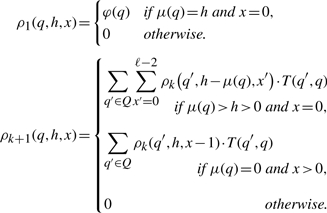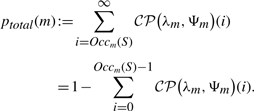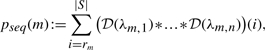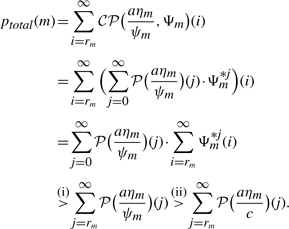Efficient exact motif discovery

Abstract

Motivation: The motif discovery problem consists of finding over-represented patterns in a collection of biosequences. It is one of the classical sequence analysis problems, but still has not been satisfactorily solved in an exact and efficient manner. This is partly due to the large number of possibilities of defining the motif search space and the notion of over-representation. Even for well-defined formalizations, the problem is frequently solved in an ad hoc manner with heuristics that do not guarantee to find the best motif.

Results: We show how to solve the motif discovery problem (almost) exactly on a practically relevant space of IUPAC generalized string patterns, using the p-value with respect to an i.i.d. model or a Markov model as the measure of over-representation. In particular, (i) we use a highly accurate compound Poisson approximation for the null distribution of the number of motif occurrences. We show how to compute the exact clump size distribution using a recently introduced device called probabilistic arithmetic automaton (PAA). (ii) We define two p-value scores for over-representation, the first one based on the total number of motif occurrences, the second one based on the number of sequences in a collection with at least one occurrence. (iii) We describe an algorithm to discover the optimal pattern with respect to either of the scores. The method exploits monotonicity properties of the compound Poisson approximation and is by orders of magnitude faster than exhaustive enumeration of IUPAC strings (11.8 h compared with an extrapolated runtime of 4.8 years). (iv) We justify the use of the proposed scores for motif discovery by showing our method to outperform other motif discovery algorithms (e.g. MEME, Weeder) on benchmark datasets. We also propose new motifs on Mycobacterium tuberculosis.

Availability and Implementation: The method has been implemented in Java. It can be obtained from http://ls11-www.cs.tu-dortmund.de/people/marschal/paa_md/

Contact: tobias.marschall@tu-dortmund.de; sven.rahmann@tu-dortmund.de

1 INTRODUCTION

De novo motif discovery is the task of uncovering exceptional patterns in texts. Especially in the context of biological sequences, this problem has been extensively studied in the hope that over-represented motifs carry structural, regulatory or other biological significance. Many different measures of ‘exceptionality’ have been proposed. In a review article, Sandve and Drabløs (2006) survey more than 100 published algorithms for motif discovery. Due to space constraints, we can review only a few of the methods here. Weeder (Pavesi et al., 2004) models motifs as strings. Given a set of sequences, it searches for motifs that occur (with a bounded number of mismatches) in as many sequences as possible. This is achieved by a pattern-driven search using a suffix tree of the given sequences. In an assessment by Tompa et al. (2005), Weeder outperformed 12 other competitors with respect to most measures. MEME (Bailey and Elkan, 1994) is an almost classical alignment-based motif discovery algorithm. Motifs are represented as position weight matrices (PWMs) and optimized using an expectation–maximization (EM) strategy. Although not as good as Weeder, MEME performed well in the assessment by Tompa et al. (2005). Seeder (Fauteux et al., 2008) is a recently published algorithm that tries to combine the merits of a pattern-driven search (used in a first phase) and alignment-based search (used in a second phase). MotifCut (Fratkin et al., 2006) approaches the motif discovery problem from a graph theoretic point of view and represents every k-mer in a given set of sequences as a vertex. Then, a motif is represented by a subgraph. For motif discovery the maximum density subgraph is searched. For a detailed overview of the field, we refer the reader to the review of Sandve and Drabløs (2006).

Despite all these efforts, the problem has not satisfactorily been solved yet, as shown in the assessment of 13 common motif discovery algorithms by Tompa et al. (2005). Recently, steps have been taken to precisely understand what makes the problem so difficult. Sandve et al. (2007) studied the ability of popular motif models (PWMs, IUPAC strings, mismatch models) to separate the true motifs from the background. Remarkably, all these models turn out to have comparable discriminative power, but are not sufficient to capture all motifs. Consequently, a split benchmark set is proposed: the first part contains datasets with motifs that can in principle be recognized and can therefore serve as a benchmark for algorithms based on such models; the second part contains the remaining datasets, useful to evaluate more powerful models. Besides the motif model, the scoring function plays an important role. Li and Tompa (2006) complement their earlier paper (Tompa et al., 2005) by assessing several scoring functions. They compare, for each dataset, the predicted motif's scores to the score of the true motif. The evaluated scoring functions are the log-likelihood of a PWM [as used by MEME, see Bailey and Elkan (1994)], Z-scores [as used by YMF, see Sinha and Tompa (2003)], and a sequence specificity score [as used by Weeder, see Pavesi et al. (2004)]. The authors conclude that the sequence specificity score outperforms the others with respect to the used dataset, but is not perfect. They also propose a new score function learned from the used data, but we are not aware of any motif discovery procedure that optimizes it.

A natural motif score is the probability that, under a suitable background model or null model, the given motif m occurs at least as frequently as observed in the given sequence(s) s, that is, ℙ(X^m_|s|≥Occ_m(s)), where X^m_n denotes the random variable counting the occurrences of m in a random text of length n, and Occ_m(s) is the number of occurrences of m in s. This probability is called p-value or significance of motif m. Computing the p-value or, more generally, the whole distribution of the occurrence count, exactly is complicated, because motif occurrences may overlap each other or their reverse complements and therefore occur in clumps (maximal groups of overlapping occurrences), making simple moment-based approximations of the distribution inaccurate. The problem has been studied by various authors, including Lladser et al. (2008); Marschall and Rahmann (2008); Nicodème et al. (2002); Régnier (2000) and Reinert et al. (2000). All these methods, however, are too slow to be used directly for exhaustive motif discovery, where one evaluates the score of each single motif in the motif space.

1.1 Our contributions

We bring together rigorous motif statistics and motif discovery. We demonstrate that a compound Poisson approximation is an excellent approximation to the exact distribution of occurrence counts. In contrast to earlier methods, we use the exact clump size distribution in the compound Poisson approximation. In particular, we show how to use probabilistic arithmetic automata [PAA, introduced by (Marschall and Rahmann (2008)] to calculate the exact clump size distribution for a motif under either an i.i.d. or Markovian background model (Section 2). Based on the compound Poisson approximation, we develop a pattern-driven approach to discover IUPAC motifs with low p-values (either with respect to the total number of occurrences or to the number of sequences the motif occurs in). The returned motif has the optimal score within a pre-defined pattern space. Exhaustive search of the motif space becomes possible because we exploit certain monotonicity properties of the Poisson distribution (Section 3), allowing us to prune a large fraction of the motif space. To evaluate the method, we run experiments on a benchmark set proposed by Sandve et al. (2007). Our method outperforms the other methods evaluated by Sandve et al. (2007), namely Weeder (Pavesi et al., 2004) and MEME (Bailey and Elkan, 1994) (Section 4). We also present previously unknown motifs on Mycobacterium tuberculosis that are strikingly overrepresented.

1.2 Notation and motif space

Let Σ = {A, C, G, T} be the alphabet of nucleotides and 2^Σ its power set. Define Λ ≔ 2^Σ∖{∅} and note that each c ∈ Λ uniquely maps to a IUPAC one-letter code; e.g. {A, G} corresponds to the IUPAC code R. Let Σ^* be the set of finite strings over Σ. Each m ∈ Λ^* is called generalized string. We define a motif of length l to be an element of Λ^l. In the remainder of this article, we use the terms motif, pattern and generalized string interchangeably. Given a motif m ∈ Λ^* and a string s ∈ Σ^*, we write Occ_m(s) to denote the number of occurrences of m in s. When S is a set of strings, we define Occ_m(s)≔∑_s∈S Occ_m(s). For a random variable A, its distribution is denoted ℒ(A).

Discovering motifs in practice requires us to choose a suitable space of motifs to be searched. Different motifs models are used in practice, such as PWMs, IUPAC (consensus) strings, string sets, and others. In this article, we use motifs of length 10 over the IUPAC alphabet Λ. We further restrict the space to patterns containing at most six c ∈ Λ with |c| = 2 (IUPAC codes R, Y, W, S, K, M), zero characters with |c| = 3 (IUPAC codes B, D, H, V) and at most two characters with |c|=4 (IUPAC code N). We denote this motif space by ℳ. It consists of 17 880 633 344 motifs. While this choice may seem arbitrary at first, the motifs in ℳ are neither too short nor too long nor too specific nor too degenerate; hence they cover many biologically interesting ones. Many biological motifs are shorter or longer than 10 bp, but the elements of ℳ can at least form well-conserved cores of longer (or reasonable extensions of shorter) motifs.

2 APPROXIMATING THE OCCURRENCE COUNT DISTRIBUTION

The most principled measure of exceptionality of a motif m is a p-value (or its negative logarithm) of its observed occurrence count, i.e. score(m)≔−log ℙ(X^m_|s|≥Occ_m(s)), where the probability measure ℙ refers to a random sequence model to be specified, and X^m_n denotes a random variable counting motif occurrences in a random text of length n. Theoretically, we can compute score(m) for all 17.8 billion m ∈ ℳ exactly with PAAs (see below), but this would take years of CPU time. Therefore, we have developed a set of techniques to prune a large part of the motif space without missing relevant motifs.

The first technique, developed in this section, is a highly accurate compound Poisson approximation of ℒ(X^m_n). Section 3 then shows how to exploit monotonicity properties of this approximation to obtain an efficient motif discovery algorithm.

2.1 Compound Poisson approximation

The main difficulty in obtaining simple accurate approximations of the occurrence count distribution of a motif lies in the fact that the strings constituting a motif may occur in clumps.

Definition 1. —

Given a sequence s ∈ Σ^* and a motif m ∈ ℳ, a clump is a maximal set of overlapping occurrences of m in s.

For example, let m≔ACA and s≔GACACATTACAAA. Then s contains three occurrences of m in two clumps (bold).

To approximate the distribution of the occurrence count, we assume the number of clumps to be Poisson distributed and the size of each clump to follow a yet unknown distribution. We further assume that the number of clumps and all clump sizes are independent. Thus, the random number of occurrences is expressed as a sum of a (random Poisson) number of independent random variables with the same unknown distribution.

Definition 2 (Compound Poisson distribution). —

Let C be a Poisson distributed random variable and (B_i)_i∈ℕ independent, identically distributed random variables with arbitrary common distribution Ψ≔ℒ(B_i). Then ∑_i=1^C B_i is said to have a compound Poisson distribution 𝒞𝒫(λ, Ψ), where λ=𝔼(C).

Compound Poisson distributions have previously proven useful for approximating occurrence count distributions (Roquain and Schbath, 2007; Schbath, 1995; Waterman, 1995). We interpret B_i in Definition 2 as the size of (number of motif occurrences in) the i-th clump. In contrast to the cited articles, we use exact clump size distributions Ψ=ℒ(B_i).

Stefanov et al. (2007) compare the exact clump number distribution to the Poisson approximation and find that the latter performs well for rare words, motivating the above assumption. The Poisson distribution with expectation λ is denoted by 𝒫(λ); the probability to see exactly j clumps equals 𝒫(λ)(j)=e^−λ ·λ^j/j!.

We denote the j-fold convolution of Ψ with itself by Ψ^*j. Then the probability mass function of the compound Poisson distribution can be written as a Poisson-weighted linear combination of Ψ's j-fold convolutions: 𝒞𝒫(λ, Ψ)(i)=∑_j≥0 𝒫(λ)(j) · Ψ^*j(i).

We need to compute Ψ and the expected number of clumps λ. For Ψ, we use a framework called PAA (Marschall and Rahmann, 2008), which we briefly describe below to make this exposition self-contained.

2.2 Exact motif statistics with PAA

In a nutshell, a PAA is a Markov chain plus state emissions (i.e. an HMM) plus a value set with state-specific arithmetic operations on the values. PAAs provide a unifying framework for a variety of exact probability computations in sequence analysis. Among other things, the exact distribution of the occurrence count can be obtained, as shown by Marschall and Rahmann (2008). Alternative methods to compute the occurrence count distribution exist (Boeva et al., 2007; Lladser et al., 2008; Nicodème et al., 2002; Nuel, 2008), but they do not provide a general framework. We briefly re-state the essentials of the PAA formalism here.

Definition 3 (PAA). —

A PAA is a tuple (Q, q₀, T, E, (π_q)_q∈Q, N, n₀, (θ_q)_q∈Q), where (1) (Q, q₀, T) is a Markov chain: Q is a finite set of states, q₀ ∈ Q is called start state (it may be alternatively replaced by a probability distribution over all states), (T(p, q))_p,q∈Q is a stochastic transition matrix. (2) (Q, q₀, T, E, (π_q)_q∈Q) is a hidden Markov model: E is a finite set called emission set, each π_q is a probability distribution on E associated with state q. (3) N is a finite set called value set, n₀ ∈ N is called start value, each θ_q :N·E → N is an operation associated with state q.

The semantics are as follows: the automaton begins in its start state q₀. In state p, T(p, q) gives the probability of going to state q. While going from state to state, a PAA performs a chain of calculations on a set of values N. In the beginning, it starts with the value n₀. Whenever a state transition is made, the entered state, say state q, generates an emission according to the distribution π_q. The current value and this emission are then subject to the operation θ_q, resulting in the next value.

Let (Y_k)_k∈ℕ0 denote the automaton's random state process, i.e. ℙ(Y_k=q) is the probability of being in state q after k steps. Analogously, we write (Z_k)_k∈ℕ0 and (V_k)_k∈ℕ0 to denote the sequence of emissions and the sequence of values resulting from the performed operations, respectively. Then V₀≡n₀ and V_k = θ_Yk(V_k−1, Z_k).

Usually, we are interested in the value distribution after k steps, ℙ(V_k=n) for all times k and values v. These probabilities are obtained from the joint state-value distribution by marginalization over states. The state-value distribution can efficiently be computed using dynamic programming (Marschall and Rahmann, 2008). The resulting algorithm is closely related to the forward algorithm known from HMMs [see, for example, Durbin et al. (1998)].

2.2.1 Motif statistics with PAAs

To study the pattern matching statistics for a motif m, we first construct a deterministic finite automaton (DFA) that recognizes Σ^* m. This can be done in a variety of ways, e.g. via the Aho-Corasick automaton of all strings constituting m, or via a simple linear non-deterministic automaton that recognizes a generalized string, which is subsequently converted into a DFA using the standard subset construction.

Based on this DFA, we define a PAA that operates on the same state set Q and has the same start state q₀. In case of an i.i.d. text model, the transition function T can be derived from the DFA's transition function by ‘replacing’ all characters with their probability. For Markovian text models of order k, a similar procedure is possible after cloning each state to accommodate for different k-mer histories.

To count motif occurrences, both emission set and value set are the natural numbers (or a finite subset thereof). Each state corresponds to a recently read substring; so for each state's emission distribution, we employ a deterministic distribution that simply emits the number of matches to be counted upon entering the state. For convenience, we denote this number μ(q). Note that in this article usually μ(q)=0 for states that do not correspond to a word in m and μ(q)=1 otherwise. In general, for motifs that consist of words of unequal length, we may have μ(q) > 1 for some states.

To sum up the occurrences, we start with value n₀≔0 and define all operations to be additions, that is, θ_q :(n, e)↦n+e. (In practice, we cut off the distribution at a maximal value of interest M and set θ_q :(n, e)↦min{n+e, M}.)

The above exposition sketches exact pattern matching statistics with PAAs. For more details, refer to Marschall and Rahmann (2008). This concludes our review of previous material on PAAs. Recall that it is impractical to compute the distribution of each potential motif in ℳ.

2.3 Computing the exact clump size distribution

We now explain how PAAs can be used to exactly calculate a pattern's clump size distribution. By definition, a clump consists of at least one match. We call a match's last character match position and consider the first match position in a clump. Further, we call the distribution of PAA states at such positions clump start distribution and denote it by ϕ; i.e. given that k is the first match position in a clump, then ℙ(Y_k=q)≔ϕ(q). For now, we assume ϕ to be known and come back to the task of its calculation later.

If ℓ≥2 is the length of the given motif, then a clump ends if ℓ − 1 consecutively visited states do not emit a match. That means we need to keep track of (i) the number of non-match states consecutively visited and (ii) the number of matches the clump contains so far.

The PAA framework allows us to achieve this by modifying the PAA described in Section 2.2. We define a new value set N′≔ℕ·ℕ with the start value n₀′≔(0, 0) and attach the following semantic: if we are in state q and the current value is (h, x), we have seen h matches in the current clump and the last of these matches occurred x steps in the past; i.e. if x=0, a match has been emitted from the current state. We define the operations accordingly:

In other words, if a match has been found (e>0), we increase the number of matches h by e and reset the distance to the last match to 0. Otherwise (e=0, no match occurred), h remains unmodified, but the number of steps since the last match x is increased.

To incorporate the clump start distribution ϕ, we need one additional state q₀′ that becomes the new start state; consequently, we set Q′≔{q₀′}∪Q and define the new transition function to be

(1)

In practice, we cannot handle the infinite value set N′. We can, however, truncate the clump size distribution to be calculated and use the value set N″≔{1,…,M}·{0,…,ℓ − 1} along with adapted operations θ_q″. Employing one of the algorithms given by Marschall and Rahmann (2008), we can then calculate the joint state-value distribution. To make the resulting recurrence better accessible to the reader, we state it explicitly in terms of the table ρ_k(q, h, x)≔ℙ(Y_k=q, V_k=(h,x)).

Lemma 1 (Explicit recurrence relation for ρ_k). —

Let ρ_k be defined as above, then

While the lemma can be proven directly from the definition of the ρ_k and θ′_q, using the Markov property on the state process, the reader should keep in mind that the PAA framework makes it unnecessary to state and prove the lemma explicitly, as the whole mechanism is inherent in the generic PAA state-value computation of Marschall and Rahmann (2008).

Updating from table ρ_k to table ρ_k+1 takes 𝒪(|Q|²·M·ℓ²) time, as can be seen from the recurrence. Note, however, that by construction of the PAA from a DFA, each states out degree is bounded by the alphabet size. Therefore, the transition matrix is sparse, and the runtime for an update is bounded by 𝒪(|Σ|·|Q|·M·ℓ²).

A clump ends if no new match has occurred ℓ − 1 steps after the previous match. Using the ρ_k, the clump length distribution Ψ is thus given by

(2)

To actually compute Ψ, we start with the initial table ρ₁ and iteratively calculate the tables ρ_k for larger k. Each ρ_k contributes to the sought distribution through the inner sum from Equation (2) and we can successively add the contributions to an intermediate clump size distribution. Observe that the total probability mass in ρ_k is an upper bound for the difference between the intermediate clump size distribution and the exact one. Thus, we iterate until the total probability mass drops under an accuracy threshold. The number of necessary steps, however, is bounded by 𝒪(M·ℓ), because a clump containing M matches can have a length of at most 𝒪(M·ℓ). In total, we need 𝒪(|Σ|·|Q|·M²·ℓ³) time to compute the exact clump size distribution. In practice, for motif discovery, Σ=4, and M and ℓ are small constants.

2.3.1 State distribution at clump start

Let us come back to computing the clump start distribution ϕ needed in Equation (1).

The PAA's state process (Y_k)_k∈ℕ0 is a Markov chain (Marschall and Rahmann, 2008) and, hence, the classical theorems [see, for instance, Brémaud (1999)] about existence of and convergence to an equilibrium distribution apply: irreducibility and aperiodicity are sufficient for convergence to a unique equilibrium distribution. Assuming that (i) a pattern does not start with a wildcard and (ii) for a Markovian text model of order k, all (k + 1)-mers have positive probability of occurring, these conditions can be verified to be fulfilled by construction of the PAA.

We consider the joint distribution of state and steps since the last match position. We define L_k as the number of steps since we last encountered a match before step k. Thus

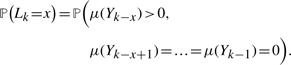Again we use the PAA framework to compute the joint state-value distribution ℒ(Y_k, L_k) for any desired k. The clump start distribution is now given by

(3)

In practice, the limits for k → ∞ exist and converge in a few steps to double precision. On a test set of 1000 motifs from ℳ (Section 2.5), convergence is reached after k = 54.6 iterations on average.

2.4 Distribution of clump number

To complete the construction of a compound Poisson approximation, we need the expected number of clumps λ(k) in a text of length k and thereby parametrize the Poisson approximation of the clump number.

The expected number of pattern occurrences 𝔼(V_k) is easily computed (Robin et al., 2005) as 𝔼(V_k)=(k−|m| + 1)·η_m, where η_m is the motif's (stationary) occurrence probability at any text position (in other words, its expected number of occurrences in a string of length |m|). Since we know the exact clump size distribution Ψ, we can also calculate its expectation 𝔼[Ψ]≔ψ. Then we obtain

2.5 Quality of approximation

In an earlier article (Marschall and Rahmann, 2008), we presented a method to exactly compute the distribution of the occurrence count. This gives us the possibility to compare the approximation introduced in the last section to the exact distribution. We randomly sample 1000 motifs from the motif space ℳ described in Section 1.2 and calculate exact distribution and compound Poisson approximation (using clump size distributions truncated at size 25). To assure a realistic background model, a third-order Markov model is estimated from the genome of M. tuberculosis. For background models estimated from other species, similar results are to be expected.

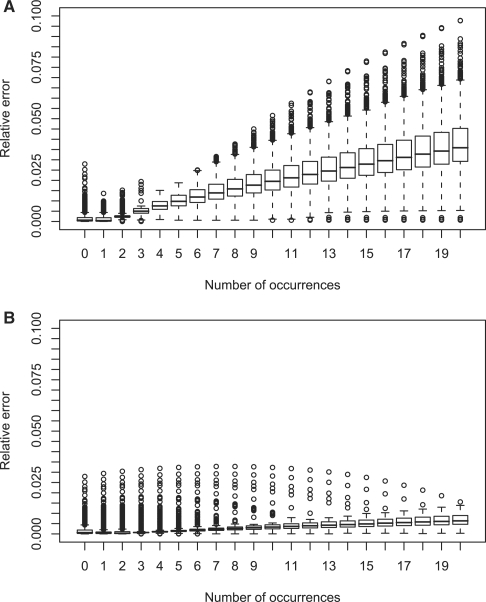
Figure 1 shows boxplots of the relative errors of log-probabilities in the occurrence count distributions for 0 to 20 occurrences and random texts of length 1000 and 10 000. The probabilities themselves range over many orders of magnitude; the probability of observing 20 matches lies in an average order of magnitude of 10⁻⁴³ for text length 1000 and 10⁻²³ for text length 10 000. Therefore, we consider log-probabilities. A relative error of 4% (for text length 1000 and 20 occurrences, 75% of motifs have lower error) here means that we miss the correct order of magnitude (e.g. −43) by 4%. We see that the relative errors increase towards the right tail of the distributions. This can be explained by observing that the length of a clump (in terms of number of characters) is not taken into account by our approximation. When the text ‘gets filled up’ with occurrences, the approximation becomes inaccurate. Note that 20 occurrences of length 10 would occupy up to 200 characters (depending on overlap). This is one-fifth of a 1000 character sequence. This explains why the accuracy decreases much slower towards the right tail for text length 10 000 (Figure 1B).

Fig. 1.

Boxplots showing the relative error of log probabilities made by compound Poisson approximation. (Top) On random texts of length 1000. The expected number of occurrences is 0.184 (averaged over all motifs). (Bottom) On random texts of length 10 000. The expected number of occurrences is 1.857 (averaged over all motifs).

It is worth noting that the occurrence count distributions are governed by an exponential decay towards the right tail. Thus, when calculating p-values (i.e. summing over a distribution from a fixed k to infinity), errors do not accumulate significantly; i.e. the summands, and hence the introduced errors, rapidly become insignificantly small.

On average, computing the distribution for text length 1000 took 97.4 ms using the compound Poisson approximation and 121.1 ms using the exact method on an Intel Core 2 Duo CPU at 2.66 GHz, running Linux 2.6.24. For text length 10 000, we measured 97.8 ms and 1209.1ms, respectively. Note that the runtime of the approximation is independent of the text length, while the exact method's runtime increases linearly with the text length.

3 MOTIF DISCOVERY

As stated in Section 2, to evaluate the significance of a motif, we compute the compound Poisson approximation of its p-value.

Depending on the situation, two different ways of counting occurrences can be reasonable. First, we may consider the total occurrence count in a sequence (or in a set of sequences) as usual (see Definition 4 below). Second, especially when considering a set of many short sequences, it may be more desirable to consider the number of sequences with at least one occurrence instead (Definition 6).

For an i.i.d. background model, we present an algorithm that finds an optimal scoring motif with respect to either of these significance measures (Sections 3.2 and 3.3). For Markovian background models, we use the i.i.d. model as a pre-filter (Section 3.4).

3.1 Motif scores

Assume we are given a finite set of strings S={s₁,…, s_n} over the alphabet Σ. For any motif m ∈ ℳ, we write Ψ_m, ψ_m and η_m to denote its clump size distribution, expected clump size and the expected number of occurrences on a string of length |m|, respectively. Ψ_m, ψ_m and η_m implicitly refer to a (i.i.d. or stationary Markovian) text model estimated from S. The first score we introduce is the compound Poisson p-value approximation for the total number of motif occurrences.

Definition 4 (Total count p-value). —

For a motif m ∈ ℳ, let a≔∑_s∈S(|s|−|m| + 1) be the adjusted total sequence length, and define λ_m≔a·η_m/ψ_m (expected number of clumps in S) and

(4)

The second measure to be introduced regards the number of sequences that contain at least one motif occurrence. Before we define it, we make an auxiliary definition to ease notation:

Definition 5 (Binary distribution 𝒟). —

For λ>0, define

Notice that for every clump size distribution Ψ, we have Ψ(0)=0 and, hence, 𝒟(λ)(0)=𝒞𝒫(λ, Ψ)(0) and 𝒟(λ)(1)=∑_i=1^∞𝒞𝒫(λ, Ψ)(i).

Definition 6 (Sequence count p-value). —

For a motif m ∈ ℳ, let (number of observed sequences with an occurrence), λ_m,i≔(|s_i|−|m| + 1)·η_m/ψ_m for 1 ≤i≤n (expected number of clumps in sequence i). Define

where * denotes the convolution operation.

3.2 Pruning the search space

The goal in the next section is to find the motif with the best p_total(m) or best p_seq(m) value. To this end, we now present two lemmas of central importance to the practicability of exact motif discovery based on the above scores. They give, for p_total and p_seq, thresholds for the number of matches necessary to obtain a p-value below a given constant T. The thresholds can be calculated provided that we know a motif's expectation η_m and an upper bound for the expected clump size c > ψ_m.

Let us analyze the right-hand side of Equation (4). We can separately consider the contributions of each possible clump count hidden in the compound Poisson distribution. When the clump count is at least Occ_m(s), there are necessarily at least Occ_m(s) matches; in this case we do not need to evaluate the clump size distribution! Furthermore, when parametrizing a Poisson distribution with a decreased expected clump count, the probability of observing more than k clumps decreases as well (for every k). These two ideas are formalized in the following lemma.

Lemma 2 (Monotonicity of p_total). —

Let m ∈ ℳ, c > ψ_m, T ∈[0, 1). Define

(5)

where a is chosen as in Definition 4. Then

Proof. —

Let Ψ_m^*j denote the j-fold convolution of Ψ_m with itself. Starting from Definition 4, we get

Inequality (i) is true because clumps have, by definition, at least size one and, hence, ∑_i=rm^∞ Ψ_m^*j(i)=1 for j≥r_m. Inequality (ii) holds due to c > ψ_m and the fact that the cumulative distribution function of a Poisson distribution is monotone in the parameter λ. If r_m ≤K, it follows from (5) that . Thus, p_total(m) > T. ▪

In an analogy to the above lemma, we can exploit a monotonicity property of 𝒟(λ_m,1)*…* 𝒟(λ_m,n) to get a lower bound for the number of motif occurrences necessary to obtain a score p_seq > T.

Lemma 3 (Monotonicity of p_seq). —

Let m ∈ ℳ, c > ψ_m, and T ∈ [0, 1). Define λ′_m,i≔(|s_i|−|m| + 1)·η_m/c for 1 ≤i ≤n, and let

Then

Proof. —

Follows directly from the fact that the cumulative distribution function of 𝒟(λ′_m,1)*…* 𝒟(λ′_m,n) is monotone in each λ′_m,i. ▪

We now explain how to exploit the above lemmas for motif discovery. Our goal is to find all motifs with a p-value below a given threshold T. We assume an upper bound to the expected clump size, denoted c=ψ_max, to be known and come back to its choice below (for the impatient, ψ_max ≔ 3 works for the motif space ℳ defined in Section 1.2). Then either lemma provides a lower bound K on the number of necessary occurrences. Motifs with fewer occurrences do not need to be evaluated in detail.

While the above lemmas help in finding a safe occurrence threshold K, they do not save us much work yet, since the Poisson parameter in Lemma 2 and the λ′_m,i in Lemma 3 depend on the frequency of the motif η_m. The punch line now is that, in an i.i.d. model, η_m is independent of the order of characters; i.e. η_m is invariant under permutations.

We call a set of all permutations of a motif abelian pattern and write, for example, C4N3 to denote the set of patterns consisting of four Cs and three Ns. For an abelian pattern, we compute η_m and derive a threshold for the number of required matches by applying Lemma 2 or Lemma 3 just once.

3.2.1 Bounding expected clump size

For the application of Lemma 2 or Lemma 3, an upper bound for the expected clump size needs to be known. In our implementation, we use the hard-coded value 3.0 as a bound, which is, from our experience, sufficient for all relevant cases. For the motif space ℳ considered in this article, let us verify that the bound holds. The motif with the largest expected clump size must consist of the most frequent characters. (Otherwise, replacing all characters with the most frequent one would yield a larger expected clump size. Wildcard characters representing two characters [R, Y, W, S, K, or M] would have to be replaced by the wildcard character that represents the most and the second most frequent character, etc.) Furthermore, the expected clump size grows with the probability of the most frequent character. We assume p_A=0.4, p_C=0.1 and p_G=0.1 and p_T=0.4, a distribution much more biased than all distributions encountered in known biological organisms. More biased distributions lead to more extreme clump sizes, as the more frequent characters can conspire to overlap. Thus, the worst-case motif must consist of As, Ws (the IUPAC symbol for {A, T}), and Ns. We enumerate all those, calculate the expected clump sizes and find the largest value to be 2.21, a safe distance from 3.0.

3.3 Exact algorithm for i.i.d. background models

In order to run an exhaustive motif discovery algorithm, the only component missing is an efficient way to count the number of occurrences of a generalized string in a set of sequences S. To this end, we walk an annotated suffix tree of S, as introduced by Sagot (1998). The annotation of the suffix tree nodes with occurrence counts permits a fast calculation of occurrence counts even for generalized strings (where we need to branch the search path) and allows us to skip many instances. This technique is often called pattern-driven search; it has been used by many different motif discovery algorithms (Ettwiller et al., 2005; Pavesi et al., 2004; Sinha and Tompa, 2003). We skip the details and refer the reader to Sagot (1998). We obtain the following algorithm:

1. Construct a suffix tree containing all sequences from S.

2. Enumerate all abelian patterns that constitute the search space ℳ. For each abelian pattern do:

   1. Compute the motif frequency η_m (constant over all m in the abelian pattern).
   2. Compute the distributions in Lemma 2 or 3 to obtain a lower bound K for the number of matches necessary for a p-value below T.
   3. Spell instances of the abelian pattern in lexicographic order while walking the annotated suffix tree, skipping instances where possible. Report motifs occurring more than K times.
   4. For reported motifs, calculate exact clump size distribution and compute p-value. Output motif if p-value is below T; discard otherwise.

3.4 Markovian background models

In practice, the i.i.d. model is too coarse for genomic motif discovery and higher order contexts need to be taken into account. This creates a problem: instances of an abelian pattern do not necessarily have the same expectation under a higher order background model and, hence, the described algorithm would not be applicable. Even though it can be modified, it would lose efficiency.

However, we can use a two-stage algorithm as follows: (i) find all motifs with a p-value below a threshold T with respect to the i.i.d. model as described above. (ii) Re-evaluate these motifs with respect to the Markovian model and discard them if their Markovian p-value is not low enough (they can be explained by inter-character dependencies found in DNA).

This efficiently discards motifs that have a too high p-value with respect to the i.i.d. model or the Markov model. It may thus happen that we miss motifs with low Markovian p-value but high i.i.d. p-value. However, one could argue that such a motif merely appears interesting because of low background frequencies of its components, not because of its high occurrence count. While from a computational point of view, this procedure is thus a heuristic, it has the potential to lead to more biological meaningful (because more frequent) motifs.

3.5 Suboptimal motifs

So far, we find the best motif (with respect to either p-value score from Definition 4 or Definition 6). In practice, we are interested in several good motifs. However, good motifs usually come in groups. For instance, making one character in a motif more general or more specific will in general not change its p-value very much. Therefore, we are interested in a set of good independent motifs. The present article does not discuss this problem in detail (which has no easy solution). For now, we take a brute-force approach and initially discover the best motif, report it, mask its occurrences in S, and re-evaluate the occurrence counts and p-values of the remaining motifs. Motifs whose p-value then rises above the threshold due to lost occurrences are discarded. The remaining best motif is reported, and the procedure is repeated until no good motifs remain.

4 EVALUATION

4.1 Benchmark data

Designing good benchmark sets for motif discovery is not trivial. While synthetic sequences involve a somewhat arbitrary choice of background and motif model, real datasets are never annotated perfectly. To evaluate our algorithm, we use the carefully crafted benchmark suites proposed by Sandve et al. (2007). They generated different datasets by either implanting transcription factor binding site (TFBS) occurrences into a background generated from a third-order Markov model or by extracting their original neighborhood from the respective genome. For each dataset, they analyzed whether or not the motif can, in principle, be discriminated from the background by popular motif models (namely, mismatch models, PWMs or IUPAC strings). They propose to use the datasets with good theoretical discrimination to benchmark algorithms and the rest to benchmark more powerful models. This makes the performance analysis of a new algorithm more informative, as effects originating from motif model and algorithm are not mixed up. Consequently, we use their ‘algorithm’ suite to assess our method. This benchmark suite is again divided into two parts: algorithm Markov and algorithm real. The former contains true binding sites from the TRANSFAC database implanted into synthetic backgrounds generated by third-order Markov models (50 datasets). The latter contains the same binding sites in their original genomic context (50 datasets). Refer to Sandve et al. (2007) for more details on the dataset generation.

For each of the 100 datasets, we estimated an i.i.d. model from the data. Then, we extracted all motifs with a p_seq score <10⁻⁸ with respect to this i.i.d. model (10 358 patterns on average). Subsequently, these patterns were re-evaluated with respect to a third-order Markov model (again estimated from the data for each dataset). The highest scoring motif was reported as the result. We used the web service accompanying the paper by Sandve et al. (2007) to calculate the nucleotide-level correlation coefficient (nCC) defined as follows:

where TP, TN, FP, and FN are the numbers of true/false positive/negative predicted characters (nucleotides). The use of this measure allows an integrated assessment of sensitivity and specificity.

The obtained scores in comparison to Weeder Pavesi et al. (2004) and MEME Bailey and Elkan (1994) are listed in Table 1. None of the resulting nCC values indicates good performance, and one could question whether in this range it has any meaning at all. Nevertheless, the reported performance represents that state of the art on this benchmark dataset, and the use of the proposed exact exhaustive method improves the mark somewhat.

Table 1.

nCC on benchmark suites proposed by Sandve et al. (2007)

Benchmark	Weeder	MEME	Our method
Algorithm Markov	0.052	0.082	0.120
Algorithm real	0.110	0.068	0.149

The results given for Weeder and MEME are taken from Sandve et al. (2007).

Best results in each row are printed in bold.

We followed Sandve et al. (2007) in choosing Weeder and MEME as competitors, because, on the one hand, they are known to peform well on this type of benchmark. [In fact, Weeder outperforms its 12 competitors with respect to most evaluated measures in Tompa et al. (2005).] On the other hand, they represent different approaches to motif discovery. While MEME models motifs as PWMs and optimizes them using an EM approach, Weeder is based on mismatch models and employs a pattern-driven search on a suffix tree.

Because of the large number of datasets (100), we ran the algorithm on a compute cluster. Since it consists of heterogeneous machines (CPU clock rates ranging from 1.6 GHz to 2.0 GHz), the measured runtimes must be interpreted with care. We give them in CPU time, i.e. the time a single (average) CPU would have needed to perform the task. The exact motif search using i.i.d. models took 11.8 CPU hours on average per dataset. The re-evaluation of top scoring motifs took 10.7 CPU minutes on average per dataset. Had we performed an exhaustive enumeration and calculated the p_seq (with respect to an i.i.d. model) for each motif separately, the computation would have lasted ∼ 4.8 years per dataset (extrapolated runtime). Our method has provided a speedup factor of at least 3500 or three to four orders of magnitude.

4.2 Motifs in non-coding regions of M. tuberculosis

Mycobacterium tuberculosis is a species of pathogenic bacteria causing tuberculosis. Its genome has been completely deciphered (GenBank accession number AL123456). To demonstrate the utility of the proposed motif discovery algorithm in a whole genome setting, we search for motifs in the non-coding (i.e. putatively regulatory) regions of M. tuberculosis. The non-coding parts of the genome comprise 2402 regions consisting of 398 419 bp, which is about one-tenth of the whole genome.

We employ the two-stage procedure described in Section 3 to search forward and backward strand in parallel. In a first phase, we discover all motifs from ℳ with a p-value below a pre-selected threshold with respect to an i.i.d. model. Here, we choose a threshold of 10⁻⁵⁰, resulting in 494 575 motifs. In a second phase, those motifs are re-evaluated with respect to a third-order Markov model derived from the regulatory regions. To obtain several motifs, we used the strategy described in Section 3.5. Due to the large input, the computations took 247.5 CPU hours for the first phase and 44.7 CPU hours for the second-phase; subsequent second phase re-evaluations took less and less time. Again, the calculations were performed in parallel on a mixed cluster. These results show that exact motif discovery based on rigorous statistics, although still a considerable computational burden, now lies within the reach of today's computers.

To judge whether this computational effort pays off in practice, we again seek to compare our method with other motif discovery algorithms. Unfortunately, many available software packages are not applicable to this dataset. Weeder, for instance, restricts its search to motifs occurring in at least half of all sequences, which renders it useless in this setting. One software package usable for our purpose is MEME. We used the command line version of MEME 4.0.0 (http://meme.sdsc.edu/meme4/meme-download.html) compiled on a Linux machine. To make the competition as ‘fair’ as possible, we instructed MEME to search for 10 motifs of length 10 on both DNA strands and allowed any number of motif occurrences in each sequence¹. MEME was run on a 2 GHz PC and reported its results after 15.2 h of CPU time (about 1/20 of our method's time).

Tables 2 and 3 show the motifs found by our method and MEME, respectively. Both methods agree on the two top-scoring motifs. The third best motif discovered by MEME is as well found by our algorithm. Note that the E-value score reported by MEME considerably drops from the fourth to the fifth motif, i.e. the last six motifs reported are not strong ones (and therefore maybe noise). But why did our algorithm fail to find the fourth MEME motif? We calculated the p-value of the IUPAC string that represented the PWM returned by MEME best and found it to be 3.6 · 10⁻⁴⁰. That means, we missed this motif due to the quite demanding p-value threshold of 10⁻⁵⁰. We did find, however, four other motifs with an even better p-value, which were missed by MEME.

Table 2.

Overview of IUPAC-motifs found by our method in non-coding regions of M. tuberculosis

	Motif	Expectation	Occurrences	p-value
1	AGACSCARAA	1.7	122	6.5 · 10−176
2	GCATCGTCRC	5.2	99	7.1 · 10−88
3	CGWCGWCGNN	195.2	313	1.9 · 10−72
4	CTCCTCMTCR	3.5	77	1.9 · 10−69
5	GGGACGGAAA	0.5	42	3.5 · 10−63
6	NYTCGNCGAR	94.6	191	3.6 · 10−56
7	NNYWGATCWR	120.6	211	3.3 · 10−52

Table 3.

Overview of motifs (consensus strings of reported PWMs) found by MEME in non-coding regions of M. tuberculosis

Consensus	Occurrences	E-value	Similar to Table 2
AGACGCAAAA	161	4.6 · 10−190	(1)
GCATCGTCGC	115	7.0 · 10−108	(2)
GTTTCCGTCC	44	1.1 · 10−31	(5)a
CGGCGTGTCG	104	1.5 · 10−34	—
AGTCTCCGGA	31	1.8 · 10−14	—
GGGCGGTTCA	41	2.7 · 10−9	—
TTCTTGGAAA	32	4.2 · 10−11	—
GATCGCAAGC	37	2.1 · 10−15	—
GATCTGAGAC	17	4.4 · 102	—
AACGTGAACT	23	2.7 · 10−2	—

The right most column references are row numbers of motifs in Table 2.

^aSimilar to the reverse complementary motif.

The AGACSCARAA motif appears to have two different functions: on the one hand, as part of a transcription terminator; on the other hand, as part of a clustered regularly interspaced short palindromic repeat (CRISPR) involved in bacteriophage response (C. Kaleta, personal communication). The function of the remaining motifs is apparently unknown. Because of their high statistical significance, they are excellent candidates for further investigations about their biological meaning.

5 DISCUSSION

In this article, we bridge the gap between rigorous motif statistics and motif discovery. On the motif statistics side, we describe a new algorithm to exactly compute the clump size distribution with respect to Markovian text models. Furthermore, we experimentally verify that the resulting compound Poisson approximation is highly accurate. On the motif discovery side, we show that, in the i.i.d. case, an exact, pattern-driven approach is feasible in practice. The main ‘tricks’ here are the decomposition of the motif space into abelian patterns and the use of the monotonicity properties proven in Lemmas 2 and 3. To the best of our knowledge, these properties have not been used before. In the concluding evaluation, we demonstrate that our method outperforms Weeder and MEME on the benchmark suite proposed by Sandve et al. (2007). It should be noted that, to avoid obfuscating the results, we did not perform any post-processing. That means all returned motifs had a length of 10. Most probably the results can further be improved by extending the motifs into both directions.

The described motif discovery procedure works equally well when searching forward and backward strand of DNA in parallel; the PAA used for statistics can be constructed for a joint motif consisting of both, the forward pattern and its reverse. Another advantage of the approach lies in its parallelizability. Different abelian patterns can simply be evaluated on different CPUs. Note that, using all cores, the algorithm will evaluate almost 18 billion motifs in <3 h on a recent quad core system.

Future work.

The filtering step can be optimized in several ways: We used a fixed upper bound of 3.0 for the expected clump size and showed that it holds by exhaustively checking it for all motifs in ℳ. It would be more elegant to have a direct proof and tighter bounds. In the Markov model, we may be able to skip the i.i.d. filtering step if we can find a tight and easily computable lower bound on η_m for certain groups of motifs: note that Lemmas 2 and 3 still hold when η_m is replaced by a lower bound.

Another optimization of practical interest is to speed up and find alternative ways of formalizing the discovery process of suboptimal motifs. The present brute-force approach works, but using conditional probabilities given the already discovered motifs may provide a more elegant solution.

Even though the motif space ℳ was chosen with some care, it cannot cover all potentially interesting motifs. However, we may speculate that most biologically relevant motifs can be discovered by starting a local hill-climbing search from the ℳ-motifs using operations such as generalizing/specializing sites of the motif, extending or shortening the motif at its left or right border. This remains to be evaluated in future work. In any case, the shortcuts introduced in this article show that efficient exact motif discovery is now possible for fairly large and biologically relevant motif spaces.

Recently, Hannenhalli (2008) reviewed current trends in TFBS search. He points out that better TFBS models and integrative searching (using additional information as evolutionary conservation, TF interactivity, etc.) are important lines of future improvements. Therefore, the method we present here should be seen as one component in a larger pipeline for TFBS discovery. In this context, it may prove especially useful that the presented method returns statistically meaningful scores.

Conflict of Interest: none declared.