Grouped graphical Granger modeling for gene expression regulatory networks discovery

Abstract

We consider the problem of discovering gene regulatory networks from time-series microarray data. Recently, graphical Granger modeling has gained considerable attention as a promising direction for addressing this problem. These methods apply graphical modeling methods on time-series data and invoke the notion of ‘Granger causality’ to make assertions on causality through inference on time-lagged effects. Existing algorithms, however, have neglected an important aspect of the problem—the group structure among the lagged temporal variables naturally imposed by the time series they belong to. Specifically, existing methods in computational biology share this shortcoming, as well as additional computational limitations, prohibiting their effective applications to the large datasets including a large number of genes and many data points. In the present article, we propose a novel methodology which we term ‘grouped graphical Granger modeling method’, which overcomes the limitations mentioned above by applying a regression method suited for high-dimensional and large data, and by leveraging the group structure among the lagged temporal variables according to the time series they belong to. We demonstrate the effectiveness of the proposed methodology on both simulated and actual gene expression data, specifically the human cancer cell (HeLa S3) cycle data. The simulation results show that the proposed methodology generally exhibits higher accuracy in recovering the underlying causal structure. Those on the gene expression data demonstrate that it leads to improved accuracy with respect to prediction of known links, and also uncovers additional causal relationships uncaptured by earlier works.

Contact: aclozano@us.ibm.com

1 INTRODUCTION

Recent advances in molecular biology make it possible to measure the genome-wide program of gene expression of an organism over time. The availability of such time course data raises the possibility of addressing a key objective: the discovery of gene regulatory networks. Since the directionality of information flow is a key aspect of the regulatory mechanisms, the crux of the problem is thus to identify causal relationships between genes rather than mere correlations.

Granger (1980) causality (Granger, 1980) is an operational definition of causality well known in econometrics, and essentially defines one time series as ‘causing’ another, if the first series contains additional information for predicting the future values of the second series, beyond the information in the past values of this second series. By combining this notion with regression algorithms, and applying them to perform graphical modeling over the lagged temporal variables, effective methods for modeling causality involving many variables can be obtained. Recently, these methods, collectively referred to as ‘the graphical Granger modeling methods’, have received considerable attention in the areas of computational biology and data mining, and specifically to address the problem of analyzing causality among gene expressions (Dahlhaus and Eichler, 2003; Mukhopadhyay and Chatterjee, 2007).

The existing algorithms for graphical Granger methods, however, have neglected an important aspect of the problem, which is critical for formulating the graphical modeling problem appropriately—the group structure among the lagged temporal variables naturally imposed by the time series they belong to. For example, lagged variables x_t−1, x_t−2, x_t−3, etc., of the same time series {x_t} can be naturally considered to form a group of related variables. This observation suggests that it would prove useful to apply variants of regression methods that make use of group information among variables, such as group Lasso (Yuan and Lin, 2006; Zhao et al., 2006), into the domain of graphical Granger modeling, resulting in our proposed methodology which we refer to as the ‘grouped graphical Granger modeling method’.

As it turns out, past works in the computational biology literature considered one unit time lag only (Fujita et al., 2007; Li et al., 2006; Mukhopadhyay and Chatterjee, 2007; Ong et al., 2002; Opgen-Rhein and Strimmer, 2007), due to either algorithmic constraints, or to computational limitations. This means that they ignore the possibility that a given gene may influence another with a delay of more than one time unit, which is an oversimplification, since time delayed regulation mechanisms with lags greater than one time unit do exist with significant frequency [e.g. as identified in Li et al. (2006)]. Such limitations will become increasingly problematic as microarray data with finer sampling period becomes available in the future. While the restriction to a unit time lag may explain why the group structure among temporal variables has been ignored to date (since the issue does not arise for this restricted case), it is clear that if the existing methods were to be extended to encompass additional lags, making effective use of such group structure would be critical.

The objective of the present article is to demonstrate that leveraging group structure among the temporal variables can indeed help improve their accuracy as methods of Granger graphical modeling, and specifically provide a more effective method for analyzing causality among gene expressions.

Note that our method is computationally efficient and can accommodate a very large number of time series, which is critical in analyzing genome-wide microarray data. The efficiency of our method is largely due to the use of regression methods with variable selection in graphical Granger modeling (i.e. Lasso and its variant). See, for example Arnold et al. (2007), for an empirical comparison of computational complexity of a number of methods, which shows in particular that Lasso-based methods are more efficient than the pairwise Granger test approach, or other traditional approaches to Bayesian network structure learning. We note that some of the existing methods (Li et al., 2006; Mukhopadhyay and Chatterjee, 2007; Ong et al., 2002; Segal et al., 2003; Yamaguchi et al., 2007) are unable to handle full-fledged Granger causality tests, and therefore either (i) resort instead to suboptimal versions involving pairwise causality tests only rather than simultaneously encompassing all the times series (Mukhopadhyay and Chatterjee, 2007); or (ii) consider a small subset of genes only (Li et al., 2006; Ong et al., 2002) or (iii) perform dimensionality reduction via clustering and obtain module networks rather than gene networks, which tend to generate results that are more difficult to interpret (Segal et al., 2003; Xu et. al., 2004; Yamaguchi et al., 2007).

The last two approaches often rely on extensive domain knowledge to preselect the most relevant genes or modules [as in Ong et al. (2002)] or to divide the genes into groups such as ‘Regulators’ versus ‘Regulated’ [as in Segal et al. (2003)]. While using domain knowledge in such a manner can be helpful, and critical for practicality of some of the methods, we prefer to cast our method in a completely general framework, where no prior knowledge about the roles of genes or likely candidates thereof is available in advance.

We perform empirical evaluation to demonstrate the advantage of the grouped graphical Granger method over the standard (non-grouped) methods. In our first set of experiments, we conduct systematic experiments using synthetic data, in which we randomly generate a true causal graph, generate time series data from it, and then apply the various alternative algorithms to estimate and infer the true causal structure. The simulation results show that indeed our grouped graphical Granger method attains significantly higher accuracy over the corresponding standard (non-grouped) methods, albeit subject to the underlying assumptions of the simulation models employed, e.g. there being a strong group structure among the variables.

In our experiments using the human cancer cell (HeLa S3) cycle data (Whitfield et al., 2002), available at http://genome-www.stanford.edu/Human-CellCycle/Hela/, we apply our method to three different datasets, corresponding to three experiments under basically the same conditions but having different sample sizes (each with 12, 26 and 48 time points). Our results are consistent with the observations made by past research (Mukhopadhyay and Chatterjee, 2007), using a related method that is inherently restricted to lag 1 (time delay of unit time 1), while they also uncover additional causal relationships uncaptured by the earlier method. By measuring the accuracy of prediction against a database of known causal links (BioGRID), we show that our method significantly improves the predictive accuracy over an existing method (Sambo et al., 2008). Our experiments also confirm that the efficiency of our method, by allowing us to analyze datasets with larger sampling sizes, contributes to the robustness and stability of the discovered causal relationships.

2 THE METHODOLOGY

2.1 Preliminaries: Granger causality and graphical Granger modeling

2.1.1 Granger causality

We begin by introducing the notion of ‘Granger Causality’ (Granger, 1980). This notion was introduced by the Nobel prize winning economist, Clive Granger, and has proven useful as an operational¹ notion of causality in time-series analysis in the area of econometrics. It is based on the intuition that a cause should necessarily precede its effect, and in particular that if a time-series variable causally affects another, then the past values of the former should be helpful in predicting the future values of the latter, beyond what can be predicted based only on their own past values.

More specifically, a time series x is said to ‘Granger cause’ another time series y, if the accuracy of regressing for y in terms of past values of y and x is statistically significantly better than that of regressing just with past values of y. Let {x_t}_t=1^T denote the time-series variables for x and {y_t}_t=1^T the same for y. The so-called Granger test first performs the following two regressions:

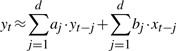(1)

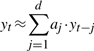(2)

where d is the maximum ‘lag’ allowed in past observations, and then applies an F-test, or some other statistical test, to determine whether or not (1) is more accurate than (2) with a statistically significantly advantage. In this article, we often use the term ‘feature’ to mean a time series (e.g. x) and use temporal variables or lagged variables to refer to the individual variables (e.g. x_t). In the context of microarray time series, a feature denotes the time series of expression levels for a gene, while a temporal variable or a lagged variable refers to the expression level for a gene at a given time point.

2.1.2 Graphical Granger modeling

The notion of Granger causality, as introduced above, was defined for a pair of time series. We are interested in cases in which there are many time-series variables present and we wish to determine the causal relationships between them. For this purpose, we naturally turn to graphical modeling over time-series data to determine conditional dependencies between the temporal variables, and obtain insight and constraints on the causal relationship between the time series.

A particularly relevant class of methodologies is those that apply regression algorithms with variable selection to determine the neighbors of each variable, such as the Lasso (Tibshirani, 1996), which minimizes the usual sum of squared errors plus a penalty on the sum of the absolute values of the regression coefficients. That is, one can view the variable selection process in regression for y_t in terms of y_t−1, x¹_t−1, x²_t−1, etc., as an application of the Granger test on y against x¹, x², etc. By extending the pairwise Granger test to one involving an arbitrary number of time series, it makes sense to say that x¹ Granger causes y, if x¹_t−d is selected for any time lag d in the above variable selection. Where and to the extent that such regression-based variable selection coincides with the conditional dependence between the variables, the above operational definition can be interpreted as the key building block of the graphical Granger model. [See, for example, Meinshausen and Buhlmann (2006) for a related theoretical result.]

2.2 Grouped graphical Granger modeling method

An important aspect that is overlooked in the existing methods in the literature is the following: for graphical Granger modeling, the question we are interested in is whether the entire series x_t−1, x_t−2,… provides additional information for the prediction of y_t. Emphatically, the question is not whether for a given lag d x_t−d provides additional information for predicting y_t. That is, as a method of Granger graphical modeling, the relevant variable selection question is not whether an individual lagged variable is to be included in regression, but whether the lagged variables for a given time series as a group (i.e. the feature), are to be included. We thus argue that a more faithful implementation of graphical Granger modeling methods should take into account the group structure imposed by the time series into the modeling approach and fitting criteria that are used in the variable selection process. This is the motivation for us to turn to the recently developed methodology, group Lasso, which performs variable selection with respect to model fitting criteria that penalize intra- and inter-group variable inclusion differently.

The foregoing argument leads to the generic procedure of grouped graphical Granger modeling method, exhibited in Figure 1. We now turn to the description of regression methods with both non-grouped and grouped variable selection: Lasso, Adaptive Lasso and Group Lasso. The latter is the preferred version of the sub-procedure REG as it performs regression with group variable selection, while the former two are not grouped methods and will be used for comparison purposes in the simulations of Section 3.

Fig. 1.

Generic group graphical Granger modeling method.

2.2.1 Sub-procedures for regression with variable selection

In the following, we state the regression methods with variable selection as generic methods for regression. Consider linear regression models. Let Y=(y₁,…, y_n)^T be an n×1 response vector and X=[x¹, x²,…, x^p] be the predictor matrix, where x^j=(x^j₁,…, x^j_n)^T, j=1,…p, are the covariates. Typically, the pairs (X_i, Y_i) are assumed to be independently identically distributed (i.i.d.) but most results can be generalized to stationary processes given reasonable decay rate of dependencies (e.g. certain conditions on the mixing rates).

We are interested in selecting the most important predictors. Hence, the ordinary least squares estimate (OLS) is not satisfactory, while procedures performing coefficient shrinkage and variable selection are desirable. A popular method for variable selection is the Lasso (Tibshirani, 1996), which is defined as:

where λ is a penalty parameter. Here, the l₁ norm penalty ‖β‖₁ automatically introduces variable selection, that is, 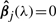for some j′s, leading to improved accuracy and interpretability. The Lasso procedure is employed in Fujita et al. (2007) (with lag of one time unit only).

It is well known that the Lasso suffers from a tendency to over-select the variables. To address this issue, Zou (2006) proposed the Adaptive Lasso, a two-stage procedure solving

where 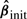is an initial root n consistent estimator, e.g. that obtained by OLS or Ridge Regression. Notice that if 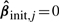then ∀λ>0, 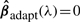In addition if the penalization parameter λ is chosen appropriately, Adaptive Lasso is consistent for variable selection, and enjoys the so called ‘Oracle Property’, which in broad terms signifies that the procedure performs as well as if the true subset of relevant variables were known.

In many situations, natural groupings exist between variables, and variables belonging to the same group should be either selected or eliminated as a whole. The group Lasso procedure (Yuan and Lin, 2006; (Zhao et al., 2006) was invented to address this issue, which we leverage in our present context by choosing the group Lasso algorithm as our sub-procedure REG.

Given J groups of variables which partition the set of predictors, the group Lasso estimate of Yuan and Lin (2006) solves

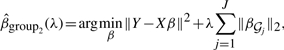where β_𝒢j={β_k; k∈𝒢_j} and 𝒢_j denotes the set of group indices. In our case groups are of equal length (since they correspond to the number of sampling points allowed in regression), so the objective does not need to account for unequal group size.

Here notice that by electing to use the l₂ norm as the intra-group penalty, one encourages the coefficients for variables within a given group to be similar in amplitude (as opposed to using the l₁ norm, for example).

3 SIMULATION EXPERIMENTS

In our first set of experiments, we conducted systematic experimentation using synthetic data in order to test the performance of the proposed methods of group graphical Granger modeling, primarily against that of the non-group variants.

As models for data generation, we employed the Vector Auto-Regressive (VAR) models (c.f. Enders, 2003). Specifically, if we let X_t denote the vector of all feature values at time t, a VAR model is defined as X_t=A_t−1·X_t−1+···+A_t−T · X_t−T. Here, the A matrices are coefficient matrices over the features. In each of these experiments, we randomly generate an adjacency matrix over the features that determines the structure of the true VAR model, and then randomly assign the coefficients (A) to the edges in the graph. We then apply the obtained model on a random initial vector x₁ to generate time-series data {X_t}_t=1,…,T of a specified length T.

In this process of data generation, we made use of the following parameters, basically following Arnold et al. (2007), which were set as follows: the affinity, which is the probability that each edge is included in the graph, was set at 0.2; the sample size per feature per lag which is the total data size per feature per maximum lag allowed, was set at 10. We sampled the coefficients of the VAR model according to a normal distribution with mean 0 and SD 0.25. The noise SD was set at 0.1, and so was the SD of the initial distribution.

In the various variable selection sub-procedures, the penalty parameter λ is tuned so as to minimize the Bayesian Information Criterion (BIC) criterion [as recommended in Zou et al. (2007)], with degrees of freedom estimated as in Zou et al. (2007) for Lasso and Adaptive Lasso, and as in Yuan and Lin (2006) for Group Lasso.

We evaluate the performance of all methods using the so-called F₁-measure, viewing the causal modeling problem as that of predicting the inclusion of the edges in the true graph, or the corresponding adjacency matrix, also following Arnold et al. (2007). Recall that, given precision P and recall R, the F₁-measure is defined as F₁=2PR/(P+R), and hence strikes a balance in the trade-off between the two measures.

Table 1 summarizes the results of our experiments. In the table, the average F₁ values over 18 runs are shown, along with the standard error. These results clearly indicate that there is a significant gap in performance between the proposed method based on Group Lasso and those of the non-group counterparts.

Table 1.

The accuracy (F₁) and standard error in identifying the correct model of the two non-grouped graphical Granger methods, compared with that of the grouped graphical Granger method on synthetic data

Method	Lasso	AdaLasso	GrpLasso
Accuracy (F1)	0.62±0.09	0.65±0.09	0.92±0.19

In Figure 2, we exhibit some typical output graphs along with the true graph. In this particular instance, it is rather striking how the non-group methods tend to over-select, whereas the grouped method manages to obtain a perfect graph.

Fig. 2.

Output causal structures on one synthetic dataset by the various methods (a) True graph, (b) Lasso, (c) Adaptive Lasso and (d) Group Lasso. In this example, the group-based method exactly reconstructs the correct graph, while the non-group ones fail badly.

The simulation results thus confirm the advantage of the proposed grouped graphical Granger method (using Group Lasso) over the standard (non-grouped) methods (i.e. based on Lasso or Adaptive Lasso), albeit subject to the underlying assumptions of the simulation experiments, e.g. there is a clear group structure present among the variables. Note that the non-grouped method based on Lasso can be considered as an extension of the algorithm proposed in Fujita et al. (2007) to lags greater than one time unit.

4 APPLICATION TO HELA CELL CYCLE DATA

We now apply our grouped graphical Granger modeling method to the gene expression data of the human cancer cell (Hela) cycle (Whitfield et al., 2002). We consider the first three experiments where cell synchronization is achieved by double thymidine block. The corresponding data contain 12, 27 and 48 time points, respectively. Whitfield et al. (2002) identified 1134 genes as periodically expressed during the cell cycle. We focus on those genes only. For Experiments 1 and 3, the first two measurements are at t=0 so we take their average. Some time points in the first two experiments are not equally spaced, so we interpolate the data using cubic smoothing splines (Green and Silverman, 1994) to get hourly data for all experiments. Note that for Experiment 1, we decided to exclude the last sample in the original data, for it was taken 10 h after the previous one, which we considered to be too large an interval to interpolate accurately. We ran experiments for maximum lags of L_max=2 and 4, respectively.

4.1 Global characteristics of inferred causal structure

We begin by examining some overall characteristics of the causal graphs output by our method to confirm their consistency with the results of earlier investigations, as well as pinpoint ways in which they differ, particularly those that are attributable to the ability to consider different time lags.

We first discuss the distributions of sizes of the connected components in the network. For that purpose, we vary the penalty parameter λ in the REG sub-procedure (i.e. the Group Lasso) so as to enforce more or less sparsity. More precisely, we restrict λ to be in the range (cλ_max, λ_max) for multiple values of c (0.5, 0.9).

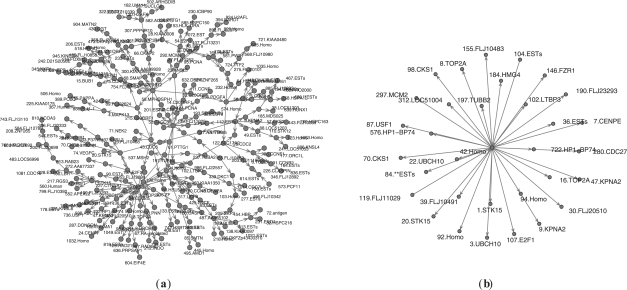
The distributions of sizes are presented in Table 2. For c=0.5, we consistently uncovered a ‘giant’ component as already observed in Mukhopadhyay and Chatterjee (2007), which means that such a phenomenon seems to be persistent across experiments and various maximum lags. The largest component for experiment 3, L_max=4 and c=0.9 is represented in Figure 3a.

Table 2.

Distribution of the sizes of the connected components in Experiments 1, 2 and 3 with L_max=2, 4 and for c=0.5 and 0.9

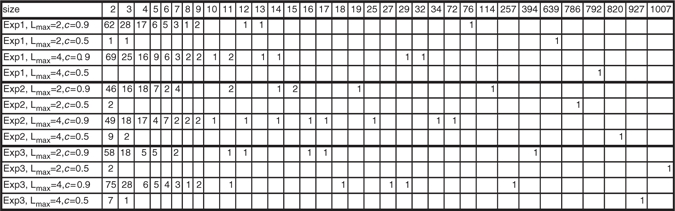Fig. 3.

Subnetworks corresponding to (a) the largest component, (b) the gene with the largest degree using the Experiment 3 dataset and L_max=4. [The number at the beginning of each gene name indicates the row number in data from Whitfield et al. (2002), which contain the full gene names.]

We now discuss the persistence of the genes with highest degrees when the maximum lag changes from 2 to 4. The genes identified as having high degrees are reported in Table 3.

Table 3.

Genes with highest degrees in Experiments 1, 2 and 3 with L_max= 2 and 4

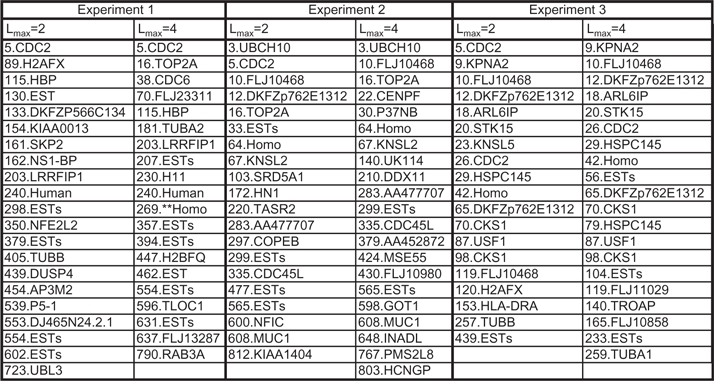The number at the beginning of each gene name indicates the row number in data from Whitfield et al. (2002), which contain the full gene name.

For Experiment 1, out of the top 21 genes, only 5 of them were persistent between lag 2 and 4. Hence, for this experiment larger lags significantly impact the structure of the network.

As we consider experiments with larger original data sizes (Experiments 2 and 3), however, the proportion of persistent genes among those with highest degrees increases significantly. More specifically, 10 out of 20 genes with highest degrees with lag 2 were persistent for lag 4 in Experiment 2, and 13 out of 19 were persistent for Experiment 3. In particular, the gene with the maximum degree for Experiment 3 is ‘Homo sapiens, clone IMAGE:2823731, mRNA, partial cds Hs.70704 R96941’. The sub-network corresponding to this gene is depicted in Figure 3b.

4.2 Causal structure on a restricted subset of genes

Next we inspect the discovered causal networks, when focusing on the subset of 20 genes preselected by Li et al. (2006), particularly with regard to the influence of different time lags as well as the three time course experiments. Out of these 20 genes, 19 are present in the datasets used in our experiments.

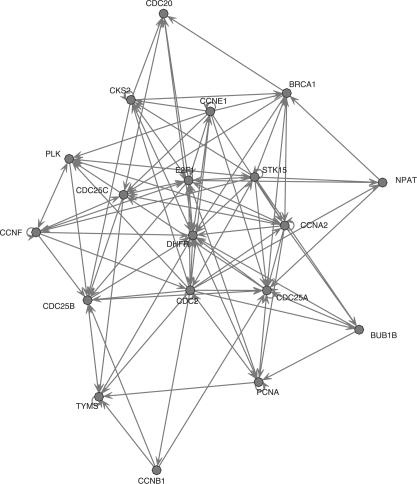
The result of applying our grouped graphical Granger modeling method on this subset of genes is depicted in Figure 4 for the case of Experiment 3 and L_max=4. The genes with highest degrees are: CDC2, PCNA, CDC25B, E2F1, CDC25A, DHFR, CCNF for Experiment 1 and L_max=2; CDC2, CDC25A, PCNA, E2F1, CDC25B, DHFR, NPAT for Experiment 1 and L_max=4; CCNF, CDC2, CCNA2, PCNA, CCNE1, DHFR, PLK for Experiment 2 and L_max=2; CCNF, CCNA2, DHFR, PLK, CDC2, BRCA1, CDC25B for Experiment 2 and L_max=4; DHFR, CCNF, STK15, CKS2, CDC25B, CDC2 for Experiment 3 and L_max=2; E2F1, DHFR, CCNA2, STK15, CDC2 for Experiment 3 and L_max=4, respectively.

Fig. 4.

Output causal structures for the genes identified by Li using the Experiment 3 dataset and L_max=4.

So the genes DHFR and CDC2 are consistently recognized as a gene with the highest degree, while CDC25B and CCNF are recognized as such most of the time.

4.2.1 Discovered pathways

One can observe that allowing a disjunction over multiple lags, as our method does, has a significant effect on the discovered pathways, since some causal relationships may exist for certain lags only. In Mukhopadhyay and Chatterjee (2007), it was discovered that (i) CCNF and CCNE1 are strong ‘regulating’ genes; (ii) STK15 and E2F1 are intermediate ‘traffic hubs’; and (iii) CDC20 and PLK are important ‘regulated’ genes. Our results confirm these observations, but present others that were overlooked by the method of Mukhopadhyay and Chatterjee (2007), due to higher lags that are involved.

In the output causal graph in Figure 4, we see that CCNF has four outgoing edges and two incoming edges, and CCNE1 has eight outgoing and one incoming edges, which is consistent with their observation that they are strong regulators. We also find that STK15 has six outgoing and three incoming edges, while E2F1 has four outgoing and six incoming edges, consistent with their observation that these are intermediate traffic hubs. We then find that CDC20 has one outgoing and three incoming edges, and PLK has one outgoing and four incoming edges, again confirming their claim that they are strongly regulated.

Our results show, however, some significant genes that were not captured by the method of Mukhopadhyay and Chatterjee (2007). Specifically, CDC25A, CDC25B, CDC25C and CCNA2 are identified as some of the largest ‘sinks’, i.e. those that are strongly regulated, with CDC25A having one outgoing and eight incoming edges, CDC25B with two outgoing and six incoming, CDC25C having four outgoing and six incoming, and CCNA2 with four outgoing and five incoming edges.

Inspecting the list of identified time-delayed gene regulations [Table 2 in Li et al. (2006)] reveals why such discrepancy may have resulted. That is, these four genes have many delayed causal links with time delays >1. CDC25A has links with 2, 4 and 5 unit time delay; CDC25B has links with 1, 2, 4 and 5 unit time delay; CDC25C has links with 1, 2, 3 and 4 unit time delay; and CCNA2 CDC25C has links with 1, 2, 4 and 5 unit time delay. Consideration of greater time lags allowed in our causal modeling thus has been critical in the identification of these regulated genes.

In addition, we note that these findings are largely consistent with what is known in the literature: CDC25A is known to be specifically degraded in response to DNA damage, which prevents cells with chromosomal abnormalities from progressing through cell division Ray and Kiyokawa (2007); CDC25B is responsible for the initial dephosphorylation and activation of the cyclin-dependent kinases, thus initiating the train of events leading to entry into mitosis (Aressy et al., 2008); abnormal expression of CDC25B in human tumors may have a critical role in centrosome amplification and genomic instability; CCNA2 binds and activates CDC2 or CDK2 kinases, and thus promotes both cell cycle G1/S and G2/M transitions.

4.3 Evaluating output causal networks against BioGRID

We cannot evaluate the performance of our methodology by comparing the discovered network to the true network for the simple reason that the latter is unknown. Here, we focus on the particular subsets of genes as selected in Sambo et al. (2008), and compare the discovered interactions to those previously reported in the BioGRID database (www.thebiogrid.org). It is important to note that (i) the list of interactions reported in the database is far from being exhaustive, (ii) the interactions documented are either physical or genetic, which implies that they may not be direct interactions. So caution should be exercised when interpreting the results of such comparison: the precision may be lower than the actual precision since links may be missing in the BioGRID database; and the recall may be lower than the actual recall in part because some of the links reported in the BioGRID database may be indirect rather than the direct interactions.

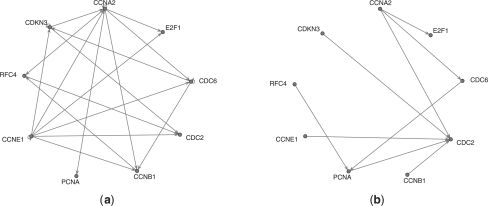
The BIOGRID network and the network discovered by our method are presented in Figure 5. The precison, recall, and F₁ scores obtained are P=0.5, R=0.72, F₁=0.59, respectively, which are superior to those reported in Sambo et al. (2008) (i.e P=0.36, R=0.44, F₁=0.40).

Fig. 5.

(a) Network from the BioGRID database and (b) network discovered by our method.

In addition, we also evaluate the performance of our method by applying the Bootstrap procedure, which is a technique widely used in statistics for evaluating statistical accuracy [see, Davison and Hinkley (2006) for a review]. More precisely, given the original lagged data matrix, we randomly draw B datasets by sampling with replacement the rows of the original data matrix, so that each dataset has the same number of rows as the original lagged data matrix. We then apply our method to each of the B bootstrap datasets.

Comparing the ‘original network’ (i.e. the network obtained by using the original dataset) with the ‘bootstrap networks’ (i.e. those obtained using the bootstrap datasets) allows us to get a measure of confidence in the causal relationships identified in the ‘original network’. In particular, for each causal relationship identified in the ‘original network’, we can get confidence in that relationship by counting the number of times it appears in the ‘bootstrap networks’.

We now report the results of the above evaluation procedure for Experiment 3, L_max=4, for the subsets of genes considered by Li et al. (2006) and Sambo et al. (2008). For the subset of genes identified in Li et al. (2006) and B=100 bootstrap sample, the causal relationships identified by our method in the ‘original network’ appear on the average 72.5% (± 1.74%) of the time in the ‘bootstrap networks’. The top 20 relationships identified by our methods for this subset are listed in Table 4 (left panel). For the subset of genes identified in Sambo et al. (2008) and B=1000 bootstrap sample, the causal relationships identified by our method in the ‘original network’ appear on the average 78.6% (± 5.31%) of the time in the ‘bootstrap networks’. The relationships identified by our methods for this subset are listed in Table 4 (right panel).

Table 4.

Appearance percentage of causal relationships in (left) 100 bootstrap networks and the subset of genes preselected by Li et al. (2006) (top 20 percentages), (right) 1000 bootstrap networks and the subset of genes preselected by Sambo et al. (2008), for experiment 3 and L_max=4.

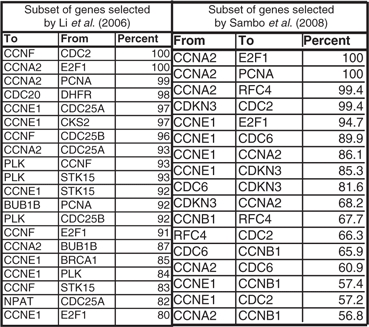As we noted earlier, the ‘false positives’ in the output causal network with respect to BioGRID may not necessarily be ‘false’, and may contain actual links that are unknown to date, or known but have not been incorporated into the database. For example, inspecting the list in Table 4 (right panel) for those links identified by our method with high confidence, and yet are not included in BioGRID, may reveal some interesting facts. Indeed, we found that such link with the highest rank, CCNA2 (Cyclin A2) → PCNA, has been confirmed in the literature—Liu et al. (2007) states that ‘the cyclin A2-depleted MG-63 cells showed decreased levels of PCNA’, evidencing the existence of a link between these two genes. Similarly, a direct functional interconnection between CCNE1 and E2F1 has been identified in Salon et al. (2007). We also found that a physical interaction between CCNE1 and CDC6 has been confirmed in the literature (Furstenthal et al., 2001). So for the top 6 links in Table 4 (right panel) two links (CCNA2→E2F1, CDKN3→CDC2) are present in the BioGRID database, and three links have been confirmed in the literature.

Another insight provided by the bootstrap method is that we can build confidence intervals for precision, recall and F₁ score in the ‘original network’ using the corresponding scores for the ‘bootstrap networks’. Specifically, if the 2.5–97.5% confidence interval for a given score on the ‘bootstrap networks’ is estimated to be [a, b] and the score on the ‘original network’ is c, then the confidence interval for the population value of the score is estimated to be [c−max((b−c), (c−a)), c+max((b−c), (c−a))] (Carpenter and Bithell, 2000). For our earlier comparison results with the BioGRID database on the subset of genes identified in Sambo et al. (2008), the 2.5–97.5% confidence interval (CI) obtained are: for precision P=0.5, CI(P)=[0.37, 0.63]; for recall R=0.72, CI(R)=[0.61, 0.83]; for the F₁ score F₁=0.59, CI(F₁)=[0.48, 0.70]. Notice that these intervals are all above the results in Sambo et al. (2008) confirming the improved accuracy of our method.

5 CONCLUDING REMARKS

We proposed a novel method for graphical Granger modeling that leverages group structure among the temporal variables according to the time series they belong to, thus allowing to efficiently model causality involving a large number of variables and time lags >1 time unit, which had not been effectively addressed previously. We applied our method to uncover gene regulatory networks for the human cancer cell (Hela) cycle data. We confirmed that by grouping of multiple lags and representing more faithfully the disjunctive nature of the relationships over different lags, we are able to detect some causal links that would otherwise be overlooked. As future work we plan to consider a variant of our method where in addition to the grouping by time series, grouping by functions or by UNIGENE clusters is considered.