Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2009 May 27;25(12):i348–i355. doi: 10.1093/bioinformatics/btp216

Modeling interactions between adjacent nucleosomes improves genome-wide predictions of nucleosome occupancy

Shai Lubliner 1, Eran Segal 1,2,*
PMCID: PMC2687970  PMID: 19478009

Abstract

Motivation: Understanding the mechanisms that govern nucleosome positioning over genomes in vivo is essential for unraveling the role of chromatin organization in transcriptional regulation. Until now, models for predicting genome-wide nucleosome occupancy have assumed that the DNA associations of neighboring nucleosomes on the genome are independent. We present a new model that relaxes this independence assumption by modeling interactions between adjacent nucleosomes.

Results: We show that modeling interactions between adjacent nucleosomes improves genome-wide nucleosome occupancy predictions in an in vitro system that includes only nucleosomes and purified DNA, where the resulting model has a preference for short spacings (linkers) of less than 20 bp in length between neighboring nucleosomes. Since nucleosome occupancy in vitro depends only on properties intrinsic to nucleosomes, these results suggest that the interactions we find are intrinsic to nucleosomes and do not depend on other factors, such as transcription factors and chromatin remodelers. We also show that modeling these intrinsic interactions significantly improves genome-wide predictions of nucleosome occupancy in vivo.

Contact: eran.segal@weizmann.ac.il

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Eukaryotic DNA is highly compacted within the cell nucleus by the wrapping of 147-bp-long DNA stretches around histone protein octamers, forming nucleosomes (Kornberg and Lorch, 1999). Adjacent nucleosomes are separated by short DNA sequences, called linkers. The positioning of nucleosomes along genomic DNA is the first order of chromatin organization. Past analyses of nucleosomal DNA and linker sequences have revealed specific sequences that are enriched within the nucleosome or within linkers (Ioshikhes et al., 1996; Kaplan et al., 2009; Lee et al., 2007; Satchwell et al., 1986; Segal et al., 2006; Yuan and Liu, 2008). Based on these nucleosome sequence preferences, several models for predicting nucleosome occupancy were suggested (Ioshikhes et al., 2006; Kaplan et al., 2009; Lee et al., 2007; Peckham et al., 2007; Segal et al., 2006; Yuan and Liu, 2008). Two of these were incorporated into a thermodynamic model (Kaplan et al., 2009; Segal et al., 2006) that was shown to predict in vitro and in vivo genome-wide nucleosome occupancy with high accuracy.

The thermodynamic model assigns a statistical weight for each possible configuration of nucleosomes that are placed along a genomic sequence, such that no two nucleosomes overlap. In this model, the association of each nucleosome to a 147-bp-long sub-sequence within a configuration is weighted according to the nucleosome sequence preferences, and is independent of associations of other nucleosomes elsewhere on the DNA. However, given the several factors that are known to affect chromatin folding and higher order chromatin organization, this independence assumption does not hold. First, different linker lengths allow different relative conformations between neighboring nucleosomes, resulting from steric hindrance constraints and the helical turns of the DNA (Schalch et al., 2005; Widom 1992). Second, many experiments and analyses have suggested that linker length distributions demonstrate a preference for quantized length patterns, of the form d + r · n, where n is a running integer, r is a repeat length, and d is a length offset (d < r) (Cohanim et al., 2006]; Kato et al., 2003; Wang et al., 2008). In most cases, r was found to be ∼10, in accordance with the DNA helical repeat, while the value of d varied. Third, the binding of the linker histone H1 to linker DNA greatly affects chromatin folding and condensation. Long linker lengths enable H1 binding, giving condensed chromatin, while short ones disable H1 binding, resulting in open chromatin (Routh et al., 2008). Finally, electrostatic interactions may occur between two nucleosomes that are spatially close (Chodaparambil et al., 2007; Dorigo et al., 2004; Luger et al., 1997), and may contribute to chromatin folding.

Here, we model interactions between adjacent nucleosomes using a nucleosome cooperativity function (NCF), resulting in a new thermodynamic model for predicting nucleosome occupancy. We consider several types of functions as NCF candidates, based on an analysis of in vivo linker length distributions in yeast, and devise an algorithm to estimate these functions from data measurements of nucleosome occupancy. All of the functions we consider are simple and defined by a small number of parameters (between two and five parameters). When applied to synthetic data, we show that our model can accurately reconstruct NCF parameters, even in the presence of large degrees of noise in the input data.

Our results suggest that reported preferences for quantized linker lengths result from the previously observed periodic sequence preferences of the single nucleosome (Satchwell et al., 1986; Segal et al., 2006). We show that modeling interactions between adjacent nucleosomes significantly improves nucleosome occupancy predictions in an in vitro system consisting of purified histones assembled on naked yeast genomic DNA, demonstrating that the preferred interactions that we find are intrinsic to nucleosome-DNA associations. The interactions that we learn introduce a preference for short linkers of less than 20 bp in length. Finally, modeling these intrinsic interactions also significantly improves predictions of nucleosome occupancy in vivo in both yeast and in Caenorhabditis elegans, showing that they also play a role in nucleosome positioning in vivo, and suggesting that they may be universal to all eukaryotes.

2 METHODS

2.1 New thermodynamic model for predicting nucleosome occupancy

A thermodynamic model for the genome-wide prediction of nucleosome occupancy has been published by our lab (Field et al., 2008; Segal et al., 2006). This model assigns a statistical weight for each possible configuration of nucleosomes that are placed along a genomic sequence. The association of each nucleosome to a 147 bp long sub-sequence within a configuration is weighted by a probabilistic model that represents the nucleosome sequence preferences, assigning different statistical weights to different 147 bp long sequences. The association of a nucleosome to DNA at a certain genomic region is independent of the associations of other nucleosomes elsewhere, other than the fact that no two nucleosomes can overlap in the same configuration.

Our new thermodynamic model relaxes the above independence assumption and models interactions between adjacent nucleosomes by incorporating a nucleosome cooperativity function (NCF). An NCF, denoted L(x), is a positive function that assigns different statistical weights to different linker lengths. These weights are used as multiplicative factors, with 1 being a neutral weight. In the Results section we refer to the actual types of functions selected to represent NCFs. The probabilistic model that we use to describe the nucleosome sequence preferences was learned from in vitro bound sequences that we previously published (Kaplan et al., 2009). We will denote this model of single nucleosome sequence preferences by Nuc, where Nuc(i) is the statistical weight that the Nuc model assigns to a nucleosome being positioned on the input sequence, S, starting at position i. By Si,j we denote the sub-sequence of S starting at position i and ending at position j. By Bg(i, j) we denote the statistical weight given by a background model to an unoccupied sub-sequence Si,j. Since the Nuc model includes a background component that is used to normalize statistical weights, we used a simple uniform 0-order Markov model (i.e. P(A) = P(C) = P(G) = P(T) = 0.25) as the Bg model. Using the above definitions, we compute the distribution over nucleosome configurations on an input sequence S of length N. We take the partition function to be the space of all legal nucleosome configurations on S, denoted by C. A legal configuration c ∈ C is defined by a set of nucleosome start positions on S, c[1],…, c[k], such that no two nucleosomes overlap. Assuming thermodynamic equilibrium, its statistical weight (its Boltzmann factor) is:

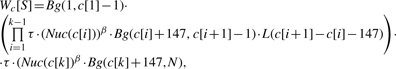graphic file with name btp216um1.jpg

where τ represents an apparent nucleosome concentration, and β is a temperature parameter. For conciseness of representation, we assume that if i > j then Bg(i,j) = 1.

The probability of configuration c is given by:

graphic file with name btp216um2.jpg

where c′ traverses over the space C of all legal configurations.

The probability of placing a nucleosome at start position i on S, denoted P(i), can be computed as follows:

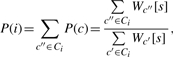graphic file with name btp216um3.jpg

where c″ traverses over the space Ci of all legal configurations in which a nucleosome starts at position i. To efficiently compute P(i) for all positions i on S we employ a dynamic programming procedure (Rabiner, 1989). This demands that we limit the effect of any NCF to a window of reasonable length ML, such that its contribution will only be added for linker lengths shorter than ML. In this work we used ML = 100. For any NCF L this is equivalent to transforming L to a new function L′ such that:

graphic file with name btp216um4.jpg

The first part of our dynamic program is a forward step, in which we compute two sets of random variables: {FiNuc} and {FiBg} (1 ≤ i ≤ N). FiNuc represents the sum of the statistical weight of all legal configurations over the prefix S1,…, Si of S, that end with a nucleosome (the last nucleosome end position is i). FiBg is similarly defined, where position i is not covered by a nucleosome. The forward step computation is as follows:

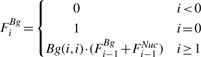graphic file with name btp216um5.jpg
graphic file with name btp216um6.jpg

This concise representation is assisted by extending the definition of FiNuc and FiBg also over negative positions.

The second part of the dynamic program is a backward step, in which we compute two more sets of random variables: {RiNuc} and {RiBg} (1 ≤ i ≤ N). RiNuc represents the sum of the statistical weight of all legal configurations over the suffix Si,…, SN of S, in the event where a nucleosome ends at position i − 1 (exactly before the suffix Si,…, SN). RiBg is similarly defined, where position i − 1 is not covered by a nucleosome. The backward step computation is as follows:

graphic file with name btp216um7.jpg
graphic file with name btp216um8.jpg

This concise representation is assisted by extending the definition of RiNuc and RiBg also over positions i > N + 1, and by defining: Bg(i, i − 1) = 1.

Having computed the above, we can now compute P(i) for any position i in S:

graphic file with name btp216um9.jpg

The probability of position i in S being covered by a nucleosome, also referred to as the average nucleosome occupancy over position i, is predicted by our model to be:

graphic file with name btp216um10.jpg

2.2 Learning the parameters of a nucleosome cooperativity function

Having chosen a type of function as our NCF, we want to learn an optimal choice of its parameter values. Our model produces a vector 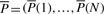Inline graphic of predicted average nucleosome occupancy, per position of an input sequence S. Therefore, for the purpose of learning NCF parameters, we require as input a vector 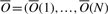Inline graphic of the measured cell population average nucleosome occupancy per position of S. 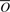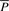Inline graphic and Inline graphic after normalization (by subtracting the mean and dividing by the SD) to mean 0 and SD 1 are denoted Ô and 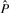Inline graphic, respectively. 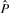We define our objective function to be the L2-distance between Ô and Inline graphic:

graphic file with name btp216um11.jpg

and our learning algorithm searches for NCF parameters assignments for which the model generates a prediction 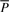Inline graphic that minimizes 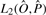Inline graphic. We chose the (Nelder-Mead) simplex method for the function optimization task at hand, since it requires only the computation of the objective function at each point in the space of NCF parameter values. We refrained from using methods, such as conjugate gradient, that require computing the partial derivatives of the objective function according to the NCF parameters (see Supplementary Methods), as such computations are quite costly, and as they limit the choices of NCFs to differentiable ones.

3 RESULTS

Previous approaches for predicting nucleosome occupancy (Ioshikhes et al., 2006; Kaplan et al., 2009; Lee et al., 2007; Peckham et al., 2007; Segal et al., 2006; Yuan and Liu, 2008) relied on modeling the nucleosome sequence preferences, and used them to generate nucleosome occupancy predictions assuming that the association of one nucleosome to the DNA is independent of the associations of other nucleosomes. We relax this independence assumption by modeling interactions between adjacent nucleosomes through a nucleosome cooperativity function (NCF). In the previous section we presented how an NCF is incorporated into our model, and how we can learn its parameters. In this section we use our model to learn NCFs from synthetic data, as well as in vitro and in vivo measurements of nucleosome occupancy.

3.1 Selecting the types of nucleosome cooperativity functions

A good candidate for an NCF would be the organism's linker lengths distribution. This distribution can be easily derived from single cell data of mono-nucleosome sequences that are uniquely mapped to the organism's genome, as linker lengths are simply the distances between any two mapped nucleosomes. However, existing experimental methods cannot measure genome-wide nucleosomes from single cells. Rather, existing nucleosome data comes from cell populations. We therefore resort to an approximation of the linker lengths distribution, derived from cell population data of mapped nucleosome sequence reads, similar to that used in (Valouev et al., 2008). Instead of counting appearances of true linker lengths, we count appearances of putative linker lengths. For any pair of nucleosomes that are d bps apart, such that d < 100, we count a single occurrence of a (putative) linker of length d. We smooth the resulting linker lengths distribution with a moving average window of 5 bps. Using this procedure, whenever we encounter a pair of nucleosomes that were adjacent within a single cell then we count a true linker length appearance. In all other cases, we falsely add appearance counts, adding noise to the distribution.

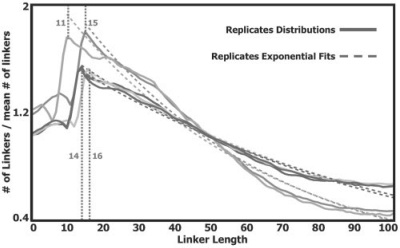
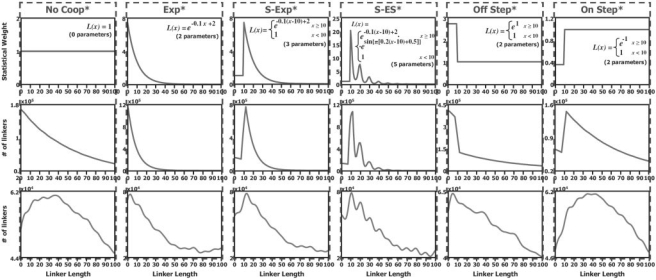
We used in vivo mono-nucleosome data, extracted from wild-type S. cerevisiae that were grown in rich medium and uniquely mapped to the S. cerevisiae genome (Kaplan et al., 2009). The linker lengths distributions that we computed from cell population data of five different experiment replicates are shown in Figure 1. These five distributions are highly similar, and share several main features. First, they all exhibit an apparent disfavoring of linker lengths shorter than ∼15 bps. Second, a single prominent peak exists at 11–16 bp, and seems to decay exponentially at longer linker lengths (see exponential fits in Fig. 1). Third, with this dominant decaying pattern, a periodic pattern of subtle peaks that are approximately 10 bps apart is combined. This pattern concurs with past analyses that revealed a preferentially quantized linker lengths pattern in yeast (Cohanim et al., 2006; Wang et al., 2008). The above linker lengths distributions derived from yeast cell populations are approximations of the unknown true linker lengths distribution in yeast. We assume that the above three features that appear in the approximate distributions reflect features of the true one. This suggests that biologically relevant NCFs will also include them. We therefore selected simple functions that represent at least one of the above three features, and are defined by a small number (between 2 and 5) of parameters. These functions are: an exponentially decaying function (Exp, two parameters), a right-shifted exponentially decaying function (S-Exp, three parameters), a right-shifted exponentially decaying sinusoid (S-ES, five parameters) and a step function (Step, two parameters, may represent both an Off Step or an On Step). The function formulas are presented in the Supplementary Data section. All functions have a parameter assignment for which they are equivalent to the constant 1 function (No Coop) that represents no nucleosome cooperating interactions. Examples of the selected functions for specific parameter assignments are shown in Figure 2.

Fig. 1.

Fig. 1.

Open in a new tab

Linker lengths distributions derived from mono-nucleosome genome-wide positioning data, extracted from in vivo yeast cell populations. The data includes five different replicates, all for wild-type yeasts grown in rich medium. For each replicate, the distribution of linker lengths in the range 0–100 is shown (divided by its mean value), along with an exponential curve that was fit to its decaying part (starting at the main peak).

Fig. 2.

Fig. 2.

Open in a new tab

Nucleosome cooperativity functions and their linker length distributions. The figure is organized in a table-like fashion, with columns per NCF and rows per graph type. In the first row (in blue) are the NCFs, along with their formulas (after parameters were assigned). In the second row (in red) are the sampled linker lengths distributions derived from sampled nucleosome configurations that represent data at single cell resolution. In the third row (in green) are the sampled linker lengths distributions derived from sampled mono-nucleosome data that represents data at cell population resolution.

3.2 Using the model to explore linker length preferences in yeast

Having selected the types of NCFs to examine, we sought to compare the in vivo linker length distributions to linker length distributions that are sampled using our model with each of the chosen NCF types. For this purpose, we selected particular parameter assignments for each NCF type (see Supplementary Data). The resulting NCFs are plotted in Figure 2. For each NCF, we sampled 5000 nucleosome configurations over a 500 000 bp long sub-sequence of yeast chromosome 4 using our model with that NCF (denoted ModelNCF), with the temperature and nucleosome concentration parameters set to 1. Each sampled configuration represents sampled nucleosome positioning data in single cell resolution. Thus, by counting linker lengths appearances in the 5000 sampled configurations we derived the sampled linker lengths distribution, plotted in Figure 2. Next, we collected all mono-nucleosome reads out of the sampled configurations, generating the sampled mono-nucleosome positioning data of the cell population. Following the same procedure described in Section 3.1 we further produced the sampled linker lengths distribution derived from cell population data, also plotted in Figure 2. Examining properties of the sampled linker lengths distributions, we find a high similarity between the shape of the NCF functions themselves (Fig. 2, blue graphs) and their respective sampled single cell linker lengths distributions (Fig. 2, red graphs). Similarities are also evident between the shape of the NCFs and their respective sampled cell population linker lengths distributions (Fig. 2, green graphs). This supports our approach in Section 3.1 of selecting NCF types reflecting features that appear in the yeast in vivo cell population linker lengths distributions. Second, all sampled linker lengths distributions (Fig. 2, red graphs) show an exponential decay as linker lengths get longer, even for NCFs that do not represent such a decay, in particular the No Coop NCF. Thus, any sampled linker lengths distribution can be decomposed to an exponentially decaying component that is NCF-independent, and other components that depend on the particular NCF type. Third, all sampled cell population linker lengths distributions (Fig. 2, green graphs), except in the S-ES case, demonstrate a periodic pattern of subtle peaks. In the S-ES case, a periodic pattern of high peaks appears, concurring with the 10n (n=1, 2,…) peak pattern of the S-ES NCF. The periodic pattern of subtle peaks apparent in all other cases starts around linker length 5, with a period slightly longer than 10 bp.

The periodic pattern of subtle peaks observed in the sampled cell population linker lengths distributions is similar in all NCF cases except S-ES, and does not depend on the NCF type. Therefore, other elements that the model accounts for produced this periodic pattern. Genomic sequences are known to encode periodic signals (Cohanim et al., 2005, 2006; Widom, 1996) that follow a ∼10-bp periodic pattern. One possibility is that the periodic pattern of subtle peaks is mainly a result of these periodic signals. Alternatively, these peaks may result from the nucleosome sequence preferences, since aligned nucleosome sequences exhibit a ∼10bp periodic dinucleotide pattern (Ioshikhes et al., 1996; Satchwell et al., 1986; Segal et al., 2006), and since the model we use (the Nuc model, see Section 2.1) includes these periodic dinucleotide preferences.

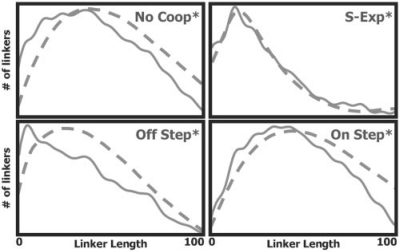
If the latter possibility is true, then using a non-uniform and non-periodic model of nucleosome sequence preferences would not produce a periodic pattern of subtle peaks. To examine this, we created an alternative model of the nucleosome sequence preferences, denoted NucU, which replaces the Nuc model (see Section 2.1), with a model in which the periodic dinucleotide preferences are removed (see Supplementary Methods). We repeated the above process of generating sampled linker lengths distributions from cell population data for several of the above NCFs using the NucU model, and compared them with the ones generated using the Nuc model. The results of this comparison appear in Figure 3, where for each NCF we present both sampled cell population linker lengths distributions, with the original Nuc model (in green), and with the NucU model (in orange). Notably, whereas the general theme of the distribution is similar for both cases, the periodic pattern of subtle peaks is abolished as a result of the removal of the periodic component of the nucleosome sequence preferences model. This demonstrates that the periodic subtle peaks pattern is mainly a result of the periodicity of the nucleosome sequence preferences. This suggests that the previously reported preferentially quantized linker lengths distribution (Cohanim et al., 2006; Wang et al., 2008) results mainly from the periodic sequence preferences of the nucleosome itself, rather than from periodicity of certain signals encoded in genomic sequences.

Fig. 3.

Fig. 3.

Open in a new tab

A comparison of sampled linker lengths distributions derived from cell population data that was sampled by one of two models: a model that recognizes nucleosome periodic sequence preferences (using the Nuc model, in green) and a model that does not (using the NucU model, in orange). The comparison was performed for four different NCFs. For each NCF, the distribution was similar in both cases, but the preference for quantized linker lengths was abolished when periodic nucleosome sequence preferences were removed. This demonstrates that preferentially quantized linker lengths distributions are mainly the result of the periodic sequence preferences of the nucleosome itself.

3.3 Learning nucleosome cooperativity functions from synthetic data

Before trying to learn NCFs from real nucleosome positioning data, we sought to test our ability to learn NCFs from the controlled setting of synthetic data. For each of the six NCFs presented in Figure 2 we used the sampled mono-nucleosome reads cell population data described in Section 3.2 as six synthetic data sets. Due to experimental limitations of the nucleosome mapping experiments, in the real yeast data that we use, each nucleosome read is mapped to the genome with an estimated inaccuracy of up to 20 bp shifts from its true location. To reflect that in the synthetic setting, we randomly shifted the location of each sampled read by a number of Pnoise bp, sampled from a Normal distribution of mean 0 and SD Stdnoise (we varied Stdnoise between 0, 10, 20, 50 and 100). After adding noise to the sets, we counted for each position on the sequence the number of sampled reads that cover it. The vector of counts per position was normalized to have mean 0 and SD 1, resulting in the normalized nucleosome occupancy data required for learning NCF parameters (the Ô vector, see Section 2.2). For each of the 30 synthetic sets (five noise levels for each of the six NCFs that we use), we partitioned the data into training data and test data, in a 5-fold cross validation (CV) manner. For each of the five CV groups, we tried to learn parameters for the Exp, S-Exp, S-ES, Step and No Coop NCFs that minimize the L2-distance between the normalized training data and the normalized model predictions (see Section 2.2). Along with the NCF parameters, we learned the model's temperature and nucleosome concentration parameters. For the No Coop NCF we learned only the last two. In all cases, a small number of parameters were learned (between 2 and 7). In the Supplementary Methods we address the issue of choosing an initial parameters assignment. Let 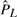Inline graphic be the normalized nucleosome average occupancy predicted by the model with a learned NCF L over the sequence positions that correspond to the normalized test data Ô. We use the R2 statistic as a test of the learned NCF L:

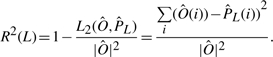graphic file with name btp216um12.jpg

This measure quantifies the fraction of the variance in the test data that the model learned from the training data explains. The same score can be applied on the training data itself to produce a training score.

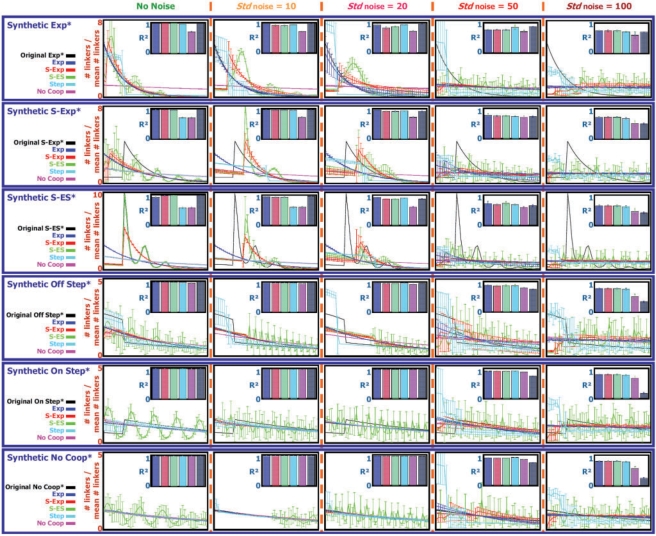
The results over the different synthetic sets appear in Figure 4. In all cases, when no noise is introduced, we are able to reconstruct the original model (when learning parameters of an NCF of the same type that was used to sample the data) with high accuracy. One exception is in the S-Exp* synthetic case, where we do not reconstruct the exact “shift” of the function. At high noise levels (Stdnoise 50 and 100), using the original model yields worse results than other models with learned NCFs, showing that the task of learning the ‘true’ NCF parameters is hard. However, at noise levels that correspond to the estimated noise in the real yeast data that we use (when Stdnoise is up to 20, see above) we are still able to learn models that fit the data well. In the S-Exp* and S-ES* synthetic cases, as more noise is introduced, learning the parameters that determine the ‘shift’ (of S-Exp and S-ES) and the ‘preferred quantized lengths’ (of S-ES) becomes harder, and the Exp and Step functions yield better results. This shows that if an Exp or a Step function scores slightly better than an S-Exp or an S-ES function on real noisy data, we cannot rule out the possibility that the ‘true’ function is one of the latter two. Taken together, we conclude that we are able to learn NCFs in a synthetic setting, even when a realistic level of noise is introduced.

Fig. 4.

Fig. 4.

Open in a new tab

A summary of results of learning NCFs from synthetic datasets. Synthetic sets were sampled over a 500 000-bp-long sub-sequence of yeast chromosome 4, using the model with each of the NCFs: Exp*, S-Exp*, S-ES*, Off Step*, On Step* and No Coop* (shown in Fig. 2). To each sampled set different levels of noise (different SDs for Gaussian perturbations of sampled nucleosome locations, denoted Stdnoise) were introduced. On each resulting synthetic set, parameters of five types of NCFs were learned (Exp, S-Exp, S-ES, Step and No Coop), together with the model's temperature and nucleosome concentration parameters, in a 5-fold cross validation manner. The results are organized in a table-like fashion, with rows per synthetic data type and columns per noise level introduced into the synthetic set. Each cell shows results attained for each of the learned NCFs, along with results attained for the original NCF (with original temperature and nucleosome concentration) used for sampling the synthetic data. Results per learned NCF are color coded according to a color legend appearing in the left part of the respective row. For each learned NCF shown are: in the bar plot, the cross validation mean (bar) and SD (blue error bar) of the test R2 statistic (quantifying the fraction of the variance in the test data that is explained by the model with the learned NCF), as well as the cross validation mean and SD of the train R2 statistic (light green error bar). In the graphs plot, shown are the cross validation mean and SD (per linker length) of the linker lengths distribution (over linker lengths 0–50) sampled using the model with the learned NCF.

3.4 Learning nucleosome cooperativity functions from yeast in vitro and in vivo data

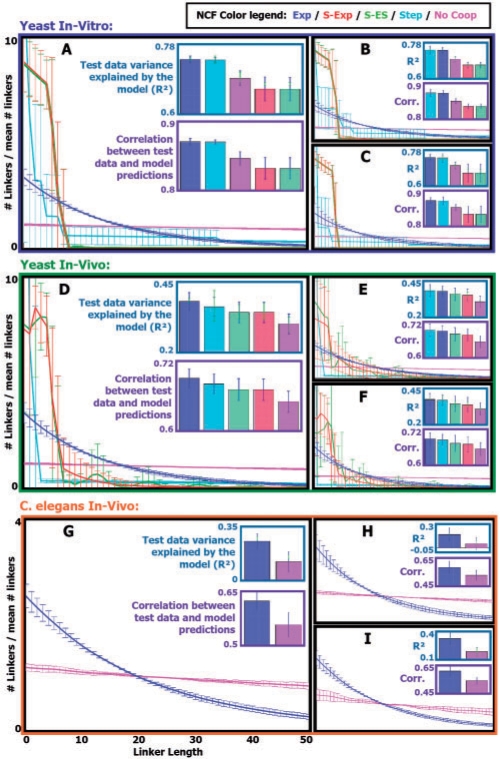
We now turn to learning NCFs from real data. First, we learned NCFs from yeast nucleosome mapping data taken from two in vitro experiment replicates that we previously measured (Kaplan et al., 2009). Since in vitro there are only purified histones and naked DNA, NCFs learned from this data can represent only interactions that are intrinsic to the association of nucleosomes and DNA, and that do not depend on other factors such as transcription factors and chromatin remodeleres that are present in living cells. From the in vitro data, we produced in vitro normalized nucleosome occupancy over the yeast genome (see Supplementary Methods). We randomly chose a 1M bp long sub-sequence of yeast chromosome 4 and used the normalized nucleosome occupancy data over it in a 5-fold CV manner, similar to the synthetic cases in Section 3.3, learning parameters of the Exp, S-Exp, S-ES, Step and No Coop NCFs. We repeated this procedure twice more over randomly chosen 1M bp long sub-sequences of yeast chromosomes 7 and 12. The results are presented in Figure 5A–C, and are similar for all three chromosomes. We find that the learned ModelExp and ModelStep models explain ∼74% of the variance in the test data, significantly better (Wilcoxon signed-rank test P-values 6 × 10−5 and 3 × 10−4, respectively) than the learned ModelNoCoop model that explains ∼69.5% of the variance in the test data. This result demonstrates that modeling intrinsic interactions between adjacent nucleosomes improves the accuracy of yeast in vitro nucleosome occupancy predictions. The learned intrinsic interactions display a preference for short linkers, evident in the linker lengths distributions sampled by the ModelExp and ModelStep models. The ModelS−Exp and ModelS−ES models that were learned were highly similar, and explained ∼66.5% of the variance in the test data, significantly worse (each with a Wilcoxon signed-rank test P-value 6 × 10−5) than the ModelNoCoop model. The reason for this may be that the learned S-Exp and S-ES NCFs show a very strong disfavoring of linkers longer than 10 bp that may be too extreme.

Fig. 5.

Fig. 5.

Open in a new tab

(A) Parameters of five NCF types (together with the model's temperature and nucleosome concentration parameters) were learned from yeast in vitro data of nucleosome mapping over a 1M-bp-long sub-sequence of chromosome 4, in a 5-fold cross validation manner. Results for each NCF type are color coded according to a color legend that appears at the center of the figure. For each learned NCF shown are: in the top bar plot, the cross validation mean (bar) and SD (blue error bar) of the test R2 statistic (quantifying the fraction of the variance in the test data that is explained by the model with the learned NCF), as well as the cross validation mean and SD of the train R2 statistic (light green error bar). In the bottom bar plot, shown is the cross validation mean (bar) and SD (blue error bar) of the correlation between the test data and the model predicted average occupancy. In the graphs plot, shown is the cross validation mean and SD (per linker length) of the linker lengths distribution (over linker lengths 0–50) sampled using the model with the learned NCF. (B) Same as in (A), for chromosome 7. (C) Same as in (A), for chromosome 12. (D–F) Same as in (A–C), respectively, for yeast in vivo data. (G) Same as A, for in vivo data of C.elegans chromosome I. (H) Same as (G), for chromosome II. (I) Same as (G), for chromosome III.

Next, we examined whether interactions between adjacent nucleosomes play a similar role in vivo. We repeated the above procedure for learning NCFs over the same three sub-sequences of chromosomes 4, 7 and 12, this time using the yeast in vivo data that was analyzed in Section 3.1. From this data we produced in vivo normalized nucleosome occupancy over the yeast genome (see Supplementary Methods). The results are presented in Figure 5D–F, and are again similar for all three chromosomes. The learned ModelExp, ModelStep, ModelS−ES and ModelS−Exp models explain ∼37.5%, ∼37%, ∼34.5% and ∼34% of the variance in the test data, respectively, all significantly better (Wilcoxon signed-rank test P-values 6 × 10−5, 6 × 10−5, 10−3 and 10−3, respectively) than the learned ModelNoCoop model that explained ∼30.5% of the variance in the test data. Importantly, the linker lengths distributions sampled using all these models are highly similar to those sampled using the models that were learned from the in vitro data, with the exception that in the in vivo case the learned S-Exp and S-ES NCFs show a weaker disfavoring of linkers longer than 10 bp. Thus, we find that modeling intrinsic interactions between adjacent nucleosomes also improves the accuracy of yeast in vivo nucleosome occupancy predictions.

3.5 Learning nucleosome cooperativity functions from c.elegans in vivo data

To examine whether the intrinsic interactions between adjacent nucleosomes that we find in yeast play similar roles in higher eukaryotes, we applied our approach for learning parameters of the Exp and No Coop NCFs from in vivo nucleosome positioning data of C.elegans. We randomly chose 1M bp long sub-sequences of C.elegans chromosomes I, II and III, and used published in vivo nucleosome occupancy data over these sub-sequences (Valouev et al., 2008). The results are presented in Figure 5G–I. The results are qualitatively similar over the three chromosomes. The ModelExp model explained ∼13% more of the variance in the test data than the ModelNoCoop model, and this improvement was significant (Wilcoxon signed-rank test P-value 6 × 10−5). Moreover, the resulting linker length distributions sampled by the two models are highly similar to those sampled for yeast, with the one sampled using the learned Exp NCF demonstrating the same preference for short linkers. This shows that, as in yeast, modeling intrinsic interactions between adjacent nucleosomes improves the accuracy of nucleosome occupancy predictions of C.elegans in vivo.

4 DISCUSSION

We presented a new thermodynamic model for genome-wide prediction of nucleosome occupancy, extending a model previously published by our lab (Field et al., 2008; Segal et al., 2006). The model assigns a statistical weight for each possible configuration of nucleosomes that are placed along a genomic sequence, such that no two nucleosomes overlap. The previous model assumed that the association of a nucleosome to the DNA at one place is independent of the associations of other nucleosomes elsewhere. Our new model relaxes this independence assumption by modeling interactions between adjacent nucleosomes through a nucleosome cooperativity function (NCF).

Based on an analysis that involves our model we suggest that the previously reported preference for quantized linker lengths in yeast (Cohanim et al., 2006; Wang et al., 2008) results mainly from the periodic sequence preferences of the nucleosome itself.

Our results show that by modeling interactions between adjacent nucleosomes, such that short linkers (less than 20 bp long) are preferred, we improve the accuracy of predictions of yeast in vitro nucleosome occupancy. The in vitro system contains only nucleosomes and naked yeast genomic DNA. Thus, the modeled interactions are intrinsic to the association of nucleosomes and DNA and are independent of other factors such as transcription factors and chromatin remodelers that affect chromatin organization in living cells.

Notably, modeling these same interactions also improves the accuracy of nucleosome occupancy predictions of yeast in vivo. Moreover, these intrinsic interactions also improve the accuracy of nucleosome occupancy predictions of C.elegans in vivo, suggesting that these interactions may be universal across eukaryotes.

It will be interesting to understand the mechanistic basis for the preferred nucleosome interactions that we find. One possibility is that such interactions results from direct interaction between spatially close nucleosomes, which are known to occur (Chodaparambil et al., 2007; Dorigo et al., 2004; Luger et al., 1997). The fact that the modeled interactions are accompanied by a preference for short linkers may hint at that direction. Direct interaction between two adjacent nucleosomes (that may involve their histone tails) may also assist with the chromatin fiber folding, energetically justifying a shift of nucleosomes away from positions that would have been otherwise favored according to the single nucleosome sequence preferences.

Funding: European Research Council (to E.S.). E.S. is the incumbent of the Soretta and Henry Shapiro career development chair.

Conflict of Interest: none declared.

REFERENCES

  1. Chodaparambil JV, et al. A charged and contoured surface on the nucleosome regulates chromatin compaction. Nat. Struct. Mol. Biol. 2007;14:1105–1107. doi: 10.1038/nsmb1334. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Cohanim AB, et al. Yeast nucleosome DNA pattern: deconvolution from genome sequences of S. cerevisae. J. Biomol. Struct. Dyn. 2005;22:687–694. doi: 10.1080/07391102.2005.10507035. [DOI] [PubMed] [Google Scholar]
  3. Cohanim AB, et al. Three sequence rules for chromatin. J. Biomol. Struct. Dyn. 2006;23:559–566. doi: 10.1080/07391102.2006.10507081. [DOI] [PubMed] [Google Scholar]
  4. Dorigo B, et al. Nucleosome arrays reveal the two-start organization of the chromatin fiber. Science. 2004;306:1571–1573. doi: 10.1126/science.1103124. [DOI] [PubMed] [Google Scholar]
  5. Field Y, et al. Distinct modes of regulation by chromatin are encoded through nucleosome positioning signals. PLoS Comput. Biol. 2008;4:e1000216. doi: 10.1371/journal.pcbi.1000216. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Ioshikhes IP, et al. Nucleosome DNA sequence pattern revealed by multiple alignment of experimentally mapped sequences. J. Mol. Biol. 1996;262:129–139. doi: 10.1006/jmbi.1996.0503. [DOI] [PubMed] [Google Scholar]
  7. Ioshikhes IP, et al. Nucleosome positions predicted through comparative genomics. Nat. Genet. 2006;38:1210–1215. doi: 10.1038/ng1878. [DOI] [PubMed] [Google Scholar]
  8. Kaplan N, et al. The DNA-encoded nucleosome organization of a eukaryotic genome. Nature. 2009;458:362–366. doi: 10.1038/nature07667. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Kato M, et al. Dinucleosome DNA of human k562 cells: experimental and computational characterizations. J. Mol. Biol. 2003;332:111–125. doi: 10.1016/s0022-2836(03)00838-6. [DOI] [PubMed] [Google Scholar]
  10. Kornberg RD, Lorch Y. Twenty-five years of the nucleosome, fundamental particle of the eukaryote chromosome. Cell. 1999;98:285–294. doi: 10.1016/s0092-8674(00)81958-3. [DOI] [PubMed] [Google Scholar]
  11. Lee W, et al. A high-resolution atlas of nucleosome occupancy in yeast. Nat. Genet. 2007;39:1235–1244. doi: 10.1038/ng2117. [DOI] [PubMed] [Google Scholar]
  12. Luger K, et al. Crystal structure of the nucleosome core particle at 2.8Å resolution. Nature. 1997;389:251–260. doi: 10.1038/38444. [DOI] [PubMed] [Google Scholar]
  13. Peckham HE, et al. Nucleosome positioning signals in genomic DNA. Genome Res. 2007;17:1170–1177. doi: 10.1101/gr.6101007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Rabiner LR. A tutorial on Hidden Markov Models and selected applications in speech recognition. Proc. IEEE. 1989;77:257–286. [Google Scholar]
  15. Routh A, et al. Nucleosome repeat length and linker histone stoichiometry determine chromatin fiber structure. Proc. Natl Acad. Sci. USA. 2008;105:8872–8877. doi: 10.1073/pnas.0802336105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Satchwell SC, et al. Sequence periodicities in chicken nucleosome core DNA. J. Mol. Biol. 1986;191:659–675. doi: 10.1016/0022-2836(86)90452-3. [DOI] [PubMed] [Google Scholar]
  17. Schalch T, et al. X-ray structure of a tetranucleosome and its implications for the chromatin fibre. Nature. 2005;436:138–141. doi: 10.1038/nature03686. [DOI] [PubMed] [Google Scholar]
  18. Segal E, et al. A genomic code for nucleosome positioning. Nature. 2006;442:772–778. doi: 10.1038/nature04979. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Valouev A, et al. A high resolution, nucleosome position map of c. elegans reveals a lack of universal sequence-dictated positioning. Genome Res. 2008;18:1051–1063. doi: 10.1101/gr.076463.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Wang J-P, et al. Preferentially quantized linker DNA lengths in Saccharomyces cerevisiae. PLoS Comput. Biol. 2008;4:e1000175. doi: 10.1371/journal.pcbi.1000175. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Widom J. A relationship between the helical twist of DNA and the ordered positioning of nucleosomes in all eukaryotic cells. Proc. Natl Acad. Sci. USA. 1992;89:1095–1099. doi: 10.1073/pnas.89.3.1095. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Widom J. Short-range order in two eukaryotic genomes: relation to chromosome structure. J. Mol. Biol. 1996;259:579–588. doi: 10.1006/jmbi.1996.0341. [DOI] [PubMed] [Google Scholar]
  23. Yuan GC, Liu JS. Genomic sequence is highly predictive of local nucleosome depletion. PLoS Comput. Biol. 2008;4:e13. doi: 10.1371/journal.pcbi.0040013. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES