A multivariate regression approach to association analysis of a quantitative trait network

Abstract

Motivation: Many complex disease syndromes such as asthma consist of a large number of highly related, rather than independent, clinical phenotypes, raising a new technical challenge in identifying genetic variations associated simultaneously with correlated traits. Although a causal genetic variation may influence a group of highly correlated traits jointly, most of the previous association analyses considered each phenotype separately, or combined results from a set of single-phenotype analyses.

Results: We propose a new statistical framework called graph-guided fused lasso to address this issue in a principled way. Our approach represents the dependency structure among the quantitative traits explicitly as a network, and leverages this trait network to encode structured regularizations in a multivariate regression model over the genotypes and traits, so that the genetic markers that jointly influence subgroups of highly correlated traits can be detected with high sensitivity and specificity. While most of the traditional methods examined each phenotype independently, our approach analyzes all of the traits jointly in a single statistical method to discover the genetic markers that perturb a subset of correlated triats jointly rather than a single trait. Using simulated datasets based on the HapMap consortium data and an asthma dataset, we compare the performance of our method with the single-marker analysis, and other sparse regression methods that do not use any structural information in the traits. Our results show that there is a significant advantage in detecting the true causal single nucleotide polymorphisms when we incorporate the correlation pattern in traits using our proposed methods.

Availability: Software for GFlasso is available at http://www.sailing.cs.cmu.edu/gflasso.html

Contact: sssykim@cs.cmu.edu; ksohn@cs.cmu.edu;

1 INTRODUCTION

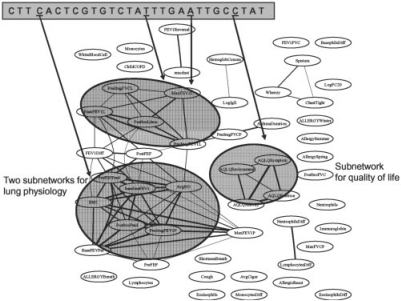
Recent advances in high-throughput genotyping technologies have significantly reduced the cost and time of genome-wide screening of individual genetic differences over millions of single nucleotide polymorphism (SNP) marker loci, shedding light to an era of ‘personalized genome’ (The International HapMap Consortium, 2005; Wellcome Trust Case Control Consortium, 2007). Accompanying this trend, clinical and molecular phenotypes are being measured at phenome and transcriptome scale over a wide spectrum of diseases in various patient populations and laboratory models, creating an imminent need for appropriate methodology to identify omic-wide association between genetic markers and complex traits which are implicative of causal relationships between them. Many statistical approaches have been proposed to address various challenges in identifying genetic locus associated with the phenotype from a large set of markers, with the primary focus on problems involving a univariate trait (Li et al., 2007; Malo et al., 2008). However, in modern studies the patient cohorts are routinely surveyed with a large number of traits (from measures of hundreds of clinical phenotypes to genome-wide profiling of thousands of gene expressions), many of which are correlated among them. For example, in Figure 1, the correlation structure of the 53 clinical traits in the asthma dataset collected as a part of the Severe Asthma Research Program (SARP) (Moore et al., 2007) is represented as a network, with each trait as a node, the interaction between two traits as an edge and the thickness of an edge representing the strength of correlation. Within this network, there exists several subnetworks involving a subset of traits, and furthermore, the large subnetwork on the left-hand side of Figure 1 contains two subgroups of densely connected traits with thick edges. In order to understand how genetic variations in asthma patients affect various asthma-related clinical traits in the presence of such a complex correlation pattern among phenotypes, it is necessary to consider all of the traits jointly and take into account their correlation structure in the association analysis. Although numerous research efforts have been devoted to studying the interaction patterns among many quantitative traits represented as networks (Friedman, 2004; Mehan et al., 2008) as well as discovering network submodules from such networks (Hu et al., 2005; Segal et al., 2003), this type of network structure has not been exploited in association mapping (Cheung et al., 2005; Stranger et al., 2005). Many of the previous approaches examined one phenotype at a time to localize the SNP markers with a significant association, and combined the results from a set of such single-phenotype association mapping across phenotypes. However, we conjecture that one can detect additional weak associations and at the same time reduce false signals by combining the information across multiple phenotypes under a single statistical framework.

Fig. 1.

Illustration of association analysis using phenotype correlation graph for asthma dataset.

In QTL mapping studies with pedigree data, a number of approaches have been proposed to detect pleiotropic effect of markers on multiple correlated traits by considering the traits jointly. However, these approaches involve only a weak and indirect form of structural information present in the phenotypes. The methods based on multivariate regression with multiple outcomes (Knott and Haley, 2000; Liu et al., 2007; Xu et al., 2005) were concerned with finding genetic loci that influence all of the phenotypes jointly, rather than explicitly taking into account the complex interaction patterns among the phenotypes. A different approach has been proposed that first applies a principal component analysis (PCA) to find the directions in which phenotypes are the most correlated, and then uses a multivariate regression on the projected phenotypes (Mangin et al., 1998; Weller et al., 1996). The transformation via PCA allows one to extract the components that explain the majority of variation in phenotypes, but has a limitation in that it is not obvious how to interpret the derived phenotypes.

More recently, in expression quantitative trait locus (eQTL) analysis which treats microarray gene expression measurements as quantitative traits, researchers have begun to combine an explicit representation of correlation structure in phenotypes, such as gene networks, with genotype information to search for genetic causes of perturbations of a subset of highly correlated phenotypes (Chen et al., 2008;; Emilsson et al., 2008; Lee et al., 2006; Zhu et al., 2008). A module network (Segal et al., 2003), which is a statistical model developed for uncovering regulatory modules from gene expression data, was extended to incorporate genotypes of regulators, such that the expression of genes regulated by the same regulator was explained by the variation of both the expression level and the genotype of the regulators (Lee et al., 2006). Although the model was able to identify previously unknown genetic perturbations in yeast regulatory network, the genotype information used in the model was limited to markers in regulators rather than the whole genome. Several other studies incorporated a gene co-regulation network in a genome-wide scan for association. In a network eQTL association study for mouse (Chen et al., 2008), a gene co-regulation network was learned, a clustering algorithm was applied to this network to identify subgroups of genes whose members participate in the same molecular pathway or biological process, and then, a single-phenotype analysis was performed between genotypes and the phenotypes within each subgroup. If the majority of phenotypes in each subgroup were mapped to the common locus in the genome, that locus was declared to be significantly associated with the subgroup. Using this approach, new obesity-related genes in mouse were identified by examining the network module associated with the genetic locus previously associated with obesity-related traits such as body mass index and cholesterol level. A similar analysis was performed on yeast, where clusters of yeast genes were mapped to a common eQTL hotspots (Zhu et al., 2008). One of the main disadvantages of this approach is that it first applies a clustering algorithm to identify subgroups of phenotypes in the network, rather than directly incorporating the network itself as a correlation structure, since the full network contains much richer information about complex interaction patterns than the clusters of phenotypes. Another disadvantage of this approach is that it relies on a set of single-phenotype statistical tests and combines the results afterwards in order to determine whether a marker is significantly affecting a subgroup of phenotypes, thus requiring a substantial effort in conducting appropriate multiple hypothesis testing. We believe that an approach that considers markers and all of the phenotypes jointly in a single statistical method has the potential to increase the power of detecting weak associations and reduce susceptibility to noise.

In this article, we propose a family of methods, called the graph-guided fused lasso (GFlasso), that fully incorporates the quantitative-trait network as an explicit representation for correlation structure without applying additional clustering algorithms to phenotypes. Our methods combine multiple phenotypes in a single statistical framework, and analyze them jointly to identify SNPs perturbing a subset of tightly correlated phenotypes instead of combining results from multiple single-phenotype analyses. The proposed methods leverage a dependency graph defined on multiple quantitative traits such as the graph for the asthma-related traits shown in Figure 1, assuming that such a graph structure is available from preprocessing steps or as prior knowledge from previous studies. It is reasonable to assume that when a subset of phenotypes are highly correlated, the densely connected subgraphs over these correlated traits contain variables that are more likely to be synergistically influenced by the same or heavily overlapping subset(s) of SNPs with similar strength than an arbitrary subset of phenotypes.

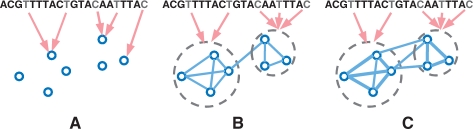
The proposed approach is based on a multivariate regression formalism with the L₁ penalty, commonly known as lasso, that achieves sparsity in the estimated model by setting many of the regression coefficients for irrelevant markers to 0 (Tibshirani, 1996). This property of lasso makes it a natural approach for genome-wide association analysis, where the marker genotypes are treated as the predictors, the phenotype in question is treated as the response, and the (sparse) set of markers having non-zero regression coefficients are interpreted as the markers truely associated with the phenotype. However, when applied to association mapping with multivariate traits, lasso is equivalent to a single-trait analysis that needs to be repeated over every single trait. In other words, for a collection of traits, each trait would be treated as independent of all other traits, and every trait would be regressed on a common set of marker genotypes via its own lasso (Fig. 2A), ignoring the possible coupling among traits. Our innovations in GFlasso that enable a departure from the baseline lasso for a single trait is that, in addition to the lasso penalty, we employ a ‘fusion penalty’ that fuses regression coefficients across correlated phenotypes, using either unweighted or weighted connectivity of the phenotype graph as a guide. This additional penalty will encourage sharing of common predictors (i.e. associated markers) to coupled responses (i.e. traits). The two fusion schemes lead to two variants of the GFlasso: a graph-constrained fused lasso (G_cFlasso) based on only the graph topology (Fig. 2B), and a graph-weighted fused lasso (G_wFlasso) that offers a flexible range of stringency of the graph constraints through edge weights (Fig. 2C). We developed an efficient algorithm based on quadratic programming for estimating the regression coefficients under GFlasso. The results on two datasets, one simulated from HapMap SNP markers and the other collected from asthma patients, show that our method outperforms competing algorithms in identifying markers that are associated with a correlated subset of phenotypes.

Fig. 2.

Illustrations for multiple output regression with (A) lasso; (B) GFlasso; and (C) G_wFlasso.

2 LASSO REGRESSION FOR MULTIPLE INDEPENDENT PHENOTYPES

Let X be an N × J matrix of genotypes for N individuals and J SNPs, where each element x_ij of X is assigned 0, 1 or 2 according to the number of minor alleles at the j-th locus of the i-th individual. Let Y denote an N × K matrix of K quantitative trait measurements over the same set of individuals. We use y_k to denote the k-th column of Y. A conventional single-trait association via linear regression model can be applied to this multiple-trait setting by fitting the model to X and each of the K traits y_k's separately:

(1)

where β_k is a J-vector of regression coefficients for the k-th trait that can be used in a statistical test to detect SNP markers with significant association, and ε_k is a vector of N independent error terms with mean 0 and a constant variance. We center each column of X and Y such that ∑_i y_ik = 0 and ∑_i x_ij = 0, and consider the model in Equation (1) without an intercept. We obtain the estimates of B = {β₁,…, β_K} by minimizing the residual sum of squares:

(2)

In a typical genome-wide association mapping, one examines a large number of marker loci with the goal of identifying the region associated with the phenotypes and markers in that region. A straight-forward application of the linear regression method in Equation (2) to association mapping with large J can cause several problems such as an unstable estimate of regression coefficients and a poor interpretability due to many irrelevant markers with non-zero regression coefficients. Sparse regression methods such as forward stepwise selection (Weisberg, 1980), ridge regression (Hoerl et al., 1975; Malo et al., 2008) and lasso (Tibshirani, 1996) that select a subset of markers with true association have been proposed to handle the situation with large J. Forward stepwise selection method iteratively selects one relevant marker at a time while trying to improve the model fit based on Equation (2), but it may not produce an optimal solution because of the greedy nature of the algorithm. Ridge regression has an advantage of performing the selection in a continuous space by penalizing the residual sum of square in Equation (2) with the L₂ norm of β_k's and shrinking the regression coefficients toward 0, but it does not set the regression coefficients of irrelevant markers to exactly 0. We use lasso that penalizes the residual sum of square with the L₁ norm of regression coefficients and has the property of setting regression coefficients with weak association markers exactly to 0, thus offering the advantages of both forward stepwise selection and ridge regression. The lasso estimate of the regression coefficients can be obtained by solving the following:

(3)

where λ is a regularization parameter that controls the amount of sparsity in the estimated regression coefficients. Setting λ to a large value increases the amount of penalization, setting more regression coefficients to 0. Many fast algorithms are available for solving Equation (3) (Efron et al., 2004; Tibshirani, 1996).

Lasso for multiple-trait association mapping in Equation (3) is equivalent to solving a set of K independent regressions for each trait with its own L₁ penalty, and does not provide a mechanism to combine information across multiple traits such that the estimates reflect the potential relatedness in the regression coefficients for those correlated traits that are influenced by common SNPs. However, several traits are often highly correlated such as in gene expression of co-regulated genes in eQTL study, and there might be genotype markers that are jointly associated with those correlated traits. Below, we extend the standard lasso and propose a new penalized regression method for detecting markers with pleiotropic effect on correlated quantitative traits.

3 GFLASSO FOR MULTIPLE CORRELATED PHENOTYPES

In order to identify markers that are predictive of multiple phenotypes jointly, we represent the correlation structure over the set of K traits as an edge-weighted graph, and use this graph to guide the estimation process of the regression coefficients within the lasso framework. We assume that we have available from a preprocessing step a phenotype correlation graph G consisting of a set of nodes V, each representing one of the K traits and a set of edges E. In this article, we adopt a simple and commonly used approach for learning such graphs, where we first compute pairwise Pearson correlation coefficients for all pairs of phenotypes using y_k's, and then connect two nodes with an edge if their correlation coefficient is above the given threshold ρ. We set the weight of each edge (m, l) ∈ E to the absolute value of correlation coefficient |r_m,l|, so that the edge weight represents the strength of correlation between the two nodes. This thresholded correlation graph is also known as a relevance network, and has been widely used as a representation of gene interaction networks (Butte et al., 2000; Carter et al., 2004). It is worth pointing out that the choice of methods for obtaining the phenotype network is not a central issue of our method. Other variations of the standard relevance network have been suggested (Zhang and Horvath, 2005), and any of these graphs can also be used within our proposed regression methods. Below, we first introduce G_cFlasso that makes use of unweighted graph, and further extend this method to G_wFlasso to take into account the full information in the graph including edge weights.

Given the correlation graph of phenotypes, it is reasonable to assume that if two traits are highly correlated and connected with an edge in the graph, their variation across individuals might be explained by genetic variations at the same loci, possibly having the same amount of influence on each trait. In G_cFlasso, this assumption is expressed as an additional penalty term that fuses two regression coefficients β_jm and β_jl for each marker j if traits m and l are connected with an edge in the graph, as follows:

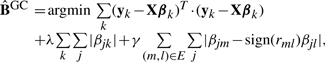(4)

where λ and γ are regularization parameters that determine the amount of penalization. The last term in Equation (4) is called a fusion penalty (Tibshirani et al., 2005), and encourages β_jm and sign(r_m,l)β_jl to take the same value by shrinking the difference between them toward 0. A larger value for γ leads to a greater fusion effect, or greater sparsity in |β_jm − sign(r_m,l)β_jl|'s. We assume that if two traits m and l connected with an edge in G are negatively correlated with r_ml < 0, the effect of a common marker on those traits takes an opposite direction and we fuse β_jm and (−β_jl), or equivalently, β_jm and sign(r_m,l)β_jl. When the fusion penalty is combined with the lasso penalty as in Equation (4), the lasso penalty sets many of the regression coefficients to 0 and for the remaining non-zero regression coefficients, the fusion penalty flattens the values across multiple highly correlated phenotypes for each marker so that the strength of influence of each marker becomes similar across those correlated traits. The idea of fusion penalty has been first used in the classical regression problem over univariate response (i.e. single output) from high-dimensional covariates to fuse the regression coefficients of two adjacent covariates when the covariates are assumed to be ordered such as in time (Tibshirani et al., 2005). This corresponds to coupling pairs of elements in the adjacent rows of the same column in the coefficient matrix B in Equation (4). In G_cFlasso, we employ a similar strategy in a multiple-output regression in order to identify pleiotropic effect of markers, and let the trait correlation graph determine which pairs of regression coefficients should be fused. Now, every such coupled coefficient pair corresponds to the elements of the corresponding two columns in the same row of matrix B in Equation (4).

In a multiple-trait association mapping, networks of clinical traits or molecular traits (i.e. gene expressions) typically contain many subnetworks within which nodes are densely connected and we are interested in finding the genetic variants that perturb the entire set of traits in each subnetwork. This can potentially increase the power of detecting weak associations between genotype and phenotype that may be missed when each phenotype is considered independently. When used in this setting, G_cFlasso looks for associations between a genetic marker and a subgraph of phenotype network rather than a single phenotype. Unlike other previous approaches for detecting pleiotropic effect that first apply clustering algorithms to learn subgroups of traits and then search for genetic variations that perturb the subgroup, G_cFlasso uses the full information on correlation structure in phenotypes available as a graph, where the subgroup information is embedded implicitly within the graph as densely connected subgraphs. Although the fusion penalty in G_cFlasso is applied locally to a pair of regression coefficients for neighboring trait pairs in the graph, this fusion effect propagates to the regression coefficients for other traits that are connected to them in the graph. For densely connected nodes, the fusion is effectively applied to all of the members of the subgroup, and the set of non-zero regression coefficients tend to show a block structure with the same values across the correlated traits given a genotype marker with pleiotropic effect on those traits, as we demonstrate in experiments. If the edge connections are sparse within a group of nodes, the corresponding traits are only weakly related and there is little propagation of fusion effect through edges in the subgroup. Thus, G_cFlasso incorporates the subgrouping information through the trait correlation graph in a more flexible manner compared to previous approaches.

Now, we present a further generalization of G_cFlasso that exploit the full information in the phenotype networks for association mapping. Note that the only structural information used in G_cFlasso is the presence or absence of edges between two phenotypes in the graph. G_wFlasso is a natural extension of G_cFlasso that takes into account the edge weights in graph G in addition to the graph topology. G_wFlasso weights each term in the fusion penalty in Equation (4) by the amount of correlation between the two phenotypes being fused, so that the amount of correlation controls the amount of fusion. More generally, G_wFlasso weights each term in the fusion constraint in Equation (4) with a monotonicaly increasing function of the absolute values of correlations, and finds an estimate of the regression coefficients as follows:

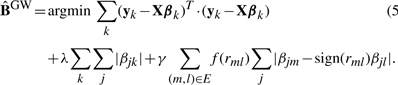(5)

If the two phenotypes m and l are highly correlated in graph G with a relatively large edge weight, the fusing effect increases between these two phenotypes since the difference between the two corresponding regression coefficients β_jm and β_jl is penalized more than for other pairs of phenotypes with weaker correlation. In this article, we consider f₁(r) = |r| for G¹_wFlasso and f₂(r) = r² for G²_wFlasso. We note that the G_cFlasso is a special case of G_wFlasso with f(r) = 1.

The optimization problems in Equations (4) and (5) can be formulated as a quadratic programming as described in Appendix A, and there are many publicly available software packages that efficiently solve such quadratic programming problems. The regularization parameters λ and γ can be determined by a cross-validation or a validation set.

4 RESULTS

We compare the results from our proposed methods, G_cFlasso, G¹_wFlasso and G²_wFlasso, with the ones from the single-marker analysis as well as multivariate regression methods such as ridge regression and lasso that do not use any structural information in the phenotypes. For ridge regression, lasso and our methods, we selected the regularization parameters using a validation set. We used [−log(P-value)] for the standard single-marker analysis, and the absolute value of regression coefficients |β_jk|'s for the multivariate regression methods and our proposed methods, as a measure of the strength of association. We also compared our methods with reduced-rank regression, which is a multivariate-output approach that first applies CCA to find canonical variables before applying multivariate regression.

4.1 Simulation study

We simulated genotype data for 250 individuals based on the HapMap data in the region of 8.79–9.20 M in chromosome 7. The first 60 individuals of the genotype data came from the parents of the HapMap CEU panel. We generated genotypes for additional 190 individuals by randomly mating the original 60 individuals on the CEU panel. We included only those SNPs with minor allele frequency >0.1. Since our primary goal is to measure the performance of the association methods in the case of multiple correlated phenotypes, we sampled 50 SNPs randomly from the 697 SNPs in the region in order to reduce the correlation among SNPs from the linkage disequilibrium.

Given the simulated genotype, we generated the true associations represented as regression coefficients B and phenotype data as follows. We assumed that the number of phenotypes is 10, and that there are three groups of correlated phenotypes of size 3, 3 and 4, respectively, so that the phenotypes in each group form a subnetwork in the correlation graph of phenotypes. For simplicity, we assumed that there were no environmental factors or other genetic effects, and that all of the covariance components in the traits came from the relevant SNPs in the given set of SNPs. We randomly selected three SNPs as affecting all of the phenotypes in the first subnetwork, and four SNPs as influencing each of the remaining two subnetwork. We assumed that there is one additional SNP affecting phenotypes in the first two subnetworks, which corresponds to the case of a SNP perturbing a super network consisting of two subnetworks such as the large subnetwork on the left-hand side of Figure 1. In addition, we assumed one additional SNP affecting all of the phenotypes. We set the effect size of all of the true association SNPs to the same value. Once we set the regression coefficients, we generated the phenotype data with noise distributed as N(0, 1), using the simulated genotypes as covariates.

We evaluate the performance of the association methods based on two criteria, sensitivity/specificity and phenotype prediction error. The sensitivity and specificity measure whether the given method can successfully detect the true association SNPs with few false positives. The (1-specificity) and sensitivity are equivalent to type I error rate and (1-type II error rate), and their plot is widely known as a receiver operating characteristic (ROC) curve. The phenotype prediction error represents how accurately we can predict the values of phenotypes given the genotypes of new individuals, using the regression coefficients estimated from the previously available genotype and phenotype data. We generate additional dataset of 50 individuals, y^new and X^new, and compute the phenotype prediction error as sum of squared differences between the true values y^new and predicted values ŷ^new of the phenotypes, ∑_k (y_k^new − ŷ^new)′ · (y_k^new − ŷ^new), where 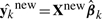.For both criteria for measuring performance, we show results averaged over 50 randomly generated datasets.

In the results shown below, for each dataset of size N, we fit lasso and the graph-guided methods using (N − 30) samples, and use the remaining 30 samples as a validation set for determining the regularization parameters. Once we determine the regularization parameters, we use the entire dataset of size N to estimate the final regression coefficients given the selected regularization parameters.

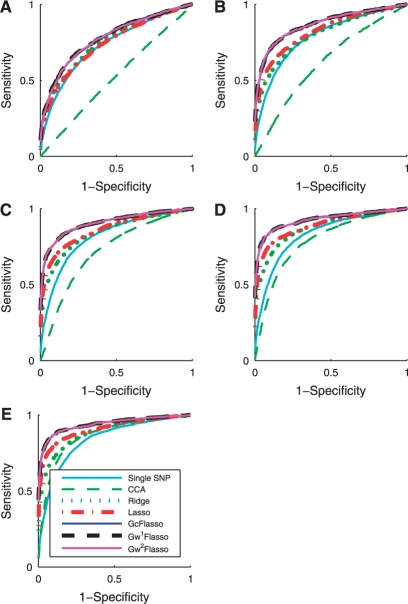
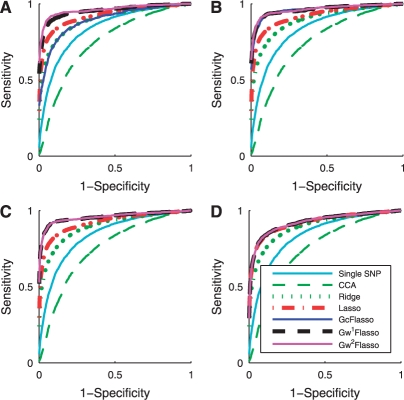
We apply the various association methods to datasets with varying sample sizes, and show the ROC curves in Figure 3. We used the threshold ρ = 0.3 to obtain the phenotype correlation graph and set the effect size to 0.5. The results confirm that lasso is an effective method for detecting true causal SNPs and is affected less by the irrelevant SNPs, compared to the single-marker analysis, ridge regression and CCA-based regression. When we use the weighted fusion penalty in addition to the lasso penalty as in G_cFlasso, G¹_wFlasso and G²_wFlasso, the performance significantly improves over lasso across all of the samples sizes shown in Figure 3.

Fig. 3.

ROC curves for comparison of association analysis methods with different sample size N. (A) N = 50; (B) N = 100; (C) N = 150; (D) N = 200; and (E) N = 250. The effect size is 0.5, and the threshold ρ for the phenotype network is set to 0.3. Note that the curves for G_cFlasso, G¹_wFlasso and G²_wFlasso almost entirely overlap.

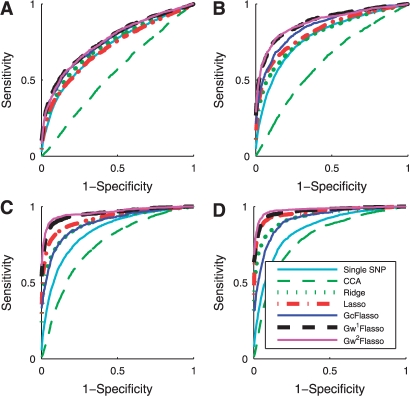
In order to see how the effect size affects the performance of the methods for association analysis, we vary the effect size and show the ROC curves in Figure 4, for the threshold ρ = 0.1 of the phenotype correlation network and sample size N = 100. G¹_wFlasso and G²_wFlasso outperform all of the other methods across all of the effect sizes. Because of the relatively low value of the threshold ρ = 0.1, the correlation phenotype contains many edges between a pair of phenotypes that are only weakly correlated. Thus, G_cFlasso that does not distinguish edges for strong correlation from those for weak correlation does not show a consistent performance across different effect size, performing better than lasso at effect size 0.3 but worse than lasso at effect size 1.0. G¹_wFlasso and G²_wFlasso have the flexibility to handle different strengths of correlation in the graph, and consistently outperforms G_cFlasso as well as the methods that do not consider the structural information in the phenotypes.

Fig. 4.

ROC curves for comparison of association analysis methods with varying effect size. Effect size is (A) 0.3; (B) 0.5; (C) 0.8; and (D) 1.0. The sample size is 100, and the threshold ρ for the phenotype correlation graph is 0.1.

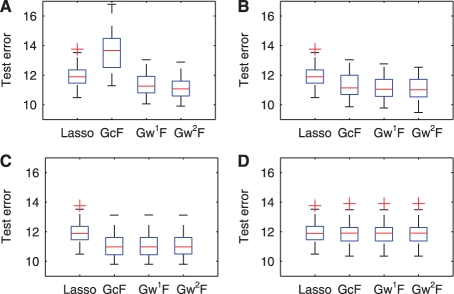
In order to examine the effect of the threshold ρ for the phenotype correlation graph on the performance of our methods, we evaluate the GFlasso methods with ρ at 0.1, 0.3, 0.5 and 0.7, and show the ROC curves in Figure 5. We include the ROC curves for the single-marker analysis, the ridge regression, lasso and the CCA-based method that do not use the thresholded phenotype correlation graph in each panel of Figure 5 repeatedly for the ease of comparison. We use the sample size N = 100 and the effect size 0.8. Regardless of the threshold ρ, G¹_wFlasso and G²_wFlasso outperform all of the other methods or perform at least as well as lasso. As we have seen in Figure 4, G_cFlasso does not have the flexibility of accommodating edges of varying correlation strength in the phenotype correlation graph, and this negatively affects the performance of G_cFlasso at the low threshold ρ = 0.1 in Figure 5A. As we increase the threshold ρ_k in Figure 5B and C, the phenotype correlation graph include only those edges with significant correlations. Thus, the performance of G_cFlasso approaches that of G¹_wFlasso and G²_wFlasso, and the curves of the three methods in the GFlasso family almost entirely overlap. When the threshold is relatively high at ρ = 0.7, the number of edges in the graph is close to 0, effectively removing the fusion penalty. As a result, the performance of the graph-guided methods becomes close to lasso. Overall, taking into account the correlation structure in phenotypes improves the detection rate of true causal SNPs. Once the phenotype correlation graph includes the edges that capture strong correlations, including more edges by further lowering the threshold ρ does not significantly affect the performance of G¹_wFlasso and G²_wFlasso. The same tendency is shown in the prediction errors in Figure 6.

Fig. 5.

ROC curves for comparison of association analysis methods with different values of threshold (ρ) for the phenotype correlation network. (A) ρ = 0.1; (B) ρ = 0.3; (C) ρ = 0.5; and (D) ρ = 0.7. The sample size is 100, and the effect size is 0.8.

Fig. 6.

Comparison of association analysis methods in terms of phenotype prediction error. The threshold ρ for the phenotype correlation network is (A) ρ = 0.1; (B) ρ = 0.3; (C) ρ = 0.5; and (D) ρ = 0.7.

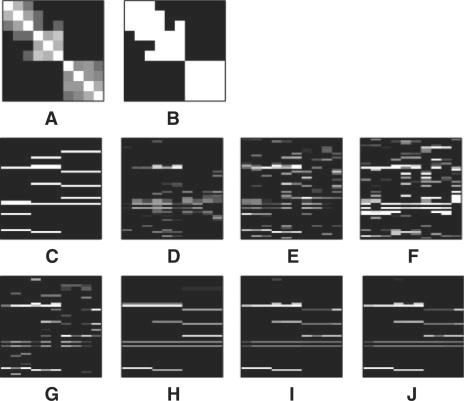
We show an example of a simulated dataset and the estimated association strength in Figure 7, using the sample size N = 100 and effect size 0.8. Although lasso is more successful in setting the regression coefficients of irrelevant SNPs to 0 than the ridge regression and the CCA-based method, it still finds many SNPs as having a non-zero association strength. G_cFlasso, G¹_wFlasso and G²_wFlasso remove most of those spurious SNPs, and shows a clear block structure in the estimated regression coefficients, with each causal SNP spanning subgroups of correlated phenotypes. Since G_cFlasso uses only the information on the presence or absence of edges, when edges of weak correlation connect nodes across two true subgraphs, G_cFlasso is unable to ignore the weak edges and fuses the effect of SNPs on the phenotypes across those two subgraphs. This undesirable property of G_cFlasso disappears when we incorporate the edge weights in G¹_wFlasso and G²_wFlasso.

Fig. 7.

Results of association analysis by different methods based on a single simulated dataset. Effect size 0.8 and threshold ρ = 0.3 for the phenotype correlation graph are used. Bright pixels indicate large values. (A) The correlation coefficient matrix of phenotypes; (B) the edges of the phenotype correlation graph obtained at threshold 0.3 are shown as white pixels; (C) The true regression coefficients used in simulation. Rows correspond to SNPs and columns to phenotypes; (D) −log(P-value). Absolute values of the estimated regression coefficients are shown for ((E) ridge regression; (F) CCA; (G) lasso; (H) G_cFlasso; (I) G¹_wFlasso; and (J) G²_wFlasso.

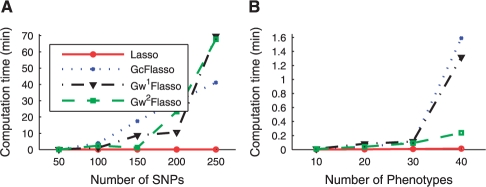
We show the computation time for solving a single optimization problem for lasso, G_cFlasso and G_wFlasso in Figure 8 for varying number of SNPs and phenotypes.

Fig. 8.

Comparison of the computation time for lasso, G_cFlasso, G¹_wFlasso and G²_wFlasso. (A) Varying the number of SNPs with the number of phenotypes fixed at 10. The phenotype correlation graph at threshold ρ = 0.3 with 31 edges is used. (B) Varying the number of phenotypes with the number of SNPs fixed at 50. The phenotype networks are obtained using threshold ρ = 0.3. The number of edges in each phenotype network is 11, 34, 53, 88 and 142 for the number of phenotypes 10, 20, 30, 40 and 50, respectively.

4.2 Case study using asthma dataset

We apply our methods to data collected from 543 asthma patients as a part of the Severe Asthma Research Program (SARP). The genotype data were obtained for 34 SNPs within or near IL-4R gene that spans a 40 kb region on chromosome 16. This gene has been previously shown to be implicated in severe asthma (Wenzel et al., 2007). We used the publicly available software PHASE (Li and Stephens, 2003) to impute missing alleles and phase the genotypes. The phenotype data included 53 clinical traits related to severe asthma such as age of onset, family history and severity of various symptoms. The phenotype correlation graph thresholded at 0.7 as shown in Figure 1 reveals several subnetworks of correlated traits. Our goal is to examine whether any of the SNPs in the IL-4R gene are associated with a subnetwork of correlated traits rather than an individual trait. We standardized measurements for each phenotype to have mean 0 and SD 1 so that their values are roughly in the same range across phenotypes.

Figure 9A shows the correlation matrix of the phenotypes after reordering the phenotypes using the agglomerative hierarchical clustering algorithm so that highly correlated phenotypes are clustered with a block structure along the diagonal. Using threshold ρ = 0.7, we obtain a phenotype correlation graph as shown in Figure 9B, where the white pixel at position (i, j) indicates that the i-th and j-th phenotypes are connected with an edge in the graph. The graph shows several blocks of white pixels representing densely connected subgraphs. We show the full graph in Figure 1. We present results for the single-marker regression analysis, ridge regression, lasso, G_cFlasso, G¹_wFlasso and G²_wFlasso in Figure 9C–H, respectively, where the rows represent phenotypes, and the columns correspond to genotypes, with bright pixels indicating high strength of association. The phenotypes in rows are rearranged according to the ordering given by the agglomerative hierarchical clustering so that each row in Figure 9C–H is aligned with the phenotypes in the correlation matrix in Figure 9A. In the fusion penalty in our proposed methods, we use the edges in Figure 9B obtained at threshold ρ = 0.7. The graph obtained at threshold ρ = 0.7 seems to capture the previously known dependencies among the clinical traits such as subnetworks corresponding to lung physiology and quality of life. We select the regularization parameters in lasso, G_cFlasso, G¹_wFlasso and G²_wFlasso using a 5-fold cross validation.

Fig. 9.

Results for the association analysis of the asthma dataset. (A) Phenotype correlation matrix. (B) Phenotype correlation matrix thresholded at ρ = 0.7. (C) −log(P-value) from single-marker statistical tests using a single-phenotype analysis. Estimated β_k's for (D) ridge regression; (E) lasso; (F) G_cFlasso; (G) G¹_wFlasso; and (H) G²_wFlasso.

As shown in Figures 9C and E, both the single-marker regression analysis and lasso find a SNP near the top row, known as Q551R, as significantly associated with a block of correlated phenotypes. This subset of traits corresponds to the bottom subnetwork (consisting of baselineFEV1, PreFEFPred, AvgNO, BMI, PostbroPred, BaseFEVPer, PredrugFEV1P, MaxFEV1P, FEV1Diff and PostFEF) that resides within the large subnetwork on the left-hand side of Figure 1, and represents traits related to lung physiology. This Q551R SNP has been previously found associated with severe asthma and its traits for lung physiology (Wenzel et al., 2007), and our results confirm this previous finding. In addition, the results from the single-marker analysis in Figure 9C show that on the downstream of this SNP, there is a set of adjacent SNPs that appears to be in linkage disequilibrium with this SNP and at the same time has generally a high level of association with the same subset of phenotypes. On the other hand, lasso in Figure 9E sets most of the regression coefficients for this block of SNPs in linkage disequilibrium with Q551R to 0, identifying a single SNP as significant. This confirms that lasso is an effective method for finding sparse estimates of the regression coefficients, ignoring most of the irrelevant markers by setting corresponding regression coefficients to 0. The ridge regression as shown in Figure 9D does not have the same property of encouraging sparsity as lasso. In fact, in statistical literature, it is well-known that the ridge regression performs poorly in problems that require a selection of a small number of markers affecting phenotypes.

Since our methods in the GFlasso family include the lasso penalty, the results from G_cFlasso, G¹_wFlasso and G²_wFlasso show the same property of sparsity as lasso in their estimates, as can be seen in Figure 9F–H. In addition, because of the fusion penalty, the regression coefficients estimated by our methods form a block structure, where the regression coefficients for each SNP are set to the same value within each block. Thus, each horizontal bar indicates a SNP influencing a correlated block of phenotypes. It is clear that the horizontal bars in Figure 9F–H are generally aligned with the blocks of highly correlated phenotypes in Figure 9A. This block structure is much weaker in the results from lasso in Figure 9E. For example, Figure 9F–H show that the SNPs rs3024660 and rs3024622 on the downstream of Q551R are associated with the same block of traits as Q551R, generating an interesting new hypothesis that these two SNPs as well as Q551R might be jointly associated with the same subset of clinical traits. These two SNPs were only in a weak linkage disequilibrium with SNP Q551R (r² = 0.48 and 0.012, respectively). This block structure shared by the two SNPs is not obvious in the results of single-marker tests and lasso.

We fit lasso and our methods in the GFlasso family, while varying the threshold for the correlation graph, and summarize the results in Table 1. When the threshold is high at ρ = 0.9, only a very small number of edges are included in the phenotype correlation graph and the contribution of the graph-guided fusion penalty in GFlasso is low. Thus, the number of non-zero regression coefficients found by G_cFlasso, G¹_wFlasso and G²_wFlasso is similar to the result of lasso that does not have the fusion penalty. When we lower the threshold to ρ = 0.7, the number of non-zero regression coefficients decreases significantly for our methods. As can be seen in Figure 9B, most of the significant correlation structure is captured in the thresholded correlation graph at ρ = 0.7. Thus, as we further lower the threshold, the number of non-zero regression coefficients generally remains unchanged.

Table 1.

Summary of results for the association analysis of the asthma dataset

ρ	Number of edges	Number of non-zero βjm's
		Lasso	GcFlasso	G1wFlasso	G2wFlasso
0.3	421	125	105	106	108
0.5	165	125	108	107	107
0.7	71	125	105	105	110
0.9	11	125	125	123	123

5 DISCUSSION

In this article, we proposed a new family of regression methods called GFlasso that directly incorporates the correlation structure represented as a graph and uses this information to guide the estimation process. Often, we are interested in detecting genetic variations that perturb a sub-module of phenotypes rather than a single phenotype, and GFlasso achieves this through fusion penalty in addition to the lasso penalty that encourages parsimony in the estimated model. Using simulated and asthma datasets, we demonstrated that including richer information on phenotype structure as in G_wFlasso and G_cFlasso improves the accuracy in detecting true associations.

One of the possible directions for future research is to explore the use of more sophisticated graph-learning algorithms such as graphical Gaussian models within the GFlasso framework instead of simply using a thresholded correlation graph. Another possible extension is to learn the graph structure and the regression coefficients jointly by combining GFlasso with graphical lasso (Friedman et al., 2008) that learns sparse covariance matrix for phenotypes. Also, in this work, we considered only continuous-valued traits, but the method can be extended to include logistic regression for discrete-valued traits. Scalability of the method to a large dataset is another important issue that needs to be addressed in the future research. Since the problem is formulated as a convex optimization, we can directly benefit from advances in convex optimization research to speed up the process of parameter estimation. Finally, in addition to the structural information in the phenome, we would like to incorporate the structure in the genome such as linkage disequilibrium structure in order to identify a block of correlated markers influencing a set of correlated phenotypes.

APPENDIX A

A1. PARAMETER ESTIMATION

In this section, we describe the procedure for obtaining estimates of the regression coefficients in G_wFlasso. Since G_cFlasso is a special case of G_wFlasso with f(r) = 1, the same procedure can be applied to G_cFlasso in a straight-forward manner. The optimization problem in Equation (5) is the Lagrangian form of the following optimization problem:

(6)

where s₁ and s₂ are tuning parameters corresponding to λ and γ in Equation (5).

Since the objective function and constraints in Equation (6) are convex, we can formulate this problem as a quadratic programming (QP) as follows. Let β_c denote a (J · K)-vector that can be obtained by concatenating β_k's such that β_c = (β₁^T,…, β_K^T)^T. We represent β_jk = β_jk⁺ − β_jk⁻, where β_jk⁺ ≥ 0 and β_jk⁻ ≥ 0, and let β_c⁺ and β_c⁻ denote (J · K)-vectors of β_jk⁺'s and β_jk⁻'s, respectively. We define θ_j,(m,l) = β_j,m − sign(r_ml)β_j,l for all (m, l) ∈ E and j = 1,…, J, and let θ_j,(m,l) = θ_j,(m,l)⁺ − θ_j,(m,l)⁻ with θ_j,(m,l)⁺ ≥ 0 and θ_j,(m,l)⁻ ≥ 0. Let θ_c = (θ₁^T,…, θ_|E|^T)^T, where θ_e = (θ_1,e,…, θ_J,e)^T for e = (m, l) ∈ E. We define θ_c⁺ and θ_c⁻ similarly. Let M be a (J · |E|) × (J · K) matrix, or equivalently a |E| × K matrix of J × J sub-matrices. Each sub-matrix B_e,k of M for e = 1,…, |E| and k = 1,…, K is an identity matrix if e = (m, l) and k = m. If e = (m, l) and k = l, B_e,k is set to a diagonal matrix with -1 along the diagonal. Otherwise, B_e,k is set to a matrix of 0's. Let R be a (J · |E|)-vector of |E| sub-vectors with length J. Each sub-vector in R is set to f(r_m,l) · 1_J, where 1_J represents a J-vector of 1's. Then, the QP problem for Equation (6) can be written as

subject to

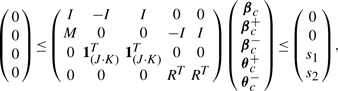where I is a (J · K) × (J · K) identity matrix, and 1_(J·K) is a (J · K)-vector of 1's.