Abstract
Motivation: Personalized medicine based on molecular aspects of diseases, such as gene expression profiling, has become increasingly popular. However, one faces multiple challenges when analyzing clinical gene expression data; most of the well-known theoretical issues such as high dimension of feature spaces versus few examples, noise and missing data apply. Special care is needed when designing classification procedures that support personalized diagnosis and choice of treatment. Here, we particularly focus on classification of interferon-β (IFNβ) treatment response in Multiple Sclerosis (MS) patients which has attracted substantial attention in the recent past. Half of the patients remain unaffected by IFNβ treatment, which is still the standard. For them the treatment should be timely ceased to mitigate the side effects.
Results: We propose constrained estimation of mixtures of hidden Markov models as a methodology to classify patient response to IFNβ treatment. The advantages of our approach are that it takes the temporal nature of the data into account and its robustness with respect to noise, missing data and mislabeled samples. Moreover, mixture estimation enables to explore the presence of response sub-groups of patients on the transcriptional level. We clearly outperformed all prior approaches in terms of prediction accuracy, raising it, for the first time, >90%. Additionally, we were able to identify potentially mislabeled samples and to sub-divide the good responders into two sub-groups that exhibited different transcriptional response programs. This is supported by recent findings on MS pathology and therefore may raise interesting clinical follow-up questions.
Availability: The method is implemented in the GQL framework and is available at http://www.ghmm.org/gql. Datasets are available at http://www.cin.ufpe.br/∼igcf/MSConst
Contact: igcf@cin.ufpe.br
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
The use of gene expression profiling allows clinical diagnosis to be made on a molecular level, thereby substantially increasing diagnosis accuracy and facilitating choice of treatment based on the patients' genetic traits, which decisively supports the desirable idea of personalized medicine (Spang, 2003). Moreover, identifying disease-related genes and monitoring their activity levels provide insights into disease mechanisms. A prominent example is cancer where gene expression profiling was successfully used to distinguish between tumor and healthy cells with high accuracy and, in addition to that, has led to the discovery of new cancer sub-types and paved the way to personalized medicine (van't Veer and Bernards, 2008).
Such clinical data usually have very peculiar characteristics; while there are only few samples (patients) there are many features (genes) (Kaminski and Bar-Joseph, 2007; Lottaz et al., 2008). Gene expression data of all kinds is notoriously noisy and missing data is a particularly relevant issue in clinical time-series experiments, since patients can miss single experiments for a variety of reasons (Irizarry et al., 2005). Last but not least, individual patient variability is also an issue (Irizarry et al., 2005). Overall, such clinical classification tasks can be considered to be among the hardest; most of the well-known theoretical issues such as high-dimensional feature spaces, few examples, noise and missing data apply [Kaminski and Bar-Joseph, 2007; Lottaz et al., 2008; see Hastie et al. (2001) for a general treatment]. As a consequence, they require the careful development of suitable classification methods that have to refer to the experimental design of the clinical studies in order to make reliable and sound predictions.
Here, we investigate the problem of classification of Multiple Sclerosis (MS) patients with respect to their response to interferon-β (IFNβ) treatment based on their gene expression profiles alone. IFNβ can still be considered to be the standard treatment in MS. Of the treated patients, ∼50% experience a reduced number of relapses as well as no further increase in the disability status scale. However, the other half of the patients do not seem to be positively affected by IFNβ treatment. For these bad responders, treatment should be ceased to mitigate side effects (Ro et al., 2002). To classify and further explore clinical differences between the groups of good and bad responders, Baranzini et al. (2005) followed 52 patients for 2 years after initiation of IFNβ therapy. Every 3 months expression profiles of 70 genes were measured using one-step kinetic reverse-transcription PCR. Patients were divided into good and bad responders based on clinical criteria such as relapse rate and disability status. They demonstrated that the patients' response could be predicted by studying gene expression profiles of the first-time point after treatment alone (Baranzini et al., 2005).
Since then, two supervised learning methods have been applied to the very same dataset. Borgwardt et al. (2006) used support vector machines, based on dynamic systems kernels. Lin et al. (2008) based their classifier on hidden Markov models (HMM) using discriminative learning. Both of these methods profited from exploring the temporal aspects of the data. For example, a main contribution of the HMM based method proposed by Lin et al. (2008) was to show that patients have specific treatment response rates; the HMMs have the power to reveal these rates automatically, which in turn helps to reveal the features (genes) that differ between good and bad responders. These studies have improved the classification accuracy over the ones reported by Baranzini et al. (2005), setting the current standard of ∼88% prediction accuracy. Lin et al. (2008) also pointed out some possible methodological flaws in the classification setup of Baranzini et al. (2005), which resulted in overly optimistic prediction accuracy values in the original paper. Clearly, in a clinical diagnosis problem, every percentage point, reflecting correct classification of at least one more patient, counts.
1.1 Our contributions
We propose a constrained mixture estimation method for time-series data in order to reliably predict good and bad response to a particular treatment. As a result, we obtain a prediction accuracy of exceeding 90% in IFNβ treatment response classification, which is a substantial improvement over the previous approaches.
The idea behind clustering with constraints, which is a semi-supervised learning method (Castelli and Cover, 1994; Chapelle et al., 2006), is to use pair-wise constraints between patients in order to restrict or penalize particular solutions. In the traditional approach, these constraints can be of two types: positive constraints, which indicate that two patients should be in the same group; and negative constraints, which indicate that two patients should be put into separate groups. In general, the constraints are soft, which means that they may be violated at a certain penalty to the objective function.
Our choice of method is motivated by two particular aspects inherent to datasets from patient expression profiles. First, in diseases with multiple molecular causes, such as MS, there could be more than one expression signature related to a response type of the patient (van Baarsen et al., 2006). Second, we also assume that some patients can have a wrong label (Ro et al., 2002), or simply that their expression signature does not match the ones of patients with similar treatment response. A classification method for clinical purposes should indicate such patients and these samples should not affect the estimation of the parameters needed for the predictions.
Here, we integrate the constrained clustering method, which was proposed by Lange et al. (2005) and Lu and Leen (2005) into a mixture estimation classification framework, where mixture components are linear HMMs (Lin et al., 2008; Schliep et al., 2003, 2004, 2005). This is done by inferring negative constraints from the labels of the patients and subsequent estimation of mixtures consisting of two or more HMM mixture components. By using only negative constraints, the estimation method penalizes solutions in which patients of distinct classes are assigned to the same model, but it allows patients from a particular responder class to be assigned to more than one model. Therefore, we can go beyond performing binary classification and investigate the presence of sub-classes among the bad or good responders (Fig. 1). Also, the constraint-based framework allows potentially mislabeled patients to be assigned to virtually wrong classes, which mitigates their misleading effects on the estimated parameters. Theoretically, the idea of using constrained mixture estimation for classification is novel. Beyond the general advantages of mixture estimation such as robustness and soft assignment of data points to classes, it allows to subdivide classes, which is of particular interest here.
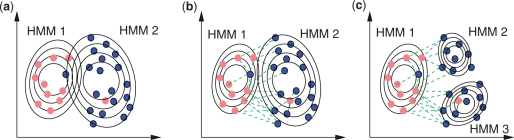
Fig. 1.
Schematic example of the classification problem in a 2D space in the presence of mislabeled examples and unknown sub-classes. Dark blue dots correspond to good responders and light red dots to bad responders. With a supervised training of a classifier with two HMMs (a), the mislabeled examples are mistakenly assigned to the class indicated by the wrong label which leads to higher SD in the respective model parameters, thereby weakening the predictive power of the model. Our approach, which uses the negative constraints (dashed lines) to guide the training (b), allows the mislabeled patients to be assigned to the closest HMM, if the assignment improves the overall model likelihood, leading to more discriminative parameters. In other words, the soft negative constraints resulting from wrongly labeled patients are overruled if this leads to improved overall model likelihood. Exploring the existence of sub-classes, as in the case of three HMMs depicted in (c), can further improve class discrimination.
Furthermore, we have put special emphasis on appropriately handling missing data and noise by extending the linear HMM models used by Lin et al. (2008) to have mixtures of multivariate Gaussians as state emission probability density functions (pdfs). This appropriately accounts for the fact that Gaussian densities have small tails. As a consequence, adding noise to single values can easily break the mixture estimation (MacLachlan and Peel, 2000). Our solution was to add a noise component to the emission pdfs, as suggested by Fraley and Raftery (1998). The noise component is also a Gaussian with mean equal to that of the whole dataset and with a high variance.
Last but not least, we have developed a novel feature selection criterion that is suitable for mixture estimation based classification tasks in general and supports the existence of sub-classes of patients. See Section 2 for more detailed descriptions.
To summarize, we classified MS patients according to IFNβ treatment response and outperformed all prior approaches. Beyond improving on prediction accuracy, we found evidence of sub-groups of good responders and mislabeled patients, which raises clinical questions that may be of particular interest. To demonstrate the general applicability of our method, we have also tested it on data simulating general clinical time series including noise and mislabeled patients.
1.2 Related work
The first microarray analyses of the late 1990s (Eisen et al., 1998) considered mostly static gene expression profiles. Since then the field expanded considerably. For gene expression time courses, statistical modeling approaches, which take the temporal interdependencies into account have proven to be superior over approaches which do not (Bar-Joseph et al., 2002; Ernst et al., 2005; Schliep et al., 2003, 2004, 2005). Note that Schliep et al. (2004) also demonstrated that mixture estimation (MacLachlan and Peel, 2000) was superior over hard assignment clustering methods in terms of robustness and noise handling.
Semi-supervised learning was suggested as a promising approach to profit from both labeled and unlabeled data at a time (Castelli and Cover, 1994). Most importantly, it was shown that adding only little labeled data to the unlabeled data can decisively improve classification. A first application of the idea in combination with the expectation maximization (EM) algorithm was presented by Nigam et al. (1999). In the meantime, the inherent classification philosophy has become very popular; it has been used in a variety of application domains (Chapelle et al., 2006).
The specific idea of constraint-based (semi-)supervised learning was presented by Basu et al. (2004) and Lange et al. (2005). Further technical aspects were investigated by Lu and Leen (2005). This methodology was successfully used in biological applications to estimate mixtures of multivariate Gaussians to analyze gene expression time-course data that was augmented with additional information such as regulatory data (Schönhuth et al., 2006) and expression location in Drosophila embryos (Costa et al., 2007).
2 METHODS
2.1 Notation
In the following, let
t ∈ {1,…, T} denote the time points;
k ∈ {1,…, K} be a running index for the mixture components (groups/classes of patients);
g ∈ {1,…, G} be a running index for the genes;
i ∈ {1,…, N=N+ + N−} be a running index for the patients where N+ resp. N− are the numbers of good resp. bad responders; and
c(i) ∈ {+, −} denote the class of the patient i (+ and − for good resp. bad responders).
Oi,g ∈ ℝT is the expression time course of gene g of patient i.
Oi,t ∈ ℝG is the expression of all genes at time t of patient i.
Oi,g,t ∈ ℝ is the expression value of gene g of patient i at time point t.
- Oi ∈ ℝT×G is the collection of all expression values for patient i for all genes g across all time points t. To summarize,
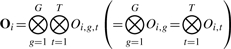
θ resp. Θ denote the parameters of a HMM with uni- resp. multivariate emission probability densities,
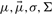 are for uni-, multivariate means, variances, covariance matrices referring to the uni- resp. multivariate Gaussian emission probability densities.
are for uni-, multivariate means, variances, covariance matrices referring to the uni- resp. multivariate Gaussian emission probability densities.
2.2 Mixture estimation
A mixture model (MacLachlan and Peel, 2000) is defined as
| (1) |
The overall model parameters Λ = (α1,…, αK, Θ1,…, ΘK) are divided into the prior probabilities αk, k = 1,…, K, which add to unity for the model components ℙ(Oi|Θk) and the Θk, k = 1,…, K, which describe the density functions that represent the components. In our case, the Θk are the parameterizations that describe the density functions of linear HMMs with multivariate emission distributions, which are discussed below. The observed data Oi then corresponds to the multi-dimensional time-courses that reflect the gene expression profiles of the patients.
One now aims at maximizing (1) by choosing an optimal parameter set Λ. This problem is routinely solved by the EM algorithm, which finds a local optimum for the above function by involving a set of hidden labels Y = {yi}i=1N, where yi ∈ {1,…, K} is the component, which generates data point Oi. For details of the EM algorithm, see Bilmes (1998).
Figure 2 (top) is a schematic illustration of a mixture estimation for two-dimensional data. The procedure starts with the data points as well as an initial guess Λ of the parameterization of the mixture. After termination of the EM algorithm, the mixture optimally explains the data in terms of having generated it. Each data point has a posterior distribution over the components which indicates a degree of membership of the data points to the components (or groups). This form of statistically consistent soft assignment of patients to groups has a variety of advantages, one of which is the increased robustness w.r.t. noise. Moreover, we will exploit the posteriors for our novel feature selection procedure (see below).
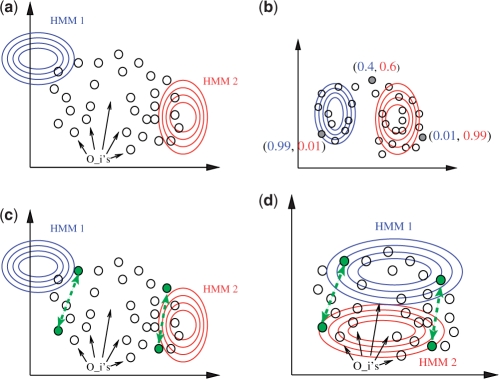
Fig. 2.
Schematic illustration of a mixture estimation with and without constraints. (a) The algorithm starts with an initial guess of the mixture components. (b) After termination, the mixture optimally explains the data points. Instead of a hard assignment to the components, each data point has a posterior distribution over the components. (c and d) By including constraints (dashed arrows in green), the EM algorithm strives for an optimum that discriminates the negatively constrained data points.
2.3 Constraints
In addition to the data, Oi one is now given a set of positive, respectively, negative constraints w+ij resp. w−ij ∈ [0, 1], which reflect the degree of linking of a pair of data points Oi, Oj, 1 ≤ i < j ≤ N. The task is to integrate these constraints meaningfully and consistently into the EM routine. We will explain the essence of the solution proposed by Lange et al. (2005). In each E-step of the EM algorithm, one has to compute the posterior distribution ℙ(Y|X, Λ) over the hidden labels yi, where Λ is an actual guess for the parameters and X = {𝕆i}Ni=1 is the set of (observed) data. By Bayes' rule we have
| (2) |
where Z is a normalizing constant. The constraints are now incorporated by, loosely speaking, choosing as prior distribution ℙ(Y|Λ) the one, which is most random without that the constraints and that the prior probabilities αk in Λ get violated. In other words, we choose the distribution, which obeys the maximum entropy principle and is called the Gibbs distribution [see Lange et al. (2005) and Lu and Leen (2005) for formulas and further details]:
| (3) |
where Z is a normalizing constant and δ is the Kronecker delta function. The Lagrange parameters ρ+ and ρ− define the penalty weights of positive and negative constraints violations. This means that increasing ρ+, ρ− leads to an estimation, which is more restrictive with respect to the constraints. Note that computing (2) is usually infeasible and thus requires a mean field approximation [see again Lange et al. (2005) and Lu and Leen (2005) for details]. Note, finally, that when there is no overlap in the annotations—more exactly, w+ij ∈ {0, 1}, w−ij ∈ {0, 1}, w+ijw−ij=0, and ρ+ = ρ− ∼ ∞—we obtain hard constraints as the ones used by Schliep et al. (2004).
In our case, only negative constraints were employed. To be more precise, we set
| (4) |
where c(i) denotes the responder class of patient i (in the following, we will formally write c(i) = + resp. c(i) = − in case that patient i is a good resp. bad responder) where both patients i, j have to belong to the training data. Also, we set ρ− = 5.0, as to make constraints to have a strong influence on solutions. This choice was motivated by experience in previous approaches (Costa et al., 2007).
Figure 2 (bottom) is a schematic illustration of a mixture estimation with negative constraints for 2D data. As for the ordinary case without constraints, the procedure starts with the data points as well as an initial guess Λ of the mixture. However, the negative constraints drive the algorithm to look for an optimal solution that discriminates between the negatively constrained data points.
2.4 Linear HMMs, noise and missing data
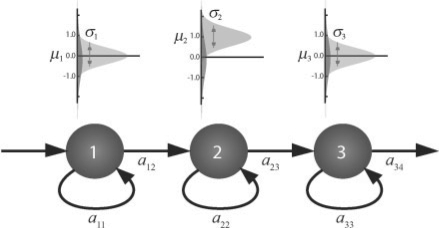
An HMM is a probabilistic model composed of a Markov chain with M discrete states and emission pdfs assigned to each state. At a given time point, an HMM is at a particular unknown state and it emits a symbol in accordance to the density function assigned to that state. In particular, we are interested in linear HMMs that follow a linear chain topology, i.e. hidden states are linearly ordered and there are only self-transitions or a transition to the next state. For example, in the HMM depicted in Figure 3—with three emitting states—the first one with a mean emission of zero and the second one with a mean emission of one and the third around zero, we model time courses displaying an upregulation pattern. Such models have already been applied in a variety of previous gene expression time course studies and described in detail (Schliep et al., 2003, 2004, 2005, Lin et al. 2008).
Fig. 3.
Example of an HMM with three hidden states modeling time courses with an upregulation pattern. Above each state, the emission densities for the univariate case, light grey corresponds to the expression emission with parameters μm and σm and dark gray to the noise component.
More formally, an HMM is parameterized by a transition matrix A = {aml}M×M, where aml is the probability of going from state m to l. As we restrict the topology to a linear chain of states, we only need to define the self-transition probability amm for a given state m, as am(m+1) = 1 − amm and all other transitions from state m are set to zero. We also have an initial probability vector Π, where πm is the probability of starting at state m, which in the linear HMM is π1 = 1 and 0 otherwise.
Finally, we have an emission function for each state for which we use mixtures of multivariate Gaussians. They consist of three components: component one is a multivariate Gaussian with diagonal covariance matrices modeling patient expression values as in Lin et al. (2008), component two— the noise component—is a multivariate Gaussian with means equal to the data center and a broad covariance matrix responsible for modeling observations due to noise (Fraley and Raftery, 1998). The third component finally is for handling missing data. Therefore, we define a special symbol Nan and extend the variable space for Oi,t from ℝG to ℝ𝔾 ∪ {Nan}. If the values Oi,t of patient i at time point t are missing, we set Oi,t ≔ Nan. As a density function ℙkm for emitting a (multivariate) expression value Oi,t from state m of the kth HMM Θk we obtain
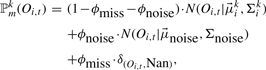 |
where 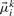 and Σki denote the mean values and diagonal covariance matrices of the G-dimensional expression vectors, ϕmiss is the proportion of missing observations in the data and ϕnoise the proportion of noise observations. For the noise component,
and Σki denote the mean values and diagonal covariance matrices of the G-dimensional expression vectors, ϕmiss is the proportion of missing observations in the data and ϕnoise the proportion of noise observations. For the noise component, 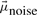 is a vector containing the average expression values of the genes across all patients and time points and Σnoise has diagonal entries set to a high value, e.g. σgg = 5.00, and all other entries are set to 0. In the experiments, we set ϕmiss to be equal to the proportion of missing observations in the real data and ϕnoise = 0.05.
is a vector containing the average expression values of the genes across all patients and time points and Σnoise has diagonal entries set to a high value, e.g. σgg = 5.00, and all other entries are set to 0. In the experiments, we set ϕmiss to be equal to the proportion of missing observations in the real data and ϕnoise = 0.05.
In summary, each linear HMM Θk corresponds to the parameterization
where
are the emission parameters. We can then apply the Baum–Welch algorithm for estimating the parameters of the HMMs for a given assignment of patients derived from the mixture estimation. The parameters 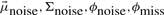 are kept fixed in the estimation. We refer the reader to Bilmes (1998) for a detailed description of the Baum-Welch algorithm.
are kept fixed in the estimation. We refer the reader to Bilmes (1998) for a detailed description of the Baum-Welch algorithm.
2.5 Core Classification Algorithm
Assume that one is given both {+, −}-labeled (training) and unlabeled (test) data, where the aim is to infer labels for the unlabeled data. Based on the idea of constrained mixture estimation, we employed the following algorithmic procedure:
Estimate a constrained mixture, in the supervised case only using training data (HMMConst) and using all data in the semi-supervised case (HMMConstAll). In both cases, constraints are available only for the training data.
Assign each of the mixture components to one of the classes +, − by determining to what degree, in terms of their posteriors, the labeled data points contribute to it.
Assign the unlabeled data to the components by determining the maximum entry in their posterior distribution. In the semi-supervised case, posteriors are readily available. In the supervised case, posteriors have to be computed upon termination of the mixture estimation procedure. This way, the class labels of the components determine the labels of the datapoints.
2.6 Feature selection
As feature selection in mixture estimation-based classification has not been presented elsewhere as of yet, we will go into a little more detail.
After application of the semi-supervised procedure, we remain with a mixture of multivariate HMMs such that the likelihood of the multivariate time course of patient i w.r.t. that mixture is computed as
| (5) |
where Λ comprises all parameters of all HMMs Θk with multivariate emissions together with the priors αk of the components Θk. In order to select features (genes) g that help classify the data best, we apply the following algorithm:
- For each gene g define new HMM components θk,g with univariate emissions by adopting the topology of Θk for all θk,g. That is, we set
which means that the transition probabilities αijk,g of changing from state i to state j in model component θk,g is just aijk, the equivalent transition probability in the multivariate Θk. Furthermore,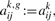
(6)
that is, we define the means of the Gaussian emission pdfs of θk,g to be those of the dimension of the multivariate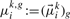
(7) 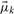 referring to gene g. Likewise,
referring to gene g. Likewise,
where (Σki)gg is the main diagonal entry of Σki at row resp. column referring to gene g. Overall, the θk,g can be perceived as ‘univariate copies’ of the multivariate Θk, where there is one copy for each gene g.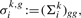
(8) - For each gene g, we compute ‘positive’ priors αgk+ (for the good responders) as well as ‘negative’ priors αgk− (for the bad responders). Therefore, we assume that the mixture
has generated all time courses Oi,g of gene g of the patients i where αk is just the prior of the estimated multivariate mixture (5). Computation of ‘positive’ and ‘negative’, gene-specific priors αgk+ and αgk− then is done by adopting the usual procedure of the EM algorithm. In more detail, let Λg = (α1,…, αK, θ1,g,…, θK,g) be the entirety of the parameters that describe the univariate mixture (9) for gene g. We define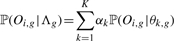
(9) 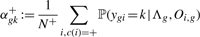
(10)
where ygi is the (hidden) variable that specifies which component has generated time course Oi,g and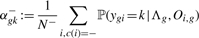
(11) 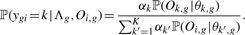
(12) - For each gene g, compare the positive prior distribution
with the negative prior distribution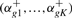
(13)
Note first that one has declared the multivariate components Θk in (5) to be either positive or negative ones. If the sum of the positive priors, running over the negative components k is greater than the sum over the positive components, or vice versa, the sum of the negative priors is greater over the positive components, discard gene g. If not, compute the Kullback–Leibler divergence of the positive prior distribution and the negative prior distribution. The greater it is, the better the gene discriminates. Rank the genes accordingly and choose an appropriate cut-off. Select the genes above the cut-off as appropriate features.
(14) Recompute a multivariate mixture using only the selected genes according to the procedure in Subsection 2.5 to perform class prediction.
2.7 Clustering consensus
In analogy to the classification procedures adopted by Baranzini et al. (2005), Borgwardt et al. (2006), and Lin et al. (2008), we performed classifications of the patients for several re-samples of the dataset. In detail, we performed 20 classifications from a five-replications 4-fold scheme. As a consequence, we need a procedure that combines the possibly different classifications into one single classification of each patient. Such an analysis is also important from two aspects: it will indicate if candidate (sub-)groups of patients are stable, i.e. if they reappear in the same (sub-)class in many solutions. Also, it indicates if particular patients are consistently grouped with patients of distinct labels, and/or if patients are potentially mislabeled.
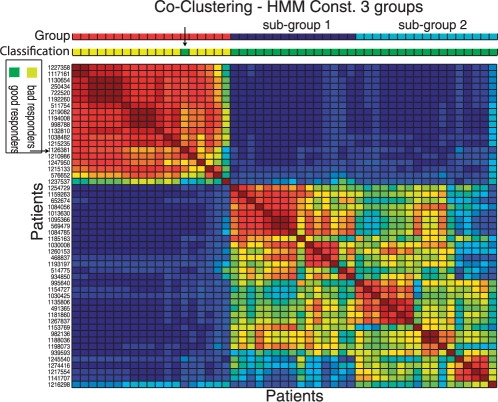
For this task, we use a procedure described by Monti et al. (2003) and Brunet et al. (2004). First, we build a co-clustering matrix by counting for each pair of patients the number of times they appear in the same group across the different solutions. This matrix is used as a similarity measure for a subsequent hierarchical clustering procedure where the rows and columns of the matrix are reordered such that patients with similar co-clustering patterns become neighbors. Finally, the resulting dendrogram is cut as to return the same number of groups as in the individual solutions. An example of such a matrix can be seen in Figure 5, where red squares represent pairs of patients in the same group at several solutions, while blue squares represent pairs not in the same group in the same solutions. Red squares indicate stable groups shared over several solutions.
Fig. 5.
Matrix depicting the co-clustering of patients for HMMConst with three groups. A particular position in the matrix represents proportion of times the pair of patients was in the same group; red values indicating higher values. Red squares indicate stable groups of patients that tend to be grouped in several solutions. The bars above the matrix indicate the groups found by HMMConst (red for bad responders, dark blue for good responders 1 and light blue for good responders 2); and the classification of patient response based on clinical criteria only. The arrow indicates the putative mislabeled patient.
2.8 Datasets
2.8.1 Simulated dataset
We resort to simulated data for a general analysis of the performance of the currently available methods on data with the specific characteristics of clinical time series. As a basis for such a comparative analysis, we use the simulated data that was proposed by Lin et al. (2008). It consists of 100 patients divided into two classes of 50 patients each. Each patient has 100 genes with 8 time points. Out of the 100 genes, only 10 had expression patterns which are substantially different between the two patient groups. The corresponding genes should preferably be chosen by feature selection subroutines. The generation mechanism behind the simulated data is to sample time series from a piecewise linear function. At a later step, patient-specific response rate is included by shrinking and expanding the curves. However, noise in form of outliers and mislabeled data had not been taken into account.
To take these issues into account, we expanded the previous analysis by (i) including outlier values at individual time points of a gene and (ii) including mislabeled time series. This way, we can compare the performance of the methods w.r.t. these two characteristics, which are ubiquitous in clinical studies on gene expression. For the first procedure, we select combinations of genes and time points according to a probability pγ. When a gene time point had been selected, we added to it a value sampled from a normal density function N(1, 1). We generate five such datasets by varying pγ from 0.01 to 0.05. Mislabeling was simulated by changing the labels c(i) of l patients. We generated four datasets by setting l from 1 to 4.
2.8.2 MS treatment response data
Blood samples enriched with mononuclear cells from 52 relapsing-remitting MS patients were obtained 0, 3, 6, 9, 12, 18 and 24 months after initiation of IFNβ therapy, which resulted on an average seven measurements across the 2 years (Baranzini et al., 2005). Expression profiles were obtained using one-step kinetic reverse-transcription PCR over 70 genes selected by the specialists to be potentially related to IFNβ treatment. Overall, 8% of measurements were missing due to patients missing the appointments. We applied a log transformation in the expression values.
After the 2 year endpoint, patients were classified as either good or bad responders, depending on strict clinical criteria. Bad responders were defined as having suffered two or more relapses or having a confirmed increase of at least one point on the expanded disability status scale (EDSS). In short, a good responder was to have a total suppression of relapses and not allowed to have an increase on the EDSS. From the 52 patients, 33 were classified as good and 19 as bad responders. Note, however, that the reliability of these criteria has not been conclusively settled (Ro et al., 2002).
3 DISCUSSION
For both simulated and real data, we analyzed the classification accuracy of the HMM mixtures resulting from the constrained estimation procedure where mixtures consisted of 2, 3 or 4 groups and were estimated from the labeled data alone, reflecting a supervised learning scenario (HMMConst). We compared it with the generative HMM classifier (HMMClass) and discriminative HMM classifier (HMMDisc), both from Lin et al. (2008). We also included IBIS (Baranzini et al., 2005) and Kalman Filter SVM (Borgwardt et al., 2006) in the comparison. For constrained estimation of mixtures of HMMs, we also investigated the use of unlabeled patients during training (HMMConstAll). This case reflects a semi-supervised scenario, where, in contrast to the purely supervised case, estimation and classification are merged into one step by integrating the unlabeled data into the estimation procedure. Note that semi-supervised learning reflects a perfectly realistic classification scenario; no assumptions about the unlabeled data are made. For each particular method, a five replications 4- fold procedure is applied, as performed in previous approaches (Baranzini et al., 2005; Borgwardt et al., 2006; Lin et al., 2008). Training accuracies are used to select the number of features and to choose the optimal number of groups. For sake of fair comparison, we used HMMs with three states for simulated datasets and four states for real datasets, just as suggested by Lin et al. (2008). Comparison of the methods, as usual, then is based on the prediction accuracy achieved on the test sets. The method is available at http://www.ghmm.org/gql and data sets at http://www.cin.ufpe.br/∼igcf/MSConst.
3.1 Simulated data
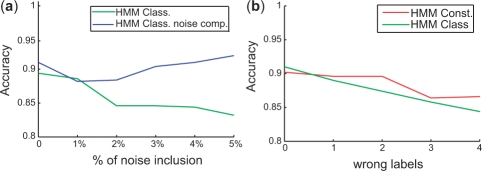
One of the aspects we analyzed is the benefit of adding the noise component, as described in subsection 2.4, into the generative classifier HMMs. As can be seen in Figure 4a, for HMMClass without the noise component, the accuracy deteriorates from around 90–85%, in case of adding noise to 5% of the time points. When employing a noise component, the accuracy of HMMClass stays at around 90%. A t-test confirms significance of the higher accuracy of HMMClass with a noise component when > 1% of noise is added (P-value > 0.05). As shown before, with the noise component the emission distributions have longer tails (Fraley and Raftery, 1998) which makes the model estimation more robust to outlier points.
Fig. 4.
Accuracy on simulated data (a) after addition of noise to x% of time points and (b) after inclusion of wrong labels.
The second aspect we analyzed was the inclusion of wrong labels into the patient response data. In this scenario, we compared the performance of the classifiers with generative HMMs and constrained mixture estimation with HMMs. As can be seen in Figure 4, the accuracy of both methods deteriorates with the inclusion of random labels. However, HMMConst has an overall better accuracy than HMMClass. Indeed, HMMConst assigned 92% of the mislabeled examples to their original class. This agreed with our intuition that the constrained mixture estimation can take care of mislabeled data points, which corresponds to the situation of constraints being overruled by the location of the data points which yields more discriminative models.
3.2 Classification of MS treatment response
In Table 1, we have displayed the training and test classification accuracy on the MS data. Overall, both semi- and purely supervised versions of HMMConst with two and three mixture components have the best classification performance among the competing classifiers. Accuracies of HMMConstAll2, HMMConstAll3, HMMConst3 with feature selection are higher than IBIS, HMMDisc, Kalman SVM (t-tests indicate P-value < 0.05) and accuracy of HMMConst2 with feature selection is higher than IBIS and HMMDisc (t-tests indicate P-value < 0.05). On the other hand, HMMConst4 has a very poor performance, which indicates that there is no support for four different responder groups in the data. Also, all methods based on all 70 genes (HMMClass, HMMConst2, HMMConst3) had a poor performance, which reinforces the importance of feature selection. Note that there is no clear statistical distinction between the accuracies resulting from using two or three mixture components in both HMMConst and HMMConstAll. However, we will put particular emphasis on the results with three groups in the next sections, as it reflects the existence of sub-groups of MS patients, which has recently been confirmed in the MS literature. Note also that HMMClass is higher than the closely related discriminative classifier proposed by Lin et al. (2008). While results from Lin et al. (2008) show that both methods are similar, the superior classification performance displayed here results from the employment of the noise component, as discussed above, in our implementation.
Table 1.
Classification accuracy of distinct methods in the MS patient response data
| Method | Number of genes | Training | Test |
|---|---|---|---|
| Accuracy (%) | Accuracy (%) | ||
| IBIS | 3 | – | 74.20 |
| HMMClass | 70 | 87.15 | 76.52 (+/− 0.03) |
| HMMConst4 | 35 | 89.62 | 78.08 (+/− 17.0) |
| HMMConst2 | 70 | 87.12 | 80.49 (+/− 9.5) |
| HMMConst3 | 70 | 88.26 | 81.38 (+/− 10.0) |
| HMMDisc | 7 | – | 85.00 |
| Kalman SVM | – | – | 87.80 |
| HMMClass | 17 | 93.66 | 89.34 (+/− 8.5) |
| HMMConst2 | 17 | 92.31 | 89.62 (+/− 8.1) |
| HMMConst3 | 17 | 92.60 | 90.39 (+/− 7.2) |
| HMMConstAll3 | 17 | 93.64 | 92.31 (+/− 7.6) |
| HMMConstAll2 | 17 | 93.47 | 92.70 (+/− 6.1) |
Overall, the HMMConstAll2 and three groups achieve the best classification performance. As this is due to the integration of the unlabeled observations (Chapelle et al., 2006) this indicates superiority of semi-supervised over purely supervised classifiers. Indeed, for the small study we analyze here semi-supervised approaches are expected to deliver particularly favorable results from purely theoretical considerations. Note, that employing our method within a purely supervised setting also performs best when compared to purely supervised approaches.
3.2.1 Selected genes
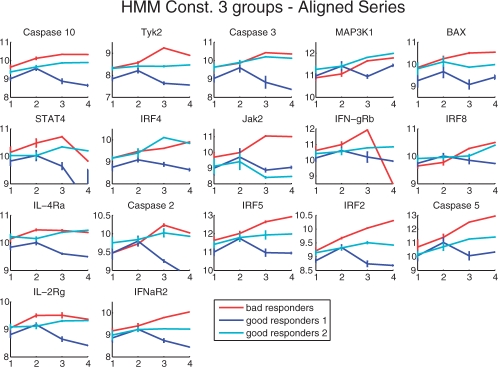
A particularly interesting aspect from a biological point of view is to compare the sets of genes selected as classification features by the different methods. Overall, our method preferred greater numbers of genes as features (17 genes in most cases) than the HMM Discriminative learning proposed by Lin et al. (2008), which select seven genes: Caspase 2, Caspase 3, Caspase 10, IL-4Ra, Jak2, MAP3K1, RAIDD. Out of these, only RAIDD is not present in the genes selected by our method (see Fig. 7 and Supplementary Material for the list of genes). When comparing our sets of genes to the 12 genes selected by Baranzini et al. (2005), we find that eight genes are shared by our method HMMConst (Caspase 2, Caspase 3, Caspase 10, IL-4Ra, IRF2, IRF4, STAT4, MAP3K1). Our approach also identifies some genes that are not indicated by others. Out of those, we stress two proteins with high-discriminative scores: Tyk2, which is part of the Jak-Stat pathway and related interferon signaling (Yang et al., 2005), and BAX, which is a known apoptosis regulator. While it is hard to evaluate, the sets of selected genes, as being highly overlapping with those of the previous studies, it is clear that the genes exclusively identified as classification features by our method helped us decisively to increase the prediction accuracy.
Fig. 7.
Time series aligned to the HMMs are shown as log expression (y-axis) versus time points (x-axis).
3.3 Constraint based mixture estimation: sub-classes of patient responders
To inspect the existence of stable sub-classes of patient responders, we performed the consensus analysis in the results of HMMConstAll3. As can be seen in Figure 5, the matrix reveals two big blocks, one in the upper left corner, referring mainly to bad responders; and another one in the lower right corner, consisting only of good responders. Furthermore, the consensus method indicates that the class of good responders is formed by two sub-classes: good responders 1 and good responders 2 (indicated by dark blue and light blue bars on the top).
The consensus matrix also indicates one patient (1 126 381) which is labeled as a good responder, but grouped together with the bad responders (the same patient is also misclassified in the HMMConst2 as indicated in the Supplementary Material). A closer inspection of the criteria used to define the patient response revealed that patient 1 126 381 was likely misclassified in the original study (Baranzini et al., 2005). One of their criteria to classify a patient as bad responder was an increase by one in the EDSS over the 2 years of treatment. According to the data present in Supplementary Material, patient 1 126 381 had a change in EDSS = 1, which just meets one of the criteria to classify a patient as a bad responder. This mislabeled example was later confirmed by the author of the original study (S.E. Baranzini, personal communication).
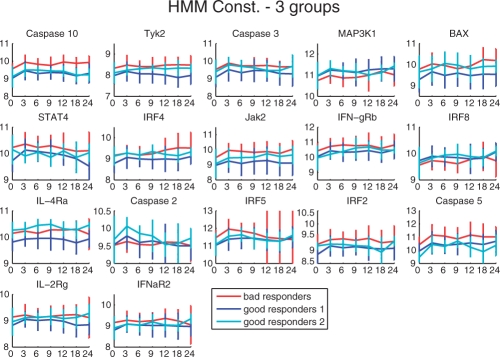
The existence of two sub-classes of good responders is further supported by the average time-series profiles and their alignments to the respective HMMs. In Figure 6, we display the average expression profiles of the genes in the three groups of patients found: bad responders (red), good responders 1 (dark blue) and good responders 2 (light blue). Final list of genes are obtained by ranking all features selected during training, summing their rank values and selection the top genes. In the figure, genes order reflect their relevance.
Fig. 6.
Mean expression profiles of genes are shown as log expression (y- axis) versus time points (x-axis).
For some genes, both sub-classes of good responders exhibit similar profiles (Caspase 10, MAP3K1, STAT4, IFN-gRB, IRF8, IRF5, IRF2, Caspase 5 and IFNaR2). Interestingly, for some genes (Tyk2, Jak2, IFNaR2, ILR-2rg), bad responders had the highest expression whereas the good responders 1 had lowest expression and good responders 2 had expression values between those groups, while for other genes (Caspase 3, BAX, IL-4Ra and IRF4), the expression profiles of bad responders and good responders 2 are similar and display higher expression values than the good responders 1. KEGG pathway (Kyoto Encyclopedia of Genes and Genomes) enrichment analysis, which was performed with the tool GOST (Reimand et al., 2007), indicates that genes in the first two groups are related to Jak-Stat pathway, while genes in the last group are involved in the apoptosis pathway. One particular gene, Caspase2 has an overexpression pattern for good responders 2, while good responders 1 and bad responders both had a lower, but similar expression values. These profiles indicate that patients belonging to the sub-class of good responders 2 share some expression marker characteristics with good responders in general, but also some marker characteristics of bad responders.
An example of a gene of potentially particular interest that is differentially expressed between the two sub-types of good responders is IL-4Ra, which is involved in the regulation of B-cell mediated immune response (Nelms et al., 1999). Note that there has been a recent debate on the role of B cells in MS and the definition of disease subtypes based on the individual types of antibodies acting as key players in the disease (Archelos et al., 2000).
4 CONCLUSION
We have presented a statistically sound and reliable methodology for analysis and classification of clinical time series. It is based on the novel idea of employing constraint-based mixture estimation to perform semi- and purely supervised clinical classification tasks. As a result, we outperformed all prior approaches w.r.t. prediction accuracy on both simulated and MS treatment response data. Moreover, we found that classification of treatment response data was best when subdividing the positive responders into two subclasses, which might raise some interesting clinical questions to be pursued further. This also coincides with recent findings on MS pathology (Satoh et al., 2006; van Baarsen et al., 2006), which indicated that MS patients display distinct expression profiles signatures.
Furthermore, we found out after submission that one of the patients that we putatively misclassified was originally mislabeled (S.E. Baranzini, personal communication). Consequently, prediction accuracy increases by 2% for all methods; 95% of accuracy from HMMConst3 and 90% of the Kalman Filter SVM. This would not only mean that we have been able to decrease the relative error rate by 50%, but also that we come close to perform accurate personal medicine diagnosis when evaluating IFNβ treatment in MS patients.
A general explanation for the superiority of our approach is its capacity of handling of noisy, missing data and mislabeled patients. This could be confirmed by, respectively, designed experiments on simulated data. It has been widely noted that mixture estimation is more robust when it comes to processing noisy and incomplete data (e.g. Schliep et al., 2005). Last but not least, note that the idea of employing mixture estimation for classification tasks allowed us to flexibly perform sub-classification, which was of particular use here. We would like to point out that, beyond the specific usage of our method outlined here, it could be applied in classifications task on other diseases with multiple genetic causes, such as cancer (van't Veer and Bernards, 2008).
ACKNOWLEDGEMENTS
We would like to thank Benjamin Georgi for help with the PyMix software. Special thanks to Katrin Höfl and Peter van den Elzen from the Department of Pathology and Laboratory Medicine, University of British Columbia for helpful comments on MS pathology and Sergio Baranzini from the Department of Neurology University of California San Francisco for clarifications concerning the MS dataset.
Funding: Pacific Institute for the Mathematical Sciences (to A.S.); Programa de Apoio a Projetos Institucionais com a Participação de Recèm-Doutores/Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (Brazil) (to I.C.).
Conflict of Interest: none declared.
REFERENCES
- Archelos J, et al. The role of b cells and autoantibodies in multiple sclerosis. Ann. Neurol. 2000;47:694–706. [PubMed] [Google Scholar]
- Bar-Joseph Z, et al. A new approach to analyzing gene expression time series data. Proceedings of the 6th Annual International Conference on Research in Computational Molecular Biology. 2002 [Google Scholar]
- Baranzini SE, et al. Transcription-based prediction of response to ifnbeta using supervised computational methods. PLoS Biol. 2005;3:e2. doi: 10.1371/journal.pbio.0030002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basu S, et al. Proceedings of the 2004 SIAM International Conference on Data Mining (SDM-04). Lake Buena Vista, Florida, USA: 2004. Active semi-supervision for pairwise constrained clustering; pp. 333–344. [Google Scholar]
- Bilmes J. Technical Report TR-97-021. Berkeley: International Computer Science Institute; 1998. A gentle tutorial of the em algorithm and its application to parameter estimation for gaussian mixture and hidden markov models. [Google Scholar]
- Borgwardt KM, et al. Class prediction from time series gene expression profiles using dynamical systems kernel. Pac. Symp. Biocomput. 2006;11:547–558. [PubMed] [Google Scholar]
- Brunet J-P, et al. Metagenes and molecular pattern discovery using matrix factorization. Proc. Natl Acad. Sci. USA. 2004;101:4164–4169. doi: 10.1073/pnas.0308531101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castelli V, Cover TM. On the exponential value of labeled samples. Patt. Recog. Lett. 1994;16:105–111. [Google Scholar]
- Chapelle O, et al. Semi-supervised Learning. Cambridge, MA: MIT Press; 2006. [Google Scholar]
- Costa IG, et al. Semi-supervised learning for the identification of syn-expressed genes from fused microarray and in situ image data. BMC Bioinformatics. 2007;8:S3. doi: 10.1186/1471-2105-8-S10-S3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eisen M, et al. Cluster analysis and display of genome-wide expression patterns. Proc. Natl Acad. Sci. USA. 1998;95:14863–14868. doi: 10.1073/pnas.95.25.14863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ernst J, et al. Clustering short time series gene expression data. Bioinformatics. 2005;21:i159–i168. doi: 10.1093/bioinformatics/bti1022. [DOI] [PubMed] [Google Scholar]
- Fraley C, Raftery AE. How many clusters? which clustering method? answers via model-based cluster analysis. Comput. J. 1998;41:578–588. [Google Scholar]
- Hastie T, et al. The Elements of Statistical Learning: Data Mining, Inference and Prediction. New York: Springer; 2001. [Google Scholar]
- Irizarry RA, et al. Multiple-laboratory comparison of microarray platforms. Nat. Methods. 2005;2:345–350. doi: 10.1038/nmeth756. [DOI] [PubMed] [Google Scholar]
- Kaminski N, Bar-Joseph Z. A patient-gene model for temporal expression profiles in clinical studies. J. Computat. Biol. 2007;14:324–338. doi: 10.1089/cmb.2007.0001. [DOI] [PubMed] [Google Scholar]
- Lange T, et al. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Vol. 1. San Diego, CA, USA: 2005. Learning with constrained and unlabelled data; pp. 731–738. [Google Scholar]
- Lin TH, et al. Alignment and classification of time series gene expression in clinical studies. Bioinformatics. 2008;24:i147–i155. doi: 10.1093/bioinformatics/btn152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lottaz C, et al. Computational diagnostics with gene expression profiles. Meth. Mol. Biol. 2008;453:281–296. doi: 10.1007/978-1-60327-429-6_15. [DOI] [PubMed] [Google Scholar]
- Lu Z, Leen T. Semi-supervised learning with penalized probabilistic clustering. In: Saul LK, et al., editors. Advances in Neural Information Processing Systems 17. Cambridge, MA, USA: MIT Press; 2005. pp. 849–856. [Google Scholar]
- MacLachlan G, Peel D. Wiley Series in Probability and Statistics. Hoboken, NJ, USA: Wiley; 2000. Finite Mixture Models. [Google Scholar]
- Monti S, et al. Consensus clustering: a resampling-based method for class discovery and visualization of gene expression microarray data. Mach. Learn. 2003;52:91–118. [Google Scholar]
- Nelms K, et al. The il-4 receptor: signaling mechanisms and biologic functions. Annu. Rev. Immunol. 1999;17:701–738. doi: 10.1146/annurev.immunol.17.1.701. [DOI] [PubMed] [Google Scholar]
- Nigam K, et al. Text classification from labeled and unlabeled documents using EM. Mach. Learn. 1999;39:795–801. [Google Scholar]
- Reimand J, et al. g:profiler–a web-based toolset for functional profiling of gene lists from large-scale experiments. Nucleic Acids Res. 2007;35:W193–W200. doi: 10.1093/nar/gkm226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ro J, et al. Assessment of different treatment failure criteria in a cohort of relapsing-remitting multiple sclerosis patients treated with interferon beta: implications for clinical trials. Ann. Neurol. 2002;52:400–406. doi: 10.1002/ana.10290. [DOI] [PubMed] [Google Scholar]
- Satoh JI, et al. T cell gene expression profiling identifies distinct subgroups of japanese multiple sclerosis patients. J. Neuroimmunol. 2006;174:108–118. doi: 10.1016/j.jneuroim.2006.02.004. [DOI] [PubMed] [Google Scholar]
- Schliep A, et al. Using hidden Markov models to analyze gene expression time course data. Bioinformatics. 2003;19(Suppl. 1):255–263. doi: 10.1093/bioinformatics/btg1036. [DOI] [PubMed] [Google Scholar]
- Schliep A, et al. Robust inference of groups in gene expression time-courses using mixtures of HMMs. Bioinformatics. 2004;20(Suppl. 1):283–289. doi: 10.1093/bioinformatics/bth937. [DOI] [PubMed] [Google Scholar]
- Schliep A, et al. Analyzing gene expression time-courses. IEEE/ACM Trans. Comput. Biol. Bioinform. 2005;2:179–193. doi: 10.1109/TCBB.2005.31. [DOI] [PubMed] [Google Scholar]
- Schönhuth A, et al. Japanese-German Workshop on Data Analysis and Classification. Springer; 2006. Semi-supervised clustering of yeast gene expression data. (in press) [Google Scholar]
- Spang R. Diagnostic signatures from microarrays: a bioinformatics concept for personalized medicine. BIOSILICO. 2003;1:64–68. [PubMed] [Google Scholar]
- van Baarsen LGM, et al. A subtype of multiple sclerosis defined by an activated immune defense program. Genes Immun. 2006;7:522–531. doi: 10.1038/sj.gene.6364324. [DOI] [PubMed] [Google Scholar]
- van't Veer LJ, Bernards R. Enabling personalized cancer medicine through analysis of gene-expression patterns. Nature. 2008;452:564–570. doi: 10.1038/nature06915. [DOI] [PubMed] [Google Scholar]
- Yang CH, et al. Interferon alpha activates nf-kappab in jak1-deficient cells through a tyk2-dependent pathway. J. Biol. Chem. 2005;280:25849–25853. doi: 10.1074/jbc.M413721200. [DOI] [PMC free article] [PubMed] [Google Scholar]