Proteome coverage prediction with infinite Markov models

Abstract

Motivation: Liquid chromatography tandem mass spectrometry (LC-MS/MS) is the predominant method to comprehensively characterize complex protein mixtures such as samples from prefractionated or complete proteomes. In order to maximize proteome coverage for the studied sample, i.e. identify as many traceable proteins as possible, LC-MS/MS experiments are typically repeated extensively and the results combined. Proteome coverage prediction is the task of estimating the number of peptide discoveries of future LC-MS/MS experiments. Proteome coverage prediction is important to enhance the design of efficient proteomics studies. To date, there does not exist any method to reliably estimate the increase of proteome coverage at an early stage.

Results: We propose an extended infinite Markov model DiriSim to extrapolate the progression of proteome coverage based on a small number of already performed LC-MS/MS experiments. The method explicitly accounts for the uncertainty of peptide identifications. We tested DiriSim on a set of 37 LC-MS/MS experiments of a complete proteome sample and demonstrated that DiriSim correctly predicts the coverage progression already from a small subset of experiments. The predicted progression enabled us to specify maximal coverage for the test sample. We demonstrated that quality requirements on the final proteome map impose an upper bound on the number of useful experiment repetitions and limit the achievable proteome coverage.

Contact: manfredc@inf.ethz.ch; jbuhmann@inf.ethz.ch

1 INTRODUCTION

Over the last few years, mass spectrometry-based proteomics has emerged as the most powerful approach to comprehensively characterize a proteome. The experimental workflows for mass spectrometry-based proteomics have sufficiently advanced to enable extensive exploration of complex biological samples (Domon and Aebersold, 2006). While conceptional studies provided rough a priori insights about the scope of these workflows (Eriksson and Fenyo, 2007), there are still no means to dynamically infer the a posteriori potential, i.e. to predict the increase in proteome coverage for their real-world implementations. This work contributes the extended infinite Markov model DiriSim to predict proteome coverage (in terms of peptide discoveries) upon repetition of liquid chromatography tandem mass spectrometry (LC-MS/MS) experiments. By explicitly modeling false and true positive peptide identifications, DiriSim enables us to specify the maximally achievable proteome coverage for a specified quality constraint on the final set of peptide discoveries.

The most successful strategy to achieve extensive proteome coverage is referred to as shotgun proteomics. In its simplest implementation, protein samples are extracted from their biological source, subjected to enzymatic digestion and the resulting peptide mixtures are finally analyzed by LC-MS/MS. More elaborate strategies essentially adopt the same workflow, additionally augmented by fractionation steps for proteins/peptides before LC-MS/MS analysis. Finally, peptide identities are inferred from the acquired fragment ion spectra and they are used to recover the protein composition of the initial biological sample.

The complexity of the protein, and hence peptide mixtures, poses a formidable challenge to mass spectrometrical analysis. The reversed phase liquid chromatography step effectively reduces the complexity of the peptide mixture by selecting peptides for tandem mass spectrometry analysis according to their polarity. For the duration of the LC-MS/MS experiment, the mass spectrometer coupled to the liquid chromatography system constantly acquires tandem mass spectra from eluting peptides. The elution time of a particular peptide is defined by its polarity. Any time during the LC-MS/MS experiment, the mass spectrometer is thus exposed to a local peptide mixture that is less complex than the initial mixture (Fig. 1a). Nevertheless, these mixtures are typically still far too complex to allow the mass spectrometer to acquire tandem mass spectra for all peptides in a single LC-MS/MS experiment. Consequently, LC-MS/MS experiments are usually repeated extensively, in order to increase the number of peptides for which tandem mass spectra are acquired.

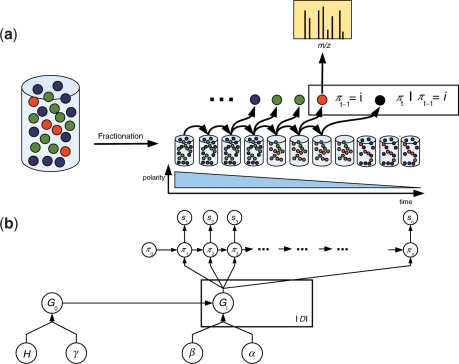
Fig. 1.

Illustration of an LC-MS/MS experiment. (a) Liquid chromatography fractionation generates a sequence of local peptide ensembles from the initial ensemble. Each of these ensembles is derived from the initial ensemble by pooling peptides of similar polarity. The sequence of ensembles features descending overall polarity in the course of the experiment. During the experiment peptides π_t are drawn from the sequence of ensembles and analyzed by the mass spectrometer coupled to the liquid chromatography system. (b) Graphical representation of the infinite Markov model. The initial ensemble is represented by its peptide distribution G₀. G₀ is assumed to have a Dirichlet process prior with concentration parameter γ and uniform distribution H over the protein database 𝒟 as base probability measure. Local ensembles for which representative peptides have been detected are represented explicitly. Each of these ensembles is indexed by its representative peptide i and characterized by its peptide distribution G_i. G_i is assumed to be sampled from a biased Dirichlet process with G₀ as base probability measure. The peptide π_t following the series π₁,…, π_t−1 = i of detected peptides is sampled from G_i. Each peptide π_t gives rise to an observable fragment ion spectrum s_t, defining the peptide-spectrum match (s_t, π_t). The error model for peptide-spectrum matches is omitted for clarity. See Section 2.5 for details.

Using one of a range of database search engines, tandem mass spectra are then assigned to peptide giving rise to a series of peptide-spectrum matches (Nesvizhskii et al., 2007). Note that peptide-spectrum matches are typically highly redundant, i.e. the number of peptide discoveries covered by the peptide-spectrum matches is typically much smaller than the total number of peptide-spectrum matches. Not all peptide-spectrum matches are correct. Various approaches are available to estimate the reliability of peptide-spectrum matches (Elias and Gygi, 2007; Keller et al., 2002). Target–decoy strategies have shown to be a generic and reliable strategy to estimate false discovery rates for peptide-spectrum matches, i.e. the expected fraction of false positive peptide assignments (Elias and Gygi, 2007). At this point, the preliminary result of a series of LC-MS/MS experiments reduces to a series of peptide-spectrum matches that is additionally characterized by some false discovery rate.

Shotgun proteomics studies should ideally be designed such that proteome coverage, i.e. the number of discovered peptides increases efficiently with consecutive measurements. For a given series of already performed LC-MS/MS experiments, this requirement translates into the task of estimating the required number of additional experiments that have to be performed to achieve a reasonable increase in proteome coverage. If the estimated effort turns out to be too large, it might be more convenient to consider other experimental setups to analyze the underlying sample. Besides simply giving existing workflows a try, there have been approaches to rationally design promising setups according to statistical analysis of the already acquired peptide-spectrum matches (Brunner et al., 2007). To the best of our knowledge, no method specifies the remaining potential of the currently performed experiments by predicting their proteome coverage progression.

To close this gap, we present DiriSim, an extended infinite Markov model for LC-MS/MS experiments that yields a posterior prediction of the proteome coverage progression. DiriSim explicitly accounts for true and false positive peptide-spectrum matches by modeling a set of LC-MS/MS experiments as a mixture of an infinite Markov model (Beal et al., 2002) and an error model distribution. The expected proteome coverage progression for additional experiments is estimated by sampling from the posterior predictive distribution. We have assessed this approach by cross validation on a set of 37 LC-MS/MS measurements of a complete proteome sample. We show that the extended infinite Markov model outperforms simple extrapolation methods and correctly predicts proteome coverage progression. Extrapolation of the proteome coverage progression further enabled us to specify the maximal coverage of the test set.

2 METHODS

The data utilized by DiriSim consists of a list of LC-MS/MS experiments where peptide-spectrum matches have been generated by searching against a protein database 𝒟. Each peptide-spectrum match (s, π) corresponds to a tandem mass spectrum s and its peptide assignment π ∈ 𝒟. Each LC-MS/MS experiment R_l defines a series of n_l peptide assignments π^(l)=π₁^(l),…, π_nl^(l). A fraction q of all peptide-spectrum matches is assumed to be erroneously assigned.

The following sections describe how to predict the progression of proteome coverage conditioned on the given data. In summary, this estimate is achieved by sampling from the posterior predictive distribution given a series of LC-MS/MS experiments and counting the amount of newly discovered peptides.

Section 2.1 briefly introduces Dirichlet processes and how these can be used to formally characterize peptide distributions arising in shotgun proteomics experiments. Section 2.2 characterizes the distribution from which peptides are sampled during an ideal LC-MS/MS experiment without false positive peptide-spectrum matches. Section 2.3 describes how to sample a series of peptides from such a distribution. Section 2.4 first describes how to sample from this distribution conditioned on the given data and second how to predict the progression of proteome coverage from the a posteriori sampled trajectories. Section 2.5 completes the framework description by introducing a component accounting for false positive peptide-spectrum matches.

Unless otherwise noted, in the following π will denote a series of sampled peptides π_t. Capital italic latin letters like G, H will denote distributions.

2.1 Dirichlet processes priors for peptide distributions

In the course of a shotgun proteomics experiment, peptides are sampled from an unknown distribution and then identified by mass spectrometrical analysis. This distribution is defined by the biological sample contributing a characteristic set of proteins/peptides and by the experimental setup enriching/depleting particular types of proteins/peptides. The more samples we draw from this distribution, i.e. the more experiments we perform, the better we are able to characterize the distribution and thereby predict the future progression of peptide discoveries.

The incremental estimation procedure is captured by a non-parametric Bayesian technique, denoted as Chinese restaurant processes (Blackwell and MacQueen, 1973). The Chinese restaurant process can be envisioned as a schematic task where n customers are to be seated in a restaurant with an infinite number of tables. At each table a particular dish is served that is denoted by its number in the menu. The first customer is seated at the first table and offered the corresponding dish π₁. The t-th subsequent customer is offered his dish π_t after having been seated either at an already populated table or at a new unpopulated table according to the following probabilities:

(1)

where n_i corresponds to the number of customers already sitting at the table serving dish i. In case a customer happens to be seated at a new table, the dish served at this table is drawn from the base probability measure H. γ is referred to as the concentration parameter of the process. The larger γ, the higher the chances that a new customer is seated at a new table. The more customers have already been seated, the less likely it will open up a new table.

Let us now assume that we do not know γ and have seated n customers. We want to estimate how many tables will be occupied, or equivalently how many different dishes will be served after m additional customers have been seated. In a first step, we characterize the seating distribution by fitting γ according to the observed seating arrangement, i.e. the more tables we find populated the larger we choose γ. We can now simulate m additional seating events using the γ estimate and thereby estimate the number of tables occupied afterwards.

By identifying dishes with peptides and, respectively, customers with mass spectra, we obtain a simple model to sample peptide assignments, i.e. simulate experiments and in particular estimate the expected number of new peptide discoveries. Although being overly simple, this model captures an essential property of shotgun proteomics experiments. While always allowing to discover a novel peptide with non-zero probability, the overall progression of new discoveries slows down for a growing number of experiments.

It turns out that a Chinese restaurant process with concentration parameter γ implements draws π_t from a discrete distribution G that itself is drawn from a prior distribution referred to as Dirichlet process DP with concentration parameter γ and base probability measure H (Antoniak, 1974; Ferguson, 1973):

(2)

Dirichlet processes have proven to be useful to formally express and deal with the uncertainty of an unknown discrete distribution, e.g. mixing distributions of mixture models. In this work, we assume Dirichlet process priors for distributions over peptides and sample from them by using the Chinese restaurant process construction.

2.2 Infinite Markov model for LC-MS/MS experiments

During an LC-MS/MS experiment, peptides designated for tandem mass spectrometry are sampled from a multitude of unknown distributions (Fig. 1). This section describes how to model these distributions with an infinite Markov model.

The peptides in the initial ensemble are distributed according to an unknown discrete distribution G₀. We assume a Dirichlet process prior DP(γ, H) for G₀ with base probability measure H and concentration parameter γ. H is assumed to be the uniform distribution over the peptides defined by the protein database 𝒟. Note that the prior DP(γ, H) does not necessarily identify G₀ with H, i.e. the uniform distribution over the protein database 𝒟.

Peptides are not directly sampled from G₀ in an LC-MS/MS experiment (Fig. 1). In the course of liquid chromatography, the mass spectrometer is exposed to a subpopulation of the initial ensemble, confined to members within a time-dependent polarity range. Depending on the time point t, peptides are thus sampled from a characteristic peptide distribution G_t that is ‘related’ to G₀. The prior for G_t has to capture the dependency on G₀. We particularly require the support of G_t to be contained in the support of G₀. While retaining flexibility, this requirement is met by choosing the prior for G_t to be a Dirichlet process with base probability measure G₀ and concentration parameter β (Teh et al., 2006).

Due to technical difficulties to reproduce absolute time courses for a series of LC-MS/MS experiments, we abstain from explicitly modeling polarity and, thereby, G_t. Instead, we represent time or, respectively, ensemble polarity by peptide identities. We denote G_i as the local peptide distribution at the time points where peptide i has been identified. Assume that we have sampled π_t−1 = i in the course of an experiment. Since π_t−1 = i is indicative for the current polarity, we assume the subsequent peptide π_t to be sampled from the local distribution G_i (Fig. 1).

This representation induces a Markov chain whose states correspond to the identified peptides. We assume each state sequence π to begin at a distinguished start state π^∗, i.e. we assume π₀∼δ_π^∗. Following (Beal et al., 2002), we define the prior of G_i to be a biased Dirichlet Process DP_i with base probability measure G₀, concentration parameter β and additional prior weight α on state i. Thereby, α explicitly controls the rate of sampling self−transitions π_t = π_t−1 = i. Having a Dirichlet process prior on G₀, the number of sampled states is not fixed a priori and steadily grows with the number of sampled transitions. Due to the Dirichlet process prior on the local probability distributions G_i, the occurrence of transitions evolves in a similar fashion. We obtain the full characterization of the distribution that is sampled in the course of an LC-MS/MS experiment:

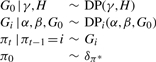(3)

2.3 Sampling sequences of peptide identifications

In the following, we describe how to sample series of peptides from the distribution defined in the preceding section. Assume that α, β, γ, H, q are given and m series π = π⁽¹⁾,…, π^(m) are to be sampled sequentially.

We assume each series π^(k) to begin at a distinguished start state π^∗. π can be sampled in ascending order. To see this, assume that we already sampled the trajectory π₀, π₁,…, π_t−1. In order to sample the subsequent peptide, we have to specify the distribution for π_t | π₀, π₁,…, π_t−1, α, β, γ, H. Starting from the hierarchy of Dirichlet processes (3) and after integrating out G_πt−1 and G₀ we obtain a nested variant of the Chinese restaurant process construction (1) for the infinite Markov model:

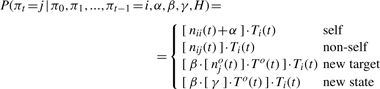(4)

n_ij(t) corresponds to the number of occurrences of observing the transition from peptide i to peptide j in the series π₀,…, π_t−2. n^o_j(t) denotes how many times peptide j has been observed as a new transition target in the series π₀,…, π_t−1. T_i(t) is shorthand for (∑_jn_ij(t)+α+β)⁻¹ and T^o(t) for (∑_jn^o_j+γ)⁻¹.

The outcome ‘self’ denotes a self-transitions π_t = π_t−1. Accordingly, ‘non-self’ corresponds to already observed transitions π_t ≠ π_t−1. Note the distinguished role of self-transitions by the prior weight α. While the event ‘new target’ refers to the discovery of a new transition to a peptide already observed in another context, ‘new state’ denotes the discovery of a yet unobserved peptide. It is straight forward to sample the random variable π_t | π₀, π₁,…, π_t−1 = i, α, β, γ, H since its distribution has a closed form and only depends on the given parameters and quantities defined by the series of preceding peptide assignments.

2.4 Posterior prediction of proteome coverage progression

This section describes how to sample peptide series conditioned on already observed series. This task translates to sampling the posterior predictive distribution for π_new given the observed peptides π. Proteome coverage progression for future experiments is estimated by approximating the expected number E[|𝒰(π_new)| | π, H] of new peptide discoveries 𝒰(π_new) upon posterior predictive sampling.

The posterior predictive distribution for π_new | π, H has no closed form. For sufficiently large series π, the posterior predictive distribution can be reasonably approximated by π_new | π, θ_ML, H where θ_ML corresponds to the maximum likelihood estimate for θ ≔(α, β, γ)

(5)

We predict the proteome coverage progression by approximating E[|𝒰(π_new)| | π, H] by averaging over a set of trajectories π₁, π₂,… sampled from π_new | π, θ_ML, H as described in Section 2.3.

2.5 Proteome coverage progression with false identifications

Sequences π of peptide assignments were assumed to be perfect in the preceding sections. Obviously this assumption does not hold in practice. This section describes an extension of the infinite Markov model by an error model that is able to deal with series of peptide assignments that are afflicted with a non-zero false discovery rate q.

We observe that false positive peptide assignments map to the decoy database in a non-redundant fashion, i.e. 83% of all decoy peptide discoveries of the test dataset (see Section 3) are supported only by a single peptide assignment. Assuming that false positive peptide assignments distribute like decoy peptide assignments (Elias and Gygi, 2007), we approximate the distribution of false positive peptide assignments with H, i.e. the uniform distribution over the protein database. In order to model the fraction q of false positive peptide assignments, we assume that peptide assignments are sampled from a mixture model with two components. The first component accounting for the true positive peptide assignments is given by the infinite Markov model as described in Section 2.2. The second component is given by the distribution of false positive peptide assignments, i.e. H. Component weights are chosen according to the false discovery rate q. Consequently, the first and second component are weighted 1−q or q, respectively.

Series of peptide assignments are generated by sampling each peptide assignment π_t either from the infinite Markov model as described in Section 2.3 or directly from H, according to the components weights. Posterior sampling requires the estimate θ_ML from an already observed series π. Exact computation of θ_ML though involves an intractable sum over configurations of false positive peptide assignments. We approximate θ_ML by assuming that the number of false positive peptide assignments equals the expected value n(1−q) and that these distribute uniformly over π. This assumption allows us to approximate P(π | θ, H, q) with adjusted transition counts, e.g. .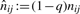

(6)

Proteome coverage progression is then predicted as described in Section 2.4.

3 RESULTS

In the following, we show results that first, demonstrate that prediction of proteome coverage progression is a non-trivial task that is not solved satisfactory by simple extrapolation methods and second, that the extended infinite Markov model can confidently predict proteome coverage progression from a small number of already performed experiments and third, that we can identify the putative number of LC-MS/MS experiments to be carried out until reaching maximal coverage.

We conducted simulation studies to ensure that we can confidently estimate α, β, γ. Therefore, we generated a dataset by simulating peptide series with false discovery rate of 1% as described in Section 2.5. Parameters α, β, γ were chosen in a range also observed in the real-world test dataset that is introduced later. We assessed the estimates on 20 simulated series, each corresponding to multiple LC-MS/MS experiments. Each set of 20 series was chosen to be of length ranging from 1000 to 15 000 peptide assignments. For each of these series we estimated α, β, γ as described in Sections 2.4 and 2.5 (Fig. 2). It can be seen that α, β, γ can be reasonably recovered even from the smallest training series. The larger the series grows the more precise the estimates become. The approximations introduced in Section 2.5 to account for false positive peptide assignments do not compromise the parameter estimates. Considering the equivalent of six or more LC-MS/MS experiments already yielded satisfactory estimates.

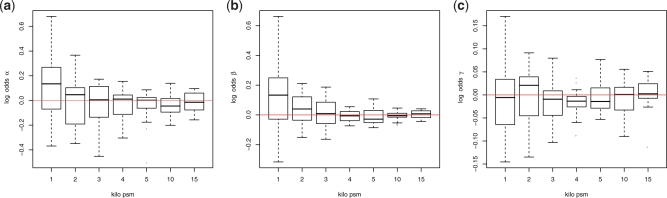
Fig. 2.

θ_ML estimate on simulated data. Performance is evaluated for different training set sizes, i.e. series of peptide assignments (psm) of length ranging from 1000 to 15 000. Performance is reported as log odds of predicted and true parameter value. Results are shown for parameters α, β, γ, respectively, governing the events of self-transitions (a), new transitions (b) and globally new discoveries (c). It can be seen that the parameters can be confidently estimated considering a training series of 10000 peptide assignments.

We assessed DiriSim's ability to predict proteome coverage progression for real LC-MS/MS experiments. We consider proteome coverage to be the number of peptide discoveries, i.e. the number of different peptides represented in the series of peptide assignments. We were particularly interested to see how many LC-MS/MS experiments are needed to confidently extrapolate the progression of peptide discoveries. We expected that confident extrapolation is feasible after training DiriSim on a small training series of peptide assignments corresponding to a small number of LC-MS/MS experiments.

To this end, we applied DiriSim to a test dataset covering 37 LC-MS/MS experiments of the complete Drosophila melanogaster proteome (Schmidt et al., 2008). Peptide-spectrum matches were generated by searching against a target–decoy protein database (tryptic, ≤1 missed cleavage), for details see (Schmidt et al., 2008). For our study, we selected top-scoring peptide-spectrum matches mapping to the target database at a false discovery rate of 1% as described in (Elias and Gygi, 2007). By this means, we finally considered 61 582 peptide-spectrum matches. We generated training series of varying size by subsampling the dataset, extrapolated the progression of peptide discoveries for each training series and compared to the observed progression of the complete dataset.

In total, we subsampled 120 training series of peptide assignments. Note that the subsampling procedure has to preserve the peptide assignments order within the individual LC-MS/MS experiments. Therefore, we generated the training series by subsampling complete LC-MS/MS experiments. We subsampled 1, 2, 3, 4, 5 and 10 LC-MS/MS experiments, giving rise to 6 training series of peptide assignments. By repeating this step 20 times we generated a total of 120 training series. For instance, one of the training series comprised the series of 1139 peptide assignments defined by the two LC-MS/MS experiments with index 14 and 18 (out of all 37 experiments). The 120 training series varied in size, ranging from 596 to 20 277 peptide assignments, i.e. covering up to one-third of the complete dataset's peptide assignments. Note that two training series that were generated by subsampling the same number of LC-MS/MS experiments do not necessarily comprise the same number of peptide assignments. This is due to the heterogeneous number of peptide assignments contributed by the individual LC-MS/MS experiments.

We extrapolated the progression of peptide discoveries for each training sequence and compared to the observed progression of the complete dataset. Therefore, we estimated α, β, γ and estimated the expected proteome coverage progression by averaging over 50 series sampled from the posterior predictive distribution of the extended infinite Markov model (see Sections 2.4 and 2.5). Goodness of the prediction was evaluated as rmsd from the observed progression of the complete dataset. Training series in corresponding to six or more average LC-MS/MS experiments (approximately 1600 peptide assignments) yield good matches (Fig. 3a and b). These results demonstrate that first, the principles governing the yield of LC-MS/MS experiments seem to be well captured by the extended infinite Markov model and second, proteome coverage progression can be confidently predicted from a considerably small set of experiments.

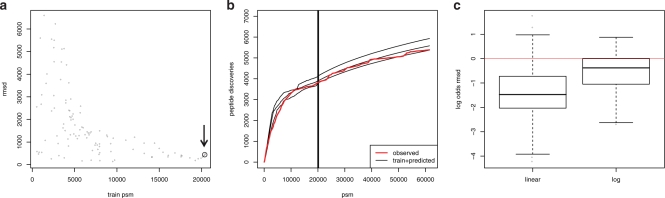
Fig. 3.

Prediction of proteome coverage progression for a dataset comprising 37 LC-MS/MS experiments each giving rise to a series of peptide assignments (psm). We generated 120 training series of varying size (train psm) by subsampling complete LC-MS/MS experiments. We predicted the progression of proteome coverage (peptide discoveries) for each training series and compared to the progression observed for the series of the complete dataset. (a) Prediction accuracy for the 120 training series. Prediction accuracy is given as root mean square deviation (rmsd) from the observed progression of peptide discoveries. (b) Concatenated training and respective predicted progressions (black) from the largest three training series [corresponding items in (a) are encircled] compared to observed progression (red). Vertical lines denote the size of the training series. Vertical lines overlap due to similar sizes around 20 000. (c) Comparison of DiriSim with linear extrapolation of proteome coverage progression of last LC-MS/MS experiment in training series (linear) or respectively extrapolation of logarithmic regression of training series (log). Box plot of log odds of rmsd [log(rmsd_DiriSim/rmsd_compare)] for DiriSim and compared method (linear, log) on the 120 training series. Median log odds for comparison with the extrapolation methods linear and log are lower than 0, indicating weaker performance than DiriSim.

We compared DiriSim with other extrapolation methods. We chose two simple general purpose extrapolation methods since there do not exist specific methods for proteome coverage prediction. We first considered an extrapolation scheme that linearly extrapolated proteome coverage progression of the last LC-MS/MS experiment of a training series. Second, we considered the extrapolation of a logarithmic regression (y=alogx + b). We assessed prediction performance on the 120 training series as described above and observed that DiriSim clearly outperforms both extrapolation methods (Fig. 3c). These results indicate that proteome coverage prediction is a non-trivial task that is not solved satisfactory by ad hoc extrapolation methods.

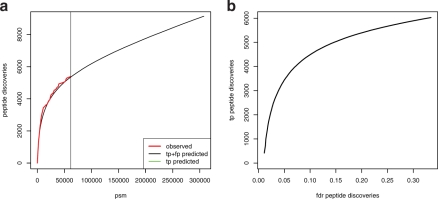
We further extrapolated the coverage progression 5-fold beyond the range covered by the test dataset (Fig. 4a). The progression of peptide discoveries for all peptide assignments shows a linear increase. Since DiriSim explicitly models true and false positive samples, we could exclusively monitor the series of true positive peptide assignments. We observe a pronounced divergence of the progression for all assignments and the exclusively true positive ones. We particularly see that the progression of true positive discoveries stagnates considerably. While the fraction of false positive peptide assignments is constantly held at 1%, the fraction of false positive peptide discoveries at the end of the predicted progression amounts to >30%. The fraction of false positives among the novel discoveries beyond the range of the test set even surmounts 60%. Tolerating a limited amount of false positive peptide discoveries, bounds the maximal number of possible peptide discoveries as well as the number of experiments having to be performed (Fig. 4b). For instance, assume that we require that at most 15% of all peptide discoveries are false positive. This constraint restricts the maximally achievable coverage since we can discover at most 5000 distinct true positive peptides. According to Fig. 4a we will have reached this point after having acquired 90 000 peptide assignments.

Fig. 4.

The 5-fold extrapolation beyond the range of the test dataset. (a) Observed progression of the test dataset in red, predicted progression with standard deviations of all (black) and only true positive (green) peptide discoveries. The progression of true positive discoveries stagnates considerably. (b) Relates the absolute number of true positive (tp) peptide discoveries to the fraction of false positive discoveries (fdr peptide discoveries). The fraction of false positive peptide discoveries grows steadily with the total amount of peptide discoveries. Quality requirements on the final set of peptide discoveries limit the maximally achievable proteome coverage as well as the sensible number of LC-MS/MS experiments.

4 DISCUSSION

To date, it is not clear beforehand how often to repeat an LC-MS/MS experiment on a single biological sample in order to efficiently achieve satisfactory proteome coverage. Furthermore, the maximally achievable proteome coverage with a particular method is not known. We address these issues by presenting DiriSim, a framework to predict the progression of proteome coverage for LC-MS/MS experiments.

DiriSim models a series of LC-MS/MS experiments as an infinite Markov model, whose states correspond to peptides. We apply DiriSim to extrapolate the proteome coverage progression of a small number of already performed LC-MS/MS experiments. Note that this task is different to the a posteriori inference of the state sequence of these experiments. In contrast to previous applications (Beal et al., 2002; Sohn and Xing, 2007), a posteriori inference of the state sequence is furthermore not necessary, since the states (peptides) are already assigned to the observable variables (tandem mass spectra) by means of the corresponding peptide-spectrum matches. Besides its application in proteome coverage prediction, the infinite Markov model could though serve as a prior in a Bayesian peptide identification setting and, in particular, prevent the accumulation of false positive peptide discoveries coming along with increasing dataset size.

LC-MS/MS experiments are typically analyzed by database searching. The underlying protein databases are large but still of finite size and therefore define a finitely large set of possibly identified peptides. De novo sequencing approaches infer peptide identities without relying on protein databases and thereby implicitly support an infinite number of possible peptide identities. Using an appropriate base probability measure H, the proposed infinite Markov model for LC-MS/MS experiments naturally lends itself to predict the proteome coverage in this context.

We have shown that DiriSim correctly extrapolates proteome coverage progression from at most 10 LC-MS/MS experiments and outperforms ad hoc extrapolation methods. Proteome coverage prediction appears to be a non-trivial task due to the intricate dependency structure of an LC-MS/MS experiment. DiriSim provides a comprehensive non-parametric Bayesian characterization of an LC-MS/MS experiment that enabled us to confidently predict proteome coverage. Although capturing the dependencies of LC-MS/MS experiments, DiriSim remains a robust, non-complex model since it only needs three parameters that are to be learnt from data.

By explicitly modeling false and true positive peptide assignments, DiriSim enables us to specify the maximally achievable proteome coverage with regards to true positive peptide discoveries. We have seen in the simulations that new peptide discoveries from extensive repetition of LC-MS/MS experiments mostly accumulate false positive discoveries. This observation reflects the difference between the distributions for true and false positive peptide assignments. While true positive peptide assignments concentrate over a small subset of the protein database, false positive peptide assignments distribute broadly over the protein database and therefore mostly contribute false positive peptide discoveries. Due to the exceedingly broad distribution of decoy matches, we do not expect that errors possibly introduced by the uniformity approximation compromise the observed accumulation of false positive peptide discoveries. We conclude that performing more and more experiments seeking for maximal coverage mainly deteriorates the overall quality of the complete peptide discovery set. Depending on the false discovery rate of the peptide assignments, a quality requirement on the set of peptide discoveries imposes an upper bound to the total number of experiments, which therefore, potentially limits the maximally achievable proteome coverage before the progression of true positive peptide discoveries is fully saturated. This limitation accrues from the occurrence of erroneous peptide-spectrum matches and their broad distribution over the protein database. As long as peptide-spectrum matches are afflicted with uncertainty, this reasoning holds for any proteome being studied. It will though be interesting to apply DiriSim to other datasets in order to study the quantitative impact of factors like proteome size and experimental setup on the maximally achievable proteome coverage. In summary, our results suggest that the design of large shotgun proteomics studies should focus on efficiency not only to save resources but, most importantly, to yield reliable peptide discoveries.