Causal Mediation Analyses for Randomized Trials

SUMMARY

In the context of randomized intervention trials, we describe causal methods for analyzing how post-randomization factors constitute the process through which randomized baseline interventions act on outcomes. Traditionally, such mediation analyses have been undertaken with great caution, because they assume that the mediating factor is also randomly assigned to individuals in addition to the randomized baseline intervention (i.e., sequential ignorability). Because the mediating factors are typically not randomized, such analyses are unprotected from unmeasured confounders that may lead to biased inference. We review several causal approaches that attempt to reduce such bias without assuming that the mediating factor is randomized. However, these causal approaches require certain interaction assumptions that may be assessed if there is enough treatment heterogeneity with respect to the mediator. We describe available estimation procedures in the context of several examples from the literature and provide resources for software code.

1. Introduction

With randomized studies, researchers want to know not only if randomized interventions work, but how they work by post-randomization mechanism or mediating variables. Knowing how an intervention works allows researchers to tailor specific elements of an intervention to achieve a specific effect or to search for other interventions that might affect the mediation variables. The analysis of mediating variables is crucial both to understanding and developing effective interventions by assessing if baseline interventions directly impact outcome holding post-baseline mediation factors constant and/or impact outcomes indirectly by assessing how the baseline intervention factor affects the mediating factor with a subsequent effect on outcome.

The motivation for the investigation of mediators of reported significant interventions arises from completed and ongoing randomized intervention studies and from policy papers on mediation. In response to advocacy papers on mediation in such contexts as community interventions, psychiatry, and substance abuse (Kraemer et al. (2002); Baranowski (1997); Kazdin (2007)), these studies have focused on intervention/mediation contexts such as: 1) family and social support mediating the effect of care manager-based interventions on depression in elderly primary care patients (Bruce et al. (2004)); pain interference and depression mediating the effectiveness of integrated mental health care on alcohol-dependence in elderly primary care patients (Mavandadi et al. (2007)); adjuvant talk therapy mediating the effect of cognitive behavioral therapy (CBT) on risk factors for suicide re-attempts among suicide-attempters (Brown et al. (2005)); and provider prescription and patient adherence behavior mediating the effect of nurse-based interventions on safe sex behavior among community-based seriously mentally ill patients with HIV.

It is well known that randomization minimizes unmeasured confounding when comparing treatment groups in intervention studies, but not when analyzing post-randomization factors, such as mediation variables. Holland (1986) used the example of a study in which students were 1) encouraged to study for a test, or 2) not encouraged to study. The meditating variable would be how much they then studied for the test, but the experimenter has no direct control over the amount of studying. Suppose the encouragement caused the lower performing students to study more, but they were unable to benefit from their ineffcient study habits, while the better students studied somewhat less because the encouragement condition had recommendations for minimum study times. Randomizing students to encouragement or not would not preclude potential confounding of the mediation relationships between non-randomized study time and the outcome.

Because baseline randomization does not protect against confounding of the mediation relationship, standard mediation approaches (e.g., regression, path, and structural equation (SEM)) require the sequential ignorability assumption for validity. That is, study participants are assumed to be randomized to their observed levels of the baseline intervention and also to the observed levels of the post-randomization mediating variables (e.g., Robins (1999)). While this is a reasonable assumption for the intervention assignment, it may not be feasible for post-randomization mediators. Hence, standard approaches have been cautiously used for randomized trials with only randomization of the baseline intervention. Additionally, interpretation of mediation effects under the standard mediation methods requires that one can manipulate the mediator such that it can be fixed to be a specific level by an investigator or clinician. With post-randomization factors that are based on behavior of either patients or their care providers, strategies for manipulating such behavior may not be plausible (Robins (1999); Pearl (2001)).

The sequential ignorability assumption may be untenable in many clinical and behavioral intervention trials even when adjusting for observed covariates. This untenability was highlighted with a discrepancy between results from a Women’s Health Initiative (WHI) clinical trial and observational studies in the context of hormonal replacement therapy (HRT) for post-menopausal cardiovascular disease (Prentice et al. (2005)). More in the context of mediation, Ten Have et al. (2007) presented contradicting evidence for the mediation of CBT on suicidality by adjuvant therapy depending on whether the sequential ignorability assumption is made. These examples reveal practical vulnerabilities of methods and studies that assume sequential ignorability and thus the need for sensitivity analyses including methods that do not make this assumption.

There is much literature on mediation approaches assuming sequential ignorability in a variety of contexts (Judd and Kenny (1981); Baron and Kenny (1986); MacKinnon et al. (2002); Kraemer et al. (2001, 2002); Gollob and Reichardt (1987, 1991); Krull and MacKinnon (1999, 2001); MacKinnon and Dwyer (1993); Cole and Maxwell (2003); Kenny et al. (2003); Cole and Maxwell (2003)). With a standard regression approach, Baron and Kenny (1986) brought the concept of mediation to the forefront in psychological research. Their article suggested a sequence of steps for testing the mediation model. Recent work has extended this approach to more complex designs (Krull and MacKinnon (1999, 2001); Kenny et al. (2003)) and to settings involving multiple measurements of intervention level, mediators, and outcomes over time (Cole and Maxwell (2003)).

To understand these steps, the mediation context is defined as follows. We refer to the intervention, which is randomized at baseline, as the baseline intervention. The group randomized to the baseline intervention is the randomized intervention group, and the group randomized to the non-intervention group (e.g., usual care) is the randomized comparison group. The mediator is the post-randomization factor measured for all study participants and occurring after the baseline intervention is assigned but not necessarily finished. The outcome is the measured response variable occurring after the baseline intervention and mediator. The pathway between the randomized baseline intervention and the outcome through this mediation variable is the indirect effect, and the pathway between the randomized baseline intervention and outcome around this mediator is the direct effect. The overall effect of the baseline intervention on outcome (i.e., intent-to-treat effect on the outcome) represents some combination of the direct and indirect effects. In the linear model, the intent-to-treat effect is a linear combination of the direct and indirect effects. In this context, Baron and Kenny (1986) presented a strategy based on estimating the direct effect and its significance, along with evaluation of relationships pertaining to the indirect effects. To illustrate and compare the causal mediation methods with this standard strategy, we focus on estimating the direct effect, as the research on estimating causal indirect effects is still underway.

The decomposition of the intent-to-treat effect on outcome into direct and indirect effects under both standard and causal approaches presents several methodological challenges (e.g., Robins (1999); Pearl (2001)). First, the decomposition does not accommodate very easily more complex models such as linear models with interactions between the baseline intervention and mediator or non-linear models even without interactions. Second, as discussed in Section 5, the interpretation of the direct effect under the decomposition assumes that the mediator can be manipulated by a clinician to a fixed level, which may be implausible for hard-to-control behavioral or clinical mediation factors such as pain interference and intermediate risk factors for depression.

Relying on baseline randomization and other assumptions, several different causal methods relax the sequential ignorability assumption in precluding the need for randomization of the post-randomization mediation factors. Without this assumption, there are not enough likelihood or estimating equations for all of the model parameters under the standard mediation approaches. Thus solving these equations leads to multiple solutions or sets of estimates of model parameters (i.e., non-identifiability; Robins and Rotnitzky (2005)). The causal methods that do not assume randomization of the mediator require other assumptions to increase the number of estimating equations with unique solutions. These assumptions entail relationships among baseline covariates, the randomized baseline intervention, and the post-randomization mediators and also model assumptions involving the outcome.

In this paper, we present such causal mediation approaches in terms of the “Rubin Causal Model” (RCM) (Rubin (1974); Holland (1986)). We will not consider alternative causal frameworks such as acyclic graph theory that lead to equivalent inference as under the RCM (Pearl (1999)). Under the RCM, causal inference is defined in terms of contrasts among multiple prospective outcomes defined under different conditions for the same individual, holding all other factors, observed and unobserved, constant (Neyman (1923)). Therefore, an obvious difficulty of causal inference is that only the prospective outcome under the intervention condition that actually took place is observed for each individual. For causal inference, Neyman (1923) introduced the concept of potential outcomes to accommodate the set of multiple prospective outcomes defined by different intervention conditions. The observed outcome is the potential outcome for which the intervention index is observed; the remaining potential outcomes for an individual are not observed and sometimes called counterfactuals. Because causal inference defined in terms of the RCM entails contrasts of the observed outcome with unobserved counterfactual outcomes, assumptions need to be made about the relationship of these unobserved potential outcomes with observed factors to establish identifiability of causal parameters in terms of a suffcient number of non-collinear estimating equations.

We present two casual modeling approaches under the RCM framework in the randomized trial-mediation context: 1) the structural mean model (SMM) (e.g., Robins (1994); Ten Have et al. (2004, 2007); and 2) principal stratification (PS) (e.g., Frangakis and Rubin (2002); Frangakis et al. (2004). These two causal approaches represent very different mediation strategies. The SMM-based approach follows more closely the traditional regression method of Baron and Kenny (1986), but trades the sequential ignorability assumption for assumed interactions between baseline covariates and the baseline intervention in terms of their impact on the mediator. These interactions lead to a suffcient number of estimating equations for the causal parameters. In contrast, the principal stratification method stratifies the population into partially latent classes (principal strata) based on potential observations for the mediator variable under each of the levels of the randomized intervention. Mediation analyses are then based on intent-to-treat effects of the randomized intervention on outcome within selected principal strata. Identification of these stratified intent-to-treat effects relies on relationships between baseline covariates and the probabilities of membership in these principal strata in addition to model assumptions for the outcome. Heterogeneity of intent-to-treat effects on outcome across these select principal strata provides one way of assessing the interactions involving the outcome as the dependent variable. Current research is focusing on a SMM approach to assessing such interactions (e.g., Joffe et al. (2007); Ten Have et al. (2007)).

We compare the above methods in this paper with respect to two behavioral intervention studies, which offer divergent conditions for illustrating the differences and similarities between the traditional and causal approaches. The first study is a suicide therapy study, which evaluated the effect of CBT versus usual care in treatment of suicide attempts, suicide ideation, hopelessness and depression in 120 patients who had recently attempted suicide (Brown et al. (2005)). The sample size for this investigation at 6 months is 101 due to drop-out, which appears to be weakly associated with the factors used in this analysis as well as others (p > 0.35; Brown et al. (2005)). We assess if the significant intent-to-treat effect of CBT on 6 month depression outcome as measured by the Beck Depression Inventory-II (BDI) was due to a direct effect apart from use of adjuvant therapy (mediator) between 4 and 6 months. Potential confounders of the mediator-outcome relationship include economic and personal stress reducing the motivation for adjuvant therapy and increasing the likelihood of depression in suicide attempters.

The second study, a suicide prevention study, compared collaborative care management for treating depression (and thus reducing the risk of suicide) with usual care in 293 elderly depressed primary care patients (Bruce et al. (2004)). The collaborative care management program in the intervention group was based on patient, primary care, staff and physician interactions with a nurse-level care manager. We evaluate if the significant intent-to-treat effect of the intervention on the 4 month Hamilton depression outcome was due to a direct effect apart from use of prescriptive anti-depressant medication (mediator) between baseline and 4 months. Potential unmeasured confounders of the medication-depression relationship include medical comorbidities at follow-up, which deter elderly depressed patients from taking anti-depressant medications because of so many other medications necessitated by their medical comorbidities, which also predispose patients to depression. As with the first study, potential baseline factors such as baseline depression and suicide ideation may have modified the significant effect of the care manager intervention and also the mediator, anti-depressant medication, on the follow-up depression outcome.

In the remainder of the paper, we first present notation in Section 2, and then assumptions, the standard and causal models, and corresponding estimation procedures in Section 3. We illustrate the approaches with two applications in Section 4. Finally, we summarize the presentation in Section 5.

2. Notation

In this section, we define notation for observed and potential variables for both the SMM and PS approaches. For causal inference, we then link the observed variables to the potential variables with causal models and assumptions.

2.1 Notation: Observed Random Variables

First, we define the observed random variables, distinguishing them from the corresponding potential outcomes that would be observed under certain intervention and mediating factor conditions. Let Y denote the observed random variable for the outcome, which for this paper is assumed to be continuous. Let R denote the observed binary random variable for the randomized baseline intervention assignment such that R = 1 if randomized to the baseline intervention; and R = 0 if randomized to the comparison group. We assume the observed mediator variable, denoted by M, is binary, such that M = 1 if the participant exhibits a positive level for the mediator (e.g., adjuvant psycho-therapy is not used); and M = 0 if the participant does not exhibit a positive level for the mediator (e.g., adjuvant psycho-therapy is used). The causal SMM approach extends in a straightforward way to continuous M, which is not necessarily the case with the PS approach. Finally, let X represent a vector of baseline, pre-randomization covariates. We suppress the index i to simplify notation, but note here that all subsequent notation applies to the i^th of n participants.

2.2 Notation: Potential Random Variables and Counterfactuals

In defining the potential variable notation, we index the potential variables with a randomized intervention level, r, and the mediation level, m. The indices, r and m, are not necessarily the observed levels of the randomized baseline intervention and mediation factors, but instead are specified or “set” to define contrasts of the potential outcome variables for an individual participant.

Before proceeding to the potential outcome notation for the causal mediation models, we consider as an introduction the potential outcome notation for the simple intent-to-treat effect in a randomized trial. In this context, the RCM distinguishes between the observed outcome, Y and the two potential outcomes denoted by Y_r (r ∈ {1, 0}), each of which would have been observed for that subject, had they been randomized to the the comparison group or the intervention, respectively. One of these potential outcomes will be observed, while the other will be an unobserved, or counterfactual, outcome. The corresponding causal effect in this simple case is the intent-to-treat (ITT) contrast between these two potential outcomes: i.e. E[Y₁ − Y₀], which can be estimated in an unbiased way with the observed ITT difference between baseline intervention sample means. The PS approach specifies ITT contrasts within each principal stratum defined by potential mediation behavior under each baseline intervention level.

We extend the potential outcomes framework to accommodate the mediation variable by using doubly indexed potential outcomes. Specifically, we let Y_rm denote the potential outcome for participant i that would occur if the baseline intervention, R, were set to level r, and if the mediator, M, were manipulated to level m. The goal of the SMM approach is then to estimate the average of the individual causal direct effect, Y_1m − Y_{0 m}, across individual participants. For the example studies in this paper, the mediator is binary, so that m ∈ {0, 1}. As a result, there are four potential outcomes (Y₁₁, Y₁₀,Y₀₁,Y₀₀) for each participant.

3. Models, Assumptions, and Estimation

We now present the standard, SMM, and PS mediation approaches separately in Sections 3.1, 3.2 and 3.3, respectively with corresponding assumptions and estimation procedures. We first review the common assumptions for the causal approaches: SUTVA (no interference and consistency assumptions) and randomization. After presenting each of the three approaches, we then compare them in Section 3.4 and discuss software in Section 3.5.

The “no interference between study units” part of SUTVA is needed to use the above potential variable notation with scalar indices rather than vector indices representing treatment assignment and/or mediation status of other subjects. That is, Y_rm is used rather than Y_{r m}, where r and m are the vectors of manipulated baseline intervention and mediator levels for all subjects. Departures from this assumption may occur when interventions such as behavioral or educational interventions are administered at the primary practice or provider level, such as in our examples. For example, when a provider administers the intervention to encourage depressed patients to take prescribed treatment for depression, the provider may learn from previous study patients and apply what he or she learns to subsequent study patients.

The consistency assumption of SUTVA is needed for estimation by linking the potential outcomes to the observed outcomes. In words, the consistency assumption implies that the observed random variable will equal one of the corresponding potential random variables even if the administration of treatment assignment and mediation behavior vary slightly (e.g., Rubin (1986)). The consistency assumption is violated when there are different versions of a treatment not reflected in the variable notation. Such violations may occur when there are different forms of administration such as interactions between the provider and patients through phone or in-person contact.

The randomization assumption implies interventions are randomly assigned to participants and that baseline variables, including potential outcomes and potential mediation behavior, are independent of randomization. That is, all unmeasured factors are equally distributed between the two groups. A weaker form of the randomization assumption requires that the potential random variables are independent of randomization, given baseline covariates. The randomization assumption is necessary for estimation in combination with SUTVA to relate the models for the observed random variables to the causal models of their respective potential variables (e.g., Angrist et al. (1996)). Furthermore, to identify causal effects within principal strata, the PS approach depends on the independence assumption between randomization and the potential mediation behavior variables, upon which the the principal stratification classes are defined. Randomized trials where the randomization unit is a cluster such as in the practice-randomized study in our example may be vulnerable to departures from this assumption. First, the number of randomized clusters is often small (e.g., 20), which increases the chances of unobserved covariate imbalance between randomization arms. Second, patients are often recruited into the clusters after the clusters are randomized. Hence, there may be selection bias in spite of randomization.

The causal SMM and PS approaches described below require additional assumptions beyond the ones specified above, but not the sequential ignorability assumption. Some of these additional assumptions involve the baseline covariates and baseline intervention in terms of their impact on the mediation factor. The stronger the impact of the baseline covariates on the mediator, the more identified the causal parameters under both the SMM and PS approaches.

3.1 Models: Standard Mediation Model, Assumptions, and Estimation

The standard linear regression model that corresponds most closely to the causal models under consideration is given by:

$$Y={\theta }_{MS}\stackrel{\sim }{m}+{\theta }_{RS}\stackrel{\sim }{r}+{\mathit{\beta }}_S^T\mathbf{x}+{\epsilon }_S$$ (1)

for all participants, where r̃ and m̃ denote the observed levels of R and M, respectively, because the “set” or fixed levels of R and M are denoted by r and m, respectively, in the definition of Y_rm. Here, β^T_S is the transpose of a column vector of regression coeffcients corresponding tothe column vector of observed baseline covariates x for the random variable vector X, and ε_S is an error term with finite variance equal to ${\sigma }_S^2$. Under sequential ignorability, we have E(ε_S | R = r, M = m, X = x) = 0, indicating the error term is mean independent of both R and M and also X. We contrast this with the conditional expectation of the error term under the SMM below, which is conditional on only R = r, and therefore independent of R but not M and X.

Without the sequential ignorability assumption, θ_RS and θ_MS still represent casual effects, but are not identified. Accordingly, the corresponding estimands of the ordinary least squares (OLS) estimators, say θ̃_RS and θ̃_MS, are defined as comparisons of expectations from different sample subgroups defined by observed r̃ and m˜, but not as causal contrasts. That is, θ̃_RS =E(Y | R = 1, M = m˜, X = x) − E(Y | R = 0, M = m˜, X = x); and θ̃_MS = E(Y | R = r̃ , M = 1, X = x) − E(Y | R = r˜, M = 0, X = x). These estimands will only equal the corresponding causal contrasts under sequential ignorability.

3.2 Models: Structural Mean Mediation Model, Assumptions, and Estimation

For the SMM approach, we actually use the rank preserving model (RPM) that is more analogous to the standard linear regression model in (1), but yet yields the same inference and estimation procedure as the SMM approach (e.g., Joffe et al. (1998); Ten Have et al. (2007)). Because of this equivalence, we continue with the SMM nomenclature to simplify the presentation of the RPM below. By analogy with the standard mediation model in (1), we have the following SMM for all of the potential outcomes denoted by Y_rm. In the case of two levels for R and M, we need separate causal models for each of the four potential outcomes (Y₁₁, Y₁₀, Y₀₁), and Y₀₀), in contrast to the standard linear regression model in (1), where we have only one model for Y :

$$Y_{rm}={\beta }_T\mathbf{X}+{\theta }_{M}m+{\theta }_{R}r+{\mathit{\beta }}^T\mathbf{x}+\epsilon$$ (2)

for all possible values of r and m. Here, β^Tis the transpose of a column vector of regression coeffcients corresponding to the vector of observed baseline covariates x, and the θ terms are the causal coeffcients. The ε term is a random error with distribution discussed below in terms of model assumptions.

The causal interpretation of the parameters θ_R and θ_M is dependent on the additive or linear nature of the part of the model involving these parameters and additional assumptions. However, we note that estimation of θ_R and θ_M as proposed by Ten Have et al. (2007) is asymptotically unbiased (i.e., for large sample sizes) even when the relationship between Y_rm and X as represented by the linear relationship β^Tx is not correctly specified (e.g, Robins 1994). The following assumptions do, however, need to hold. First, we assume we know or have unbiased estimates of the correct randomization probabilities (i.e., E(R|X = x) = p(x)), as investigators control the randomization process. Second, we assume that unlike the residual under the standard regression model in (1), ε is independent of R but not X and M : E(ε | R = r) = 0.

A number of no-interaction assumptions are implied by the linear SMM in (2). First, the causal effects (θ_R and θ_M ) do not differ across subgroups defined by observed covariates, i.e. there are no interactions involving the X variables in the above SMM. In addition, a causal interaction between M and R is assumed to be absent. Ten Have et al. (2007) showed the sensitivity of the SMM model in (2) to these no-interaction assumptions. Vansteelandt and Goetghebeur (2003), Ten Have et al. (2007), and Joffe et al. (2007) proposed some strategies for assessing these interactions causally under the SMM. Finally, the PS approach may offer one way of assessing causal interactions between R and M.

Under the above assumptions and model specifications for a specific individual participant, θ_M = Y_r1 −Y_r0 (i.e., the effect of changing mediation levels while fixing the baseline intervention at a specific level); and θ_R = Y_1m − Y_0m (i.e., the effect of changing baseline intervention levels while fixing the mediation variable at a specific level). Note that these causal contrasts represent differences for each individual participant in comparison to the contrasts between means representing different groups of participants under the standard regression model in (1). Accordingly, under sequential ignorability along with causal no interaction assumptions and correct specification of the covariate-outcome relationship, the causal parameters in (2) equal their respective association parameters in (1): θ_M = θ _{M S}; θ_R = θ_RS. That is, the association contrasts among group means distinguished by different observed values of R and M equals the corresponding individual level causal contrasts for individual participants under sequential ignorability.

Also under the above assumptions, the estimation procedure proposed by Ten Have et al. (2007) produces asymptotically unbiased estimators of θ_M and θ_R and corresponding standard errors under (2). That is, while these estimators may be somewhat biased for small sample sizes, this bias goes to zero as the sample size gets larger. Ten Have et al. (2007) showed with simulations that this estimation procedure produces accurate inference under two separate samples sizes ranging from 100 to 300. Estimation is implemented using G-estimation equations (Robins (1994)). The G-estimation equations represent extensions of randomization tests, relying on the correctly specified distribution for the randomized assignment of the baseline intervention, but also requiring a mapping of the observed outcome Y to the potential outcome Y₀₀ by subtracting off the estimated linear combination of parameters and observed values of R, M, and X in (2). A two-dimensional weight vector for each participant is incorporated into the G-estimation equations to obtain non-collinear identifying equations for each of the causal parameters, θ_R and θ_M. The specification of the weight elements is crucial in two ways. For identifiability, it is imperative that collinearity between the elements of the weights is minimized. For effciency of the G-estimation estimators, one of the weights requires strong baseline-covariate modification of the baseline intervention effect on the mediator. Then because of the correct specification of the randomization model, the resulting, identifying G-estimation estimating equations have zero expectation given R. Accordingly, they yield consistent estimators of θ_R and θ_M without assuming randomization of M but under the other assumptions described above. The estimating equations and resulting standard errors obtained from sandwich estimators are presented in Ten Have et al. (2007).

3.3 Models: Principal Stratification Mediation Model, Assumptions, and Estimation

The PS approach relies on estimating the baseline intervention effect within those latent sub-groups (i.e, principal strata) of participants who would naturally not change their mediator level regardless of the baseline intervention assignment (e.g., someone who would seek adjuvant psychotherapy regardless of whether they had CBT or not). This stratification occurs on the basis of their potential mediator behavior under each of the two randomized baseline intervention arms. Assuming the mediator is binary, two of the resulting four strata correspond to sub-classes of participants who wouldn’t change their mediator behavior if their baseline intervention assignment changed. Hence, the mediator is controlled for participants in these two separate classes, and as a result, the estimated baseline intervention effect in each of these classes is the direct effect of the intervention at least for these sub-groups of participants.

More specifically, with a binary mediator (e.g., adjuvant psychotherapy), four possible principal strata exist and have been interpreted as follows (Mealli and Rubin (2003) and Rubin (2004)). For the first principal stratum, the participant would exhibit a positive level for the post-randomization factor (e.g., no adjuvant therapy) if the patient were to be randomly assigned to the intervention arm, and vice versa if the patient were to be assigned to the comparison arm. In the adherence literature, this group would be called compliers. For the second principal stratum, the participant would exhibit a negative level for the post-randomization factor (e.g., adjuvant therapy) if the participant were to be randomly assigned to the intervention arm, and vice versa if the patient were to be assigned to the comparison arm. For adherence, this class would be called defiers. For the third principal stratum, the participant would exhibit a negative level for the post-randomization factor (e.g., adjuvant therapy) regardless of randomization status. This stratum would be called never takers in the adherence context. For the fourth principal stratum, the participant would exhibit a positive level for the post-randomization factor (e.g., no adjuvant therapy) regardless of randomization status. This group would be called always takers in terms of adherence. In the two principal strata for which the prospective post-randomization factor behavior (e.g., adjuvant therapy) is held constant when changing intervention conditions (e.g., CBT versus non-CBT), the baseline intervention effects within these “fixed mediator” principal strata (second and third strata above) are direct effects.

Given an observed baseline assignment status and also observed mediator level, each participant can potentially belong to either of two of the four principal strata. For example, a participant randomized to CBT and who did not seek adjuvant therapy would belong to either the principal stratum that never seeks adjuvant therapy or the one that does not seek adjuvant therapy only under CBT. In contrast, a participant randomized to the comparison group and who did not seek adjuvant therapy would belong to either the principal stratum that never seeks adjuvant therapy or the one that seeks adjuvant therapy only under CBT.

To estimate the ITT contrasts within each of the principal strata along with the probabilities of membership in each principal stratum, we need to specify a fully parametric model in addition to the SUTVA and baseline randomization assumption. The model that we consider for this mediation context is specified as follows for the potential outcome for the rth baseline intervention assignment and cth principal stratum:

$$Y_r={\theta }_{PSc}r+{\mathbf{x}}^T{\mathit{\beta }}_{PSc}+{\epsilon }_{rc}.$$ (3)

where c = 1 − 4 for the four principal strata. Here, β_{PS c} is the vector of covariate effects for the cth principal stratum. The causal parameter θ_{PS c} is the ITT effect for the cth principal stratum:

$${\theta }_{PSc}=E[Y_1\mid \mathbf{X}=\mathbf{x},C=c]-E[Y_0\mid \mathbf{X}=\mathbf{x},C=c].$$

The direct effects correspond to the ITT effects of the baseline intervention (θ_{PS c}) in the “fixed mediator” principal strata. Moreover, the standard ITT effect for the population equals the weighted sum of the stratum-specific ITT effects across all four strata with weights corresponding to probabilities of membership in each principal stratum, π_c = Pr(C = c|X = x), such that Σ_c π_c = 1:

$$E[Y\mid \mathbf{X}=\mathbf{x},R=1]-E[Y\mid \mathbf{X}=\mathbf{x},R=0]=\sum _{c}E[Y_1-Y_0\mid \mathbf{X}=\mathbf{x},C=c]{\pi }_c.$$ (4)

Additional model specification and corresponding assumptions are needed to identify the θ_{PS c} parameters. Principal Stratification models have often been identified, especially in the context of adherence to randomized treatment contexts, by a monotonicity assumption and then an exclusion restriction (e.g., Angrist et al. (1996)). Under the monotonicity assumption, the principal stratum that is analogous to the defier principal stratum in the adherence context does not exist. Several forms of the exclusion restriction have been specified, such as θ_{PS c} = 0 for the “fixed mediator” principal strata (e.g., Hirano et al. (2000); Frangakis et al. (2002)). That is, in this case, the exclusion restriction implies that the direct effect is zero in these two principal strata. The exclusion restriction and monotonicity assumptions are not consistent with the goal of mediation analyses in that there is no reason to believe that any one of the principal strata does not exist (unlike in adherence contexts), and clearly mediation analyses would not be possible if direct effects were assumed to be absent in the “fixed mediator” principal strata.

As a trade-off for monotonicity, the exclusion restriction, and sequential ignorability, the PS approach we consider requires assumptions involving strong covariate predictors of the principal strata and also parametric model assumptions for the outcome. First, a multinomial logit model is specified for the π_c probabilities as a function of baseline covariates. Also, unlike the SMM in (2), the error term in (3) is assumed to have a fully parametric distribution, such as normal with mean zero and finite variance ${\sigma }_S^2$. Inference based on such models appears to be sensitive to these distribution assumptions (Imbens and Rubin (1997); Hirano et al. (2000); Frangakis et al. (2004)). Assuming a normal distribution for ε_{r c}, Imbens and Rubin (1997) showed that the ITT effects in certain principal strata are biased under violations of this normality assumption. Observed and model-based posterior estimates of cumulative distribution functions for outcomes may be plotted to identify departures from the normality assumption. Additionally, separate variances may be assumed for the different principal strata under proper prior distributions to account for any departures from normality due to heteroscadacicity.

Estimation for the principal stratification procedure is based on a mixture of distributions across principal strata. Specifically, each participant’s likelihood is a mixture of two of the four densities corresponding to the possible principal strata given the observed M and R variables. Because of the identifiability problems with relaxing the sequential ignorability, monotonicity, and exclusion restriction assumptions, Bayesian techniques have been used to fit PS models in the mediation context (e.g., Hirano et al. (2000); Frangakis et al. (2002); Ten Have et al. (2004). The Markov Chain Monte Carlo (MCMC) technique may be used to implement this Bayesian mixture estimation with the specification of proper prior distributions (Hirano et al. (2000); Ten Have et al. (2004, 2007)).

3.4 Relationship between the standard, SMM, and PS approaches

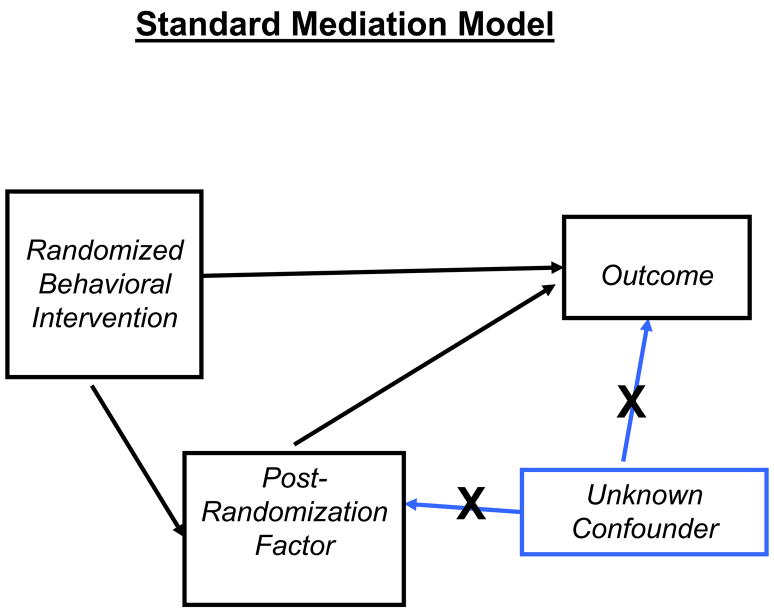
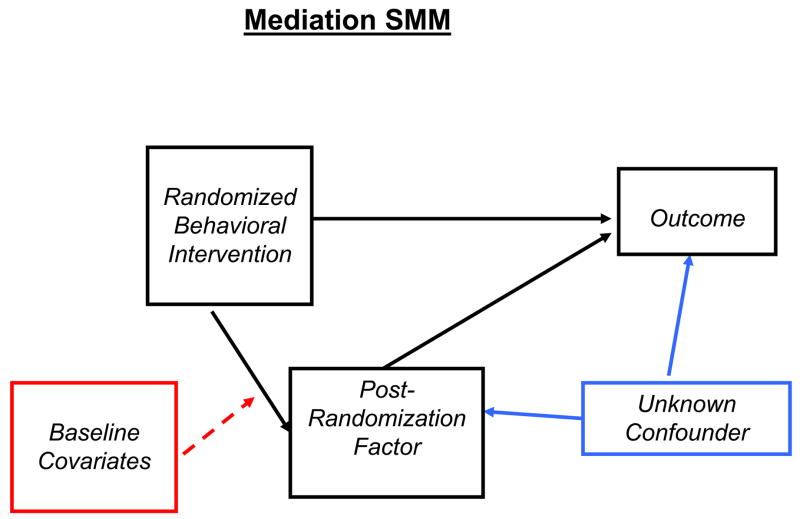
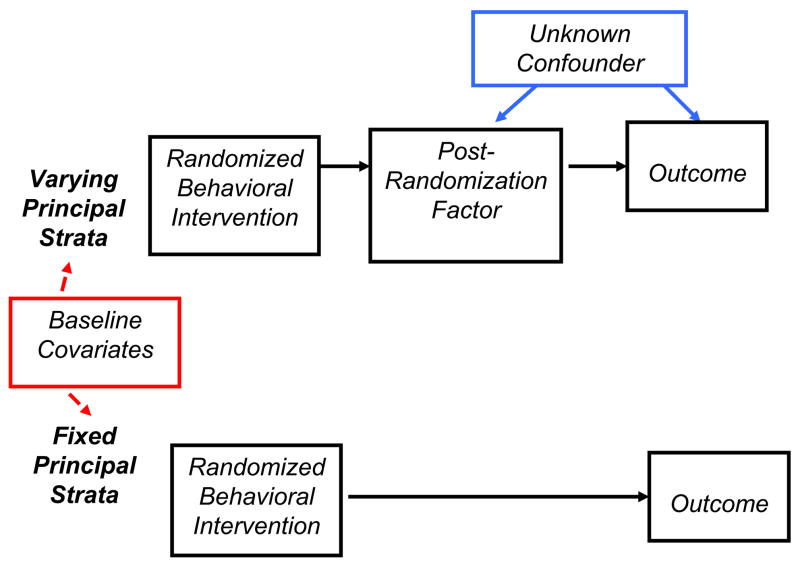
Figures 1, 2, and 3 highlight the differences and similarities between the standard, SMM, and PS mediation approaches. The differences are governed by how the causal approaches control for the confounded mediation effect on outcome when estimating the direct effects. As Figure 1 shows, the standard approach assumes the absence of unmeasured confounding represented by the “X’s” on the arrows from the unmeasured confounder to the mediator and outcome (i.e., sequential ignorability). Figure 2 also shows the tradeoff with the sequential ignorability assumption under the SMM approach represented by an arrow from the baseline covariates to the arrow from the baseline intervention to the mediator. This arrow, which does not appear in Figure 1 for the standard method, indicates the necessary interaction between baseline covariates and baseline intervention in terms of their effect on the outcome for the SMM. Such an interaction corresponds to one of the elements in the multi-dimensional weight vector that helps identify the causal parameters under the SMM. These differences notwithstanding, the similarity between Figures 1 and 2 indicates the common mediation strategy underlying these two approaches. In contrast, Figure 3 shows that the PS strategy controls for the potentially confounded mediator by stratifying the population of participants into latent sub-groups based on potential mediation behavior and then estimating baseline intervention ITT effects within these latent principal strata. The direct effects of the baseline intervention are the ITT effects in the principal strata in which the participants do not change their potential mediation behavior regardless of the baseline intervention assignment, as shown for the two “fixed mediator” principal strata in Figure 3.

Figure 1.

Schematic representation of the standard regression approach.

Figure 2.

Schematic representation of the structural mean model (SMM).

Figure 3.

Schematic representation of the principal stratification (PS) model.

The PS approach may be particularly more useful for hard-to-control behavioral mediation factors such as hopelessness in the context of the CBT suicide study. The traditional and SMM approaches assume that with the baseline intervention or a supplemental intervention, the mediator variable can be manipulated to equal particular levels (e.g., external therapy is obtained). This may be implausible with behavioral mediators, such as hopelessness, which are diffcult to control with such specificity under any intervention. In contrast, the PS approach stratifies the population into groups according to potential mediator behavior, precluding any manipulation of mediators.

Alternatively, several researchers (e.g., Pearl (2001) and Robins (2003)) have proposed the “natural” direct effect. Such an effect is interpreted as the effect of the baseline intervention on outcome assuming that the baseline intervention and possibly unmeasured (“natural”) factors have resulted in setting the mediator factor equal to a level potentially exhibited by the individual patient under a given level of the baseline intervention. Operationally, this amounts to averaging across the distribution of the potential mediation variable under a given baseline intervention, thus precluding the need to manipulate the mediation variable to a specific level.

3.5 Software Implementation

The causal mediation software necessary for the above approaches is not available commercially except for a limited case for the PS approach. For this strategy, we know of two available approaches for implementation. First, MPLUS produced by Statmodel Corp offers an estimate and standard error for the causal effects under a two-principal strata model, but not a four-principal strata model, with a macro “mix12.std” at http://www.statmodel.com/examples/mixture.shtml#r Moreover, a SAS macro for the principal stratification approach is available at http://www.cceb.upenn.edu/pages/tenhave/CausalMacro.zip with documentation at http://www.cceb.upenn.edu/pages/tenhave/CausalModelGuide.doc. This software was used for published analysis in Ten Have et al. (2004.

We do not know of any commercial software that implements the SMM and G-estimation, although SAS and SPLUS macro software is available. Specifically, the SAS macros for the SMM’s as they apply to the two example datasets in this paper (Suicide Prevention and Therapy Studies in Section 4) are available under the Paper Information link at the Biometrics website http://www.tibs.org/biometrics. More general software for more than two covariates will be available from the first author at ttenhave@upenn.edu. Additionally, the group led by Els Goetghebeur at the Ghent University, Belgium offers SAS and R (SPLUS) macro software at http://www.cvstat.ugent.be/noncompliance.htm.

4. Results for two behavioral intervention studies

The ensuing results for the two studies are taken from Ten Have et al. (2007). First, the descriptive statistics in Table 1 suggest similarities between the two examples in terms of the ITT comparisons of outcome but not in terms of the ITT comparison of the mediator factor. First, the ITT contrasts for outcome and mediator are significant in both studies. Hence, an analysis of the mediation of these significant ITT effects is justified. Second, Table 1 also indicates differences between the two examples in terms of the level of use of the mediator factor by patients and also the sign of the ITT effect on the mediator factors. Most of the depressed patients in the suicide prevention study used medication regardless of whether they were in the care manager arm or not. In contrast, in the suicide therapy study, fewer of the suicidal patients used adjuvant therapy in either arm, although a higher proportion of the usual care group used adjuvant therapy than the randomized study therapy group. Given the differences between the two examples with respect to the mediator results in Table 1, we now compare the SMM and standard regression results in Table 2 and then these results with those of the PS approach in Table 3.

Table 1.

For the suicide prevention (“prevention”) and therapy (“therapy”) studies, means (standard deviations in parentheses) and proportions for the Hamilton or BDI depression outcomes, respectively, and proportion of patients taking anti-depressant medication or adjuvant therapy, respectively, by randomized intervention group or by whether they took anti-depression medication or adjuvant therapy.

Suicide Study	Group	Hamilton	Medication
Prevention	Usual Care	13.55 (8.35)	0.45
	Intervention	11.50 (7.38)	0.85
	No medication	13.14 (8.09)
	Medication	12.23 (12.23)
		BDI	Non-Study Therapy
Therapy	Usual Care	19.33 (12.07)	0.25
	Study Therapy	14.02 (14.77)	0.08
	No Non-study Therapy	17.08 (14.78)
	Non-study Therapy	15.11 (12.07)

Table 2.

For the suicide prevention (“prevention”) and therapy (“therapy”) studies, ITT, standard regression, and SMM estimates are presented for the direct effects of the randomized baseline intervention (care manager or CBT) and the mediator (anti-depressant medication or adjuvant therapy). Standard errors and nominal 95% confidence intervals are in parentheses.

Suicide Study	Method	Direct Effect	Mediator Effect
Prevention	ITT	−3.12 (0.82) (−4.72, −1.51)
	Standard	−2.67 (0.89) (−4.41, − 0.93)	−1.19 (0.94) (−3.03, 0.65)
	SMM	−2.58 (1.27) (−5.07, −0.10)	−1.43 (2.34) (−6.01, 3.15)
Therapy	ITT	−6.35 (2.53) (−11.37, − 1.33)
	Standard	−6.86 (2.60) (−12.01, −1.70)	−3.05 (3.46) (−9.92, 3.82)
	SMM	−3.93 (3.09) (−9.98, 2.12)	14.59 (15.87) (−16.52, 45.69)

Table 3.

For the suicide prevention (“prevention”) and therapy (“therapy”) studies, PS estimates are presented for the direct effects of the randomized baseline intervention (care manager or CBT) separately in the “fixed mediator” principal strata groups. Standard errors and nominal 95% confidence intervals are in parentheses.

Suicide Study	Principal Stratum	Direct Effect
Prevention	Never (7%)	−8.93 (6.01)
	Medication	(−17.06, 1.37)
Prevention	Always (36%)	−1.94 (2.18)
	Medication	(−5.23, 1.50)
Therapy	Never (66%)	−7.07 (4.44)
	Therapy	(−24.51, 15.67)
Therapy	Always (6%)	−8.14 (17.79)
	Therapy	(−99.57, 91.38)

Suicide Prevention Study

The SMM and standard regression estimates for the suicide prevention study in Table 2 are in agreement in estimating a statistically significant direct effect of the care manager intervention on the 4 month Hamilton outcome apart from increasing anti-depressant use among the depressed patients. The estimated direct effect of this intervention under both the SMM and standard regression approaches is an approximate reduction of 2.5 Hamilton units. However, the SMM confidence interval is wider than the standard regression confidence intervals, as one would expect from the MSE results in the simulations. The significant direct effect of the presence of care manager on reducing depression could be the result of the impact of this specialist on the staff and physicians of the practices. That is, one would expect that the presence of the care manager in the intervention practices raised the sensitivity of the staff and providers in treating depression. We also see that both the SMM and standard regression approaches indicate a non-significant effect of the mediator (anti-depressant use) on outcome.

Estimating the direct effect of the care manager intervention under the SMM approach required covariates that interact with the significant randomized intervention factor on the mediator, i.e, varying the compliance score-based weight element, η(x). One strategy for identifying such predictors is to perform logistic regression of medication use on baseline covariates stratified by randomization arm. Comparing these predictive relationships between the two randomization arms, the test of the overall X * R interaction on M yielded a p-value of 0.006.

Finally, the PS results in Table 3 reveal more heterogeneity in the direct effects across principal strata for the Prevention Study than for the Therapy Study. In particular, the direct effect estimate in the principal stratum that would always take mediation is much larger than that in the principal stratum group that would never take medication, as well than the SMM and standard estimates. The very wide confidence intervals for the ITT effect under the PS approach, surround zero for the ITT effects. Nonetheless, there seems to be some evidence that the central locations of these confidence intervals differ between the two “fixed mediator” principal strata (always and never medication strata), thus not supporting the no-interaction assumption for baseline covariates and the Prospect intervention.

Suicide Therapy Study

In contrast to the suicide prevention study, the SMM and standard regression estimates for the suicide therapy study in Table 2 are not in agreement, indicating possible unmeasured confounding of the standard regression results and/or a violation of the no M * R, X * R, and X* M interactions assumption for Y_rm. Specifically, for the suicide therapy study, the estimate of θ_R under the SMM is smaller than the standard regression estimate of θ _RS. Hence, under the standard approach there is a significant direct effect of the study therapy on the 6 month depression outcome, apart from any impact on this outcome through the use of adjuvant therapy, whereas the SMM approach indicates that there is not suffcient evidence for such inference. There are three alternative explanations for this discrepancy in direct effect estimates between the SMM and standard approaches: 1) confounding of the adjuvant therapy vs. depression outcome relationship; 2) effect modification of the adjuvant therapy mediator on outcome by CBT; and 3) modification of the effect of baseline CBT on outcome by baseline depression or suicide ideation.

Ten Have et al. (2007) discuss the clinical implications of these three alternative explanations of the discrepancy in direct effect estimates between the SMM and standard approaches. The study investigators believed that the unmeasured stress-based source of confounding violating sequential ignorability was as likely as the possibility of effect modification of the adjuvant therapy effect on depression outcome by the baseline CBT intervention. Hence, clinical information and statistical evidence suggests that departures from sequential ignorability and/or departures from the assumption of no X * R interaction on Y_rm may be leading to differences between the standard and SMM approaches with respect to the direct effect of the baseline CBT intervention.

Inferentially, the SMM and standard approaches also disagree with respect to the sign of the effect of adjuvant therapy on the depression outcome, although both approaches yielded confidence intervals surrounding one. Moreover, the SMM-based estimate of θ_M and corresponding standard error are much larger in magnitude than the analogous standard regression estimates. This result conforms to the large simulation-based MSE for θ_M in Table 1 in Ten Have et al. (2007). Nonetheless, Table 1 in Ten Have et al. (2007) indicates such variability in the θ_M estimate does not preclude more accurate inference of the G-estimation estimate of θ_R under the structural no-interaction assumption.

In assessing the effectiveness of the multidimensional weighting for identifying the causal direct effects, Ten Have et al. (2007) evaluated the predictors of the the mediator, taking adjuvant therapy, stratified by randomization arms. The corresponding test of the overall X*R interaction on M yielded a p-value of 0.59, which is much less significant than the p-value of 0.006 for the larger suicide intervention study. Nonetheless, the suicide therapy study appeared to have a wider range of estimated weight elements than did the suicide prevention study, suggesting that the weights in the therapy study were still effective in improving identifiability of the causal parameters.

Finally, the PS results in Table 3 reveal little heterogeneity in the direct effects across principal strata for the Therapy Study, thus supporting in a limited way the assumption of no baseline covariate-CBT interactions with depression as the outcome. In particular, the direct effect estimates in the separate “fixed mediator” principal strata (always and never adjuvant therapy strata) are similar to each other and to the direct effect estimates under the standard and SMM approaches. Again, these results are qualified by the fact that the confidence intervals are very wide under the PS approach, surrounding zero for the ITT effects.

5. Summary

In the context of mediation analyses for baseline randomized behavioral intervention studies, we have reviewed two causal methods and one standard approach to estimating direct intervention effects. Traditionally, randomized studies have become the gold standard in establishing the causal effects of interventions on outcomes by allowing us to compare experimental groups using the ITT approach, which provides unbiased estimates of the effect of randomization. Understanding how such interventions work is needed for making these interventions more cost effective and more robust with more heterogeneous populations than the study populations on which they were tested (e.g., Baranowski (1997); Kazdin (2007)). Mediation analyses may satisfy these needs. However, current standard mediation methods are not protected by randomization against potential unmeasured confounding. Consequently, causal mediation methods such as the structural mean model and principal stratification approaches for obtaining more accurate inference under such confounding have been proposed in recent years (e.g., Mealli et al. (2004); Rubin (2004); Ten Have et al. (2007)). While these causal approaches differ in terms of controlling for the possibly confounded mediator effect while estimating the direct effect of the baseline intervention, they all make tradeoffs with the no confounding or sequential ignorability assumption for other assumptions involving treatment heterogeneity with respect to the mediator and outcome.

The tradeoffs that are made to relax the no confounding or sequential ignorability assumption under these two approaches involve model assumptions and also requirements for baseline covariate modification of baseline intervention effects on the mediator. First, there are bias versus variability tradeoffs shown in the simulations of Ten Have et al. (2007). The SMM was shown to exhibit more variability and less bias than the standard approach under unmeasured confounding of the mediator effect on outcome. Gallop et al. (2007) shows through simulations that the PS approach also exhibits more variability but less bias than the standard mediation approach. Such variability under the PS approach was exhibited in the empirical results presented above for the two psychiatry studies. In addition, the SMM approach exchanges the untestable sequential ignorability assumption for no-interaction assumptions among baseline covariates and the baseline intervention and mediator. The PS approach makes fewer and thus more robust no-interaction assumptions. Moreover, it provides an assessment of the no-interaction assumptions made by the SMM approach. In both of the studies presented above, there was clinical conjecture about potential unmeasured confounders that would violate the sequential ignorability assumption. However, there was also clinical weight given to interactions between baseline study interventions and follow-up adjuvant therapies on the follow-up depression outcome. Balancing these assumptions is a clinical judgment.

Future research will focus on assessing the structural R * M, X * R, or X * M interactions under the SMM in (2). An additional element involving X will be added to the weight vector for each additional structural interaction parameter based on the criteria of Robins et al. (1992). The diffculty of testing these structural interactions arises because X would be required to satisfy several strong constraints. For example for R * M, X (e.g., baseline depression) would need to satisfy two conditions: 1) x leads to strong interaction with R on M (i.e., variation in compliance score across x); and 2) P r(M = 1 | R = 1, X) is not perfectly collinear with the compliance score. For assessing R * X, condition 2) would need to be that X itself is not perfectly collinear with the compliance score. Our future research will focus on determining such baseline covariates satisfying these conditions for either of the two example studies. While the above weights yield consistent estimators under departures from sequential ignorability, they are not effcient under these departures. Additional future research will develop weights leading to consistent estimators that are also effcient under departures from sequential ignorability.

Additional extensions of these approaches to binary outcomes have been presented but not in the mediation context. The principal stratification approach has been extended to causal odds ratios for different principal strata (e.g., Hirano et al. (2000) and Frangakis et al. (2004). Robins and Rotnitzky (2005) showed that additional unverifiable assumptions are needed for inference with causal odds ratios under the logistic SMM. Accordingly, ? presented an approach that relies on an additional unverifiable assumption that a dose response of treatment on outcome can be modeled correctly in the group that receives treatment. As a tradeoff to additional unverifiable assumptions, Ten Have et al. (2003) presented an estimation method that approximates the true causal odds ratio under the logistic SMM.

Finally, as we have noted, the three approaches discussed in this paper differ in how the mediator is treated in defining direct effects. The standard and SMM approaches require a hypothetical mechanism that fixes even uncontrollable mediation factors (e.g., medication use by patients at home) at a given level when specifying direct effects of the baseline intervention. In contrast, the PS approach resolves this situation by forming the principal strata on the basis of each participant’s potential mediator behavior and then only focuses on those strata for whom participants would exhibit the same mediator behavior regardless of the baseline intervention. Alternatively, following the common mediation strategy of the standard and SMM mediation models, “natural” direct and indirect effect have been defined for which the mediator is not assumed to be fixed at a specific value by a hypothetical and potentially implausible mechanism (e.g. Robins (1999); Pearl (2001)). Rather, these alternative definitions of the direct and indirect effects assume the mediator is fixed at a “natural” level. In practice, the natural level corresponds to averaging the mediator factor with respect to its distribution under one of the two baseline arms. The resulting “natural” direct and indirect effects offer ways of specifying directly the indirect effect, which is not possible under the standard approach, except as a product of parameters but not as a contrast of means. Moreover, these natural effects offer a way of specifying direct and indirect effects under nonlinear models and models with interaction terms. Under a linear model such as in either (1) or (2), these natural effects equal their respective effects under the standard definitions.