Biomechanical assessment of evolutionary changes in the lepidosaurian skull

Abstract

The lepidosaurian skull has long been of interest to functional morphologists and evolutionary biologists. Patterns of bone loss and gain, particularly in relation to bars and fenestrae, have led to a variety of hypotheses concerning skull use and kinesis. Of these, one of the most enduring relates to the absence of the lower temporal bar in squamates and the acquisition of streptostyly. We performed a series of computer modeling studies on the skull of Uromastyx hardwickii, an akinetic herbivorous lizard. Multibody dynamic analysis (MDA) was conducted to predict the forces acting on the skull, and the results were transferred to a finite element analysis (FEA) to estimate the pattern of stress distribution. In the FEA, we applied the MDA result to a series of models based on the Uromastyx skull to represent different skull configurations within past and present members of the Lepidosauria. In this comparative study, we found that streptostyly can reduce the joint forces acting on the skull, but loss of the bony attachment between the quadrate and pterygoid decreases skull robusticity. Development of a lower temporal bar apparently provided additional support for an immobile quadrate that could become highly stressed during forceful biting.

Lepidosauria is composed of 2 subgroups: Rhynchocephalia (Sphenodon and its extinct relatives) and Squamata (lizards, snakes, and amphisbaenians). Several stem taxa (as part of the more inclusive Lepidosauromorpha) are known from fossil deposits of Permian to Jurassic age (≈250 million to 164 million years ago; ref. 1). In relation to lepidosaurian evolution, paleontologists, comparative anatomists, and functional morphologists have focused particularly on changes in cranial morphology, most notably with respect to the evolution of streptostyly (anteroposterior quadrate movement) and cranial kinesis. A long-standing hypothesis held that the ancestral lepidosaur possessed a fully diapsid skull (upper and lower temporal openings) with a complete lower temporal bar (2–6). Loss of that bar supposedly “freed” the quadrate, resulting in streptostyly. Elements of this hypothesis persist in the literature, even though it has been demonstrated unequivocally (1, 7–9) that the ancestral lepidosauromorph, the ancestral lepidosaur, and the ancestral rhynchocephalian (7, 8) all had a fixed quadrate (strong quadrate–pterygoid and squamosal–quadrate joints) but no lower temporal bar (Fig. 1). Indeed, the same seems to have been true for the last common ancestor of lepidosaurs and archosaurs (Fig. 1) (9). A complete lower temporal bar was developed de novo one or more times within Rhynchocephalia (7, 8). The ancestral squamate, on the other hand, inherited a skull without a lower temporal bar but underwent a reduction of the palatoquadrate and its derivatives, as well as a reduction of the connections between those derivatives (quadrate and epipterygoid) and the rest of the skull (quadrate–pterygoid, quadrate–squamosal, and epipterygoid–pterygoid) (8). Fig. 2 illustrates the difference in the relationships of the quadrate, pterygoid, and epipterygoid in Sphenodon and a modern lizard (Varanus). In the former, the 3 bones overlap extensively and are firmly sutured. In the latter, the contacts are substantially reduced, and the epipterygoid has a synovial joint with the pterygoid, the base resting in a pit (fossa columellae) on the dorsolateral pterygoid surface. Thus, the question at issue in relation to the lepidosaurian lower temporal bar is not the functional advantage of its loss (13), but rather of its gain in some rhynchocephalians and, very rarely, in lizards (12, 14). This, in turn, raises questions as to the selective advantages of the different lepidosaurian skull morphologies.

Fig. 1.

Simplified phylogeny of diapsid reptiles showing variation in lower temporal bar (ltb) development. Black indicates quadrate; dark gray, jugal. Key: (A) Carboniferous Petrolacosaurus (9); (B) Triassic early rhynchosaur, Mesosuchus (10); (C) Triassic Prolacerta (8); (D) Triassic archosaur Protorosuchus (11); (E) Triassic Kuehneosaurus (8); (F) Jurassic Marmoretta (8); (G) Recent Iguana (8); (H) Cretaceous Polyglyphanodon (12); (I) Cretaceous Tianyusaurus (12); (J) Jurassic Gephyrosaurus (8); and (K) Recent Sphenodon (8). Nodes: 1, Diapsida, hypothesized primitive state with ltb, fixed quadrate, robust epipterygoid; 2, Sauria, no ltb, quadrate and epipterygoid fixed; 3, Archosauromorpha, no ltb in basal taxa, developed in some lineages (e.g., Rhynchosauria, Archosauria); 4, Lepidosauromorpha and 5, Lepidosauria, no ltb in basal taxa quadrate and epipterygoid sutured to pterygoid large squamosal; 6, Squamata, quadrate/pterygoid overlap reduced, ligamentous, squamosal reduced, epipterygoid with synovial pterygoid joint, rare development of ltb in 1 lineage; and 7, Rhynchocephalia, no ltb in basal taxa, developed in some descendants, quadrate, pterygoid, and epipterygoid firmly sutured.

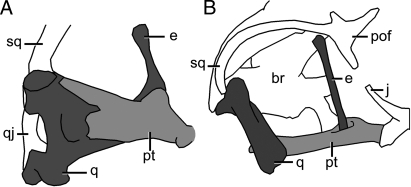
Fig. 2.

Relationship between the quadrate (q), pterygoid (pt), and epipterygoid (e) in Sphenodon, medial view (8) (A), and Varanus, lateral view (original) (B). Not to scale. br, braincase; j, jugal; pof, postorbitofrontal; qj, quadratojugal; sq, squamosal.

Morphological changes in the lepidosaurian skull have been the subject of theoretical and experimental studies (6, 8, 9, 15–19) that aimed to understand the underlying selective criteria. It is widely accepted that such factors as genetic history and lifestyle play a pivotal role in the evolution of cranial structure (20), but there has been less discussion on the degree to which biomechanical necessities are among the selective factors that direct evolutionary pathways. Bite performance should be an important driving factor. Changes in skull architecture influence muscle structural design and gape angle, which in turn influence bite force (6), whereby higher forces require a more robust structure to withstand them. This reinforcement can take place through increased levels of cranial ossification or by strengthening of the soft tissues.

The application of 2 powerful computational tools—multibody dynamic analysis (MDA) and finite element analysis (FEA)—is becoming widespread in the field of functional morphology to answer questions surrounding the biomechanical significance of cranial design (21–33). We implemented both of these techniques on Uromastyx hardwickii, a streptostylic but otherwise akinetic herbivorous lizard. In the MDA part of this study (Fig. 3), we predicted the loading conditions imposed on the skull and assessed the role of streptostyly (movement of the quadrate) on the rest of the skull. In the FEA, we applied the MDA load data and assessed the role and function of the epipterygoid, the quadrate–pterygoid joint, and the lower temporal bar via a series of virtual reconstructions based on the Uromastyx skull (Fig. 4).

Fig. 3.

Lateral view of the Uromastyx MDA model showing muscles and ligaments. The MPST, MAMEP, and MPTM are internal muscles, and they are not visible in this figure. Lig, ligament. For full names of muscles, see Materials and Methods.

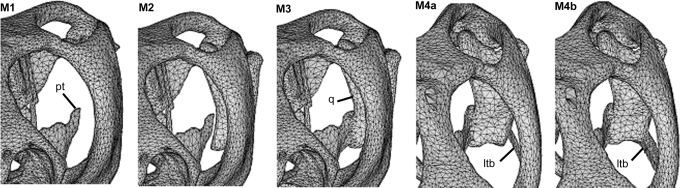
Fig. 4.

An illustration of the different models constructed for this study. In M1, the quadrate (q) is not present (but its effect was included; see text); in M2, the quadrate is present. M3 shows the connection between the quadrate and pterygoid (pt). M4a and M4b show artificial thin and thick lower temporal bars (ltb), respectively, which were added to the Uromastyx skull. Note that models are viewed through the left orbit to highlight the differences in the internal anatomical structures.

Results

MDA.

The MDA simulations were used to predict the loading experienced by the skull when the quadrate was either mobile or fixed. Table 1 summarizes the results corresponding to biting at a 7° gape angle and shows that the magnitudes of the muscle, ligament, and joint forces were higher when the quadrate was fixed, although bite force remained similar in the mobile- and fixed-quadrate models. It should be noted that the joint force acting on the skull in the first MDA simulation, in which quadrate is allowed to move, acts through the quadratosquamosal joint (joint 1 in Fig. 3), whereas in the second MDA simulation, where the quadrate is fixed, the only joint force acting on the quadrate, and through it the skull, is the quadratomandibular joint force (joint 2 in Fig. 3).

Table 1.

Loading conditions applied to the skull

	Streptostylic quadrate (L1)				Fix quadrate (L2)
	Fx	Fy	Fy	Mag	Fx	Fy	Fy	Mag
MAMEM1	−2.55	−4.88	7.32	9.16	−2.54	−4.93	7.48	9.31
MAMEM2	−1.21	−7.10	5.55	9.09	−1.22	−7.17	5.72	9.25
MAMESP1	—	—	—	—	2.27	−4.6	3.88	6.43
MAMESP2	—	—	—	—	1.77	−4.07	4.98	6.67
MAMEP1	—	—	—	—	0.16	−4.17	2.33	4.78
MAMEP2	−1.40	−4.16	1.64	4.68	−1.40	−4.21	1.78	4.78
MPTE1	3.16	1.41	7.77	8.50	3.10	1.59	7.86	8.60
MPTE2	1.46	−0.90	7.57	7.76	1.49	−0.81	7.79	7.97
MPTE3	0	0	0	0	0	0	0	0
MPTM1	−2.47	−1.12	6.87	7.38	−2.40	−0.77	6.97	7.41
MPTM2	0	0	0	0	0	0	0	0
MPTM3	0	0	0	0	0	0	0	0
MPST1	−0.91	−0.59	0.65	1.26	−0.92	−0.61	0.74	1.33
MPST2	−0.52	−0.78	0.96	1.34	−0.51	−0.78	1.00	1.37
MAMESA1	1.98	−1.09	5.69	6.12	1.95	−0.95	5.76	6.15
MAMESA2	2.40	−1.31	5.49	6.13	2.36	−1.14	5.60	6.18
Lig1	−0.16	−1.50	−1.34	2.02	−0.47	−4.32	−3.83	5.79
Lig2	0	0	0	0	−0.14	−0.68	−1.97	2.09
Bite force	0	−0.84	−21.84	21.86	0	−1.43	−21.86	21.91
Joint force 1	0.20	22.87	−26.37	34.91	—	—	—	—
Joint force 2	—	—	—	—	−3.49	39.07	−34.26	52.30

A summary of the loading conditions applied to the skull on one side of the FEA model, as obtained from the MDA study of a model with a fixed quadrate and with a streptostylic quadrate. MAMESPs 1 and 2 and MAMEP1 originate from the jaw and insert on the quadrate, and therefore do not apply any force directly on the skull; hence, their values are not reported here. In the first MDA simulation, where quadrate is streptostylic, joint force 2 (quadratomandibular joint force) does not apply to the skull, and in the second simulation, where the quadrate is fixed, we assumed that there is no movement around joint 1 (quadratosquamosal joint); therefore, no force was applied to the skull at this point. Values are in newtons. F_x, F_y, and F_y represent force components, and Mag represents the force magnitude. The empty cells are not applicable, and the coordinate system is defined in Fig. 3.

FEA.

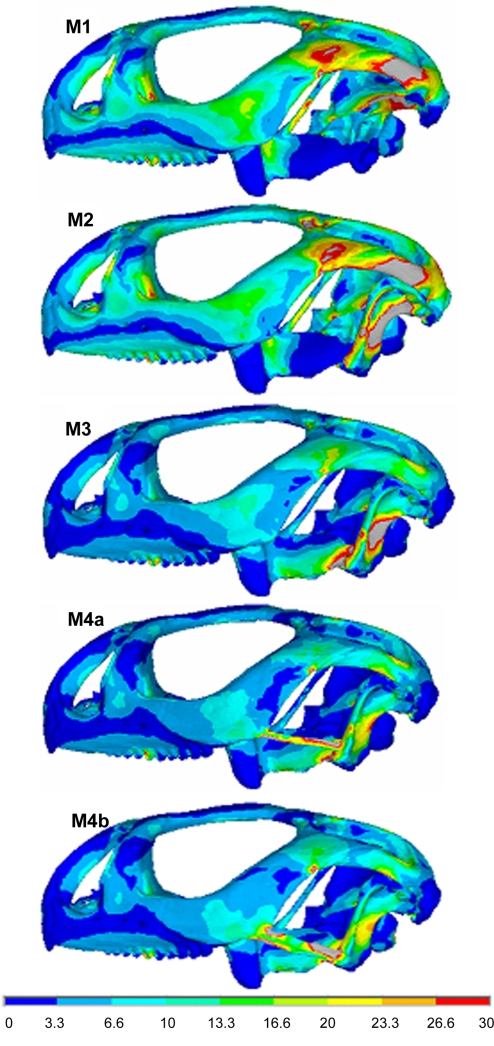
Plots of mean stress (i.e., von Mises stress) in lateral view are shown in Fig. 5 for each of our models [from the first model (M1) to the 2 alternatives of the fourth model (M4a and M4b)]. Despite the different loading conditions that are imposed on M1 (mobile quadrate) and model 2 (M2; quadratosquamosal joint fixed), a comparable pattern of stress is observed in most regions of these models. However, M2 shows that the fixed quadrate is under a relatively higher stress. In model 3 (M3), where the quadrate is also attached to the pterygoid, the stress distribution across the whole skull is significantly reduced (compared with M1 and M2), although a high-stress concentration is created around the attachment which extends to meet the pterygoid. The addition of a lower temporal bar (M4a and M4b) leads to a greater reduction in quadrate stress compared with M3. Differences in bar thickness (M4a vs. M4b) yield slightly different local patterns of stress in the quadrate and jugal but have little or no global effect on the pattern of stress across the skull (for the thicknesses considered here).

Fig. 5.

Comparison of mean stress in models M1 to M4b. Note the gray color shows values greater than 30 MPa.

Discussion

In the tuatara, Sphenodon, the quadrate is rigidly fixed to the skull by its bony attachments to the pterygoid, squamosal, quadratojugal/jugal, the last of these being a secondary development (7–9). In most squamates, by contrast, the streptostylic quadrate can swing anteriorly and posteriorly during jaw opening and closing, although this movement is restricted, to various degrees, by the stiffness of the joints between the quadrate and neighboring bones (squamosal, pterygoid, supratemporal, opisthotic) and by associated quadratopterygoid and temporal (quadratojugal/jugomandibular) ligaments. In forceful biting, a combination of these ligaments and muscle action can temporarily fix the quadrate (static biting; ref. 34). However, a new Chinese fossil lizard, Tianyusaurus (12, 14), is unique among squamates in having immobilized the quadrate in a manner analogous to that of Sphenodon, by developing a deep bony quadrate/pterygoid overlap and by linking the quadrate to the jugal via a bony bar. Computational techniques have the potential to address questions surrounding the selective value of such adaptations during evolutionary time frames. Our results shed light on the effects of these changes (streptostyly, a lower temporal bar) on the mechanical performance of the lepidosaurian skull.

Streptostyly.

The role and function of streptostyly was assessed through the MDA part of this study, where the analysis was run in separate simulations on the same model, with the quadrate either streptostylic or fixed (but no lower temporal bar). The variation in the MDA load data between the streptostylic- and fixed-quadrate simulations is shown in Table 1. These results show first that the skull with a fixed quadrate in the simulation is able to generate only marginally higher muscle forces than that with a streptostylic quadrate. Second, both sections of the modeled temporal ligament go into tension in the fixed-quadrate simulation to prevent posterior displacement of the jaw during biting (as predicted by refs. 6, 34, and 35). Third, the joint force acting on the skull was significantly higher in the fixed-quadrate model compared with the streptostylic quadrate model, although bite force was the same. Together, these results show that under the same conditions (i.e., muscle force, bite position, and angle) and yielding the same bite force, higher joint reaction forces would be generated in a nonstreptostylic lepidosaurian skull than a streptostylic one. Therefore, one advantage of a mobile quadrate is a reduction of the quadratomandibular joint force during biting, but it may have limited the maximum bite force that could be generated (6).

The results of the FEA performed here show that in the fixed-quadrate model (M2 in Fig. 4), the level of stress on the quadrate is so high that it could have led to failure of this structure. This exceptionally high degree of stress may result from the fact that the muscle forces representing the action of the external adductor (MAMESP1, MAMESP2, and MAMEP1) muscle slips on the quadrate were applied as point loads rather than a distributed load, an effect addressed in more detail by Grosse et al. (27). However, it seems likely that even with a distributed force load on the quadrate, a fixed quadrate without the support of a lower temporal bar would experience high stress in hard biting.

Quadrate–Pterygoid Joint, Epipterygoid, and Lower Temporal Bar.

A representative connection was made in the Uromastyx model between the quadrate and the pterygoid to simulate the overlap present in extinct lepidosauromorphs and basal lepidosaurs, as well as the living Sphenodon (see Fig. 4) and the unique Chinese fossil lizard Tianyusaurus (12, 14). An exact comparison with these taxa is difficult because of the different anatomy (and we are engaged in a parallel study of Sphenodon to test the hypotheses developed here), but the effect of this attachment in Uromastyx is still interesting. M3 in Fig. 5 demonstrates a general reduction in stress across the whole skull, and more specifically in the epipterygoid, when compared to M1 and M2. This is significant because on the one hand, it may help to explain the development in early squamates of a synovial joint between the base of the epipterygoid and the pterygoid, instead of the firm suture found in Sphenodon and basal taxa (Fig. 2). On the other hand, this reduction in stress implies that M3 is more robust compared with M2 under the same loading conditions. M3 (Fig. 5) also shows a high-stress concentration at the connection between the quadrate and pterygoid. However, this is probably an artifact of the relatively small attachment area that was created in this model from the micro computed tomography (microCT) data, rather than the broad overlap found in Sphenodon and basal taxa (Fig. 2). Finally, the reconstruction of an attachment between the jugal and the quadrate (via a lower temporal bar) reduced the mechanical stress on the quadrate (compare M3 to M4a and M4b) and on the skull as a whole. As expected, an increase in bar thickness did not show a global effect in the pattern of stress distribution across the skull. This suggests that the acquisition of a lower temporal bar in some reptile lineages may have been driven by the necessity of providing additional support for a quadrate that became highly stressed during hard biting.

Some generalizations have been made in these comparative studies that show higher levels of stress in the anatomical Uromastyx skull compared with the modified versions. It is likely that different, probably higher, muscle forces were acting on the modified skull versions. The quadratopterygoid ligament (between the quadrate and pterygoid; refs. 36 and 37) was not included in our models. This ligament has a role in stabilizing the streptostylic quadrate, so including it in the MDA model might transfer some of the tensile forces carried by the temporal ligament to the pterygoid. In addition, permitting movements of the epipterygoid about its basal joint could significantly reduce the stress levels in this bone. Herrel et al. (6, 34) showed that the temporal ligaments play an important role in balancing the jaw adductor muscle forces and limiting backward rotation of the quadrate in lizards such as Uromastyx. A complete lower temporal bar together with a firm pterygoid–quadrate contact may behave in an analogous way as a quadrate stabilizer in Sphenodon and in the recently described fossil lizard Tianyusaurus (12, 14).

Conclusions

From an evolutionary perspective, our results suggest that lepidosauromorphs and basal lepidosaurs with a bony attachment between the quadrate and the pterygoid have had a more mechanically robust skull architecture than squamates with a streptostylic quadrate. However, hard biting puts considerable stress on the quadrate and the epipterygoid and on their connections with the rest of the skull. Reducing those connections and increasing the degree of soft tissue involvement (as in streptostyly) provide one solution, albeit with some potential loss of bite force (6). Concomitant changes in muscle architecture may have compensated for this (6). The alternative strategy was to maintain (or redevelop) the bony connections (quadrate–pterygoid, epipterygoid–pterygoid, squamosal–quadrate) and attach the quadrate to the jugal via a lower temporal bar (4), thus creating a more robust skull able to withstand and generate stronger bite forces. However, it is important to get the polarity of these changes correct. Although the presence of a robust quadrate–pterygoid overlap is primitive for lepidosaurs, the possession of a complete lower temporal bar is not (refs. 1, 7, and 8, vs. refs. 4, 6, 34, and 38).

Materials and Methods

MDA.

The development of the MDA model of Uromastyx has been described in detail elsewhere (30). In brief, a 3D model of the skull, jaw, and quadrates of U. hardwickii were constructed from microCT data and then imported into MSC ADAMS in preparation for the MDA. The skull was fixed throughout all of the simulations, and the quadrates were connected to the skull at one end (quadratosquamosal joint, specified as joint 1) and the jaw at the other (quadratomandibular joint, specified as joint 2) via hinge joints. The temporal ligament (jugal to quadrate and lower jaw) was modeled in the form of tension-only springs (with stiffness of 50 N/mm), and the jaw-closing muscles [adductor mandibulae externus superficialis anterior (MAMESA), adductor mandibulae externus superficialis posterior (MAMESP), adductor mandibulae externus medialis (MAMEM), adductor mandibulae externus profundus (MAMEP), pterygoideus externus (MPTE), pterygoideus medialis (MPTM), and the pseudotemporalis superficialis (MPST)] were modeled, including the active and passive force–length and force–velocity characteristics of the muscles as described by van Ruijven and Weijs (39) (see Fig. 3). It was necessary to define a food particle for the biting simulations (jaw-closing phase). This was performed by including a resisting spring located between the teeth (with stiffness of 50 N/mm and damping constant of 9 N·s/mm).

Two simulations were performed: (i) quadrate allowed to move anteriorly and posteriorly during jaw opening and closing (streptostyly) and (ii) quadrate fixed (i.e., the hinge joint connecting the quadrate to the skull modified to form a suture) so that the only part moving during jaw opening and closing was the jaw itself. Both simulations were started from an initial position as shown in Fig. 3 and were performed in 2 phases. The first phase was jaw opening, which was performed via a motion control and lasted for 0.32 s, leading to a gape angle of 35° (here, muscle forces could be estimated while the modeled strands were elongated—inverse dynamic analysis). The second phase was jaw closing to a 7° gape, simulating a perpendicular bite on a food bolus located at the back of the mouth, 13 mm from the anterior tip of the jaw (here, estimated muscle forces were applied to close the jaw and bite, and all joint and ligament forces were calculated—forward dynamic analysis).

FEA.

The 3D model of the skull developed for the MDA was transformed into a meshed solid model by using the Amira image segmentation software (Mercury Computer Systems) for input into ANSYS finite-element software. In M1, only the skull was represented (i.e., the quadrate was not modeled), with the forces at the quadratosquamosal joint applied directly to the skull rather than via the quadrate, without any loss of accuracy (31, 32). M2 incorporated both the skull and quadrate, such that the quadrate was immobile. We further investigated the effect of connections between the quadrate and pterygoid, as well as the quadrate and jugal (via a lower temporal bar). This was achieved during the image segmentation process by modifying the original microCT data of the Uromastyx skull (M3, M4a, and M4b models). In model M3, the quadrate and pterygoid bones were firmly connected (Fig. 4, M3). M4a and M4b were based on M3 but also included an artificial lower temporal bar that had a thickness of 0.32 mm in M4a and 1.04 mm in M4b (resembling the condition in Sphenodon; Fig. 1). The number of elements within each of these models was typically 215,000.

The loading conditions imposed on the above models were obtained from the MDA. The muscle, ligament, joint, and bite forces were all imported in text format (.txt) into the FE software package (ANSYS). The forces were applied in the FEA at one node, which was chosen by finding the closest coordinate in the FE model to the force application in the MDA model. The L1 load data from Table 1 were applied to M1 (Fig. 4), with L2 load data applied to the other FE models (i.e., M2–M4b in Fig. 4). Three nodes were constrained at the occipital condyle in all directions in all of the models, and the bone was assigned a Young's modulus of 10 GPa and a Poisson ratio of 0.3 as in previous studies (21, 31).