Turning a plant tissue into a living cell froth through isotropic growth

Abstract

The forms resulting from growth processes are highly sensitive to the nature of the driving impetus, and to the local properties of the medium, in particular, its isotropy or anisotropy. In turn, these local properties can be organized by growth. Here, we consider a growing plant tissue, the shoot apical meristem of Arabidopsis thaliana. In plants, the resistance of the cell wall to the growing internal turgor pressure is the main factor shaping the cells and the tissues. It is well established that the physical properties of the walls depend on the oriented deposition of the cellulose microfibrils in the extracellular matrix or cell wall; this order is correlated to the highly oriented cortical array of microtubules attached to the inner side of the plasma membrane. We used oryzalin to depolymerize microtubules and analyzed its influence on the growing meristem. This had no short-term effect, but it had a profound impact on the cell anisotropy and the resulting tissue growth. The geometry of the cells became similar to that of bubbles in a soap froth. At a multicellular scale, this switch to a local isotropy induced growth into spherical structures. A theoretical model is presented in which a cellular structure grows through the plastic yielding of its walls under turgor pressure. The simulations reproduce the geometrical properties of a normal tissue if cell division is included. If not, a “cell froth” very similar to that observed experimentally is obtained. Our results suggest strong physical constraints on the mechanisms of growth regulation.

In many pattern-forming systems in physics, such as viscous fingering or needle crystallization (1–4), the observed structures have very different morphologies depending on whether their growth is isotropic or anisotropic. The understanding of these systems progressed through experiments in which this aspect of their behavior was altered, either imposing an artificial anisotropy to normally isotropic systems, or suppressing their natural anisotropy. Here, we address this issue for a living system, the growing plant. Plants grow through the osmosis-driven uptake of water from the soil (5). Were this process to supply a homogeneous, isotropic structure, the plant would grow into the shape of a balloon. In reality, a seedling has a heterogeneous and anisotropic growth, leading, for instance, to the formation of an elongated stem bearing a variety of organs with diverse shapes. In the following we will show that it is possible to suppress this anisotropy and we will discuss the resulting growth patterns.

We consider the development of the shoot apical meristem (SAM) of Arabidopsis thaliana, a group of dividing cells located at the tip of the stem, which generates all aerial organs. The growth of the SAM results from cell enlargement and divisions. These processes are coordinated in such a way that the meristem summit forms a dome with a steady shape (6). Cells are continuously advected away from the tip, and their average size remains roughly constant in time and space (7). During normal growth, multicellular protrusions, the primordia, appear at the periphery of the SAM, and later give rise to leaves or flowers. As the stem grows, new primordia emerge above the previous ones, at well-defined locations (8). The isotropy or anisotropy of meristematic cells is thought to depend on the presence of highly ordered arrangements of cellulose microfibrils in the extracellular matrix. The orientation of these fibrils depends in turn on the presence of microtubules, small protein filaments attached to the cytoplasmic side of the plasma membrane (9). It was shown recently (10) that, in the central zone of the meristem, the orientation of the cortical microtubules fluctuates constantly thus resulting in an effective isotropy. As the cells are advected into the lateral regions of the meristem the orientation of the microtubules becomes predominantly azimuthal. Correlatively the cell divisions are similarly oriented and growth becomes increasingly a longitudinal elongation. Growth thus becomes spontaneously anisotropic. In this article, we revisit the effect of oryzalin, a drug that causes microtubule depolymerization (11). We find that growth becomes isotropic; by using a joint experimental and theoretical investigation of the development and geometry of the network of cells, we conclude that differences in turgor pressure are involved in growth regulation, and propose a plausible form for this regulation. This finding could have a broader significance because the mechanical regulation of growth was also suggested to be important in animal tissues (12–14).

Experimental Results

To optically access the shoot apical meristem more easily, we artificially prevented organ initiation at the periphery of the meristem with 1-N-naphthylphthalamic acid (NPA), an inhibitor of hormone-induced organ initiation, by using a protocol described earlier (15). This resulted in the formation of a pin-shaped stem bearing a naked meristem at the tip (Fig. 1A). Two situations were investigated, where the NPA treatment was either maintained or interrupted. In the latter case, after NPA removal, the meristems started to reinitiate primordia, as in Fig. 2. The seedlings were then immersed in a solution containing 10 μg/mL oryzalin for 3 h. To prevent repolymerization of the microtubules, the same treatment was repeated 24 h later. To observe the geometry of the cells, we used the GFP-LTI6b transgenic line that expresses a fluorescent fusion protein addressed to the plasma membrane. Serial optical sections of the apex were taken immediately before and at regular intervals after oryzalin treatment by using a confocal microscope.

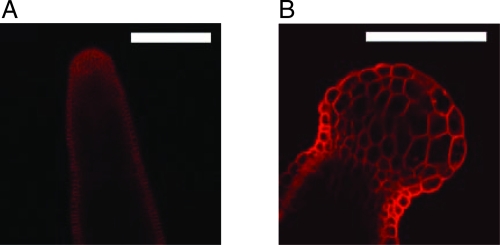
Fig. 1.

Anisotropic and isotropic growth forms in the plant A. thaliana. (Scale bar, 100 μm.) (A) The “normal” shape of the stem of A. thaliana grown on an NPA-treated substrate before oryzalin treatment. (B) Shape of an apex 72 h after treatment with oryzalin. The isotropic growth of the tip gives rise to a spherical meristem (from ref. 15)

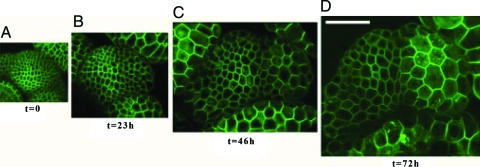
Fig. 2.

Evolution toward a living froth. Four confocal microscopy reconstructions of the same shoot apical meristem (stem tip) in a GFP-LTI6b transgenic plant as a function of time. The central zone (meristem summit) is on the left of the center of these images and a primordium grows on the right. The scale being the same for all images, cell enlargement is obvious. (Scale bar, 50 μm.) (A) Initial structure at time t = 0, immediately before treatment with oryzalin; (B–D) The structure after the treatment, at times 23 h, 46 h, and 72 h, respectively. The evolution of individual cells can be followed along all images.

The application of oryzalin had no immediate effect on either the shape of the cells or that of the organs. This reflects the maintenance of the mechanical properties of the cell wall immediately after the treatment. Later on, however, growth subsequent to oryzalin treatment resulted in a drastic change in organ shapes suggesting a loss of anisotropy. This change was particularly obvious in plants grown in the presence of both NPA and oryzalin, where the pin-shaped tips became spherical (Fig. 1B; see also ref. 15). In plants where NPA inhibition had been stopped, the initiated primordia, as well as the meristem itself, grew into globular shapes.

At the scale of the cells, the absence of microtubules had several major effects (Fig. 2; ref. 15):

1. All cell divisions were inhibited, whereas growth was maintained. As a result, the meristematic and primordium cells increased their size dramatically.

2. The growth rate in the primordia was higher than in the meristem proper, as observed in untreated meristems, showing that the oryzalin treatment did not affect the overall distribution of growth rates in the shoot apex.

3. The differentiated cells of the stem below the meristem kept growing but the effect of the treatment was less dramatic than in the undifferentiated cells of the meristem, consistent with the presence of stiffer cell walls in the stem.

Seventy-two hours after the first application of oryzalin, the increase in cell volume was of the order of 3,000% in volume. At that time, while the organs had become globular, we observed striking similarities between the geometry of the cells and that of bubbles in a soap froth (16). This comparison can be made more quantitative by examining several features of the distribution of angles between cell walls at wall junctions. Indeed, one of the governing features of the geometry of soap froths is the requirement, related to the balance of capillary forces, that soap films meet in threes at angles of 120°.

In an untreated plant, the SAM has two outer cell layers (called L1 and L2), in which cell divisions are mostly perpendicular to the surface (anticlinal divisions), justifying in part the consideration of each one as a 2D system. In what follows, when refering to the cells of these layers, “cell sides” refers to walls perpendicular to the surface, and “neighbors” to those belonging to the same layer.

To quantify the angles between neighboring cell walls, we developed a graphical interface allowing a precise reconstruction of the 3D shape of the outer envelope of the living meristems from confocal optical sections. Sections of the apex parallel to this envelope are taken, at a constant distance from the surface. With a proper choice of the distance, a section at mid-level of the L1 layer is obtained. By tilting the resulting curved surfaces, each region is then observed in a plane perpendicular to the local tangent to the surface (Fig. 3). Three cells (and three cell walls) were found to meet at each vertex, so that three angles were measured for each vertex. To verify our measurements, we checked that the sum of the angles at each vertex was equal to 360°. In addition, each angle was measured 3 times (corresponding to the three neighboring cells), with slightly different projections. Using this protocol, the resulting values were found to be consistent.

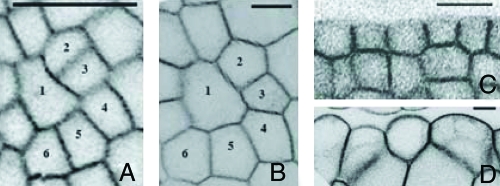
Fig. 3.

Sections showing the evolution of the shape of individual cells of the apex of Fig. 2. A and C correspond to time t = 0 immediately before the oryzalin treatment, whereas B and D correspond to t = 72 h. To allow a better comparison of the cell shapes, B and D have been scaled down by a factor of 2.5. (Scale bar, 10 μm.) A and B show sections parallel to the surface of the same cells of the meristem. At time t = 0, the two walls separating cells 2 and 3 and cells 5 and 6 had been recently formed. These new cell walls connect to the existing ones approximately at right angles; 72 h later, all the angles of these vertices have relaxed to 120°. C and D show the evolution of the L1 layer on two transverse sections of a primordium at time t = 0 and t = 72 h. On the latter image, the outer cell walls exhibit a larger outward curvature.

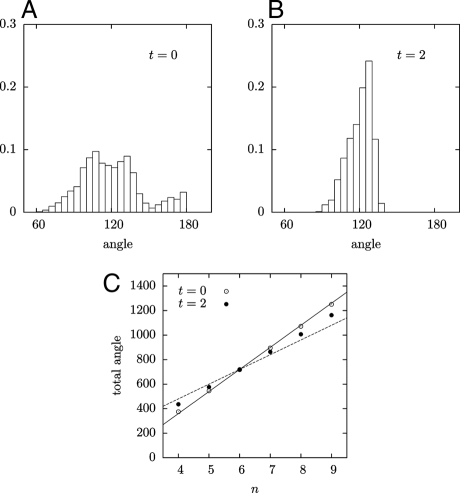
The internal angles of cells in an apical meristem before oryzalin treatment are broadly distributed, ranging from 90° to 180° (Fig. 4A). Because all groups of 3 angles add up to 360°, the average value is necessarily 120°, but the standard deviation is large: δθ = 23°. Furthermore the histogram has a characteristic complex shape. This distribution of angles results from the superimposition of vertices of different “ages”: the angles at a vertex depend essentially on the time elapsed since the cell division that produced it. Newly formed vertices account for the extreme values: during cell divisions, the new wall connects two walls of the mother cell, meeting them approximately at right angles; at first, the shapes of the older walls are unaffected, so that in newly formed vertices, one angle is equal to 180°, whereas the two others are close to 90°. Over time, the older walls bend and the angles slowly shift toward 120°. The overall angle distribution results from the combination of these different stages of vertex evolution.

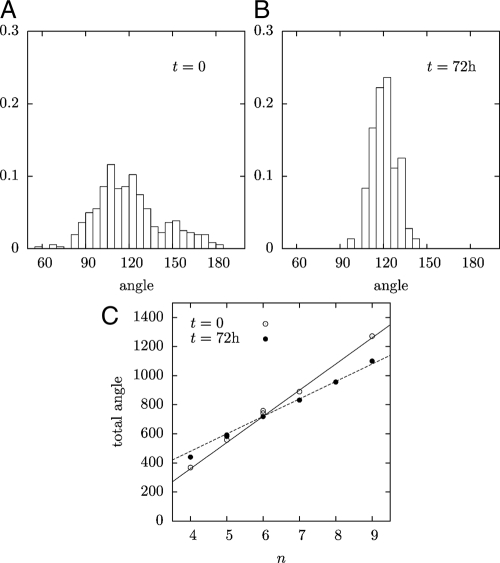
Fig. 4.

Geometry of the meristem. (A,B) Histograms of the angles at the vertices of the L1 cellular layer for t = 0, and t = 72 h. (C) Sum of all the angles of a cell versus the number of its edges. Solid line, (n − 2) × 180° corresponding to straight walls and a polygonal cell; dotted line, n × 120° corresponding to curved walls and all vertex angles equal to 120°.

After oryzalin treatment, all angles converge toward 120° (Fig. 4B). At 23 h of treatment, the standard deviation had already decreased to 17.5°, at 46 h, to 10.6°, and at 73 h, to 8.6°. This evolution was also reflected in the variation of the sum of cell internal angles. As in 2D soap froths, the number of cell sides was broadly distributed (4–8, with an average of 6, following Euler's theorem). Before oryzalin treatment, the cells are nearly polygonal, so that the sum of the inner angles of an n-sided cell is close to (n − 2) × 180° (Fig. 4B). After treatment, this sum tends to n × 120° (Fig. 4B), as each angle approaches 120°.

This angle distribution is the same as in a 2D soap froth, where it results from the equality of the tensions in the 3 soap films meeting at a vertex. This condition is naturally met by an array of hexagonal bubbles separated by straight films. If the bubble lattice is irregular, however, the soap films bordering nonhexagonal bubbles must become curved. This is also what is observed in oryzalin-treated meristems: the walls of cells having <6 sides become convex, whereas those of cells having more sides become concave (see Figs. 2 and 3). This is responsible for the soap froth aspect of the cellular array. Moreover, due to Laplace's law in the soap froth, the pressure inside a bubble is modified if it has curved walls, so that the pressure in bubbles with convex walls is larger than in bubbles with concave walls. Thus, the curved walls of the cells in the SAM suggest a nonuniform turgor; this might be surprising knowing that cell cytoplasmic membranes are connected by plasmodesmata, which, in principle, allow free diffusion of solutes. Therefore, our observations on the geometry hint to a closing of plasmodesmata, at least for meristems treated with oryzalin. This has been observed in a different context: the rapid elongation of cotton fibers is accompanied by the closing of plasmodesmata (17).

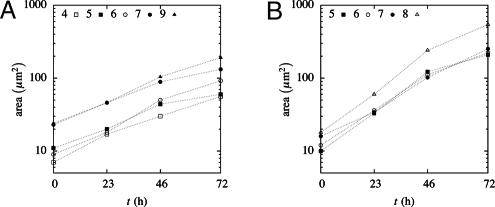
However, the 2 systems evolve in a different way. In a soap froth, the 120° angles are achieved instantaneously. The pressure difference between bubbles generate a slow evolution, as it induces a gas diffusion from the bubbles with a small number of sides (which are convex) into those with a large number of sides (which are concave). The latter grow larger, but the former shrink and ultimately vanish. This phenomenon is responsible for the coarsening of soap froths (16). In contrast, the 120° angles in oryzalin-treated meristems result from a slow evolution. Moreover, we measured the rate of growth of cells as a function of time and found it roughly constant and independent of the number of sides, as shown on Fig. 5.

Fig. 5.

Geometry of the meristem: time evolution of the area of the cross-sections of cells of the L1 layer having different numbers of sides (the sections are parallel to the surface). The growth is approximately exponential but slows down slightly between 46 and 72 h. Cells from the meristem (A) exhibit a weaker rate of growth that those from primordia (B). However, in both regions, the rate of growth of the cells is found to be independent of the number of sides.

Model and Simulation Results

In what follows, we discuss the mechanisms needed for the geometrical structure of the meristem to arise, relying on a theoretical and numerical model of plant cell growth. As mentioned above, the 120° angles in a soap froth result from a balance of equal forces and generate pressure differences between bubbles with different numbers of sides. Conversely, that the angles tend toward 120° in the SAM implies that the tensions in the walls are becoming uniform, whereas the turgor pressure is getting nonuniform, suggesting a regulation of growth.

As in the experiments, we consider a single layer of cells, delimited by a network of walls (18, 19), and two successive regimes. Starting from a small number of cells, we allow cell proliferation to proceed until the chosen number of cells has formed. Subsequently, cell division is stopped, and enlargement continues. The simulation is eventually terminated when the increase in cell size is of the same order as in the experiments. To avoid edge effects, the simulations presented below are performed with periodic boundary conditions.

Each wall is modeled as a viscoelastic rod of negligible bending rigidity [this is justified by the small ratio between wall thicknesses and cell sizes (20)]. Growth is similar to a plastic deformation of cell walls under turgor pressure (21, 22). In accordance with experimental observations, a clear separation of timescales between the equilibration of water potential through water redistribution, turgor regulation, and growth is assumed (orders of magnitude reported in, e.g., ref. 23 are 10 min, 1 h, and 1 day, respectively). At any given time, the system is thus in a state of equilibrium. As in soap froths, each wall supports a uniform tension T_i (because there are no tangential forces), and exhibits a constant curvature κ_i related to T_i and to the pressure difference δP between the cells on either side of the wall by an equation similar to Laplace's law:

Wall yielding is described by Maxwell's model, i.e., the rate of irreversible deformation is proportional to the elastic strain; if l_i⁰ and l_i are the rest length and actual length (augmented by elastic stretching) of wall i, then the tension in this wall is given by

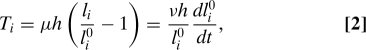where uniform wall thickness h, elastic modulus μ, and viscosity ν are assumed. Note that this viscoelastic model is fundamentally different from those used for animal tissues, in which growth is driven solely by cell division (see, e.g., ref. 13). At each time step, the state of the system is determined by minimizing its mechanical energy, which comprises its elastic energy and pressure potential energy, e.g., if turgor is uniform,

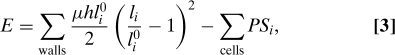where S_i is the area of cell i, then the rest lengths are updated according to Eq. 2. Until it is stopped, cell division occurs when the area of a cell exceeds a given threshold, through the insertion of a new wall. The location of the division plane is chosen so as to minimize the length of the new wall while dividing the cell into 2 daughter cells of approximately equal size (18). The unit length is such that the threshold area for cell division is one, so that the average cell size in the proliferating tissue is of order one. The tension in each wall is of order PS^1/2. Measuring stress in units such that μh = 1, the strains are also of order PS^1/2, which is assumed small with respect to one so that the strains remain small (e.g., P = 0.02). The timescale is chosen such that the strain rate in the proliferation regime is close to one. More specifically, we set νh = P.

In support of the proposed modeling approach, we first note that it reproduces the detailed structure of the angle distribution in a proliferating tissue. As in the measured histograms three peaks can be distinguished (compare Fig. 4A and Fig. 8A), which result from the coexistence of new vertices with older ones in which the angles have relaxed to 120°.

Fig. 8.

Simulation of growth with regulated turgor pressure. Distribution of the angles at the vertices (A) for t = 0, to be compared with Fig. 4A; and (B) for t = 2, to be compared with Fig. 4B. (C) Sum of all the angles of a cell versus number of edges. Solid line, straight walls; dotted line, curved walls and vertex angles equal to 120°, as in Fig. 4C.

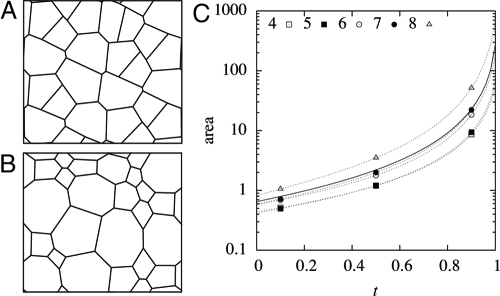
We first consider the situation where turgor is uniform and constant. In this case, there are no pressure differences and the walls remain straight. After divisions are stopped, the tension in the walls and the strain rate increase rapidly, as S^1/2, and the evolution of the tissue is catastrophic, reaching an infinite size in a finite time. Until this happens, all cells do not grow at the same rate: cells having more edges grow more rapidly, and the differences in cell sizes also increase without limit (Fig. 6). The angle standard deviation does decrease over time, yet only slightly, from 26.0° at t = 0 to 17.0° at t = 1 (during the same time, cell areas increase by over a hundredfold). Indeed, as stated earlier, the angles cannot converge without the walls becoming curved.

Fig. 6.

Simulation of growth with uniform turgor pressure—all cell walls remain straight. (A) Normal growth of a 2D cellular structure giving the initial state at t = 0 when cell divisions become inhibited (dimensions of simulation box ≈4.2 × 3.7). (B) The 2D cellular structure resulting from the same simulation at time t = 1 after the inhibition of cell divisions (dimensions ≈86 × 75); cells with <6 sides tend to vanish relatively. (C) Cell area versus time; dotted lines correspond to individual cells having different numbers of sides, the solid line to an average over all cells.

The above outcome of the model suggests that turgor is not uniform and constant. This may seem incompatible with the existence of plasmodesmata, which allow the diffusion of water and solutes between cells; possible explanations would be that plasmodesmata are closed or partially closed, or that diffusion is too slow to allow turgor equilibration. From the curvatures observed in experiments and Laplace's law Eq. 1, we may infer that turgor is negatively correlated with cell area. For simplicity, we will assume in what follows that turgor depends directly on cell size, discussing later a more realistic, indirect mechanism for such a correlation.

More specifically, a cell of size S tends to adjust its pressure to P(S), through changing the concentration of a solute. Assuming uniform water potential,

where n_i is the quantity of solute in cell i (in units such that the constant of proportionality is one). The pressure is equal to its target value if n = P(S)S. To account for a finite response time, we assume that the quantity of solute evolves according to

We have used the numerical value τ = 0.1 (turgor regulation is faster than growth), which is consistent with the above-mentioned orders of magnitude found in experiments. However, turgor regulation is slower than water redistribution, so the quantity of solute n_i in each cell can be considered constant in determining the state of equilibrium of the system, which is done by minimizing the energy

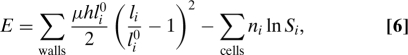instead of Eq. 3. Regarding the target pressure P(S), the relatively constant overall growth rate (Fig. 5) is consistent with

which yields

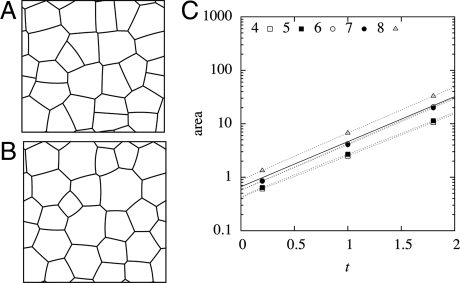
In that case, cells having fewer edges, which are generally smaller to begin with, initially grow less rapidly, leading to higher turgor pressures and an convex curvature of the walls, while cells having more edges exhibit concave walls (Fig. 7). The angles between walls progressively become closer to 120 degrees (Figs. 7B and 8), with the deviation decreasing from 24.2° at t = 0 to 9.6° at t = 2. Thus, this form of turgor regulation allows to reproduce the observed convergence to a froth-like geometry.

Fig. 7.

Simulation of growth with regulated turgor pressure—cell walls may be curved. (A) Normal growth of a 2D cellular structure giving the initial state at t = 0 when cell divisions become inhibited (dimensions of simulation box ≈4.2 × 3.9). (B) The 2D cellular structure resulting from the same simulation at time t = 2 after the inhibition of cell divisions (dimensions ≈29 × 28); cells with <6 sides become convex, and cells with more sides become concave. (C) Cell area versus time; dotted lines correspond to individual cells having different numbers of sides, the solid line to an average over all cells.

Discussion

In soap froths, the pressure differences needed for bubbles to acquire curved walls and angles to become equal to 120° may build up because gas content is each bubble is fixed. (This is only true on timescales that are short with respect to the coarsening of the foam.) In constrast, water may freely diffuse between plant cells, and pressure differences are established only over time, through variations in cell solute contents. The rapid convergence of angles to 120° in soap froths is related to the balance of capillary forces, and conversely, the progressive convergence in the growing regions of oryzalin-treated plants implies that wall tensions are becoming more uniform. We conclude that the state of mechanical forces underlying the observed tissue geometry is in fact equivalent to that in a soap froth, with the difference that it is not a static, rapidly attained equilibrium, but rather a dynamical one, resulting from growth and toward which the tissue progressively tends. As tensions become more uniform, growth should progressively become more uniform, with the shapes of the cells tending to a stationary state. This is in fact the case in our simulations, and is consistent with observations. Note that this conclusion holds irrespective of the particular material behavior of the walls, whether linear or not. Our results may also be extended straightforwardly to the 3D shapes of cells. Although a systematic study would be more difficult, it seems that the geometry of cells in an oryzalin-treated meristem as a whole is similar to that of a 3D soap froth. In particular, the segregation between the outer layers and the inner tissue gradually disappears (Figs. 1 and 3D), an observation that would deserve a more thorough investigation, because it could shed light on the mechanisms by which this segregation is maintained during normal growth. Finally, we note that the picture of a soap froth does not seem to apply either to wild-type (anisotropic) plant tissues or to animal tissues (26).

Additional support for the hypothesis of a correlation between cell area and turgor may be found in the observed curvatures of epidermal cells. From Laplace's law and the uniform wall tensions indicated by the angles at junctions, it may be concluded that the curvature of epidermal walls is proportional to the pressure inside epidermal cells. Examination of cross-sections of the meristem suggests that smaller cells indeed have a higher curvature (Figs. 1B and 3D). Besides, we have checked that different turgor regulation rules yield results similar to those reported above. One plausible mechanism would involve mechanosensing, which is known to play a role in turgor regulation, in particular, through mechanosensitive ion channels (24). More specifically, cell osmolarity could be regulated so as to maintain a constant average tension in cell walls (25). As is evident from the fact that this ensures a constant overall growth rate, this would yield the same scaling relation between area and turgor as that assumed in our simulations.

Our results may also have implications on growth in untreated meristems. Because it seems unlikely that such a mechanism should be specific to oryzalin-treated plants, we propose that turgor is also correlated with cell area in untreated plants. Within an organismal view of plant development, this could be thought of as a homeostatic loop serving to smooth out the local variations in growth rate that inevitably arise from the disordered nature of proliferating plant tissues, providing a rather homogeneous “canvas” for patterning mechanisms operating on a multicellular scale. Similar mechanisms might be at play in animal tissues (12, 13). However, much further experimental work is needed to confirm these proposals.

Concerning isotropy and anisotropy, the role of the microtubules in controlling anisotropy had already been noted. It was shown recently that the orientation of the microtubules was correlated with the principal stress direction in wild-type meristems (10). This phenomenon appears to give rise to a self-induced anisotropy: the orientation of microtubules and hence of cellulose microfibrils results in circumscribing the growth of the stem into an elongated structure. Conversely, when we suppressed microtubules, we found that younger cells, and hence the tip of the meristem, become isotropic, whereas older cells retain the anisotropy imposed by previously deposited microfibrils. In the light of this finding, the microtubules are very likely to represent an important target of the patterning genes acting in the meristem, in particular, when translating gene expression patterns into complex shapes. Therefore, the link between the regulatory network and morphogenesis, one of the key challenges of today's developmental biology, will have to explore in plants how the regulators of microtubules behavior and dynamics are acting within the gene-shape nexus.