Interactions between zebrafish pigment cells responsible for the generation of Turing patterns

Abstract

The reaction–diffusion system is one of the most studied nonlinear mechanisms that generate spatially periodic structures autonomous. On the basis of many mathematical studies using computer simulations, it is assumed that animal skin patterns are the most typical examples of the Turing pattern (stationary periodic pattern produced by the reaction–diffusion system). However, the mechanism underlying pattern formation remains unknown because the molecular or cellular basis of the phenomenon has yet to be identified. In this study, we identified the interaction network between the pigment cells of zebrafish, and showed that this interaction network possesses the properties necessary to form the Turing pattern. When the pigment cells in a restricted region were killed with laser treatment, new pigment cells developed to regenerate the striped pattern. We also found that the development and survival of the cells were influenced by the positioning of the surrounding cells. When melanophores and xanthophores were located at adjacent positions, these cells excluded one another. However, melanophores required a mass of xanthophores distributed in a more distant region for both differentiation and survival. Interestingly, the local effect of these cells is opposite to that of their effects long range. This relationship satisfies the necessary conditions required for stable pattern formation in the reaction–diffusion model. Simulation calculations for the deduced network generated wild-type pigment patterns as well as other mutant patterns. Our findings here allow further investigation of Turing pattern formation within the context of cell biology.

The reaction–diffusion system is one of the most studied and well-known nonlinear mechanisms that are able to generate spatially periodic structures. In the original article, Turing (1) presented the idea that the periodic structures generated by the reaction–diffusion mechanism may provide correct positional information that is used in the course of animal development. On the basis of many mathematical studies using computer simulations (2–5), animal coat pattern is assumed to be the most typical example of the Turing pattern. However, the mechanism underlying pattern formation remains unknown because the molecular or cellular basis of the phenomenon has yet to be identified. Recently, the zebrafish (Danio rerio), a small fish with distinctive stripes on the body trunk and fins, was selected as one of the model animals for molecular genetic research (6). Studies using this model animal have made it possible to uncover the basic mechanism that generates the Turing pattern in biological systems.

The stripes of zebrafish are composed of a mosaic-like arrangement of 3 types of pigment cells: melanophores, xanthophores, and iridophores (7). Evidence from recent molecular and genetic studies (8–10) on the altered patterns of mutant fish has suggested that the interaction between the melanophores (black) and xanthophores (yellow) are critical to the patterning process. However, such interactions have yet to be measured directly in the skin of adult fish. The pigment patterns of zebrafish are highly regenerative and are capable of correcting pattern disturbances induced artificially (7, 11). Our previous studies (11) and those of other groups (9) have shown that when all pigment cells in a wide area were killed, new pigment cells developed randomly in the vacant field regardless of their original position (11), followed by the segregation of pigment cells by cell type, through migration and cell death of pigment cells (11). Although the spacing of the regenerated stripes was as wide in the original pattern, the conformation of the new pattern was sometimes changed (7, 11). These results suggest that the stripe pattern is generated in the skin by interactions between pigment cells, rather than by a prepattern mechanism. In this study, we performed a series of ablations to measure the relationship between regenerating cells and those surrounding the ablated region. We then deduced the control network between the melanophores and xanthophores. Finally, we used computer simulation to determine whether the deduced network is capable of forming the pigment patterns of wild-type and mutant zebrafish.

Results

Long-Range Interaction to Influence the Development of New Pigment Cells.

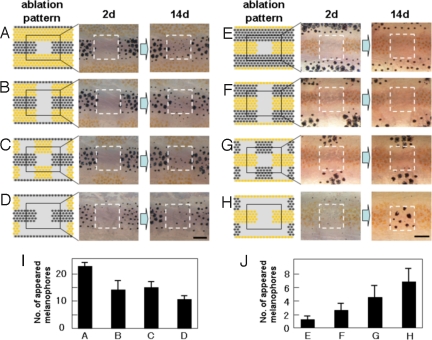
In the first experiment, we observed the regeneration of pigment cells and how this process was influenced by cells in the neighboring stripes. When we ablated the melanophores in the square region in the black stripe, melanophores developed to regenerate the original pattern (Fig. 1A). However, when we simultaneously ablated the xanthophores in the neighboring stripes, the number of regenerated melanophores decreased corresponding to the number of xanthophores ablated (11) (Fig. 1 B–D). This observation suggests that the development of melanophores was positively affected by xanthophores in the neighboring stripes. When we ablated the xanthophores in the square region in the yellow stripe, only xanthophores developed to regenerate the original pattern (Fig. 1E). However, when melanophores in the neighboring stripes were ablated at the same time, melanophores quickly developed in the original xanthophore region (11) (Fig. 1 F–H), and xanthophore did not. This result suggests that the melanophores in the neighboring stripes had a repressive effect on the development of melanophores in the distant place. Because the xanthophores do not develop in the region already occupied by melanophores, the effect of melanophores on developing xanthophores cannot be determined from this experiment.

Fig. 1.

De novo pigment cell development induced by laser ablation. (A–H) To measure the influence of distant region on cell regeneration in the center region, pigment cells in the neighboring stripes were ablated by laser with the pattern shown (Left). The ablated pattern (day 2) and the regenerated pattern (day14) are shown (Center and Right). (I) The number of melanophores that appeared in the center square area for the ablation patterns a–d. (J) The number of melanophores that appeared in the center square area for the ablation patterns e–h. Pigment cells on the right side of 34-dpf fish were ablated as described (11), and the pigment cells that appeared in the center square area were recorded. Pigment cells developed in the surrounding ablated area were ablated daily to maintain the cell density of the surrounding area. n = 5 for experiment a–d, and n = 8 for e–h. SD values were presented at the top of each bar. For the details of laser ablation of the pigment cells, see ref. 11.

Long-Range Interaction to Influence the Survival of Pigment Cells.

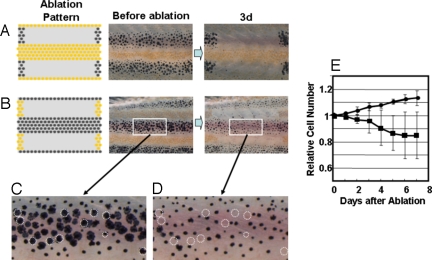
In the second experiment, we tried to determine how the survival of pigment cells is influenced by the cells in the neighboring stripe. In Fig. 2A, melanophores in 2 black stripes located dorsal and ventral to the central yellow stripe were ablated to abolish the influence of melanophores. In this case, xanthophores did not appear damaged, and no cell death was observed. However, when we ablated the xanthophores in the yellow stripes sandwiching the black stripe (Fig. 2B), melanophores became less dendritic in shape, and 10% to ≈15% of melanophores died.(Fig. 2 C and D). Very few newly developed melanophores were observed in the region, whereas an ≈10% increase in the number of melanophore was observed on the other side of the identical fish. At day 6 after the ablation, the melanophore density decreased ≈20% compared with the control (Fig. 2E). This observation suggests that the xanthophores in the neighboring stripes aided in melanophore survival. Because the melanophores in the middle of the black stripe disappeared, the xanthophores should have influence over a long range (at least half the width of a stripe in distance).

Fig. 2.

Survival of pigment cells after loss of the pigment cells in neighboring stripes. (A and B) To measure the long-range effect from the neighboring stripes to help the survival, all of the pigment cells in the neighboring stripes were ablated, and the survival of the cells in the center stripe was observed at day 3. (C and D) Magnified picture of the white square area in day 0 and day 3 of experiment B. Dotted circles are the cells that were no longer present at day 3. (E) Time course of the number of melanophores in the middle stripe region. Cell number is represented by the value relative to the original number. Black circle, number of melanophores in the control region; black square, number of the melanophores in the middle region. Pigment cells of 34-dpf fish were ablated as in Fig. 1. For all test fish, laser ablation was performed only on the left side of the trunk. The right side was used as the control. To avoid the influence of newly developed pigment cells in the ablated (yellow stripe) region, developing pigment cells were ablated daily. Number of the cells in the test region (white square) was counted and represented as value relative to the original number. SD value is represented at each point. The number of the fish used for this experiment was 8.

Short-Range Effect of Xanthophores Against Melanophores.

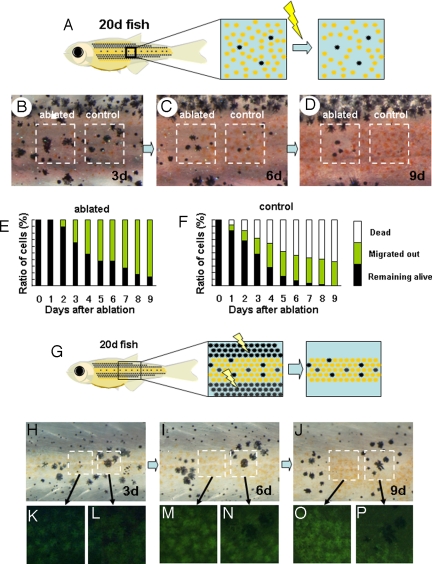
In the third experiment, we identified the short-range effect of the adjacent cells. In the body trunk of a young zebrafish [20 days after fertilization (dpf)], those ≈10 days before the adult stripes are completed, the melanophores are sparsely distributed in the region of future black stripe but also in the future yellow stripe.(Fig. 3B) We selected lone melanophores in the future yellow stripe region and observed their behavior (Fig. 3 A–D). In the normal course of stripe formation (Fig. 3 B–D, right square), these melanophores disappeared quickly either by cell death (50%) or by migration (40%) toward the black-striped region (Fig. 3F). However, when we ablated those xanthophores located at the nearest neighboring region (Fig. 3A), very little cell death was observed, and ≈40% of the melanophores remained alive in the yellow-striped region until at least 6 d after ablation (Fig. 3 B–D, left square and Fig. 3f). These results suggest that the elimination of the melanophores in the control experiment were caused by the xanthophores directly surrounding those melanophores. In the experiments in Figs. 1 and 2, we showed that the distantly located xanthophores enhanced the development and the survival of melanophores. Therefore, xanthophore cells exhibit 2 different and opposing effects on melanophore cells, depending on their distance.

Fig. 3.

Competitive effect between adjacent pigment cells. (A) Schematic drawing of the experiment to measure the short-range effect of xanthophores on melanophore. In a 20 dpf-fish, melanophores are dispersed in the middle region where xanthophores become dominant soon after. Xanthophores adjacently surrounding each melanophore were ablated, and the survival of these cells was tracked. (B, C, and D) Survival of the melanophores in relation to the adjacent cells. In the control region, no ablations were made, and the dispersed melanophores were surrounded by xanthophores (B, right square) the number of the melanophore decreased (day 6) and disappeared at day 9. In the left square region, the xanthophores adjacently surrounding the melanophores were ablated.(B, right square) A half of melanophores survived at day 6. (E and F) Time course of melanophore survival after ablation. Survival ratio is shown as the relative value against the original number. Total number of the tested melanophores was 50 for each graph. Black bar, melanophores remained alive in the yellow stripe region; yellow bar, melanophores migrated into the black stripe region; white bar, melanophores disappeared (dead). (G) Schematic drawing of the experiment to measure the short range effect of melanophores on xanthophores. Melanophores in the black stripe region were continuously ablated to enhance the survival of melanophores in the middle region. (see Figs. 1 and 2). (H, I, and J) Survival of the pigment cells at days 3, 6, and 9 after ablation of black stripes. The region in the left square is filled with xanthophores. As the time passed, all of the xanthophores in the left region accumulated the fluorescent pigment and looked very healthy. The right square region is occupied by the mixture of melanophores and xanthophores, at day 3. As the time passed, melanophores became dominant, and the xanthophores disappeared. This should be caused by the adjacent melanophores because the xanthophore in the left region stayed alive in the same period. (K–P) Magnified picture of the outlined area in H–J.

Short-Range Effect of Melanophores Against Xanthophores.

In the fourth experiment, we identified the short-range effect of melanophores on xanthophores. We used 20-dpf young zebrafish again because these specimens have a mixed distribution of pigment cells (Fig. 3G). Normally, xanthophores develop in this center region, and all melanophores disappear quickly. Therefore, it is difficult to observe the short-range effects of melanophores on xanthophores. To enhance the survival of melanophore in this region, we ablated the melanophores in the neighboring black-striped regions (Fig. 3G). (Loss of melanophores in the neighboring stripe has a positive effect for the melanophores. See Fig. 1.) Three days after ablation, some melanophore colonies survived in the region normally occupied by the yellow stripe (Fig. 3 H, K, and L). The left square region, which consisted solely of xanthophores, showed an increase in endogenous xanthophore pigment fluorescence, corresponding to the growth of the fish (Fig. 3 K, M, and O). This result suggests that ablation of melanophores does not affect xanthophore activity. However, in the right region where the melanophore colony survived, xanthophore cells disappeared within and around the melanophore colony (Fig. 3 L, M, and P), suggesting that melanophores compete with xanthophores at short range.

Discussion

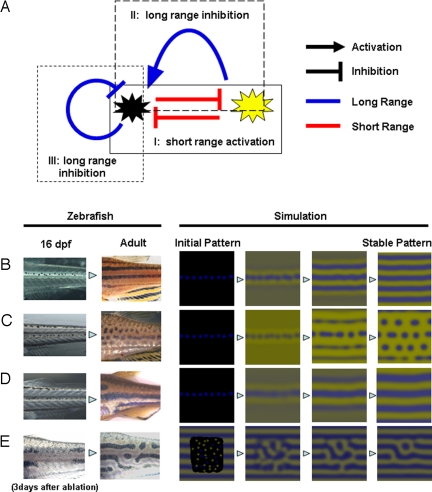
In the above 4 experiments, we observed the in vivo interactions between melanophores and xanthophores with respect to the distance between the cells and how these interactions affect the development and survival of pigment cells. The deduced control network is shown in Fig. 4A. Each arrow does not represent a particular molecular signal but, instead, represents the formal interactions that exist between the pigment cells. Therefore, an arrow could be the sum of a number of parallel signals or could be a relay of indirect signals. To determine the network at the molecular level, identification of the molecules mediating these interactions is required.

Fig. 4.

Deduced interaction network between pigment cells and simulation. (A) Control network among the pigment cells deduced by the results described in this report. There are 3 control loops that start with and return to the melanophores. Control loop I (experiment shown in Fig. 3) contains 2 short-range negative effects and functions as a short-range positive-feedback mechanism. Control loop II (experiment shown in Figs. 1 and 2) contains a negative (short) and a positive (long) effect and functions as a long-range negative-feedback mechanism. Control loop III (experiment shown in Fig. 1) is a long-range negative-feedback mechanism. As a whole network, this system satisfies the need for local activation and long-range inhibition, which have been cited by mathematical studies as necessary conditions for Turing pattern formation. (B–D) Development of pigment patterns in real zebrafish and computer simulation. In the left 2 panels, fish pigment pattern of 16-dpf and adult (3 months) are shown for wild type (B), leo^t1 (C), and obe^tc271d (D). Sixteen-dpf patterns are almost identical because the juvenile melanophore lines along the horizontal myoseptum. Therefore, we used identical initial pattern in the simulation for B, C, and D. In the right 4 panels, the results of the simulation are represented. In E, the pattern of 3 days after the ablation and regenerated pattern (11) are shown in the left 2 panels. Initial pattern for this regeneration is a random pattern in the ablated region. Details of the simulation are in Experimental Methods and Simulation.

The most important characteristic of this deduced network is the opposing effects of cells positioned in close or distal regions. According to the deduced network, the activation of melanophores inhibits xanthophores in the local region, resulting in further activation of melanophores in this region (Fig. 4A, control loop I). Conversely, the inhibition of xanthophores causes a decrease of melanophores in distant regions (Fig. 4A, control loop II), creating a long-range inhibitory loop; control loop III (Fig. 4A) also acts as a long-range inhibitory loop. The deduced network involves local activation and long-range inhibition, which have been cited by mathematical studies (12, 13) as necessary conditions for periodic pattern formation in the reaction–diffusion system. The computer simulation that generated the network can reproduce the normal and regenerative process of pigment patterns and the patterns of mutant lines (Fig. 4 B–E). (For simulation details, see Experimental Methods and Simulation) From these results, we conclude that the network we have identified is the core mechanism for zebrafish pigment pattern formation. Our current results do not address or rule out the possibility that other cells (iridophores, keratinocytes, and fibroblasts) in the skin also have some effect on stripe formation. However, we assume that these cells can only modify the pattern generated by the core mechanism because the deduced network is enough to generate the pigment pattern.

Theoretical studies (2, 13–15) have suggested that the reaction–diffusion mechanism underlies the skin patterning of animals. However, these mathematical models have been difficult to apply to studies at the molecular level because these models are too abstract. In the present report, we show that the variables of the model equation correspond to the interactions between pigment cells. This finding will aid in the identification of a more detailed mechanism for pigment pattern formation.

Although we showed that interactions between pigment cells possess the necessary conditions of Turing pattern formation, the molecular and genetic mechanisms responsible for the interactions between pigment cells remain unidentified. Identification of the molecular signaling pathways is required to understand pigment pattern formation in animals. Comprehensive genetic screening (6, 16) has isolated many mutant genes responsible for the alteration of pigment pattern in zebrafish, and the function of these genes were studied (8, 9, 17–21). The most relevant area of research is the characterization of the in vivo function of such molecules during adult pigment pattern formation. Recent reports (22–24) on developmental processes in several vertebrates have shown that the reaction–diffusion mechanism functions in pattern-forming events other than skin pigmentation, which suggests the importance of the dynamic mechanism in the understanding of animal morphogenesis. Fish pigment pattern development is an ideal system in which to study the reaction–diffusion mechanism because it occurs in the 2-dimensional field, and the dynamics of this pattern are visible. Further clarification of the molecular mechanisms involved in zebra fish pigment pattern development will give a greater understanding of dynamic and complex phenomena occurring in living systems.

Experimental Methods and Simulation

Fish Stock.

Zebrafish were bred and maintained under standard laboratory conditions (25). The wild-type strain used was Tü (6). The age of the fish used in the experiments was ≈3 weeks after hatching, the point at which the first 3 stripes appear on the body.

Laser Ablation of Pigment Cells.

Before ablation, the fish were anesthetized by using 0.01% MMS (ethyl-m-aminobenzoate methanesulphonate) (25) and mounted on a chamber glass slide. During ablation, fish were always maintained under moist conditions with a weaker anesthesia than full anesthetization. Ablation was performed by using a 365-nm multiple light-pulse laser from the MicroPoint pulse laser system (Photonic Instruments) that was focused to a 40× objective on a microscope. In general, each pigment cell was broken down sufficiently by 4–5 laser pulses. Cell death from ablation was checked the next day, and remnants were ablated if there were any.

Simulation (Fig. 4).

Simulations were carried out as a variation of the reaction–diffusion model that contains 3 factors. The differential equations are as follows,

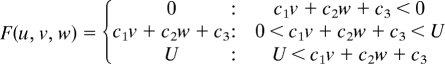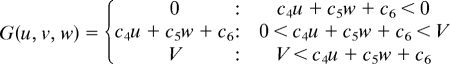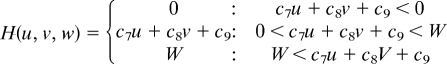(To avoid the unrealistic production rates of the substances, lower (equal to 0) and upper limits of U, V, and W were set for the function F, G, and H.)

Two of the variables, u and v, represent the density of the 2 types of pigment cells, melanophores and xanthophores. The variable w represents a long-range factor that is expressed by u. The short-range ligands produced by these cells have small diffusion constants, and the distribution of them should be almost the same as that of pigment cells. Therefore, we assumed that u and v also represent the concentration of the short-range factor. This simplification has been made to avoid the complexity of the differential equations. Because there are no data about molecular devices that mediate the interaction, the temporal model should be as simple as possible.

Parameters for each simulation are as follows: for wild type, c₁ = −0.04; c₂ = −0.055; c₃ = 0.37; c₄ = −0.05; c₅ = 0.0; c₆ = 0.25; c₇ = 0.016; c₈ = −0.03; c₉ = 0.24; c_u = 0.02; c_v = 0.025; c_w = 0.06; D_u = 0.02; D_v = 0.02; D_w = 0.2; U = 0.5; V = 0.5; and W = 0.5. For the leopard mutant, c₃ = 0.385 and other parameters are identical to the wild type. For the jaguar/obelix mutant, D_u = 0.04; D_v = 0.04; D_w = 0.4; and other parameters are identical to the wild type.

Simulations were done in a 128 × 128 square field with a no-diffusion boundary condition. Results of the calculations were shown by the mix of green and blue color that represents the concentrations of u and v, respectively.

Because the width of the zebrafish stripes is the size of only 7–12 pigment cells, it is expected that the pattern formation may be influenced by the stochastic effect of cellular behaviors. To simulate such phenomenon, it is better to use a cell-based model in which each cell's behaviors (development, cell death, and migration) are calculated by stochastic functions. However, such complex and detailed simulation is temporally unrealistic because we do not have enough experimental information to determine the functions specifying the behaviors of pigment cells. Therefore, we used in Fig. 4 the continuum model in which the number of parameters can be minimized. We confirmed that the stripe patterns made by the stochastic simulation are as stable as those made by continuum simulation, using a prototype cell-based simulator [see supporting information (SI) Text and Fig. S1].