Change in Conduction Velocity due to Fiber Curvature in Cultured Neonatal Rat Ventricular Myocytes

Abstract

Computer modeling of cardiac propagation suggests that curvature of muscle fibers modulates conduction velocity (CV). The effect could be involved in arrhythmogenesis by altering the dynamics of reentrant wavefronts or by causing propagation block.

To verify the existence of this effect experimentally, we measured CV in anisotropic neonatal rat ventricular myocyte monolayers. The orientation of the cells was directed by scratches machined into plastic coverslips. Each substrate contained a region in which scratch radius-of-curvature varied from 0.25 to 1.0 cm. The CV anisotropy ratio (longitudinal CV / transverse CV in straight-fiber regions) was 2.3±0.3 (n=38). We initiated wavefronts transverse to fibers with the fibers either curving toward or away from the wavefronts. Action potentials were recorded using a potentiometric dye and a video camera. Propagation was faster (p=0.0003) when fibers curved toward wavefronts than when fibers curved in the opposite direction. The mean CV difference was 0.38±0.44 cm/s (n=24), which is 3.5% of nominal straight-fiber transverse CV (11.0±3.2 cm/s). The effect was also present when pacing was slowed from 350 ms to 500 ms (n=6). In a control group (n=8) with uncurved fibers, CV was the same in both directions (p=NS). We conclude that fiber curvature is a factor in modulating cardiac propagation.

Introduction

Cardiac myocytes are elongated and align axially along cardiac fibers [1, 2]. Intercellular connectivity is anisotropic: gap junctions (the primary pathway for intercellular ionic currents) are found predominantly at the ends of the myocytes (the longitudinal direction), with comparatively few gap junctions between the sides of adjacent cells (the transverse direction) [2, 3]. Electrical anisotropy results from this structure. Transverse intercellular resistance is higher than longitudinal intercellular resistance, resulting in slower conduction velocity in the transverse direction [4−6].

Propagation transverse to the fibers is asymmetric when the fibers are curved. In two dimensions, the wavefront can cross the curved fibers either from their convex or their concave side. Computer modeling has shown that conduction velocity (CV), upstroke rate, and action potential amplitude are all increased relative to the straight-fiber case when fibers curve toward the wavefront (i.e., the wavefront propagates toward the concave side). These effects are all reversed when waves propagate in the opposite direction relative to the fibers. The effects are due to directional differences in the electrical load on the wavefront [7, 8].

Fiber curvature is clearly present in the heart. The spatial orientation of cardiac fibers has been measured in dog [9], rabbit [10], and pig [11] hearts. Regions are present in which fibers are curved in planes parallel to the epicardium [9−11]. More pronounced fiber curvature is present where the right and left ventricles join at the septum [11] and is also very likely to occur where endocardial structures such as trabeculae and papillary muscles join the bulk myocardium.

In computer models, fiber curvature has been shown to affect the dynamics of reentrant waves by causing nominally stationary reentry to drift [7]. Other models have shown that fiber curvature may be important in defibrillation [12]. Computer modeling of the effect of surface curvature, which modulates wavefront loading in a similar manner to fiber curvature, has shown that even very small loading effects (CV changes on the order of 2%) can convert a stable reentrant activation pattern to a complex VF-like state [13]. It has been proposed that the insertion points of ventricular trabeculae and papillary muscles are involved in wavebreak and reentry [14, 15]. Although the mechanism of this involvement is not well understood, fiber curvature may play a role.

Despite the potential importance of the effects of fiber curvature on cardiac propagation, it has not yet been demonstrated experimentally. Native tissue preparations are not well suited for such studies because it is difficult to isolate fiber curvature's role from that of other heterogeneities. In the present study, we test for the effects of fiber curvature on transverse CV using anisotropic monolayers of cultured cardiac myocytes with controlled fiber orientation. We find that as predicted, propagation is faster when fibers curve toward the wavefront than when they curve in the opposite direction.

Materials and Methods

All protocols involving animals were approved by the Institutional Animal Care and Use Committee at the University of Alabama at Birmingham.

Cell Culture Substrate Preparation

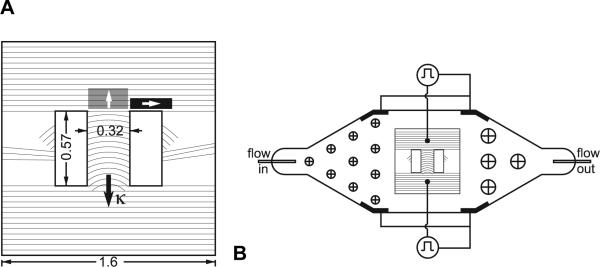
Polyvinyl chloride (PVC) coverslips (Fisher Scientific) were scratched using a razor blade with a finely serrated edge. Controlled serrations were made in the edge of the razor blade using a fly-cutter on a tabletop milling machine (Sherline Products, Vista, CA). Serrations were produced with 18μm spacing, consistent with the width of scratches previously shown to maximize anisotropy [5]. The serrated blade was then fixed in place and PVC coverslips were mounted below it on the milling machine's stage. Scratches were produced by moving the coverslips under the blade using computer control of rotation and X-Y translation. Figure 1A illustrates the pattern of scratches. The radius of curvature of the scratches varied from 0.25 cm at one end of the curved-fiber region to 1 cm at the other end. Although the radius of fiber curvature has not been explicitly quantified throughout the myocardium in whole hearts, we believe that fiber curvatures of this order of magnitude are reasonable at structurally complex regions such as the apex and at the insertions of the right ventricular free wall, trabeculae, and papillary muscles. A range of curvatures, rather than a single curvature value, results from the concentric geometry of the scratching pattern. The concentric geometry ensures constant spacing between the scratches. Nonuniform spacing may have resulted in side-to-side gradients of the anisotropy ratio across the curved-fiber region. Straight scratches were produced above and below the region of curved scratches to promote transverse propagation on entry to and exit from the curved-fiber region. Two rectangular holes were punched in the coverslip to create parallel boundaries on either side of the region of curved scratches. These boundary conditions were designed to maintain approximately transverse wavefronts in the resulting channel of curved fibers. The symmetrical geometry of the substrate boundaries was designed to produce the same electrophysiological boundary conditions for wavefronts entering from either end of the curved-fiber region. We also produced control substrates that were identical to those described above, but with straight scratches replacing the curved scratches. To remove any machining residues, coverslips were sonicated in a detergent solution (containing Alconox, White Plains, NY) for 30 minutes and then thoroughly rinsed with deionized water. The substrates were then gas sterilized. To promote cell adhesion, substrates were coated with collagen (extracellular matrix protein collagen type IV from human placenta, Sigma) dissolved in a phosphate buffer at a concentration of 100 ug/mL.

Figure 1.

A. Geometry of the growth directing substrates. Hatch marks indicate the scratch pattern. Scratches were spaced by 18 μm. Isotropic regions on both sides of the culture were scratched three times with a scalpel to prevent wavefront reentry. Shaded boxes represent regions of measurement of longitudinal (black) and transverse (gray) velocities used in anisotropy ratio calculations. White arrows denote propagation direction in those measurements. The κ vector points toward the center of curvature. All dimensions are in cm. B. Geometry of the perfusion bath. The bath was machined in a block of clear acrylic and is approximately 3 mm deep. Arrays of circles with crosses on either side of the cell culture represent cylindrical obstacles to smooth perfusate flow. All electrodes are shown in black. Two grounding electrodes were paired with each unipole to ground stimuli from either side of the cell culture.

Cell Culture

Cell cultures were plated and incubated using ventricular myocytes from two to three day old Sprague-Dawley rats (Harlan, Indianapolis, IN) as previously described [16]. Measurements were made between the fourth and sixth days in culture.

Optical Mapping of Wavefronts

Cell culture confluence was assessed using phase contrast microscopy, and monolayers with visible gaps in the curved-fiber channel were excluded. Cell cultures exhibiting fast spontaneous rhythms (cycle length < 350ms) were also excluded because the spontaneous wavefronts would interfere with the wavefronts paced at slower rates.

For experiments, cell cultures were placed in a perfusion bath that was custom fabricated from clear acrylic (Figure 1B). The perfusate was regulated to 37°C and had the following composition (mmol/L): NaCl 150, KCl 5, CaCl₂ 1.2, MgCl₂ 1, NaHCO₃ 5.8, HEPES 5, and glucose 5 (Hanks Balanced Salt Solution supplemented with Sodium Bicarbonate and HEPES, Sigma). Perfusate flow rate was 3.6mL/min. pH was regulated to 7.4. A piece of clear acrylic was placed on top of the perfusion bath in contact with the fluid surface to prevent ripples from distorting optical signals. Cultures were allowed to equilibrate in the perfusion bath for at least 35 minutes prior to data acquisition.

Cell cultures were stained with the voltage-sensitive fluorescent dye di-4-ANEPPS (11μmol/L in Hanks solution, Invitrogen) by perfusing with the dye solution for 23 minutes and then rinsing with dye-free perfusate for 8 minutes. Excitation light was provided by an array of 39 LEDs (470 nm, BL-3000, Lamina Ceramics, Westampton, NJ) placed below the perfusion bath. The LED output was passed through a 510nm shortpass filter (Edmund Optics, Barrington, NJ) to reduce background fluorescence and a diffuser for more uniform illumination (Edmund Optics, Barrington, NJ). Emitted fluorescence was recorded at 1000 frames per second and 32×32 spatial resolution with a CCD camera (iXon DV860DC-BV, Andor Technologies, Ireland). The camera was fitted with a video lens (6mm, f/1.0, Pentax), a series of close-up lenses with a diopter of +27 for magnification (Kodak), and a 610 nm longpass filter (Edmund Optics, Barrington, NJ). This configuration provided a spatial resolution of 0.28mm per pixel.

Rogers and McCulloch characterized fiber curvature with a vector that points toward the center of curvature (κ, Figure 1A) [7]. Following the terminology of this previous paper, we refer to transverse wavefronts propagating in the same direction as the curvature vector as transverse-with (TW) and wavefronts propagating in the opposite direction as transverse-against (TA). Fibers curve away from TW wavefronts and toward TA wavefronts.

Two unipolar stimulating electrodes were extended through the clear window on top of the perfusion bath to within 400μm of the cell culture (Figure 1B). TW and TA wavefronts were initiated with the upper and lower electrodes, respectively. Stimuli were grounded by a pair of stainless steel mesh electrodes on the same side of the perfusion bath as the stimulating electrode (Figure 1B). The stimuli were threshold cathodal pulses, 5 ms in duration. Twenty four curved-fiber cultures and eight straight-fiber controls were paced with a 350 ms interval. An additional 6 curved-fiber cultures were paced at 500 ms.

Sixteen optical mapping recordings were made per culture, each 3 seconds in length. To control for gradual changes in CV over the course of the experiment that were not related to fiber curvature, recordings were divided into 4 series of 4 recordings each. Recordings of TW and TA wavefronts were alternated as follows: (TA, TW, TA, TW), (TW, TA, TW, TA), (TA, TW, TA, TW), (TW, TA, TW, TA). After switching the stimulus site between recordings, the new stimulus site was paced for several cycles before recording optical data. Adjacent runs within each four run series were never separated by more than 20s. Series were separated by at least 120s, with continued same-side stimulation during the interval. The same procedure was followed for the control cultures (those with straight scratches throughout) to verify that there was no systematic asymmetry in the perfusion/mapping apparatus.

Determination of CV

Optical mapping data were processed in MATLAB (MathWorks, Natick, NJ). First, background fluorescence was removed by subtracting a background image from each frame of the dataset. Baseline drift (due to dye bleaching) in the signal associated with each pixel was removed by linear trend subtraction. A 60 Hz bandstop filter with a width of 1.66 Hz was used to minimize 60-cycle noise.

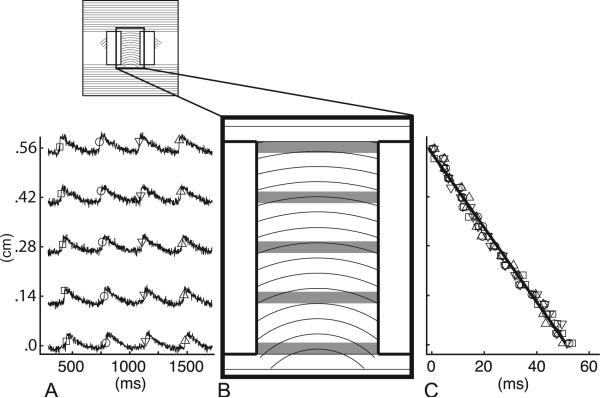
Figure 2 illustrates the procedure used to compute CV for each recording. First, signals from pixels in rows crossing the channel were averaged together and the resulting signals were 3-point median filtered (Figure 2A,B; approximately 11 pixels per row). This averaging was possible because the wavefronts traversing the curved-fiber region were essentially straight and perpendicular to the substrate boundaries (see Analysis of Wavefront Curvature below). There were approximately 20 rows of pixels spanning the channel. Peaks in the derivative of the fluorescence upstroke identified activation times in each averaged row of pixels. At the 350ms pacing rate, each three-second recording contained eight or nine wavefronts. At the 500ms pacing rate, each three-second recording contained five or six wavefronts. The activation times associated with each wavefront were shifted in time so that all wavefronts had the same mean activation time. A straight line was then fit to the displacement vs. activation time data for all the wavefronts in each recording (Figure 2C), and the slope of this line was taken as the CV for that recording. This analysis is designed to test for an overall CV difference between TW and TA propagation. Because scratch curvature changes from one end of the curved-fiber channel to the other, CV may change as wavefronts traverse the channel. The overall TW-TA CV difference was expected to be small, so in the present study, we did not attempt to resolve CV changes within one type of propagation, which would be even smaller. Although both TW and TA wavefronts encounter the same range of fiber curvatures, they do so in the opposite sequence. From equation B4 of our previous publication [7], wavefront loading does not depend on changes in fiber orientation in the direction normal to the wavefront. Thus, we do not expect the average CV computed over the length of the channel to be affected by progressively increasing or decreasing fiber curvature.

Figure 2.

Method for CV calculation. A. The signals shown were constructed by averaging across pixels in rows crossing the channel (gray bars in B). Activation times, determined by the maximum derivative of the upstroke for each depolarization, are shown by symbols, with different symbols corresponding to different wavefronts. B. Channel of curved fibers (0.32 by 0.57 cm). C. Displacement vs. time for all wavefronts, showing data from all rows of pixels. Each symbol type represents one wavefront, with symbols matching the symbols of activation times in A. The linear regression is shown as a thin black line. CV calculated from the data shown was 11.0cm/s.

Analysis of Anisotropy

The anisotropy ratio (longitudinal CV / transverse CV) in straight-fiber regions was computed for each cell culture. This was done by computing CV, in the same manner described above, for wavefronts exiting the curved-fiber channel (Figure 1A). Longitudinal CV was measured in the black region, and transverse CV was measured in the gray region.

To assess the conformance of cell orientation to the curved scratches, at the conclusion of mapping, eight cultures were fixed in 3.7% formaldehyde and stained for actin (Alexa Fluor 488-phalloidin, Invitrogen) [17]. The cultures were imaged with phase-contrast microscopy to show the scratches, and then, without moving the culture, with fluorescent microscopy to show cell orientation.

Analysis of Wavefront Curvature

Wavefront curvature can also influence CV [18, 19]. To determine if wavefront shapes were different between the TA and TW cases, we used cross-correlation to find the temporal lags between signals recorded across rows of pixels for both TA and TW propagation. For each row of pixels analyzed, we averaged signals from the two leftmost, two rightmost and two center pixels to yield three new signals (left, right, and center). This was done for three different rows in each recording (¼, ½, and ¾ of the way through the channel). The cross-correlation between two signals gives the temporal lag that optimally aligns the signals. Thus, without explicitly picking activation times, this analysis gives an indication of the difference in wavefront arrival time averaged over the 8 or 9 waves in each recording. Cross correlation lags are limited in resolution to one temporal sample. The temporal resolution of the alignment can be improved by interpolating the signals to a higher sampling rate [20, 21]. Before computing the cross correlations, we used the MATLAB resample() function to increase the sampling rate from 1 kHz to 10 kHz. The lag between the left and right signals (lag_full-width) in a row approximates the wavefront orientation across the full width of the channel. The lag between the left and center signals (lag_half-width) indicates the wavefront position at the center of the channel. The half-width lag, relative to the full-width lag, is the “bend” of the wavefront (wavefront bend = lag_half-width – lag_full-width /2 ). At the 10kHz interpolated sampling rate, the smallest detectable wavefront bend is 0.1ms. This corresponds to a maximum detectable wavefront radius of 11.7cm for a wavefront with nominal CV=11cm/s.

Statistical Analysis

Because successful TW and TA runs were never separated by more than 20s and TW preceded TA exactly half the time, to control for the effects of time on CV, we simply averaged the eight runs in each direction to get a single TW and TA value for each culture. For each group of cultures with curved fibers, a one-sided paired t-test was used to test the hypothesis that TA propagation is faster than TW propagation. For the control cultures (those with straight scratches throughout the substrate), a two-sided paired t-test was used to test for a CV difference in the two possible directions. We used two-way analysis of variance (ANOVA) to test for the effects of distance through the channel and propagation direction (TW or TA) on wavefront bends. Differences were considered significant for p<0.05. Averaged measurements are expressed as mean±SD.

Results

Thirty curved-fiber cell cultures and eight straight-fiber control cell cultures from four different litters of neonatal rats were used in this study.

CV anisotropy ratio averaged over all 350ms paced cultures was 2.3±0.3 (n=32). Mean transverse and longitudinal CVs during 350ms pacing, from the values used in anisotropy ratio calculations, were 11.0±3.2 and 24.9±7.0 cm/s, respectively. CV anisotropy ratio averaged over all 500ms paced cultures was 2.5±0.3 (n=6). Mean transverse and longitudinal CVs during 500ms pacing, from the values used in anisotropy ratio calculations, were 8.4±2.8 and 20.8±5.8 cm/s, respectively.

Fluorescent actin staining was used to image the alignment of cells with the machined scratches in eight of the cultures. Figure 3 shows one example. The white strands in panel A are actin filaments. Panel B shows the scratches in the same region. The strands are in general alignment with the scratches.

Figure 3.

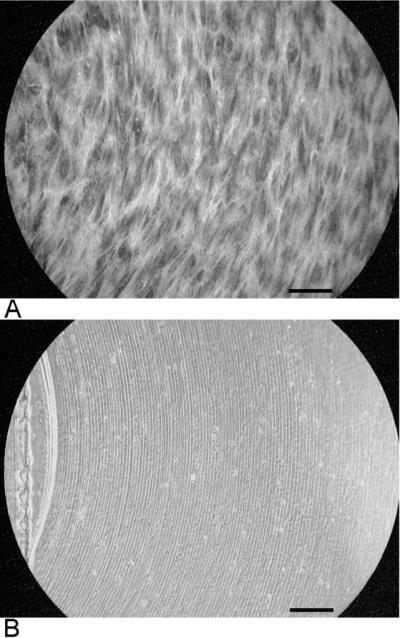
Alignment of cells with curved scratches. A. Cell orientation imaged with fluorescent actin filament staining. B. Phase contrast image showing scratches in the same region. Bars are 200μm.

TA wavefront bends at ¼, ½, and ¾ distances through the channel (all 350ms paced, curved fiber samples, n=24) were 0.4±1.8, −0.3±1.8, and −0.0±2.5 ms, respectively. At the same distances, TW wavefront bends were 0.4±1.8, −0.2±0.6, and −0.4±1.9 ms, respectively. A positive bend indicates convex wavefront curvature, relative to the stimulus site; a negative bend indicates concave wavefront curvature. From the nominal transverse CV of 11 cm/s, these bends and their standard deviations are very small—less than a single pixel (0.28 mm). Neither distance through the channel nor TW vs. TA propagation affected wavefront bend (p=0.26, p=0.86, respectively). The interaction between the two factors was also insignificant (p=0.50).

Example signals and activation time vs. displacement plots from one recording are shown in Figure 2. To demonstrate the alternating sequence of TW and TA recordings, velocity measurements from a single cell culture vs. time of data acquisition are shown in Figure 4A.

Figure 4.

A. Velocity measurements vs. time of data capture for a single cell culture. Squares denote TA runs; circles denote TW runs. The first recording in this cell culture is TA propagation (first square, t=0), the second recording is TW propagation (first circle, t=16). Starting from t=0, the order of the recordings is as follows: Series 1: TA, TW, TA, TW; series 2: TW, TA, TW, TA; series 3: TA, TW, TA, TW; series 4: TW, TA, TW, TA. The measurement sequence is reversed in each subsequent series of four measurements to control for temporal changes in CV. Recordings within each series are no more than 20s apart. Series are separated by at least 120s. B. Average conduction velocities for TW and TA propagation in all curved-fiber samples. Each line represents one cell culture. Solid lines represent cultures paced at 350ms, dashed lines represent cultures paced at 500ms.

The mean CVs for 350ms paced TA, TW, and control runs in both directions were 11.4±2.5 cm/s, 11.0±2.1 cm/s, and 11.4±2.3 cm/s, respectively. By one-way ANOVA, which does not take into account the same-culture pairing between TW and TA runs, there was no difference among these means (p=0.8). Solid lines in Figure 4B show the paired 350ms paced CV measurements for TA and TW propagation in each culture. The mean CV difference (TA – TW) was 0.38±0.44 cm/s, which is approximately 3.5% of nominal transverse CV. By a paired t-test, the difference was highly significant (p=0.0003). Two of the cell cultures exhibited a >1 cm/s difference between TA and TW propagation velocities, while two other cultures exhibited the reverse of the hypothesized effect (TW propagation was faster than TA propagation in these two samples). The CV difference for the two propagation directions in the control group was much smaller than in the curved-fiber group (0.06±0.18 cm/s) and was not statistically significant. This indicates that there was no significant systematic asymmetry in the mapping apparatus.

The mean CVs for 500ms paced TA and TW wavefronts were 8.5±2.9 cm/s, and 7.9±2.1 cm/s, respectively (n=6 cultures). The mean CV difference (TA – TW) was 0.62±0.88 cm/s, which is approximately 7.6% of nominal transverse CV. Although this mean difference was larger than in the 350 ms samples, it did not reach significance by a one-sided paired t-test (p=0.07). Dashed lines in Figure 4B show the paired 500ms paced CV measurements for TA and TW propagation in each culture. One of the six 500ms paced cultures exhibited the reverse of the hypothesized effect (TW propagation was faster than TA propagation in that culture).

Discussion

The major result of the present study is that fiber curvature modulates conduction velocity in anisotropic cultures of ventricular myocytes. Specifically, transverse waves propagating into the fiber curvature (TA propagation) are faster than waves propagating in the opposite direction (TW propagation). This finding experimentally confirms predictions derived from theory and computer modeling [7, 8].

The effect of fiber curvature on CV can be understood qualitatively by considering current diffusing from a differential wavefront segment. Because current diffuses preferentially along the longitudinal direction of cells, cells angled away from the center of the wavefront (as in TW propagation) act to disperse the depolarizing current, slowing CV. In the reverse case, when cells are angled towards the center of the wavefront (TA propagation), cellular geometry focuses the depolarizing current [7]. Thus, fiber curvature affects propagation by modulating the effective electrical load at the leading edge of the wavefront. This mechanism is broadly similar to the CV changes that result from wavefront curvature [18, 19]: Wavefronts that are concave (with respect to propagation direction) move faster by focusing current toward the center of the wavefront, effectively increasing depolarization current density; convex wavefronts disperse depolarizing current, and therefore reduce CV.

Mathematically, the effects of both wavefront and fiber curvature are consequences of the diffusive term of the monodomain equation that governs cardiac propagation in a continuum [22]. We previously showed that this term can be expanded into three components [13]: one that relates the spread of depolarizing current to wavefront curvature, a second that involves fiber curvature, and a third that accounts for surface curvature (in 2D). The effect of wavefront curvature has previously been demonstrated experimentally [23], and the present experiments have illustrated the validity of the fiber curvature component. However, although the role of surface curvature has been demonstrated in computational models [13], it has yet to be validated experimentally.

Wavefront curvature is a potential confounding factor in these experiments. In computer simulations of TW and TA propagation with sealed lateral boundaries, the wavefronts were concave with essentially identical shapes for both TW and TA propagation [7]. In earlier simulations in which the lateral boundaries were made inexcitable to decouple the wave ends from the boundaries, the fast TA wavefronts were convex, while the slow TW wavefronts were concave. Thus, the relative speed of TA and TW wavefronts was opposite to that predicted by wavefront shape [8]. Comparison of these simulations shows that wavefront shape is not determined solely by the fiber orientation and that wavefront curvature does not dominate fiber curvature in determining CV. In the present experiments, wavefronts were observed with convex as well as concave wavefront bends (approximated with a cross-correlation technique) for both TW and TA propagation. On average, the bends were very slight. There was no difference in bend for TA vs TW propagation (p=0.86). Thus, wavefront curvature does not appear to play a role in the TW vs. TA CV differences we observed.

For a wave propagating in the y direction, the contribution of fiber curvature to the rate of depolarization or repolarization is proportional to the product of the spatial derivative of fiber angle parallel to the wavefront (∂θ/∂x) and the spatial derivative of transmembrane potential normal to the wavefront (∂u/∂y) (ref [7], Equation B4). Because ∂u/∂y has opposite sign at the waveback relative to the wavefront, during TA propagation, when fiber curvature speeds the wave by making the depolarization rate (∂u/∂t) more positive, it also speeds repolarization by making ∂u/∂t at the waveback more negative. Therefore, at high pacing rates, when CV becomes a function of diastolic interval (DI), this abbreviated action potential duration could lead to a longer DI, and consequently, faster propagation of the following wave. The opposite situation pertains during TW propagation. It is therefore possible that the effect of fiber curvature on repolarization could play a role in modulating CV. We believe that this effect is a minor contributor to CV because the absolute value of ∂u/∂y is much smaller at the waveback than the wavefront. This is supported by the data from the 6 cultures that were paced with a 500 ms interval. Although the trend did not reach significance, in 5 of 6 of these cultures , TA propagation was faster than TW propagation as it was in the 350 ms cultures. The TW vs. TA difference was greater in the 500 ms cultures (0.62±0.88 cm/s) than the 350 ms cultures (0.38±0.44 cm/s). Because the repolarization effects are in the same direction as the depolarization effects (speeding TA and slowing TW propagation), if they were playing a major role, we would expect to see the TW-TA CV difference to be attenuated or abolished when pacing at 500 ms, which is slow enough not to engage CV restitution [24].

Because fiber curvature is not constant throughout the myocardium, fiber curvature can produce local heterogeneity even in tissue that is otherwise completely uniform. Patchy heterogeneity has long been known to be a key factor in arrhythmogenesis [25]. For example, a wavefront propagating into a region of sharp local fiber curvature could experience local propagation failure leading to wavebreak formation and reentry. Because the effect of fiber curvature is fairly small—about 3.5% in these experiments—we do not expect it to cause propagation block in normal circumstances. However, at high activation rates, when wavefronts are already on the verge of failure and the CV restitution effect discussed above potentially comes into play, fiber curvature could be a synergistic factor that results in block. This is what we found in our previous study that modeled the effects of surface curvature on reentrant propagation [13]. In this study, surface curvature produced only subtle CV changes of about 2%. However, this was enough to cause wavebreak when tissue was driven at high rates and to convert nominally stable reentry to a complex fibrillation-like pattern. Thus, it is possible that fiber curvature plays a role in the arrhythmogenic effects of geometric structures such as trabeculae and papillary muscle insertions [14, 15]. Computer simulations have also suggested that fiber curvature may play a role in defibrillation [12].

Anisotropy in vivo is a product of both cell geometry and nonuniform gap junction distribution. Gap junctions in cultured myocyte preparations do not reproduce such directionally preferential organization, but are instead isotropically distributed [5, 26]. However, the anisotropic propagation effects achieved in culture as a result of elongated cellular geometries are functionally similar to the anisotropic effects observed in whole hearts. The growth-directing substrates used in this experiment produced monolayers with an anisotropy ratio (2.30±0.28) that is within the range of anisotropy ratios measured for wavefront propagation in adult ventricular myocardium (1.7 to 3.5) [6].

In this study, the magnitude of the difference in CV for TA versus TW propagation varied from one culture to another. This variability may be a result of microscopic gaps that occur randomly throughout the cultured monolayers or the presence of nonexcitable cells (such as fibroblasts) embedded in the monolayer. The presence of such nonexcitable regions may also explain the difference in transverse and longitudinal CVs we observed (11.0±3.2 cm/s and 24.9±7.0 cm/s, respectively) compared with those recorded in similarly anisotropic monolayers (anisotropy ratio = 1.89±0.38) at a microscopic scale by Fast and Kleber (19.0±4.3 cm/s and 34.6±4.5 cm/s, respectively) [6]. While microscopic CV measurements can be made in regions selected for optimal confluence, our measurements spanned a larger area that is more likely to contain defects.