How can mathematics help us explore vertebrate segmentation?

Abstract

Since the discovery of gene products oscillating during the formation of vertebral segments, much attention has been directed toward eluciating the molecular basis of the so-called segmentation clock. What research has told us is, that even in the most simple vertebrates, enormously complicated gene networks act in each cell to give rise to oscillations, and that cell-cell communication synchronizes these oscillations between neighboring cells. A number of theories have been proposed to explain both the initiation and maintenance of oscillations in a single cell and the synchronization of such oscillations between cells. We discuss these theories in this Commentary.

The development of living organisms has evolved to be a highly dynamic process: there is a precise temporal structure to growth that ensures correct specification of the body plan. This temporal structure is regulated, in part, through a number of rhythmic events taking place in both the internal and external environments of the embryo. The response to such occurrences is generally recognized as a series of nonrandom events and may lead to temporal or spatial pattern.

Rhythms in physiological systems are generally controlled via biochemical processes that cause oscillations in a number of genes and their protein products. In special cases the oscillators may act as clocks, providing a temporal readout, and in others as pacemakers that direct or influence other oscillators. These oscillators create natural cycles with specific physiological functions, which include controlling the temporal dynamics of the developing organism.

OSCILLATORS DURING VERTEBRATE SEGMENTATION

The first developmental process to be identified with oscillatory gene activity was somitogenesis: the formation of the vertebral precursors, known as somites. The somites are transient features, epithelial balls of cells that later differentiate to make up the axial skeleton, the skeletal muscles, and parts of the dermis of the back (Gossler and Hrabě de Angelis, 1998). What is most interesting about these structures is that their formation is tightly controlled in space and time. Somites form in pairs in a strict head-tail order from two longitudinal bands of mesenchymal tissue, known as the presomitic mesoderm (PSM), that lie on either side of the presumptive spinal chord (see Fig. 1 for more details). At regular intervals, precisely defined groups of cells at the cranial-most ends of the PSM undergo changes in their adhesive and migratory properties and condense together to form a new pair of somites. The intervals between each round of segmentation are tightly controlled and characteristic of the species—ranging from 90 min in the chick to 120 min in the mouse and about 4 to 5 h in humans (Dequéant and Pourquié, 2008).

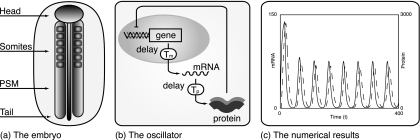
Figure 1. Somite formation.

(a) A diagram of the head-tail axis during somite formation. The somites and PSM are clearly marked. (b) The basic gene regulatory network modeled in individual cells. Down-regulation of mRNA transcription by the protein products, coupled with delays in transcription and translation, lead to oscillations in mRNA and protein levels. (c) Results from numerical solution of the model given by Eqs. 1, 2. mRNA dynamics is indicated by the solid line and, as expected, peaks precede those in protein levels, indicated by the dashed line. The equations were solved using the MATLAB solver dde23 with parameter values as follows: a=5.00, b=0.23, c=0.23, T_p=2.50, and T_m=12.00. The nonlinear function used was f(p)=30∕[1+(p∕40)²].

A widely agreed hypothesis for the process is that a somite prepattern arises via a clock and wavefront mechanism (Cooke and Zeeman, 1976; Dubrulle et al., 2001; Pourquié, 2001; Baker et al., 2006, 2008): the interaction of a wavefront of segmental determination and a segmentation clock gates cells into somites, such that the clock determines the timing of somite formation and the wavefront the position of the somite boundaries. Differential gene expression patterns arising from such a mechanism direct the morphological changes that give rise to somites (Kulesa et al., 2007). Firm evidence for both the clock and wavefront has been gathered over the past 10 yrs, so that both are now characterized to good extent by the molecular players that seem to play key roles in their existence.

In 1997, oscillatory expression of c-hairy1, a homolog of the Drosophila pair-rule gene hairy, was identified in the PSM. During the time taken to form one somite, wide bands of c-hairy1 expression travel along the PSM in the chick, from the tail to the head, narrowing as they move, until they come to rest as thin bands that define the posterior half of the somitic prepattern. Since this initial discovery, many further genes exhibiting rhythmic expression during somitogenesis have been identified. In particular, microarray studies of the mouse PSM transcriptome (Dequéant et al., 2006) have revealed that the segmentation clock is driven by a large network of cyclic genes involved in cell signaling. The clock arises as an autonomous property of PSM cells. Cell-cell communication, controlled by components of the Notch–Delta pathway, seems to play a fundamental role in the synchronization of the oscillators locally (Dequéant and Pourquié, 2008).

Molecular constituents of the wavefront were discovered more recently, with gradients of FGF8 along the axis shown to control the commitment of cells to their future differentiation path (Dubrulle et al., 2001). The connection between the wavefront of segmental determination and the clock is only just being elucidated: gradients of Wnt signaling activity, controlled by components of the β-catenin pathway, are thought to be central to both clock and wavefront (Aulehla et al., 2008). It is thought that the segmentation clock oscillations slow down and arrest at different stages of their cycle due to the interaction of the wavefront with the oscillatory network of the segmentation clock.

Oscillations in other developmental processes

Similar oscillatory processes are involved elsewhere in embryonic development. The vertebrate limb is segmented along the proximodistal axis. In chick embryos, hairy2 is periodically expressed every 6 h during limb outgrowth and segmentation. However, a new autopod limb is formed every 12 h and, as a consequence, it has been suggested that a new limb forms every two oscillations (Pascoal et al., 2007). Hairy and enhancer of split homology (Hes1) oscillations are also observed in neural progenitor cells located in the telencephalon of mouse embryos, though cells do not synchronize their oscillations (Shimojo et al., 2008).

The discovery of periodic Hairy homolog gene expression during development suggests that biological clocks might coordinate a number of developmental processes. However, despite all the work done in the last 10 yrs, the sheer complexity of the oscillators involved in development means that key underlying mechanisms have yet to be identified. Simple intuition is not enough: we need mathematics to help!

MODELS FOR CELL-LEVEL OSCILLATIONS DURING SOMITOGENESIS

Many theoretical models have been proposed for the cyclic gene oscillations observed in a single cell during somitogenesis. Beginning with the work of Lewis (2003) and Monk (2003), much attention was directed toward models of negative regulation of mRNA transcription by protein products, with delays in transcription and translation resulting in oscillations with periods defined, for the most part, by the total delay in the system. Such models have often assumed the following form:

$$\frac{dp}{dt}=am(t-T_p)-bp\left(t\right),$$ (1)

$$\frac{dm}{dt}=f\left[p(t-T_m)\right]-cm\left(t\right),$$ (2)

where m denotes mRNA concentration and p protein concentration. a, b, and c are positive constants representing protein translation, protein decay, and mRNA decay rates, respectively. T_m and T_p represent the delays in mRNA transcription and protein translation, and the function f represents the negative regulation of mRNA transcription by promoter binding (Lewis, 2003). We refer readers to Fig. 1 for more details and results of numerical simulation of the model.

Genes such as Her∕Hes in zebrafish and∕or mouse and chick were attributed to the model components but with the wealth of genetic data available it quickly became obvious that a greater degree of the complexity of the clock network must be taken into account for theoretical models to begin to give us much further insight into the mechanisms underlying somitogenesis. The inclusion of increasing numbers of genes, such as Lfng, has enabled the models to account for observations from more mutant studies. Cell-cell communication has been added by including components of the Notch–Delta pathway and the link with the determination wavefront by including components of the Wnt∕Axin2∕β-catenin pathway. In almost all models, sets of nonlinear delay differential equations describing the dynamics of gene products in each cell are written down (Goldbeter and Pourquié, 2008; Santillan and Mackey, 2008), with parameter values determined, as far as possible, from experimental observations.

While a good degree of understanding has been gained from such models, the majority of them are incredibly difficult to analyze mathematically, and computer simulation is the only way forward. The snag here is that computer simulation cannot be used to explore the behavior of the models for all the possible parameter values (many of which we are still guessing due to lack of information) and for all types of cell-cell interactions, etc. What is needed are other types of model framework, which allow one to forget the minute details of the oscillators and concentrate on the global behavior of the system. This problem is addressed in a paper published in this issue, and we outline some of the background below.

Models for coupled oscillators

Suppose that we could forget about the internal machinery of each cell’s segmentation clock and concentrate solely, for a moment, on the coupling of a cell’s clock with that of its neighbors. Would we be able to analyze the degree of synchrony in the PSM and gain insight into the importance of cell-cell communication upon somitogenesis? This is precisely the question investigated by Oates and co-workers in this issue (Morelli et al. 2009).

The ability of oscillators to synchronize phase and frequency was first documented by Christiaan Huygens, the inventor of the pendulum clock. Huygens noted that two pendulum clocks hung on the same wall would start to swing with the same frequency and in antiphase. Following disturbance to one of the clocks, synchrony was observed again within about an hour. Although it did not achieve its goal of solving a major problem in maritime navigation, Huygens’ experiment went on to inspire modern studies of coupled oscillations in many areas of nonlinear science.

One such area is that of phase-coupled oscillators, and a paradigm study to illustrate this is that of the Kuramoto model (Kuramoto, 2003), originally motivated by the phenomenon of collective synchronization in which a large system of oscillators may spontaneously lock to a common frequency, despite variation in the natural frequency from oscillator to oscillator. Suppose that each oscillator in a field may be represented by phase θ_i, where the subscript i denotes the ith oscillator. Then the rate of change of phase can be written

$$\frac{d{\theta }_i}{dt}={\omega }_i+\frac{K}{N}\sum _{j=1}^N\sin ({\theta }_i-{\theta }_j),$$ (3)

for i=1,…,N. K>0 is the coupling strength, ω_i is the natural frequency of the ith oscillator, and the coupling is assumed to be equally weighted, sinusoidal, and between all oscillators.

An order parameter can be defined to aid in visualization of the collective dynamics of the phase:

$$Z=r{e}^{i\psi }=\frac{1}{N}\sum _{j=1}^N{e}^{i{\theta }_j}.$$ (4)

The phases θ_j are all plotted on a unit circle, and their average gives a measure of the order: r gives the phase coherence, and ψ gives the average phase (see Fig. 2 for a graphical representation). For this model Kuramoto showed that the governing phase equations can be written in terms of Z as

$$\frac{d{\theta }_i}{dt}={\omega }_i+Kr\sin (\psi -{\theta }_i),$$ (5)

for i=1,…,N. When written in this form it is easy to see that each individual oscillator interacts with all others only through the mean-field, with oscillators entrained toward the mean frequency, ψ, with forcing proportional to the coherence, r. In this way there is positive feedback between the synchrony of the population and the rate at which oscillators become entrained.

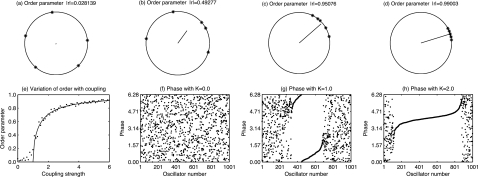
Figure 2. The Kuramoto model for coupled oscillators explains synchronization between oscillators despite variation in their natural frequencies.

(a)–(d) The order parameter may be thought of as the length of the resultant vector when each of the phases are plotted as an angle on a circle of unit radius. The direction of the vector indicates the average phase. As the phases are more closely aligned the length of the vector increases, indicating more closely synchronized oscillators. (e) The change in order parameter with coupling strength. Below a critical value, K_c=1 here, no synchronization takes place. Progressively more synchronization occurs as K increases above K_c. The solid line indicates a theoretical prediction of K while the dots indicate the results of numerical simulation of the system. (f)–(h) The individual phases of each oscillator plotted so that the oscillators are ordered in terms of increasing natural frequency, ω_i. This again demonstrates the progressive synchronization of the field as K increases. In each of the numerical simulations shown in (e)–(h), 1000 oscillators were coupled with frequencies drawn from a Lorentzian distribution with width parameter Γ=0.5. The initial phases were drawn uniformly from the range θ_i∊[0,2π] and the MATLAB solver ode45 was used to solve the system until the order parameter reached an approximately steady value.

Numerical simulations of the model show that, in general, there is a critical value of the coupling parameter, K=K_c, such that for K<K_c the oscillators behave as if they were uncoupled while for K>K_c clusters of oscillators synchronize, thereby generating a collective oscillation. Results from numerical simulation of the model for 1000 oscillators with natural phase of oscillation distributed according to a Lorentzian distribution are shown in Fig. 2.

It is precisely this kind of model that lends itself openly to investigating the effects of cell-cell coupling in the segmentation clock. Oates and co-workers first developed the idea by supposing that we can represent the segmentation clocks arising in PSM cells as a population of identical, mutually coupled phase-oscillators (Riedel-Kruse et al., 2007). Using their model they are able to estimate the time taken to produce the first defective somite boundary in wild type zebrafish embryos treated with DAPT—a substance which blocks the response of the Notch intercellular domain to binding of the receptor’s extracellular domain. The hypothesis being that when the field has order parameter, r, below some critical value proper segmentation fails.

Work presented in this issue by Oates and co-workers (Morelli et al., 2009) furthers this investigation. Using the same basis the authors assume: (i) the presence of a frequency profile along the PSM, which accounts for the change in oscillation period as the clock interacts with the wavefront of determination; (ii) a time delay in the transfer of clock information between cells. Using this basis spatiotemporal patterns of gene expression arise with wavelength dependent upon the natural frequency of oscillation, coupling strength, and the frequency profile. Measurable, tissue-level phenomena are observable and arise as a result of events taking place on a cellular level, but knowledge of the exact molecular mechanisms is not necessary. In short, the model provides a platform that allows in-depth investigation of the role of cell-cell communication in synchronizing the segmentation clock and generating coherent somites, without the added complexity of modeling the core of the clock mechanism.

CONCLUSIONS

The development of increasingly sophisticated methods for exploring, perturbing, and visualizing biological systems is resulting in an explosion in our knowledge of the genes and associated products playing a role in development. However, integrating this knowledge into mathematical models requires that theoreticians remain alert and responsive to developing new methods of characterizing such systems—in order that each model framework remains explorable from an analytic point of view yet includes enough information to give insight into the biological mechanisms under study.

The use of mean-field theory to describe coupled oscillators in biological systems is not necessarily new. On the other hand, application to somitogenesis, where increasingly detailed descriptions of the segmentation clock network are available, allows us to concentrate on the role of cell-cell communication without the worry of describing a complex gene network.

Somitogenesis makes an excellent paradigm for studying the role of multiple, competing factors in pattern formation during development. In return, insights into the process from theoretical exploration could one day lead to huge advances in the field and have implications in the understanding of human segmentation syndromes such as congenital scoliosis.