A critical view of metabolic network adaptations

Abstract

There has been considerable recent interest in deciphering the adaptive properties underlying the structure and function of metabolic networks. Various features of metabolic networks such as the global topology, distribution of fluxes, and mutational robustness, have been proposed to have adaptive significance and hence reflect design principles. However, whether evolutionary processes alternative to direct selection on the trait under investigation also play a role is often ignored and the selection pressures maintaining a given metabolic trait often remain speculative. Some systems-level traits might simply arise as by-products of selection on other traits or even through random genetic drift. Here, we ask which systems-level aspects of metabolism are likely to have adaptive utility and which could be better explained as by-products of other evolutionary forces. We conclude that the global topological characteristics of metabolic networks and their mutational robustness are unlikely to be directly shaped by natural selection. Conversely, models of optimal design revealed that various aspects of individual pathways and the behavior of the whole network show signs of adaptations, even though the exact selective forces often remain elusive. Comparative and experimental approaches, which so far have been relatively rarely employed, could help to distinguish between alternative adaptive scenarios.

One of the major goals of biology is to understand phenotypes in the light of evolution. Recent advances in molecular biosciences has enabled the characterization of cellular networks and uncovered biochemical phenotypes that were invisible before (Bruggeman and Westerhoff, 2007). Despite the unprecedented progress in elucidating the structure and operation of molecular networks, it remains poorly understood what aspects of these networks are adaptive, that is, increase the fit of the organism to their environment, and by which evolutionary forces they have become established. Although it is often suggested that some systems-level network properties, such as scale-free topology (Jeong et al., 2000) (see Table 1 for a glossary of terms), robustness against mutations (Wagner, 2000), pathway regulation (Zaslaver et al., 2004), metabolic flux states (Varma and Palsson, 1994), are direct products of natural selection and have certain adaptive utility, it is rarely examined whether these properties could arise by nonadaptive evolutionary processes (e.g., mutation and genetic drift) or as indirect by-products of other adaptive processes (Lynch, 2007b; Wagner, 2007). For example, it has been theoretically shown that the evolution of transcriptional regulatory pathways could be, to a large extent, driven by mutation and drift (Lynch, 2007a), and the connectivity distribution of metabolic networks could emerge as a consequence of selection for growth rate without the need to invoke selection for mutational robustness (Pfeiffer et al., 2005). Understanding the evolutionary forces and selection pressures shaping biochemical networks would be important not only to gain insight into the design principles that govern cellular behavior but also to know which biochemical traits are amenable to engineering principles, such as optimization. Engineering principles can be utilized to fill in gaps of our knowledge, and enable us to make predictions for systems behavior without knowing all mechanistic details (see Table 2 on constraint-based modeling) and also could facilitate the design of novel synthetic biochemical circuits (Pharkya et al., 2004).

Table 1.

Glossary.

Adaptations: properties (or phenotypes) that increase the fit of the organism to its environment and which are favored by natural selection.
Degree distribution: gives the probability, P(k), that a selected node in the network has exactly k links (i.e., number of connections with other nodes).
Dispensable gene: a gene whose deletion (or inactivation) does not have a detectable fitness effect.
Enzyme kinetics: study of metabolic (biochemical) reactions in terms of rates.
Fitness landscape: visualizes the relationship between genotype and fitness. The plane of the landscape contains all possible genotypes in such a way that similar genotypes are located close to each other on the plane and the height of the of the landscape reflects the fitness of the corresponding genotype.
Genetic drift: stochastic changes in allele frequencies in a population that occur owing to random sampling effects in the formation of successive generations.
Metabolic flux: turnover rate of substrates through metabolic reactions or pathways.
Mutation accumulation experiments: spontaneous mutations are allowed to accumulate over many generations by ensuring a very small effective population size where genetic drift overwhelms natural selection (hence the sampling of mutations is nearly unbiased).
Mutational robustness: phenotypic constancy in the face of mutations.
Natural selection: the process by which favorable heritable properties of individuals become more common (and unfavorable traits become less common) in successive generations of a population of reproducing organisms.
Network diameter: the average shortest distance (or minimal number of links) between any two nodes in the network. Scale-free networks show small diameters due to the existence of highly connected nodes.
Scale-free network: a network whose degree distribution follows a power law, i.e., P(k)∼k−γ (that is, it contains a small number of highly connected nodes (called “hubs”) and a high number of nodes with few links).
Trade-off (in evolutionary biology): two traits are in trade-off relation when an increase in fitness due to a change in one trait is opposed by a decrease in fitness due to a concomitant change in the second trait.
Yield: a ratio indicating how many moles of product are obtained per mole of substrate used.

Table 2.

Constraint-based modeling of metabolism.

The recent availability of complete genome sequences enabled the reconstruction of large-scale metabolic networks for various microbial species. These networks are constructed on the basis of genome annotations in which genes encoding enzymes are associated to reactions (Francke et al., 2005). In addition, modeling techniques have been developed to study the functional capabilities of metabolic networks in terms of metabolic fluxes through the network, including the biomass production (growth) rate. Modeling of metabolism involves the formalization of a model, characterized by the network itself and its interaction with the environment. This interaction is represented by so-called exchange reactions that allow nutrients and metabolic products to flow in or out the system. The influx of nutrients is an important capacity constraint. Balancing of mass by the constituent reactions is another essential constraint representing a (pseudo)-steady-state assumption. At steady state there is no accumulation of metabolites, i.e., the production rates must equal the consumption rates for each compound. In mathematical terms this is written as S⋅v=0, where S is a matrix containing the stoichiometry of all reactions and v is a vector of reaction rates. The capacity constraints, for each internal as well as exchange reaction, are written as vmin⩽v⩽vmax. The mass balance and capacity constraints together define the space of allowable metabolic flux states (i.e., phenotypes), which is called the solution space in mathematical terms. A number of constraint-based techniques have been developed to explore the solution space to predict metabolic fluxes and in silico growth (for detailed reviews see Price et al., 2004 and Teusink and Smid, 2006). One such method is flux balance analysis (FBA) in which linear optimization is performed to predict an optimal flux state of the network that maximizes a predefined objective function, e.g., the flux through the biomass reaction.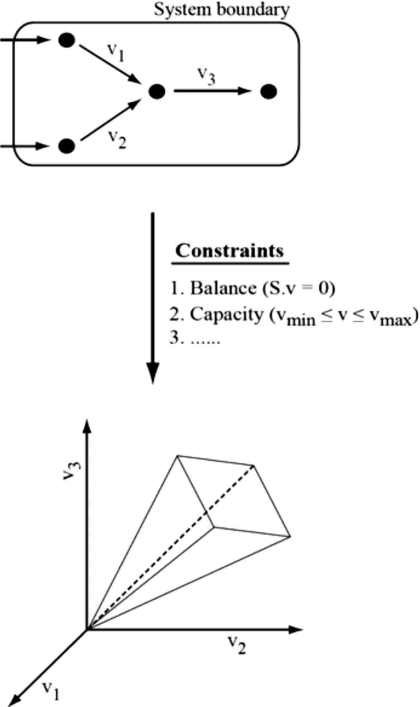

What tools are available for revealing adaptations in biochemical networks? Just as comparisons of an explicit null model to alternative models of molecular evolution can be employed to detect adaptive evolution in protein sequences (Yang and Bielawski, 2000), it is, in principle, also possible to formulate mechanistic models of biochemical network evolution and ask which one is sufficient and necessary to explain the observed network properties. Although, ideally, network evolution models should be constructed within a population-genetic framework, models with such details have so far been put forward for transcriptional regulatory networks only (Lynch, 2007a). A general limitation of this approach is that biologically relevant null models of network evolution are difficult to construct (Artzy-Randrup et al., 2004).

Applying optimality theory is a far more common approach to study adaptation above the level of biological sequences, and involves the construction and testing of hypotheses about the adaptive utility of the trait under investigation (Parker and Smith, 1990). Indeed, optimization principles have not only been applied to understand the adaptive value of macroscopic and behavioral traits, such as clutch size in birds, but also to analyze adaptation at the level of biochemical pathways and networks (Weber, 1998). Constructing an optimality hypothesis also requires specifying a range of alternative phenotypes, which are considered physically and chemically plausible and would be also possible for evolution to achieve. Although the physicochemical plausibility of alternative biochemical phenotypes might be straightforward to judge, it is much less clear how far the availability of genetic raw material or population genetic processes constrain the possible outcomes of molecular network evolution. It has, for example, been suggested that the mechanism of gene duplication could be responsible for the evolutionary origin of certain universal topological properties of molecular networks (Barabasi and Oltvai, 2004), but the role of duplication in network evolution clearly differs between eukaryotes and bacteria (Pál et al., 2005). Thus, until we have a better understanding of how the generation of genetic variation influences the range of possible phenotypes available for natural selection, the best one can do is to define biochemically plausible alternative molecular networks.

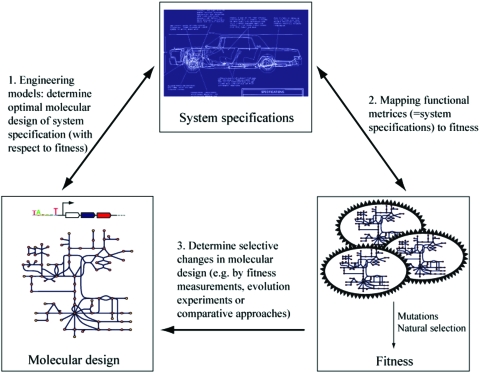
Given a well-formulated adaptive hypothesis, it can be, in principle, tested by three main approaches: (i) engineering models (comparing the actual trait to the one predicted by a hypothesis about optimal design, e.g., an engineering model; see Fig. 1); (ii) comparative method (if different species are predicted to have altered forms of an adaptation as a result of different selective pressures); and (iii) experiments (if the trait can be manipulated experimentally and the performance of the alternative forms can be investigated). The usefulness of applying different complementary techniques to test adaptive hypotheses can be best demonstrated by examples from behavioral and evolutionary ecology where these methods are extensively utilized (Krebs and Davies, 1993). For example, to understand how the sex ratio (the ratio of males to females) is adaptive, theoretical models have been put forward with the ability to predict both the frequently observed 1:1 ratio and deviations from it (Bull and Charnov, 1988). Bias in sex ratios can also be investigated by comparing species with different sex ratios: for instance, a female-biased sex ratio was observed in a wasp species where sons are more costly to produce than daughters compared to a related wasp where the two sexes have similar costs (Metcalf, 1980). Furthermore, monitoring the dynamics of sex ratio after establishing laboratory populations with skewed sex ratios can be used to experimentally demonstrate that natural selection drives the population towards the theoretically predicted stable sex ratio (Basolo, 1994). In contrast to the widespread use of comparative methods and experimental manipulations in the field of behavioral ecology, these approaches are rarely applied to test hypotheses on the adaptive utility of cellular network properties, and most studies on biochemical adaptations exclusively employ engineering models (Alon, 2006; Heinrich et al., 1991; Schuetz et al., 2007).

Figure 1. Common approaches in the study of design principles in metabolic networks.

In general, one is interested in mapping molecular design to fitness. How can this be done? One route is to define a hypothesis about what system specifications confer a fitness contribution in the system under study (process 2). For example, the hypothesis could be that growth rate is the main (or only) determinant for fitness under constant environments. With this hypothesis in mind, engineering models can be used to test what molecular design of the system specification (e.g., a genome-scale metabolic network) would be optimal with respect to growth rate (process 1). The results can then be compared to the actual behavior of cells. Although suggestive, this does not strictly prove that the molecular design was actually selected for that trait, because the hypothesis about fitness cannot be independently proven. Therefore, process 3 is very important, i.e., show either by fitness measurements of alternative forms of the molecular design, by comparative studies between organisms with well-defined environmental niches, or by adaptive evolution studied under well-defined conditions that the molecular design in question can be directly shaped by natural selection instead of merely being a by-product of other evolutionary processes.

Microbial metabolic networks are excellent candidates to gain insights into systems-level cellular adaptations not only because they are well characterized and available for a large number of organisms, hence amenable to comparative approaches, but also because their phenotypic behavior can be more readily predicted than those of other molecular networks. Thus, in the present Perspective we will focus on metabolic networks to revisit which systems-level aspects are adaptive and what selective forces might be driving the emergence of these properties (e.g., selection for higher growth rate or efficiency, selection to increase robustness against mutations or environmental changes). We will also propose experimental and comparative approaches to test alternative adaptive hypotheses of metabolic systems properties.

GLOBAL TOPOLOGICAL PROPERTIES OF METABOLIC NETWORKS ARE UNLIKELY TO BE ADAPTIVE

Large-scale structures of biochemical networks are often described by abstract topological metrics borrowed from graph theory, such as degree distribution and network diameter (see Table 1, Glossary), and several structural properties of metabolic networks have been reported, which are absent in random networks (Jeong et al., 2000). For example, the connectivity of metabolites follows a power-law distribution (i.e., few highly connected “hub” metabolites dominate the overall connectivity of the network), a scaling property shared with other complex systems, such as the Internet, but not observed in random networks (Barabasi and Oltvai, 2004). As networks with power-law degree distributions demonstrate a high robustness against random errors (i.e., random removal of nodes), it has been proposed that such a property of metabolic networks reflects the design principle of error tolerance, and therefore it has adaptive utility for the organisms (Jeong et al., 2000). Furthermore, a comparison of metabolic networks across prokaryotes showed that several graph metrics are correlated with the optimal growth temperature (Takemoto et al., 2007). Therefore, it might be tempting to conclude that both simple engineering models and interspecies comparisons support the view that global topological properties of metabolic networks can be shaped by natural selection. But, could it be possible that these properties emerge as indirect by-products of evolutionary processes unrelated to direct selection on the property itself?

Indeed, several lines of theoretical reasoning and empirical evidence are consistent with the latter possibility. First of all, the functional relevance of some graph-theoretical metrics has been questioned (Arita, 2004), and it is generally unclear how global topological properties are connected to observable biological functions and organismal fitness (Mahadevan and Palsson, 2005; Wagner, 2007). For example, a closer inspection of error tolerance in metabolic networks showed that metabolite connectivity does not correlate with the essentiality of enzymatic reactions (Mahadevan and Palsson, 2005). Although this finding is incompatible with the idea that robustness against enzyme deletions is a consequence of power-law connectivity distribution, it is unsurprising given that organismal fitness depends on the ability of metabolism to produce certain key output molecules (e.g., biomass components) from nutrients, and even lowly connected nodes embedded in linear pathways can be crucial for this function. As we shall discuss later, tolerance against random mutations can be better explained by other properties of metabolism, such as the presence of functionally distinct parallel pathways. In a similar vein, it remains unclear how differences in the topological properties of metabolic networks can confer adaptedness to different environmental temperatures. Second, it seems that the degree distribution observed in metabolic networks is a very general property of chemical reactions networks: it has been reported that the chemical networks of planetary atmospheres also display similar degree distributions (Gleiss et al., 2001), despite the fact that they do not exist in living organisms and hence cannot be the result of natural selection. Finally, using an explicit computer simulation of early metabolic network evolution, it has been demonstrated that power-law-like connectivity distributions can emerge as a by-product of selection for growth rate (Pfeiffer et al., 2005). Thus, available observation and reasoning supports the view that some global topological properties, such as connectivity distribution and network diameter, are unlikely to be the result of direct selection for such properties, but rather emerge as indirect by-products of other evolutionary processes.

EVIDENCE FOR ADAPTIVE STRUCTURAL AND REGULATORY FEATURES IN WELL-STUDIED METABOLIC PATHWAYS

In contrast to the properties derived from the global network topology (i.e., graph theory), the structural (stoichiometric) and kinetic properties of individual metabolic pathways can easily be related to functional metrics, such as flux level, thermodynamic efficiency, metabolic concentrations, transient times, among others (Heinrich et al., 1991). Hence, one might expect direct selection on these properties to increase some fitness components (e.g., production rates or yields of key metabolic compounds). Various studies have been conducted to investigate whether the structural and kinetic properties of commonly observed pathways, such as glycolysis, are likely to be shaped by selection. These studies mainly relied on engineering models in which the actual observed properties of the pathway were compared to those resulting from optimization approaches. The crux—and weakness—in these approaches is the mapping between fitness and functional metrics (Fig. 1). As we will see, in most cases in this and the next section, output flux is taken as the optimization criterion, but this alone cannot explain many observations.

The most intensively studied pathway is glycolysis, a pathway that converts glucose into pyruvate by investing ATP and subsequently gaining a surplus of ATP. The production and consumption of ATP at certain locations in the pathway is one structural property that is recovered in optimal solutions of mathematical models when ATP production rate is maximized in comparison to other possible pathway structures (Heinrich et al., 1997; Stephani and Heinrich, 1998). More recently, it has been shown that this structural property also correlates with pathway stoichiometries that were identified by optimizing ATP production rate by a genetic algorithm (evolutionary optimization) (Stephani et al., 1999). Besides elucidating adaptive features of glycolysis, other pathways have been investigated, such as the pentose phosphate pathway (Melendez-Hevia et al., 1994). For this pathway it has been shown theoretically that, when one again maximizes flux through the pathway, a structure emerges that is characterized by the least number of reaction steps (referred to as “simplicity”), which corresponds well to the “real” pathway. Additional findings suggest that metabolic pathways, in general, have evolved to have the least number of steps and, at the same time, the maximum number of excess ATP produced (Beasley and Planes, 2007).

It has been reported that pathway structures, such as glycolysis or citric acid cycle, vary among species with different ecological niches and phylogenetic positions (Huynen et al., 1999; Verhees et al., 2003). Taken together with the fact that most studies focus on adaptations in pathways of single organisms, such as E. coli or S. cerevisiae, it raises the question whether variations among species reflect adaptation to different ecological niches or rather the result of chance historical events without any adaptive significance. Comparative studies may shed light on this question. For example, a recent comparison of two strains of the photosynthetic marine green alga Ostreococcus showed that the strain living in the deep sea environment has an alternative electron flow to oxygen not observed in the strain living close to the water surface. It has been proposed that differences in photosynthetic electron flow might reflect an adaptation to sustained light and∕or nutrient limitations in deep sea environments (Cardol et al., 2008).

An alternative strategy to infer adaptations would be a combination of comparative and engineering approaches. For instance, one might construct species-specific engineering models reflecting the organisms’ actual ecological niche and primary fitness components (e.g., growth yield or rate). Subsequently, the computationally predicted optimal pathway structures would be compared to those observed in the organisms living under different ecological conditions. A similar strategy demonstrated that some of the differences in the metabolic gene content between two related endosymbiotic bacteria can be explained by differences in their lifestyles and interactions with the host organisms (Pál et al., 2006). It remains to be elucidated, however, whether different optimal pathway stoichiometries have actually been realized by organisms thriving under different environmental conditions.

In addition to structural design in certain well-studied metabolic pathways, adaptations in the regulation of pathways have also been uncovered using engineering models. For example, precise timing of gene expression, also referred to as “just-in-time” transcription, of the enzymes that catalyze the consecutive reactions along a linear pathway, is a property that becomes apparent when optimizing for a rapid production of end products with minimal protein investments (Klipp et al., 2002; Zaslaver et al., 2004). Another example of regulation comes—again—from the stoichiometric design of glycolysis. This “design” of glycolysis in S. cerevisiae has been compared to a turbo engine, with important implications for its regulation (Teusink et al., 1998). In short, the autocatalytic or turbo design of glycolysis requires a negative feedback (or brake) at the early steps in glycolysis to prevent substrate-accelerated death caused by uncontrolled uptake of substrate. The nature and strength of this feedback, however, can be related to the environmental conditions of the pathway, i.e., to whether the pathway is likely to experience large fluctuations in the substrate (Iynedjian, 1998). Interestingly, where S. cerevisiae appears robust against large fluctuations in glucose levels, it cannot handle similar fluctuations in maltose as it lacks the negative feedback (Jansen et al., 2004). This may reflect the environmental history of this organism, and would possibly allow one to conclude that this particular regulation of glycolysis is adaptive, conferring robustness to specific fluctuating environments.

It appears, therefore, that even though studies on structural design of metabolic pathways point to a relationship with maximal output of that pathway, other functional requirements, largely driven by environmental factors experienced throughout the evolutionary history of an organism, are needed to explain all aspects of metabolism. Although this conclusion may be trivial, it once again stresses the difficulty of mapping fitness to functional metrics if the evolutionary history of the organism is unknown. We therefore either need comparative studies between organisms with a well-defined evolutionary history (or ecological niche), or adaptive evolution experiments in which adaptation is followed under well-defined environmental conditions (Elena and Lenski, 2003). Nevertheless, on the pathway level there are several lines of support for adaptive properties. However, since pathways are embedded in large metabolic networks, the question arises whether such evidence for adaptation can be found at the global level of intermediary metabolism.

ADAPTATIONS IN METABOLIC NETWORK BEHAVIOR

The phenotypic behavior of large and complex metabolic networks can be arguably best described by intracellular reactions rates (i.e., fluxes) as these are the functional end points emerging from protein-metabolite interactions and various levels of regulatory interactions (Sauer, 2006). There have been many experimental and theoretical studies that deal with flux distributions in metabolic networks (for reviews, see Christensen and Nielsen, 2000; Price et al., 2004; Sauer, 2006). Most of these studies fall within the engineering approach. The most popular approach is constraint-based modeling (see Table 2), in which mass balance and capacity constraints are used to define a space of all feasible flux states—the so-called solution space. Within this space, optimal states, i.e., flux distributions of the network, can be found that maximizes or minimizes a certain objective function (flux balance analysis, FBA). These engineering models show clear support for the adaptive utility of flux states under some circumstances: studies applying optimization principles to intracellular flux states demonstrated that, under some environmental conditions, in vivo fluxes are distributed in such a way as if biomass production was maximized (Schuetz et al., 2007; Segrè et al., 2002).

An important indication that flux states can indeed be adaptive comes from adaptive evolution experiments. In these experiments, cells are grown for longer periods (500–1000 generations) in relatively constant environments, a condition in which strains are selected mainly on the basis of growth rate (Elena and Lenski, 2003). In a number of studies the flux state of evolved strains was altered to reflect the optimal flux distribution for producing biomass in a predefined environment (Ibarra et al., 2002). Although these studies do not directly prove that flux states are adapted in the wild type, they strongly suggest that flux states can be easily shaped by natural selection.

It is, however, important to discuss cases where optimality models fail as it highlights important limitations to the use of constraint-based modeling techniques (Schuster et al., 2008). The argument is rather subtle: even though in the mathematical formalism (see Table 2) the growth rate is being maximized, the necessary input constraints (or normalization procedure, needed to bound the solution space) force the optimization solution towards a flux distribution in which the yield on the limiting input flux is maximal (Schuster et al., 2008; Teusink et al., 2006). Hence, FBA always predicts the most efficient conversion from the input flux (limiting nutrient) to the output flux (growth rate). It therefore fails to predict the behavior of cells that do not metabolize nutrients most efficiently. It can however be questioned whether one can be sure that, in an experiment, suboptimal yield is due to a deliberate evolved strategy of the cell (i.e., inefficient operation), rather than by the presence of another hidden limiting factor (therefore still operating efficiently relative to this factor)? In this context, oxygen (or respiratory capacity) is often considered as a possible limiting factor (Famili et al., 2003; Vemuri et al., 2007). However, we will give here a clear example of deliberate inefficient metabolism from our own experience: the behavior of lactic acid bacteria [Schuster gives other examples (Schuster et al., 2008)]. These bacteria produce lactic acid where FBA predicts mixed acids to be formed, resulting in much higherin silico growth rates than observed experimentally (Teusink et al., 2006). This takes place anaerobically, so there is no uncertainty with respect to limitations in oxygen or respiration. Crucially, Lactobacillus plantarum is still homolactic (i.e., inefficient) in a glucose-limited chemostat at a dilution rate that is only 20% of its maximal growth rate on that medium. Under these conditions, the addition of glucose led to an increased biomass in the fermentor, indicating a glucose limitation [(Teusink et al., 2006) and unpublished data]. Moreover, many regulatory mechanisms exist in lactic acid bacteria (e.g., Neves et al., 2005) that actively inhibit the mixed acid branch in the presence of glucose, strongly suggesting that these bacteria change metabolic strategy in disfavor of yield (but possibly in favor of growth rate, see below).

Despite the L. plantarum counter example, FBA with growth rate maximization tends to work on poor carbon sources or in glucose-limited chemostats at relatively low growth rates, conditions where efficiency is likely to be a relevant strategy towards increased fitness and thus the resulting flux states of the network are likely to be adaptive. For other conditions, either alternative objectives have been formulated (Schuetz et al., 2007), or ad hoc (experimentally derived) specific capacity constraints on efficient pathways are used to steer flux towards suboptimal pathways (Famili et al., 2003; Oliveira et al., 2005). In the latter case models become more descriptive, and less predictive. An alternative approach with a higher predictive value is to impose a general upper limit constraint on the total concentration of enzymes, hence intracellular fluxes, representing the phenomenon of molecular crowding (Beg et al., 2007). However, it remains to be seen how far the adaptive value of inefficient use of nutrients can be addressed within the constraint-based modeling framework.

The adaptive value of inefficient metabolism has been also discussed in the context of game theory. On the basis of thermodynamic (and partly experimental, see MacLean, 2008; Novak et al., 2006) arguments, a trade-off between yield and rate in ATP production was shown theoretically to lead to a “tragedy of the commons” (MacLean, 2008; Pfeiffer et al., 2001). The basic idea is that organisms have two options: either convert substrate into biomass efficiently, but slowly, or consume the substrate fast with concomitant fast growth, but inefficiently. The latter means that less offspring is produced per substrate quantity. These studies show that inefficient metabolism is optimal at the level of the individual cells (as it leads to higher growth rates in these models) at the cost of the fitness of the population as a whole (in terms of the number of offspring from the resource). Efficient metabolism is only stable in these models when there is a structural distribution of the substrate, stimulating kin selection in local patches, or when frequency-dependent costs associated with the toxic by-products of inefficient metabolism (such as lactate or ethanol) are included.

The game-theoretical approaches so far have been relatively simple, ignoring important aspects such as phenotypic plasticity (Aledo and del Valle, 2004), allowing single cells to switch in strategy, rather than looking at pairwise competition between fixed strategies. What is perhaps the most important contribution of game-theoretical approaches to metabolism is the emphasis on cost-benefit analyses and trade-offs within metabolism for understanding metabolic strategies. The importance of such trade-offs has also been stressed by an empirical cost-benefit study showing how a trade-off between metabolic benefit and protein cost (both in terms of growth rate changes) affects the fine-tuning of expression levels in E. coli (Dekel and Alon, 2005). Indeed, in both constraint-based modeling and game-theoretical approaches the costs of alternative pathways in terms of protein synthesis are not (or not explicitly) taken into account. Yet, the protein cost argument was implicitly used in the understanding of pathway topology in the previous section, through the use of flux (or number of steps) minimization.

Within the context of stoichiometric models, there has been—to our knowledge—one other approach where a rudimentary cost-benefit analysis was explicitly used to predict regulation of metabolic enzymes. In this approach, a combined measure of pathway yield and length was used to predict the relative contribution of an enzyme under certain environmental conditions (Stelling et al., 2002). The authors showed a good correlation between the relative contribution of an enzyme and the expression level of the associated genes. Although this study has not been followed up extensively, it is an interesting example of combining different functional metrics to predict global regulation of metabolic pathways. It also illustrates that multiple objectives will probably have to be combined to understand all aspects of design and regulation of metabolic pathways. We therefore expect extension of this research in the direction of multiple objective optimization, highlighting important trade-offs that cells face in adapting to the environment.

ROBUSTNESS AGAINST GENE DELETIONS APPEARS TO BE A BY-PRODUCT OF ENVIRONMENTAL ADAPTATION

Organisms show considerable robustness against the effects of mutations, including gene deletions, and it has been suggested that this property might be an evolved capacity of genetic networks to compensate for mutations (Wagner, 2000). Although large-scale functional genomics screens conducted in different organisms have established that most genes appear to be “dispensable” (or have only very weak effects) under standard laboratory conditions (Hurst and Pál, 2007), the presence of dispensable genes does not necessarily imply evolved compensation capacity against null mutations. First of all, some dispensable enzymatic genes might catalyze reactions that are inactive under the tested condition (i.e., carry zero flux); hence, there might be no need to invoke any compensatory mechanisms to explain their dispensability (Blank et al., 2005; Papp et al., 2004). These functionally inactive genes might become important under some other environmental conditions, and a recent large-scale chemical genomic assay in yeast indicates that genes with condition-specific functions are rather common in the genome: 97% of gene deletions exhibited a measurable growth phenotype in at least one of hundreds of tested conditions compared to only 34% in rich medium (Hillenmeyer et al., 2008). Second, even if organisms have a substantial capacity to compensate for null mutations, either by redundant gene copies or by alternative metabolic routes, this might be the by-product of other evolved properties of metabolism. But, what are the selective forces maintaining parallel pathways and isoenzymes with redundant functions?

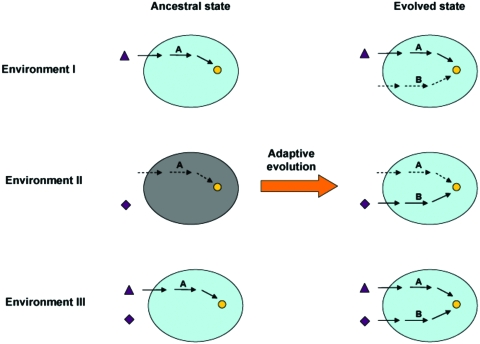
Although selection for resilience against harmful mutations could, in principle, increase the mutational robustness of biochemical networks, population genetic models show that the selection pressure is weak at best, of the order of mutation rates (Proulx, 2005). Alternatively, distinct, but functionally overlapping metabolic pathways might evolve as a result of selection for utilization of various nutrients and, as a correlated response, some of these pathways may also increase robustness against mutations under some circumstances (Harrison et al., 2007) (see Fig. 2). One appeal of this latter scenario is that the evolution of robustness against environmental changes is unproblematic from a population genetics point of view. Furthermore, evidence suggests that insensitivity to environmental perturbations and robustness against mutations are generally correlated (Meiklejohn and Hartl, 2002; Remold and Lenski, 2004); hence, natural selection to promote survival under a large variety of environments might indirectly increase mutational resilience. As a further support, it has been recently demonstrated that a large fraction of the compensating gene pairs in cellular networks bears distinct functional roles and are not redundant under all conditions (Harrison et al., 2007; Ihmels et al., 2007), suggesting that these genes are unlikely to be maintained by direct selection for mutational robustness. Importantly, parallel metabolic pathways could evolve not only to metabolize qualitatively different nutrient molecules, but also in response to variation in the quantitative availability of nutrients. For example, E. coli has two pathways of glutamate synthesis, one of which can fix ammonium into organic molecules when the external concentration of ammonium is low, while the other plays an important role when the cell is limited for energy, but is not under ammonium restriction (Helling, 1994). Finally, the evolutionary maintenance of compensating isoenzymes in metabolic networks could be explained by selection to increase gene dosage (i.e., to increase flux) (Conant and Wolfe, 2007; Papp et al., 2004), filter nongenetic noise (Kafri et al., 2006), or provide differential regulation of isoforms (Ihmels et al., 2004).

Figure 2. A conceptual model to explain the evolution of genetic robustness as a by-product of adaptation to new environments.

Pathway A and pathway B both synthesize a key metabolite (yellow circle), but start from different external nutrients. In the ancestral state only pathway A is present and therefore the microbe is able to grow only in Environment I or III. Pathway B evolves as an adaptation to enable growth in Environment II as well. In the evolved state the microbe is able to grow in both Environment I and II, and also under a condition where the starting nutrients of both pathways are present (Environment III). Importantly, although pathway A and B have distinct functional roles, they have the capacity to compensate each other’s loss in Environment III.

Thus, instead of regarding apparently redundant pathways and enzymes in metabolic networks as adaptations against mutations, their presence more likely reflects the fact that metabolism has evolved to operate under a variety of environmental conditions and in the face of stochastic perturbations. Future synthetic biology studies could, in principle, provide more direct tests of this idea by introducing novel metabolic pathways into a wild-type microbe in order to extend its range of growth regimes. Then, mutation accumulation experiments (Montville et al., 2005) could be employed to test whether the modified strain shows increased genetic robustness under a condition where both the wild-type and the modified strain has similar growth performance.

Despite the general conclusion on the evolutionary maintenance of dispensable genes, further comparative studies are needed to decipher the interspecies variation in pathway and isoenzyme redundancies. For example, the highly reduced genome of Mycoplasma genitalium has an especially low fraction of dispensable genes (Glass et al., 2006), which is compatible with the idea that a strict host associated lifestyle leads to the loss of condition-specific genes, hence compensating capacity (Papp et al., 2004). However, it remains to be explored whether the dimensionality of the environment experienced by a given organism can, in general, explain its mutational robustness.

FUTURE DIRECTIONS

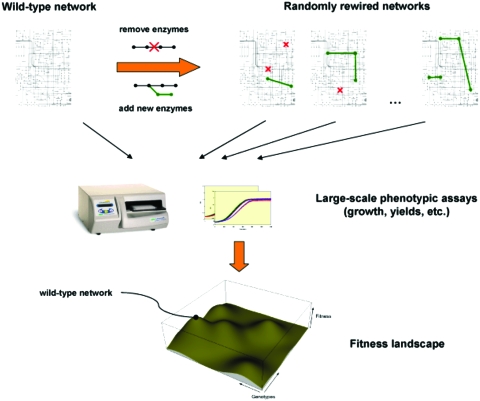
Despite suggestions to the contrary, there is no convincing evidence for the view that some of the global properties of metabolic networks are directly shaped by natural selection: the degree distribution of metabolic graphs or their resilience against random mutations can be better explained as by-products of other adaptive evolutionary processes. In contrast, various properties of some well-studied metabolic pathways and, in many cases, the phenotypic behavior of the whole network, can often be explained as a result of natural selection for higher pathway fluxes and∕or higher molar yields. However, further progress in understanding metabolic adaptations will certainly benefit from systematic cost-benefit analyses of metabolic network properties, from comparative studies on organisms with different ecological niches, and from new experimental approaches. More specifically, we expect that future formulation of adaptive hypotheses will incorporate information on trade-offs between different functional properties of the metabolic system (e.g., yield and rate) and on metabolic costs (e.g., enzyme levels or intermediate concentrations). Second, there is a great need for comparative studies on the ecological and metabolic characteristics of a set of species. The most informative comparative analyses are based on reconstructed phylogenies (Harvey and Purvis, 1991) and can be used both to discover correlations between certain metabolic properties and environmental variables, hence to suggest adaptive explanations, and also to test well formulated hypotheses. Thus, it might be particularly fruitful to focus on closely related groups of organisms where genome sequence and biochemical data are available and where the phylogenetic relationships can be reliably inferred (e.g., yeast species or various groups of well-studied bacteria). Finally, we expect that advances in synthetic biology and metabolic engineering tools will open new possibilities in studying systems-level adaptations. For example, systematic addition of new links into the gene regulatory network of E. coli has been carried out recently (Isalan et al., 2008). Applying analogous rewiring approaches to metabolic networks (i.e., inactivation and addition of pathways) could, in principle, contribute to the elucidation of metabolic designs in at least two ways (Fig. 3). First, with the in vivo construction of different metabolic network forms, it will become possible to explore the space of plausible alternative molecular circuits and to identify potential trade-offs that are needed to formulate more realistic engineering models. Second, fitness measurement of strains carrying different network forms could be employed to experimentally test whether the wild-type form is adaptive and, in addition, will offer an unprecedented insight into the fitness landscape of metabolic systems.

Figure 3. A synthetic biology approach to map the fitness landscape of metabolic network structures.

A large set of randomly rewired metabolic networks is constructed using high-throughput synthetic biology and genome engineering tools (e.g., addition of new pathways and deletion of enzymes). By measuring the metabolic performance and fitness of rewired networks, the fitness landscape of metabolic network structures can be mapped and the adaptedness of the wild-type can be examined.