Vocal tract resonances in speech, singing, and playing musical instruments

Abstract

In both the voice and musical wind instruments, a valve (vocal folds, lips, or reed) lies between an upstream and downstream duct: trachea and vocal tract for the voice; vocal tract and bore for the instrument. Examining the structural similarities and functional differences gives insight into their operation and the duct-valve interactions. In speech and singing, vocal tract resonances usually determine the spectral envelope and usually have a smaller influence on the operating frequency. The resonances are important not only for the phonemic information they produce, but also because of their contribution to voice timbre, loudness, and efficiency. The role of the tract resonances is usually different in brass and some woodwind instruments, where they modify and to some extent compete or collaborate with resonances of the instrument to control the vibration of a reed or the player’s lips, and∕or the spectrum of air flow into the instrument. We give a brief overview of oscillator mechanisms and vocal tract acoustics. We discuss recent and current research on how the acoustical resonances of the vocal tract are involved in singing and the playing of musical wind instruments. Finally, we compare techniques used in determining tract resonances and suggest some future developments.

The development of our vocal system allowed extraordinary changes in human evolution and cultural development. Speech and∕or singing (their order of development is still debatable, e.g., Mithen, 2007; Wolfe, 2002) enabled the transmission of detailed information and contributed to the development of extremely subtle social relations and structures. Speech and singing involve processes requiring fine muscular control as well as extensive neurological involvement. As a result, controlling the acoustic resonances of the vocal tract is an important skill mastered by nearly all children when learning to speak: they learn to move their tongue, jaw, lips, and soft palate to adjust some of these resonances to specific frequencies. These resonances in turn produce broad peaks in our speech spectrum that are characteristic of vowels and some consonants. For this reason, these broad peaks have been intensively studied in this context (e.g., Peterson and Barney, 1952; Fant, 1960; Lindblom and Sundberg, 1971; Ladefoged et al., 1988; Hardcastle and Laver, 1999; Stevens, 1999; Clark et al., 2007).

A further landmark in cultural evolution has been the development of a wide variety of musical instruments. Wind instruments use the breath of the player as their energy source, and so the vocal tract can be intimately involved, and its resonances can contribute both to timbre (Berio, 1966; Erikson, 1969; Fletcher, 1996; Wolfe et al., 2003; Tarnopolsky et al., 2005, 2006) and to pitch control (Chen et al., 2008a, 2008b; Scavone et al., 2008).

This article reviews knowledge about the influence of vocal tract resonances on the voice and on wind instrument performance, techniques to measure these resonances and to investigate their effects, and research perspectives on these topics.

In the first section, interesting insights arise from comparing and contrasting the voice and wind instruments: all involve a vibrating valve or airstream (vocal folds, lips, reed, air jet), which converts breath energy into sound. In both voice and wind instruments, this source is coupled, weakly or strongly, to both a downstream duct (vocal tract or instrument bore, respectively) and an upstream duct (subglottal tract or vocal tract, respectively). The frequency of the lips or reed vibration in wind instruments is usually governed primarily by the acoustic resonances of the downstream resonator, i.e., the instrument’s bore. In contrast, for the normal voice, the frequency of the vocal folds’ vibration can usually be controlled almost independently of the vocal tract resonances, especially at low pitch.

For the voice and for some wind instruments, the vocal tract has primarily a filtering effect, especially when the sounding frequency is well below the tract resonance frequencies. In the second section of this article, we briefly review the principles of that filtering effect and its consequences on phoneme production, voice quality and musical timbre.

In a third section, we discuss interactions between the vocal tract and the excitation source, in particular when the excitation frequency is comparable to a vocal tract resonance frequency and∕or when the vocal tract resonance is of comparable strength to that of the instrument’s bore. We will illustrate how these interactions are used in some phonation modes when one vocal tract resonance is tuned to one harmonic of the voice (Lindblom and Sundberg, 1971; Sundberg and Skoog, 1997; Joliveau et al., 2004a, 2004b; Henrich et al., 2007). We show how tract resonances are used to determine playing pitch in some wind instruments (high range of the clarinet and saxophone), by increasing the magnitude of a vocal tract resonance and adjusting its frequency close to the played note (Chen et al., 2008a, 2008b; Scavone et al., 2008).

In the fourth section, we review techniques currently available to measure or to estimate vocal tract resonances. We discuss their principles, advantages, and drawbacks. Until recently, vocal tract resonances have been mainly studied from the output sound, especially in phonetic science. New techniques allow the investigation of vocal tract resonances independently of the output sound and suggest perspectives for new research about the contribution of vocal tract resonances in speech, singing, and playing wind instruments.

OSCILLATOR MECHANISMS AND COUPLING TO THE DUCTS

Valve mechanics

Structurally, there are strong similarities between the voice and some wind instruments.

In the case of the voice, vocal folds are adducted during phonation so the aperture between them, also called the glottis, decreases. Flow of air through this constriction produces a pressure drop. The pressure excess produced in the lungs and trachea tends to force the folds apart and to accelerate air through the glottis. The air flow between them creates a suction that tends to draw the folds back together (via the “Bernoulli effect,” Van den Berg et al., 1957), as does the tension in the folds themselves and, in the case of a such a response in the upstream airways, a fall in the upstream pressure. These alternating effects tend to excite a cycle of closing and opening of the folds, which is assisted by their inherent springiness or elasticity (which provide a restoring force), their mass (which provides inertia), and the inertia of the air flow itself, which maintains high flow rates even as the folds are closing. Muscles do not directly contribute to the vocal fold vibration, which is a passive aeromechanical effect (Van den Berg, 1958), but participate in its control (Titze, 1994).

The lip valve family includes the brass instruments, whose orchestral members are trumpet, horn, trombone, and tuba. In this family, the player’s lips vibrate in a way that is a little similar to the vibration of the vocal folds: to oversimplify somewhat, air passing between the lips produces a suction that draws them closed, and an excess of pressure in the mouth and∕or a suction in the mouthpiece opens them (see, e.g., Yoshikawa, 1995; Fletcher and Rossing, 1998).

Reed instruments include clarinets and saxophones. These are called single reeds because a single reed, usually cane, is fixed to the mouthpiece. This leaves a small aperture, whose area is varied as the reed vibrates, thereby modulating the flow of air from the mouth into the bore. In double reeds (oboe, bassoon, shawm), two pieces of cane vibrate against each other to perform a similar function. The main physical difference between reeds and lip valves is that high steady pressure in the mouth tends to close the reed of a clarinet, but tends to open the lips of a trombonist (for a review, see, e.g., Fletcher and Rossing, 1998).

In each case, a valve converts quasisteady air flow and pressure to oscillating air flow and pressure by nonlinear processes in the valve (the vocal folds, lips, reeds) or air jets (in flutes and whistles). The mechanics of the valve itself is often nonlinear, especially in high amplitude oscillation when, for example, vocal folds, lips, or reeds completely occlude the airway. Somewhat analogous to “clipping” in electronics, this saturation of the displacement produces strong, high frequency harmonics in the source signal. In most cases, the vocal folds and brass players’ lips operate in this strongly nonlinear mode, coming into contact and remaining closed for a fraction of the cycle. Reeds can also operate in this way but, at very small amplitude, the motion of a single reed can remain nearly sinusoidal. In such cases, another nonlinearity is still present, and produces higher harmonics.

This further nonlinearity, present for all such valves even at small amplitudes, occurs due to the loss of kinetic energy of the air flow in turbulence downstream from the folds, lips, or reed: the pressure difference has a term proportional to the square of the flow velocity. Such a pressure difference, generated across the valve with appropriate phase, can produce self-sustained oscillation.

Helmholtz (1877) identifies a brass player’s lips as a “striking outwards” valve: a steady, positive, upstream pressure excess (or downstream suction) tends to open the valve. Conversely, a woodwind reed is a “striking inwards” valve. Since then, a number of researchers have addressed the general problem of how such valves convert direct current (dc) flow into alternating current (ac) flow (Flanagan and Landgraf, 1968; Fletcher, 1979; Elliot and Bowsher, 1982).

Fletcher (1993) develops a simple but general model to explain the interaction of a linear oscillator with this nonlinear pressure term to explain several features of valve-resonator interaction and also includes a “striking sideways” valve, which opens due to pressure excess on either side. Simple models of the lips of brass instruments are striking outwards, while more elaborate models of lips and of vocal folds include components of striking sideways or combinations of both (Ishizaka and Flanagan, 1972; Yoshikawa, 1995; Titze, 2008).

Influence of the ducts on the valve

In a simple model discussed below, the upstream and downstream ducts have somewhat similar effects on the valve. However, in normal operation, the resonances of the upstream duct (trachea for voice, vocal tract for wind instrument) are much weaker than those of the downstream resonator and have little effect. On the other hand, the downstream duct (vocal tract for voice, internal bore of an instrument) has several strong resonances, whose frequencies may be varied by making geometric changes (varying mouth opening and the internal geometry for the voice, changing the length of tubing for a brass instrument, or closing or opening holes in woodwind instrument).

Several important consequences emerge naturally from the simple valve models described above.

Under suitable conditions, a sufficiently strong resonance (whether upstream or downstream) can “control” the valve. For example, a resonance at a frequency slightly above the natural frequency of a striking outwards valve or slightly below that of a striking sideways valve can, under some circumstances, produce sustained oscillations. This explains some of the behavior of brass instruments. On the other hand, when the valve frequency is well below that of the first resonance (as in low pitched speech and singing), this simple, general model predicts little influence of the duct geometry on the operating frequency f₀, but the duct dimensions do determine the predicted threshold for oscillation (Fletcher, 1993).

This result is consistent with some observations about the voice, but remember that the model includes only the nonlinearity associated with airflow: it is more comparable with a high pitched, very breathy voice, in which the vocal folds never touch and less comparable with the normal voice, in which the tract is completely occluded for part of the cycle. Similarly, it is a better approximation to the high range of a brass instrument than to the low. To include the nonlinearities of the valve as well, numerical rather than analytical models are required. Some of these are reviewed by Titze (2008). We return to this topic below.

Nevertheless, despite qualitatively similar excitation mechanisms, the operation of the voice and that of brass instruments are qualitatively different. A major cause is a quantitative difference: to take a specific example, a trombone has a frequency range similar to that of a male voice, but a trombone (or any other brass instrument) is much longer (a few meters) than a man’s vocal tract (∼0.2 m). The brass instrument operates at one or other of the resonant frequencies of the instrument bore, but the male voice usually operates at frequencies below that of the lowest resonance of the tract. Another quantitative difference concerns the “strength” of the resonance, which we quantify later.

These quantitative differences give a profound functional difference. In normal operation, one of the resonances of the instrument bore controls the playing frequency (Elliot and Bowsher, 1982; Fletcher, 1979). The trombonist (to continue our example) can change the lip tension and other relevant variables continuously but, unless s∕he moves the slide, the playing frequency “jumps” among several nearly discrete values, which correspond to resonant frequencies of that particular length and shape of tubing. Thus, a skilled player can usually select which of typically ten or so possible instrument resonances to play by adjusting parameters of his∕her embouchure (including lip tension and pressure)—and perhaps also by adjusting the resonances of the (upstream) vocal tract. The behavior of a bugle, trumpet, etc., is similar. For a woodwind instrument, a strong resonance of the bore can control the vibration of the reed over a large range of frequencies below the reed’s natural frequency.

For the normal voice, especially at low pitch, there is no simple analogy for this behavior. Indeed, if one pronounces several different phonemes in a monotone voice, one is demonstrating that the voice frequency is easily held constant, while resonances of the tract are varied. Alternatively, if one sings a melody using a single vowel (as in vocalise), one demonstrates that the frequency can be controlled rather independently of the resonant frequencies.

The frequency of the lowest resonance of the vocal tract varies typically from 300 to 800 Hz. The fundamental frequency f₀ of the voice therefore usually falls below the frequencies of the tract resonances. Consequently, the resonances usually have little effect on f₀. However, certain harmonics of the voice fall near these resonances and are efficiently radiated, while those that fall between resonances are not. So, in normal operation, vocal tract resonances usually control the spectral envelope of the voice, rather than f₀.

Another difference between the vocal tract and wind instruments is that the resonances of the bore of a wind instrument are, in a sense to be quantified later, usually “stronger” than those of the vocal tract. This also helps explains why they can control the playing frequency f₀, and why, in most circumstances, it is the instrument rather than the player’s vocal tract that predominantly determines f₀.

We may regard these two behaviors as extremes of a continuum: for a low pitch and for mouth configurations in which the first tract resonance frequency is high, the tract resonance has little effect on the valve, but it does modify the output sound. On the other hand, a strong resonance at a frequency near that of the valve can determine the f₀.

VOCAL TRACT RESONANCES AND FILTERING EFFECT

The origin of vocal tract resonances

For non-nasalized phonation, the vocal tract approximates a tube of irregular shape, typically 0.15–0.20 m from lips to glottis for a man. The resonance frequencies of the air in a tube depend on its length and upon the variation in its cross section along the length.

To discuss the vocal tract properties, a useful quantity is the acoustic impedance, Z, which is the ratio of acoustic pressure, p (the variation of the pressure from its steady value) to the acoustic or oscillating component of the flow, U, measured over a specified area at a specific place—such as the glottis. (Informally, Z could be said to be a measure of how difficult it is to produce oscillatory air flow through that area at a given frequency.) Z often varies strongly with frequency and it is a complex quantity, i.e., it may have both a real component, with pressure and flow in phase, and an imaginary component, with pressure and flow 90° out of phase. The real component dissipates sound energy, often turning it into heat, while the imaginary component temporarily stores sound energy. When the imaginary component is positive (pressure phase is ahead of flow), the impedance is inertive, meaning related to its inertia. A small mass of air, free to move but requiring a pressure difference to be accelerated, is an inertance or has an inertive reactance, and sound energy is stored in its kinetic energy. On the other hand, a small confined volume of air is a compliance. In this case, the imaginary component is negative, and energy is stored in alternately compressing and dilating the air. In general, a duct whose length is not negligible compared to the wavelengths of interest has acoustic pressure, flow, and impedance that all vary along its length. Measured at any position, the imaginary component of its impedance varies with frequency and changes sign at each resonance. Fletcher and Rossing (1998) give a good introduction and review.

A sound wave emitted from the open lips encounters the impedance Z_rad of the radiation field outside the mouth. Oversimplifying only a little, the pressure p at the lips that is required to produce an acoustic flow U_rad is that needed to accelerate a mass of air just outside the mouth. This mass is small, so Z_rad is small, especially at low frequencies, when only small accelerations are required. Inside the vocal tract (or a pipe), acoustic flow cannot spread out so much, so impedances are typically rather higher than Z_rad.

As in a pipe, Z in the vocal tract depends strongly on reflections of sound waves and one of the strongest occurs at the lips because of the sudden transition from high Z inside to low Z outside. If a burst of high-pressure air is emitted from the glottis at the moment when a high pressure burst resulting from previous reflections arrives back at the glottis, the pressures will add, so Z will be high. Conversely, if the emitted high pressure pulse is canceled by an arriving pulse of suction, Z is small. This explains the large variation in the input impedance of the simple cylindrical pipe without glottal constriction shown in Fig. 1. High sound levels occur when the acoustic flow through the glottis produces large changes in acoustic flow or pressure at the lips. This will occur at minima in the impedance Z.

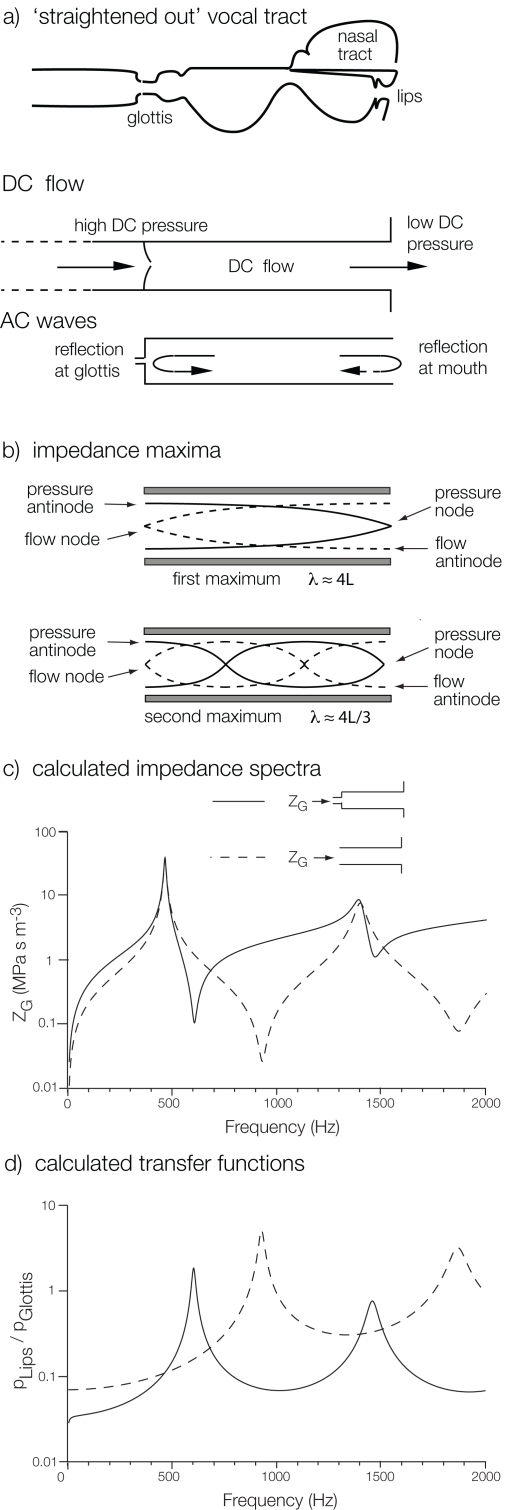
Figure 1. Simplified vocal tracts.

In the sketch in (a), the vocal tract has been “straightened out” to show the effects of dc and ac flows. (b) shows the modes of vibration in a simple pipe leading to impedance maxima measured at the left hand end. (c) shows the theoretical calculations for the magnitude of the input impedance and (d) a transfer function for a cylindrical “vocal tract” of length=170 mm and radius=15 mm (dashed line). The variation is large, so both vertical scales are logarithmic. The continuous line includes the effect of a model “glottal” constriction: a cylinder with a radius of 2 mm and an effective length (including end effects) of 3 mm.

Oversimplifying considerably, we can picture the tract as a tube that is open at the lips and nearly closed at the vocal folds. For the vowel ɜ in the word “heard,” the tract behaves approximately like a cylindrical tube that is open at the lips with a short, narrow constriction at the glottis. So, for simplicity, we begin by considering a simple, cylindrical tube with length L, open at the lips and with no glottal constriction. The maxima in the impedance Z occur for wavelengths approximately λ₁=4L, λ₃=4L∕3, λ₅=4L∕5, etc., and thus at frequencies f₁=c∕4L, f₃=3c∕4L=3f₁, f₅=5c∕4L=5f₁, etc. Minima in Z occur at frequencies roughly half way between the maxima (dashed lines in the figure) in this unrealistic situation.

However, the glottis is effectively a short, narrow constriction, and this has significant effects on the acoustic impedance and transfer functions. To illustrate the effect, we plot the impedance that would be measured upstream from a very simple model of a glottis in Fig. 1. The maxima in Z are hardly changed: these correspond to pressure antinodes (maximum p) and flow nodes (minima in U). A short constriction of the pipe at the input has little effect for a frequency that produces negligible input flow, i.e., at a maximum in Z. In contrast, at frequencies that require maximal flow, the mass of the air in and near the glottis must be accelerated to produce substantial flow, and the pressure difference that supplies this force acts on only a small area, while the area admits small volume flow. Consequently, the minima in Z (pressure node, flow antinode) are all substantially lowered in frequency. For a sufficiently small glottis, the falling slopes in Z(f) are almost vertical,as shown. Thus both the maxima and minima in Z(f) occur at similar frequencies, as do the maxima in the transfer functions.

As mentioned above, the acoustic pressure at the lips is small, but not zero, because of the finite pressure in the radiation field. This difference is called an end effect: compared to an “ideally open” pipe, which would have zero acoustic pressure at an open end, the impedance of the radiation field lowers slightly the frequencies of resonances. For a pipe, the end effect may often be usefully approximated as an extra length, which, in the case of the mouth opening would typically be several millimeters, and which would depend on mouth opening and shape. For the purposes of calculation, complicated vocal tract shapes are often approximated with a series of small conical or cylindrical sections.

Resonances, formants, and spectral peaks

Unfortunately, the meaning of the word “formant” has expanded to describe two or three different things. Fant (1960) gives this definition: “The spectral peaks of the sound spectrum ∣P(f)∣ are called formants.” Resonance frequencies are then defined in terms of the gain function T(f) of the tract by “The frequency location of a maximum in ∣T(f)∣, i.e., the resonance frequency, is very close to the corresponding maximum in spectrum P(f) of the complete sound.” Fant then writes: “Conceptually these should be held apart but in most instances resonance frequency and formant frequency may be used synonymously.” Benade (1976) uses a similar definition of formant: “The peaks that are observed in the spectrum envelope are called formants.”

More recently, the acoustical properties of the vocal tract are often modeled using an all-pole autoregressive filter (Atal and Hanauer, 1971). For many voice researchers, formants now refer to the poles of this filter model. To others, formant means the resonance frequency of the tract. Finally, many researchers, particularly in the broader field of acoustics, retain the original meaning: a broad peak in the spectral envelope of a sound (of a voice, musical instrument, room, etc.). The original meaning of formant is also retained, almost universally, when discussing the singers formant and actors formant: these terms refer to a peak in the spectral envelope around 3 kHz (discussed below).

As Fant observes, while these uses are often closely related, they are conceptually quite distinct. Further, the resonant frequency, the pole of the fitted filter function and the peak spectral maximum need not coincide. Moreover, it is now possible to measure resonances of the vocal tract quite independently of the voice. Consequently, it is sometimes essential to make a clear distinction among a resonance frequency (a physical property of the tract), a filter pole (a value derived from data processing), and a spectral peak (a property of the sound). In this article, we refer to the first, second and ith resonances as R1, R2, ..Ri.. We minimize use of the word formant but, where it appears, it has its original meaning and we name formants F1, F2, ..Fi…

Filtering effect in voice and musical instruments

The energy of the sound which excites the vocal tract is more effectively radiated at or near resonance frequencies of the vocal tract, resulting in broad peaks in the output sound spectrum, while other frequencies are less well radiated.

In the case of the voice, this filtering effect of the vocal tract is modeled by the source-filter theory (Fant, 1960) shown in Fig. 2: the vibrating vocal folds modulate air flow and produce a harmonically rich source. This is filtered by the tract to enhance the output spectrum at frequencies close to those of vocal tract resonances. In this simplest model of voiced speech and singing, the influence of sound waves in the vocal tract on the motion of the vocal folds is neglected. Although oversimplified, this model shows many important characteristics of voice production, especially for low-pitched voices and high frequency tract resonances. We discuss the interaction between source and filter in the fourth part.

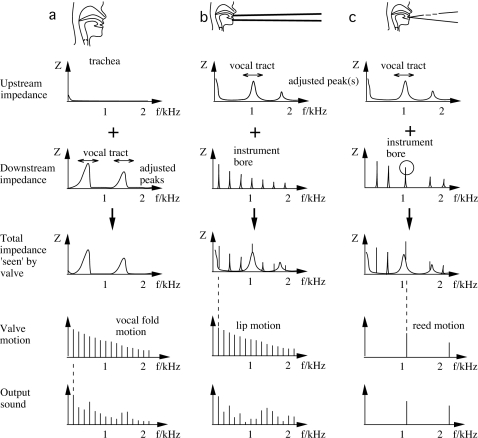
Figure 2. Schematic figures show idealizations of the duct-valve interactions in the voice (a), a lip valve instrument (b), and a reed instrument (c).

The upstream and downstream impedances add to give the total impedance Z. (a) Illustrates the source-filter theory: the vocal fold motion is assumed independent of Z, but tract resonances transmit certain harmonics more efficiently into the sound field at the open mouth. The vocal tract impedance spectrum has a different form when seen from the glottis (a) and from the lips (b) and (c). In (b) and (c) the mouth is closed so it will be difficult to change low frequency impedance peaks significantly by altering the mouth geometry. An impedance peak may be changed over a range near 1 kHz, which alters the total impedance (instrument+tract) over the same range. The timbre effect, as used by didjeridu players, is shown in (b) where vocal tract impedance peaks inhibit output sound. For a high pitched instrument, such as a saxophone played in the altissimo range (c), a vocal tract resonance may help determine the playing range by selecting which of the sharp peaks in the impedance spectrum of the instrument bore will determine the playing regime.

In the case of brass and woodwind instruments, Backus (1985) showed that, for a simple model, the impedances Z_b of the bore (downstream duct) and Z_m of the vocal tract (upstream duct) are acoustically in series. Inwards- or outwards-striking valves and the air passing between them are acted on by the difference P_m−P_b between the pressure upstream P_m and that downstream P_b. The volume flow U_b into the downstream duct approximately equals the flow out of the downstream duct, i.e., U_m=−U_b. By definition, the acoustic impedance of the upstream duct is Z_m=p_m∕U_m, where p_m is the acoustic or oscillatory component of P_m, and similarly Z_b=p_b∕U_b. Consequently p_m−p_b=−(Z_m+Z_b)U_b=(Z_m+Z_b)U_m. So the impedance of the up- and down-stream ducts are in series. The situation is more complicated for sideways-striking valves: the series impedance acts on the air flow, but not on the valve.

For musical instruments, if the playing frequency is determined by a strong resonance of the bore with frequency below the resonance frequencies of the tract, vocal tract resonances may then influence the timbre of wind instruments. Thus, the acoustical flow into the instrument is admitted for some frequency bands, while at other frequencies the flow is inhibited, thereby producing broad spectral peaks in the output sound. This filtering effect, though smaller for most wind instruments than for voice, is audible and well known to musicians (Berio, 1966; Erikson, 1969; Wolfe et al., 2003). We discuss it in more detail below.

Consequences for speech phonemes and voice quality

This filtering effect has some obvious consequences on speech production as well as on voice timbre. To a large extent, vowels in non-tonal languages are perceived according to the values of formants F1, F2 and, to a lesser extent, F3 (Peterson and Barney; 1952, Nearey, 1989; Carlson et al., 1970). For most vowels, higher formants have little effect on the vowel sound produced, but are important to the timbre of the voice (Sundberg, 1987). Nasal vowels or consonants are produced when the oral and nasal cavities are coupled by lowering the velum (or soft palate, see Fig. 1). The nasal tract also exhibits resonances. Coupling the nasal to the oral cavity not only modifies the frequency and amplitude of the oral resonances, but also adds further resonances and hence changes in the output sound (Feng and Castelli, 1996; Chen, 1997). When the vocal tract is constricted during the production of consonants, the variation in formants during the constricting or opening are important to recognition of the phoneme, as is the broadband sound associated with the opening or closing (Smits et al., 1996; Clark et al., 2007).

Movements of the articulators mentioned above are capable of a wide range of modifications of the acoustical properties of the tract. Some regions, however, such as the hypopharyngeal cavity (the region between above the larynx but below the pharynx), have an almost fixed geometry, and may play a role in the qualities of an individual speaker’s voice (Kitamura et al. 2005).

On the other hand, some vocal tract shapes are similar between speakers for some emotional states or modes of production, so that vocal tract resonances can participate, among other cues, in the perception, from the sound of the voice only, of smiling (Tartter, 1990), of different emotions (Siegwart and Scherer, 1995, Burkhardt and Sendlmeier, 2000) or of vocal effort (Liénard and Di Benedetto, 1999; Eriksson and Traunmuller, 2002).

Many singers practice controlling their vocal tracts to enhance the sound energy in some parts of the spectrum; perhaps to vary voice quality for interpretation, or for more efficient production. Studies have already characterized formants or tract resonances for different singing styles (classical, belting, see Stone et al., 2003; Sundberg et al., 1993), or different qualities or techniques (twang, “forward,” “throaty,” “resonant,” or “open” singing; see Bloothooft and Pomp, 1986a; Hertegard et al., 1990; Steinhauer et al., 1992; Ekholm et al., 1998; Titze, 2001; Vurma and Ross, 2002; Titze et al., 2003; Bjorkner, 2006; Garnier 2007b).

The singers formant

A number of studies of the spectral envelopes of male singers trained in the Western operatic tradition show a peak in the 2–4 kHz region that has been called the singers or singing formant (Sundberg, 1974, 2001; Bloothooft and Plomp, 1986b; Rzhevkin, 1956). Because the power produced by a symphony orchestra declines steadily with frequency above several hundred hertz (Hz), a voice exhibiting a strong singers formant may exceed the orchestral power in this range. This assists opera soloists to “project” or to be heard above a large orchestra in a large opera hall.

Singers formants in the voices of women opera singers, especially sopranos, seem either to be weaker, or nonexistent or else difficult to document (Weiss et al., 2001). In part, this is because the wide spacing of harmonics in high voices, particularly in the high soprano voice, makes it impossible to define a formant (in its original sense) in the spectrum of any single note. (A peak in the envelope of a spectrum averaged over a long time is not necessarily the same as a formant, because it may depend on which notes are sung over that time, particularly for high voices.) Further, the existence of a resonance in this range is of rather less use when singing in the high alto or soprano range. If the gain in a singer’s vocal tract had a bandwidth of a few hundred Hz (the typical width of the singers formant), then for many notes in the high range it would fall between two adjacent harmonics. Further, high voices have the advantage that several of the low harmonics and even sometimes the fundamental fall in the region where hearing sensitivity is greatest. Finally, high voices can take advantage of resonance tuning, as explained below.

The singers formant is usually attributed to the proximity in frequency of the third, fourth, and∕or fifth resonances of the tract (Sundberg, 1974). If two or more of these resonances fall close to each other, they can produce a single broad peak in the spectrum. There seem to be no published direct measurements of the resonances associated with the singers formant, although this is the subject of ongoing research.

Singers produce the singers formant by keeping the larynx low and by narrowing the epilaryngeal tube—a constriction in the vocal tract just above the larynx (Sundberg, 1974; Imagawa et al., 2003; Dang and Honda, 1997;Kitamura et al., 2005; Takemoto et al., 2006a, 2006b). Of course, R3, R4, and R5 are properties of the tract as a whole, rather than just of the epilaryngeal tube (Sundberg, 1974). Because its diameter is intermediate between that of the glottis and the upper tract, the epilaryngeal tube typically has intermediate values of impedance (formally, its characteristic impedance has an intermediate value). Consequently, at some frequencies, it may act as an effective impedance matcher between the two. An impedance matcher increases power transfer in both directions. It may therefore both increase sound output at some frequencies and increase the influence of pressure waves in the tract on the vocal folds.

When a strong singers formant is combined with the strong high harmonics produced by rapid closure of the glottis, the effect is a very considerable enhancement of output sound in the range 2–4 kHz: i.e., in a range in which human hearing is very acute and in which orchestras radiate relatively little power. It is not surprising that these are among the techniques used by some types of professional singers who perform without amplification.

Increasing the fraction of power at high frequencies has a further advantage: at wavelengths long in comparison with the size of the mouth, the voice radiates almost isotropically. As the frequency rises and the wavelength decreases, the voice becomes more directional, and proportionally more of the power is radiated in the direction in which the singer faces, which is usually towards the audience (Flanagan 1960; Katz and D’Alessandro, 2007, Kob and Jers, 1999). So increasing the power at high rather than low frequencies via rapid glottal closure and∕or a singers formant helps the singer not to “waste” sound energy radiated away from the audience.

A number of studies have investigated a speakers formant or speakers ring in the voice of theatre actors or in the speaking voice of singers (Pinczower and Oates, 2005; Bele, 2006; Cleveland et al., 2001; Barrichelo et al., 2001; Nawka et al., 1997). Leino (1993) observed a spectrum enhancement in the voices of actors, but of smaller amplitude than the singing formant, and shifted about 1 kHz towards high frequencies. This was interpreted as the clustering of R4 and R5. Bele (2006) reported a lowering of the formant F4 in the speech of professional actors, which contributed to the clustering of F3 and F4 in an important peak. Garnier (2007a) also reported such a speaker’s formant in speech produced in noisy environment, with a formant clustering that depended on the vowel.

Consequences on the timbre of lip valve instruments

Instruments of the brass family have a bore that, at the input end, has a cross section rather smaller than that of the vocal tract. Further, the mouthpiece has a constriction with a diameter of only several mm. The peaks in the bore impedance Z_b are therefore usually rather greater than those in the mouth or vocal tract impedance Z_m, and consequently the effects of the vocal tract are often modest.

A notable exception is the didjeridu, in which the effects of vocal tract configuration on the sound are very prominent. The didjeridu is a traditional Australian instrument made from the termite-hollowed trunk of a small tree. Its bore has no mouthpiece constriction and has a cross sectional area comparable with or larger than that of the vocal tract. This instrument usually plays a single, long, sustained note at a frequency near its lowest resonance, with notes at higher resonances used only rarely. The musical interest comes largely from variations in timbre produced by changes in the configuration of the vocal tract (Fletcher, 1996).

In traditional didjeridu performance, a rhythmic variation in timbre is produced by what is called circular breathing: during the exhalation phase, most of the air from the lungs goes into the instrument while a portion is used to fill the player’s cheeks. During the next phase, the palate seals the mouth and the player inhales through the nose, while simultaneously expelling the air from the cheeks into the instrument, thus maintaining a continuous note. The changes in timbre that accompany these large, repeated changes in vocal tract configuration are usually used to establish the rhythmic structure of the performance. Other changes in timbre are produced by changing the position of the tongue in the mouth.

Peaks in Z_m are very closely correlated with minima in the spectral envelope, and vice versa, as shown in Figs. 3c, 4. This is because when Z_m just inside the lips is large, very little acoustic current enters the instrument, so there is little sound output at that frequency. It is as though players use the tract resonances to “sculpt” the spectral envelope: broad peaks in the tract impedance suppress certain harmonics, leaving the remaining bands of harmonics as broad peaks in the spectral envelope (formants in the original sense) (Tarnopolsky et al., 2005, 2006; sound files in Music Acoustics, 2005). The same auditory system that readily follows formants in speech presumably tracks the formants in the sound of the didjeridu.

Figure 3. Three different uses of vocal tract resonances are shown here.

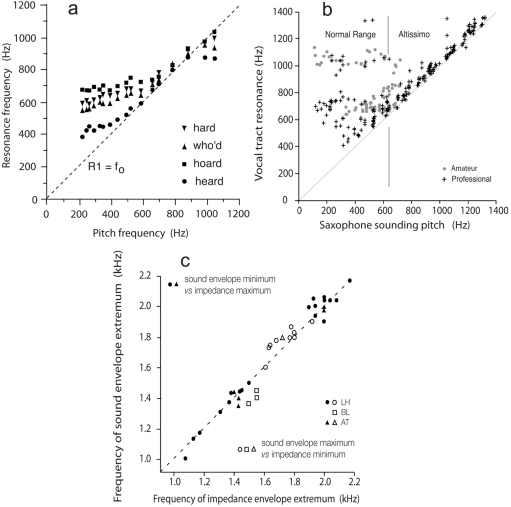
(a) Shows resonance tuning by sopranos. At low frequencies, the first resonance R1 is different for each vowel. As f₀ approaches R1, however, R1 is tuned to a frequency slightly above f₀. (From Joliveau et al., 2004a.) (b) shows how saxophonists tune the vocal tract to produce the altissimo range (here for a tenor saxophone). In the normal range of the instrument, below about 700 Hz, there is no simple relation between the frequencies of the note played and the tract resonance. In the high altissimo range, however, a vocal tract resonance is consistently tuned a little above the frequency of the note played—by those experienced musicians who can play in this register. (From Chen et al., 2008a.) (c) shows how didjeridu players use resonances to produce maxima and minima in the impedance of the tract that form minima and maxima respectively in the spectral envelope of the output sound. (From Tarnopolsky et al., 2006.)

Figure 4. Contrasting the timbre effect and the tuning effect of the vocal tract in wind instruments.

The top graph (Tarnopolsky et al., 2005) shows how vocal tract impedance peaks (dark line) control the timbre by suppressing harmonics in the sound of the didjeridu. The next two graphs (Chen et al., 2008a) show how, in the high pitch range (b), experienced saxophonists tune a resonance of the tract to select the note to be played (the spike near 1000 Hz). [In the low range (a), accessible to amateurs, resonance tuning is not needed.]

For brass instruments, similar but smaller effects on timbre are audible and well known to musicians (Berio, 1966; Erikson, 1969). However, to date, only preliminary measurements of Z_m during performance have been made. The size of the glottis affects both the frequency and the magnitude of peaks in Z_m. For this reason Mukai’s observation (1992) that the glottis size during playing was smaller for experienced brass players than for amateurs suggests that experienced players may use their glottis, among other vocal tract parameters, to adjust resonances.

SOURCE-TRACT INTERACTIONS

In the simple model of valve-duct interactions discussed above, the effect of the ducts on the operating frequency of the valve is small when that operating frequency lies well below those of the resonances of the ducts. It is also small if the valve and duct are weakly coupled because of an impedance mismatch (Titze, 2008). Consequently, the vocal tract resonances have little influence on the glottal source at low pitches. The relatively weak resonances of the subglottal tract also have little effect. In wind instrument performance, the tract resonances also have little effect on pitch at low frequencies, because the peaks in Z_m are not only at much higher frequencies those of Z_b, but also have (usually) much smaller magnitude.

Nevertheless, the source and the vocal tract resonances may be interrelated in a number of ways. First, there are direct, physical interactions: the mode of phonation affects the reflections of sound waves at the glottis, and so affects standing waves in the tract. Second, the varying sound pressure in the vocal tract certainly does exert oscillatory force on the valve (vocal folds, reed, lips) and on the air passing through it, so the vocal tract must to some extent influence the “source,” especially when f₀ and R1 are close. Third, speakers, singers, and wind players may consciously or unconsciously use combinations of fundamental frequency and resonance frequency for different effects, in particular to improve their efficiency or to facilitate producing high pitches. We discuss these in turn.

Effect of the glottis aperture on vocal tract resonances

In the simple approximation mentioned above, we treated the vocal tract as a pipe open or closed at the lips, for, respectively, voice and wind instrument, but nearly closed at the glottis in both cases. This approximation is suggested by the fact that the glottis aperture is very much smaller that the tract section.

In the case of voice, however, depending on the laryngeal mechanism or on the mode of phonation, the mean glottis aperture can change, as can the time ratio of the opening phase over the fundamental period, i.e., the open quotient (Klatt and Klatt, 1990; Alku and Vilkman, 1996; Gauffin and Sundberg, 1989). This changes the boundary condition at the glottal extremity of the tube and affects its resonance frequencies. Thus, for in vitro measurements, the first resonance frequency of a cylindrical tube tends to increase with glottal aperture and open quotient (Barney et al., 2007). As for in vivo measurements, first resonances have been shown to fall at higher frequencies for whispering than for normal speech, for the same vocal tract shape (the same vowel articulation) (Kallail and Emanuel, 1984a, 1984b; Matsuda and Kasuya, 1999; Itoh et al., 2002; Swerdlin et al., 2008). This can be explained by the larger aperture of the glottis in that mode of phonation (Solomon et al., 1989). Matsuda and Kasuya (1999) attributed it to the combined effect of a narrowing of the tract above the glottis and weak acoustic coupling with the tract below the glottis.

In the case of brass instruments, although the vocal folds are not vibrating (the lips do instead), the size of the glottis affects both the frequency and the magnitude of peaks in Z_m. For this reason Mukai’s observation (1992) that the glottis size during playing was smaller for experienced brass players than for amateurs suggests that experienced players may use the glottis size, among other vocal tract parameters, to adjust resonances.

The effect of acoustic pressure on the excitation source

In models, both the flow of air through the glottis and the motion of the vocal folds are predicted to depend on the pressure difference across the glottis and folds, and thus on the pressure in the tract immediately above the glottis (Flanagan and Landgraf, 1968; Rothenberg, 1981; Fletcher, 1993; Titze, 1988, 2004; 2008). As one would expect, the models suggest that the relative phase of the motion of the vocal folds and the arrival of a pressure pulse reflected from the mouth opening is important. This phase changes sign as the frequency passes through a resonance of the tract: below the resonance frequency, the pressure pulse is ahead in phase of the flow into the tract (the load is inertive, or behaves somewhat like a mass) but at frequencies above that of resonance, the pressure maximum follows that of flow (the load is compliant or behaves somewhat like a spring). Nonlinear models of the vocal folds typically have two or more masses connected by springs, plus parameters to represent the nonlinearity in their motion, and others concerning the geometry of the opening elements. Such models comprise a large literature. A review of such models and a set of simulations representing a range of different conditions are given by Titze (2008).

Experimental tests of these models are necessarily indirect: few mechanical properties of operating vocal folds can be measured, and there are considerable difficulties in measuring or estimating the pressures on either side. Hardware (in vitro) models have the advantage that the properties may be measured in considerable detail (Titze et al., 1995; Kob, 2002; Ruty et al., 2007), but the disadvantage that we do not know how well the behavior of their valves resembles that of living, controlled, vocal folds.

Similarly, measuring vocal tract effects on brass instruments can be achieved using artificial “lips” driven by compressed air. The geometry of the upstream plumbing may then be modified to simulate the effect of changing mouth geometry. Some preliminary results have been reported for very simple systems (Wolfe et al., 2003), but the technical difficulties of producing reliable, reproducible models of human lips are considerable (Fréour et al., 2007; Newton and Campbell, 2007).

It is also possible to observe the effect of pressure waves on the motion of vocal folds directly. Hertegard et al., (2003) used an endoscope to film the larynx while singers mimed singing, and while a range of acoustic signals was injected into the mouth via a tube sealed at the lips. The variation in glottal area was greatest for frequencies not far from those of normal phonation. In a recent study (Wolfe and Smith, 2008), we used electroglottography (EGG) to monitor the motion of the vocal folds, while they were subjected to sound waves generated independently. The EGG signal for the passive response of adducted vocal folds to a sound signal generated in the mouth by didjeridu playing, without phonation, was comparable in magnitude with that generated by phonation at a similar sound level. All the above evidence suggests that the standing waves in the “filter” have a strong interaction with the source.

We now turn to less direct interactions between the resonances and the source: those that involve strategies of the singer or speaker that may increase the loudness of the voice at constant vocal effort, or which allow production of a given sound level more efficiently.

Resonance tuning in singing and speech

Interactions between vocal tract and glottal source can be exploited by singers to improve their efficiency. The first vocal tract resonance poses a particular problem for sopranos, the highest common voice range, and to a lesser extent other voices in their high range. The range of R1 (about 300–800 Hz) roughly overlaps the range of fundamental frequencies of the soprano voice. If the resonances were maintained at the values typical of speech, this would have two consequences. First, for many note-vowel combinations, the fundamental would fall above R1, so the singer would lose the impedance-matching benefit of R1, which allows production of a loud voice with relatively little vocal effort. Second, the loudness and timbre of the voice would vary considerably from one note-vowel combination to the next.

Sopranos in the Western tradition are often taught to increase the mouth aperture, by lowering the jaw, smiling or “yawning,” as they ascend in pitch. Sundberg and colleagues (Lindblom and Sundberg, 1971; Sundberg and Skoog, 1997) studied the aperture of the mouths of sopranos as a function of pitch and deduced that they were tuning R1 to a value near the fundamental frequency of the note sung. (It is worth noting that opening the mouth also improves the impedance matching between the vocal tract and the radiation field.)

Measurements of the resonances, using acoustic excitation at the mouth opening, confirmed this (Joliveau et al., 2004a, 2004b): at low pitches, sopranos use values of R1 and R2 typical of those of the vowel they were asked to sing. In the range where f₀ was equal to or greater than the normal value of R1, they systematically increased R1 so that it was usually slightly higher than f₀. This tuning of R1 to f₀ began at lower frequencies for vowels with lower R1. It continued over most of the range to above 1 kHz (see Fig. 3). At the highest frequencies, tuning was not maintained for vowels requiring lip rounding, perhaps because of the difficulty of opening the mouth wide enough in this case. Over the range of tuning of R1, R2 also rose, but it was not tuned to match harmonics of the voice. The explanation here is that both R1 and R2 increase with increased mouth opening, so that tuning R1 to f₀ increases R2 as a side effect.

We explained above that the resonances R1 and R2 determine the corresponding spectral envelope maxima F1 and F2, and that the combination of F1 and F2 are important determinants of the perceived vowel sound. A consequence of the resonance tuning we have just described is that, for sufficiently high pitches, the pitch of a note determines R1, independently of the vowel written in the libretto or lyrics, and that R2 is increased above its usual value. Would this mean that all vowels would sound very similar? The answer is yes, they do and sound samples demonstrate this (Music Acoustics, 2004). However, this does not mean that much phonetic information is lost by resonance tuning itself. Once f₀ exceeds R1, no information is conveyed by R1, because there is no acoustic energy at that frequency. There is consequently no F1. Further, in this range, the spacing of harmonics is so high that there is no F2 either: there are just widely separated harmonics. So sopranos have virtually nothing to lose by tuning resonances in this range (Berlioz, 1882), and much to gain: increased power for the same effort and improved homogeneity of timbre.

How do they learn to do this? Beyond the suggestions of teachers, there is audio feedback: as the tract resonance approaches that of the fold vibration from above (or vice versa from below), the sound output is presumably louder for the same effort. Singers also use proprioceptive feedback (Scotto di Carlo, 1994). A simple model shows that autonomous valves that open sideways or in the direction of the steady flow (as described above) tend to be driven most easily at frequencies a little below the resonance: they “drive” inertive loads better than compliant ones (Fletcher, 1993). Is it possible that it is simply easier to sing in this condition? Apart from anecdotal reports, we know of no direct evidence.

The range in which f₀ exceeds typical values for R1 comprises much of the soprano range, less of the alto range, only the upper range for tenors and only affects a few vowels at the top of the range for basses. Resonance tuning in these voice classes has been much less studied. However, those studies show that, for the vowel and pitch ranges where f₀ exceeds R1, some singers in these ranges do use the technique of tuning R1 to f₀. In some but not all cases, altos and baritones were also observed to tune R1 to the second harmonic (i.e., to 2f₀) over a limited range (Smith et al., 2007).

An interesting example of resonance tuning comes from a style of folk singing practised by Bulgarian women, in which the second harmonic is especially prominent. This style is usually performed out of doors and is very loud. A study of one practitioner, an alto, showed that, for most vowels, R1 is consistently tuned near to 2f₀ over the whole pitch range used for this style (Henrich et al., 2007).

Tuning of a resonance to higher harmonics of f₀ is the chief feature in a range of styles known as harmonic or overtone singing. The fundamental frequency is usually at a rather low pitch (falling in a range where the ear is not very sensitive) and is usually held constant, both of which features make it less obvious. One (or sometimes more) resonances are then tuned to select one of the high harmonics, typically from the about the 5th to the 12th. Several studies have concentrated on the source involved. A key feature, however, must be the presence of a strong resonance with a narrow bandwidth that can selectively radiate one harmonic (Adachi and Yamada, 1999; Kob, 2003; Music Acoustics, 2003; Smith et al., 2007). This seems to have been little studied.

Is resonance tuning used in speech? Actors, orators, and teachers sometimes face the same challenge of communicating in a large hall and sometimes with accompaniment of different sorts. However, they have the advantage over most singers that the pitch is not specified for them: in principle, they might achieve resonance tuning by a combination of vowel modification and appropriate f₀. Some preliminary research suggests that resonance tuning is used in shouted speech (Garnier et al., 2008) but more experiments are needed.

Resonance tuning in reed instruments

In reed instruments, the series combination Z_m+Z_b is important and the peaks in Z_m are usually rather smaller than those in Z_b, at least at low frequencies. Consequently, the effects of vocal tract configuration on pitch and timbre are expected usually to be modest at low frequencies. In the case of vocal tract effects on clarinet performance, acousticians had expressed opinions ranging from “negligible” (Backus, 1985) to “vocal tract resonant frequencies must match the frequency of the required notes” (Clinch et al., 1982). Measuring the impedance spectrum Z_m while the player plays is technically difficult and so early investigations involved measuring while players mimed (Fritz and Wolfe, 2005).

The saxophone, whose single reed mouthpiece is rather like that of a clarinet, provides an interesting example. The saxophone has a nearly conical bore with a small bell and large tone holes. A consequence of this is that the magnitudes of the peaks in Z_b decrease relatively rapidly over the upper frequencies of the playing range. The “normal” range of the saxophone is about 2.6 octaves and beginners quickly learn to play to the top of this range. Playing higher notes (the “altissimo” range), however, usually requires considerable training.

Figure 3 shows the data for amateur and professional players over a large range. In the normal range, there is no evidence of systematic tuning of the tract for either amateur or professional players. For some players, the tract resonance varies little with note played. In the altissimo range, there are no data for amateurs because they were unable to play in this range. However, the professional players, when they reach this range, consistently tune a strong peak in Z_m to be a little above the frequency of the note to be played. Specific examples are shown in Fig. 4 (Chen et al., 2008a; sound files in Music Acoustics, 2008.)

Scavone and colleagues (2008) used one microphone inside the mouthpiece and another just inside the player’s mouth to study tract effects. Because U_m=−U_b, the ratio of the two pressures gives the ratio Z_m∕Z_b at the harmonics of the note played. These measurements show Z_m<Z_b at the pitch frequency in the normal range, and Z_m>Z_b in the altissimo range.

Similarly, although clarinetists rarely use vocal tract resonances in most of the range of the instrument and under normal playing conditions, they do adjust the tract resonances for exotic effects, including the “throat glissando” at high pitch (Fritz and Wolfe, 2005; Chen et al., 2008b).

To summarize: at low pitch, Z_b has strong peaks that determine the playing regime. At high pitch, the player must learn to tune a large peak in Z_m to the desired frequency. This seems to be difficult to do, perhaps in part because feedback is only available once one can do it. Scavone’s technique offers the possibility of visual feedback to players.

Although experiments are being conducted on other reed instruments, there are no comparable data yet published. Nevertheless, the reports of musicians suggest that similar effects have some importance in timbre and intonation.

TECHNIQUES FOR STUDYING VOCAL TRACT RESONANCES

New techniques for resonance measurements, improvements to established measurements, and combinations of complementary techniques have led to some of the recent discoveries mentioned above, and may lead to new discoveries. It is therefore interesting to compare and to contrast some of these techniques.

A quantity of great interest is the transfer function T(f)=p_m(f)∕p_g(f), where p_g(f) and p_m(f) are, respectively, the pressure spectra at the glottis and the mouth opening. This cannot usually be measured directly. However, formants (in the original sense) are commonly assumed to occur at frequencies close to those of the maxima of T(f). Extrema in this and the other transfer functions are closely related to the resonances. This leads to the longest established technique, which uses the voice itself as the stimulus. An external stimulus is another possibility, as is modeling based on images. Variants of these three different categories of measurement are summarised in Table 1.

Table 1.

A summary of the methods for estimating vocal tract resonances. Horizontal lines separate the three basic methods mentioned in the text. In this table, “ecological” refers to normal conditions of speech or singing, as distinct from special laboratory conditions.

	Excitation source	Measured parameters	Advantages	Disadvantages
	Vocal fold vibration (vocalization)	Sound output	• Natural source	• Unknown source spectrum
			• Ecological	• Poor frequency resolution
			• Minimal hardware	• Unusable at high pitch
			• No subject discomfort
			• Nonperturbing
	Turbulent air flow (whisper)	Sound output	• Natural source	• Unknown source spectrum
			• Minimal hardware	• Different mechanism causes  shift in formant frequencies
			• No subject discomfort
			• Non perturbing	• Not ecological
			• Good frequency resolution
	Mechanical excitation near glottis	Sound output and force input	• Can choose source spectrum • Good frequency resolution	• Perturbs subjects • Unknown transfer function   from skin to glottal flow • Not ecological • Requires hardware
	Acoustic current at lips	Tract and radiation impedance in parallel	• Can choose source spectrum • Good frequency resolution	• Measures “from wrong end” • Radiation impedance is low • Not ecological • Requires hardware
	None	Tract geometry inferred from tomography, acoustic properties calculated	• Gives explicit dependence   of acoustical properties   on articulation geometry	• Discomfort of subjects • Not ecological • Reduced frequency precision

Output sound when excited at the glottis

One method involves analysing the response of the vocal tract to a glottal excitation, including normal speech. A common way of using the output sound to determine tract characteristics consists of estimation by linear prediction of the parameters of an autoregressive filter that would best fit the measured spectrum (Atal and Hanauer, 1971; Markel and Gray, 1982; Makhoul, 1975; Alku, 1991). Poles (characteristic frequencies) of this filter correspond approximately to the resonances of the tract. This technique requires little specialized technology and a range of analysis software is available (Boersma and Weenink, 2005; Childers, 1999). It has therefore been very widely used and is responsible for much of our knowledge of voice acoustics. Several variants of this method use different types of source to excite the vocal tract and are shown in the Table 1.

Usually, normal quasiperiodic vibration of the vocal folds is used as the source of excitation. This method has the great advantages of minimal perturbation of the system under investigation, and of studying the tract under the conditions of interest, i.e., during speech and singing. Speech and singing may be recorded in laboratory or more natural conditions and the sound analyzed later.

However, for studying resonances of the vocal tract, the voice signal has two disadvantages. One is that the source functions, i.e., the vibrations and sound flow at the glottis, are in general not known. [It is possible to position a microphone near the vocal folds, but it is reported to be uncomfortable, and there is chance of vocal fold cramp if the microphone touches the folds (Kob, 2002)]. Thus, we cannot simply compare the source and the output and directly deduce properties of the tract. One approach involves making some strong assumptions about the source spectrum (and the lip radiation), based on theoretical models.

A second and more significant drawback of the normal voice as a probe can be limited frequency resolution. As shown in Fig. 2, information in the frequency domain is limited to multiples of the fundamental frequency. For the low voice (f₀=150 Hz) used in this example, this sampling gives an approximate picture of the spectral envelope, but for high pitched voices (e.g., 500 or 1000 Hz, to take high examples in the tenor and soprano range), relatively little information is given about the frequency response of the tract. For example, imagine removing most of the harmonics in the left column of Fig. 2, to yield fundamental frequencies of 450 or 1050 Hz. In speech, the fundamental frequency varies with time, and so the voice “scans” across a frequency range. In principle, this could give more frequency information about a particular articulation. In practice, however, articulation and thus the properties of the tract also vary rapidly in time during normal speech, which would make it difficult to use the variation of f₀ to improve the estimation of resonances from normal speech.

Some studies have also used a broadband (but still natural) excitation of the vocal tract, for example by producing whispered (Pham Thi Ngoc, 1995; Dowd, 1995), creak voice or “ingressive” phonation (i.e., produced on inspiration rather than expiration) (Miller et al., 1997). Whispering is produced by a glottis whose area does not oscillate. This area is larger than that used in normal speech, but small compared to that used in breathing. Airflow through it is turbulent, and has a mix of all frequencies (Itoh et al., 2002; Matsuda and Kasuya, 1999). The creak voice or vocal fry has an oscillating glottis, but the variations are not periodic (Hollien and Michel, 1968).

Thus, unlike periodic phonation, the whisper and the creak voice have the advantage that their excitation spectrum is broadband rather than harmonic. Consequently, the formants may be estimated rather more precisely than is the case for singing and speech. However, as with the normal voice, the source function is still not known, so the frequencies of the formants may not coincide precisely with those of the resonance. The main drawbacks of these methods are that glottal aperture may be larger for these modes of phonation than for normal speech (discussed later), giving rise to an increase of the first vocal tract resonance frequencies for a similar tract configuration (Matsuda and Kasuya, 1999; Itoh et al., 2002), and that articulation may change from normal to whispered or creak phonations (Kallail and Emanuel, 1984a, 1984b), changing the resonance characteristics as well.

Another solution consists of exciting the vocal folds mechanically from outside the neck using a mechanical vibrator, while the subject is phonating in a natural mode. For this technique, Fujimura and Lindqvist (1971) used sinusoids, Castelli and Badin (1988) used white noise and Djeradi et al. (1991) used pseudorandom excitation. One limitation of this method is the requirement that the subject maintain a constant articulatory position for a sustained period. Another is the power of the excitation, which has to be large to produce good signal to noise ratio, and which has been reported as uncomfortable for the subject (Djeradi et al., 1991). In addition, the proportion of the external vibration that is transmitted to the glottis via the cartilage and skin around the neck is unknown (Pham Thi Ngoc, 1995).

Output sound when excited at the lips

Another approach consists of analysing the response of the vocal tract to an excitation, but this time from the lips (see Table 1). A large impulsive signal, produced by an electrical discharge or even a gunshot, has a broadband signal, but is potentially disturbing for nervous subjects (Karlsson and Rothenberg, personal communication). Continuous, synthesized acoustic currents have also been used (Epps et al., 1997, Dowd et al., 1997; Kob, 2002; Kob and Neuschaefer-Rube, 2002; Joliveau et al., 2004a, 2004b; Stoffers et al., 2006). The acoustic impedance measured at the mouth opening is then given by Z=p_m(f)∕U_m(f), where U_m(f) is the acoustic current flow and p_m(f) is the pressure signal recorded at the mouth opening.

This method, however, has different disadvantages. First, when the mouth is open, as in speech or singing, the vocal tract impedance is measured in parallel with the relatively low impedance of the radiation field. Consequently, a moderately loud measurement signal may be needed to obtain good signal to noise ratios during loud phonation, especially at low frequencies where the radiation impedance is low. Further, the technique of exciting and recording at the lips has the disadvantage, when analyzing speech or singing, that the acoustic impedance is measured “at the wrong end,” i.e., at the lips rather than the normal place of excitation at the glottis. However, maxima of the acoustic impedance measured at the mouth opening allow relatively precise measurement of the resonance frequencies of the vocal tract (Epps et al., 1997) that are close to those seen at the glottis (Smith et al., 2007). Neither disadvantage listed above applies when investigating vocal tract effects on most wind instruments because the mouth is closed and because the impedance just inside the lips is the quantity of interest.

Computational estimation of the vocal tract transfer function from imaging

A less direct approach (see Table 1) is to make a magnetic resonance imaging or x-ray tomographic image of the tract, to deduce from this the cross section as a function of distance, and then to use acoustic models to calculate the expected properties (Sulter et al., 1992; Baer et al., 1991; Miller et al., 1997; Story et al., 1998; Honda et al., 2004; Story, 2005; Takemoto et al., 2006). The images are helpful for their anatomical details and they have been used as the basis for articulatory models. They provide convincing speech simulations (animations and sound files on Story, 2008). This research has yielded a wealth of information. Nevertheless, several steps are required between tomographic data and calculated acoustical properties, all of which can limit the confidence in the precision of estimates thus obtained.

Another, related way of avoiding the measurement difficulties of the real vocal tract is to study instead a hardware model of it (e.g., Fant, 1960; Kob, 2002). Usually, such model tracts are made of materials that are both more rigid and denser than that of human tissues. However, at the frequencies of greatest interest, the differences in behavior thereby introduced are assumed negligible. Such models may be excited acoustically at the glottis, and pressure may be measured at any point. So, if the geometry of a particular tract configuration is sufficiently well known, its linear acoustical properties may be measured in considerable detail.

CURRENT AND FUTURE DIRECTIONS

There are currently considerable technical difficulties in precisely measuring the acoustic properties of the vocal tract, particularly in real time. Complications can arise due to interference from the very high sound levels that occur during loud singing or while playing a musical instrument. There are also difficulties of access to the tract whilst playing musical instruments. However, as the measurement technologies described above are improved and as they and combinations of them are applied to studies of singing, speaking, and wind instrument performance, we are likely to learn much more about how we use our vocal tracts.

Improved measurements of vocal tract resonances may result in improved solutions to the inversion problem: estimating the area function of the vocal tract from properties of its transfer function. It has been suggested that this could have clinical applications (Stoffers et al., 2006).

The skills involved in adjusting vocal tract resonances to produce speech, and in controlling the vocal folds to produce a range of pitches in different laryngeal mechanisms, are so widespread and learned so early, that we hardly notice them. Indeed the skills so become deeply entrained that it can be very difficult to modify them or to learn new ones. One common example is learning a foreign language: it is widely observed and regretted that adult learners have difficulty acquiring an authentic pronunciation. This is usually attributed, at least in part, to processes of categorization, whose result is that speakers never learn the resonance frequencies associated with phonemes in the new language. Direct feedback using the resonance frequencies of the vocal tract rather than those inferred from hearing should not suffer from this problem. For example, a study found that the acoustic properties and recognizability of French vowels produced by monolingual anglophone subjects were significantly superior when the subjects used real-time visual feedback on the acoustic resonances of their vocal tract (Dowd et al., 1997). Nonacoustic feedback on tract resonances might also help hearing-impaired subjects achieve improved and more natural pronunciation.

Appropriate real-time feedback on their resonance behavior could also provide useful training in situations outside normal speech. Thus, some speakers, actors, orators, or singers might learn how to use their tract resonances (among other skills) to enhance sound power by altering the spectrum of the sound they produce. It could also help singers learn to tune the resonances of their vocal tracts to an harmonic of their voice. This can facilitate singing at high pitch, enhancing vocal power, and∕or controlling the timbre of the voice. Players of wind instruments could also use appropriate feedback to learn how to use their tract to influence pitch and timbre.

The very fine muscular control of tract resonances (and also pitch) could also possibly be used for a number of purposes outside those described in this article. The broad peaks in the sound spectrum produced by resonances have been used for many years to control the spectrum of other sound sources via devices such as vocoders. Indeed the resonance frequencies themselves could be used for real time control of various parameter(s) in electronic synthesisers. The precise control of resonances may ultimately be useful in areas quite unrelated to sound, for example in providing control signals for use by the disabled.