Delayed coupling theory of vertebrate segmentation

Abstract

Rhythmic and sequential subdivision of the elongating vertebrate embryonic body axis into morphological somites is controlled by an oscillating multicellular genetic network termed the segmentation clock. This clock operates in the presomitic mesoderm (PSM), generating dynamic stripe patterns of oscillatory gene-expression across the field of PSM cells. How these spatial patterns, the clock’s collective period, and the underlying cellular-level interactions are related is not understood. A theory encompassing temporal and spatial domains of local and collective aspects of the system is essential to tackle these questions. Our delayed coupling theory achieves this by representing the PSM as an array of phase oscillators, combining four key elements: a frequency profile of oscillators slowing across the PSM; coupling between neighboring oscillators; delay in coupling; and a moving boundary describing embryonic axis elongation. This theory predicts that the segmentation clock’s collective period depends on delayed coupling. We derive an expression for pattern wavelength across the PSM and show how this can be used to fit dynamic wildtype gene-expression patterns, revealing the quantitative values of parameters controlling spatial and temporal organization of the oscillators in the system. Our theory can be used to analyze experimental perturbations, thereby identifying roles of genes involved in segmentation.

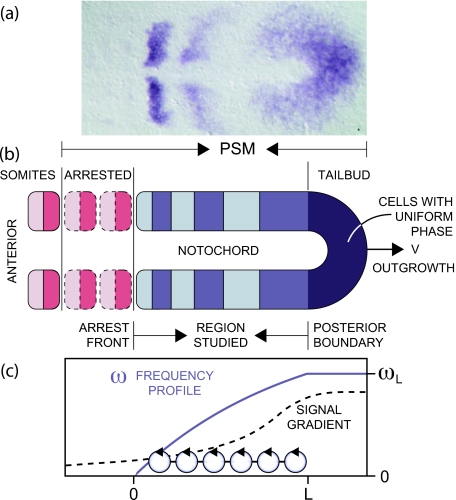
During vertebrate development, segmentation of the continually elongating embryonic body axis occurs rhythmically and sequentially from head to tail in a process termed somitogenesis (Wolpert et al., 2006). Somites are regularly sized cell clusters that bud off periodically from the anterior end of the posterior-most unsegmented tissue, the pre-somitic mesoderm (PSM), with a species-specific frequency. These transient, left-right symmetric structures are the embryonic precursors of adult bone and muscle segments, and defects in their formation lead to congenital birth defects (Bulman et al., 2000). Underlying the morphogenetic rhythm of somitogenesis, repeated waves of oscillating gene expression sweep through the cells of the PSM from the posterior to the anterior (Palmeirim et al., 1997), see Fig. 1a and Supplementary Movie 1. These genetic oscillations are thought to slow down and arrest at different phases of their cycles at an anteriorly positioned arrest front that moves in concert with embryonic elongation (Dubrulle et al., 2001) [Fig. 1b], translating the temporal periodicity into a striped spatial pattern of gene expression.

Figure 1. Representation of the PSM. Anterior is to the left and posterior to the right.

(a) In situ hybridization (Oates and Ho, 2002) showing the expression of deltaC mRNA in the zebrafish PSM (dorsal view). (b) Schematic PSM together with the already determined segments—arrested—and the most recently formed pair of somites. The studied region lies between the arrest front and the posterior end of the notochord. (c) Schematic representation of the signal gradient spanning the PSM (broken line). The frequency profile ω related to this gradient is depicted as solid purple line, using Eq. 2 with the width σ given in Table 1. The length of the studied region is denoted by L. A linear array of N coupled oscillators is indicated.

Given the existence of genetic oscillators in the cells of the PSM (Hirata et al., 2002; Masamizu et al., 2006), several questions still remain unanswered: how does a collective segmentation period arise from the population of individual oscillators, and what is the relation between the overall pattern of gene expression observed in the PSM and the oscillating expression at the cellular level. To investigate this, we develop a theoretical description based on phase oscillators and four key ingredients motivated by the biology: (i) a frequency profile along the PSM, slowing down the oscillations; (ii) coupling of oscillators; (iii) a time delay in the information transfer between neighboring oscillators; and (iv) the existence of a moving front that arrests the oscillations at the anterior end of the PSM, while the posterior end moves due to embryonic outgrowth. This delayed coupling theory provides an excellent fit to the existing biological data, allows perturbations to the system to be analyzed in terms of underlying processes, and predicts how intercellular communication affects the collective period of the segmentation clock. Below, we introduce the elements of the delayed coupling theory.

Phase oscillators

To provide a simple picture of the segmentation process, Cooke and Zeeman proposed a clock and wavefront model more than 30 years ago (Cooke and Zeeman, 1976). However, to understand the role of collective processes in the emergence of dynamic gene expression patterns in the PSM a more detailed analysis is needed, for which methods from other pattern forming systems can be borrowed (Cross and Hohenberg, 1993). In particular, the periodic expression of genes in the oscillating PSM cells can be described at tissue level using a set of phase oscillators, disregarding at this stage the underlying biochemical and genetic mechanisms that generate the oscillations and their pattern. In this phase description, each cell, or group of synchronous cells, is represented by an oscillator, and the state of each oscillator is characterized only by its phase in the cycle of periodic gene expression. Oscillators with the same phase represent cells with equivalent expression level of cyclic genes. Previous models described the PSM as a continuous oscillatory medium with a phase defined at each point of the PSM, see Supplementary data of Palmeirim et al. (1997) and Kaern et al. (2000), Jaeger and Goodwin (2001), Giudicelli et al. (2007), Gomez et al. (2008). In this work we show that a phase description is sufficient to compute the overall spatiotemporal patterns of gene expression and the collective period of the oscillations.

Frequency profile

It has been suggested that the arrest of the oscillations and the observed oscillating gene expression patterns are shaped by a spatial dependence of the frequency of the individual oscillators (Palmeirim et al.; 1997, Kaern et al., 2000; Jaeger and Goodwin, 2001; Giudicelli et al., 2007; Gomez et al., 2008). A frequency profile could be controlled by the molecular gradients observed in the PSM, see Fig. 1c, e.g., the gradients of the growth factor FGF (Dubrulle et al., 2001; Sawada et al., 2001; Dubrulle and Pourquié, 2004; Wahl et al., 2007) or of Wnt signaling (Aulehla et al., 2003; 2008). Several models have recently proposed regulatory mechanisms by which the genetic oscillations are affected by the gradients of signaling molecules along the PSM (Cinquin, 2007; Tiedemann et al., 2007; Santillán and Mackey, 2008; Mazzitello et al., 2008). Motivated by the changing width of the stripes of gene expression in the PSM and the necessity that the oscillations slow down and finally stop at the arrest front, we include such a frequency profile in our theory. As with the assumption of cellular oscillators, our theory does not rely on the molecular origin of this frequency profile, and hence, its inclusion is purely phenomenological.

Coupling of oscillators

Recent theoretical works seeking to describe spatiotemporal patterns in somitogenesis using phase oscillators have not included coupling between oscillators (Kaern et al., 2000; Jaeger and Goodwin, 2001; Giudicelli et al., 2007; Gomez et al., 2008), although intercellular coupling has been considered in reduced models of regulatory circuits (Lewis, 2003; Cinquin, 2003; Horikawa et al., 2006). Here, coupling means that oscillators can influence the phase of their neighbors. Coupling is essential to stabilize tissue-scale patterns against the unavoidable noise present in biological systems (Jiang et al., 2000; Horikawa et al., 2006; Riedel-Kurse et al., 2007; Özbudak and Lewis, 2008), and also to explain the resynchronization of surgically inverted pieces of the PSM (Dubrulle et al., 2001). Thus, in this work we propose a description based on coupled phase oscillators.

Time delay

Coupling between cells via signaling macromolecules, e.g., through the Notch pathway (Jiang et al., 2000; Horikawa et al., 2006; Riedel-Kruse et al., 2007; Özbudak and Lewis, 2008), involves synthesis and trafficking of such molecules within cells. These dynamics imply the existence of time delays, which have been recently estimated to be in the range of tens of minutes in cell culture (Heuss et al., 2008). Time delays in the coupling can have an impact on the self-organization of coupled oscillators (Schuster and Wagner, 1989; Niebur et al., 1991; Yeung and Strogatz, 1999; Earl and Strogatz, 2003; Lewis, 2003), making their inclusion in our theory important. For simplicity, we will use here a deterministic time delay; a more realistic description would include a distribution of delays (MacDonald, 1989).

Moving borders due to embryonic elongation

The embryo is a rapidly growing system, elongating about one somite length per oscillation cycle, which takes around 25 min in zebrafish, 90 min in chick, and 120 min in mouse. Cells are continuously in transit from the tailbud through the PSM, exiting it anteriorly as somites form. Additionally, cell proliferation plays a role during elongation, but since in the PSM it has a stochastic character it can be considered as a potential noise source (Horikawa et al., 2006) not otherwise significantly affecting the oscillatory dynamics (Zhang et al., 2008), and we do not consider it further here. To correctly understand the formation of patterns of gene expression and how the frequency is regulated, it is necessary to consider the geometry and boundaries of the arena in which the process occurs. Here, we neglect changes in the antero-posterior length of the PSM or the rate of axial growth, which occur during development at time scales larger than the somitogenesis period (Tam, 1981; Schröter et al., 2008; Gomez et al., 2008). Consequently, both the arrest front and the posterior boundary move at the same velocity v, see Fig. 1b.

RESULTS

This section contains technical details of our theory. Readers who are more interested in the basic ideas and the biological justifications should note that a careful understanding of the equations is not a requisite to follow the arguments we introduce in this section.

Formulation of the delayed coupling theory

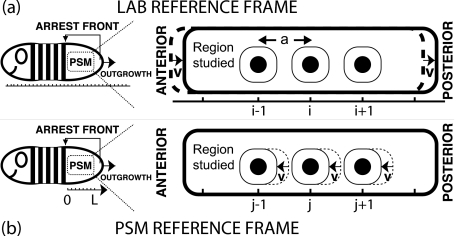
Our model equations in the lab reference frame, Fig. 2a, consist of a lattice of discrete phase oscillators. This lattice comprises N oscillators in the antero-posterior direction, labeled by an index i. Each oscillator occupies a positionx_i=ia along the PSM axis in the lab reference frame, wherea is the characteristic distance between oscillators, i.e., the average cell diameter. Hence, the total physical length of the considered system in the antero-posterior direction is L≡Na.

Figure 2. Two different coordinate systems to describe genetic oscillations in the PSM.

(a) Lab reference frame: oscillators labeled by index i hold fixed positions x_i=ia, where a is the distance between oscillators. The PSM boundary moves posteriorly with velocity v as the embryo extends. (b) PSM reference frame: the PSM boundaries do not move but oscillators move through the PSM from posterior to anterior with velocity v. Oscillators are constantly relabeled using symbols j to denote discrete positions relative to the arrest front. Dashed lines indicate the state of the system at slightly earlier times.

As the embryo elongates with velocity v, the arrest front is positioned at vt, where t is time. Oscillators anterior to the arrest front, x_i⩽vt, are arrested. New oscillators are added at the posterior boundary, situated at vt+L, as elongation proceeds. The oscillators in the studied region, with indices vt∕a⩽i<(N+vt∕a) are weakly coupled to their n nearest neighbors, denoted by the index k. In one dimension n=2, while in a two-dimensional square lattice n=4. The phase dynamics of the coupled oscillators can be described by

$${\dot{\theta }}_i\left(t\right)={\omega }_i\left(t\right)+\frac{{\epsilon }_i\left(t\right)}{n{a}^2}\sum _k\sin [{\theta }_k(t-{\tau }_i\left(t\right))-{\theta }_i\left(t\right)]+{\zeta }_i\left(t\right),$$ (1)

where the dot denotes time derivative, θ_i is the phase of oscillator i, ω_i is its intrinsic frequency, ε_i is the coupling strength, τ_i is the time delay in the coupling, and ζ_i is a random variable with zero average representing different noise sources. Our objective in this work is to characterize the basic model in the synchronized state, and if not otherwise stated, we ignore the effects of noise. According to experimental evidence (Riedel-Kruse et al., 2007), coupling strength is weak compared to other time scales in the system. This justifies the use of the sine function in the coupling, as it is the dominant term of any more general periodic coupling function (Kuramoto, 1984).

To specify the shape of the frequency profile we choose, for vt∕a⩽i<(N+vt∕a),

$${\omega }_i\left(t\right)={\omega }_{\infty }(1-e^{-(ia-vt)∕\sigma }),$$ (2)

where ω_∞ is a characteristic frequency scale of individual oscillators, and σ is a measure of the characteristic distance over which the frequency profile decreases from high to low values [see Fig. 1c]. Below we will show that our choice of Eq. 2 is consistent with experimental observations, and we will determine σ from the width of the stripes of gene expression in the PSM. Qualitatively similar choices for the frequency profile have been used before (Kaern et al., 2000; Jaeger and Goodwin, 2001). For simplicity, we have chosen the frequency to be strictly zero at the arrest front. Note, however, that this is not biologically necessary: a very low value of the frequency at the arrest front means a very large period of oscillation. If this period is much larger than any other time scale involved in the process, it determines in practice an arrested oscillation, which can specify the downstream fixed pattern that eventually sets the position of somite boundaries. Furthermore, since the oscillations can be coupled to a bistable system arising from opposing signaling gradients in the PSM, long period oscillations at the arrest front could be stopped by a bistable transition (Goldbeter et al., 2007; Santillán and Mackey, 2008).

For convenience we introduce the parameter ω_L≡ω_∞(1−e^−L∕σ), that represents the intrinsic frequency of the oscillators at the posterior boundary of the system. Based on in situ experiments that show a largely uniform spatial expression of cyclic genes in the tailbud at any given stage of the cycle [Fig. 1a], we define a uniform phase [Fig. 1b] and homogeneous frequency ω_L [Fig. 1c] in the tailbud, posterior to the notochord and the region we study here. This homogeneity would be favored by the strong cell mixing (Mara et al., 2007), and high, potentially saturating uniform levels of the signaling molecules that establish the gradient anterior to this region (Sawada et al., 2001;Dubrulle et al., 2001; Dubrulle and Pourquié, 2004; Wahl et al., 2007; Aulehla et al., 2003, 2008). Furthermore, the shape of ω_i described by Eq. 2 resembles the posterior branch of FGF receptor saturation proposed in Goldbeter et al. (2007).

The coupling could also be position dependent. In particular, since the oscillators anterior to the arrest front stop cycling, they can not influence the active oscillators in the interval vt∕a⩽i<(N+vt∕a). We take this into account imposing ε_i=ε₀=0 for i<vt∕a. For simplicity, in this work we consider the coupling strength ε_i≡ε and the time delay τ_i≡τ to be constant posterior to the arrest front.

Numerical simulations in two dimensions

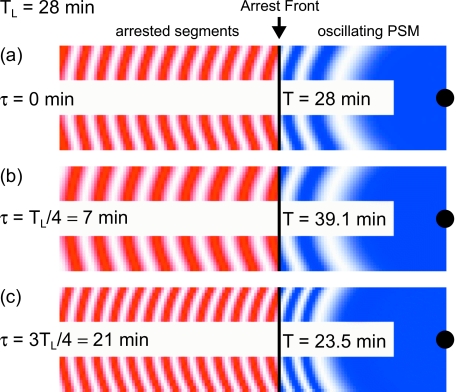
To gain insight into the role of delayed coupling in setting the period and the pattern of the genetic oscillations, as well as to illustrate the formation of realistic wave patterns within our theory, we performed computer simulations of Eq. 1 in a two-dimensional geometry using different values of the time delay (Fig. 3 and Supplementary Movies 2, 3, and 4). Although the theory represents generic vertebrate segmentation, here we use parameters from the zebrafish embryo, Table 1. For the intrinsic frequency at the posterior we chose ω_L=0.224 min⁻¹, corresponding to an intrinsic period ofT_L=2π∕ω_L=28 min. We show simulations with no time delay (τ=0 min), a short delay compared to the intrinsic period (τ=T_L∕4=7 min), and a long delay close to the intrinsic period (τ=3T_L∕4=21 min). The latter is consistent with the experimental observation of tens of minutes for intercellular communication times (Heuss et al., 2008).

Figure 3. Numerical simulation of segmentation using Eq. 1 in a growing two-dimensional geometry.

Color intensity indicates the value of sin θ of the phase θ: white is sin θ=1 and dark (red or blue) is sin θ=−1. Vertical line indicates the position of the arrest front, with the oscillating PSM to its right (blue) and the arrested pattern to the left (red). Intrinsic frequency is a decaying function of the distance to the black dot at the posterior boundary, causing the curvature of the stripes. Open boundary conditions are used in the lateral borders: no coupling is considered to cells outside the simulated geometry. We have used parameters determined for zebrafish at 28 °C, see Table 1, and ω_L=0.224 min⁻¹, see main text for details. We have chosen to display three illustrative values of the time delay (a) τ=0 min, (b) τ=T_L∕4≈7 min, and (c) τ=3T_L∕4≈21 min. Delayed coupling affects the collective frequency of oscillations according to Eq. 5. The stripes of the oscillating PSM pattern and the segment length of the frozen pattern change accordingly. Movies available as Supplementary Material.

Table 1.

Parameters of the delayed coupling theory and their values in zebrafish embryo at 28 °C near the ten somite stage. The first five parameters have been determined before or come from our observations. PSM length L and decay length of the frequency profile σ come from fits of our theory to experimental data in Giudicelli et al. (2007). The parameters ω_L and τ could not be determined independently in this work, but they are related by Eq. 5. Note that parameters change with temperature and throughout development (Schröter et al., 2008). We choose as length unit one cell diameter (cd), in terms of which the distance between neighbor oscillators is a=1 cd.

T	Period of somite formationa	23.5 min
Ω	Collective frequency, 2π∕T	0.267 min−1
S	Somite size (our own experimental estimation)	6 cd
v	Velocity of the arrest front, v=S∕T	0.255 cd min−1
ε	Coupling strengthb	0.07 cd2 min−1
L	PSM length	39 cd
σ	Decay length of the frequency profile	36 cd
τ	Time delay	Not determined
ωL	Intrinsic frequency in the posterior PSM

^aSchröter et al. (2008).

^bRiedel-Kruse et al. (2007).

Figure 3a shows a snapshot of the simulation with no time delay. Not surprisingly, the collective period—the time needed to form one new arrested segment, and also the time after which the oscillating pattern in the PSM repeats itself—is unchanged with respect to the intrinsic period at the posterior. The arrested segments have a length of S≈7 cell diameters. The case of short delay with respect to the period, τ=T_L∕4, qualitatively represents the situation in species with a relatively long segmentation period, such as mouse. Figure 3b shows that in this case, the effect of the delay in coupling is to slow down the collective period (T=39.1 min) with respect to the intrinsic period (T_L=28 min). Further, the arrested segments are longer (S≈10 cell diameters) than in the case without delay, and there is a smaller number of gene expression stripes in the PSM, with increased size. Surprisingly, when the delay is made longer, the trends observed with the short delay are inverted. Figure 3c shows that for the time delay of τ=3T_L∕4, the collective period (T=23.5 min) is shorter than the intrinsic period. Moreover, the arrested segments are also shorter (S≈6 cell diameters) than in both previous cases, as are the stripes of oscillating gene expression in the PSM.

This puzzling results show that delayed coupling introduces nontrivial effects to the system, large enough to be observable in real experiments. In order to understand these effects, in the following we perform an analysis of Eq. 1, studying first the emergence of the collective period from the parameters of the theory and then turning our attention to the spatial pattern. For this purpose, we will write Eq. 1 in a more convenient manner.

PSM reference frame

It is useful to consider the dynamics in the PSM reference frame, Fig. 2b, where the oscillations can be characterized by a stationary phase profile and a collective frequency. For simplicity from here on we use a one dimensional description of the system, with n=2. In the lab reference frame [Fig. 2a] the symbol i represents a fixed oscillator. In the PSM reference frame [Fig. 2b] we introduce the symbol j to label fixed discrete positions relative to the arrest front. The label j runs from j=0 at the arrest front to j=N at the posterior boundary of the PSM. Discrete position j is occupied by different oscillators as the system evolves in time. For convenience we have included in the description the last arrested oscillator, j=0.

In the PSM reference frame, the frequency profile is stationary, ω_j=ω_∞(1−e^−ja∕σ). Reexpressing Eq. 1 in this PSM reference frame, an extra term describes the drift of the phase due to the movement of the cells relative to the PSM boundaries. The resulting phase dynamics are given by

$${\dot{\phi }}_j\left(t\right)={\omega }_j+v[{\phi }_{j+1}\left(t\right)-{\phi }_j\left(t\right)]+\frac{\epsilon }{2a^2}\sum _{k=j+p\pm 1}\sin [{\phi }_k(t-\tau )-{\phi }_j\left(t\right)].$$ (3)

Here φ_j is the phase at position j relative to the arrest front and p=[vτ∕a] is the nearest integer to vτ∕a, representing the distance a cell moves during the time it takes for a signal from a neighbor to arrive. Note that now the coupling is nonlocal: due to the time delay and cell movement, the neighbors of an oscillator with position j had positionsj+p+1 and j+p−1 at the time the signal was sent.

Steady state ansatz and collective frequency

The oscillating gene expression pattern in the PSM repeats after a full period T=2π∕Ω of oscillation (Palmeirim et al., 1997; Masamizu et al., 2006), where Ω is the collective frequency of the oscillation. This leads to the steady state ansatz φ_j(t)=Ωt+ϕ_j, where ϕ_j is the stationary phase profile describing the pattern in the PSM. With this ansatz we obtain from Eq. 3,

$$\Omega ={\omega }_j+v[{\varphi }_{j+1}-{\varphi }_j]+\frac{\epsilon }{2a^2}\sum _{k=j+p\pm 1}\sin [{\varphi }_k-{\varphi }_j-\Omega \tau ].$$ (4)

The collective frequency of oscillations Ω is equivalent to the rate of somite formation. Note that the instantaneous frequencies ${\dot{\theta }}_i$ of individual oscillators depend on position and are in general different from Ω.

Anterior boundary condition sets the segment length

To determine the collective frequency Ω we need to specify the boundary conditions, namely the conditions that ϕ_j fulfills at the borders of the studied region [j=0 and j=N, Fig. 1b]. This boundary should not be confused with somite boundaries, which we do not discuss in this paper.

At the arrest front (j=0), the fact that ω₀=0 and ε₀=0 implies with Eq. 4 that (ϕ₁−ϕ₀)=Ω∕v=2π∕vT. Thus, the anterior boundary condition determines the wavelength of the arrested pattern, which is the segment lengthS=2π∕(ϕ₁−ϕ₀)=vT: the segment length is the distance advanced by the arrest front during one oscillation period (Cooke and Zeeman, 1976).

Coupling and delay affect the collective period

At the posterior boundary of the PSM, we assume that new cells are added into the system with phase ϕ_N. To implement this we impose in Eq. 4p boundary conditions, ϕ_j=ϕ_N for j=N+1,…,(N+p), accounting in this way for the effective nonlocality of the coupling. We base this choice on the experimental observation of cyclic gene mRNA patterns, which maintain a smooth expression profile, and hence, approximately homogeneous phase, across the interface between tailbud and posterior PSM [e.g., Fig. 1a].

Substituting the posterior boundary condition ϕ_N+1=ϕ_N in Eq. 4 we obtain a relation for the collective frequency of oscillations [see also (Schuster and Wagner, 1989; Niebur et al., 1991; Yeung and Strogatz, 1999; Earl and Strogatz, 2003)],

$$\Omega ={\omega }_L-\epsilon \sin \left(\Omega \tau \right).$$ (5)

The solutions to this equation are shown in Figs. 4a, 4b. Results from numerical simulations of Eq. 1 in two spatial dimensions show that the collective frequency indeed fulfills Eq. 5, see blue dots in Fig. 4a.

Figure 4. Collective frequency Ω of somitogenesis as a function of time delay and coupling strength.

(a) Dimensionless collective frequency Ω∕ω_L and time delay τω_L are displayed for constant coupling ε=0.07 (cell diameter)² min⁻¹, and intrinsic frequency ω_L=0.224 min⁻¹. Analytical solutions of Eq. 5 shown as blue lines: solid lines stable solutions of Eq. 5, dashed lines unstable solutions of Eq. 5. Blue dots correspond to numerical integration of the discrete model in two dimensions as given by Eq. 1, for the three cases illustrated in Fig. 3. Red lines: collective frequency as a function of delay in the continuum limit, showing its ranges of validity. (b) Collective frequency Ω as a function of time delay for different coupling strengths obtained from the solution of Eq. 5 with ε=0.11 (cell diameter)² min⁻¹ (green), ε=0.07 (cell diameter)² min⁻¹ (blue), and ε=0.03 (celldiameter)² min⁻¹ (red). Solid lines are stable solutions, dashed lines are unstable solutions. Dotted line at Ω∕ω_L=1 corresponds to vanishing coupling, ε=0 (cell diameter)² min⁻¹.

For a given set of parameters ω_L, ε, and τ, Eq. 5 allows for multiple solutions for the collective frequency Ω. Independent measurement of coupling strength ε, collective frequency ω_L, and collective frequency Ω would allow the determination of possible values of the delay τ consistent with Eq. 5. Experimentally, this can be done studying situations where the intrinsic cellular oscillations are altered (modified ω_L) or where the coupling strength is altered (modified ε) and using the observed values of Ω to fit τ.

A linear stability analysis following (Yeung and Strogatz, 1999; Earl and Strogatz, 2003) reveals that when cos(Ωτ)>0 the solution to Eq. 5 is stable, and unstable otherwise, see continuous and dashed lines in Fig. 4. Consequently, multistability occurs for large values of ε and τ. As seen in Fig. 4a, for the biologically plausible parameters that we use in the figure, there is a small gap of time delay values between the first and the second stable branches of the solution. This happens around τω_L=π, which means that the delay is close to half the intrinsic period of the cellular oscillators in the posterior PSM, τ≈T_L∕2≡π∕ω_L. For the parameters in Fig. 4a, larger values of the delay always involve at least one stable solution. Note that values of the collective frequency equal to the intrinsic frequency, Ω=ω_L, are only possible for delays equal to integer and semi-integer multiples of the intrinsic period T_L: these solutions are stable in the case of integer multiples (τ=integer×T_L) and unstable in the case of semi-integer multiples (τ=(integer+1∕2)×T_L). However, stable solutions are possible for these latter delays, albeit with the collective frequency Ω different than the intrinsic frequency ω_L.

Equation 5 provides an explanation for the non-monotonic behavior of the collective period observed in Fig. 3. Moreover, the simulation results coincide quantitatively with the prediction of Eq. 5, as shown by the three dots in Fig. 4a. Equation 5 is biologically relevant: the collective frequency or period of somitogenesis emerges as a self-organized property and depends not only on the intrinsic frequency of individual cells, but also on the coupling strength and the time delay (Fig. 4). Note that Ω does not depend on the specific shape of the frequency profile, and the period is set by the uniform phase cell population in the tail, which is the pacemaker of the whole oscillatory process.

Delayed coupling keeps the oscillations synchronized

We have seen how the presence of time delay in the coupling can have an important effect in the spatiotemporal patterns of gene expression. A critical biological function of intercellular coupling is to keep neighboring cells oscillating in synchrony (Jiang et al., 2000; Horikawa et al., 2006; Riedel-Kruse et al., 2007; Özbudak and Lewis, 2008). To demonstrate that delays in the coupling allow this function, and to showcase the role of noise in our theory, we simulate the phenotype of a class of mutant embryos in which coupling is strongly reduced (Jiang et al., 2000; Riedel-Kruse et al., 2007). To do this we include an additive white Gaussian noise in the simulations, with zero mean and correlations ⟨ζ_i(t)ζ_k(t^′)⟩=2Qδ(t−t^′)δ_ik, and choose $\sqrt{2Q}=0.036{\min }^{-1}$ for illustrative purposes. With coupling as in Table 1, the process is not disrupted by noise, Fig. 5a and Supplementary Movie 5. When coupling is disrupted, the simulation exhibits posterior segmentation defects, Fig. 5b and Supplementary Movie 6, resembling Delta–Notch mutant phenotypes in zebrafish (Holley et al., 2000, 2002; Itoh et al., 2003; Jülich et al., 2005; Oates et al., 2005). A more subtle feature of Fig. 5b is the change in segment length after coupling has been disengaged. As soon as the coupling is removed, the effects of time delays are no longer present, and cells can oscillate at their intrinsic frequencies. Because at the time the coupling is turned off there is an established pattern in the oscillating PSM, it takes a few cycles for this information to be wiped out and to reach the new steady state value of the segment length.

Figure 5. Effects of noise in the delayed coupling theory.

We include a white Gaussian noise as discussed in the text. Open boundary conditions for the lateral borders as in Fig. 3. (a) Delayed coupling is robust against the influence of noise. Parameters as in Fig. 3b. (b) Impaired coupling results in segmentations defects. After initial synchronization with resulting segments not shown, coupling is turned off (ε=0 (cell diameter)² min⁻¹). The first segments have recognizable boundaries, but posterior segments are increasingly disrupted due to the effect of noise. Parameters as in (a). Movies available as Supplementary Material.

Although out of the scope of this work, our model provides a simple framework to study the effects of different kinds of noise on segmentation. This interesting possibility remains open for future work.

Spatial patterns of gene expression

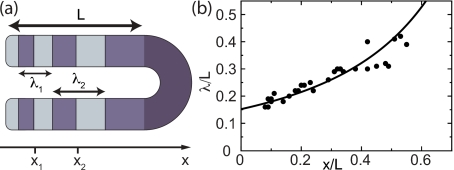
While the collective frequency Ω describes the temporal regularity of somitogenesis, the spatial pattern of gene expression in the PSM is characterized by the phase profile ϕ_j. To evaluate the phase profile it is convenient to introduce a continuum limit where the spatial coordinate takes continuous values, denoted by x, replacing the discrete index j, see the Methods section. The stationary phase profile ϕ(x), see Fig. 6a, can be compared to quantitative experimental measurements of the pattern, such as the width of the stripes of gene expression reported in Giudicelli et al. (2007). We define the wavelength λ as the distance of two points in the PSM with a phase difference of 2π, see Fig. 7a. The wavelength is large close to the tail and becomes smaller close to the arrest front where it matches the segment length. Using the continuum formalism we find an expression for the dependence of λ with the position x of the stripe’s center relative to the arrest front

$$x\approx \sigma \log \left[\frac{\sinh (\lambda ∕2\sigma )}{\pi {\nu }^{-1}{(1+\eta )}^{-1}+(\lambda ∕2\sigma )e^{-L∕\sigma }}\right].$$ (6)

Here, ν and η are dimensionless parameters relating intrinsic frequency, coupling, time delay, elongation speed, and the frequency profile, as defined in the Methods section. In Fig. 7b we show the fit of Eq. 6 to the wavelengths obtained from the raw data in Giudicelli et al. (2007): distances between consecutive points with equal level of her1 expression in zebrafish embryos around the ten somite stage andraised at 28 °C. The equation fits very well to the data, showing that our choice of Eq. 2 for the frequency profile is consistent with observations.

Figure 6. Phase profile in the PSM in the continuum limit.

(a) Phase profile as a function of relative position, given by Eq. 11. Left axis: phase relative to the arrest front. Right axis: corresponding number of gene expression stripes. The green solid line corresponds to the set of parameters obtained from zebrafish data, see Table 1, using T_L=28 min and τ=21 min for illustration. Orange dotted line corresponds to σ=6 cell diameters. (b),(c) Wave form of the expression pattern represented as sin ϕ. (d) Number of stripes in the PSM as a function of σ from Eq. 7, where σ is the parameter describing the decay length of the frequency profile. Black solid line corresponds to parameters in Table 1, with σ variable. Green square dot: σ obtained from zebrafish data, see Table 1. Orange circular dot: mouse mode, see orange dotted curve in (a),(c). Dotted and dashed curves correspond to higher and lower values of collective frequency, which can potentially be affected by the intrinsic frequency, the coupling strength, or the time delay, see Eq. 5. (e),(f) Numerical simulations using the methods of Fig. 3. (e) Zebrafish mode, reproducing panel (c) of Fig. 3 for comparison with panel (f). (f) Mouse/chick mode: zebrafish parameters as in (e), but with a sharper frequency profile, σ=6 cell diameters. Only one wave of expression appears in the PSM, in contrast to the almost three waves in (e). Movies available as Supplementary Material.

Figure 7. Wavelength of the pattern as a function of the position x in the PSM.

L is the length of the part of the PSM considered. (a) Schematic representation of the wavelength λ. (b) Fit of Eq. 6 to the experimental data obtained from wildtype zebrafish in Giudicelli et al. (2007). Best fit parameters are μ=1.08 and ν(1+η)=57.8. (μ, ν, and η are dimensionless quantities defined in the Methods section.)

Parameter values

From the fit to data obtained from wildtype zebrafish shown in Fig. 7b we determine L∕σ=1.08 and ν(1+η)=57.8. We estimate the parameters L and σ using the definitions of ν and η and the measured values of T and S, see Table 1. Time delay affects both the collective frequency and the wavelength of the gene expression patterns. As we show in the Methods section, delayed coupling introduces a renormalization of both frequency and coupling strength. The effects of the time delay are thus included in the dimensionless renormalized parameters of Eq. 6, but the fit of spatial gene expression patterns does not allow the separation of the contribution of the time delay from that of the intrinsic frequency, and hence, these two parameters remain undetermined from this fit. The intrinsic frequency at the posterior ω_L, and the time delay τ, are related through Eq. 5. Thus, experimental determination of one would suffice to calculate the other if the coupling strength and collective frequency are known.

From our estimated parameters in Table 1 the value of the frequency ω_L can be up to 30% higher or lower than the collective frequency Ω, see Fig. 4a. For an intrinsic period T_L=2π∕ω_L around 28 min, this implies that changing delay time could situate the collective period in a range between 21 and 40 min, in qualitative agreement with the magnitude of period change from simulations of the genetic regulatory network model in Lewis (2003) for two coupled cells (Leier et al., 2008). Note that this period change is only possible due to the presence of delays in the coupling, both in our theory [see Eq. 5] and in the model in Leier et al. (2008). This difference in period is large and should be accessible to experimental observation, allowing at the same time for numerical determination of the values of the time delay τ and the intrinsic frequency ω_L.

DISCUSSION

We have constructed a phenomenological theory describing the tissue-level dynamics of the vertebrate segmentation clock employing phase oscillators to represent cyclic gene expression in the cells of the PSM. As key ingredients of the theory, we considered: (i) the existence of a frequency profile; (ii) coupling between oscillators; (iii) time delay in this coupling; and (iv) moving boundaries corresponding to embryonic elongation and the moving arrest front. Although these four elements have been considered before, here we combine them in a unified framework. In this theory, tissue-level phenomena are generated by the interaction of cellular properties. For example, the collective frequency of oscillation of the PSM, related to the segmentation rate, depends on the intrinsic frequency at the posterior, the coupling strength and the time delay in the coupling, Eq. 5; the spatial wavelength of gene expression stripes in addition depends on the shape of the frequency profile. Knowledge of the molecular underpinnings is not necessary for this mesoscopic description. By fitting the phase profiles obtained in our continuum limit to the existing data from a vertebrate embryo, we obtained a description of the tissue- and cellular-level processes controlling period and pattern in the system that is both quantitative and predictive. This framework can now be used to analyze experimental and evolutionary variants of embryonic segmentation or other permutations of growing, oscillating systems.

Note that the basic relationship of a clock and wavefront type model for embryonic segmentation, as initially proposed by Cooke and Zeeman (1976), is that the length of a segment is the product of the arrest wavefront velocity and the period of the clock. In our description the population of oscillators create a pattern with a collective frequency, that together with the movement of the arrest front gives rise to a segment length consistent with the clock and wavefront picture.

Variation of stripe patterns for different animal species

We have compared our theory to zebrafish data, but it applies equally well to other vertebrate species, since it does not involve species-specific details. The difference between what is termed a zebrafish mode of oscillation in somitogenesis and a mouse∕chick mode, observed also in medaka (Gajewski et al., 2006), can be characterized as follows: in the zebrafish mode, several waves of gene expression sweep simultaneously through the PSM, i.e., multiple stripes of expression are detected in in situ experiments; in mouse∕chick mode, only one wave is observed. The zebrafish mode applies also to snakes, where up to nine waves of gene expression have been observed (Gomez et al., 2008). Within our theory these different modes are characterized by the phase difference between the arrest front and the posterior border: the number of stripes of gene expression in the PSM is (ϕ(L)−ϕ(0))∕2π, see Figs. 6a, 6b, 6c. From Eq. 11 in the Methods section we find

$$\text{Number}\text{of}\text{stripes}\approx \frac{\sigma }{vT}-\frac{L}{(e^{L∕\sigma }-1)vT}=\frac{1}{\mu s}-\frac{1}{(e^{\mu }-1)s}.$$ (7)

This expression can be written as a function of only two dimensionless parameters: the ratio μ=L∕σ between the system length and the decay length of the frequency profile and the ratio s=S∕L=vT∕L between the segment length and the system length. The number of stripes is a decreasing function of both these ratios: smooth frequency profiles with long decay lengths, as well as small segment lengths, favor a large number of stripes of gene expression, as in the zebrafish mode, see Fig. 6d. The coupling strength and time delay do not appear in Eq. 7 because we have neglected for simplicity higher order terms in ε where they show up explicitly. Note, however, that the collective period T=2π∕Ω in Eq. 7 does depend on both the coupling strength and the time delay through Eq. 5, see Fig. 6d. Thus, in the same way that it may modify the collective period (as discussed in the parameter values section), the effect of delayed coupling can vary up to 30% the number of stripes of gene expression observed in the PSM compared to a system without coupling, see Fig. 3.

A similar formalism for calculating the number of stripes has recently been published as Supplementary Material in Gomez et al. (2000). The underlying theory was previously proposed in Kaern et al. (2000) and Jaeger and Goodwin (2001), and is the same as our continuum theory (see Methods), but without coupling, and hence, without the effects caused by the delay in the coupling. However, in Gomez et al. (2008) no explicit choice for the shape of the frequency profile is made, hence, the resulting formula for the number of stripes is a function of an unknown integral, rather than a closed formula. Our Eq. 7 allows for direct quantitative comparison with data. The choice of Eq. 2 for the frequency profile comes from phenomenological observations and it is not derived from the underlying molecular interactions of the signalling gradients with PSM cells. Nevertheless, our function for the frequency profile is well supported by experimental data, see Fig. 7.

It is important to note that a switch between modes can be achieved while preserving the timing of somitogenesis by changing the shape of the frequency profile: in Fig. 6f we show results of simulations of a mouse mode in zebrafish with all parameters given as in Table 1 except for σ, which is 6 cell diameters instead of 36 cell diameters, see also Supplementary Movie 7. This implies that the number of stripes can change by changing the shape of the frequency profile while leaving the collective period and segment length unaffected. Previous hypotheses for the different modes include changes in period, loss of stripe specific cyclic gene enhancers, changes to the stability of cyclic mRNA or different elongation velocities (Gajewski et al., 2006; Holley, 2007; Elmasri et al., 2004; Gomez et al., 2008). The delayed coupling theory indicates that changes to the frequency profile, potentially through changes to FGF or Wnt signaling gradients in the PSM, and different sizes of the PSM must be considered as well. This is consistent with recent experiments reported in Aulehla et al. (2008), where extra stripes of gene expression appear in a mutant with an expanded PSM.

Relation to regulatory network models

Current regulatory network models for the genetic oscillations in somitogenesis (Jensen et al., 2003; Lewis, 2003; Monk, 2003; Cinquin, 2007; Rodríguez-González et al., 2007; Goldbeter and Pourquié, 2008), undergo a Hopf bifurcation—a generic mechanism by which oscillations can appear in a dynamical system—when varying some parameters of the models, as for instance the transcriptional delays (Bernard et al., 2006; Tiana et al., 2007; Feng and Navaratna, 2007; Verdugo and Rand, 2008; Momiji and Monk, 2008). Although it is also valid in more general settings, our Eq. 1 can be obtained as the phase equation associated to the normal form of a Hopf bifurcation when variations in the amplitude of the oscillations can be neglected, and as such it can in principle be derived from any of the dynamical systems associated with these regulatory networks following standard procedures (Hassard and Wan, 1978; Kuramoto, 1984; Nishii et al., 1994). Hence, our formulation represents a simplification that captures general features and properties of more detailed models.

The mechanism arresting the oscillations at the arrest front is a different problem not addressed in our present work. While the above mentioned models undergo a Hopf bifurcation when varying one of their parameters, something completely different (another kind of bifurcation triggered by the variation of a different parameter of the models, for instance) may be happening at the arrest front. The possibility that the oscillations are coupled to a bistable switch related to the signaling gradients in the PSM has been proposed (Goldbeter et al., 2007; Santillán and Mackey, 2008). In this scenario the arrest of the oscillators would not be a result of the intrinsic mechanism of the oscillations, but would result from an external signal.

Implications of multistability

Only stable solutions of our theory can be biologically relevant. In addition, we hypothesize that unique solutions are required to guarantee a robust behavior in the developing embryo. In the presence of multiple stable solutions for the collective frequency, fluctuations could drive the system to switch between these different states, with dramatic consequences for healthy development. For this reason, we conjecture that if several time delays are consistent with a fit to experimental data, those yielding a unique value of the collective frequency should be favored. Biochemical evidence indicates that coupling time delays should be relatively short compared to other signaling processes in the vertebrate segmentation clock (Heuss et al., 2008), thus likely precluding the observation of multistability in such an embryonic system. Multistability has been observed in other systems where coupling delays can be large, with applications in biochemistry (Casagrande et al., 2007), chemistry (Kim et al., 2001; Manrubia et al., 2004), control theory (Beta and Mikhailov, 2004), or laser physics (Wünsche et al., 2005; Franz et al., 2008), for example.

Applications in somitogenesis and comparison to experiments

Key quantitative experiments in vertebrate segmentation include determination of segmentation rates (Schröter et al., 2008), and the analysis of expression patterns from in situ experiments (Giudicelli et al., 2007) and fluorescent reporter genes (Masamizu et al., 2006). Our theoretical description allows for quantitative analysis of these experiments.

The comparison to experimentally observed dynamic patterns of gene expression permits the determination of the model parameters, which are provided for wildtype zebrafish in Table 1. Future studies in mutant embryos or embryos treated with different inhibitors will reveal which parameters are affected. The parameters in our model can be related to different cellular functions such as molecular synthesis and trafficking of intercellular signals (coupling delay τ); the strength of intercellular signaling (coupling strength ε); the speed of a cell autonomous oscillator (intrinsic frequency ω_L); changes in the signaling gradients responsible for the frequency profile (decay length σ); and changes in the position of the arrest front (reflected by the system length L). Thus, analysis of experimental results using our theory can provide a deeper understanding of how molecular changes lead to new phenotypes from the altered collective dynamics of tissues.

Our framework can be extended to other developmental processes that combine growth with a molecular clock. These are for instance fore-limb autopod outgrowth and patterning (Pascoal et al., 2007), or segmentation in short germ band insects, spiders, centipedes, and other invertebrates that might form segments by a mechanism similar to the one we described (Damens, 2007; Chipman and Akam, 2008).

Summary

The delayed coupling theory describes spatiotemporal patterns of gene expression during morphogenesis in agreement with experimental observations. Most importantly, our phenomenological theory provides a unified quantitative framework relating the segmentation period and cyclic patterns of gene expression to underlying properties, such as the characteristics of intercellular communication, cell autonomous oscillations, the spatial profile of the slowing of the oscillators in the PSM, the rate of axial growth, and the size of the PSM. Our results indicate that the specific spatial pattern of cyclic gene expression in the PSM does not affect the overall timing of somitogenesis, but intercellular communication should be considered as a fundamental mechanism in regulating the collective frequency of the segmentation clock.

METHODS

Continuum limit

Starting from Eq. 3 a continuum limit describing the evolution of the phase can systematically be derived for any value of the time delay. This continuum limit is valid when the typical length scale of the modulations of the pattern is much larger than the distance between oscillators, a. The limit is obtained by letting the distance a tend to zero, while the total number of oscillators N tends to infinite, in such a way that the length of the PSM, L=Na, remains finite and constant. In the continuum limit, we require a finite coupling strength ϵ_c≡lim_a→0ε∕a² to exist, which implies that ε scales as a².

The description based on discrete oscillators with phase φ_j(t) at a distance aj from the arrest front (where j is a discrete label) is substituted by a description defined in a continuous field spanning from x=0 to x=L, where x is a real positive value giving the distance to the arrest front of a point of the field with phase φ(x,t). The resulting continuum equation reads

$$\dot{\phi }(x,t)=\overline{\omega }\left(x\right)+v\nabla \phi (x,t)+\frac{{\overline{ϵ}}_c}{2}{\nabla }^2\phi (x,t),$$ (8)

where v is the velocity of the arrest front, ∇ denotes spatial derivatives (∇=(∂∕∂x) in one dimension, ∇=(∂∕∂x,∂∕∂y) in two dimensions, and so on), $\overline{\omega }\left(x\right)$ is a position dependent effective frequency given by

$$\overline{\omega }\left(x\right)=\omega \left(x\right)\frac{1+2\pi m{ϵ}_c∕{\omega }_L}{1+{ϵ}_c\tau },$$ (9)

and ${\overline{ϵ}}_c={ϵ}_c(1+2\pi m{ϵ}_c∕{\omega }_L)∕(1+{ϵ}_c\tau )$ is the effective coupling strength. The effect of the time delay appears through τ and m=[τω_L∕2π], the nearest integer to τω_L∕2π. In analogy with ω_j in the discrete case, the intrinsic frequency is defined as ω(x)=ω_∞(1−e^−x∕σ). Note that for simplicity we have assumed that the intrinsic coupling ϵ_c is constant throughout the PSM (as we did with ε); it is straightforward to include a positional dependence by substituting ϵ_c by ϵ_c(x) in all the previous expressions.

We can simplify Eq. 8 using the steady state ansatz φ(x,t)=Ωt+ϕ(x) as we did in the discrete case

$$\Omega =\overline{\omega }\left(x\right)+v\nabla \varphi \left(x\right)+\frac{{\overline{ϵ}}_c}{2}{\nabla }^2\varphi \left(x\right).$$ (10)

The boundary conditions for Eq. 10 are _{∣∇²ϕ(x)∣x=0}=0 and _{∣∇ϕ(x)∣x=L}=0. As in the discrete case, we assume that the phase is defined and uniform in the tailbud, ϕ(x>L)=ϕ(L). This implies that at x=L all the derivatives in Eq. 10 vanish and $\Omega =\overline{\omega }\left(L\right)$. In fact the right-hand side of Eq. 9 coincides with the expression for Ω obtained from solving Eq. 5 after linearization around values of the delay τ=2πm∕ω_L. In Fig. 4a we show in red the dependence of $\Omega =\overline{\omega }\left(L\right)$ with τ given by Eq. 9 for several values of m; note that almost the whole range of stable solutions of Eq. 5 (solid blue) can be well approximated by the continuum limit (red).

Equation 8 with $\overline{\omega }\left(x\right)$ given by Eq. 9 is valid when τ≈2πm∕ω_L for an integer m. A different equation can be obtained in the cases where τ≈2π(m+1∕2)∕ω_L: it corresponds to the continuum approximation of the unstable solutions of Eq. 5 shown by the broken blue lines in Fig. 4a.

Equation 10 can be solved and the corresponding phase profile reads

$$\varphi \left(\xi \right)=\nu {(1-\eta )}^{-1}\{(1-{\eta }^2)-\mu \xi [e^{-\mu }-\eta e^{-\mu ∕\eta }]+{\eta }^2{e}^{-\mu \xi ∕\eta }-e^{-\mu \xi }\},$$ (11)

where we have defined the dimensionless coordinate ξ=x∕L and parameters μ=L∕σ, $\nu ={\overline{\omega }}_{\infty }\sigma ∕v$, and $\eta ={\overline{ϵ}}_c∕2\sigma v$; ϕ(0) has been set to ϕ(0)=0 to fix an arbitrary constant. Figure 6a shows the shape of this phase profile.

The wavelength of the patterns of gene expression can be measured as a function of the relative position ξ. InGiudicelli et al. (2007) this is done experimentally, using a definition of the wavelength λ that in our notation can be expressed as the condition ϕ(ξ+λ∕2)−ϕ(ξ−λ∕2)=2π. In the limit of small coupling strength η⪡1, we obtain a simple relation between the local wavelength of the pattern λ and the position ξ along the PSM given by Eq. 6 of the main text.

SUPPORTING INFORMATION

Supplementary Movie S1.

Repeated waves of oscillating gene expression sweep through the cells of the PSM from the posterior (right) to the anterior (left). Each frame of the movie shows an in situ hybridization experiment from a different embryo detecting the expression of deltaC mRNA in the zebrafish PSM (dorsal view), at different phases of cyclic gene expression. For a better visualization of the wave pattern, set the loop option while viewing this cartoon.

Supplementary Movie S2.

Numerical simulation of segmentation using coupled oscillators in two dimensions with a geometry inspired by the real PSM shape. The arrested pattern is red, and the oscillating PSM is blue. Color intensity indicates the value of the sine of the phase: white is 1 and red/blue is -1. See text and Fig. 3 caption for further details. Parameters as in Table I, with ɷ_L=0.224 min^-1 and τ=0 min. See Figure 3a.

Supplementary Movie S3.

The same as Movie S2 but with τ=7 min. See Figure 3b.

Supplementary Movie S4.

The same as Movie S2 but with τ=21 min. See Figure 3c.

Supplementary Movie S5.

Numerical simulation of segmentation using coupled oscillators in two dimensions with a geometry inspired by the real PSM shape. Here we include Gaussian white noise in the instantaneous frequencies of individual cells, see text for details. Other parameters as in Movie S3. See Figure 5a.

Supplementary Movie S6.

The same as Movie S5, but coupling is turned off at the beginning of the Movie, when the arrest front is at the left-most boundary of the picture. See Figure 5b.

Supplementary Movie S7.

Numerical simulation of segmentation corresponding to a mouse mode in zebrafish. Parameters are the same as in Movie S3, but the decay length of the frequency profile is much smaller. Compare with Movie S3. See also Figure 6f.