Abstract
Social animals regularly face consensus decisions whereby they choose, collectively, between mutually exclusive actions. Such decisions often involve conflicts of interest between group members with respect to preferred action. Conflicts could, in principle, be resolved, either by sharing decisions between members (‘shared decisions’) or by one ‘dominant’ member making decisions on behalf of the whole group (‘unshared decisions’). Both, shared and unshared decisions, have been observed. However, it is unclear as to what favours the evolution of either decision type. Here, after a brief literature review, we present a novel method, involving a combination of self-organizing system and game theory modelling, of investigating the evolution of shared and unshared decisions. We apply the method to decisions on movement direction. We find that both, shared and unshared, decisions can evolve without individuals having a global overview of the group's behaviour or any knowledge about other members' preferences or intentions. Selection favours unshared over shared decisions when conflicts are high relative to grouping benefits, and vice versa. These results differ from those of group decision models relating to activity timings. We attribute this to fundamental differences between collective decisions about modalities that are disjunct (here, space) or continuous (here, time) with respect to costs/benefits.
Keywords: collective decisions, conflict resolution, consensus decisions, cooperation, information pooling, speed versus accuracy trade-off
1. General introduction
A major challenge to most social animals, including humans, is the regular need to make ‘consensus decisions’, i.e. to choose, collectively, between mutually exclusive actions (Conradt 1998). Such decisions may involve choosing between different activities (Conradt 1998; Ruckstuhl & Neuhaus 2000), movement destinations (Trillmich et al. 2004; Couzin et al. 2005), nest sites (Seeley & Buhrman 1999), migration routes (Simons 2004) or hunting strategies (Conradt & Roper 2005).
In principle, three main factors influence consensus decisions, namely, information, conflict and time constraints. Firstly, the relevant information held by individual group members, and how this information is shared within the group, influences decision outcomes and accuracy (Seeley & Buhrman 1999; Conradt & Roper 2003; List 2004; Simons 2004; Couzin et al. 2005; Ame et al. 2006; Biro et al. 2006; Passino & Seeley 2006; Codling et al. 2007; Lusseau 2007; Ward et al. 2008; Dyer et al. 2009; Franks et al. 2009; List et al. 2009; Skyrms 2009; Sumpter & Pratt 2009). Secondly, conflicts of interest between group members, in the form of conflicting preferences for different decision outcomes, affect the fitness of individual group members and the evolution of the decision-making process (Conradt 1998; Ruckstuhl 1998, 1999; Conradt & Roper 2000, 2003, 2005, 2007; Ruckstuhl & Neuhaus 2000, 2002; Rands et al. 2003; Austen-Smith & Feddersen 2009; Hix & Noury 2009). Thirdly, time constraints and the resultant trade-offs (e.g. between speed and accuracy of decision making) limit the options for potential decision outcomes (Passino & Seeley 2006; Franks et al. 2009; Sumpter & Pratt 2009). Here, we concentrate on the second of these three factors, namely, conflicts of interest between group members.
To reach a consensus, conflicts of interest with respect to decision outcomes have to be resolved (Conradt & Roper 2003, 2007; Rands et al. 2003; Couzin et al. 2005). In principle, this can be achieved in two ways: decisions can either be ‘shared’ (some or all group members contribute to the decision outcome) or ‘unshared’ (the decision outcome is dictated by a single individual; Conradt & Roper 2003; List 2004; Austen-Smith & Feddersen 2009). Shared and unshared decisions influence the fitness of individual group members differently. Here, we are interested in the conditions under which shared decision making might be expected to evolve when there are conflicts of interest between group members. We provide a brief overview of published work on conflicts of interest and the evolution of decision sharing in animals and then investigate the evolution of decision sharing using a novel approach in which we integrate self-organizing systems simulations with game theory modelling.
2. Short review: conflicts of interest and the evolution of decision sharing
Consensus decisions in animals vary in the extent to which they involve conflicts of interest between group members (Conradt & Roper 2005). For example, nest site choice in eusocial insects (Seeley & Buhrman 1999; Visscher & Seeley 2007; Franks et al. 2009), or navigation in homing or migrating birds (Wallraff 1978; Simons 2004; Biro et al. 2006), involve relatively little conflict of interest because the optimal decision outcome is the same for all group members. By contrast, synchronization of group activities and choice of short-term travel destinations in birds, fishes and mammals can involve significant conflict (Conradt 1998; Ruckstuhl & Neuhaus 2000), since individual group members often differ in physiological requirements (e.g. Clutton-Brock et al. 1982) and therefore in their optimal requirements with respect to activity timing and travel destinations (e.g. Gompper 1996; Prins 1996; Ruckstuhl 1998).
Where there is conflict, reaching a consensus decision will necessarily involve compromise for at least some group members. Formally, this means that at least some members will pay a ‘consensus cost’, defined as the fitness cost to an individual of foregoing its own optimal action in order to comply with the consensus decision (Conradt & Roper 2003, 2005, 2007). Consensus costs, and their distribution between group members, are crucial for group stability (Conradt 1998; Ruckstuhl & Neuhaus 2000).
The consensus cost to individual group members depends on their own ability to influence the decision outcome versus that of other group members (Conradt & Roper 2003). For example, if a dominant individual dictates the decision (unshared decision making), it will not incur a cost because it can choose the decision outcome that is optimal for itself, whereas subordinate members will incur costs according to how different their own optima are from that of the dominant. By contrast, if all group members contribute equally to the decision outcome (‘equally shared’ decision making) the consensus costs will be relatively lower for most members other than the dominant (Conradt & Roper 2003). Decision-making processes that are intermediate between these two extremes (i.e. ‘partially shared’ decisions in which a subset of group members contributes to the decision outcome) are also possible.
Historically, scientists working on relatively small groups (i.e. groups in which global communication between group members is possible; Conradt & Roper 2005), especially in mammals, have tended to assume that decision making is unshared, no doubt because such groups usually exhibit obvious dominance hierarchies (e.g. Sapolsky 2005). By contrast, scientists working on large groups (i.e. groups in which only local communication between neighbouring members is possible; Conradt & Roper 2005), especially those using self-organizing system approaches, have tended to assume equally shared decision making insofar as they apply similar behavioural parameters to all group members (see Couzin & Krause 2003 for a review). The reason for this is no doubt the intrinsic difficulty of imagining that any individual member of a large self-organizing group could exert meaningful control over the behaviour of the group as a whole.
However, emerging empirical evidence challenges the assumption that a dominant individual always dictates what happens in small groups of animals (primates: Stolba 1979; Stewart & Harcourt 1994; Boinski & Campbell 1995; Byrne 2000; Milton 2000; Meunier et al. 2006; Sellers et al. 2007; ungulates: Conradt & Roper 2003; bats: Kerth et al. 2006; birds: Black 1988). Conversely, there is no intrinsic reason why self-organizing systems should only produce equal sharing of decisions (Conradt et al. in press). Indeed, several empirical observations suggest that in self-organizing groups individuals that have greater ‘needs’ might be able to gain a disproportionate weight in decision outcomes (fishes: Krause et al. 1992; Krause 1993; ungulates: Prins 1996; Fischhoff et al. 2007).
One of the most important outstanding theoretical questions is to explain how shared decision making can evolve in decisions that involve conflict, without invoking ‘good-for-the-group’ arguments (Gächter & Herrmann 2009). The main challenge in addressing this question is the complexity arising from multi-individual interactions in group decisions. Rands et al. (2003) modelled a group of two in which each member tries to maximize its own chance of survival and both gain from foraging together, but in which the optimal times for foraging can differ between individuals. In such a situation, if one member starts to forage because its reserves drop below a crucial threshold, the other member should also start to forage, because the advantages of foraging together outweigh the disadvantages of foraging at a less preferred time. The result is high activity synchrony. This constitutes, in principle, a shared consensus decision, because neither of the members has intrinsically more weight in the decision than the other, or differs in principle from the other at the start of the simulations. The decision threshold in this shared decision is one since, if at least one of the two starts to forage, this determines the collective behaviour. However, because group members differ in reserves, and this difference is likely to be preserved for some time, it is likely that during several consecutive occasions it will be the same individual that starts to forage first. Thus, this individual will seem to be the apparent ‘leader’ of the activity. It is not clear what would happen if one were to extend Rands et al.'s model to a group of more than two.
Dostalkova & Spinka (2007) also modelled activity synchronization between two group members. Similar to Rands et al. (2003), they predict that individuals maximize their benefits by switching activities simultaneously when the first prefers a change, provided that there is no communication between members. However, if there is communication, and acting too late is ‘cheaper’ (in terms of consensus cost) than acting prematurely, the group should switch activity only when both members prefer to do so (i.e. when a decision threshold of two is reached). In order to explain this difference, Dostalkova & Spinka (2007) raised the interesting notion of the inherent informational asymmetry of time. Without communication, information about members' preferred leaving times becomes available only once members attempt to leave, resulting in an informational bias towards earlier preferred leaving times. This can affect synchronization decisions in an asymmetric manner. Again, it is not clear what will happen if the model is extended to a group larger than two.
A model by Conradt & Roper (2003), again focusing on activity synchronization, suggests that the consensus costs to a group as a whole are considerably lower for equally shared than for unshared decisions under most conditions and for group sizes larger than two. However, without invoking group selection arguments this does not necessarily lead to the evolution of decision sharing. Indeed, Conradt & Roper (2007) showed that, in principle, unshared decisions, as well as equally shared decisions, can be evolutionarily stable in groups of all sizes. The authors identified five factors that favour the evolution of shared versus unshared decisions in the context of activity synchronization, namely, (i) large conflicts of interest between group members (resulting in high potential consensus costs), (ii) long-term differences between group members with respect to requirements (i.e. high heterogeneity within the group), (iii) asymmetric consensus costs (i.e. one decision outcome is potentially much more costly than another), (iv) marginal grouping benefits, and (v) a group size that is close to, or above, optimal group size.
The predictions of all three of these models still require empirical testing. Moreover, all three models deal with activity synchronization, leaving it unclear as to whether the same results apply to the evolution of consensus decisions involving, say, movement destinations. Decisions about the latter often differ in principle from those about activity synchronization in an important respect, as follows. While an average or median timing might often offer a sensible compromise between different optimal timings (Conradt & Roper 2003), such a procedure would more rarely be valid when compromising between different spatial targets (Conradt et al. in press). For example, if a flock of geese were trying to decide which of two lakes to land on, it would make no sense for it to land halfway between the two lakes where there was no water at all. Another limitation of all three models is that they assume (at least implicitly) that group members have a global overview of the activities of other group members, and that this global overview can influence their behaviour. This assumption does not hold in many of the large groups that we observe in nature (Couzin & Krause 2003; Couzin et al. 2005; Sumpter 2006; Sumpter & Pratt 2009). In §3, we address the evolution of consensus decisions about movement destinations. We avoid the assumption of global overview by considering a self-organizing system.
3. Evolution of decision sharing during movements by self-organizing groups
(a) Introduction
Many animal groups, in particular many economically important groups, are thought to be ‘self-organizing’ (see Couzin & Krause 2003 and Sumpter 2006 for reviews), in the sense that (i) pattern at the global level (e.g. group movement direction, group movement speed, group composition, group formation, etc.) emerges solely from numerous local interactions among the individual group members (i.e. nobody is in overall ‘command’) and (ii) the local behavioural rules specifying the interactions among the group members are executed using only local information, without reference to the global pattern (i.e. nobody has a global ‘overview’ of the group; Camazine et al. 2003). Typical examples for self-organizing groups are swarms of honeybees or locusts, colonies of ants, large shoals of fish, large flocks of birds and large herds of ungulates. Here, we are investigating the evolution of shared and unshared decision making in such self-organizing groups during group travel.
Studying the evolution of shared decision making in self-organizing systems poses some logistic challenges. Self-organizing animal systems are often studied with the help of computer simulations. However, these simulations can require considerable computing power (e.g. Couzin et al. 2005). Linking self-organizing systems modelling directly with evolutionary simulations, in order to answer evolutionary questions, would therefore require prohibitively large computing resources. We avoid this problem by adopting a novel approach in which we combine two different modelling techniques, namely, self-organizing system modelling and game theory modelling.
First, we modify a self-organizing system model by Couzin et al. (2005) in order to enable individual group members to differ in their local behaviours. We then use self-organizing system simulations to determine global group behaviour (e.g. group spatial position, group movement efficiency, group fragmentation risk) depending on all members' local behaviours (cf. Conradt et al. in press). Next, we translate this group-level outcome into fitness consequences for individual group members (Conradt & Roper 2003, 2007). In this manner, we determine fitness consequences for each individual group member, depending both on its own local behaviour and on that of all other group members. The resulting pay-off matrices to individuals can then be used in multiplayer game theory models to determine evolutionarily stable strategies (‘ESSs’; Maynard-Smith 1989). Because multiplayer game theory models are complex, we use computer simulations to determine the relevant ESSs. Here, we use this method for the first time to investigate the evolution of decisions about movement destinations in a self-organizing group containing three members.
(b) Methods
(i) Conflicts of interest
To create conflicts of interest between members, we assume that two of the three members (‘majority members’) prefer to move to one spatial target, while the third member (‘minority member’) prefers to move to another spatial target. The spatial targets are equidistant (500 spatial units) from the group's starting point, but lie in opposite directions. ‘type 1’ animals prefer to move to target 1 and ‘type 2’ animals to target 2. Thus, a group consists either of two type 1 and one type 2 animal, or vice versa.
(ii) Self-organizing group movement simulation model
The model is based on one by Couzin et al. (2005). The mathematical details are given in appendix Aa(i). All members move simultaneously in discrete time steps. Each individual member moves at each time step according to behavioural rules that depend only on local information (‘local movement rules’), as follows. The highest priority for an individual at any time is to avoid collision by moving away from neighbours that come too close. If (and only if) there is no immediate danger of collision, an individual has the following two aims: (i) to keep cohesion with other group members and (ii) to move towards its own preferred spatial target, as follows. In order to maintain group cohesion, the individual is attracted to neighbours within a given spatial range, so as to move towards them and align travel direction with them (‘social attraction’). However, the resulting ‘social attraction direction’ might differ from the direction towards the individual's preferred spatial target. Therefore, the individual ‘balances’ attraction to its preferred spatial target against social attraction to neighbours with its own individual factor ωi (‘degree of assertiveness’). In other words, it decides to move in the following direction:
| (3.1) |
It follows that, if ωi is large (and the individual is highly assertive), the individual decides to move at each time step predominantly in the direction of its preferred target; if ωi is small (and the individual is of low assertiveness), it decides to move predominantly towards, and align with, neighbours; and if ωi is intermediate (medium assertiveness), the individual compromises between its own target preference and moving towards, and aligning with, neighbours. Should the individual have no neighbours within the given spatial range, the individual has, at least for that time step, lost contact with other group members and cannot move towards, or align with, neighbours. Thus, it simply moves towards its own preferred spatial target (see above). According to these local behavioural rules, at each time step, for each individual, the next movement step direction was calculated (constrained by a maximum turning angle and including a random movement error; see appendix Aa(ii) for details), and then all individuals simultaneously moved in their new direction with a constant speed.
(iii) Variation in individual behaviours
The degree of assertiveness ωi determines an individual's readiness to compromise (see above). Therefore, it is the behavioural parameter that is most likely to influence the sharing/non-sharing of consensus decisions and the fitness of individual group members (Conradt et al. in press). Hence, we varied ωi between individual members, such that they could exhibit low (ωlow=0.05), medium (ωmedium=0.5) or high (ωhigh=5.0; see Couzin et al. 2005 for a biologically meaningful range of values for ωi) assertiveness. We consider all possible combinations ω1, ω2, ω3 (with ω1, ω2, ω3∈{ωlow, ωmedium, ωhigh}) for three members (i.e. 18 biologically different sets of behaviours; see also table 1). For each set of behaviours, we ran 500 simulations since, in pilot runs, results had stabilized to the required accuracy well below this number of replicates.
Table 1.
Standardized relative pay-off matrixa to focal animal depending on its own and the other group member's assertiveness, and on majority/minority relationships within the group.
| (a) focal player is minority type in group | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| one majority player plays | |||||||||
| ωlow | ωmedium | ωhigh | |||||||
| other majority player plays | |||||||||
| focal animal plays | ωlow | ωmedium | ωhigh | ωmedium | ωhigh | ωhigh | |||
| ωlow | −0.6 | −1 | −1 | −1 | −1 | −1 | |||
| ωmedium | −0.1 | −0.7 | −1 | −1 | −1 | −1 | |||
| ωhigh | 0 | 0 | 0.4· | −0.2· | |||||
| (b) focal player is majority type in group | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| other majority player plays | |||||||||
| ωlow | ωmedium | ωhigh | |||||||
| minority player plays | |||||||||
| focal animal plays | ωlow | ωmedium | ωhigh | ωlow | ωmedium | ωhigh | ωlow | ωmedium | ωhigh |
| ωlow | −0.4 | −0.9 | −1 | 0 | −0.4 | −1 | 0 | 0 | −0.4+ |
| ωmedium | −0.1 | −0.4 | −1 | 0 | 0 | 0.2·()−1 | 0 | 0 | |
| ωhigh | 0 | 0 | 0.6· | 0 | 0 | 0 | 0 | − | |
Note that if all animals within a group preferred the same target, the group always remained cohesive and moved towards the common preferred target; thus, for the evolution of behaviours, only those groups were relevant in which there was conflicts of interest between group members, and only those combinations are shown in the table.
(iv) Results of self-organizing system simulations
At the end of every simulation (after 5000 time steps), we determined for each group member (i) with how many other group members it was still in a group (see Couzin et al. 2005 for criteria of group cohesion) and (ii) its end position. If the individual had moved more than 500 steps towards target 1 or 2, respectively, it was considered to head towards target 1 or 2, respectively. Otherwise, it was considered to move too inefficiently (i.e. less than 10% movement efficiency) to be heading towards either target.
(v) Translating the results into individual fitness and pay-off matrices
We determined for each group member at the end of each simulation (i) the remaining number of members in their group and (ii) which target they were moving to (see above). This information can be translated into individual benefits, as follows. Firstly, social animals usually benefit by being in a group, and these ‘grouping benefits’ depend on group size (Krause & Ruxton 2002). We can, thus, determine the grouping benefits to an individual at the end of a simulation, depending on how many other group members it was still together with (solitary individuals gain no grouping benefits). Secondly, individuals are likely to gain from moving towards their preferred spatial target and from moving towards the target preferred by other group members, and more so from the former than the latter (e.g. Conradt 1998; Ruckstuhl & Neuhaus 2000; Conradt & Roper 2003, 2007). The difference in fitness gains between moving towards a non-preferred target versus a preferred target constitutes a ‘consensus cost’ (Conradt & Roper 2003, 2005). Therefore, from the final position of individuals, we could determine what moving-to-preferred/non-preferred-target benefits an individual had gained, and whether an individual had incurred a consensus cost, or not. In this manner, we could, for each combination of behaviours, determine the net gains (grouping benefits+spatial target benefits) for each group member at the end of each simulation. We averaged those gains over the 500 replicated simulations for each combination of behaviours.
For the purpose of the game theory model, only differences in relative benefits for different behavioural strategies are relevant (rather than absolute benefits; Maynard-Smith 1989). Therefore, in order to keep parameters to a minimum, we expressed the relative benefits to individuals in each combination of behaviours in terms of grouping benefits relative to potential consensus costs. That is, and were the grouping benefits of remaining in a group with three and two members, respectively, relative to the potential consensus costs (i.e. the difference in benefits between moving to preferred versus non-preferred spatial target). Based on these two parameters, we could calculate the standardized relative pay-off matrix for majority and minority group members depending on their own behaviour and that of other group members (table 1). This pay-off matrix is the basis for the game theory model that follows below.
(vi) Game theory model
We make the conservative assumption that individuals in self-organizing groups do not have information about whether they are majority or minority types (Couzin et al. 2005). Thus, individuals behave independently of whether they are in a majority or minority. A focal individual can play the pure strategies ωlow, ωmedium or ωhigh. It can also play any combination of these pure strategies. Assume that rlow, rmedium and rhigh are the probabilities that the focal plays ωlow, ωmedium or ωhigh, respectively. All possible complex behaviour strategies for a focal can, thus, be described as {rlow, rmedium, rhigh} (with 0≤rlow≤1; 0≤rmedium≤1−rlow; and rhigh=1−rlow−rmedium). Individuals drawn randomly from the population can also play the pure strategies ωlow, ωmedium or ωhigh, or complex combinations. Assume that plow, pmedium, phigh and qlow, qmedium, qhigh are the respective probabilities with which individuals that are drawn randomly from the population, and that have the same (pxx) or opposite (qxx) target preference as the focal, play ωlow, ωmedium or ωhigh, respectively. Thus, all possible complex behaviour strategies in the population can be described as {plow, pmedium, phigh, qlow, qmedium, qhigh} (with 0≤plow≤1; 0≤pmedium≤1−plow; and phigh=1−plow−pmedium; 0≤qlow≤1; 0≤qmedium≤1−qlow; and qhigh=1−qlow−qmedium). Using our derived pay-off matrix (table 1), and assigning animals drawn from the population into groups randomly with respect to preferred target, we can now calculate the expected relative net gains to a focal individual playing any focal behaviour strategy {rlow, rmedium, rhigh} in a population with any behaviour strategy {plow, pmedium, phigh, qlow, qmedium, qhigh}, as follows:
| (3.2) |
where t is the proportion of individuals in the population, which have the same target preference as the focal. We assumed that these relative gains translate into fitness consequences to individual players (Maynard-Smith 1989) and, thus, that plow, pmedium, phigh and qlow, qmedium, qhigh evolve accordingly (see also appendix Ab). We have further assumed that the proportion of different types of members (t) does not evolve. The rationale for this is as follows. Group members usually differ with respect to target preference because they are of different sex, age, size or physiological state (Conradt & Roper 2007), so t is commonly determined by factors (e.g. reproduction) that are independent of group decision making. However, this is not invariably so (see Rands et al. 2003) and, by covering a wide parameter range for t (0.1–0.9), we will be able to assess the potential effect t could have had if it had been allowed to co-evolve.
(vii) Evolutionarily stable strategies
We assume that relative gains (see equation (3.2)) translate into fitness consequences to individuals, and that the system evolves until it either reaches an evolutionarily stable strategy (Maynard-Smith 1989) or starts to oscillate. In order to find the ESSs in the system, we used a combination of analytical and simulation methods, as follows. Assume target type 1 is the focal target type, and target type 2 the other target type. First, we analytically determined stability conditions for pure strategies (i.e. plow=1, pmedium=1 or phigh=1; and qlow=1, qmedium=1 or qhigh=1; see appendix Ab(i)). The biological effect of the emerging pure ESSs (e.g. whether certain individuals or the majority led the group, and whether the group fragmented or not) can be derived from the self-organizing system simulations, given the pure strategies of both types (table 2). To examine the system for more complex ESSs, we used simulations. Starting from different ‘starting population strategies’, we simulated the evolution of population strategy, based on the relative gains given in equation (3.2) (assuming that these gains translate into fitness benefits; Maynard-Smith 1989), until there was either no further change in population strategy (i.e. we had reached an ESS), or the system began to oscillate. The details for these simulations are given in appendix Ab(ii). By closely covering the whole parameter range for potential starting population strategies, we made sure we detected all potential ESSs in the system.
Table 2.
Evolutionary stability criteria for pure strategies of either target type.
| strategy of type 1 individuals | strategy of type 2 individuals | stability criteria | biological effect |
|---|---|---|---|
| play always ωlow (plow=1) | play always ωlow (qlow=1) | never stable | |
| play always ωlow (plow=1) | play always ωmedium (qmedium=1) | never stable | |
| play always ωlow (plow=1) | play always ωhigh (qhigh=1) | ESS, if (type 1)< (type 1) and | type 2 leads; mixed groups move cohesively to target 2 |
| play always ωmedium (pmedium=1) | play always ωlow (qlow=1) | never stable | |
| play always ωmedium (pmedium=1) | play always ωmedium (qmedium=1) | ESS, if (type 1)>5 and (type2)>5 | equally shared decision; majority leads cohesive group |
| play always ωmedium (pmedium=1) | play always ωhigh (qhigh=1) | ESS, if (type 1)> (type 1); and (type 2)<5 | type 2 leads mixed groups towards target 2; some group fragmentation, thus, partial segregation |
| play always ωhigh (phigh=1) | play always ωlow (qlow=1) | ESS, if (type 2)< (type 2) and | type 1 leads; mixed groups move cohesively to target 1 |
| play always ωhigh (phigh=1) | play always ωmedium (qmedium=1) | ESS, if (type 2)> (type 2); and (type 1)<5 | type 1 leads mixed groups towards target 1; some group fragmentation, thus, partial segregation |
| play always ωhigh (phigh=1) | play always ωhigh (qhigh=1) | ESS, if (type1)<1 and (type 2)<1 | complete segregation of the two types |
(c) Results
All of the ESSs that emerged were ‘pure’ ESSs, i.e. they consisted of a single pure strategy rather than an equilibrium mix of pure strategies (figures 1 and 2, table 2). There were six possible ESSs (table 2). Their biological consequence for group decisions ranged from (i) complete segregation of different target types, via (ii) partial segregation, and (iii) equally shared consensus decision making, to (iv) consensus decision making by individuals of only one of the two target types. We examine the ESSs, assembled by their biological consequences, in detail, in the following.
Figure 1.
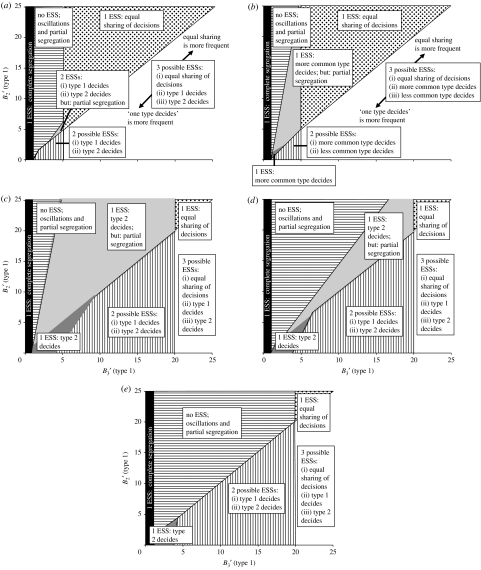
ESSs depending on the grouping benefits to type 1 of being in a group of three (, x-axis) or two (, y-axis), respectively, relative to the potential consensus costs; (a) both types with same grouping benefits to consensus cost ratio (i.e. (type 1)= (type 2); (type 1)= (type 2)), t=0.5; (b) both types with same grouping benefits to consensus cost ratio, t=0.1/0.9; (c) type 1 with four times higher grouping benefits to consensus cost ratio (i.e. (type 1)=4· (type 2); (type 1)=4· (type 2)), t=0.1; (d) type 1 with four times higher grouping benefits to consensus cost ratio, t=0.5; (e) type 1 with four times higher grouping benefits to consensus cost ratio, t=0.9 (black areas, 1 ESS, all individuals play always ωhigh, resulting in complete segregation; horizontally striped areas, no ESS, individuals oscillate between playing ωmedium and ωhigh, resulting in varying leading and partial segregation; light grey areas, 1 (or 2) ESSs, the type with the highest potential consensus costs or which is more common plays always ωhigh, the other type plays always ωmedium, resulting partially in leading by first type and partially in segregation; dark grey areas, 1 ESS, the type with the highest potential consensus costs or which is more common plays always ωhigh, the other type plays always ωlow, resulting in leading of decisions by first type; vertically striped areas, 2 ESSs, one type plays always ωhigh, the other type always ωlow, resulting in ‘leading by type 1’ or ‘leading by type 2’; spotted areas, 1 ESS, all types play always ωmedium, resulting in equally shared decision making; white areas, 3 ESSs, ‘leading by type 1’, ‘leading by type 2’ and ‘equally shared decision making’).
Figure 2.
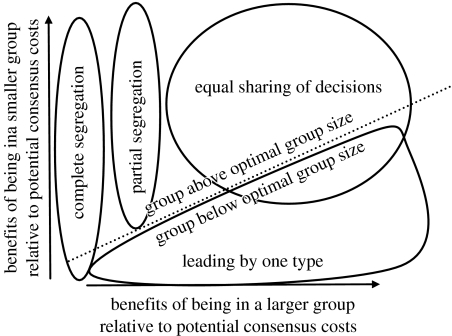
Schematic summary of model predictions. The area above the dotted line refers to groups that are above optimal group size; the area below the dotted line refers to groups of suboptimal size.
(i) Complete segregation of target types
If the benefits of being in a group of three are lower than the potential consensus costs (i.e. if <1; figure 1, black areas) for both target types, the only ESS in the system is: ‘both target types always play ωhigh’ (table 2). That is, none of the group members should compromise and incur consensus costs in order to maintain group cohesion (and gain grouping benefits that do not outweigh the consensus costs). This ESS leads to complete segregation of different target types into separate groups. In the rest of the results section, we only consider what happens if grouping benefits relative to potential consensus costs are high enough not to automatically lead to complete segregation (i.e. if it is >1 for at least one target type).
(ii) Partial segregation of target types
If group size three is above optimal group size (i.e. if ), and grouping benefits of being in a group of three are less than five times as high as potential consensus costs for at least one of the two target types (i.e. if <5), three possible situations can arise, as follows (see table 2 for criteria for each case). Firstly, no ESS exists and both types oscillate between playing ωhigh and ωmedium (figure 1, horizontally striped areas). Secondly, one ESS exists: ‘more common type/type with lower grouping benefits relative to potential consensus costs always plays ωhigh and other type always plays ωmedium’ (figure 1b–e, light grey areas). Thirdly, two ESSs exist: (i) ‘type 1 always plays ωhigh and type 2 always ωmedium’ and (ii) ‘type 2 always plays ωhigh and type 1 always ωmedium’ (figure 1a, light grey area). The biological effect is the same in all three situations, namely members will not always reach consensus and at least some group fragmentation will occur in mixed-type groups. This will lead to at least partial segregation of the two target types into separate groups.
(iii) Equally shared consensus decisions
If, and only if, grouping benefits of being in a group of three are more than five times as high as potential consensus costs for both target types (i.e. if >5), the following strategy was always an ESS: ‘both target types always play ωmedium’. The biological effect of this ESS is equally shared consensus decision making (see table 2; cf. Couzin et al. 2005). Note, however, that only disjunct parameter values for ω could be tested here, and that ‘both target types always play ωmedium’ might cease to be an ESS in a continuous parameter space for ω. It would then be likely to be replaced by another ‘equal-sharing’ ESS with a slightly higher common ω value and slightly different stability criteria, while qualitative results would be similar (Conradt & Roper 2007).
If the minimum condition >5 was met for both target types, and group size three was above optimal group size (i.e. if ), both target types always play ωmedium was the only ESS in the system, and equal sharing of consensus decisions always evolved (figure 1, spotted area). If group size three was not above optimal group size (i.e. if ; figure 1, white areas), two further ESSs could exist: ‘type 1 always plays ωlow, and type 2 always ωhigh’ (which would mean that type 2 individuals lead all decisions; tables 1 and 2) and (ii) ‘type 1 always plays ωhigh, and type 2 always ωlow’ (which would mean that type 1 individuals lead all decisions). To which ESS the system evolves in such a case depends on the starting point of the system, the proportion t of type 1 in the population and on the grouping benefits relative to potential consensus costs (i.e. and ). If grouping benefits are large relative to consensus costs (i.e. and are large), equal sharing of decision making is more likely to evolve. If grouping benefits are small relative to consensus costs (i.e. and are small), leading by one type is more likely to evolve (see also next section).
(iv) One target type leads consensus decisions
We consider only situations without complete or partial segregation (see above and table 2 for criteria). If group size three is not above optimal group size (i.e. if ), the following two strategies are potential ESSs: (i) ‘type 1 always plays ωhigh and type 2 always ωlow’ and (ii) ‘type 2 always plays ωhigh and type 1 always ωlow’. Either of these ESSs results in decisions being made by individuals of only one target type. In particular, the first ESS means that target type 1 individuals lead all consensus decisions (table 2; figure 1, dark grey and vertically striped areas), the second ESS that target type 2 individuals lead all consensus decisions. Since individuals of the leading target type always play ωhigh, they do not compromise with other group members but behave domineeringly. Decisions are no longer equally shared, and the decision is not necessarily made by members of the target type that are in the majority within the group. If only one member in a group is of the ‘leading’ target type, the decision will, strictly speaking, even be ‘unshared’.
To which ESS the system evolves, depends on the starting point of the system, the proportion t of type 1 in the population and on the grouping benefits relative to potential consensus costs (i.e. and ). If the ratio of grouping benefits to potential consensus costs is similar for individuals of both types (i.e. if (type 1)= (type 2) and if (type 1)= (type 2)), and if type 1 and 2 individuals are equally frequent in the population (i.e. if t=0.5), the ESSs ‘type 1 individuals lead all consensus decisions’ and ‘type 2 individuals lead all consensus decisions’ are equally likely to evolve (figure 1a). Otherwise, if grouping benefits are small relative to potential consensus costs (i.e. is small; figure 1, dark grey area; see table 2 for threshold), only that ESS can evolve in which those individuals lead all decisions, which are of the more common type (figure 1b) and/or of the type with lower grouping benefits relative to potential consensus costs (figure 1c–e). As grouping benefits relative to potential consensus costs increase (i.e. as increases), the system can evolve also to ‘leading by the other type’ (figure 1, vertically striped areas). If grouping benefits of being in a group of three exceed five times the potential consensus costs (i.e. if >5) for both target types, a third ESS exists that leads to equal sharing of consensus decisions (see section above). If relative grouping benefits increase further (i.e. increases further, and in particular if increases), the system is more and more likely to evolve to equal sharing of consensus decisions rather than to leading by either type (figure 1, white areas; see also section above).
(v) Potential effect of t
Qualitative results were fairly constant over a wide range of values for t (compare figure 1a,b and figure 1c–e), implying that an evolving t would not have led to greatly different results, always assuming that ultimately neither target type (e.g. sex, age or size class; Conradt & Roper 2007) would go completely extinct.
(d) Discussion
To date, hardly anything is known about the evolution of group decision-making strategies in animals. The present study is therefore pioneering work, in which we introduce a novel technique (combining self-organizing system and game theory modelling) and explore a first application. Although we were only able to model a small group (group size three) owing to computational limitations, our results provide a preliminary understanding of the evolution of spatial decisions in groups in which there is no communication between members and in which individuals are unable to perceive or react directly to global group behaviour. We show that in such groups, equally shared consensus decision making, as well as leading by one ‘domineering’ target type, could in principle evolve in decisions about movement destinations. If grouping benefits were small relative to potential consensus costs, groups either became unstable such that individuals with different preferences segregated into different subgroups (if group size was above optimal group size), or leading by one type evolved (if group size was not above optimal group size; figure 2). The leading type was likely to be either the type with the lower grouping benefits to potential consensus cost ratio, or the more common type in the overall population (although not necessarily within the group). As grouping benefits relative to potential consensus costs increased, equal sharing of decisions became more likely to evolve, in particular when group size was above optimal group size.
These results partially contradict those of Conradt & Roper (2007), who predicted that high potential consensus costs and marginal grouping benefits should favour the evolution of equally shared versus less shared decision making. The reason for this apparent contradiction lies in the different nature of decisions about activity synchronization (which were the subject of Conradt & Roper 2007) and decisions about movement destinations. In decisions about the timing of activities, compromises that can be reached in an equally shared manner (e.g. the average or median of preferred timings by group members) usually lower the average consensus costs to individual group members (Conradt & Roper 2003). This is generally true if the modality which the group decides upon (e.g. timing) is continuous with respect to benefits/costs. In such a case, a compromise can be viable. To give an example: if you want to go to a restaurant at 19.00 hours, and I want to go at 20.00 hours, going there at 19.30 hours might mean that both of us do not get inconvenienced too much. To compromise (and share a decision) on such a continuous modality will be particularly crucial if potential consensus costs are high and grouping benefits marginal, since group members should only stay in a group if grouping benefits exceed consensus costs. Thus, in such situations, one expects either equally shared decisions or group fragmentation. Group decisions about timing, while not always, will usually fall into this category.
By contrast, if the modality which the group decides upon (e.g. spatial targets) is disjunct with respect to benefits/costs, then a compromise is unlikely to be viable. To give an example: if you are hungry and want to go to a restaurant, and I need petrol and want to go to a garage, compromising and going halfway between the restaurant and the garage (where we could neither get food nor petrol) does not make sense for either of us. While not all decisions on spatial targets are necessarily ‘disjunct decisions’ in this way, the majority are, most notably in patchy landscapes. Such circumstances usually require ‘hard’ decisions, of an ‘either/or’ kind, to be made. Thus, groups in the kind of situation that we have considered here have only three viable options: move to target 1, move to target 2 or fragment. If grouping benefits are large relative to consensus costs, no group member wishes to risk group fragmentation, so being too assertive with respect to your own preference is risky and therefore disadvantageous. On the other hand, if nobody is highly assertive it pays to be somewhat assertive, because otherwise you would never move to your own preferred target. Consequently, evolution favours a medium level of assertiveness in all individuals, which leads in a self-organizing system to equally shared decision making (Couzin et al. 2005). By contrast, if grouping benefits are low relative to consensus costs, risking group fragmentation rather than moving towards a less preferred target becomes an evolutionary option. Thus, it will pay some individuals, in particular those which would face higher consensus costs if moving towards the less preferred target (or those which stand to gain less grouping benefits), to be highly assertive. As individuals of one target type evolve to be highly assertive, selection might then favour individuals of the other target type to be unassertive in order to avoid group fragmentation. The result is that ‘leading by one type’ evolves. If grouping benefits drop further, individuals with different preferences segregate into different subgroups.
An interesting implication of this is that if animals make simultaneous group decisions about continuous and disjunct modalities (e.g. about space and time), they should apply different strategies to the two different aspects of the decision. How the details of combined space-and-time decisions could look requires further modelling.
The model proves that equal sharing of decisions is not a foregone conclusion, even in self-organizing systems where individuals do not have an overview of, or could directly react to, global group behaviours (Camazine et al. 2003). On the contrary, we show that leading by one type can evolve, even if group members cannot communicate, and consequently have no knowledge about, the preferences of other group members. The model offers testable predictions about when equal sharing or leading by one type should occur in group decisions about movement destinations.
The present model is for computational reasons restricted to groups of three. However, its results provide initial insight into an important type of group decision (see Couzin & Krause 2003 for a review). Its most important qualitative result (i.e. the principal difference between decisions in continuous and disjunct modalities, and thus, usually between timing and spatial decisions) is likely to hold for larger group sizes, for the reasons given above. Whether other results also hold requires further investigation. As computer speeds increase, our approach will become feasible for studies on larger groups.
Acknowledgments
L.C. was supported by a Royal Society University Research Fellowship, and would like to thank the Royal Society particularly for its support during maternity leave and with respect to part-time working.
Appendix A
(a) Details of the self-organizing group movement simulation model
(i) Individual local behaviour rules
Collision avoidance. For each individual, the highest priority is to avoid collision. Thus, if there are neighbours within a collision range α (α=2; for adequacy of parameter choice see Couzin et al. 2005), the individual simply tries to turn away from those neighbours. Thus, if Niα(t)>0, then
| (A1) |
where Niα(t) is the number of neighbours within range α; di(t) is the preliminary movement direction; and ci(t) is the position vector, for individual i at time t.
Balance between social attraction and preferred target direction. If there are no neighbours within range α (i.e. if Niα(t)=0), the individual's movement is based on its desire to maintain group cohesion as well as to move towards its preferred target, as follows. In order to maintain group cohesion, the individual is attracted to neighbours within a range ρ (ρ=30; for adequacy of parameter choice see Couzin et al. 2005) so as to move towards them and align travel direction with them (‘social attraction’). However, the resulting ‘social attraction vector’ might differ from the vector towards the individual's preferred spatial target. Therefore, the individual ‘balances’ attraction to its preferred target against social attraction to neighbours with its own individual factor ωi (‘degree of assertiveness’). That is, an individual tries to move in the direction of social attraction+ωi·preferred target direction (where preferred target direction is the vector between the individual's position and the preferred target position, scaled to unit length). Thus, if Niα(t)=0 and Niρ(t)>0, then
| (A2) |
where Niρ(t) is the number of neighbours within range ρ; vi(t) is the unit vector of movement direction, for individual i at time step t; and gi is the position vector of the preferred target of individual i. The first term describes social attraction to neighbours, the second term alignment with neighbours (first and second term together constitute the social attraction vector), and the third term attraction to the preferred goal.
It follows that, if ωi is large (and the individual is highly assertive), the individual tries to move at each time step predominantly in the direction of its preferred target; if ωi is small (and the individual is of low assertiveness), it predominantly tries to move towards, and align with, neighbours; and if ωi is intermediate (medium assertiveness), the individual compromises between its own target preference and moving towards, and aligning with, neighbours.
Absence of neighbours. If there are no neighbours within ranges α or ρ, the individual always tries to move in the direction of its preferred target. Thus, if Niα(t)=0 and Niρ(t)=0, then
| (A3) |
Note that none of these assumptions regarding local behavioural rules requires a global overview of the group, or a view of other group members further away than distance ρ.
(ii) Self-organizing system simulations
Individual group members start with a random movement direction and a random position within a cohesive group. From the preliminary movement direction di(t) (equations (A1)–(A3), above), we derive the new movement direction for each individual at the next time step by adding an individual random directional error to di(t) (with standard deviation σ=0.01 radians; Couzin et al. 2005), and limiting the change in movement direction to a maximum turning angle of θΔt (θΔt=0.2 radians; see Couzin et al. 2005 for details and justification of parameter choice). The new position of each individual is obtained by moving it one step ahead of Δt=0.1 (equivalent to a constant speed of 1 spatial unit/time unit) in the new movement direction.
(b) Game theory model
(i) Criteria for the increases in the population of different behavioural strategies
We determine the criteria under which different pure behavioural strategies should increase or decrease in the population, using the expected relative gains given in equation (3.2). Equation (3.2) can be written shorter as
| (A4) |
These relative gains peak with rlow=1 if is relative large (which means that it is of advantage to play ωlow). Similarly, they peak with rmedium if is relatively large (which means that it is of advantage to play ωmedium). Finally, they peak with rhigh if is relative large (which means that it is of advantage to play ωhigh). We assume that relative gains translate into relative fitness increases (Maynard-Smith 1989). It therefore follows that plow (i.e. the probability with which individuals of the focal's target preference play ωlow) increases in the population relative to other strategies, if relative gains reach a maximum for rlow=1. Similarly, pmedium increases in the population if relative gains reach a maximum for rmedium=1. Finally, phigh increases in the population if relative gains reach a maximum for rhigh=1. In particular, plow increases in the population if
| (A5a) |
and
| (A5b) |
pmedium increases in the population, if
| (A6a) |
and
| (A6b) |
and phigh increases in the population, if
| (A7a) |
and
| (A7b) |
Of course, the analogue is true for the members in the population of the opposite target preference. Thus, qlow increases in the population if
| (A8a) |
and
| (A8b) |
qmedium increases in the population if
| (A9a) |
and
| (A9b) |
and qhigh increases in the population if
| (A10a) |
and
| (A10b) |
(ii) Simulations to find complex ESSs
First, we chose a starting population strategy {plow, pmedium, phigh, qlow, qmedium, qhigh}. Using equations (3.2) and (A 4), we calculated , , , , and for this starting population strategy. According to the inequality relationships listed in the previous section (equations (A 5a)–(A 10b)), we determined which pxx and qxx probabilities increase in the population. We then added a random increase to the relevant probabilities in the population strategy (with a mean of 0.001 and a standard deviation of 0.0005, but capping the probabilities at 1). The relevant increase was then deducted from the remaining non-increasing probabilities (until they reach a minimum of 0) in such a manner that the following holds true for the newly derived probabilities: and . In this manner, we derive a new, evolved population strategy. We repeated the process again using the newly derived population strategy. The process was repeated until all the probabilities stabilized and the derived population strategy was an ESS, or until the system started to oscillate.
Our starting population strategies covered the whole parameter space (in steps of 0.1) and used all biologically possible combinations of plow∈{0, 0.1, 0.2, …, 1); pmedium∈{0, 0.1, 0.2, … 1−plow); qlow∈{0, 0.1, 0.2, … 1); and qmedium∈{0, 0.1, 0.2, … 1−qlow). Thus, by closely covering the whole range of potential starting population strategies, and by using small increases at each simulation step, we made sure that we detected all potential ESSs in each system. The examined parameter range for proportion t was 0.1, 0.5 and 0.9; and that for relative grouping benefits (type 1), (type 2), (type 1) and (type 2): 0.5–25 (in steps small enough to cover all potentially different cases arising from the stability conditions in table 2). It was assumed that the ratio of grouping benefits relative to potential consensus costs ( and ) were either the same for individuals that preferred targets 1 and 2 (i.e. (type 1)= (type 2) and (type 1)= (type 2)), or they were four times higher for individuals that preferred target 1 than for those that preferred target 2 (i.e. (type 1)=4· (type 2) and (type 1)=4 (type 2)).
Footnotes
One contribution of 11 to a Theme Issue ‘Group decision making in humans and animals’.
References
- Ame J.M., Halloy J., Rivault C., Detrain C., Deneubourg J.L. Collegial decision making based on social amplification leads to optimal group formation. Proc. Natl Acad. Sci. USA. 2006;103:5835–5840. doi: 10.1073/pnas.0507877103. doi:10.1073/pnas.0507877103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Austen-Smith D., Feddersen T.J. Information aggregation and communication in committees. Phil. Trans. R. Soc. B. 2009;364:763–769. doi: 10.1098/rstb.2008.0256. doi:10.1098/rstb.2008.0256 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biro D., Sumpter D.J.T., Meade J., Guilford T. From compromise to leadership in pigeon homing. Curr. Biol. 2006;16:2123–2128. doi: 10.1016/j.cub.2006.08.087. doi:10.1016/j.cub.2006.08.087 [DOI] [PubMed] [Google Scholar]
- Black J.M. Preflight signaling in swans—a mechanism for group cohesion and flock formation. Ethology. 1988;79:143–157. [Google Scholar]
- Boinski S., Campbell A.F. Use of trill vocalizations to coordinate troop movement among white-faced capuchins—a 2nd field-test. Behaviour. 1995;132:875–901. doi:10.1163/156853995X00054 [Google Scholar]
- Byrne R.W. How monkeys find their way: leadership, coordination and cognitive maps of African baboons. In: Boinski S., Garber P.A., editors. On the move. University of Chicago Press; Chicago, IL: 2000. pp. 491–518. [Google Scholar]
- Camazine S., Deneubourg J.L., Franks N.R., Sneyd J., Theraulaz G., Bonabeau E. Princeton University Press; Princeton, NJ: 2003. Self-organization in biological systems. [Google Scholar]
- Clutton-Brock T.H., Guinness F.E., Albon S.D. University of Chicago Press; Chicago, IL: 1982. Red deer: behaviour and ecology of two sexes. [Google Scholar]
- Codling E.A., Pitchford J.W., Simpson S.D. Group navigation and the “many-wrongs principle” in models of animal movement. Ecology. 2007;88:1864–1870. doi: 10.1890/06-0854.1. doi:10.1890/06-0854.1 [DOI] [PubMed] [Google Scholar]
- Conradt L. Could asynchrony in activity between the sexes cause intersexual social segregation in ruminants? Proc. R. Soc. B. 1998;265:1359–1363. doi: 10.1098/rspb.1998.0442. doi:10.1098/rspb.1998.0442 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conradt L., Roper T.J. Activity synchrony and social cohesion: a fission–fusion model. Proc. R. Soc. B. 2000;267:2213–2218. doi: 10.1098/rspb.2000.1271. doi:10.1098/rspb.2000.1171 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conradt L., Roper T.J. Group decision-making in animals. Nature. 2003;421:155–158. doi: 10.1038/nature01294. doi:10.1038/nature01294 [DOI] [PubMed] [Google Scholar]
- Conradt L., Roper T.J. Consensus decision making in animals. Trends Ecol. Evol. 2005;20:449–456. doi: 10.1016/j.tree.2005.05.008. doi:10.1016/j.tree.2005.05.008 [DOI] [PubMed] [Google Scholar]
- Conradt L., Roper T.J. Democracy in animals: the evolution of shared group decisions. Proc. R. Soc. B. 2007;274:2317–2326. doi: 10.1098/rspb.2007.0186. doi:10.1098/rspb.2007.0186 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conradt, L., Couzin, I. D., Krause, J., Roper, T. J. In press. Leading according to need in self-organising groups. Am. Nat [DOI] [PubMed]
- Couzin I.D., Krause J. Self-organization and collective behavior in vertebrates. Adv. Study Behav. 2003;32:1–75. doi:10.1016/S0065-3454(03)01001-5 [Google Scholar]
- Couzin I.D., Krause J., Franks N.R., Levin S.A. Effective leadership and decision-making in animal groups on the move. Nature. 2005;433:513–516. doi: 10.1038/nature03236. doi:10.1038/nature03236 [DOI] [PubMed] [Google Scholar]
- Dostalkova I., Spinka M. Synchronisation of behaviour in pairs: the role of communication and consequences in timing. Anim. Behav. 2007;74:1735–1742. doi:10.1016/j.anbehav.2007.04.014 [Google Scholar]
- Dyer J.R.G., Johansson A., Helbing D., Couzin I.D., Krause J. Leadership, consensus decision making and collective behaviour in humans. Phil. Trans. R. Soc. B. 2009;364:781–789. doi: 10.1098/rstb.2008.0233. doi:10.1098/rstb.2008.0233 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischhoff I.R., Sundaresan S.R., Cordingley J., Larkin H.M., Sellier M.J., Rubenstein D.I. Social relationships and reproductive state influence leadership roles in movements of plains zebra, Equus burchellii. Anim. Behav. 2007;73:825–831. doi:10.1016/j.anbehav.2006.10.012 [Google Scholar]
- Franks N.R., Dechaume-Moncharmont F.-X., Hanmore E., Reynolds J.K. Speed versus accuracy in decision-making ants: expediting politics and policy implementation. Phil. Trans. R. Soc. B. 2009;364:845–852. doi: 10.1098/rstb.2008.0224. doi:10.1098/rstb.2008.0224 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gächter S., Herrmann B. Reciprocity, culture and human cooperation: previous insights and a new cross-cultural experiment. Phil. Trans. R. Soc. B. 2009;364:791–806. doi: 10.1098/rstb.2008.0275. doi:10.1098/rstb.2008.0275 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gompper M.E. Sociality and asociality in white-nosed coatis (Nasua narica): foraging costs and benefits. Behav. Ecol. 1996;7:254–263. doi:10.1093/beheco/7.3.254 [Google Scholar]
- Hix S., Noury A., Roland G. Voting patterns and alliance formation in the European Parliament. Phil. Trans. R. Soc. B. 2009;364:821–831. doi: 10.1098/rstb.2008.0263. doi:10.1098/rstb.2008.0263 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerth G., Ebert C., Schmidtke C. Group decision making in fission–fusion societies: evidence from two-field experiments in Bechstein's bats. Proc. R. Soc. B. 2006;273:2785–2790. doi: 10.1098/rspb.2006.3647. doi:10.1098/rspb.2006.3647 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krause J. The relationship between foraging and shoal position in a mixed shoal of roach (Rutilus rutilus) and chub (Leuciscus-Cephalus)—a field-study. Oecologia. 1993;93:356–359. doi: 10.1007/BF00317878. doi:10.1007/BF00317878 [DOI] [PubMed] [Google Scholar]
- Krause J., Ruxton G.D. Oxford University Press; Oxford, UK: 2002. Living in groups. [Google Scholar]
- Krause J., Bumann D., Todt D. Relationship between the position preference and nutritional state of individuals in schools of juvenile roach (Rutilus rutilus) Behav. Ecol. Sociobiol. 1992;30:177–180. doi:10.1007/BF00166700 [Google Scholar]
- List C. Democracy in animal groups: a political science perspective. Trends Ecol. Evol. 2004;19:168–169. doi: 10.1016/j.tree.2004.02.004. doi:10.1016/j.tree.2004.02.004 [DOI] [PubMed] [Google Scholar]
- List C., Elsholtz C., Seeley T.D. Independence and interdependence in collective decision making: an agent-based model of nest-site choice by honeybee swarms. Phil. Trans. R. Soc. B. 2009;364:755–762. doi: 10.1098/rstb.2008.0277. doi:10.1098/rstb.2008.0277 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lusseau D. Evidence for social role in a dolphin social network. Evol. Ecol. 2007;21:357–366. doi:10.1007/s10682-006-9105-0 [Google Scholar]
- Maynard-Smith J. Oxford University Press; Oxford, UK: 1989. Evolutionary genetics. [Google Scholar]
- Meunier H., Leca J.B., Deneubourg J.L., Petit O. Group movement decisions in capuchin monkeys: the utility of an experimental study and a mathematical model to explore the relationship between individual and collective behaviours. Behaviour. 2006;143:1511–1527. doi:10.1163/156853906779366982 [Google Scholar]
- Milton K. Quo vadis? Tactics of food search and group movements in primates and other animals. In: Boinski S., Garber P.A., editors. On the move. University of Chicago Press; Chicago, IL: 2000. pp. 375–418. [Google Scholar]
- Passino K.M., Seeley T.D. Modeling and analysis of nest-site selection by honeybee swarms: the speed and accuracy trade-off. Behav. Ecol. Sociobiol. 2006;59:427–442. doi:10.1007/s00265-005-0067-y [Google Scholar]
- Prins H.H.T. Chapman & Hall; London, UK: 1996. Ecology and behaviour of the African buffalo. [Google Scholar]
- Rands S.A., Cowlishaw G., Pettifor R.A., Rowcliffe J.M., Johnstone R.A. Spontaneous emergence of leaders and followers in foraging pairs. Nature. 2003;423:432–434. doi: 10.1038/nature01630. doi:10.1038/nature01630 [DOI] [PubMed] [Google Scholar]
- Ruckstuhl K.E. Foraging behaviour and sexual segregation in bighorn sheep. Anim. Behav. 1998;56:99–106. doi: 10.1006/anbe.1998.0745. doi:10.1006/anbe.1998.0745 [DOI] [PubMed] [Google Scholar]
- Ruckstuhl K.E. To synchronise or not to synchronise: a dilemma for young bighorn males? Behaviour. 1999;136:805–818. doi:10.1163/156853999501577 [Google Scholar]
- Ruckstuhl K.E., Neuhaus P. Sexual segregation in ungulates: a new approach. Behaviour. 2000;137:361–377. doi:10.1163/156853900502123 [Google Scholar]
- Ruckstuhl K.E., Neuhaus P. Sexual segregation in ungulates: a comparative test of three hypotheses. Biol. Rev. 2002;77:77–96. doi: 10.1017/s1464793101005814. [DOI] [PubMed] [Google Scholar]
- Sapolsky R.M. The influence of social hierarchy on primate health. Science. 2005;308:648–652. doi: 10.1126/science.1106477. doi:10.1126/science.1106477 [DOI] [PubMed] [Google Scholar]
- Seeley T.D., Buhrman S.C. Group decision making in swarms of honey bees. Behav. Ecol. Sociobiol. 1999;45:19–31. doi:10.1007/s002650050536 [Google Scholar]
- Sellers W.I., Hill R.A., Logan B.S. An agent-based model of group decision making in baboons. Phil. Trans. R. Soc. B. 2007;362:1699–1710. doi: 10.1098/rstb.2007.2064. doi:10.1098/rstb.2007.2064 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simons A.M. Many wrongs: the advantage of group navigation. Trends Ecol. Evol. 2004;19:453–455. doi: 10.1016/j.tree.2004.07.001. doi:10.1016/j.tree.2004.07.001 [DOI] [PubMed] [Google Scholar]
- Skyrms B. Evolution of signalling systems with multiple senders and receivers. Phil. Trans. R. Soc. B. 2009;364:771–779. doi: 10.1098/rstb.2008.0258. doi:10.1098/rstb.2008.0258 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stewart K.J., Harcourt A.H. Gorillas vocalizations during rest periods—signals of impending departure. Behaviour. 1994;130:29–40. doi:10.1163/156853994X00127 [Google Scholar]
- Stolba A. Universitaet Zuerich; Zuerich, Switzerland: 1979. Entscheidungsfindung in Verbanden von Papio hamadryas. [Google Scholar]
- Sumpter D.J.T. The principles of collective animal behaviour. Phil. Trans. R. Soc. B. 2006;361:5–22. doi: 10.1098/rstb.2005.1733. doi:10.1098/rstb.2005.1733 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sumpter D.J.T., Pratt S.C. Quorum responses and consensus decision making. Phil. Trans. R. Soc. B. 2009;364:743–753. doi: 10.1098/rstb.2008.0204. doi:10.1098/rstb.2008.0204 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trillmich J., Fichtel C., Kappeler P.M. Coordination of group movements in wild Verreaux's sifakas (Propithecus verreauxi) Behaviour. 2004;141:1103–1120. doi:10.1163/1568539042664579 [Google Scholar]
- Visscher P.K., Seeley T.D. Coordinating a group departure: who produces the piping signals on honeybee swarms? Behav. Ecol. Sociobiol. 2007;61:1615–1621. doi:10.1007/s00265-007-0393-3 [Google Scholar]
- Wallraff H.G. Social interrelations involved in migratory orientation of birds—possible contribution of field studies. Oikos. 1978;30:401–404. doi:10.2307/3543490 [Google Scholar]
- Ward A.J.W., Sumpter D.J.T., Couzin J.D., Hart P.J.B., Krause J. Quorum decision making facilitates information transfer in fish schools. Proc. Natl Acad. Sci. USA. 2008;105:6948–6953. doi: 10.1073/pnas.0710344105. doi:10.1073/pnas.0710344105 [DOI] [PMC free article] [PubMed] [Google Scholar]