Single-molecule mechanics: New insights from the escape-over-a-barrier problem

The early description of the living cell as a reaction vessel of molecules undergoing random collisions has evolved to a much more interesting picture of a small chemical factory of complex and dynamic molecular structures that carry out specialized functions in a highly-coordinated fashion. Traditional solution biochemistry has had extraordinary success in elucidating molecular structures of the cellular components. The task of capturing the dynamics and the distribution of states of these structures, however, seemed nearly impossible because the activities of the molecules in the solution are asynchronous as the result of their interactions with the surroundings. This situation has changed with the development of single-molecule biophysical methods (1, 2) that permit measurements of the response of macromolecules or individual molecular bonds to external load with the spectacular resolution of subnanometer distances and picoNewton forces, revealing details that are typically lost to ensemble averaging when studied by solution methods. Unprecedented information about the mechanisms that drive biological processes becomes encoded in the resulting wealth of unaveraged data. Recall, however, that these systems are of microscopic dimensions, which puts thermal fluctuations on equal footing with the external deterministic forces. This circumstance, along with the far from equilibrium conditions, makes a quantitative description of the molecular bond properties that can account for observed data a challenging task. The article by Freund in this issue of PNAS (3) offers a theoretical framework that does just that. A novel and concise derivation takes the reader from a very fundamental starting point to a set of analytical results that provide intriguing insights into the response of a molecular bond to an imposed mechanical load.

To probe mechanical properties of macromolecules experimentally, the molecules are attached, one at a time, to an external probe, such as a μm-sized bead, a cantilever, or a pipette. By pulling on the probe, and hence on the molecule, the response of the molecule (DNA, RNA, or protein) or a ligand–receptor pair to a controlled force or twist is examined. Given the same external load, the responses will differ from one measurement to another because of the stochastic nature of the system, but upon observing many of the responses, the entire distribution of the dynamic properties, such as dissociation times and rupture forces, can be collected. Such a systematic investigation of the dependence of molecular properties on external loading is at the heart of dynamic force spectroscopy method (4–6), brilliantly designed to probe the inner world of molecular interactions.

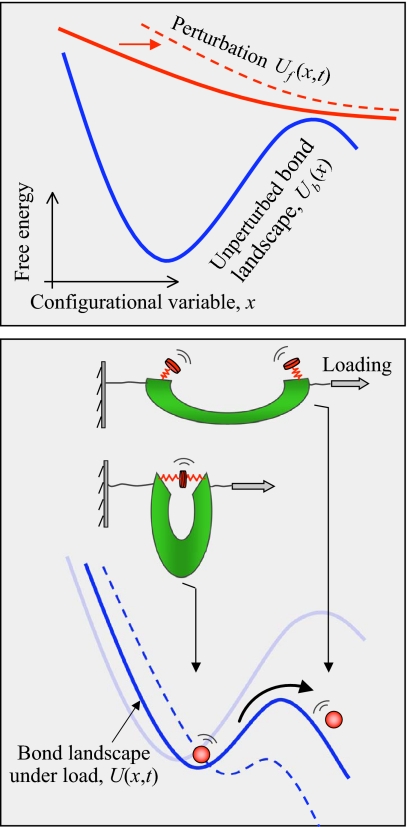
Because the thermal noise from the environment is an integral part of the bond separation process, the response of the bond to an external force can only be described in probabilistic terms. Assume that the instantaneous configuration of the bond can be fully identified by a single variable x, which can, for instance, be the bond length. The bond can only adopt configurations confined to a 1D free-energy landscape U(x, t), which is the sum of the bond natural free energy of a general shape sketched in Fig. 1 and the mechanical work of (in general, time-dependent) external force acting in the direction of x (Fig. 1). Now consider an ensemble of nominally-identical bonds that are simultaneously subjected to the same external force, responding independently of each other. It is the probability distribution of the bond configurations that is diffusing on the free energy landscape U(x, t) governed by the generalized diffusion (Smoluchowski) equation.

Fig. 1.

Conceptual picture of the process of separation of a molecular bond under external load. (Upper) Natural free-energy landscape of the bond (blue) is assumed to have 2 states (bound and dissociated) that are connected by a quasi-irreversible transition. Instantaneous state of the bond is identified by a configurational variable x, e.g., the bond length. Free-energy profile of an applied force (red solid line) is fixed in shape but translates (red dashed line) along x as specified by the Gibbs external coordinate, y(t). (Lower) The total free-energy landscape (blue solid line) of the bond subjected to external load is tilted relative to the natural profile, with the barrier lowered and the distance between the well and the barrier decreased. For given loading regime, y(t), the evolution of the probability of finding the bond at configurational state x at time t can be described as a diffusion process.

The fraction of the bonds in the ensemble that remain intact at time t is the “survival probability” of the bond. To describe force-induced molecular rupture, a common starting point is the first-order rate equation governing the evolution of the survival probability (the first-order kinetics is a signature of the “rare” character of the rupture events). The time dependence of the rupture rate in this equation can be calculated by treating bond rupture under force as a diffusive barrier crossing, a generalized version of a classical problem studied by Kramers (7). Applied to a class of simple microscopic models of the bond free-energy landscape, Kramers' theory has been used to derive analytical solutions for the rupture rate under constant external force and for the rupture-force distributions under constant loading rate (8–10). In the analysis by Freund (3), the rate equation for the survival probability, rather than serving as a starting point, is shown to emerge naturally, along with the time dependence of the rate in this equation, from the underlying Smoluchowski equation. Neither constant force nor constant force rate regimes of the external loading are presumed in the derivation of Freund (3), where the use of the concept of the Gibbs external coordinate, representing the applied loading in the present context, provides the analysis with its powerful versatility.

How does the bond respond to the external load during the process of separation? The entire time history of the bond response is reflected in a statistical representation of force, the mean force per bond in an ensemble of identical bonds. Freund (3) derives a general expression for the time history of the mean force on the bond under an arbitrary prescribed regime of loading. This result, besides its fundamental interest, is of practical importance in the light of the pulling experiments that probe the resistance of a biological system where multiple bonds in series are involved.

Armed with this general formalism, what information can be decoded about the nanoscale realm of a molecular bond directly from experimental data? First, implications of the general results are demonstrated by Freund (3) for a representative energy landscape of the bond and a linear spring compliance of the loading device, for which case an explicit asymptotic result for the time-dependent rate of the bond rupture is obtained in terms of the parameters characterizing both the bond and external loading. This result, valid for an arbitrary time dependence of the imposed loading that induces bond separation, highlights and quantifies the sensitivity of the bond response to the stiffness of the loading device (11). Second, for the data in the form of a force probability distribution, commonly reported in the constant speed loading experiments, Freund (3) suggests a practical means of extracting 3 functional characteristics of the bond of interest, namely the bond “depth” (the activation energy), “width” (the length), and diffusivity. This novel approach, based on a simple analysis of the level curves of diffusivity in the space of bond depth and bond width, is an alternative to the existing analytical methods (10, 12) of extracting kinetic information from single-molecule pulling measurements.

The rate equation for the survival probability, rather than serving as a starting point, is shown to emerge naturally.

With a general framework established and practical implementation demonstrated, the analysis by Freund (3) also highlights a number of challenges:

Interpretation of experimental data in terms of the underlying properties of a molecular bond ultimately rests on a detailed specification of the shape of the bond potential surface. How unique is this interpretation? The article by Freund (3) suggests, in agreement with earlier studies (12), that the parameters extracted from Kramers' (7) picture of diffusive barrier crossing are relatively insensitive to the precise details of a (reasonably chosen) model for the free-energy surface and may thus be considered meaningful. Hopefully, the emergence of model-independent quantitative approaches (12) will enable a higher degree of generality of conclusions drawn from single-molecule mechanics data.

Although enlightening, it is only a glimpse into the realm of molecular interactions that we acquire from learning the depth, width, and rate coefficient of the molecular bond interaction potential. Continued refinement of the quantitative methods should enable the reconstruction of a more detailed map of the macromolecular energy landscape (13). At the same time, while introducing new free parameters into a theoretical model, we have to be careful to avoid overinterpreting experimental data.

How adequate is a 1D description of force-induced rupture? 1D theories seem to be remarkably successful in reproducing and interpreting experimental data for the unfolding of short nucleic acids and small proteins (12, 14). In the case of more complex biomolecules, however, multiple unfolding pathways and populated states may be detected depending on how the force is applied, and higher-dimensional approaches thus must be considered. Such approaches certainly add a challenge into the microscopic interpretation of the data, at the same time revealing the richness and complexity of the inner world of biomolecular interactions (15). It is our hope that such more realistic models will help drive new breakthrough experiments, with an eye on a broader goal of single-molecule studies to comprehend the inner workings of the cellular factory across the scales of its organization.