Allee effect in the selection for prime-numbered cycles in periodical cicadas

Abstract

Periodical cicadas are well known for their prime-numbered life cycles (17 and 13 years) and their mass periodical emergences. The origination and persistence of prime-numbered cycles are explained by the hybridization hypothesis on the basis of their lower likelihood of hybridization with other cycles. Recently, we showed by using an integer-based numerical model that prime-numbered cycles are indeed selected for among 10- to 20-year cycles. Here, we develop a real-number-based model to investigate the factors affecting the selection of prime-numbered cycles. We include an Allee effect in our model, such that a critical population size is set as an extinction threshold. We compare the real-number models with and without the Allee effect. The results show that in the presence of an Allee effect, prime-numbered life cycles are most likely to persist and to be selected under a wide range of extinction thresholds.

True periodicity, involving synchronized adult emergences, fixed life cycle lengths, and intervals between emergences with no adults present, is rare among insects (1). The majority of periodical insects have life cycles of 2 years with geographically separated populations appearing in even and odd years, respectively. The most famous periodical insects, the periodical cicadas (Magicicada spp.) of eastern North America, have the most extreme periodical life cycles known (1–6). The seven described species of 13- and 17-year periodical cicadas are divided into a complex mosaic of 15 largely parapatric, regional “broods” on different emergence schedules (1–6). Enduring questions about these insects are why are there only two life cycles and why are these both prime numbers.

Several authors have proposed a hybridization hypothesis for the evolution of Magicicada life cycles that involves “weeding out” all but the long-length prime-numbered cycles from a spectrum of periodical cycles (7, 8). In the various models that have been presented, coemergences of different life cycles lead to hybridization and production of offspring with altered life cycles that remove them from the mating population and thereby introduce a fitness cost. Thus, brood pairs that are more likely to coemerge stand a greater chance of decline and extinction. The fact that the two extant Magicicada life cycles (13 or 17 years) are prime-numbered means that where broods of different life cycles are adjacent, coemergences of adults occur rarely (only once every 221 years). In Magicicada, the fitness costs of hybridization may be elevated by predation; periodical cicadas suffer heavy mortality at low population densities because they rely on mass numbers and a strategy of “predator satiation” for survival (9, 10). In this article, we examine the relationship between individual fitness and population density [or Allee effect (11–13)] in the evolution of Magicicada periodicity.

In our previous studies using a simple numerical model of emergence and hybridization in periodical cicadas (14), we show that the cost of hybridization causes prime-numbered cycles to persist longer than other potential life cycles. These earlier models assume implicitly a kind of Allee effect by rounding population sizes downward, which has disproportionately large effects on small populations (14). In this article, we present a simulation model with an explicit Allee effect in the form of an extinction threshold, or population density below which a brood becomes extinct. We use this model to investigate the potential strength of an Allee effect in the evolution of Magicicada periodicity.

Model

We built a deterministic discrete model of population dynamics starting with 11 pure broods of 10–20-year genetically determined life cycles (14). All population sizes were measured as real numbers with decimals (double precision). We kept track of the population sizes of all broods/hybrids including birth year with juvenile (N_l,t) and adult stages (N_A). Rates of hybridization among different broods/genotypes were assumed to be proportional to the relative population sizes of coemerging broods (15).

We applied an Allee effect to periodical cicada population dynamics (8, 11–13) in the following manner. We set a critical population size Nc, below which the population will become extinct immediately. As a control, we set Nc = 0 (without the Allee effect). To test the sensitivity of this extinction threshold Nc, we varied the critical population sizes, such that Nc = 0, 10, 20, …, 300 (step = 10).

To avoid an initial advantage to any specific cycle, the starting conditions of our model included identical population sizes for all broods of 1,000 first-instar juveniles. We also tested the sensitivity of the initial conditions with various equal and unequal population sizes. In all simulations, we explored the population dynamics of cicadas from 11 pure broods with cycles ranging from 10 to 20 years.

Results

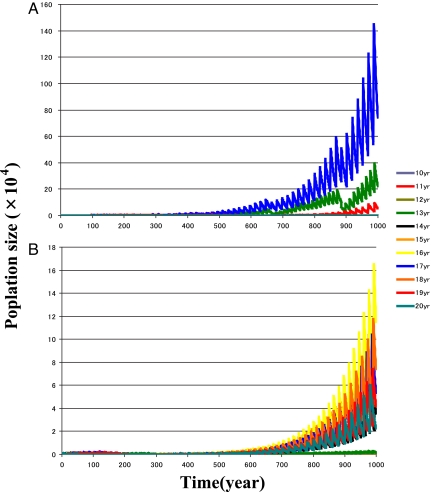
Selection for prime-numbered cycles appears only under the Allee effect (Fig. 1). With the Allee effect (Nc = 100), only a few prime-numbered cycles (17, 13, and 19) survive (Fig. 1A), and their identities depend on the initial model parameters. However, without the Allee effect (control: Nc = 0), the 16-year cycle increases most, but all cycles survive, and some increase (Fig. 1B). We also varied the initial population sizes from 1,000 to 11,000 individuals per cycle. When population sizes are small (<1,800 individuals), prime-numbered life cycles are favored; at larger population sizes, non-prime-numbered life cycles may also persist.

Fig. 1.

Temporal dynamics of periodical cicadas starting with 11 pure broods at 10- to 20-year cycles. (A) Real-number model with the Allee effect (Nc = 100). All but 13-, 17-, and 19-year cycles are extinct at an early stage. The order of population sizes at the end (100 years) is: 17 > 13 > 19. (B) Control: real-number model without the Allee effect (Nc = 0). Parameters are S = 0.95 and E = 0.5. All survive until the end (100 years), and the order of population sizes is 16 > 15 > 18 > 17 > 19 > 14 > 20 @k 13 > 12 > 11 > 10.

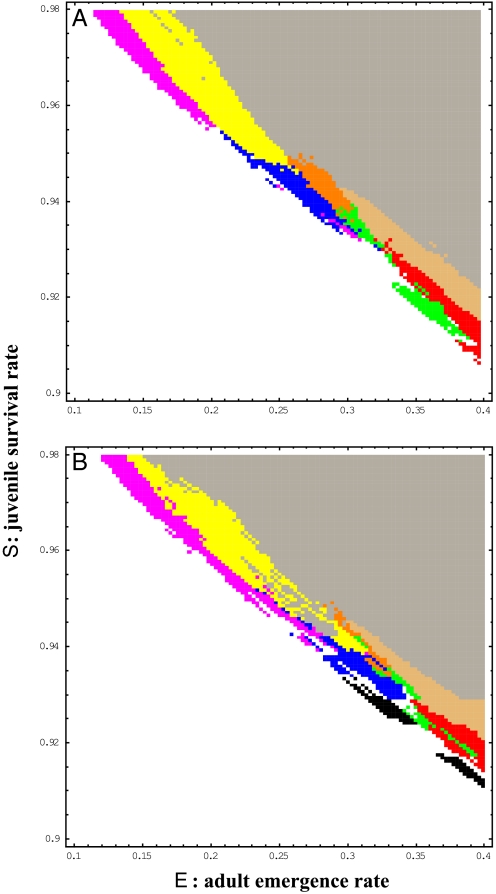
Parameter sensitivity analysis shows that survival advantages for the prime-numbered cycles appear under the Allee effect (Fig. 2). The phase planes show the survival cycles at a thousand years for the two parameters: juvenile survival rate S and adult emergence rate E with extinction threshold Nc = 100 (Fig. 2A) and 300 (Fig. 2B). Here, all of the broods have gone extinct under a combination of low juvenile survival rates and low adult emergence rates, whereas all survive when these parameters are high. Prime-numbered cycles survive at the boundaries (edge) of extinction: a single cycle at the very edge and two or more far inside with an increasing number of survival cycles (Fig. 2). The difference between Nc = 100 and 300 is rather quantitative. The phase plane for Nc = 300 is more complicated. Among non-prime-numbered cycles, only 14-year cycles appear near the edge of extinction (black in Fig. 2B). However, no non-prime-numbered cycles appear at the edge of extinction when the critical population size, Nc, is set to 100 (Fig. 2A).

Fig. 2.

Phase planes of 1,000-year survivals for juvenile survival rate S and adult emergence rate E among 11 pure broods of 10- to 20-year cycles with the Allee effect. The extinction thresholds are set as: Nc = 100 (A) and Nc = 300 (B). One or two cycles only (red: 11 only; green: 13 only; black: 14 only; blue: 17 only; pink: 19 only; beige: 11 and 13; brown: 13 and 17; yellow: 17 and 19), three or more cycles (gray) and all extinction (white) are shown. The various cycles (gray) include hybrids.

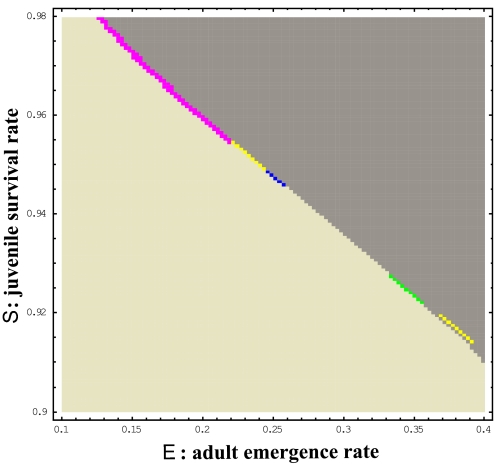
Without the Allee effect, we find no strict extinction in the phase plane at 1,000 years because hybrids suffer no costs (Fig. 3). Therefore, we evaluate the growth rate of populations as follows. If the populations at 1,000 years are ≥1,000 individuals, they are considered “increasing,” whereas if they are <1,000, they will be “decreasing.” The positive or negative growth is shown in the dark or light gray areas, respectively, in Fig. 3, where the total population size is increasing or decreasing from the initial 1,000 individuals. At the increasing/decreasing boundary, we find an extremely narrow area where only one to three prime-numbered cycles increase, whereas the rest of the cycles decrease more or less (note that these colors are different from those of Fig. 2, which indicate the survival of only one or two cycles). The increasing/decreasing boundaries are similar among all broods (Fig. 3). Thus, the advantage of prime-numbered cycles does not appear when the Allee effect is absent.

Fig. 3.

Phase planes of population sizes (relative to the initial population sizes) of 1,000-year survivals for juvenile survival rates S and adult emergence rate E among 11 pure broods of 10- to 20-year cycles without the Allee effect (control; Nc = 0). The population sizes are categorized as increasing or decreasing compared with the corresponding initial population sizes (N₀ = 1,000). The populations are shown as: three or more cycles increasing (dark gray); shown prime numbers only increasing with the rest decreasing (green: 13 only; blue: 17 only; pink: 19 only; yellow: 17 and 19); and all decreasing (light gray).

The exact tradeoff between juvenile survival rate S and adult emergence rate E is seen in the straight border of extinction (Fig. 3). The overall growth rates of populations are unity along the border. This survival border is extended largely when there is an Allee effect (Fig. 2). The individual phase plains for each cycle with Nc = 100 indicate that the survival areas are very large for all of the prime-numbered cycles, suggesting the advantage of prime-numbered cycles (Fig. 4).

Fig. 4.

Individual phase planes of 1,000-year survivals (Fig. 2A) for each of 11 pure broods of 10- to 20-year cycles (numbers shown) with the Allee effect. The extinction thresholds are set as Nc = 100. The two parameters are juvenile survival rates S (y axis: range = 0.91–0.97) and adult emergence rate E (x axis: range: 0.13–0.35). The survival areas are larger in 13- and 17-year cycles, followed by 11- and 19-year cycles. Those of non-prime-numbered cycles are all smaller.

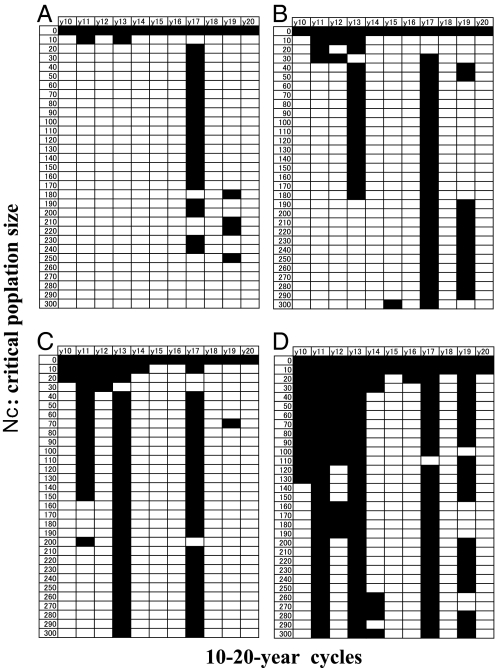
The advantage of prime-numbered cycles appears as long as there is an Allee effect, irrespective of the extinction thresholds (Fig. 5). We varied the extinction level from 0 (without the Allee effects) and 10, 20, … , to 300 (step = 10; with the Allee effects). When the emergence rate is low (E = 0.24), the survival of only one prime-numbered cycle (either 17 or 19) is seen for Nc = 20–250. When the emergence rate is increased slightly (E = 0.26, 0.27), the survival of two to three prime-numbered cycles appear in a wide rage of critical population sizes (Nc = 40–300; Fig. 5 B and C). When the emergence rate is increased further (E = 0.3), many cycles survive at different levels of Nc (Fig. 5D), but in general, prime-numbered cycles still have an advantage.

Fig. 5.

Surviving cycles among 11 pure broods at 10- to 20-year cycles with different levels of the Allee effect, where the extinction threshold is varied, such that Nc = 0 (no Allee effect), 10, 20, … , 300 (step = 10). The gray cells are surviving cycles. E = 0.24 (A), 0.26 (B), 0.27 (C), and 0.3 (D). Other parameters are S = 0.944, and C = 25. A–D correspond with the points along line S = 0.944 in the phase plane of Fig. 2A.

Discussion

The hybridization hypothesis (7, 8) must explain two evolutionary processes: (i) the fixation of perfectly synchronous periodical life cycles, and (ii) the selection of prime-numbered 17- and 13-year cycles. Our model addresses the processes that select for prime-numbered life cycles, or the second part of the hybridization hypothesis. To address the first part of the hypothesis and to resolve conflicts between this hypothesis and other hypotheses for the evolution of periodical cicada life cycles (5, 6, 16, 17), studies are needed on the genetic and environmental basis of periodicity.

Our results suggest that an extinction threshold Allee effect could facilitate the selection of prime-numbered life cycles. The various parameters in our model seem to have little effect on the eventual outcome; under a wide range of extinction thresholds, non-prime life cycles are unlikely to persist (Figs. 1–5). In addition, the numerical advantages of prime-numbered cycles appear only when an Allee effect is at work (Fig. 3). These results suggest that the mechanism of prime-number selection is extremely stable under various environmental settings. The exact form of the Allee effect may be unimportant to the general results; this model has an explicit Allee effect, whereas our previous model had an implicit but untested Allee effect (14). Both models favored prime-numbered cycles after a process of coemergence, hybridization, and extinction of non-prime-numbered cycles.

In the current model (but not our previous model), we assume constant clutch size (14). This simplification is important to elucidate the mechanisms of the selection process because the relationships among parameters and the outcomes become straightforward. The important finding is that the areas of survival of prime-numbered cycles appear only when any survival parameter is varied close to the extinction boundary (Fig. 2) and that this phenomenon is caused directly by the Allee effect.

The most unrealistic aspect of our model is that it presupposes geographic overlap of periodical life cycles; Among the modern-day periodical cicada broods, such life cycle overlap is virtually nonexistent (1). In addition, our model postulates the existence of fixed life cycles with no plasticity. Although periodical cicada life cycles are genetically determined, plasticity has been implicated in allowing periodical cicadas to switch life cycles (6, 16–18), and the phenomenon of off-cycle emergences, or “straggling” is also likely a manifestation of life cycle plasticity. Periodical cicada life cycle plasticity may itself be subject to evolutionary change (10), and we know little about the genetics of life cycle plasticity; thus, there is no simple way to include it in our models.

Another unrealistic aspect of our model is that the extinction threshold is difficult to determine empirically and is modeled as a sharp boundary condition, whereas in reality, we would expect Allee effects to operate more gradually, such that small population sizes would be at a higher risk of extinction than larger ones (11–13). Thus, we would expect some gradual shift in the probability and intensity of the Allee effect as the population sizes approached the extinction thresholds, unlike the sharp threshold of the current model. The Allee effect in our previous “round-down” integer model is more gradual (14). The round-down integer model produces relatively simple survival patterns (Fig. 2 in ref. 14), whereas the current model produces much more complicated patterns (Figs. 2 and 3). Yet the general results of both models are the same: Allee effects resulting from predator satiation seem to favor prime-numbered life cycles. A numerical demonstration that Allee effects can promote the maintenance of long, prime-numbered periodical life cycles confirms our earlier, intuitive understanding of how periodical life cycles are shaped by the interactions of predators and population densities (3, 5, 7–10).

Model Specifications

The model consists of two key parameters: juvenile survival rate S and adult emergence rate E. We assume that juvenile survival (mortality) rate S (1− S) per year is constant (0 < S < 1). Successful adult emergence rate E (0 < E < 1) is kept constant, assuming emergence failure is independent of life cycle length. To make the model simple, the clutch size C is also set to be constant (C = 25). For simplicity, we assume that the life cycle follows a single-locus Mendelian inheritance system with shorter cycle dominance, such that genotype [i, j] corresponds to phenotype i (years) if i < j. We do not know the genetics of periodical cicada life cycles, but note that the current simulation model is fairly neutral to what kind of genetic system we employ. For genotype [i, j] of a given birth year, the juvenile population size of a brood at time t (N_l, t) follows the equation:

Adult brood size N_A,t (only appear in emergence year) is

The offspring (juvenile) brood size between [i, j] and [m, n] is:

where F is the frequency of the target brood, such that

where ΣN_A is the sum of the population sizes of all coemergent adults for a given year. The genotypes of hybrid offspring between broods [i, j] and [m, n] include four possibilities: [i, m], [i, n], [j, m], and [j, n]. Thus, the offspring brood size of each genotype is determined for the sum of Eq. 3. For example, the offspring brood size of genotype [i, m] follows:

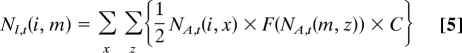The other genotypes are handled in similar fashion.