Turbulence-driven instabilities limit insect flight performance

Abstract

Environmental turbulence is ubiquitous in natural habitats, but its effect on flying animals remains unknown because most flight studies are performed in still air or artificially smooth flow. Here we show that variability in external airflow limits maximum flight speed in wild orchid bees by causing severe instabilities. Bees flying in front of an outdoor, turbulent air jet become increasingly unstable about their roll axis as airspeed and flow variability increase. Bees extend their hindlegs ventrally at higher speeds, improving roll stability but also increasing body drag and associated power requirements by 30%. Despite the energetic cost, we observed this stability-enhancing behavior in 10 euglossine species from 3 different genera, spanning an order of magnitude in body size. A field experiment in which we altered the level of turbulence demonstrates that flight instability and maximum flight speed are directly related to flow variability. The effect of environmental turbulence on flight stability is thus an important and previously unrecognized determinant of flight performance.

Locomotion is critical to the survival and reproductive success of many animals (1). Along with individual differences in physiology, morphology, and behavior, variability in the physical environment can strongly affect locomotor performance. Locomotory modes involving contact with a solid substrate, such as running (2–5), crawling (6), jumping (7), and climbing (8), can be directly affected by variability in substrate characteristics (e.g., surface roughness, texture, and geometry). Environmental variability can also affect locomotor performance in aquatic environments. Ordered, three-dimensional flows (e.g., behind objects in a stream) attract fish, which extract energy from regularly shed vortices (9), but more turbulent wave-driven flows overwhelm aquatic larvae (10) and force reef-dwelling fish to seek flow refuges (11). Laboratory studies suggest that turbulent flows decrease maximum swimming speed (12) and increase energetic costs (13) in fish, in part because of stability-enhancing fin movements that generate additional drag.

In comparison to terrestrial and aquatic systems, the effect of environmental variability on flight performance has received far less attention, despite the fact that aerial turbulence is universal in natural environments, varying temporally and spatially (14–15), as well as between different habitat types (e.g., grasslands, rolling hills, and coniferous vs. deciduous forests) (16–17). Interest in aeroecology, the interaction between flying animals and the aerial environment, is growing (18–19), but virtually all animal flight studies to date have been performed in simplified environments, such as laminar flow or still air (19). Turbulence variation in tropical forests has been linked to daily activity patterns of gliding tree frogs (14), but the effect of environmental variability on active flight has never been investigated.

In this study, we examined the effect of aerial turbulence on forward flight performance and maximum flight speed in wild orchid bees. These solitary, neotropical bees cover vast distances (tens of kilometers) (20) at high flight speeds foraging for diverse resources. Male bees are strongly attracted to aromatic compounds, which they scrape from orchids and store within pockets in their enlarged hindlegs (21) to be used during mating displays (22). We motivated male orchid bees (Euglossa imperialis) to fly at high speeds in turbulent air by placing an artificial scent source in the mouth of an outdoor air jet. We captured flight sequences with high-speed video and determined each bee's maximum flight speed, the speed beyond which flight instabilities caused the bee to crash. To explore the link between turbulence, flight instability, and maximum speed, we measured flow variability in front of the air jet, as well as in the surrounding forest, and performed a field experiment to test whether maximum flight speed changes as the turbulence level is altered.

Results and Discussion

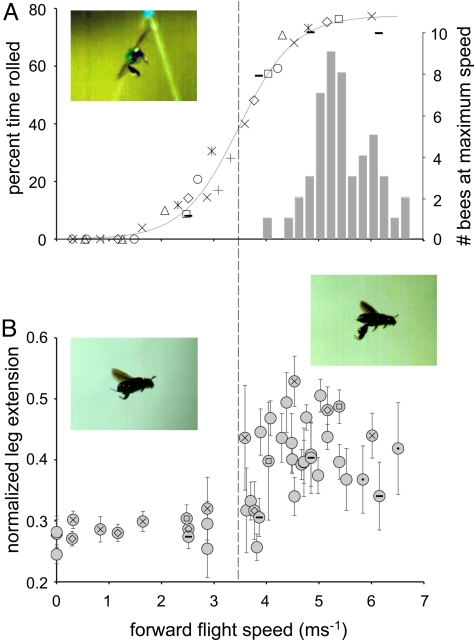
High-speed videos of bees flying in front of the outdoor air jet reveal that bees begin to roll from side to side at intermediate flight speeds, and that the incidence of rolling increases with airspeed until bees are rolled to one side or the other ≈80% of the time (Fig. 1A; Movie S1). These instabilities eventually result in aerodynamic failure (i.e., bees either crash to the ground or shoot laterally from the airstream; Movie S2), limiting maximum flight speed (average ± 1 SD = 5.32 ± 0.57 ms⁻¹, n = 49). The ability of bees to maintain stability and reach high flight speeds in turbulent air varies widely among individuals (Fig. 1A), and only 20% of this variability is explained by body mass (y = 11.516x + 3.4981, R² = 0.2045).

Fig. 1.

Roll instability, maximum flight speed, and leg extension of Euglossa imperialis flying in turbulent air. (A) Left axis: Percentage of time rolled as a function of flight speed in 8 individuals (indicated by different symbols). Solid line is a sigmoidal function of the form y = c/(1+e^a(b−x)) (a = 1.803, b = 3.433, c = 76.968, R² = 0.99); dotted line shows the inflection point. Inset shows the rear view of a bee rolling during fast flight (5.4 ms⁻¹). Right axis: Frequency distribution of maximum flight speeds in 49 bees (maximum of ≥3 independent measurements per bee). (B) Average normalized hindleg extension (± 1 SD) as a function of flight speed in 30 individuals (46 total clips). Normalized leg extension was calculated from lateral views as the distance between the center of mass and the hind tibia, divided by body length. Blank circles represent data from different individuals, each analyzed at a single speed; symbols inside circles identify data from individuals analyzed at multiple speeds. Insets show a bee with legs tucked during slow flight (Left, 1.5 ms⁻¹) and legs extended during fast flight (Right, 5.6 ms⁻¹).

At higher flight speeds, bees extend their hindlegs ventrally (Fig. 1B). Leg extension does not increase gradually with airspeed; rather, bees keep their legs tucked tightly against their bodies at low speeds (Movie S3) and extend their legs at intermediate and high speeds (Movie S4), when the incidence of rolling increases (Fig. 1). The effect of leg extension on the rolling moment of inertia can be estimated by modeling the legs as ellipsoids extended from the body's longitudinal axis (see Methods). Although the hindlegs account for only a small percentage of total body mass (average ± 1 SD of both legs = 5.9% ± 0.6%, n = 21), leg extension increases the moment of inertia by more than 50% (I_tucked = 3.65 × 10⁻¹⁰ kg m², I_extended = 5.60 × 10⁻¹⁰ kg m² for a 160-mg, 13.5-mm-long bee), decreasing roll accelerations substantially. Hindleg extension will also influence aerodynamic torques on the body, which may affect stability, but the magnitude of the inertial effects (>50% change) suggests that inertia plays an important, if not dominant, role in this method of flight stabilization.

In addition to enhancing roll stability, hindleg extension also increases overall body drag. We oriented 60 orchid bee bodies (E. imperialis) horizontally on a single-axis force transducer in front of the outdoor air jet and compared body drag of individual bees at their maximum recorded flight speed with legs tucked vs. extended. Hindleg extension increased body drag significantly (average ± 1 SE = 30.3% ± 2.6%; paired t test, P < 0.001). Because power requirements in flying bees increase in proportion to the product of body drag and forward speed, roll mitigation via hindleg extension is associated with substantial energetic cost, particularly at higher flight speeds.

Despite the associated energetic cost, leg extension during unstable forward flight appears to be a common behavior among euglossine bees. We observed leg extension during flight in front of the air jet in 10 different orchid bee species (all species surveyed), including representatives of 3 of the 5 euglossine genera: 8 species within the genus Euglossa (Eg. imperialis, tridentata, dissimula, bursigera, variabilis, heterosticta, azureoviridis, and sapphirina), as well as Exaerete frontalis and Eulaema meriana. These species possess diverse body and leg morphologies, and span over an order of magnitude in size (23).

To manipulate turbulence independently from average flow velocity, we generated 2 different flow conditions by inserting geometrically distinct flow straighteners (honeycomb vs. square grid) within the air jet. We characterized the conditions produced by measuring three-dimensional flow velocity with a sonic anemometer, and performed similar measurements of natural airflow at 6 heights in the adjacent forest. We found that flow variability of the air jet (expressed as the standard deviation of lateral velocity) increases with airspeed, but is significantly higher at any given speed with the honeycomb in place (ANOVA of speeds ≥3.6 ms⁻¹; grid effect, F = 54.728, P < 0.0001; velocity effect, F = 32.255, P < 0.0001; grid × velocity effect, F = 1.861, P = 0.15; Fig. S1). We also performed power spectral density analyses of velocity fluctuations and found that the frequency spectra are not affected by alternating flow grids (mixed model analysis of normalized power spectra with frequency as a repeated measure, grid effect, F = 0.69, P = 0.4099; velocity effect, F = 20.24, P < 0.0001; grid × velocity effect, F = 0.45, P = 0.7731). Thus, the grids affect only flow variability and not the temporal characteristics of flow. Our measurements in the adjacent forest showed that natural airflow contains more low-frequency turbulence than that produced by the air jet (Fig. S2), but the range of flow variability produced by the air jet lies within the range measured in the natural environment (Fig. S1).

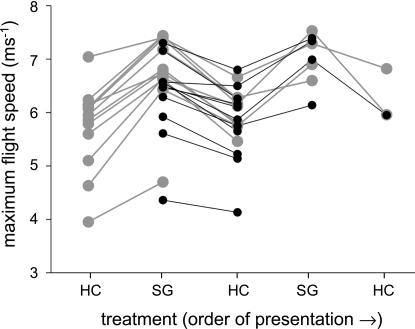
To determine whether external flow conditions are the primary cause of the observed flight instabilities (as opposed to internally generated force asymmetries, for example), we measured maximum flight speed in 24 individual bees as the flow grids were alternated. Bees reached significantly higher maximum speeds when flying in front of the square grid with less variable flow (paired t test, P < 0.0001; average difference ± 1 SD = 0.76 ms⁻¹ ± 0.32 ms⁻¹, n = 24). This difference in maximum flight speed was repeatable over multiple alternations of the 2 grids (Fig. 2), demonstrating that flow variability underlies the flight instabilities that limit maximum speed.

Fig. 2.

Effect of flow variability on maximum flight speed in Euglossa imperialis. Lines connect maximum speeds for individual bees flying in front of the air jet as honeycomb (HC; high flow variability) and square grids (SG; lower flow variability) were alternated. Some bees flew with the honeycomb in place initially (n = 13, gray) and others with the square grid (n = 11, black). Symbols represent the higher of 2 maximum speeds recorded for each treatment. Maximum speed was significantly higher when the square grid was in place (paired t test on maxima over all alternations, P < 0.0001).

Wild orchid bees forage for diverse resources, which can be found anywhere from the forest floor (e.g., rotting wood) to the top of the canopy (e.g., flowering canopy trees), and thus bees fly at all vertical levels of the forest (24). Foraging bees will encounter significantly higher flow velocities and greater variability in the upper canopy (15) (Fig. S1) as well as over open terrain (16). Orchid bees may fly at high speeds in the natural environment for a number of reasons—to cover long distances while foraging over large areas, transit quickly through exposed habitats, escape from aerial predators, or simply to progress forward in the face of a strong headwind. Although wild bees may only rarely approach their maximum flight speed or experience the severe flight instabilities observed here, active stabilization via hindleg extension is initiated at relatively low forward speeds and low levels of flow variability (Fig. 1B and Fig. S1). Thus, bees are likely to display this stabilizing behavior at times in the natural environment, particularly when flying in higher levels of the forest or over open terrain, increasing their power requirements substantially. Additionally, we found that individual bees vary widely in their ability to maintain stable flight at higher speeds (Fig. 1A), which may differentially influence their ability to collect canopy resources, cover large foraging ranges, or escape from aerial predators. These findings point to the need for further studies exploring the effects of aerial turbulence and environmental flow variability on the locomotor performance, energetic costs, and spatial habitat use of flying animals.

Materials and Methods

Flight Experiments and Drag Measurements.

Flight experiments were performed in a small forest clearing on Barro Colorado Island, Panama (09.15° N, 79.85° W). An air jet was created by removing the working section from a small wind tunnel and reversing the motor to force air through a tapering section terminating in a 10-cm square opening. Artificial scents (cineole, eugenol, methyl salicylate, or benzyl acetate) were placed inside a streamlined pipette tip, which was aligned to the flow and secured in the center of the air jet opening with monofilament. The air jet and other equipment were assembled inside a large screen enclosure, which was sealed to isolate individual bees (Euglossa imperialis) once they located the scent source. Airspeed was increased gradually, and bees were filmed at 1,000 frames s⁻¹ (Redlake MotionMeter or Fastec TroubleShooter) from a dorsal or lateral view while flying at a range of forward velocities.

For measurements of maximum flight speed, air velocity was increased until instabilities caused bees to crash vertically or laterally out of the air stream. Air velocity was measured with a TSI VelociCalc digital anemometer inserted into the air stream after each flight bout. For maximum flight speed in Fig. 1A, at least 3 separate measurements of maximum speed were obtained for each bee, and the highest value was reported. A honeycomb flow straightener with 0.3-cm round openings was placed in the wide end of the tapering section of the air jet for these measurements, all video footage, and measurements of body drag. This was alternated with a square grid with 3.175-cm square openings for the experiment presented in Fig. 2. In this experiment, maximum flight speed of an individual bee was measured twice with each grid in place, and grids were alternated until bees lost interest in the scent source. The maximum value recorded with each grid in place (over all trials) was used to calculate the maximum speed difference. After flight experiments were completed, bees were weighed and photographed.

Total body drag was measured by placing dead bees on a pin protruding laterally from a one-dimensional force transducer attached to a digital voltmeter. Bees were positioned in front of the outdoor air jet with their bodies approximately horizontal, and drag was measured at each bee's maximum flight speed with legs tucked and fully extended. A tapered shield was constructed to reduce drag on the pin, and the system was verified by comparing drag measured on a small sphere to theoretical predictions.

Video Analysis.

The percentage of time rolled was measured in 8 individuals, each filmed flying at 3–7 different speeds (34 total clips, average time per clip ± 1 SD = 1.81 ± 0.76 s; minimum = 0.748 s). Four of these individuals were filmed from a dorsal view and 4 from a lateral view. Asymmetry in leg and wing position was used to identify frames in which bees were rolled, and the number of rolled frames was divided by the total number of frames analyzed (×100) to determine the percentage of time rolled.

Leg extension was analyzed in 46 lateral video clips from 30 different individuals (5 individuals were analyzed at multiple speeds). Only frames in which the bee was perpendicular to the camera were used, and only one frame per wing stroke was analyzed (average wing strokes analyzed per clip ± 1 SD = 46 ± 19; minimum = 11). In each frame, the center of the head, tip of the abdomen, and center of the hind tibia were digitized using DLTdataviewer (by T. L. Hedrick) in Matlab. The position of the center of mass (CM) relative to the head and tip of the abdomen was determined in 2 freshly killed bees by photographing the body hanging from 3 different points of attachment; comparisons of CM position with legs tucked vs. extended revealed that leg extension has a negligible effect on the center of mass position. Based on these measurements, the CM was estimated in each analyzed video frame, and normalized leg extension was calculated as the linear distance between the CM and hind tibia, divided by total body length.

Calculation of Rolling Moment of Inertia.

Moment of inertia around the rolling axis was estimated by modeling bees' bodies and legs as simple geometric objects. The body and hind tibiae were both treated as ellipsoids, with a moment of inertia of I_z = 1/5 m(r_x² + r_y²), where I_z is the moment of inertia around the rolling axis, m is mass, and r_x and r_y are the semiaxes. When a bee has its legs tucked tightly, the body and legs can be treated as one ellipsoid, where m is total mass (average of measurements in E. imperialis) and r_x (= r_y) is the body radius (one-half of maximum body width, estimated from dorsal photographs of bees). For bees with legs extended, the moment of inertia of the body (I_body) was calculated as above, replacing total mass with the body mass (mass of body minus legs). The moment of inertia of each leg (I_leg) was calculated separately, where m is the mass of one leg (m_leg), r_x is the minor axis (one-half thickness), and r_y the major axis (one-half length) of the hind tibia, estimated from posterior photographs of bees with extended hindlegs. Using the parallel axis theorem, the total rolling moment of inertia of bees with legs extended was then calculated as I_extend = I_body + 2I_leg + 2m_legd_leg², where d_leg is the total distance (due to both vertical and lateral extension) from the rolling axis to the center of the hind tibia, based on posterior photographs.

Flow Measurements.

Flow from the air jet was measured with a 3D sonic anemometer (RM Young, model 81000) sampling an area of ≈100 cm² in front of the air jet mouth at 32 Hz. Two 10-min recordings were taken with both the honeycomb and square grid in place at mean forward velocities (U) of 0.9, 1.9, and 2.8 ms⁻¹. Three recordings were taken with each flow divider at forward velocities of 3.6, 4.5, 5.3, 6.2, and 7.1 ms⁻¹, except for the honeycomb divider at 4.5 and 6.2 ms⁻¹, where more recordings were performed (6 and 4, respectively) because of high intertrial variability. In the forest, 15-min recordings were performed with the sonic anemometer extended horizontally from a canopy tower, 3–4 m away from the tower and surrounding vegetation. Five recordings were taken at vertical heights of 5.6, 11.1, and 22.2 m; 6 recordings at 33.1 and 40.7 m; and 9 recordings at 47.8 m (above the canopy).

For all recordings, horizontal velocity components were rotated to produce a mean lateral velocity (V) of zero, and the vertical wind component (w) was unaltered (15, 17). Statistical analyses performed on the 3 velocity components produced similar results; analyses on the lateral (v) component are reported, as they may be particularly relevant to rolling instabilities. Standard deviations of velocity were calculated for each recording, and air jet data for mean forward velocities of 3.6 ms⁻¹ and above were analyzed with an analysis of variance (ANOVA) in Systat 12, testing for effects of grid type and mean forward velocity.

For spectral analysis, the mean was removed from each time series and spectral densities (S(n)) were calculated in Matlab using a fast Fourier transform and a Hamming window, based on the periodogram method of Welch (25). Nondimensional spectral densities were calculated by normalization with frequency and variance (σ²), as n * S(n)/σ². For air jet data, the effect of grid type on the normalized power spectra of frequencies above 1 Hz (the range most relevant to bee flight) (26) was analyzed using a mixed model analysis (PROC MIXED in SAS 9.1) with an autoregressive error structure, treating different frequencies as repeated measures and grid type and velocity as effects. The significance of results was unaltered by analyzing each forward velocity separately (with frequency treated as either a class or continuous variable).