Arithmetic in newborn chicks

Abstract

Newly hatched domestic chicks were reared with five identical objects. On days 3 or 4, chicks underwent free-choice tests in which sets of three and two of the five original objects disappeared (either simultaneously or one by one), each behind one of two opaque identical screens. Chicks spontaneously inspected the screen occluding the larger set (experiment 1). Results were confirmed under conditions controlling for continuous variables (total surface area or contour length; experiment 2). In the third experiment, after the initial disappearance of the two sets (first event, FE), some of the objects were visibly transferred, one by one, from one screen to the other (second event, SE). Thus, computation of a series of subsequent additions or subtractions of elements that appeared and disappeared, one by one, was needed in order to perform the task successfully. Chicks spontaneously chose the screen, hiding the larger number of elements at the end of the SE, irrespective of the directional cues provided by the initial (FE) and final (SE) displacements. Results suggest impressive proto-arithmetic capacities in the young and relatively inexperienced chicks of this precocial species.

1. Introduction

Only human adults would be considered capable of counting if numerical and language abilities were considered to be strictly correlated with one another (Dehaene 1997; Butterworth 1999; Spelke & Dehaene 1999; Hauser & Spelke 2004). Although this is likely to be correct for symbolic mathematical capacity (Carey 2004), recent evidence from clinical neuropsychology suggests a remarkable degree of independence of mathematical cognition from language grammar in human adults (Varley et al. 2005; see also Butterworth et al. 2008). Moreover, numerical competences have recently been demonstrated in a variety of species (for mammalian and bird species, see Hauser et al. 2000; Hauser & Carey 2003; Lyon 2003; Judge et al. 2005; Pepperberg & Gordon 2005; Beran et al. 2006; Cantlon & Brannon 2006a,b, 2007; Pepperberg 2006; Addessi et al. 2008; Rugani et al. 2008).

Animals and human infants are even capable of some simple arithmetic, such as addition and subtraction (reviews in Gallistel 1990; Dehaene 1997; Spelke & Dehaene 1999; Brannon & Roitman 2003).

Some of these studies employed choice paradigms involving very little or no specific numerical training. Chimpanzees (Pan troglodytes) presented with two sets of two food wells, each of which contained a number of chocolates, selected the pair of quantities whose sum was greater than the sum of the other pair (Rumbaugh et al. 1987). To choose the sets of larger overall quantity, the chimpanzees had to add up the number of chocolates in each set and then compare the two resulting values. Chimpanzees solved the task even when, on the critical trial, the correct set of wells did not contain the larger single value, demonstrating that performance was not based on choosing the largest single amount (Rumbaugh et al. 1988).

Other studies employed specific training on symbols representing numbers. Washburn & Rumbaugh (1991) trained two rhesus monkeys (Macaca mulatta) to choose between two Arabic numbers presented on a touch-sensitive screen. As a reward, the animals received the corresponding number of pellets to the number they had selected. Monkeys always chose the larger number even when they were presented with new combinations of numbers. A similar paradigm was used to test squirrel monkeys (Saimiri sciureus) on tasks requiring them to choose between pairs or triplets of Arabic numerals. Monkeys chose the larger sum and their performance could neither be attributed to choosing the largest single value nor to avoiding the single smallest value (Olthof et al. 1997). Evidence on symbolic training has been reported for apes, e.g. chimpanzees (P. troglodytes; Beran & Rumbaugh 2001).

Using the methodology of the violation of expectancy, Wynn (1992) showed that five-month-old infants can solve some simple arithmetic operations. The idea was that, if infants keep track of the numbers of toys they see being placed behind a screen, they should look longer at the screen that, once lowered, violates their expectations revealing an unexpected outcome. For example, in the 1+1=2 task, one object was placed on a stage, covered by the screen, and then another object was introduced behind the screen. When the screen was removed, infants looked longer at the ‘impossible’ outcomes of either one object or three objects, suggesting that infants expected to see exactly two objects. In the original study, continuous variables such as volume or surface area were not controlled for, thus infants might well have attended to the volume, area or contour length of the objects rather than to their actual number. Wynn's results, however, were then replicated by subsequent studies in which continuous variables were at least partially controlled for. Simon et al. (1995) replicated Wynn's paradigm, but used ‘Elmo’ dolls in the initial phase of the trials and then surreptitiously replaced ‘Elmo’ dolls with ‘Ernie’ dolls. The infants' expectations were not violated by this identity switch. They looked longer only at the numerically unexpected outcome and not at the identity of the outcome. This indicates that, in some sense, infants represent the number of objects stripped of their non-numerical features. Moreover, they do so even across sensory modalities. Five-month-old infants underwent preliminary familiarization trials in which tones were paired with objects, thereby, they learned to associate the two events. At test, the infants were presented alternatively with two types of arithmetic events: the expected, correct outcome operations (one object+one tone=two objects; and one object+two tones=three objects) or the unexpected, incorrect ones (one object+two tones=two objects; and one object+one tone=three objects). Infants looked longer at the unexpected outcomes rather than at the expected ones (Kobayashi et al. 2004).

Wynn's paradigm was also adapted to test arithmetic reasoning in rhesus monkeys (M. mulatta). Subjects viewed food items. A screen was then raised to obscure the items on the stage. Some items were then added or removed from behind the screen. Finally, the screen was lowered to reveal an expected or unexpected number of objects and looking time was measured. Monkeys looked longer when the unexpected outcome was revealed for 1+1=1 or 2 and 2−1=1 or 2 operations (Hauser et al. 1996), even when continuous variables, such as volume and surface area were partially controlled for (Hauser & Carey 2003). Cotton-top tamarins (Saguinus oedipus) and lemurs (Eulemur fulvus, Eulemur mongoz, Lemur catta and Varecia rubra), if presented with the 1+1 operation, looked longer at the unexpected outcome of 3 or 1 compared with the expected value of 2, demonstrating that subjects expected ‘exactly 2’ (Uller et al. 2001; Santos et al. 2005). Also, using a choice measure, expressed by reaching rather than looking time, Sulkowski & Hauser (2001) have shown that rhesus monkeys are remarkably precise at calculating the outcome of subtraction operations for small numbers up to 3. Even domestic dogs have been shown to be capable of solving simple additions such as 1+1=2 rather than 1 or 3 (West & Young 2002). In all these studies, regardless of the paradigm employed, participants were able to compute the correct outcome of simple arithmetic operations whenever both sets were small (upper limit of 4 for adult rhesus monkeys and upper limit of 3 for human babies), but failed whenever any of the sets exceeded such limit: rhesus monkeys failed at three versus eight (Hauser et al. 2000); infants failed at 2 versus 4, 3 versus 6, 1 versus 4 and even 0 versus 4 (Feigenson & Carey 2005). Nevertheless, several other studies showed that animals succeed when dealing with large as well as small sets. Rhesus monkeys (Brannon & Terrace 1998, 2000), socially housed hamadryas baboons, socially housed squirrel monkeys (Papio hamadnjas, Saimiri sciureus; Smith et al. 2003) and brown capuchin monkeys (Cebus apella; Judge et al. 2005) trained to order numerosities from 1 to 4, could then generalize to numbers from 5 to 9. Monkeys trained to respond (in ascending or descending order) to pairs of numerosities (1–9) spontaneously ordered in the same direction new pairs of larger values (i.e. 10, 15, 20, 30; Cantlon & Brannon 2006b). Chimpanzees were able to summate different sets of food items and to select the larger quantities in the comparison 5 versus 8; 5 versus 10 and 6 versus 10 (Beran & Beran 2004) and 2+2+3 versus 3+4+1 (Beran 2001). Monkeys could also sum different numbers of dots and select the correct response in a matching-to-sample task even when large numerosities were employed (Cantlon & Brannon 2007).

The present study aimed at extending comparative research on the spontaneous representation of number to very young birds, employing filial imprinting to familiarize the animals with a certain number of elements (see Vallortigara (2004, 2006) for general reviews on the use of imprinting as a tool for comparative cognitive investigation). Thus, no specific numerical training was performed and the results obtained allow some conclusions to be drawn on the spontaneous ability of animals to deal with simple arithmetic tasks. Moreover, the use of very young and inexperienced animals may enlighten us with regard to core knowledge mechanisms (Spelke 2000, 2003) in the vertebrate brain, in particular, concerning the extent to which arithmetic capacities depend on acquired experience versus inborn predispositions (for similar research in the domain of geometry cognition see Vallortigara (in press a,b)).

2. Experiment 1

Chicks were required to identify the larger between a set of two and a set of three elements (i.e. small balls, all identical) by walking to the location where such sets had been seen to disappear. Chicks have been shown capable of rejoining a social goal (a single imprinting ball) in the correct spatial location up to 180 s from its disappearance (Vallortigara et al. 1998; Regolin et al. 2005a,b). Here, chicks were expected to approach the larger set because, in simultaneous free-choice tests when both choice sets were visible, these birds have been shown to prefer the larger set of imprinting objects, irrespective of the number of elements that they had been exposed to during imprinting (Rugani et al. submitted). Rugani and colleagues tested chicks for their sensitivity to number versus continuous extent of artificial objects they had been reared with. When objects used during exposure were all identical to each other and were also identical to the objects used at test, chicks faced with choices between different numerosities (i.e. 1 versus 2 or 2 versus 3 objects) chose the set of larger numerosity, irrespective of the number of objects they had been reared with. When chicks were reared with objects of different aspect (colour, size and shape) and then tested with completely novel objects (of different colour and shape but controlled for continuous extent), they chose to associate with the set of objects comprising the same number of elements they had been reared with during imprinting. Note, however, that in the study presented here, the choice could not be based on direct perceptual cues associated with visible elements, but must have relied on the memory of the disappeared sets and of their spatial position.

(a) Materials and methods

(i) Subjects and rearing conditions

Subjects were 17 female ‘hybro’ (a local variety derived from the white leghorn breed) domestic chicks (Gallus gallus), obtained weekly from a local commercial hatchery (Agricola Berica, Montegalda, Vicenza, Italy) when they were only a few hours old. On arrival at the laboratory, chicks were immediately housed singly in standard metal home cages (28 cm wide×32 cm long×40 cm high) at controlled temperature (28–31°C) and humidity (68%), with food and water available ad libitum in transparent glass jars (5 cm in diameter, 5 cm high) placed at each corner of the home cage. The cages were constantly (24 h d⁻¹) lit by fluorescent lamps (36 W), located 45 cm above each cage. Each chick was placed in one cage together with a set of five identical rounded objects made of yellow plastic. Each object was a ‘Kinder surprise’ capsule (Ferrero S.P.A. Alba, Cuneo, Italy) measuring 4×3×3 cm, which we will hereafter refer to as a ‘ball’. Previous studies have shown that this kind of object is very effective in producing social attachment through filial imprinting in this strain of chicks (Vallortigara & Andrew 1991). The five balls placed in each cage constituted the chicks' imprinting stimulus and were each suspended in the centre of the cage by a fine thread, at approximately 4–5 cm from the floor, so that they were all located at about chicks' head height.

Chicks were reared in these conditions from the morning (11.00) of the first day (i.e. Monday, the day of their arrival, which was considered as day 1) to the third day (Wednesday). All chicks underwent two testing phases. In the morning (11.00) of day 3, chicks underwent the training, and approximately 1 hour later, they took part in the first testing session. A second testing session took place in the morning (09.00) of day 4.

(ii) Apparatus

Training and testing took place in an experimental room located near the rearing room. In the experimental room, temperature and humidity were controlled (respectively, at 25°C and 70%). The room was kept dark, except for the light coming from a 40 W lamp placed approximately 80 cm above the centre of the apparatus. The testing apparatus (figure 1) consisted of a circular arena (95 cm in diameter and 30 cm outer wall height) with the floor uniformly covered by a white plastic sheet. Within the arena, adjacent to the outer wall, was a holding box (10×20×20 cm), in which each subject was confined shortly before the beginning of each trial. The box was made of opaque plastic sheets, with an open top allowing the insertion of the chick before each trial. The side of the holding box facing the centre of the arena consisted of a removable clear glass partition (20×10 cm), in such a way that the subjects, while confined, could see the centre of the arena. During the training phase, a single opaque cardboard screen (16×8 cm; with 3 cm sides bent back to prevent the chicks from spotting the hidden ball) was used, positioned in the centre of the arena, in front of and 35 cm away from the front of the holding box. During testing, two opaque cardboard screens (16×8 cm), identical in colour and pattern (i.e. blue coloured with a yellow ‘X’ on them), were positioned in the centre of the arena, symmetrically with respect to the front of the confining box (i.e. 35 cm away from it and 20 cm apart from one another).

Figure 1.

The test apparatus employed in all of the experiments described. The holding box is visible to the left, both screens are present, as during the test phase. One ball is visible behind one of the screens.

(iii) Procedure

Training

On day 3 of life, in the morning, chicks underwent a preliminary training session. Each chick, together with a single ball, identical to one of the five balls constituting the chick's imprinting object, was placed within the testing arena, in front of one of the screens. The ball was held from above by the experimenter (not visible to the chick), via a fine thread, and kept between the holding box and the screen. The chick was left free to move around and get acquainted with the environment for approximately 5 min. Thereafter, the experimenter slowly moved the ball towards the screen, and then behind it, until the ball disappeared from the chick's sight. This procedure was repeated a few times, until the chick responded by following and rejoining the ball behind the screen. Thereafter, the chick was confined within the holding box, from where it could see the ball being moved behind the screen. As soon as the ball had completely disappeared from sight, the chick was set free in the arena by lifting the transparent frontal partition. Every time the chick rejoined the ball, as a reward, it was allowed to spend a few seconds with it. The whole procedure was restarted and the training ended when the chick had rejoined the ball three consecutive times. On average, approximately 15 min were required to complete the training for each chick.

Testing

During testing, the chick was confined to the holding box, behind the transparent partition, from where it could see the two screens positioned in the arena. The chick was shown two sets of elements, one made of three of the five imprinting balls and the other made of two such balls (placed at first at approx. 10 cm from the front of the holding box containing the chick). Both sets disappeared, each behind one of the two screens. Immediately after the disappearance of both sets (with a delay of 5 s), the transparent partition was removed and the chick was left free to move around and search for its imprinting balls within the arena. To prevent the chicks from seeing the hidden balls before having circled almost completely around the screen, the screens were provided with 3 cm bent back edges on the two vertical sides. A choice was defined as when the chick's head had entered the area behind one of the two screens (beyond the side edges), only the choice for the first screen visited was scored and thereafter the trial was considered over. At the end of each trial, chicks were allowed to spend 1–2 s with their ‘social companions’ behind the screen chosen by the chick. The behaviour of the chicks was entirely video-recorded and it was scored blind both online and later offline.

If the chick did not approach either screen within 3 min, the trial was considered null and void and it was repeated immediately afterwards. After three consecutive null trials, the chick was placed back within its own rearing cage (in the presence of the imprinting balls) for approximately 1 hour before being resubmitted to further trials. After another three consecutive null trials, the same procedure was repeated and if, once again, the chick scored for the third time three consecutive null trials, it was discarded from the experiment.

Each chick underwent two complete testing sessions of 20 valid trials each. The two test sessions differed in the procedure by which the balls were made to disappear behind the two screens:

Simultaneous disappearance test (SDT). Both sets of three and two elements were placed in the arena in front of the chick confined in the holding box. After approximately 3 s, both sets were simultaneously made to slowly move and disappear each behind one different screen (the whole procedure took approx. 8–10 s).

Consecutive disappearance test (CDT). For each trial, each of the balls of the first set was placed singly in front of the confined chick and then made to disappear before the next ball was introduced in the arena. In this way, all balls of the first set were made to disappear one by one behind one screen, and then the same procedure was employed for the second set. For both sets, each ball was kept for approximately 3 s in front of the chick before making it move and disappear behind either screen (the whole procedure took approx. 50 s). During the disappearance phase, the speed of motion of the items of each set was manipulated so that it took the same total time to disappear for the set of three and for the set of two. Disappearance of each whole set took approximately 18 s (i.e. 6 s for each element in the set of three and 9 s for each element in the set of two).

For both the SDT and the CDT, the order (3–2 versus 2–3) as well as the direction (left–right) of disappearance of the two sets was counterbalanced within each chick's 20 test session trials.

The number of trials in which each chick chose the screen hiding three balls (correct choice) was considered and percentages were computed as: number of correct choices/20×100. Parametric paired t-tests (to compare different conditions) or one-sample t-tests (to assess significant departures from chance level, i.e. 50%) were used. Non-parametric statistics were performed employing the binomial test.

(b) Results and discussion

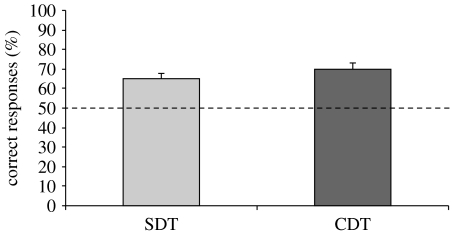
All chicks took part in the first test administered (whether SDT or CDT), but four chicks were discarded from the second test (two chicks did not take part in the SDT, and two did not take part in the CDT) due to unsatisfactory health condition. Chicks preferentially chose the screen hiding three balls over the screen hiding two balls both in the SDT (n=15; mean=65.000, s.e.m.=2.536; one-sample t-test: t₁₄=5.915; p<0.001) and in the CDT (n=15; mean=70.000, s.e.m.=3.047; one-sample t-test: t₁₄=6.564; p<0.001) trials (figure 2). There was no statistically significant difference between correct choices in the two testing conditions (two-sample t-test: t₂₈=1.261; p=0.218).

Figure 2.

Results of experiment 1. Percentage of correct responses (group means+s.e.m.) scored by chicks that underwent the SDT or the CDT. The dashed line (y=50) represents chance level.

In order to assess whether the overall performance depended on learning, occurring during testing, the first five trials of each session were considered. Since there was no difference between the two groups (two-sample t-test: t₂₈=1.684, p=0.103; SDT: n=15, mean=58.667, s.e.m.=4.563; CDT: n=15, mean=70.667, s.e.m.=5.474), data were merged and overall, chicks preferentially chose the larger set (n=30; mean=64.667, s.e.m.=3.674; one-sample t-test: t₂₉=3.992, p<0.001).

We also performed a non-parametric (binomial) analysis on chicks' initial performance. As this was the chicks' behaviour in the very first trial affected by the response to the novelty of the situation (e.g. two screens were present in the arena), the first three trials were considered. Twenty-three chicks were considered successful as they scored at least two correct trials within the first three, and seven chicks were considered as unsuccessful (they scored at least two mistaken trials out of three). The difference (23 versus 7) was significant (binomial test, one tail, p=0.0026).

Chicks' performance could not be based on the average presentation time of the two sets of stimuli, because this was identical in the SDT, and was equalized in the CDT. Results confirmed that, in the absence of any specific training, chicks spontaneously discriminated between sets of two and three elements, preferring the larger set (Rugani et al. submitted), and did so even when such a discrimination must have been based on the memory of the disappeared sets and of their relative spatial position.

3. Experiment 2

Experiment 1 showed that chicks spontaneously master the discrimination of two versus three identical elements after these had been hidden from view. In experiment 2, a similar procedure was employed using new stimuli allowing us to control for continuous variables, such as overall area and contour length. Our hypothesis predicted that chicks should be able to discriminate 2 versus 3 independently of the use of such variables, since such discrimination would still be possible when operating within a system computing small numerosities (Hauser & Spelke 2004). However, some doubt has been raised recently as to whether human infants and non-human animals really compute numerosity: when number is pitted against continuous dimensions correlating with number (e.g. area and contour length), infants sometimes respond to continuous physical dimensions (Feigenson et al. 2002a,b). Nevertheless, it has been shown that monkeys are able to compute number rather than other dimensions in a matching-to-sample numerical task (Cantlon & Brannon 2007). That is not to say that preverbal infants cannot respond to number themselves, but that they do so only sometimes. For instance, when objects to be discriminated belong to a domain in which the continuous extent is especially relevant, such as food, infants indeed tend to respond to the overall amount rather than to number (Feigenson et al. 2002a,b). But, when the task requires reaching for individual objects, number encoding prevails over physical extent (Feigenson 2005). Using conditioning procedures, even newborn chicks are able to discriminate small sets of elements on the basis of number when both area and contour length are controlled for (Rugani et al. 2008).

(a) Materials and methods

(i) Subjects

Subjects were a new group of 16 female domestic chicks. Rearing conditions were identical to those described for the first experiment.

(ii) Stimuli

Imprinting stimuli were identical for all chicks and consisted of a set of five identical, two-dimensional (approx. 1 mm thick), red plastic squares (4×4 cm).

Test stimuli also consisted of red squares, identical in material and colour to those used for imprinting, but differing in their dimensions in each of three control groups. In the two-dimensional stimuli control group (n=7), the original dimensions of the stimuli were maintained, so that the single squares were all identical in the sets of three and two elements. This control was aimed at determining whether chicks responded to two-dimensional imprinting stimuli in the same way as they did to the solid objects in experiment 1. Both in the contour length (n=5) and in the area (n=4) control groups, the set of two elements comprised squares of dimensions identical to those used during imprinting, while the set of three elements comprised smaller sized squares. The dimensions of each square in the set of three elements were computed in order to equate the overall contour length (with squares measuring 2.66×2.66 cm each) or the overall area (with squares measuring 3.26×3.26 cm each) in the two sets. The overall time of disappearance of the two sets was equalized as detailed in §2a(iii).

(iii) Procedure

The apparatus, the general training and testing procedures were identical to those described in the CDT of the previous experiment, with each chick undergoing 20 test trials on day 3.

(b) Results and discussion

No difference (F_2,13=1.824; p=0.200) emerged at an analysis of variance (ANOVA) comparing the percentage of correct responses emitted by the three groups of chicks (two-dimensional stimuli control group: n=7, mean=67.143, s.e.m.=1.844; contour length control group: n=5, mean=62.000, s.e.m.=2.000; and area control group: n=4, mean=63.750, s.e.m.=3.750). Data were therefore merged, and the resulting mean (n=16, mean=64.688, s.e.m.=1.405) was significantly above chance level (one-sample t-test: t₁₅=10.454, p<0.001).

When analysing chicks' initial performance (considering the first three trials, as described for the data of experiment 1), a statistically significant difference was found as 13 chicks out of 16 were successful (binomial test, one tail, p=0.0106).

Chicks preferentially chose the screen hiding the set of three elements in all conditions.

Results confirmed the ability of chicks to discriminate sets of 2 versus 3 elements selectively preferring the larger set even when such discrimination must be based on the actual number of the non-visible sets of objects and was not based on differences in continuous variables, such as contour length, area or time of disappearance.

4. Experiment 3

In the third experiment, we checked whether chicks can also update their representation of the sets of stimuli by processing subsequent events. After the initial disappearance of the two sets of elements (similarly to the previous experiments), some of the elements were visibly transferred from behind one screen to behind the other one. Such condition should represent a more challenging task than those of the previous experiments, since the chicks' final choice would now depend on correctly taking into account a series of subsequent displacements. The possible cues provided by the order of disappearance of stimuli in guiding chicks' discrimination were controlled for.

(a) Materials and methods

(i) Subjects

Subjects were a new group of 19 female domestic chicks. Rearing conditions were identical to those described for the previous experiments.

(ii) Procedure

Apparatus, general training and testing procedures were the same described for the previous experiments. At test, one ball at a time was placed in the arena and was slowly moved towards and behind one screen. The procedure was repeated for all five balls in such a way that a different number of them (depending on the experimental condition, see below) was eventually concealed behind either screen. This disappearance phase constituted the first event (FE). Approximately 5 s after the last ball had disappeared, and while the chick was still confined to the holding box, some of the concealed balls were slowly and visibly moved (one ball at a time) from one screen towards and behind the other screen (second event, SE). After a delay of 5 s from the end of the SE, the chick was released in the arena. Regardless of the balls position after the FE, all four tests provided, as a result of the SE, a final comparison of two versus three balls. Chicks performed a correct choice when approaching the screen hiding the three elements.

Each chick underwent only one of two different test conditions:

1. FE controlled (FEC) (n=8). In order to choose the screen hiding the larger amount, i.e. the three balls, the chicks entering this condition would need to choose against the cue provided by the initial displacement of the balls. In fact, at the end of the FE, the larger set was located behind the screen which hid two balls at the end of the SE (i.e. the wrong one). This was obtained in two different manners: ‘(4−2) versus (1+2)’ and ‘(5−3) versus (0+3)’ (the names refer to the events taking place at the correct screen).

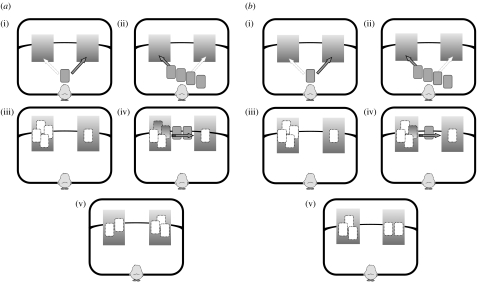
2. (4−2) versus (1+2). The chicks (n=4) saw four balls disappearing behind one screen and the remaining one disappearing behind the other screen. Subsequently, two balls moved from the screen hiding four balls to the other screen. At the end, the screen initially hiding one ball only, hid three balls and represented the correct choice (figure 3a).

3. (5−3) versus (0+3). In front of the chicks (n=4), five balls disappeared behind one screen and none disappeared behind the other screen. Then, the chick saw three balls that moved from the screen hiding the group of five, to the other screen. Therefore, the screen initially hiding no balls, at the end hid three balls and constituted the correct choice.

4. Last event controlled (LEC) (n=11). The SE now involved a movement from the screen that was to be considered as correct (hiding the larger number of elements) to the wrong screen (hiding the smaller number of elements). Therefore, in order to choose the correct screen chicks would need to choose against the directional cue provided by the final visible displacement. This was obtained in two different manners: ‘(4−1) versus (1+1)’ and ‘(5−2) versus (0+2)’ (again, the names refer to the events taking place at the correct screen).

5. (4−1) versus (1+1). Chicks (n=7) saw four balls disappear behind one screen and the remaining one behind the other screen. Then, one ball moved from the group of four to the other screen. Therefore, the screen initially hiding four balls now hid three balls and represented the correct choice (figure 3b).

6. (5−2) versus (0+2). Chicks (n=4) saw five balls disappear behind one screen and none behind the other. Two balls were then moved from the group of five to the other screen. Therefore, the screen initially hiding five balls now hid three balls and constituted the correct choice.

Figure 3.

Schematic representing, from the perspective of the confined chick, the events occurring in experiment 3 within: (a) one possible trial of the FEC test (in the ‘(4−2) versus (1+2)’ condition, see text); (b) one possible trial of the last event controlled test (in the ‘(4−1) versus (1+1)’ condition, see text). (a(i)) FE: one ball is hidden behind one screen. (ii) Four balls are hidden—one by one—behind the other screen. The sequence of events and the directions were randomized between trials. (iii) At the end of the first displacement either four or one ball(s) are hidden behind each screen. (iv) SE: two balls move—one by one—from the screen hiding four to the one hiding a single ball. (v) Test: the chick is released in the arena and should rejoin the larger number of imprinting balls, which is NOT behind the screen where the larger number of balls had initially disappeared. (b(i)) FE: one ball is hidden behind one screen. (ii) Four balls are hidden—one by one—behind the other screen. The sequence of events and the directions were randomized between trials. (iii) At the end of the first displacement either four or one ball(s) are hidden behind each screen. (iv) SE: one ball moves from the screen hiding four to the one hiding a single ball. (v) Test: the chick is released in the arena and should rejoin the larger number of imprinting balls, which is NOT behind the screen where the final hiding of balls has been observed.

For both conditions (FEC and LEC), whenever the initial displacement involved two hiding events (i.e. four balls going behind one screen and one (or two) ball(s) going behind the other screen), the order of such events (i.e. which one occurred before and which after the other) was counterbalanced throughout the 20 testing trials administered to each chick, as well as the left–right direction of the disappearance of the two sets. Sets' disappearance times could not be equalized in this experiment due to procedural contingencies (e.g. one set disappeared in one direction and no elements disappeared in the opposite direction).

Each chick underwent one single testing session (20 trials). For each chick and for each group, the mean percentage of choices of the screen hiding three elements were computed. Non-parametric statistics were performed employing the binomial test.

(b) Results and discussion

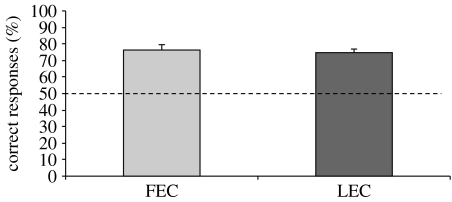
Results are represented in figure 4.

Figure 4.

Results of experiment 3. Percentage of correct responses (group means+s.e.m.) shown by chicks that underwent the FEC or the LEC conditions. The dashed line (y=50) represents chance level.

(i) FE controlled

No significant difference (two-sample t-test: t₆=0.785; p=0.463) was found between the groups: (4−2) versus (1+2) (n=4, mean=78.750, s.e.m.=3.750) and (5−3) versus (0+3) (n=4, mean=73.750, s.e.m.=5.154). Overall (n=8, mean=76.250, s.e.m.=3.098) chicks significantly chose the screen hiding the larger number of elements (one-sample t-test: t₇=8.473, p<0.001).

When limiting the analysis to the first five test trials, no statistically significant difference was found between the two conditions (two-sample t-test: t₆=0.522, p=0.620). Overall, chicks significantly approached, from the very beginning of the test, the screen hiding the larger set at the end of the SE (n=8, mean=77.500, s.e.m.=4.531; one-sample t-test: t₇=6.069, p<0.001).

(ii) LE controlled

No significant difference (two-sample t-test: t₁₀=1.053; p=0.317) was found between the (4−1) versus (1+1) (n=7, mean=76.586, s.e.m.=2.978) and the (5−2) versus (0+2) (n=5, mean=71.556, s.e.m.=3.826) conditions. Overall, chicks preferentially chose the correct screen (n=12, mean=74.490, s.e.m.=2.366; one-sample t-test: t₁₁=10.347, p<0.001).

When limiting the analysis to the first five test trials, no difference was found (two-sample t-test: t₁₀=0.078; p=0.938) between the two test conditions. Overall, chicks significantly preferred the correct screen even within the first five test trials (n=12, mean=76.667, s.e.m.=4.820; one-sample t-test: t₁₁=5.533; p<0.001).

There was no difference between FEC and LEC conditions (two-sample t-test: t₁₈=0.458; p=0.652). Chicks selectively approached the screen hiding the larger number of elements (n=20, mean=75.194, s.e.m.=1.843; one-sample t-test: t₁₉=13.667; p<0.001). Their response was based neither on the first site, where the larger number of objects had been seen to disappear, nor on the most recent directional cue provided by the very last displacement.

When chicks' initial performance was analysed with non-parametric statistics (considering the first three trials, as described for the data of experiment 1), the difference between successful and unsuccessful chicks (i.e. 13 out of 19) was marginally non-significant (binomial test, one tail, p=0.0835). We expected chicks' performance to be worse in experiment 3, as the conditions were much harder than those of the previous experiments. Nevertheless, when analysing chicks' overall scores in the 20 trials, and considering successful any chick that took at least 14 out of 20 (binomial test, one tail, p=0.0577) correct trials, then overall 14 out of 19 chicks were successful (binomial test, one tail, p=0.0318).

It should be pointed out that, although chicks were choosing against the initial or the final events, they must have properly computed such events in order to make a correct final choice.

5. General discussion

The results of experiments 1 and 2 showed that, in the absence of any specific training, chicks spontaneously discriminated between two and three, in both cases preferring the larger stimulus set. The discrimination was based on the memory of the spatial position of the disappeared objects, since any direct assessment of the sensory stimuli associated with the two sets was not possible at the time when chicks were allowed to choose between the two screens. Hence chicks' behaviour seemed to indicate an ability to perform additions, i.e. combining two or more quantitative representations (addends) to form a new representation (i.e. the sum).

Quite interestingly, the discrimination held for both the simultaneous disappearance of all the elements of a set of stimuli as well as for the one-by-one (i.e. sequential) disappearance of the single elements of the set. Indeed, the performance tended to be slightly better in the latter case, although this difference could not be due to cues provided by differences in the time of disappearance of the two sets as this variable had been equalized in the first two experiments.

The results of experiment 2 showed that discrimination was based on the number, and not on the continuous physical variables that may covary with number, such as area, contour length or time of disappearance during stimuli presentation. Evidence has been reported that when the number is pitted against continuous dimensions that correlate with number (e.g. area and contour length), infants sometimes seem to respond to continuous physical dimensions (Feigenson et al. 2002a,b). Nonetheless, evidence has been collected showing that human infants also encode discrete numbers as well as continuous extent (Feigenson & Carey 2003). It seems that when the objects in an array differ in their individual characteristics (such as colour, shape, texture), infants rely on the number rather than spatial extent, whereas the reverse is true for sets of homogeneous objects (Feigenson 2005). Somewhat similar results were obtained in the study by Rugani et al. (submitted; see §2) in which chicks, were directly facing the two sets of objects while choosing between them at test, so that encoding them as a homogeneous or heterogeneous array of elements was perceptually apparent. In the task studied here, by contrast, summation and subtraction required an updating of stored memory representations of small arrays that were no longer visible.

Updating of stored representations by chicks is particularly impressive in experiment 3. Here, after the initial disappearance of the two sets of objects behind both screens, some of the objects were again visibly transferred from one screen to the other before the chick was allowed to search. Thus, an initial addition and a subsequent subtraction of elements were needed in order to determine the screen hiding the larger number of elements at the end of the two events. Chicks correctly chose the screen hiding the larger number of elements irrespective of the directional cues provided by the initial or final movement of the elements.

Human infants seem to show a failure when an exact numerical representation has to include more than three objects (review in Hauser & Spelke 2004). A signature limit similar to that described for young infants has been reported for adult monkeys (Hauser & Spelke 2004), and it was also observed in chicks, although in a different task and on animals a few days older than those used here (Rugani et al. 2008). In the present study, however, chicks seem to go beyond such a limit, for, in order to perform the arithmetic discriminations described in experiment 3, they must have represented five distinct individuals exactly.

It can be speculated that altricial and precocial species may differ in signature limits (or in their timing of appearance in life) in exact numerical representations. Moreover, the signature limit may be task specific, in the sense that it is shaped by the specific demands of the ecological conditions in which a certain numerical computation has evolved. If so, we could perhaps expect that chicks' signature limits would be defined by their typical brood size (i.e. approx. 8–10 siblings).

The capacities exhibited by young chicks appear to be really noteworthy, particularly considering that, in the very brief period of rearing that preceded testing, the animals had no possibility to experience the sorts of events they were faced with at test, since the chicks were reared singly with the suspended balls (and without any experience of occluding surfaces in their home cage). We cannot exclude of course that, over their first days of life, chicks experience (in their home cage) would contribute to some familiarization with quantity manipulation. Besides the imprinting objects, chicks in their home cages were exposed to food, water and the dishes. For example, chicks may learn that the level of chicks' starter food decreases over the time spent eating. Nevertheless, we regard it unlikely for the chicks to experience precise computation of actual subtraction of food elements (we see no possible way for them to experience additions) while eating, as their food (i.e. standard chicks' starter crumbs) was not made of discrete elements (as would occur, for example, if the chicks were fed seeds), but rather of clumped aggregate of grain flour. Moreover, although food amount in the dish could somewhat diminish daily, new food was constantly added so that its level was kept constant.

Chicks could apparently maintain a record of the number of hidden objects comprising two distinct sets, updated by arithmetic operations of addition and subtraction computed on the basis of only the sequential visual appearance and disappearance of single separate objects. Models based on the idea of an operating ‘accumulator’ are common in the theoretical analyses of how animals can perform counting in the absence of verbal tags (Meck & Church 1983). However, to the best of our knowledge, this is the first evidence showing that sequential addition and subtraction can be successfully performed by animals on the same sets.

We believe that the findings presented here provide striking support to the ‘core knowledge’ hypothesis (Pica et al. 2004; Dehaene et al. 2006; Spelke & Kinzler 2007) according to which mental representations of number (as well as other basic representations such as those of physical objects, animate objects and geometry) would be in place at birth and shared among vertebrates.