Flight speeds of swifts (Apus apus): seasonal differences smaller than expected

Abstract

We have studied the nocturnal flight behaviour of the common swift (Apus apus L.), by the use of a tracking radar. Birds were tracked from Lund University in southern Sweden during spring migration, summer roosting flights and autumn migration. Flight speeds were compared with predictions from flight mechanical and optimal migration theories. During spring, flight speeds were predicted to be higher than during both summer and autumn due to time restriction. In such cases, birds fly at a flight speed that maximizes the overall speed of migration. For summer roosting flights, speeds were predicted to be lower than during both spring and autumn since the predicted flight speed is the minimum power speed that involves the lowest energy consumption per unit time. During autumn, we expected flight speeds to be higher than during summer but lower than during spring since the expected flight speed is the maximum range speed, which involves the lowest energy consumption per unit distance. Flight speeds during spring were indeed higher than during both summer and autumn, which indicates time-selected spring migration. Speeds during autumn migration were very similar to those recorded during summer roosting flights. The general result shows that swifts change their flight speed between different flight behaviours to a smaller extent than expected. Furthermore, the difference between flight speeds during migration and roosting among swifts was found to be less pronounced than previously recorded.

1. Introduction

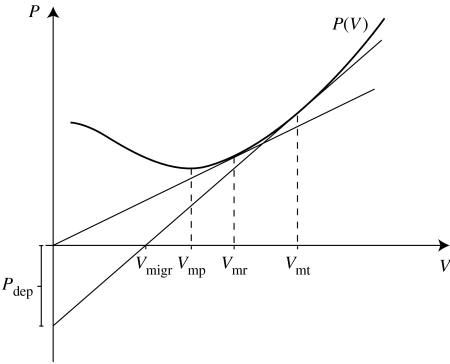
Flight mechanical theory has been recognized as a framework for understanding optimal flight speeds among migratory birds. Most central is the so-called power curve, describing the relationship between mechanical power and flight speed of the bird (Pennycuick 1968). From the power curve, three characteristic flight speeds can be derived and two of these have been proposed to be the most ecologically relevant in the migratory behaviour of birds. The exact flight speeds and the shape of the curve are often difficult to asses because many parameters are difficult to estimate (e.g. Alerstam 2003; Hedenström 2008). However, this is often not the most important issue if the relationship between flight speeds in different ecological situations can be determined. The three speeds are the minimum power speed (V_mp), the maximum range speed (V_mr) and the flight speed associated with time minimization (V_mt; Alerstam & Lindström 1990; Alerstam 1991; Hedenström & Alerstam 1995), respectively. Theoretically, V_mr will be intermediate of V_mp and V_mt (e.g. Alerstam & Hedenström 1998; figure 1). V_mp is the relevant flight speed if the aim is to minimize the energy consumption per unit time, i.e. staying aloft for as long as possible on a given amount of fuel. If the aim is instead to minimize the energy consumption per unit distance, the appropriate flight speed is V_mr, which maximizes the distance covered on a given amount of fuel. V_mt is expected in time-selected migration, likely to arise when there is something to gain from being first to occupy high-quality territories (e.g. Kokko 1999), or when matching temporally narrow peaks in food abundance is of crucial importance.

Figure 1.

A conceptual power curve. It is costly to fly slowly as well as fast. In between, the curve has its minimum that corresponds to the minimum power speed (V_mp). If a tangent is drawn from the origin to the curve, the maximum range speed (V_mr) is obtained. If the fuel deposition rate (P_dep) for a bird at stopover sites along the migratory journey is taken into account, the optimal speed is the time minimizing speed (V_mt). In this case, the y-axis is extended downwards to include the fuel-deposition rate. V_mt is found by drawing a tangent from the point of the current deposition rate to the power curve. The intercept between the tangent and the x-axis corresponds to the overall speed of migration (V_migr).

From the theory, it can also be predicted that birds adopting energy- or time-optimizing strategies should adjust their flight speed so that they increase their airspeed in headwind and reduce it in tailwind (e.g. Tucker & Schmidt-Koenig 1971; Pennycuick 1978). Liechti et al. (1994) showed that this also applies to the strength of a side wind component, with optimal airspeeds increasing with increasing side wind, provided that the birds maintain a constant track over ground.

To test whether birds adjust airspeed in accordance with predictions, we studied the nocturnal flight behaviour of common swifts (Apus apus L.) using tracking radar during spring, summer and autumn. The swift is a suitable candidate for exhibiting all of the three characteristic flight speeds. During spring migration, flight speeds are expected to be higher (closer to V_mt) than during autumn migration if the birds are time selected during spring. Swifts experience competition at the breeding areas both regarding available nest sites and mates (e.g. Lack 1956). A late arrival involves both the risk of not finding a nest and not finding a mate. During autumn migration, flight speeds closer to V_mr would be expected since the time restriction probably is less pronounced. During summer roosting flights (Weitnauer 1952, 1980; Lack 1956; Bruderer & Weitnauer 1972; Snow & Perrins 1998; Bäckman & Alerstam 2001, 2002; Tarburton & Kaiser 2001), the airspeed is predicted to be lower (V_mp) than during both spring and autumn migrations since the expected aim for the birds is to minimize energy spent per unit time during this behaviour.

2. Material and methods

(a) Study species

The common swift is renowned for its extremely aerial life style. From the moment the young swift leaves the nest, it sets out on a very long journey. It will spend almost its entire lifetime in the air, day and night. The only time swifts land for a considerable time period is during breeding, although juvenile swifts are known to roost in trees on rare occasions during extreme weather (Holmgren 2004). They forage on the wing, collect nest materials on the wing, sleep on the wing and perform yearly migrations between Europe and Africa. At night, the swifts generally roost on the wing apart from during breeding (Weitnauer 1952, 1980; Lack 1956; Bruderer & Weitnauer 1972; Snow & Perrins 1998; Bäckman & Alerstam 2001, 2002; Tarburton & Kaiser 2001). In the late evening, around sunset, swifts ascend to altitudes of 1–2 km orienting themselves into headwinds during roosting in order to minimize displacement (Bäckman & Alerstam 2001).

(b) The tracking radar

The radar used for this study is an automatic tracking radar (X-band, 200 kW peak power, 0.25 ms pulse duration, 504 Hz pulse repeat frequency and 1.5° pencil beam width). It is situated at the roof of the Ecology Building (55°42′ N, 13°12′ E, 91.5 m above sea level) at Lund University, Sweden. The radar tracking data were recorded by a computer with custom-built software that records positions every 2nd second (analysis of the effect of sampling rate on airspeed estimates, see the electronic supplementary material). The radar echo signal can be sampled for an arbitrary duration and from this wing-beat frequency is presented to the operator in real time, which makes the identification of the target being tracked relatively easy. The wing-beat frequency is derived using discrete Fourier transform analysis of echo peak amplitudes and data are stored both as the complete signal measurement as well as the calculated frequency estimates.

(c) Data acquisition and processing

(i) Bird trackings

Radar operation was performed during night time, between 23.00 and 05.00 (UTC 21.00–03.00 local time). All nights without rain clouds (which cause great disturbance to the radar signal) were chosen for operation. Data on roosting flight were collected during 1999 and 2007, and spring and autumn migration data were collected during 2006–2007. The sky was systematically searched between 5 and 35° in elevation and at approximately 2–10 km distance from the radar. Only strong and easily distinguished echoes judged to be single swifts were used for tracking. The same cues as used in Bäckman & Alerstam (2001) were used to identify swifts and distinguish them from other birds. (i) Swifts have lower wing-beat frequency (approx. 7–9 Hz) than most other birds encountered. (ii) The echo signature is characteristic, with distinct flapping and resting phases. (iii) Signal strength often changes abruptly as the swift banks during gliding bouts (Bruderer & Weitnauer 1972). Each bird was tracked during approximately 60 s during spring and autumn migrations and between 1 and 20 min during the summer roosting flights (longer tracking periods were possible for roosting birds because of their behaviour of orienting into the wind). The radar was normally operated with automatic tracking of azimuth, elevation and range, but range was sometimes tracked manually when the signal was weak. To avoid repeated measurement of the same individual, the direction of the radar antenna was changed drastically after the end of each tracking.

After acquisition, data were processed in three steps. First, each tracking was critically examined with custom-built software plotting azimuth, elevation and range separately. Obviously erroneous points in either of these were deleted and substituted by linear interpolation. Trackings with too much noise (due to rain clouds or interfering echoes) were also excluded. Second, means over 10 s intervals were calculated for each tracking to reduce noise (analysis of the effect of the length of these intervals on airspeed estimates, see the electronic supplementary material). Third, mean of these intervals was calculated to produce an estimate of the overall speed and direction for each tracking. Trackings with mean airspeeds lower than 5 m s⁻¹ or higher than 25 m s⁻¹ were considered erroneous and excluded (spring 1.7% out of total number of trackings, summer 1.6% and autumn 0.7%).

The radar echo signals were sampled and from these, the proportion of flapping and gliding phases (hereafter referred to as flap proportion) was calculated using a custom-written Matlab program that uses threshold values of signal intensity to detect when the bird was flapping its wings and when it was gliding.

(ii) Wind measurements

To measure the wind, helium balloons carrying reflectors were released from the roof of the building and tracked from the lowest possible altitude (approx. 300–500 m) up to approximately 2500 m altitude. Simultaneously, wind speed and direction at the top of the building were measured using a stationary anemometer. All recorded bird trackings were within a period of maximum 2 hours before or after a wind measurement.

Each wind tracking was post-processed in three steps. First, as with bird trackings, each file was examined and erroneous points deleted. Second, means over 30 s intervals were calculated for each tracking. Third, each averaged wind tracking was used to create a complete wind profile from the ground up to maximum altitude of each tracking with a resolution of 1 m. This was done by interpolating between the interval means. This complete wind profile was used to calculate air speed and heading of each bird tracking using wind data for the exact altitude on which the bird was flying. In order to quantify the change in wind over time, we compared the difference in calculated wind speed and wind direction between the wind profile closest in time to the tracking (the one used in the real calculation) with that calculated using the subsequent wind profile. The average difference was 2.0 m s⁻¹ in speed and 12.8° in direction.

(iii) Equivalent air speed

In order to make it possible to compare flight speeds between different trackings, airspeed was normalized by flight altitude to produce equivalent air speed (V_eq). V_eq corresponds to the air speed that represents the same dynamic pressure at sea level as the air speed at the bird's flight altitude. V_eq was calculated according to the description in the electronic supplementary material.

(d) Statistical analysis

A statistical model of the complete dataset including all three seasons; spring, summer and autumn, was derived using SPSS v. 15.0 (SPSS Inc., Chicago, IL, USA). This general linear model had V_eq as the dependent variable, season as fixed factor and side wind component (V_s), tailwind/headwind component (V_t) and vertical speed (V_z) as covariates. These are all variables that are expected to influence V_eq. V_s was calculated as the perpendicular velocity component from the recorded wind with respect to the heading direction of the bird. V_t was calculated as the velocity component from the wind parallel to the heading direction of the bird. V_eq was shown by Shapiro–Wilk test to be non-normally distributed in the spring and summer data (p<0.001; p<0.001), and therefore the complete dataset was log transformed prior to the statistical test. After this operation, spring and autumn data were normally distributed (p=0.59; p=0.12), but summer data were not (p<0.001). We found the comparison between spring and autumn to be the most crucial and chose to perform analysis on the log-transformed data. The effect of season on V_eq was analysed by examining the residuals when season was excluded from the model. Levene's test for equality of variance was performed on the residuals, which showed that the variance was significantly different between the three subsets. One-way ANOVA with post hoc test Tamhane (designed for unequal variances) was performed on the residuals to test the difference in V_eq between the three seasons.

3. Results

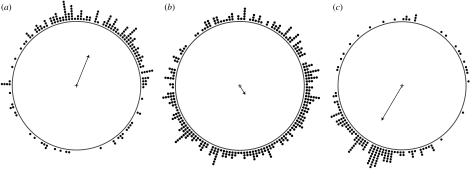
This study is based on a total of 637 trackings, of which 176 are from spring migration (May), 311 from summer roosting flights (July) and 150 from autumn migration (August). Mean directions of tracks during the three seasons are presented in figure 2, and mean values and standard deviation for variables are presented in table 1. Mean V_eq during spring was 10.6 m s⁻¹, during summer 9.0 m s⁻¹ and during autumn 9.2 m s⁻¹. Ground speed during spring was 11.5 m s⁻¹, during summer 6.4 and 8.8 m s⁻¹ during autumn. Mean vertical speed in all three cases was close to zero. Flap proportion of birds during spring was 55 per cent, during summer 66 per cent and during autumn 62 per cent. Mean track direction during spring was towards NNE (22.1°; table 1) and during autumn towards SSW (210.6°; table 1), which is expected for birds entering and leaving Sweden at the southwest corner of the country. The spring and autumn data show relatively strong mean vectors (r=0.51 and 0.63, respectively; table 1), implying low scatter, with a slightly higher scatter during spring compared with autumn. Rayleigh's test gave p<0.001, Z=46.6 and p<0.001, Z=58.7 for spring and autumn, respectively. During summer roosting flights, the track directions were highly scattered (r=0.17), while the mean vector was still significant according to Rayleigh's test (p<0.001, Z=8.8) due to large sample size.

Figure 2.

Track directions for the complete dataset with mean vector. Each of the stacked dots represents a tracking and each stack corresponds to the group of trackings within 2.5° intervals (in total 144 groups, 36 for each quadrant). The central vector in each subfigure corresponds to the mean vector, where length of the vector corresponds to the ‘directional strength’. (a) spring, (b) summer and (c) autumn.

Table 1.

Mean values and mean directions with standard deviation for the complete dataset. (Rows with track, heading and wind show r-values whereas remaining rows show s.d.)

variable	spring (N=176)		summer (N=311)		autumn (N=150)
	mean	s.d./r-value	mean	s.d./r-value	mean	s.d./r-value
ground speed (m s−1)	11.5	7.0	6.4	3.9	8.8	4.9
equivalent air speed (m s−1)	10.6	3.9	9.0	2.1	9.2	1.5
vertical speed (m s−1)	0.04	0.4	0.00	0.5	0.07	0.5
altitude (m)	980	345	1335	610	1374	474
track (°)	22	0.51	149	0.17	211	0.63
heading (°)	334	0.56	237	0.53	178	0.66
wind (°)a	271	0.54	246	0.43	110	0.25
wind speed (m s−1)	9.4	4.6	8.9	4.6	7.6	2.8

^aWind refers to the direction from where the wind is coming.

(a) Statistical model

The model that was constructed for analysing the variation in V_eq between the three seasons and description of each parameter is presented in table 2. The model includes four parameters expected to influence V_eq based on theory: V_z, V_s, V_t and season. Season had a highly significant effect on V_eq (p<0.001), while V_z did not influence V_eq significantly (p=0.750). Both wind components (V_s and V_t) were significant factors (p<0.001 and p<0.005, respectively). The effect of V_s was to increase V_eq while the effect of V_t was to decrease V_eq.

Table 2.

(a) The statistical model of the complete dataset containing all three seasons. Dependent variable is V_eq. ^** indicate significance to the level of p<0.01. R²=0.105 (Adj. R²=0.098). (b) Parameter estimates of the complete model using log-transformed V_eq. Season 1, 2 and 3 corresponds to spring, summer and autumn, respectively.

(a) parameter	d.f.	S.S.	F	p-value
season	2	0.388	21.713	0.000**
vertical speed	1	0.001	0.102	0.750
side wind	1	0.131	14.669	0.000**
tailwind	1	0.082	9.177	0.003**
error	631	5.638

			95% confidence interval
(b) parameter	B	s.e.	lower bound	upper bound
(season=1)	0.049	0.011	0.028	0.070
(season=2)	−0.013	0.010	−0.032	0.007
(season=3)	0.932	0.009	0.913	0.950
vertical speed (Vz)	0.003	0.008	−0.014	0.019
side wind (Vs)	0.004	0.001	0.002	0.006
tailwind (Vt)	−0.002	0.001	−0.003	−0.001

(b) Effect of season on flight speed

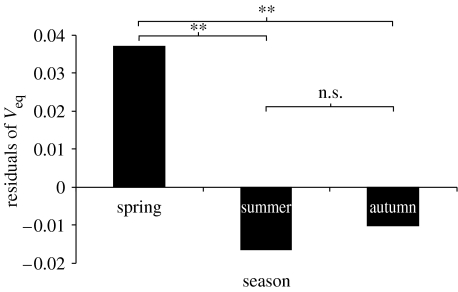
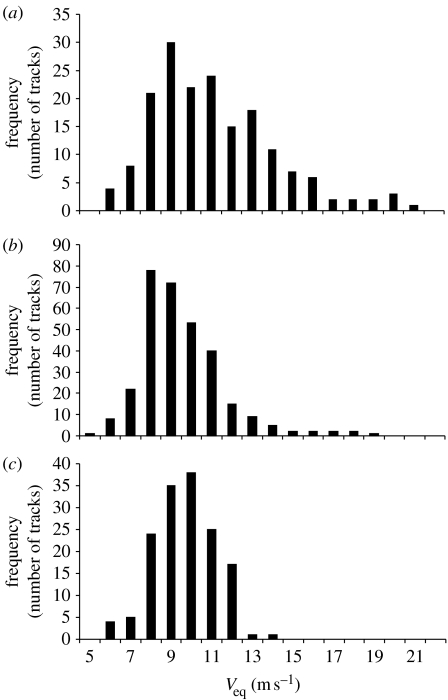
There was a significant difference in V_eq between spring and summer (p<0.001) and spring and autumn (p<0.001), but not between summer and autumn (p=0.777; figure 3). The mean flight speed during spring migration (10.6 m s⁻¹) was higher than during autumn migration (9.1 m s⁻¹), and it was the lowest during the summer roosting flights (9.0 m s⁻¹). The standard deviation in V_eq during spring (s.d.=3.04 m s⁻¹) was also higher than during autumn (s.d.=1.50 m s⁻¹), while during summer it was intermediate (s.d.=2.14 m s⁻¹). Shapiro–Wilk test of normality shows that the spring and summer data deviate from normality (p<0.001; p<0.001). For the spring data, this is due to a tail of high-speed flyers that skews the distribution towards the right (figure 4a). In summer, a similar pattern as during spring was found, but there were fewer high-speed flyers than in spring (figure 4b).

Figure 3.

Residuals of log-transformed V_eq when season was excluded from the model. ^** indicates significant difference (p<0.001). This was found by performing one-way ANOVA with Tamhane post hoc test on the residuals of V_eq between seasons when excluding season from the model.

Figure 4.

Distribution of V_eq during (a) spring, (b) summer and (c) autumn.

4. Discussion

(a) Speed differences among seasons

The main focus of this study was the difference in flight speeds during three different phases of the life of birds: spring migration, autumn migration and the special case of summer roosting flight among swifts. The choice of the swift as study species was because it was possible to reliably identify to species based on the very characteristic echo signature. The swift is expected to fly at a lower speed during roosting flight than during migration. Furthermore, the swift is predicted to fly at a higher speed during spring migration than during autumn migration, if it is of importance to arrive early at the breeding site in spring.

The prediction that swifts fly at a higher speed during migration than during roosting was supported by our observation when comparing summer and spring, but not when comparing summer and autumn.

The prediction that swifts fly faster during spring migration compared with autumn migration was in agreement with the results.

Bruderer & Weitnauer (1972) studied the spring migration and summer roosting flights of swifts. In that study, the mean air speed was found to be 11.1 m s⁻¹ during migration and 6.4 m s⁻¹ during summer roosting flights, a finding that has been generally quoted in support of adaptive speed adjustment according to flight mechanical theory. In this study, we find a less pronounced difference in flight speed between spring and summer. The difference in results between the two studies can, at least partly, be attributed to a difference in methodology; (i) spring migration was studied during night in this study and during day by Bruderer and Weitnauer, (ii) positions were logged every second in this study compared with every 20th second in the study by Bruderer and Weitnauer. Mean flight speeds during spring in the two studies are similar (10.6 compared to 11.1), suggesting that flight speeds are similar between night and day. During roosting flight, the birds typically fly along a very irregular path at very low ground speed, constantly orienting themselves towards the wind (Bäckman & Alerstam 2002). This circuitous track in combination with a lower position recording rate may have resulted in an underestimate of the length of the true flight path and thereby also the actual flight speed (Bruderer & Weitnauer 1972). On migration, the flight path is straight and the speed estimate is therefore accurately estimated also by recording one position every 20th second. The effect of sampling rate on speed estimates of summer roosting birds has been investigated and is presented in the electronic supplementary material.

Another example of adaptive speed adjustments in birds is the skylark that has been found to adjust flight speed when comparing display flight (V_mp) and migration (≥V_mr; Hedenström & Alerstam 1996).

(b) Time-selected migration and sprint migration

The prediction that swifts during spring migration have a higher flight speed than during autumn migration states that this is due to time selection in spring, meaning that birds arriving earlier to the breeding area should have a better chance of finding a mate and a nest and therefore also have higher breeding success (e.g. Kokko 1999). This advantage could introduce a tendency towards increased flight speeds in order to perform a faster migration to breeding area (flying at V_mt).

Between spring and autumn, the variance in V_eq was different. During spring, the variance of V_eq was much larger (by a factor of almost four) than during autumn. This larger variance appears to be mostly due to a ‘tail’ of high-speed flyers in spring (figure 4a). This subgroup was examined more closely by taking a subsample of the spring data containing all birds flying at V_eq≥13 m s⁻¹ (19% of the spring tracks). The group showed no abnormalities in V_z, V_s, V_t or altitude, implying that these individuals were not flying under any special wind situations or performed steep dives. Swifts are known to be able to fly at high speeds; records of up to 28 m s⁻¹ exist (Oehme 1968; Bruderer & Weitnauer 1972). We can only speculate about the reason for the fast flying individuals in the spring data: it can be heavier individuals that fly faster; it can be strong individuals that simply have the opportunity to fly faster; or it can be individuals that are close to their goal and can afford a sprint towards the final destination (Alerstam 2006). Also, the individuals during spring potentially consist of two groups, breeders and non-breeders, as swifts migrate to breeding areas also during the years before reaching sexual maturity. These non-breeders reside in proximity to breeding colonies searching for potential mates and nest sites (e.g. Lack 1956; Tarburton & Kaiser 2001), and may not be under such strong time restriction and therefore fly at lower speeds (V_mr) than individuals that are migrating to breed. If this is the case, the flight speed of the adult breeding swifts during spring migration may be underestimated by the population mean.

(c) Migration strategy

The prediction that flight speeds are higher in time-selected spring migration (V_mt) was developed based on the assumption that the birds perform stopovers to forage (Alerstam & Lindström 1990; Hedenström & Alerstam 1995). During these stopovers, the birds will have a certain net food intake rate that will determine the optimal flight speed towards the next stopover site in order to minimize time spent on migration. One could argue that the swifts are atypical in that respect, because they fly continuously and may potentially also forage on migration without doing regular stopovers. This strategy has been shown to occur among birds that have the possibility to forage on migration without making stopovers (e.g. Strandberg & Alerstam 2007). If this is the case, the optimal flight speed would depend on other factors, such as the benefit of offsetting energy consumption during migration flight and the cost of reduced effective travel speed (Alerstam et al. 1993; Hedenström & Alerstam 1995; Strandberg & Alerstam 2007) and would consequently be unknown from the basis of the current data. It may well be that a fly-and-forage behaviour is used by swifts, but in that case it would be most likely to occur during diurnal flights. We studied the nocturnal flights and during night it is unlikely that the birds forage. Bruderer & Weitnauer (1972) found that diurnal spring migrating swifts had an airspeed of 11.1 m s⁻¹, which is similar to that of nocturnal spring migration in this study (10.6 m s⁻¹). This suggests that there is no major difference between diurnal and nocturnal migratory flight speeds.

During autumn migration, we predicted that the optimal flight speed would be V_mr, while on roosting flights, the predicted optimal flight speed was V_mp (i.e. lower than during autumn), but the results show that there was no significant difference between summer and autumn flight speeds. Again, as with spring migration, one could propose that the swift perform a fly-and-forage strategy during autumn migration, but as during spring, this is likely to occur during diurnal flight only, and would not affect the flight speeds we investigate in this study. There are indications that swifts do not perform fly-and-forage migration during daytime either. Hedenström & Alerstam (1998) presented an estimate of the speed of migration of 150 km d⁻¹ or 1.7 m s⁻¹ for swifts. The mean ground speed during autumn migration in this study was 8.8 m s⁻¹ or 32 km h⁻¹. This means that, in order to advance 150 km d⁻¹, the birds need to fly for 4.7 h d⁻¹, which is easily covered during the nocturnal flight hours and would then mean that the advancement on migration during daytime is small. A simple check of the time budget thus suggests that the swifts do not perform fly-and-forage migration during autumn, but rather feed during daytime with little progress and consequently are expected to fly at V_mr during night.

(d) Specialized flight performance in the swift?

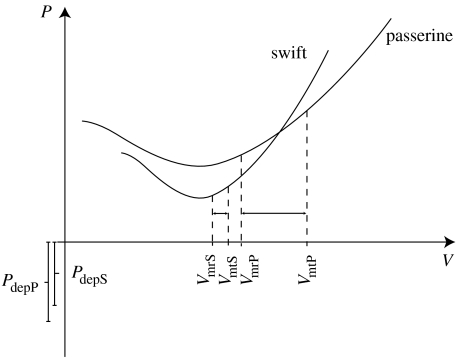
If swifts perform stopovers, it would be unlike most other birds that actually interrupt their flight for foraging. Swifts fly while foraging and would possibly have a higher cost compared with a passerine foraging in a forest patch. In that case the net intake rate is lower for the swift than for the passerine. As an example, the fuel deposition rate for the barn swallow (Hirundo rustica), which is also an aerial forager, has been found to be relatively low (Lindström 2003). On the other hand, a study of the flapping flight aerodynamics of a swift in a wind tunnel showed that the aerodynamic efficiency (meaning effective L : D) of the swift is higher than any other bird studied so far (Henningsson et al. 2008). This would imply that the power required to fly would hypothetically fall below that of a similarly sized passerine, if energetic efficiency is inferred from the aerodynamic efficiency, even though the conversion factor (output work/input work) is unknown. A conceptual comparison is presented in figure 5. With more efficient flight (lower over all mechanical power), the difference between V_mp and V_mr is decreased. Furthermore, one could speculate that swifts are optimized for flight at a certain flight speed (Lentink et al. 2007; Henningsson et al. 2008), although Oehme (1968) showed that they are capable of flying at higher speeds than found in this study. This would follow the reasoning by Thomas & Hedenström (1998), where they discuss how this would affect the shape of the power curve and the characteristic flight speeds. If a bird is specialized in flying at a certain speed, performance would decrease rapidly if operating away from the optimum, i.e. the power curve would rise more steeply both below and above this desired flight speed. As a consequence, V_mp, V_mr and V_mt would then be close to each other (figure 5) and difficult to distinguish by observations. This may possibly be part of the explanation to the small difference between summer and autumn flight speeds that was found in this study. A similar pattern was found in a wind tunnel study of the aerodynamic gliding performance of swift wings. The speed involving the highest maximum duration (the gliding flight equivalence to V_mp in flapping flight) and the speed resulting in the highest maximum glide ratio (the gliding flight equivalence to V_mr in flapping flight) were found to be similar; 7.7 and 8.1 m s⁻¹, respectively (Lentink et al. 2007). Pure gliding flight is not directly comparable with the flap-gliding flight that the swifts perform during typical flight, but the fact that the swifts in this study were shown to glide for approximately 40 per cent of the flight time justifies such a comparison. Observed flight speeds were approximately 9 m s⁻¹ during summer roosting flights and autumn migration and 10.6 m s⁻¹ during spring migration, which show that even during gliding bouts, the speed would be close to the aerodynamic glide optimum (Lentink et al. 2007). It is even possible that the birds adjust their speed slightly during both gliding and flapping phases to avoid constant acceleration/deceleration or ascent/descent, resulting in a mean flight speed that is a compromise between the optimal flapping speed and the optimal gliding speed.

Figure 5.

A conceptual comparison between swift and passerine power curves. If the overall power of flight and the net intake rate during stopover for the swift is lower than for the passerine, the same pattern as seen in this study emerges; the difference between V_mt, V_mr and V_mp is smaller for the lower curve than for the upper curve. ‘S’ and ‘P’ in the subscript denote ‘swift’ and ‘passerine’, respectively.

The possibility that the shape of the power curve differs between more or less efficient flyers and between species with different flight modes (cf. Tobalske et al. 2003; Alerstam et al. 2007) in ways that may restrict or widen the difference between significant flight speeds represents a fascinating subject for further research.

Supplementary Material

Calculation of equivalent air speed (V_eq)

Description of the method of calculating equivalent air speed

Analysis of effect on airspeed estimate by length of intervals for calculated means

Description of the analysis of effect on airspeed estimate by length of intervals used for calculated means

Analysis of effect on speed estimate by sampling rate

Description of the analysis of effect on speed estimate by sampling rate

Display of wind directions for different wind speeds during the three seasons; spring, summer and autumn

Visualization of the wind conditions by display of wind directions for different winds speeds during the three seasons; spring, summer and autumn, respectively