Degree dependence in rates of transcription factor evolution explains the unusual structure of transcription networks

Abstract

Transcription networks have an unusual structure. In both prokaryotes and eukaryotes, the number of target genes regulated by each transcription factor, its out-degree, follows a broad tailed distribution. By contrast, the number of transcription factors regulating a target gene, its in-degree, follows a much narrower distribution, which has no broad tail. We constructed a model of transcription network evolution through trans- and cis-mutations, gene duplication and deletion. The effects of these different evolutionary processes on the network structure are enough to produce an asymmetrical in- and out-degree distribution. However, the parameter values required to replicate known in- and out-degree distributions are unrealistic. We then considered variation in the rate of evolution of a gene dependent upon its position in the network. When transcription factors with many regulatory interactions are constrained to evolve more slowly than those with few interactions, the details of the in- and out-degree distributions of transcription networks can be fully reproduced over a range of plausible parameter values. The networks produced by our model depend on the relative rates of the different evolutionary processes. By determining the circumstances under which the networks with the correct degree distributions are produced, we are able to assess the relative importance of the different evolutionary processes in our model during evolution.

1. Introduction

Transcription regulation plays a key role in determining cellular function, response to external stimuli and development. Regulatory proteins orchestrate gene expression through thousands of interactions resulting in a system too complex to be easily understood in detail. This makes elucidation of gene regulation from a global perspective—that of the transcription network as a whole—an important challenge.

Genes in a transcription network either have outgoing edges, incoming edges or both. Outgoing edges from a gene represent the different targets that it regulates, while incoming edges at a gene represent the different transcription factors that regulate it. A number of studies (Thieffry et al. 1998; Guelzim et al. 2002; Maslov & Snepen 2005) have established that, in both prokaryotes and eukaryotes, the degree distributions for outgoing and incoming edges are very different. The out-degree distribution, n_out(k), follows a broad tailed distribution that is best described by a power-law:

$$n_{out}(k)\propto k^{-\gamma }.$$ (1.1)

The exponent γ is observed to be in the range 1<γ<2 (Guelzim et al. 2002; Maslov & Snepen 2005). A power-law distribution indicates that there are a small number of hub transcription factors that regulate a large number of genes (Barabási & Oltvai 2004). Interpretation of power-law degree distributions, and the small world structure they confer, has been the focus of a great deal of attention (Barabási & Albert 1999; Bahn et al. 2002; Pastor-Sorras et al. 2002; Chung et al. 2003; Wagner 2003; Barabási & Oltvai 2004; Pagel et al. 2007). In particular, it has been suggested that a power-law distribution may deliver an evolutionary advantage through increased mutational robustness and evolvability (Barabási & Oltvai 2004).

However, the in-degree distribution of transcription networks is much narrower than a power-law and has no broad tail (Thieffry et al. 1998; Guelzim et al. 2002; Maslov & Snepen 2005). It is best described by an exponential distribution

$$n_{in}(k)\propto {\text{e}}^{-\alpha k}.$$ (1.2)

The exponential in-degree distribution reflects the fact that only a few transcription factors combinatorially regulate any one gene. There exist no hub target genes. For example, in the yeast transcription network, 93 per cent of target genes are regulated by less than five transcription factors (Guelzim et al. 2002).

The extent to which the in- and out-degree distributions of transcription networks are different is intriguing, and the cause unknown. In this paper, we develop a model to explain the evolution of the asymmetrical transcription network degree distribution observed in yeast and other organisms. We focus on the different types of mutation through which the network evolves. Changes to the outgoing and incoming edges at a gene may occur as the result of mutation to a regulatory protein (trans-mutation) or as the result of mutation to transcription factor-binding sites (cis-mutation). These two processes change the network structure in different ways, but both result in either the loss or gain of regulatory interactions between existing genes. In addition, genes themselves may be lost or gained in the network through deletion and duplication.

The rates at which a gene evolves may vary according to its connectivity in the transcription network (Maslov et al. 2004; Wagner & Wright 2007). We investigate two types of connectivity-dependent evolution. It is often argued (Barabási & Oltvai 2004) that hub genes, which participate in many regulatory interactions, are particularly important for the proper functioning of the network, and are therefore constrained to evolve more slowly. This leads to the expectation of a slower rate of evolution among genes that regulate many downstream targets and a faster rate of evolution among genes that regulate only a few targets. It has also been suggested that a process of preferential attachment may occur in biological networks (Barabási & Oltvai 2004). Under preferential attachment, new interactions are gained in proportion to the number of interactions a node already participates in. Such a process has been shown to occur in protein–protein interactions networks (Wagner 2003; Pagel et al. 2007).

We construct a model incorporating evolution through trans- and cis-mutations, gene duplication and deletion along with variation in evolutionary rates depending on the connectivity of a gene. We use our model to unravel the relationship between the rates of evolution of genes through different processes in relation to the network structure.

2. Results

(a) Model

There are four types of network mutation in out model—gene deletion and duplication, plus cis- and trans-mutation. The in- and out-degree distributions of the network are determined by the rates at which these different types of mutation become fixed in the transcription network of a population. Since there is a clear functional difference between genes that code for transcription factors and those that code for other types of protein, we separate genes into two groups. Those with regulatory functions are labelled transcription factors (TFs) and those that are only regulated are labelled target genes (TGs). TGs have only incoming edges, while TFs may have either outgoing or incoming edges.

We establish the equilibrium in- and out-degree distributions for four different versions of our model. In the first version, the rates of evolution are independent of a gene's connectivity. We then consider two types of connectivity dependence in TF evolution. In the second version of our model, there is connectivity dependence such that the TFs with a large number of interactions undergo trans-evolution more slowly than those with few interactions. This is referred to as degree dependence in the rate of trans-evolution. In the third version of our model, there is connectivity dependence such that TFs gain new targets at a rate proportional to the number of targets they regulate. This is referred to as preferential attachment. The final version of our model includes both degree dependence in the rate of trans-evolution and preferential attachment.

(b) Gene deletion and duplication

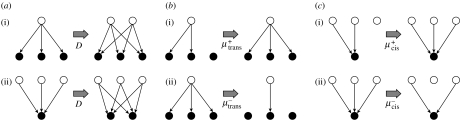
We assume that when genes are duplicated they inherit all the regulatory interactions of their parent. Evolution through duplication occurs at rate D⁺ and deletion occurs at rate D⁻ per gene (figure 1a). A TF of out-degree k gains outgoing edges due to duplication of its targets at rate kD⁺, and loses outgoing edges due to deletion of its targets at rate kD⁻. Similarly, a gene of in-degree j gains incoming edges due to duplication of TFs at rate jD⁺, and loses incoming edges due to deletion of TFs at rate jD⁻. If the rates of gene deletion and duplication are different, this will result in either growth (if the rate of duplication is greater than the rate of deletion), or decline (if the rate of deletion is greater than the rate of duplication) in the size of the network. We assume that the rate of growth (or decline) of the network is small compared to the rate of rewiring of regulatory interactions through trans- and cis-mutation (Gao & Innan 2004; Doniger & Fay 2007; Ward & Thornton 2007). Thus, we consider only networks of constant size, and therefore assume that $D^{+}=D^{-}=D$.

Figure 1.

(a)(i) Duplication of a TF and all its outgoing edges, (ii) duplication of a TG and all its incoming edges. (b) Evolution via trans-mutation: (i) gain of an interaction through trans-evolution; (ii) loss of interactions through trans-evolution. (c) Evolution via cis-mutation: (i) gain of an interaction through cis-evolution; (ii) loss of an interaction through cis-evolution.

(c) Evolution of regulatory-binding sites and transcription factors

A trans-mutation results in a change in the ability of TFs to bind to the promoter region of a gene. This may occur through a change in the binding affinity of a TF for a regulatory site. Alternatively, it may be the result of a TF gaining or losing an interaction with another TF, which helps it bind to the promoter region of a target (Tuch et al. 2008). Therefore, a trans-mutation in our model refers to a mutation affecting a transcription factor protein only. It does not refer to mutations affecting the cis-regulatory regions of trans-acting genes.

Following fixation of such a trans-mutation, a TF can cease to control some of the genes it currently regulates and can gain control over new genes. We assume that trans-evolution resulting in a TF potentially losing targets occurs at a constant rate ${\mu }_{trans}^{-}$. In this process, an existing target is lost with probability m. The probability, $P_{k,\mathrm{\Delta }k}^{-}$, that a TF with k out-edges loses Δk of its targets following a trans-mutation is given by

$$P_{k,\mathrm{\Delta }k}^{-}=\frac{k!}{\mathrm{\Delta }k!(k-\mathrm{\Delta }k)!}{m}^{\mathrm{\Delta }k}{(1-m)}^{k-\mathrm{\Delta }k}.$$ (2.1)

Similarly, we assume that trans-evolution resulting in the gain of new targets by a TF occurs at a constant rate ${\mu }_{trans}^{+}$, which is independent of the out-degree of the TF. Overall, trans-evolution results in a gene losing incoming edges at rate $m{\mu }_{trans}^{-}$ (per edge) and gaining a new incoming edge at rate ${\mu }_{trans}^{+}(1-(k/N))$ (figure 1b). The factor $(1-(k/N))$ gives the probability that the gene gaining the new incoming edge is not one of the k genes currently regulated by the mutated TF.

A cis-mutation results in the gain of a new binding site or the loss of an existing binding site in the promoter region of a gene. The rate at which binding sites are lost is ${\mu }_{cis}^{-}$. The probability that a gene, which is regulated by k TFs, loses an interaction through loss of a TF binding site is $k{\mu }_{cis}^{-}$. A gene may also gain a new regulatory binding site for any TF in the network to which it is not currently connected, at rate ${\mu }_{cis}^{+}$ (figure 1c). Therefore, a gene currently regulated by k TFs gains an incoming edge through cis-evolution at a rate ${\mu }_{cis}^{+}(1-(k/N))$. Throughout, we assume that the size of the network N is large compared to any realistic in- or out-degree k, so that the terms k/N may be neglected. Thus, new incoming edges are gained at constant rates ${\mu }_{trans}^{+}$ through trans-evolution and ${\mu }_{cis}^{+}$ through cis-evolution.

We also develop a model in which degree dependence in the rate of trans-evolution occurs. In this model, a trans-mutation, which results in TF-losing interactions, is fixed with a probability that depends on its out-degree. Since a trans-mutation affects the functioning of the transcription factor itself, it potentially alters all of the interactions in which a TF takes part. We assume that a trans-mutation at a TF with k targets has a deleterious effect on the functioning of the network that is proportional to k. Therefore, we assume that a trans-mutation resulting in the loss of edges from the network is fixed with probability proportional to 1/k. In this way, the rates of evolution of TFs are degree dependent.

A summary of all the parameters used in the model is given in table 1.

Table 1.

Model parameters.

k	number of regulatory interactions
N TG	expected number of TGs
N TF	expected number of TFs
N	expected size of the network ($N=N_{\text{TF}}+N_{\text{TG}}$)
${\mu }_{trans}^{+}$	rate of gain of interactions due to trans-evolution
${\mu }_{trans}^{\text{P}}$	in preferential attachment model—the rate at which new edges produced by trans-mutation undergo preferential attachment based on the in-degree of genes
${\mu }_{trans}^{\text{R}}$	in preferential attachment model—the rate at which new edges produced by trans-mutation undergo random attachment to genes
${\mu }_{trans}^{-}$	rate of loss of interactions due to trans-evolution
m	probability a TF loses an existing target immediately following a trans-mutation
${\mu }_{cis}^{+}$	rate of gain of TF-binding sites through cis-evolution
${\mu }_{cis}^{\text{P}}$	in preferential attachment model—the rate at which new edges produced by cis-mutation undergo preferential attachment based on the out-degree of TFs
${\mu }_{cis}^{\text{R}}$	in preferential attachment model—the rate at which new edges produced by cis-mutation undergo random attachment to TFs
${\mu }_{cis}^{-}$	rate of loss of TF-binding sites through cis-evolution
D	rate of duplication and deletion
$P_{k,\mathrm{\Delta }k}^{-}$	probability that a TF of out-degree k loses Δk edges as a result of a trans-mutation

(d) Network evolution

We allow evolution of the network by updating it at time intervals Δt, taken so that at most one mutation occurs and goes to fixation within each interval. Hence, the mean field equation for the expected number of genes with in-degree k at time t, changes in the time interval Δt by,

$$\begin{array}{l}\mathrm{\Delta }{n}_{in}=\left({\Pi }_{\text{TG}+}^{in}(k-1)+{\Pi }_{\text{TF}+}^{in}(k-1)\right)n_{in}(k-1,t)\\ +\left({\Pi }_{\text{TG}-}^{in}(k+1)+{\Pi }_{\text{TF}-}^{in}(k+1)\right)n_{in}(k+1,t)\\ -\left({\Pi }_{\text{TG}+}^{in}(k)+{\Pi }_{\text{TF}+}^{in}(k)+{\Pi }_{\text{TG}-}^{in}(k)+{\Pi }_{\text{TF}-}^{in}(k)\right)n_{in}(k,t)\end{array}$$ (2.2)

where ${\Pi }_{\text{TG}+}^{in}(k)$ and ${\Pi }_{\text{TG}-}^{in}(k)$ are the probabilities of a gene with in-degree k gaining or losing an edge through mutation at the regulated gene; and ${\Pi }_{\text{TF}+}^{in}(k)$ and ${\Pi }_{\text{TF}-}^{in}(k)$ are the probabilities of a gene with in-degree k gaining or losing an edge through mutation at a TF regulating it, in the time interval Δt. Similarly, the expected number of genes with out-degree k at time t changes in the time interval Δt by

$$\mathrm{\Delta }{n}_{out}=\left({\Pi }_{\text{TG}+}^{out}(k-1)+{\Pi }_{\text{TF}+}^{out}(k-1)\right)n_{out}(k-1,t)+{\Pi }_{\text{TG}-}^{out}(k+1)n_{out}(k+1,t)-\left({\Pi }_{\text{TG}+}^{out}(k)+{\Pi }_{\text{TG}-}^{out}(k)+{\Pi }_{\text{TF}+}^{out}(k)\right)n_{out}(k,t)+\sum _{j=k}^N{\Pi }_{\text{TF}-}^{out}(j,k)n_{out}(j,t)-\sum _{j=0}^k{\Pi }_{\text{TF}-}^{out}(k,j)n_{out}(k,t),$$ (2.3)

where N is the number of genes (TFs and TGs) in the network; ${\Pi }_{\text{TG}+}^{out}(k)$ and ${\Pi }_{\text{TG}-}^{out}(k)$ are the probabilities of a gene with out-degree k gaining or losing an edge through mutation at one of its targets; ${\Pi }_{\text{TF}+}^{out}(k)$ is the probability that a TF with out-degree k gains a target through mutation at the TF; and ${\Pi }_{\text{TF}-}^{out}(j,k)$ is the probability that a TF with out-degree j≥k loses interactions to become a TF with out-degree k due to mutation at the TF.

The equilibrium in-and out-degree distributions for the model can be found from equations (2.2) and (2.3), by setting the left-hand sides of both equations to 0 (see the electronic supplementary material). The equilibrium in-degree distribution satisfies

$$\left({\Pi }_{\text{TF}-}^{in}(k+1)+{\Pi }_{\text{TG}-}^{in}(k+1)\right)n_{in}(k+1)=\left({\Pi }_{\text{TF}+}^{in}(k)+{\Pi }_{\text{TG}+}^{in}(k)\right)n_{in}(k).$$ (2.4)

After making a number of approximations (see the electronic supplementary material), the equilibrium out-degree distribution satisfies

$$\left({\Pi }_{\text{TG}-}^{out}(k+1)+(k+1){\mu }_{trans}^{-}K(\gamma ,m)\right)n_{out}(k+1)=\left({\Pi }_{\text{TG}+}^{out}(k)+{\Pi }_{\text{TF}+}^{out}(k)-k{\mu }_{trans}^{-}K(\gamma ,m)\right)n_{out}(k),$$ (2.5a)

for the model excluding degree dependence in the rate of trans-evolution and

$$\left({\Pi }_{\text{TG}-}^{out}(k+1)+{\mu }_{trans}^{-}K(\gamma ,m)\right)n_{out}(k+1)=\left({\Pi }_{\text{TG}+}^{out}(k)+{\Pi }_{\text{TF}+}^{out}(k)-{\mu }_{trans}^{-}K(\gamma ,m)\right)n_{out}(k),$$ (2.5b)

for the model including degree dependence in the rate of trans-evolution. The positive parameter γ arises from the approximations used to obtain equations (2.5a) and (2.5b) (see the electronic supplementary material), and the functions K(γ, m) are specific to each of the models we consider and will be described below.

We now solve equations (2.4), (2.5a) and (2.5b) for the in- and out-degree distributions for four specific models of transcription network evolution. We start using a simple model and then investigate different models including degree dependence in the rate of trans-evolution and preferential attachment, to ask what conditions are required to explain the observed difference between the in- and out-degree distributions of transcription networks.

(e) Model 1: no connectivity dependence

In the first model, we assume there is neither any degree dependence nor any preferential attachment in the rate of trans-evolution. The event probabilities for the in- and out-degree distributions in this model are given in table 2a. Substituting these in equations (2.4) and (2.5a), we find for the in-degree distribution (see the electronic supplementary material)

$$n_{in}(k)\propto k^{-\lambda }{\text{e}}^{-\alpha k},$$

where

$$\begin{array}{l}\alpha =\text{ln}\left(1+\frac{{\mu }_{cis}^{-}+m{\mu }_{trans}^{-}}{D}\right),\\ \lambda =1-\frac{{\mu }_{cis}^{+}+{\mu }_{trans}^{+}}{D}.\end{array}$$ (2.6)

This is approximately an exponential distribution, characterized by α, unless α is small, which occurs if $D\gg {\mu }_{cis}^{-}+{\mu }_{trans}^{-}m$, or λ is large and negative, which occurs if $D\ll {\mu }_{cis}^{+}+{\mu }_{trans}^{+}$.

Table 2a.

Incoming edge event probabilities.

	model 1	model 2	model 3	model 4
${\Pi }_{\text{TG}+}^{in}(k)$	${\mu }_{cis}^{+}$	${\mu }_{cis}^{+}$	${\mu }_{cis}^{+}$	${\mu }_{cis}^{+}$
${\Pi }_{\text{TG}-}^{in}(k)$	$k{\mu }_{cis}^{-}$	$k{\mu }_{cis}^{-}$	$k{\mu }_{cis}^{-}$	$k{\mu }_{cis}^{-}$
${\Pi }_{\text{TF}+}^{in}(k)$	$kD+{\mu }_{trans}^{+}$	$kD+{\mu }_{trans}^{+}$	$kD+{\mu }_{trans}^{\text{R}}+k{\mu }_{trans}^{\text{P}}$	$kD+{\mu }_{trans}^{\text{R}}+k{\mu }_{trans}^{\text{P}}$
${\Pi }_{\text{TF}-}^{in}(k)$	$kD+k{\mu }_{trans}^{-}m$	$kD+k\langle 1/k\rangle {\mu }_{trans}^{-}m$	$kD+k{\mu }_{trans}^{-}m$	$kD+k\langle 1/k\rangle {\mu }_{trans}^{-}m$

The equilibrium out-degree distribution for this model obtained from equation (2.5a) is

$$n_{out}(k)\propto k^{-\gamma }{\text{e}}^{-\beta k},$$

where

$$\begin{array}{l}\beta =\text{ln}\left(\frac{{\mu }_{cis}^{-}+D+{\mu }_{trans}^{-}K(\gamma ,m)}{D-{\mu }_{trans}^{-}K(\gamma ,m)}\right),\\ \gamma =1-\frac{{\mu }_{cis}^{+}+{\mu }_{trans}^{+}}{D-{\mu }_{trans}^{-}K(\gamma ,m)},\end{array}$$ (2.7)

and K(γ, m) is as in table 2b. This distribution is a power-law characterized by γ only if β is 0. This occurs if ${\mu }_{cis}^{-}=-2{\mu }_{trans}^{-}K(\gamma ,m)$. However, as the rates, ${\mu }_{cis}^{-}$ and ${\mu }_{trans}^{-}$, are both positive constants, and $K(\gamma ,m)>0$ (table 2b), this condition cannot be met. Therefore, this model cannot produce a power-law out-degree distribution.

Table 2b.

Outgoing edge event probabilities.

	model 1	model 2	model 3	model 4
${\Pi }_{\text{TG}+}^{out}(k)$	$kD+{\mu }_{cis}^{+}$	$kD+{\mu }_{cis}^{+}$	$kD+{\mu }_{cis}^{\text{R}}+k{\mu }_{cis}^{\text{P}}$	$kD+{\mu }_{cis}^{\text{R}}+k{\mu }_{cis}^{\text{P}}$
${\Pi }_{\text{TG}-}^{out}(k)$	$kD+k{\mu }_{cis}^{-}$	$kD+k{\mu }_{cis}^{-}$	$kD+k{\mu }_{cis}^{-}$	$kD+k{\mu }_{cis}^{-}$
${\Pi }_{\text{TF}+}^{out}(k)$	${\mu }_{trans}^{+}$	${\mu }_{trans}^{+}$	${\mu }_{trans}^{+}$	${\mu }_{trans}^{+}$
${\Pi }_{\text{TF}-}^{out}(j,k)$	${\mu }_{trans}{P}_{j,j-k}^{-}$	${\mu }_{trans}^{-}(P_{j,j-k}^{-}/j)$	${\mu }_{trans}{P}_{j,j-k}^{-}$	${\mu }_{trans}^{-}(P_{j,j-k}^{-}/j)$
K(γ, m)	$(1/2(\gamma -1))(1-{(1-m)}^{\gamma -1})$	$(1/2\gamma )(1-{(1-m)}^{\gamma })$	$(1/2(\gamma -1))(1-{(1-m)}^{\gamma -1})$	$(1/2\gamma )(1-{(1-m)}^{\gamma })$

(f) Model 2: degree dependence in the rate of trans-evolution

In this model, we allow degree dependence in the rate of trans-evolution. Substituting the event probabilities for this model (table 2a) into equations (2.4) and (2.5b), we find for the in-degree distribution

$$n_{in}(k)\propto k^{-\lambda }{\text{e}}^{-\alpha k},$$

where

$$\begin{array}{l}\alpha =\text{ln}\left(1+\frac{{\mu }_{cis}^{-}+m\langle \frac{1}{k}\rangle {\mu }_{trans}^{-}}{D}\right),\\ \lambda =1-\frac{{\mu }_{cis}^{+}+{\mu }_{trans}^{+}}{D},\end{array}$$ (2.8)

and $\langle 1/k\rangle ={\sum }_{\mathit{j}=1}^N{n}_{out}(j)/j$ determines the mean rate of trans-evolution across the network. Following the same procedure as for model 1, this distribution will be approximately exponential unless α is small or λ is large and negative, which occurs when $D\gg {\mu }_{cis}^{-}+\langle 1/k\rangle {\mu }_{trans}^{-}m$ or $D\ll {\mu }_{cis}^{+}+{\mu }_{trans}^{+}$, respectively.

The equilibrium out-degree distribution for this model is

$$n_{out}(k)\propto k^{-\gamma }{\text{e}}^{-\beta k},$$

where

$$\begin{array}{l}\beta =\text{ln}\left(1+\frac{{\mu }_{cis}^{-}}{D}\right),\\ D(\gamma -1)+{\mu }_{cis}^{+}+{\mu }_{trans}^{+}={\mu }_{trans}^{-}K(\gamma ,m)\left(1+\frac{D}{D+{\mu }_{cis}^{-}}\right),\end{array}$$ (2.9)

and K(γ, m) is as in table 2b. This distribution is a power-law characterized by γ only if β is 0. This occurs if $D\gg {\mu }_{cis}^{-}$. Under this condition, equation (2.9) has solutions with γ>1 provided $m{\mu }_{trans}^{-}>{\mu }_{cis}^{+}+{\mu }_{trans}^{+}$.

(g) Model 3: preferential attachment

This model includes preferential attachment, but excludes degree dependence in the rate of trans-evolution (considered in model 2). In preferential attachment models, the rate at which nodes gain new edges is proportional to the number of edges already attaching to them. Preferential attachment has been discussed widely in the study of other biological networks (Wagner 2003; Barabási & Oltvai 2004; Pagel et al. 2007), including in the protein–protein interaction network of yeast (Wagner 2003).

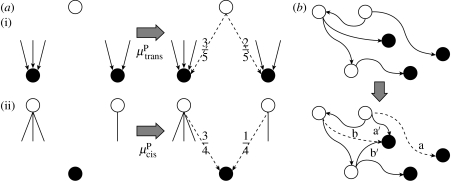
We model preferential attachment of incoming and outgoing edges separately. For incoming edges our model is as follows: new edges arise due to trans-evolution at rate ${\mu }_{trans}^{+}$. When such a new edge arises, it may be either through preferential attachment or through random attachment (i.e. the new edge attaches to each gene with equal probability) at the gene that is regulated. In the case of preferential attachment, the probability that a gene gains a new incoming edge is proportional to its in-degree. In the case of random attachment, the probability that a gene gains a new incoming edge is independent of its in-degree. We assume that such new edges undergo preferential attachment to a gene at rate ${\mu }_{trans}^{\text{P}}$, and undergo random attachment at a rate ${\mu }_{trans}^{\text{R}}$. The rate at which a gene of in-degree k gains a new edge due to preferential attachment is $k{\mu }_{trans}^{\text{P}}$, and the rate at which it gains a new edge due to random attachment is ${\mu }_{trans}^{\text{R}}$. The total rate at which TFs gain new outgoing edges is then ${\mu }_{trans}^{+}=(E/N_{\text{TF}}){\mu }_{trans}^{\text{P}}+(N/N_{\text{TF}}){\mu }_{trans}^{\text{R}}$, where E is the total number of edges in the network.

Our model of preferential attachment for outgoing edges is of the same form: new edges arise due to cis-evolution at rate ${\mu }_{cis}^{+}$. The rate at which a TF of out-degree k gains new outgoing edges due to preferential attachment is then $k{\mu }_{cis}^{\text{P}}$, and the rate at which it gains new edges due to random attachment is ${\mu }_{cis}^{\text{R}}$. The total rate at which genes gain new incoming edges is then ${\mu }_{cis}^{+}=(E/N){\mu }_{cis}^{\text{P}}+(N_{\text{TF}}/N){\mu }_{cis}^{\text{R}}$. Our model of preferential attachment is illustrated in figure 2a.

Figure 2.

(a) Preferential attachment: (i) preferential attachment of incoming edges. A TF choosing between a TG with three incoming edges and a TG with two incoming edges gains an interaction with the first with probability 0.6 and with the second with probability 0.4 due to preferential attachment; (ii) preferential attachment of outgoing edges. When choosing between a TF with three outgoing edges and a TF with one outgoing edge, a TG gains an interaction with the TF with three edges with probability 0.75 and with the TF with one edge with probability 0.25 due to preferential attachment. (b) Rewiring: (i) network prior to rewiring; (ii) edge ‘a’ is rewired to edge ‘a′’. This results in a change in the in-degree of two TGs but leaves the out-degree of the TF unchanged. Edge ‘b’ is rewired to edge ‘b′’, changing the out-degree of two TFs but leaving the in-degree of the TG unchanged.

The event probabilities for the in- and out-degree distributions in this model are given in table 2a. Substituting these into equations (2.4) and (2.5a), the in-degree distribution is

$$n_{in}(k)\propto k^{-\lambda }{\text{e}}^{-\alpha k},$$

where

$$\alpha =\text{ln}\left(\frac{D+{\mu }_{cis}^{-}+m{\mu }_{trans}^{-}}{D+{\mu }_{trans}^{\text{P}}}\right),$$

$$\lambda =1-\frac{{\mu }_{cis}^{+}+{\mu }_{trans}^{\text{R}}}{D+{\mu }_{trans}^{\text{P}}}.$$ (2.10)

This distribution will be approximately exponential unless α is small or λ is large and negative. That is, unless $D+{\mu }_{trans}^{\text{P}}\gg {\mu }_{cis}^{-}+{\mu }_{trans}^{-}m$, or $D+{\mu }_{trans}^{\text{P}}\ll {\mu }_{cis}^{+}+{\mu }_{trans}^{\text{R}}$. Therefore, we require ${\mu }_{trans}^{\text{P}}\sim {\mu }_{cis}^{-}+m{\mu }_{trans}^{-}$. The equilibrium out-degree distribution for this model is

$$n_{out}(k)\propto k^{-\gamma }{\text{e}}^{-\beta k},$$

where

$$\beta =\text{ln}\left(\frac{{\mu }_{cis}^{-}+D+{\mu }_{trans}^{-}K(\gamma ,m)}{D+{\mu }_{cis}^{\text{P}}-{\mu }_{trans}^{-}K(\gamma ,m)}\right),$$

$$\gamma =1-\frac{{\mu }_{cis}^{\text{R}}+{\mu }_{trans}^{+}}{D+{\mu }_{cis}^{\text{P}}-{\mu }_{trans}^{-}K(\gamma ,m)},$$ (2.11)

and K(γ, m) is as in table 2b. This distribution is a power-law characterized by γ only if β is 0. This occurs if ${\mu }_{cis}^{-}={\mu }_{cis}^{\text{P}}-2{\mu }_{trans}^{-}K(\gamma ,m)$. Equation (2.11) then gives $\gamma =1-(({\mu }_{cis}^{\text{R}}+{\mu }_{trans}^{+})/(D+(1/2)({\mu }_{cis}^{-}+{\mu }_{cis}^{\text{P}})))$, and the only solutions have γ<1.

(h) Model 4: degree dependence and preferential attachment

In the final model, we include degree dependence (as described in model 2) and preferential attachment (as described in model 3). The event probabilities for this model are given in table 2a. Using these with equations (2.4) and (2.5b), we find for the in-degree distribution

$$n_{in}(k)\propto k^{-\lambda }{\text{e}}^{-\alpha k},$$

where

$$\alpha =\text{ln}\left(\frac{D+{\mu }_{cis}^{-}+m\langle \frac{1}{k}\rangle {\mu }_{trans}^{-}}{D+{\mu }_{trans}^{\text{P}}}\right),$$

$$\lambda =1-\frac{{\mu }_{cis}^{+}+{\mu }_{trans}^{\text{R}}}{D+{\mu }_{trans}^{\text{P}}}.$$ (2.12)

This distribution is approximately exponential unless α is small or λ is large and negative. That is, unless $D+{\mu }_{trans}^{\text{P}}\gg {\mu }_{cis}^{-}+\langle 1/k\rangle {\mu }_{trans}^{-}m$, or $D+{\mu }_{trans}^{\text{P}}\ll {\mu }_{cis}^{+}+{\mu }_{trans}^{\text{R}}$. Therefore, we require ${\mu }_{trans}^{\text{P}}\sim {\mu }_{cis}^{-}+m\langle 1/k\rangle {\mu }_{trans}^{-}$. The equilibrium out-degree distribution for this model is

$$n_{out}(k)\propto k^{-\gamma }{\text{e}}^{-\beta k},$$

where

$$\begin{array}{l}\beta =\text{ln}\left(\frac{D+{\mu }_{cis}^{-}}{D+{\mu }_{cis}^{\text{P}}}\right),\\ \left(D+{\mu }_{cis}^{\text{P}}\right)(\gamma -1)+{\mu }_{cis}^{\text{R}}+{\mu }_{trans}^{+}={\mu }_{trans}^{-}K(\gamma ,m)\left(1+\frac{D+{\mu }_{cis}^{\text{P}}}{D+{\mu }_{cis}^{-}}\right),\end{array}$$ (2.13)

and K(γ, m) is as in table 2b. This distribution is a power-law characterized by γ only if β is 0. This requires ${\mu }_{cis}^{-}={\mu }_{cis}^{\text{P}}$. Under this condition, the third term in equation (2.13) has solutions with γ>1 provided $m{\mu }_{trans}^{-}>{\mu }_{cis}^{\text{R}}+{\mu }_{trans}^{+}$.

3. Discussion

To assess the four models we have presented, we compare their results to empirical observations from the yeast transcription network. The out-degree distribution of the Saccharomyces cerevisiae transcription network is best described by a power-law distribution with an exponent γ=1.5, while the in-degree distribution is best described by an exponential distribution with exponent α=0.4 (Maslov & Snepen 2005).

Since the exponent of the out-degree distribution for yeast is greater than 1, we conclude that models 1 and 3, which do not include degree dependence in the rate of trans-evolution, cannot account for the observed out-degree distribution of the S. cerevisiae transcription network. However, models 2 and 4, which include degree dependence in the rate of transcription factor evolution, can both produce networks with power-law out-degree distributions whose exponent is γ>1. Therefore, we conclude that degree dependence in the rate of transcription factor evolution is necessary to reproduce the structure of the yeast transcription network.

(a) Empirical rates of evolution

We can further distinguish between models 2 and 4 by referring to empirical data on the rates of evolution in the yeast transcription network. The rate of gene duplication in yeast is found to be in the range 1×10⁻⁵–6×10⁻⁵ Myr⁻¹ (Gao & Innan 2004). The rate of evolution (gain or loss) of regulatory interactions is an order of magnitude higher, approximately 36×10⁻⁵ Myr⁻¹ (Gu et al. 2005). Evolution of regulatory interactions may occur due to changes in regulatory proteins (trans-mutations in our model) or due to changes in cis-regulatory elements. A trans-mutation in our model refers to a mutation affecting a transcription factor protein only. It does not refer to mutations affecting the cis-regulatory regions of trans-acting genes. In practice, it is difficult to distinguish between the effects of the trans- and cis-mutations of our model without much more detailed comparative data. Studies on the contribution of the evolution of cis-regulatory elements and of trans-acting proteins to the evolution of gene expression have mixed findings. Variation between yeast strains have been found to be mainly due to variation in trans-acting proteins by some studies (Yvert et al. 2003; Zhang et al. 2004; Wang et al. 2007), while this has been contradicted by others (Ronald et al. 2005).

In model 2, a power-law out-degree distribution is only produced if $D\gg {\mu }_{cis}^{-}$. If we consider the case in which trans-evolution is more rapid than cis-evolution, then, given a rate of evolution of regulatory interactions of 36×10⁻⁵ Myr⁻¹ (Gu et al. 2005) and a rate of gene duplication of range 1×10⁻⁵–6×10⁻⁵ Myr⁻¹ (Gao & Innan 2004), model 2 suggests that the loss of regulatory interactions must be approximately 99 per cent due to trans-evolution. Such a disproportionate rate is not consistent with empirical data on the relative contributions of trans- and cis-change to the evolution of gene expression in yeast (Yvert et al. 2003; Zhang et al. 2004; Ronald et al. 2005; Wang et al. 2007). Therefore, we can reject model 2, as inadequate to explain the structure of the yeast transcription network.

(b) Preferential attachment

Model 4 can produce a power-law out-degree distribution provided ${\mu }_{cis}^{-}={\mu }_{cis}^{\text{P}}$. This requirement means that the rate at which transcription factors lose connections to target genes through cis-mutations must be balanced by the rate at which they gain new targets through preferential attachment. From this we also conclude that preferential attachment for outgoing edges is necessary to produce the observed yeast transcription network. The condition ${\mu }_{cis}^{-}={\mu }_{cis}^{\text{P}}$ is identical to a model in which transcription factors undergo rewiring (figure 2b), and suggests that transcription factors undergo a constant turnover of targets, without net gain or loss.

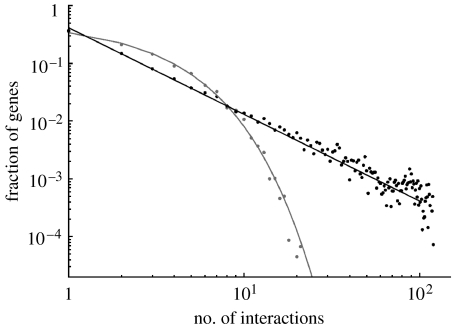
In order to determine whether preferential attachment among incoming edges occurs, we must consider the in-degree distribution of model 4. This is given by equation (2.12), with an exponential exponent, α, of approximately 0.4. Given a low rate of duplication, equation (2.12) suggests that preferential attachment of incoming edges at target genes is also necessary to reproduce the structure of the yeast transcription network. Figure 3 shows the result of simulations using model 4, which confirm that this model can reproduce the observed structure of the yeast transcription network.

Figure 3.

Simulated networks with an expected size of 100 TFs and 100 TGs. Networks have an exponential in-degree and power-law out-degree with α=0.4 and γ=1.5. Simulations consist of ensembles of 1000 networks evolved for 10⁶ mutations. Plot is on a log–log scale. Simulations were run for a range of parameter values. A typical example is shown. Data points show the degree distributions for simulated networks, solid lines are the predicted distribution. In-degree is shown in grey. Out-degree is shown in black. The networks were produced using model 4, including degree dependence in the rate of trans-evolution and preferential attachment. Here, the rate of duplication is D=0.26, the rate of gain of interactions through trans-evolution is ${\mu }_{trans}^{+}=0.04$, and through cis-evolution is ${\mu }_{cis}^{+}=0.31$. The rate of loss of interactions through trans-evolution is $m{\mu }_{trans}^{-}=0.25$ and through cis-evolution is ${\mu }_{cis}^{-}=0.14$.

(c) Evolution via trans-mutation

Our model for loss of interactions through trans-evolution includes two parameters, ${\mu }_{trans}^{-}$, the rate at which trans-mutations are fixed, and m, the probability each interaction is lost given that a trans-mutation is fixed. This means that following a trans-mutation a transcription factor will retain, on average, a fraction 1−m of its interactions. As it is difficult to estimate m, we consider two important cases: m→0 and m=1. In the first case, transcription factors evolve by small changes, one interaction at a time. In the second case, transcription factors lose all their existing interactions, and subsequently gain new ones through both cis- and trans-evolution. In this case, the TF may be seen as completely losing its old function before acquiring a new function.

When m→0, equation (2.13) for the out-degree distribution in model 4 may be used to obtain the approximation

$$\gamma =1-\frac{{\mu }_{cis}^{\text{R}}+{\mu }_{trans}^{+}}{D+{\mu }_{cis}^{\text{P}}}+\frac{m{\mu }_{trans}^{-}}{D+{\mu }_{cis}^{\text{P}}}.$$ (3.1)

Similarly, if m=1, equation (2.12) may be used to obtain

$$\gamma =\frac{1}{2}\left(1-\frac{{\mu }_{cis}^{\text{R}}+{\mu }_{trans}^{+}}{D+{\mu }_{cis}^{\text{P}}}+\sqrt{{\left(1-\frac{{\mu }_{cis}^{\text{R}}+{\mu }_{trans}^{+}}{D+{\mu }_{cis}^{\text{P}}}\right)}^2+\frac{4{\mu }_{trans}^{-}}{D+{\mu }_{cis}^{\text{P}}}}\right).$$ (3.2)

Therefore, given measurements of the relative rates of cis- and trans-evolution, it would be possible to distinguish between these two cases.

Given values for the other parameters, the value of ${\mu }_{trans}^{-}$ required in equation (3.2) to produce γ=1.5 will be greater than the value of $m{\mu }_{trans}^{-}$ required in equation (3.1) to produce the same distribution. The rate at which interactions are lost through trans-evolution is proportional to $m{\mu }_{trans}^{-}$. Therefore, the case m→0 is consistent with a slower rate of loss of interactions though trans-evolution than the case m=1. This can be compared with recent work (Gu 2009), suggesting that gene network evolution may be characterized by a 2-2-1 pattern (net gain of two genes and two edges along with loss of one edge). In our model, the ratio of gain of two edges to loss of one edge is more consistent with the case m→0 than with the case m=1.

(d) Growing and shrinking networks

We have considered networks in which the rates of gene duplication and deletion balance. However, it is well known that duplication growth models of networks can produce power-law distributions (Bahn et al. 2002; Pastor-Sorras et al. 2002; Chung et al. 2003; Gu 2009). We have not considered growing networks for two reasons. First, the observed low rate of gene duplication in yeast means that genes will undergo rewiring events at a rate that is 10-fold greater than the rate of duplication events. Second, the observed rates of gene duplication and deletion are comparable (Gao & Innan 2004) and suggests that the yeast transcription network is not undergoing constant growth. Therefore, any model that relies on network growth by duplication to reproduce the observed degree distributions in the yeast transcription network is not consistent with the data.

We have also investigated the case of shrinking networks. Although it is obvious that real networks cannot be continuously shrinking, the recent whole genome duplication in yeast (Kellis et al. 2004) means that there have been a great many redundant genes that have been lost resulting in an increased rate of gene deletion. Thus, the network has recently been undergoing a period of evolution in which it has been shrinking. We have considered a model in which a network is shrinking (see the electronic supplementary material). We show that this model is not able to reproduce the observed structure of the yeast transcription network without both degree dependence in the rate of trans-evolution and preferential attachment. Therefore, this model does not alter our conclusions.

(e) Autoregulation

In the analysis above, we neglected autoregulation of transcription factors. Autoregulation alters the consequences of transcription factor duplication. When an autoregulating transcription factor with k outgoing edges is duplicated, it gains an edge and becomes a transcription factor with k+1 outgoing edges. In our model, we assume that the transcription factors regulate each of the possible N targets with equal probability. Therefore, the probability that a transcription factor of out-degree k autoregulates is k/N. So the rate at which new transcription factors with out-degree k are produced due to duplication of autoregulators is $(k-1)(D/N)n_{out}(k-1)$, and the rate at which transcription factors with out-degree k are lost due to duplication of autoregulators is $k(D/N)n_{out}(k)$. Therefore, duplication of autoregulators provides a mechanism for a form of preferential attachment, since it results in transcription factors gaining new outgoing edges at a rate proportional to their out-degree. However, the rate at which this preferential attachment occurs is ∼(1/N) times the rate of gene duplication, D. Since N is large, duplication of autoregulating transcription factors is therefore expected to have little impact on the equilibrium degree distributions produced by our models. To verify these arguments, we carried out simulations in which autoregulation was permitted in each of the four models (data not shown). The results showed that autoregulation had only a minor quantitative effect on the outcome of the models provided the rate of duplication D was not high. We also note empirical findings in the yeast transcription network, which show that only 12 out of 131 (9%) of transcription factors admit autoregulation (Milo et al. 2004). Given this, the rate at which new edges are produced through duplication of autoregulating transcription factors is approximately an order of magnitude less than the rate of gene duplication. Even at this rate of autoregulation, duplication of autoregulating transcription factors will not have a significant impact on the degree distribution of the network.

4. Conclusion

We have compared four simple models for the evolution of transcription networks. Genes are separated into regulatory transcription factors and non-regulatory target genes, which evolve through mutation of trans- and cis-elements, as well as through deletion and duplication. When rates of evolution are constant across the network, our model can reproduce the exponential in-degree and power-law out-degree distributions characteristic of transcription networks. However, this model cannot produce networks with the power-law exponent observed in the out-degree of the yeast transcription network. It is only when the effects of variation in the rate of protein evolution are taken into account that the correct degree distributions are fully reproduced. This variation takes two forms. First, degree dependence in the rate of trans-evolution, meaning that the more regulatory interactions a transcription factor participates in, the more slowly it undergoes trans-evolution. Second, preferential attachment, meaning that genes gain new interactions at a rate proportional to the number of interactions they already participate in. The requirement for preferential attachment can be relaxed if the rate of evolution through gene duplication and deletion is high compared to the rate of cis-evolution.

We have proposed a model in which the rate of trans-evolution among transcription factors varies in inverse proportion to the number of targets they regulate. The true rate of trans-evolution depends on the rate of evolution of gene sequence and gene expression (Tirosh & Barkai 2008). The relationship between the evolution of gene expression, gene sequence and position in the transcription network is likely to be complex and is not fully understood (Wagner 2003). Our model suggests that variation in the rate of trans-evolution with the position of a gene in an interaction network significantly affects the structure of that network. We have considered these effects in relation to the structure of transcription networks, although they may also play a role in shaping the structure of protein interaction networks and metabolic networks.

Appendix A. simulations of network evolution

Simulations were carried out using ensembles of 1000 networks, each with an expected size of 100 TFs and 100 TGs. Networks were subject to 10⁶ mutations after which the average degree distributions were taken over the ensemble, and the mean degree distributions determined. The evolutionary algorithm used allowed networks to vary in size between a lower and upper boundary of 50 and 150 nodes, for both TFs and TGs. Loss of interactions through trans-mutation was executed by deleting each of a TF's outgoing edges with probability m. For gain of new interactions, random attachment was executed by selecting a gene and a TF at random and adding an edge between them. Preferential attachment of incoming edges was executed by selecting a gene with a probability proportional to its in-degree and a TF at random. A new edge was then added between them. Similarly for preferential attachment of outgoing edges, a TF was selected with probability proportional to its out-degree, and another gene was selected at random. An interaction was then added between them. Simulations were run for a range of parameter values. Data shown are for m=0.01, corresponding to the case m→0 (equation (3.1)). The rate of duplication used is D=0.26, the rate of gain of interactions through trans-evolution is ${\mu }_{trans}^{+}=0.04$, and through cis-evolution is ${\mu }_{cis}^{+}=0.31$. The rate of loss of interactions through trans-evolution is $m{\mu }_{trans}^{-}=0.25$ and through cis-evolution is ${\mu }_{cis}^{-}=0.14$.

Supplementary Material

The electronic supplementary material contains details of all derivations and approximations used in finding the equilibrium degree distributions for the four models considered in the paper

In addition it contains details of a model in which a network is shrinking, corresponding to the evolution of the yeast transcription network following whole genome duplication