Evolution in plant populations as a driver of ecological changes in arthropod communities

Abstract

Heritable variation in traits can have wide-ranging impacts on species interactions, but the effects that ongoing evolution has on the temporal ecological dynamics of communities are not well understood. Here, we identify three conditions that, if experimentally satisfied, support the hypothesis that evolution by natural selection can drive ecological changes in communities. These conditions are: (i) a focal population exhibits genetic variation in a trait(s), (ii) there is measurable directional selection on the trait(s), and (iii) the trait(s) under selection affects variation in a community variable(s). When these conditions are met, we expect evolution by natural selection to cause ecological changes in the community. We tested these conditions in a field experiment examining the interactions between a native plant (Oenothera biennis) and its associated arthropod community (more than 90 spp.). Oenothera biennis exhibited genetic variation in several plant traits and there was directional selection on plant biomass, life-history strategy (annual versus biennial reproduction) and herbivore resistance. Genetically based variation in biomass and life-history strategy consistently affected the abundance of common arthropod species, total arthropod abundance and arthropod species richness. Using two modelling approaches, we show that evolution by natural selection in large O. biennis populations is predicted to cause changes in the abundance of individual arthropod species, increases in the total abundance of arthropods and a decline in the number of arthropod species. In small O. biennis populations, genetic drift is predicted to swamp out the effects of selection, making the evolution of plant populations unpredictable. In short, evolution by natural selection can play an important role in affecting the dynamics of communities, but these effects depend on several ecological factors. The framework presented here is general and can be applied to other systems to examine the community-level effects of ongoing evolution.

1. Introduction

It is increasingly recognized that the ecology and evolution of species interactions within communities are interdependent (Antonovics 1992; Stinchcombe & Rausher 2001; Agrawal 2003; Whitham et al. 2006). On the one hand, species interactions can drive evolution within populations for traits related to competitive ability (Macarthur & Levins 1967; Grant & Grant 2006), host defence (Ehrlich & Raven 1964; Agrawal 2007), predation (Abrams 2000) and mutualistic interactions (Bronstein 1994). On the other hand, evolution within populations is hypothesized to lead to dynamic ecological changes in the structure and diversity of communities (Johnson & Stinchcombe 2007; Urban et al. 2008). Although it is well known that evolutionary change over macroevolutionary time scales has important consequences for the ecology of communities (Webb et al. 2006), it has only recently been appreciated that evolution might be an important factor affecting the ecological dynamics of communities over shorter time scales (Whitham et al. 2003; Johnson & Stinchcombe 2007), driving ecological changes in communities at a rate comparable to ecological mechanisms (Thompson 1998; Hairston et al. 2005; Ezard et al. 2009).

A combination of recent theory and experiments has supported the hypothesis that rapid evolution can affect the ecological dynamics of communities. For example, the cycles exhibited by predator and prey populations dramatically change in phase and length when models allow prey populations to evolve in response to selection by predators, compared with models that ignore evolution (Abrams & Matsuda 1997; Jones et al. 2009). These theoretical predictions have been corroborated by microcosm experiments that examined evolution in Escherichia coli attacked by phage and algae consumed by rotifers (Yoshida et al. 2007). Nevertheless, it is unclear whether the results from models and laboratory experiments reflect the dynamics and patterns of natural ecosystems, where communities are inherently more diverse and are influenced by many biotic and abiotic factors. Many recent studies have shown that genetic variation within a focal population has cascading ecological and ecosystem-level effects on communities (Shuster et al. 2006; Whitham et al. 2006; Bailey et al. 2009; Palkovacs et al. 2009), which suggests that evolution in the focal population has the potential to cause ecological changes in communities. However, community-level effects of standing genetic variation do not provide direct evidence that evolution in one population can drive temporal changes in communities (Johnson & Stinchcombe 2007). The strongest evidence for supporting the role of evolution by natural selection in driving community change comes from experiments that either measure selection on heritable plant traits shown to influence ecological interactions among species (present study), or demonstrate an association between ecotypic differences among focal populations and corresponding ecological differences in communities that coexisted with the focal species during ecotypic differentiation (e.g. Post et al. 2008; Post & Palkovacs 2009).

Here, we describe and implement an experimental approach to test the hypothesis that evolution by natural selection in plant populations can cause ecological changes in the abundance of particular arthropod species, as well as the total abundance and diversity of large arthropod assemblages associated with plants. This approach involves experimentally testing a series of necessary conditions of the hypothesis. Although our data are limited to the study of plant–arthropod interactions, we believe that this approach can be applied to any system in which it is possible to measure phenotypic traits and components of fitness from a focal population, as well as interactions between the focal population and other species in the community.

2. General approach

For evolution by natural selection in plants to cause temporal changes in arthropod community variables, such as the number of species (species richness), their abundance or species composition, we propose that three conditions are necessary: (i) a plant population exhibits genetic variation in a phenotypic trait(s), (ii) there exists measurable directional selection on the plant trait(s), and (iii) the traits under selection cause variation in one or more ecological characteristics of the arthropod community (e.g. arthropod abundance) associated with the plants. When all three conditions are satisfied, adaptive evolutionary changes in plant traits should lead to ecological change(s) in the arthropod community.

(a) Condition 1: genetic variation in plant traits

Showing that plant populations contain heritable variation in one or more traits satisfies the first condition. Plants typically exhibit genetic variation for multiple traits within and between populations (Briggs & Walters 1972). Previous research showed that there is genetic variation for morphological, phenological and putative resistance traits in the herbaceous plant Oenothera biennis (Onagraceae) (Johnson & Agrawal 2005; Johnson 2008; Johnson et al. 2008), which is the focal plant of the experiment described here. Therefore, in this system and others, the first necessary condition will usually be satisfied.

(b) Condition 2: directional selection on plant traits

This condition can be evaluated by measuring the strength of directional selection acting on plant traits. These analyses can be performed using conventional regression techniques that measure the strength of phenotypic and/or genotypic selection according to the covariation between relative fitness in a population and variation in one or more traits (Lande & Arnold 1983; Rausher 1992). Price (1970) showed that the strength of selection (S) acting on a trait is equal to the covariance (cov(ω,z)) between relative fitness (ω) and variation in a trait (z). The response to selection can then be predicted when S is multiplied by the heritability of a trait (narrow-sense heritability based on additive genetic variance [h²] for sexual populations and broad-sense heritability based on additive and non-additive genetic variances [H²] for inbreeding and asexual populations) (i.e. R=h²S, the breeder's equation). The breeder's equation can be generalized to the multivariate case to predict the response to selection on two or more traits according to the equation:

$$\left[\begin{array}{c}\mathrm{\Delta }{\overline{z}}_1\\ \mathrm{\Delta }{\overline{z}}_2\\ ⋮\\ \mathrm{\Delta }{\overline{z}}_i\end{array}\right]=\left[\begin{array}{cccc}{G}_{11}& G_{12}& \dots & G_{1j}\\ G_{21}& G_{22}& \dots & G_{2j}\\ ⋮& ⋮& & ⋮\\ G_{i1}& G_{i2}& \dots & G_{ii}\end{array}\right]\left[\begin{array}{c}{\beta }_1\\ {\beta }_2\\ ⋮\\ {\beta }_i\end{array}\right],$$ (2.1)

where $\mathrm{\Delta }{\overline{z}}_i$ describes the evolutionary change in the mean value of trait i across a single generation; the square matrix G describes the genetic variance (diagonal elements, G_ii); and covariances (off-diagonal elements, G_ij) among traits, and the ‘selection gradient’ β_i measures the strength of selection on trait i (Lande 1979; Lande & Arnold 1983).

(c) Condition 3: selected traits affect variation in the arthropod community

To test condition 3, a field experiment is needed to determine whether genetically variable plant traits subject to natural selection predict natural variation in arthropod populations or communities associated with individual plants. To do this, one can use multiple regression to determine how community variables are affected by plant traits; operationally, this can be done with genotypic means for both the plant traits and the community variables, to assess whether these relationships have a genetic or environmental basis. A genetic relationship would indicate an indirect genetic covariance between plant traits and the arthropods found on those plant genotypes. Analogous indirect genetic covariances have been studied for social interactions within populations, which result in indirect genetic effects that influence the evolution of behavioural traits (Moore et al. 1997; Wolf et al. 1997, 1998; Petfield et al. 2005). Models of indirect genetic effects show that the expression of a phenotype is influenced not only by the direct genetic and environmental factors experienced by a focal individual (Moore et al. 1997; Wolf et al. 1998), but also by the indirect effects of the expression of genes in other individuals in the population. Inclusion of these indirect genetic effects into quantitative genetics models can alter a population's predicted evolutionary response (Moore et al. 1997; Wolf et al. 1997). This concept was recently extended to the study of interspecific interactions (Shuster et al. 2006), and our implementation of these ideas here considers how the selection and genetic variance in one focal population can influence ecological changes in other species in a community. Specifically, by calculating the partial regression coefficients (α_yi) between an arthropod community variable y and the selected plant trait(s) i (hereafter ‘community–trait gradient’; analogous to ψ in models of indirect genetic effects, see Wolf et al. 1998), we can modify the Lande–Arnold equation to predict how the evolutionary response in the plant population will lead to an ecological response in the community. This equation can be written as

$$[\mathrm{\Delta }{\overline{c}}_1]=[{\alpha }_{11},{\alpha }_{12},\dots ,{\alpha }_{1i}]\left[\begin{array}{cccc}{G}_{11}& G_{12}& \dots & G_{1j}\\ G_{21}& G_{22}& \dots & G_{2j}\\ ⋮& ⋮& & ⋮\\ G_{i1}& G_{i2}& \dots & G_{ii}\end{array}\right]\left[\begin{array}{c}{\beta }_1\\ {\beta }_2\\ ⋮\\ {\beta }_i\end{array}\right],$$ (2.2)

where $(\mathrm{\Delta }{\overline{c}}_1)$ is the change in a single community variable as a function of the previously described selection gradients (β vector); the variance–covariance matrix (G) of plant traits; and the community–trait gradients (α vector) describing the relationship between each plant trait under selection and variation in the community variable.

(d) Modelling the ecological effects of evolution on communities

Although conditions 1–3 are necessary for evolution by natural selection to drive community changes, they are not sufficient as other evolutionary and ecological factors (e.g. small population sizes that increase the strength of genetic drift) may counteract the effects of selection. Although it would be best to observe directly ecological changes due to natural selection, such experiments are exceedingly difficult and we are unaware of any such study (including our own) done in the field. Modelling approaches can be useful in such circumstances and we explore the use of two methods that use field collected data to predict the effects of evolution on communities over longer time scales (see §§3 and 4).

(e) Objectives and assumptions

Our principal objective was to outline and use a conceptual framework that tests the hypothesis that evolution by natural selection can drive temporal changes in the ecological characteristics of communities. To do this, we conducted an experiment that assesses whether each of the conditions above are satisfied for interactions between the native plant common evening primrose (O. biennis) and its associated arthropod community. We then use these results to model the expected evolutionary changes in plant populations and the predicted ecological effects of this evolution on: (i) the abundance of common arthropod species, (ii) the total abundance of all arthropods on plants, and (iii) the number of arthropod species in the community.

In many instances, the traits subject to selection and correlated with variation in the community will be unknown, making it impossible to test the conditions outlined above. Using theory from path analysis (Wright 1934; Kline 2004), we develop a method of determining when natural selection is acting on unknown traits in the focal species that cause variation in community variables. This method uses the covariance between components of fitness (e.g. survival and fecundity) in a focal population and variation in an associated community variable (see §5). Although this method makes it possible to detect natural selection that is affecting community variables, it lacks the mechanistic detail about the particular traits that are responsible.

As we elaborate below (see §5), the accuracy of our predictions depends on several factors. Predictions about changes in the community will be most accurate when: arthropod populations respond to phenotypic variation in plant traits consistently over space and time; the influence of changes in plant phenotype on the preference and performance of arthropod populations are not outweighed by extrinsically driven population dynamics; the direct and indirect interactions among arthropod populations are relatively consistent through time; and rapid coevolution of arthropod populations does not buffer the community-level effects of plant evolution. Because the potential for these confounds increases through time, our approach is most valuable at making short-term predictions of the effects of evolution on community dynamics.

3. Material and methods

(a) Experimental system

The focal plant species used in our experiment, O. biennis L. (Onagraceae), is a native herbaceous plant of open habitats (e.g. fields, roadsides, lakeshores, etc.) in eastern North America, and it is widely introduced across the world (Dietrich et al. 1997). Plants typically germinate in spring, form a basal rosette of leaves and flower at the end of the first or second year of growth (Johnson 2007). Because plants are self-fertilizing and monocarpic (i.e. reproduction is fatal), the number of fruits represents equal components of total male and female fitness over a plant's lifetime. Similar to apomictic species, O. biennis is functionally asexual as it produces seeds that are genetically identical to one another and to their parent plant (Cleland 1972). We used this genetic behaviour to replicate single genotypes from seed.

Oenothera biennis plays host to over 150 specialist and generalist herbivorous, omnivorous and predaceous arthropod species (Johnson & Agrawal 2005, 2007). In the present experiment, 93 arthropod species naturally colonized O. biennis over the course of 2 years.

(b) Experimental design

This experiment was conducted in 2002 and 2003 at the University of Toronto's Koffler Scientific Reserve (www.ksr.utoronto.ca) in South-Central Ontario, Canada. The design of our experiment is reported elsewhere (Johnson & Agrawal 2005, 2007), so we provide only a concise description here. This paper expands on our previous work by exploring the untested hypothesis that natural selection on a plant population can lead to ecological changes in arthropod communities in the field. Since the main objective of the present paper was to heuristically outline and empirically test a conceptual and analytical framework of the hypothesis, we only use data from one of five habitats previously studied (i.e. Mesic habitat); results from the other habitats were similar.

In brief, we germinated seeds from 14 O. biennis genotypes at the same time and grew plants for five weeks in a greenhouse at the University of Toronto. We then transplanted plants into an old field leaving the surrounding vegetation intact. In total, we randomized 184 plants, with 12–15 replicates per genotype, into four contiguous rectangular blocks. We measured six traits from each plant that characterized the growth rate, resistance to herbivores (early season damage and leaf toughness), life-history variation (annual versus biennial reproduction and lifetime biomass) and fitness (lifetime fruit production) among O. biennis genotypes. Growth was measured as the maximum rosette diameter four weeks following germination. Rosette diameter is an accurate surrogate for early growth rate because all plants were planted at the same time and O. biennis exhibits exponential growth during the first five weeks following germination (Johnson et al. 2008); rosette diameter is also highly correlated with total plant biomass (Gross 1981). Resistance to herbivores was measured as the number of discrete chewing holes on two rosette leaves made by four specialist beetles (Tyloderma foveolatum, Tyloderma nigrum, Graphops pubescens and Altica knabi) during June of the first year of growth. The number of holes on two leaves was correlated with the total number of holes on the entire plant (r=0.58, p<0.001, n=39) and is well correlated with leaf area consumed (r=0.95, p<0.001, Johnson & Agrawal 2005). We transformed resistance to ‘relative resistance’ by taking 1−(no. holes)/(max. no. holes), so that resistance varied between 0 (low resistance) and 1 (high resistance). Leaf toughness was measured as the grams of force required to penetrate a leaf using a force-gauge penetrometer (Type 516; Chatillon, Kew Gardens, NY, USA). Life-history strategy (annual versus biennial reproduction) was determined by observing whether plants flowered and died in 2002 or 2003 as described previously (Johnson 2007). We collected the above-ground biomass of plants that flowered in the autumn of each year, dried the material at 60°C for one week in a forced-air drying oven, and weighed all material to the nearest 0.1 g. After weighing, we counted the number of fruits on plants.

We non-destructively surveyed the arthropod assemblage that naturally colonized each plant. We performed four surveys each year, every two to three weeks in spring and summer; surveys were conducted on the same dates in 2002 and 2003, for a total of eight surveys. Arthropods were visually censused by counting all arthropods on all surfaces of the plant. Arthropod species were identified by the lead author and with the assistance of Agriculture Canada's National Identification Service (Ottawa, Canada) by taking specimens from non-experimental plants. We only included species that were observed to feed directly on O. biennis or to prey on herbivores of O. biennis. For each species, we determined the maximum abundance across sampling dates within each year, thus seasonal population dynamics were decomposed into a single estimate of population size.

Using these data, we extracted several descriptors of the arthropod community. First, we quantified the five most common arthropod species (Philaenus spumarius (Cercopidae and Hemiptera), Cedusa incisa (Cicadellidae and Hemiptera), Mompha stellella (Momphidae and Lepidoptera), Schinia florida (Noctuidae and Lepidoptera) and Sparganothis recticulatana (Tortricidae and Lepidoptera)) to examine whether evolution by natural selection could lead to changes in the abundance of common arthropod species on plants. These species comprised approximately 80 per cent of the arthropod fauna on O. biennis. Second, we calculated the total abundance of all arthropod species on each individual plant, by summing the maximum abundances of each species in each of the 2 years. Because biennials live twice as long as annuals, we multiplied arthropod abundance by two on all annual plants to control for differences in plant lifespan. Finally, we determined the total number of arthropod species (arthropod species richness) that were identified over the lifetime of each plant. For species richness, we used only data from the year in which a plant flowered (year 1 for annuals, year 2 for biennials) when calculating community–trait gradients; therefore, analyses were not biased by differences in generation time or the number of surveys.

(c) Statistical analyses

(i) Measurement of genetic variance and heritability

We used restricted maximum likelihood (REML) in Proc Mixed of SAS (SAS Institute, Cary, NC, USA) to estimate the variance explained by plant genotype for each trait. The statistical model included plant genotype and spatial block as random effects, where the significance of genotype was tested using a log-likelihood ratio test. Because O. biennis is functionally asexual, a population's evolutionary response to selection will depend on the total genetic variance (V_g) within a population, including both additive and non-additive components. For this reason, heritability of O. biennis traits are most accurately estimated as H²=V_g/V_T (Lynch & Walsh 1998), where V_T is the total phenotypic variance (genetic and environmental) in the trait. The coefficient of genetic variation was calculated as $V_{\text{g}}^{0.5}/{\mu }_i$, where μ is the mean for trait i. The analyses described above were performed on untransformed data as recommended by Houle (1992).

The variance–covariance trait matrix was calculated using the genetic variances (G_ii) from REML, and the genetic covariances (G_ij) between traits. Genetic covariances were calculated according to the equation cov_g=r_g(G₁₁×G₂₂)^0.5, where r_g is the Pearson correlation coefficient of the genetic correlation between the best-linear unbiased predictors (BLUPs) of the genotypic breeding values (similar to genotypic means) of two traits. The statistical significance of genetic covariances was assessed as the p-value for r_g (Lynch & Walsh 1998, p. 641).

(ii) Measurement of natural selection on plant traits

Genotypic multivariate selection analyses were performed using the Lande–Arnold method (1983) as modified by Rausher (1992). We first calculated the BLUPs for each plant trait using the untransformed data. BLUPs were also calculated for absolute fitness (no. fruits), which was transformed to relative fitness by dividing the BLUPs for each genotype by mean fitness among genotypes. We then regressed relative fitness against the five plant traits and selected the best model using forward stepwise regression in Proc Reg of SAS, with an entry/exit p-value of 0.1 and partial partitioning of the error. Although we explored and present models with linear (directional selection) and quadratic (stabilizing and disruptive selection) parameters, we focus on linear coefficients because directional selection is principally responsible for changes in mean trait values (Lande & Arnold 1983). Quadratic selection influences the magnitude of genetic variance within populations (Lande & Arnold 1983; Stinchcombe et al. 2008), and therefore it can affect the long-term rate at which community variables change in response to selection on plant traits. Studies that wish to make long-term predictions about the community-level effects of natural selection should incorporate the effects of both directional and nonlinear selection gradients.

Phenotypic selection analyses, where individual plants are treated as replicates, were also performed and their results are provided in table 2 in the electronic supplementary material. Results from genotypic and phenotypic selection analyses were similar and our focus on the former avoids problems of confounding effects due to environmentally induced covariance between traits and fitness (Stinchcombe et al. 2002).

(iii) Measurement of community–trait gradients

We calculated the BLUPs for arthropod community variables associated with each plant genotype and then used multiple regression to regress individual community variables against the plant traits subject to natural selection. A significant partial regression coefficient (α) between a community variable and a plant trait indicated that the selected plant trait was associated with or affected the community variable. We also performed phenotypic analyses as described above; results are in table 3 in the electronic supplementary material.

(d) Models

We used two complementary modelling approaches (matrix projections and simulations) to explore the long-term community-level consequences of evolution. These models allowed us to examine how community variables are expected to change in response to selection. The matrix projection models were most useful in predicting the responses of community variables to natural selection on plant traits over a single generation. Our simulation models complemented the matrix projections as they allowed us to explore the relative roles of natural selection versus genetic drift in driving evolutionary and ecological changes under the various ecological conditions experienced by O. biennis in natural populations. Specifically, we considered how variation in population size and population dynamics might influence O. biennis evolution and changes in the community. The simulation models also enabled us to explore how non-additive community variables such as species richness might change in response to selection on plants; matrix models cannot accommodate such variables. Assumptions of these models are discussed below (see §5c).

(i) Matrix projection models

The first approach involved calculating the matrix projections of equation (2.2) (i.e. Δc=αGβ) to predict the change in mean arthropod abundance due to evolution in the O. biennis population over a single generation. The community–trait gradients and selection gradients are provided in table 2 and figure 1, respectively; the G-matrix can be found in table 1 in the electronic supplementary material. The calculation of the 95% confidence intervals around Δc is described in the methods in the electronic supplementary material. Our matrix projection method is most accurate at predicting changes in absolute and relative abundance over a single generation because these projections assume constant (i) genetic variance, (ii) selection and (iii) responses of community members to plant genetic variation. This approach cannot be used to model changes in arthropod species richness because richness is a non-additive composite measure of species' presence/absence in a community.

Table 2.

Community–trait gradients between community variables and plant traits under selection. (Community–trait gradients (α) were calculated as the partial regression coefficients between a community variable and genetic variation in plant traits. Community–trait gradients in bold indicate p≤0.05 and italicized values indicate 0.05≤p≤0.10. The covariance between relative fitness and normally standardized community variables (cov_ωc) is also shown (significant values in bold). Statistically significant negative quadratic effects are denoted by † (parameter estimates not shown); we focus on linear effects because they are primarily responsible for causing changes to the mean of community variables.)

	community–trait gradient (α)
community variable	biomass	life-history strategy	resistance	covωc
Philaenus	0.09±0.02	4.61±1.09	877.75±561.11	0.75
Cedusa	0.08±0.01	3.03±0.75	−202.10±383.29	0.68
Mompha	−0.09±0.26†	39.65±18.36	8930.34±9424.25	0.78
Schinia	0.01±0.02†	−0.88±1.66	−1129.67±852.59	0.23
Sparganothis	0.002±0.01†	1.36±0.58	517.23±296.21	0.83
total abundance	0.18±0.29†	51.30±21.05	9715.06±10804	0.89
total richness	0.05±0.02†	6.64±1.38	548.09±710.07	0.84

Figure 1.

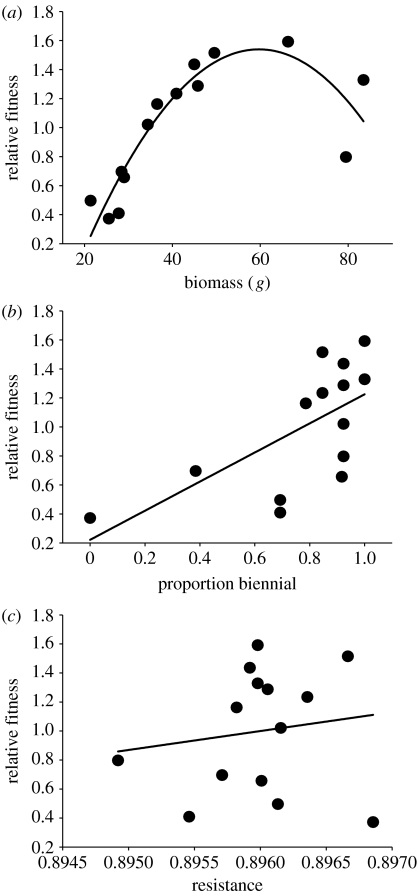
Directional and stabilizing selection on plant traits. (a–c) The uncorrected (not partialled) pairwise relationship between the breeding values of relative fitness and (a) plant biomass (β=0.01±0.005, p=0.07, r=0.58^*; γ=−0.001±0.0003, p=0.003), (b) flowering strategy (expressed as the proportion of plants biennial within a genotype; β=0.91±0.32, p=0.02, r=0.65^*) and (c) resistance to early season herbivory. Directional selection gradients (β) were calculated as partial regression coefficients between relative fitness and genetic variation in the trait (β=447.38±166.76, p=0.02, r=0.15); selection gradients were calculated using untransformed data. The selection differential (r) was estimated as the pairwise correlation between relative fitness and the normally standardized trait value. The best-fitting quadratic curve is shown in (a) because directional and stabilizing selections acted on plant biomass; the strength of stabilizing selection was estimated as two times the partial regression coefficient for the quadratic term of biomass.

(ii) Simulation models

Our second modelling approach allowed for longer term projections of changes in arthropod abundance and richness as a function of evolution in O. biennis. This approach used our field data on relative genotype fitness, life-history variation and arthropod assemblages. Using two different scenarios of O. biennis population dynamics—constant population size or exponential growth with population crashes—we simulated evolution by natural selection according to observed relative fitness variation in the field experiment, and compared the outcomes of these simulations with simulations in which all plants had equivalent fitness (i.e. only genetic drift could change genotype frequencies). A strength of these simulations is that they allow for temporal changes in the strength of selection and the magnitude of genetic variation, and they allowed us to model changes in arthropod abundance and richness across the entire plant population. Detailed methods of our simulations are available in methods in the electronic supplementary material.

4. Results

(a) Condition 1: genetic variation in plant traits

We detected significant genetic variation for four of six plant traits, including lifetime fruit production (table 1). The broad-sense heritability of traits varied from 0.001 to 0.44 and the coefficient of genetic variation ranged between 0.5 and 211 (table 1). This genetic variation in fitness and other plant traits indicates that our O. biennis population had the potential to evolve in response to selection acting on genetically variable plant traits.

Table 1.

Genetic variation in six plant traits. (Genetic variation was measured as genetic variance (V_g), broad-sense heritability (H²) and the coefficient of genetic variance (CV_g). Significance tests for the effect of plant genotype were performed using log-likelihood ratio tests and their p-values are reported.)

trait	Vg	H2	CVg	p-value
plant biomass	428.78	0.44	47.24	<0.001
leaf toughness	1.40	0.002	2.00	>0.10
resistance	<0.01	0.001	0.46	>0.10
flowering strategy	2.60	0.08	210.88	<0.001
growth rate	55.50	0.36	17.69	<0.001
fruits	3765.60	0.42	44.41	<0.001

(b) Condition 2: natural selection on plant traits

We detected natural selection on three life-history and resistance traits (figure 1). There was directional selection for an increase in lifetime biomass (figure 1a) and an increase in biennial reproduction versus annual reproduction (figure 1b). Directional selection also acted to increase resistance in plants (figure 1c), even though we did not detect significant genetic variation in this trait. Stabilizing selection also acted on biomass (figure 1a). Phenotypic selection analyses showed significant directional selection for increased plant biomass and biennial reproduction, but no selection on resistance (see table 2 in the electronic supplementary material).

(c) Condition 3: the effect of selected traits on the arthropod community

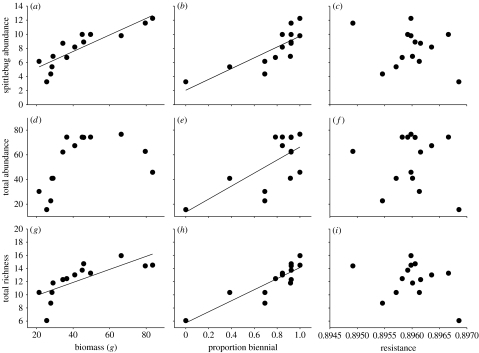
Two of the three plant traits with significant genetic variation and subject to natural selection consistently predicted variation in community variables (table 2, figure 2). Genetic variation in plant biomass and/or flowering strategy significantly predicted variation in the abundance of four of the five most abundant arthropod species on O. biennis (table 2). For example, the abundance of P. spumarius increased with greater plant biomass and a higher frequency of biennial reproduction (figure 2a,b). There were also positive effects of increasing bienniality on total arthropod abundance and arthropod richness (figure 2e,h), as well as a significant positive relationship between plant biomass and arthropod richness (figure 2g). We did not detect any effects of genetic variation in plant resistance to early season herbivores on arthropod community variables (figure 2c,f,i).

Figure 2.

Community–trait gradients of the relationship between community variables and plant traits. (a–i) The relationship between (a–c) P. spumarius abundance, (d–f) total arthropod abundance and (g–i) arthropod richness, and genetic variation in plant traits (biomass, proportion biennial and resistance) subject to directional selection. The best-fitting line is shown in figures where there was a significant linear community–trait gradient; variables exhibiting significant quadratic relationships are indicated in table 2.

(d) Modelling the ecological effects of evolution on communities

Both the matrix projections and simulation models indicate that evolution by natural selection can lead to rapid temporal changes (i.e. within 1–5 years) in arthropod community variables under some ecological conditions. Matrix projections of equation (2.2) predict that the evolutionary response of O. biennis to selection over a single generation will lead to a significant increase in the abundance of three arthropod species, as well as the total abundance of arthropods (table 3). Schinia florida was predicted to decrease in abundance, but this effect was not significant. We also used the matrix projections to predict how the relative abundance of the most common community members might change as a function of evolution in O. biennis (see figure 1 in the electronic supplementary material). These results suggest that M. stellella will quickly dominate the community, while the relative abundance of other species will decrease (e.g. P. spumarius, C. incisa) or remain unchanged (S. reticulatana).

Table 3.

Predicted change in arthropod abundance $(\mathrm{\Delta }{\overline{c}}_1)$ over a single generation. (The lower and upper 95% confidence intervals of $\mathrm{\Delta }{\overline{c}}_1$ are also shown. $\mathrm{\Delta }{\overline{c}}_1$ was calculated from equation (2.2) and the derivation of confidence intervals is described (methods in the electronic supplementary material). Significant changes at the 0.05 level are shown in bold.)

community variable	$\mathrm{\Delta }\overline{c}$	lower 95%	upper 95%
Philaenus	14.01	3.34	38.52
Cedusa	3.66	−1.78	16.75
Mompha	124.16	7.11	402.47
Schinia	−9.51	−11.39	8.05
Sparganothis	5.85	1.10	15.50
total abundance	149.39	13.25	469.59

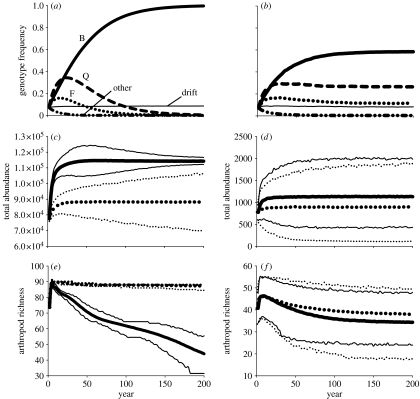
Our simulations suggest that evolution by natural selection on O. biennis can lead to rapid temporal changes in the abundance and species richness of arthropod communities, but these results depend on several ecological and evolutionary factors (figure 3). In large plant populations of constant size, natural selection on O. biennis leads to a rapid increase in the total abundance of arthropods, which reaches an equilibrium after approximately 50 years (figure 3c). This increase in abundance is significantly greater than the abundance of arthropods in plant populations not subject to selection (figure 3c). By contrast, total arthropod richness significantly decreased in populations subject to natural selection compared with populations not experiencing selection (figure 3e). These dynamics occurred because selection caused the fixation of the same O. biennis genotype (genotype B) in every simulation (figure 3a). This selected genotype was strictly biennial, had high biomass and supported a large total abundance and richness of arthropods. The total arthropod richness across the plant population declined because different plant genotypes supported unique arthropod assemblages (see Johnson & Agrawal 2007), and natural selection quickly eroded genetic diversity in the plant population (figure 3a). As a consequence, although arthropod richness increased on an individual plant level, it decreased across the entire plant population (figure 3e).

Figure 3.

Simulated evolution and community change in large (a,c,e; n=2800) and small (b,d,f; n=28) O. biennis populations. (a,b) We contrasted temporal changes in genotype frequencies in populations subject to selection (i.e. relative fitness of genotypes determined according to our experimental results; see methods in the electronic supplementary material) to populations where all genotypes had equal relative fitness and were therefore only influenced by genetic drift. We show the mean genotype frequencies (across 1000 simulations) of the three most fit genotypes in selected populations (B, F and Q), the mean frequency of all other genotypes in selected populations (‘other’ line) and the mean frequency of genotypes (‘drift’ line) in drift populations. (c,d) Mean total arthropod abundance and (e,f) mean arthropod richness summed across all plants in the population are shown from selected (bold solid curve) and drift (bold dotted curve) populations; thin solid and dotted curves show the upper and lower 95% CI around the mean selected and drift populations, respectively.

In small populations of a constant size, natural selection had no discernible effect on the temporal dynamics of arthropod communities when compared with non-selected populations (figure 3d,f). Although the mean differences in abundance and richness are in the same direction as in large populations, the 95% CI values are overlapping (figure 3d,f). This occurs because genetic drift swamps out the effects of selection, and although populations still evolve to fix a single genotype, the outcome is more stochastic (figure 3b). Therefore, evolution due to drift can still lead to changes in the arthropod community, but these changes will be unpredictable.

Similar results were found when O. biennis populations were allowed to exponentially increase and crash, as they often occur in successional and disturbed landscapes (see figure 2 in the electronic supplementary material). When populations were large, these simulations differed in that selection fixed a genotype (Q) with greater annual reproduction (figure 2a in the electronic supplementary material), and although selection caused arthropod abundance to significantly increase at first, it eventually declined to the level observed in populations without selection (see figure 2c in the electronic supplementary material). As before, selection in large populations caused a decline in arthropod richness (see figure 2e in the electronic supplementary material), and in small populations, genetic drift caused there to be no significant differences in abundance or richness between populations with selection versus without selection (see figure 2d,f in the electronic supplementary material).

5. Discussion

Using a combination of empirical and modelling results, we show that evolution in populations of O. biennis has the potential to drive ecological changes in the arthropod community associated with this plant. This conclusion follows from several results: (i) O. biennis exhibits significant genetic variation for multiple plant traits (condition 1), (ii) directional selection acts on life-history and resistance traits of O. biennis (condition 2), and (iii) two of the selected plant traits predict variation in the abundance of individual arthropod species, total arthropod abundance and the number of arthropod species on plants (condition 3). Unfortunately, few field studies have attempted to understand whether evolutionary change in natural populations causes ecological changes to communities over time (Fenner & Ross 1994; Fussmann et al. 2007). Our simulations predict that evolution due to natural selection on O. biennis populations will lead to rapid increases in the abundance of common arthropod species, and a decrease in the total number of arthropod species in plant populations. These results will probably only hold in large O. biennis populations where selection is most efficient.

(a) Evolutionary mechanisms

We have focused on natural selection as a driver of ecological change, but any of the main mechanisms of evolution (i.e. natural selection, genetic drift, dispersal, mutation and assortative mating) can potentially cause ecological changes in communities. Our simulations showed that the effects of selection lead to predictable community changes in large plant populations (figure 3c,e), while in small populations genetic drift caused stochastic community dynamics (figure 3d,f). Although we did not manipulate dispersal or mutation, they can have important effects on the evolution of populations (Moore & Hendry 2009) and potentially even the ecological changes in communities (Garant et al. 2007). When an individual disperses or a new mutant arises in a population, the effect of this variant on the rate and direction of evolution (and the subsequent effect on the community) will depend on the variant's phenotype. If the phenotype of a new mutant or dispersed individual represents a random representation of existing phenotypes in the population, then increased mutation or dispersal rates will attenuate the difference between selected and non-selected populations and decrease the community-level effects of adaptive evolution. If new variants are not random and bring a population closer to its optimum, then increasing dispersal and mutation rates will increase the rate of evolution and accentuate the effects of selection on community dynamics. Finally, if selection or drift depletes genetic diversity within populations, dispersal and mutation will increase genetic variation and potentially fuel ongoing adaptive evolution and any effects this evolution has on the community.

(b) Selection and genetic diversity

Our simulations suggest that selection on O. biennis populations will erode genetic diversity and cause a decrease in the richness of arthropod species in plant populations. This result provides support for the prediction that evolution can be an important mechanism driving community-level effects of genetic diversity (Hughes et al. 2008). Although strong selection is predicted to erode genetic variance in any closed population (Barton & Turelli 1989), our results are likely to be most accurate for highly selfing and asexual populations. By contrast, sexual populations are likely to maintain greater genetic diversity within populations, which will allow ongoing evolution that can influence community processes. Also, balancing selection that maintains genetic diversity in plant traits has the potential to positively influence community diversity through time (Lankau & Strauss 2007).

(c) Assumptions and caveats to studying the effects of evolution on communities

Several caveats arise when studying the community-level effects of evolution. For instance, although we satisfied the necessary conditions of our hypothesis, and our models suggest that ecological effects of evolution on the community are likely to occur in large O. biennis populations, several factors may still prevent ecological changes in arthropod communities in response to plant evolution. First, many factors other than plant genotype influence arthropod communities (Strong et al. 1984), which may render the influence of changes in genotypic composition unimportant unless arthropods respond to the phenotypic distribution of plant traits consistently over space and time. If arthropod populations change their preferences for different phenotypes depending on the environment, plant evolution will have little effect on their ecology. Even when arthropods do respond to plant phenotypic variation in a consistent way, the response of arthropod populations to other ecological factors (e.g. climate-driven population dynamics) could obscure the effects of evolution. Second, our approach does not explicitly incorporate the interactions between arthropod species and how they might change, but instead assumes that any interactions between species that affected the observed abundances will remain the same over time, regardless of changes in genotype frequencies. Arthropod populations can directly and indirectly influence the preference and performance of other arthropods on plants (Kaplan & Denno 2007), and changes in the relative abundance of one population may have cascading effects throughout the community, dampening or amplifying the community-level effects of evolution (Whitham et al. 2006; Bailey et al. 2009). Finally, arthropod populations can rapidly adapt to plant phenotypes (Van Zandt & Mopper 1998), or exhibit plastic behavioural and physiological responses that could buffer ecological changes (Karban & Agrawal 2002).

These caveats arise because unlike a plant's phenotype, which is influenced directly by a plant's genotype and changes in gene expression due to the environment, communities are composed of multiple individual populations, each with their own capacity to ecologically and evolutionarily respond to their environment. As such, understanding the biology underlying these caveats will be necessary to decipher when and where the effects of evolution on communities are likely. We believe that our predictions will be most accurate at making short-term predictions about the effects of evolution on communities.

It is possible to make predictions about the response of multiple arthropod populations while explicitly accounting for the effects of interactions among species. This requires estimating the genetically controlled covariance in abundance between each of y arthropod species and adding the resulting y×y matrix as the first element of equation (2.2). The left-hand side of this revised equation would be a response vector with elements describing the simultaneous changes in the abundance of y arthropod species; the community–trait gradient matrix would similarly have y rows.

(d) What to do when the traits causing variation in the community are unknown

In many instances, the selected traits associated with variation in the community will be unknown, making it difficult to test the conditions outlined above. It would still be useful, however, to have a method that determines whether community-level consequences of evolution are possible or likely in a given system. We have used theory relating to path analysis to derive such a method.

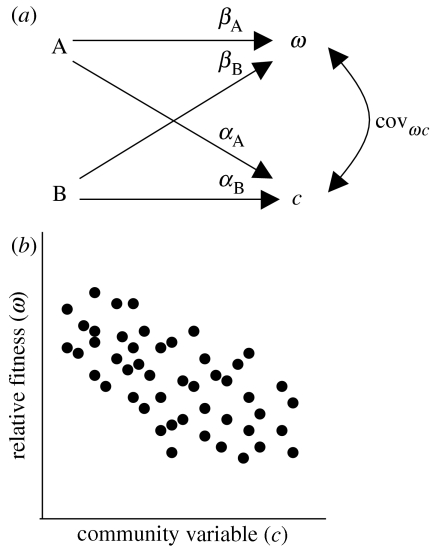
Consider the path diagram of interactions in figure 4a, which parallel the interactions observed in our study. In this example, only two plant traits A and B are subject to natural selection with path coefficients (selection gradients) β_A and β_B, respectively. These same two traits causally affect a community variable c with community–trait gradients α_A and α_B. In this example, when all of the variations in ω and c are explained by A and B, we can use path analysis to derive an empirical relationship between these variables. In particular, Wright (1934) showed that the correlation between any two variables that are not causally related, such as ω and c, can be estimated according to:

$$r_{\omega c}=\Sigma {\beta }_{i\omega }{r}_{ic},$$ (5.1)

where β_iω represents the normally standardized regression/path coefficient between variable i and ω; and r_ic is the correlation coefficient between trait i and the community variable c. When all trait and community variables are transformed to normal variates, with mean 0 and standard deviation 1, the correlation between any two variables i and j has the property that r_ij=β_ij=cov_ij. It then follows that the covariance between relative fitness in one population and variation in a community variable (cov_ωc) can be expressed as

$${\text{cov}}_{\omega c}={\text{cov}}_{\text{A}\omega }{\text{cov}}_{\text{A}c}+{\text{cov}}_{\text{B}\omega }{\text{cov}}_{\text{B}c}.$$ (5.2)

Note that the right-hand side of the equation is equivalent to the multiplication of αβ from equation (2.2) in the case of normally standardized coefficients. Therefore, anytime relative fitness in one population covaries with a community variable (figure 4b), cov_ωc provides evidence that natural selection is acting on traits that affect or are associated with community variables. It is important to note that cov_ωc provides an estimate of total selection on all unmeasured traits that affect the community variable, as equation (5.2) is a specific case of equation (5.1) and generalizes to any number of traits. Thus, estimating the genetic covariance between relative fitness and community variables provides useful information irrespective of the presence or absence of the community–trait gradients. However, the accuracy of inferences based on this covariance (or point estimates of the covariance term itself, if only phenotypic data are available) will be related to how much variation in ω and c is explained by other ecological variables as well (e.g. seasonal weather change), and a complete mechanistic understanding of how and why this process is occurring can only be gained through the trait-based approach described in equation (2.2).

Figure 4.

(a,b) Path diagram illustrating the relationship between plant traits, relative fitness and community variation. Two plant traits A and B causally influence variation in relative fitness (ω) according to path coefficients β_A and β_B. These same traits influence variation in a community variable (c) according to coefficients α_A and α_B. The resulting covariance between ω and c is denoted by cov_ωc.

(e) Practical considerations in studying the effects of evolution on communities

The most convincing evidence in support of our hypothesis will come when there is direct experimental evidence that evolution by natural selection in one population has caused temporal changes in the ecology of one or more populations of other species in a natural community. Testing this hypothesis in the field presents researchers with practical challenges, and we outline two potential experimental protocols.

One experiment involves manipulating selection on a focal species in the field and observing its evolution and the ecological effects of evolution on the community. The optimal design is one where there are replicated experimental populations that are of identical size and genotypic composition at the beginning of the experiment. Half of the populations are then randomly assigned to be selection lines (e.g. removal of herbivores), while the other half are controls (e.g. herbivores present). It is then straightforward to compare phenotypic traits and community variables between selected and control lines to examine divergence. This method will work best when selection and control lines are later assessed in a common environment, allowing plastic and evolutionary responses to be distinguished. Another alternative would be to follow changes in genotype frequencies using molecular markers (in the case of asexual/selfing species) or changes in allele frequencies for ecologically relevant Mendelian traits (Subramaniam & Rausher 2000; Barrett et al. 2008). If there are concurrent changes in the size of the focal populations, then it will be further necessary to parse out ecological and evolutionary effects on communities (Hairston et al. 2005; Ezard et al. 2009).

An alternative approach is to experimentally simulate evolution by manipulating changes in the phenotypic distribution of traits within a population over time. Using this method, the phenotypic distribution of ecologically important traits could be altered every generation to simulate directional, disruptive or stabilizing selection on a population. Community dynamics in ‘evolved’ and control (static) plant populations could then be contrasted to determine the community consequences of the simulated phenotypic evolution. This approach mitigates the practical challenges of following genotype/allele frequencies and concurrent ecological changes within the selected populations.

6. Conclusion

Understanding the importance of evolution for the ecological dynamics of communities is an important, yet unresolved problem in evolutionary ecology. Circumstantial evidence is mounting that evolution in one population can cause ecological changes to natural communities (Agrawal 2005; Lankau & Strauss 2007; Post et al. 2008; Post & Palkovacs 2009). However, no study has convincingly demonstrated that evolution drives rapid ecological changes in natural communities over time. Our own data and simulations suggest that natural selection on genetic variation in life-history traits of a native plant can drive rapid ecological changes in the abundance and species richness of arthropod communities. The experimental and analytical framework proposed here could lead to a better understanding of the community-level effects of evolution by natural selection in a wide diversity of experimentally tractable systems.

Supplementary Material

Supplementary methods

Supplementary methods for matrix projection and simulation modelling

Supplemental table 1

The G-matrix. Genetic variances of traits are shown along the diagonal and genetic covariances on the off-diagonal. These estimates were used to derive the predicted response of community variables to selection on O. biennis traits

Supplemental table 2

Directional selection gradients from phenotypic selection analyses. Analyses were performed by calulating the partial regression coefficients between relative plant fitness and phenotypic variation in Oenothera biennis traits

Supplemental table 3

Community-trait gradients between community variables and plant traits under selection based on phenotypic analyses. Gradients were calculated as the partial regression coefficient between a community variable and plant traits

Supplemental figures 1 and 2

Fig 1: Predicted changes in the relative abundance of arthropods in response to selection on O. biennis. Fig 2: Simulated evolution and community change in O. biennis populations that experience exponential growth and population crashes