Analysis of multiple SNPs in a candidate gene or region

Abstract

We consider the analysis of multiple SNPs within a gene or region. The simplest analysis of such data is based on a series of single SNP hypothesis tests, followed by correction for multiple testing, but it is intuitively plausible that a joint analysis of the SNPs will have higher power, particularly when the causal locus may not have been observed. However, standard tests, such as a likelihood ratio test based on an unrestricted alternative hypothesis, tend to have large numbers of degrees of freedom and hence low power. This has motivated a number of alternative test statistics. Here we compare several of the competing methods, including the multivariate score test (Hotelling’s test) of Chapman et al. [2003], Fisher’s method for combining p-values, the minimum p-value approach, a Fourier transform based approach recently suggested by Wang and Elston [2007] and a Bayesian score statistic proposed for microarray data by Goeman et al. [2005]. Some relationships between these methods are pointed out, and simulation results given to show that the minimum p-value and the Goeman et al. [2005] approaches work well over a range of scenarios. The Wang and Elston approach often performs poorly; we explain why, and show how its performance can be substantially improved.

1 Introduction

Current genetic association studies produce information on many SNPs in a gene, region or, in more recent studies, over the entire genome, but it is not obvious how this information should be best analysed to detect and locate causal variants affecting the trait of interest. The simplest approach is to perform a separate test at each genotyped SNP: this raises multiple testing problems, but is otherwise straightforward, and is optimal where we are searching for a single causal variant that we believe has been included in the set of genotyped SNPs. However, we will often believe that multiple causal variants exist and, more importantly, current genotyping densities make it very unlikely that the causal variant has been genotyped: instead, we rely on the causal variant being highly correlated with one or more of the genotyped SNPs. This suggests that a joint analysis of SNPs in a gene or region may be preferable, since combining information across many SNPs may better predict the unobserved causal variant than any single SNP. A very large number of such methods have been suggested, ranging from sophisticated but computationally expensive coalescent-based probability models [Morris et al., 2002; Tachmazidou et al., 2007] to more ad hoc schemes for combining single SNP p-values, the best known being Fisher’s method.

Here we restrict our attention to a subset of approaches that generate test statistics based directly on genotype data in a candidate gene: such approaches are straightforward, and there is evidence that they are at least as powerful as alternatives, for instance haplotype based tests [Chapman et al., 2003]. Such tests can be applied to larger regions, or even to genome wide studies, by dividing the region in to a number of possibly overlapping windows and then testing the SNPs within each window. It is currently an open, and important, question as to whether this will outperform the single SNP tests currently favoured for genome wide studies [The Wellcome Trust Case-Control Consortium, 2007].

The approaches we consider can be divided into two types. The first performs a set of univariate tests and then attempts to combine these tests in some way: we consider the best known such approach, Fisher’s method for combining p-values, together with the standard approach of using the smallest p value observed in a region as a measure of significance within that region. The second are true multivariate tests. These are motivated by the observation that increasing the number of SNPs in a set will increase our ability to predict an unobserved causal variant, therefore suggesting an increase in power. However as the number of SNPs increases so too does the degrees of freedom (df) “spent” and for standard tests—for example a likelihood ratio test based on a regression model fitting a parameter per SNP—-this can result in a net loss of power. Accordingly, several authors have developed test statistics which use some sort of dimension reduction to reduce the number of degrees of freedom spent by a test for a given number of SNPs. Within this class, we examine a recent approach due to Wang and Elston [2007], who suggested a test statistic that reduces the effective degrees of freedom by using a weighted Fourier transform test that puts higher weight upon the low-frequency components (i.e. those explaining the most information). This method is related to a number of simple alternatives; we discuss these and note that these will often be preferable to the original Wang and Elston [2007] test. We also investigate an approach based on work by Goeman et al. [2005] on the analysis of high dimensional gene expression data, and not previously applied to association studies. Goeman et al define a general score test within an empirical Bayesian model, which assumes a central normal prior for the appropriate regression parameters, and suggest the variance of this prior to be a multiple of the corresponding identity matrix. Within a linear model framework Goeman et al. show that their test statistic effectively forces the test to put more weight upon the higher Eigen vectors of the matrix of genotype data, rather than the most informative Fourier transform components, as in Wang’s test statistic. We compare the power of these approaches with the usual multivariate score test (Hotelling’s T² test) [Chapman et al., 2003; Xiong et al., 2002; Fan and Knapp, 2003].

We now give a more detailed description of the test statistics investigated, before comparing the methods by simulations based on real sequence data from two genomic regions. We will use two scenarios; firstly the case in which we have a set of tag SNPs representing the region and secondly the situation in which we have full sequencing data across the region. Throughout, we assume a case-control study design.

2 Methods

We begin by establishing some notation, and then give the test statistics to be considered. We assume that we have genotyped N individuals at n loci. We let X_i = (x_i1,...,x_in)^T be a column vector of length n in which x_ij represents the genotype at locus j in individual i and where we code each genotype as 0, 1 or 2 counting the number of “1” alleles present at that locus (labelling of alleles is arbitrary). We also let Y_i determine the disease status of individual i, whereby this is coded as 0 for those individuals without disease and 1 for those with the disease. We then let X = (X₁,...,X_N)^T be the N by n matrix of genotype data and Y = (Y₁,..,Y_N)^T the N by 1 vector of disease status.

2.1 Test statistics

Single SNP test

The standard score test for association between locus k and case control status is

$$t_k^2=\frac{u_k^2}{v_k},$$

where

$$u_k=\sum _{i=1}^N(Y_i-\stackrel{‒}{Y})X_{ik},$$

is the mean of * and v_k is the variance of u_k under the null of no effect within the region, which can be estimated by

$$v_k=\frac{1}{N}\sum _{i=1}^N{(Y_i-\stackrel{‒}{Y})}^2\sum _{i=1}^N(X_i-\stackrel{‒}{X}){(X_i-\stackrel{‒}{X})}^T.$$

Since we have n test statistics we need to correct for multiple testing [Schaffer, 1995] by calculating the family wise error rate, that is the probability of at least one false discovery under the global null that no loci are associated to disease. This is equivalent to combining all single locus tests into a single test statistic through their maximum value (minimum p-value), giving

$$T_{\mathit{minp}}=\underset{k=1}{\overset{n}{\max }}{t}_k^2.$$

In general this has an unknown null distribution and we therefore calculate the appropriate p-value using a standard permutation argument, in which we randomly permute the disease status across all individuals.

Fisher’s method for combining p-values

Fisher [1932] suggested combining information across multiple tests using the statistic

$$T_{\text{fisher}}=-2\ast \sum _{j=1}^n\log \left(p_j\right),$$

where p_j is the p-value corresponding to the single locus test at locus j. When the tests are mutually independent, Fisher showed that this test statistic asymptotically follows a chi-square distribution on 2n degrees of freedom, under the global null hypothesis. However in this application, the single locus tests at nearby loci are likely to be correlated and therefore the limiting distribution of Fisher’s statistic is unknown and we again calculate significance using permutation.

Standard multivariate test

Chapman et al. [2003] show that when assuming a single underlying causal locus, and a genotype based model, the appropriate multivariate score test statistic can be defined by

$$T_{\text{usual}}=U^T{V}^{-1}U,$$

where

$$\begin{array}{cc}\hfill U=& \sum _{i=1}^N(Y_i-\stackrel{‒}{Y})X_i\hfill \\ \hfill =& X^T(Y-\stackrel{‒}{Y})\hfill \end{array}$$

is a vector of length n and V is the estimated null variance-covariance matrix of U,

$$\begin{array}{cc}\hfill V=& (N-1)\ast \sum _{i=1}^n{(Y_i-\stackrel{‒}{Y})}^2\ast \sum _{i=1}^n(X_i-\stackrel{‒}{X}){(X_i-\stackrel{‒}{X})}^T\hfill \\ \hfill =& (N-1){(Y-\stackrel{‒}{Y})}^T(Y-\stackrel{‒}{Y})\ast {(X-\stackrel{‒}{X})}^T(X-\stackrel{‒}{X}).\hfill \end{array}$$

Under the null that there is no associated locus within the region, this usual test statistic has an asymptotic chi-square distribution on n degrees of freedom. This test is equivalent to the score test for a logistic regression model in which each x_ij is included as an explanatory variable of Y_i.

Bayesian score test

The test statistic of Goeman et al. [2005] is closely related to T_usual above, being based on the logistic regression model in which each x_ij is included as an explanatory variable of Y_i, but assumes an empirical Bayesian model. In particular they suggest the use of an independent prior on the SNP effects.

More precisely, the test statistic of Goeman et al. is based upon the likelihood, f (β;D), where D represents the data and β the parameters of the model, and assumes a prior for β = τb such that E(b) = 0 and E(bb^T) = Σ. Goeman et al. [2005] show that the empirical Bayesian score test then has the form

$$T_{\text{goeman}}=\frac{1}{2}(U_f^T\Sigma U_f-\text{trace}\left(\Sigma I_f\right)),$$

where U_f is the score function relating to likelihood f (β;D), with respect to β, and I_f is the corresponding observed Fisher information matrix. Goeman et al. [2005] suggest the use of Σ equal to the identity matrix, I, since in the regression framework this leads to a test that focuses more weight on the most informative eigenvectors of the X^TX matrix. In our case D = (X,Y) and β represents the coefficients of the logistic regression of Y upon X. Therefore, U_f is defined by U, above, and I_f is equal to

$$\begin{array}{cc}\hfill I_f=& \stackrel{‒}{Y}(1-\stackrel{‒}{Y})\ast \sum _{i=1}^n(X_i-\stackrel{‒}{X}){(X_i-\stackrel{‒}{X})}^T\hfill \\ \hfill =& \stackrel{‒}{Y}(1-\stackrel{‒}{Y})\ast {(X-\stackrel{‒}{X})}^T(X-\stackrel{‒}{X}),\hfill \end{array}$$

leading to a test statistic of the form

$$T_{\text{goeman}}=\frac{1}{2}({(Y-\stackrel{‒}{Y})}^{T}X{X}^T(Y-\stackrel{‒}{Y})-\stackrel{‒}{Y}(1-\stackrel{‒}{Y})\ast \text{trace}\left({(X-\stackrel{‒}{X})}^T(X-\stackrel{‒}{X})\right)).$$

Intuitively, this produces a test which ignores correlation between SNPs, relative to tests not assuming independent SNP effects; this increases power for certain alternatives and reduces it for others. In particular, this test will have increased power when positively correlated SNPs have effects in the same direction, since the deviations from expectations under the null at each SNP are combined without adjustment for the positive correlation between the SNPs, but reduced power when positively correlated SNPs act in opposite directions or negatively correlated SNPs in the same direction. Since the first situation is believed to be common in genetic association studies, arising for instance when several observed SNPs are in Linkage Disequilibrium (LD) with an unobserved causal variant, whilst the second would require two nearby loci to act in opposite directions or particular epistatic patterns, we might expect a net gain in power.

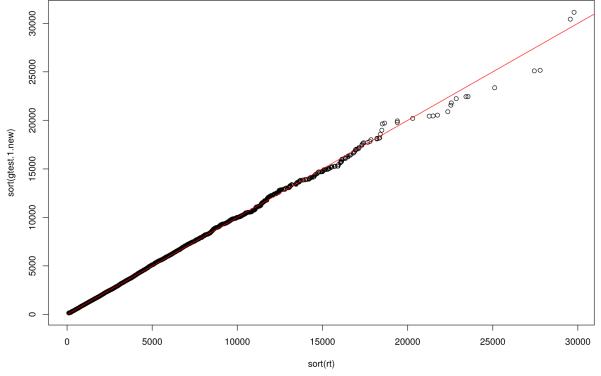
This test statistic has no known distribution and we can use the same permutation argument to estimate appropriate critical values under the global null hypothesis. Note, however, that under permutation only the first part of this test statistic, equating to U^TU, is random and that under the null the U component has known asymptotic normal distribution with zero mean and variance estimated by I_f. Therefore a quicker method for calculating p-values is to simulate a large sample of U statistics from this asymptotic null distribution, form the appropriate test statistics (U^TU) and calculate the proportion of these simulated test statistics that are more extreme than the observed test statistic. The qq-plot in figure 1 demonstrates the validity of this approach by comparing the quantiles of 10,000 true test statistics, each derived from datasets sampled under the null, with the quantiles of 10,000 of these simulated values (where the variance matrix was estimated from a single randomly chosen dataset).

Figure 1.

QQ-plot comparing the distribution of true test statistics, based upon the CTLA4 region, with the distribution of the simulated asymptotic values.

Weighted Fourier transform

Wang and Elston [2007] suggest an alternative multivariate test that aims to reduce the test degrees of freedom by using a weighted Fourier transform of the genotypes. The genotype codes for individual i, (x_i1,...,x_in) are transformed into a sequence of numbers (z_i1,...,z_in) using the real part of the discrete Fourier transform:

$$\left(z_{ik}\right)=\text{Real}\left(\sum _{j=1}^m{x}_{ij}\exp \left(-\frac{2\pi \sqrt{(}-1)(k-1)(j-1)}{n}\right)\right),$$

for i = 1,...,N. Note that we have indexed the z’s from 1 to n, rather than 0 to (n − 1) as in Wang and Elston [2007]. These new values now form n Fourier transform components, Z_j = (z_1j,...,z_Nj), for j = 1,...,n, which can be treated simply as recoded genotype values. Assuming a simple logistic regression of disease upon each of these Fourier transform components independently we are able to define a Fourier transform score and variance estimate for each Fourier component such that

$$u_{ft:k}=\sum _{i=1}^N(Y_i-\stackrel{‒}{Y})\left(z_{ik}\right),$$

and v_ft:k is simply the estimate of the null variance of u_ft:k, calculated in the same way as before. Wang and Elston [2007] then combine these Fourier score components into a single test statistic by choosing some weighting, w of the components, where more weight is given to the lower-frequency components (i.e. smaller k) since these are the components with more smoothing. The test suggested by Wang and Elston [2007] is therefore defined by

$$T_{\mathit{wang}.ft}=\frac{w^T{U}_{ft}}{\sqrt{w^T{V}_{ft}w}},$$

where U_ft = (u_ft:1,...,u_ft:n)^T and V_ft has diagonals defined by (v_ft:1,...,v_ft:n) and zeros elsewhere because the Fourier components are independent of one another. This test statistic then follows a standard normal distribution under the null and so its square is a chi-square on 1 df. In order to try to achieve an appropriate weighting, Wang and Elston [2007] choose the vector w to be simply defined by (1/(k + 1)²) for the k^th component, k = 1,...,n.

Comments and alternatives

We now make a number of comments about the Wang and Elston [2007] approach, and suggest some alternative test statistics.

First, note that the weighting w_k = (1/(k + 1)²) is arbitrary: intuition suggests that a weighting based upon the data would be preferable, though it is not immediately obvious how to choose a weighting to give a test with a convenient null distribution. Our next comment regards the use of only the real part of each Fourier component. This means that the components are based upon sums of cosine functions and as such will mean that nearly half of the components will be linearly independent. In fact only the first m = ceiling((n + 1)/2) components are possibly linearly independent and further dependencies within the data can reduce this number again. Theoretically, this means that only these linearly independent components should be included within Wang’s test statistic, although in practise this makes very little difference as it simply means that the weights are slightly higher than those defined, although still decreasing with k.

Following the standard multivariate test, the points above suggest that we could drop the linearly dependent higher-frequency Fourier components and base a test on just the the “m” linearly independent real Fourier components, since this should automatically (approximately) halve the df whilst retaining much of the information. Therefore, we can simply define a multivariate score test based on the linearly independent Fourier components:

$$T_{\mathit{li}.ft}=U_{\mathit{li}}^T{V}_{\mathit{li}}^{-1}{U}_{\mathit{li}},$$

where U_li = (u_ft:1,...,u_ft:m)^T defines the scores for the first m linearly independent Fourier components and V_li is their diagonal m by m variance matrix under the null (equivalent to the first m rows and columns of V_ft). Under the null hypothesis we would expect this test statistic to follow a chi-square distribution on m degrees of freedom.

These points also suggest that another possible test statistic might be based upon the full Fourier components, including both real and imaginary parts, since this full transformation is one-to-one and all original information is retained. However such an approach is complicated by the imaginary components and will not be considered further within this paper.

We note also that within the examples of Wang and Elston [2007] it appears that much of the information is found within the score for the first Fourier component which is of the form:

$$\begin{array}{cc}\hfill u_{ft:1}=& \sum _{i=1}^N(Y_i-\stackrel{‒}{Y})z_{i1}\hfill \\ \hfill =& \sum _{i=1}^N(Y_i-\stackrel{‒}{Y})\left(\sum _{j=1}^m{x}_{ij}\exp \left(-\frac{2\pi \sqrt{(}-1)(j-1)\ast 0}{n}\right)\right)\hfill \\ \hfill =& \sum _{i=1}^N(Y_i-\stackrel{‒}{Y})\left(\sum _{j=1}^m{x}_{ij}\right).\hfill \end{array}$$

This is equivalent to the score for the logistic regression of Y upon a single term equal to the sum of genotypes across all n loci and has a chi-square distribution on one degree of freedom under the null. We denote the corresponding test by T_1.ft.

Finally, we point out that if negative correlation exists between pairs of loci, T_1.ft (and perhaps T_wang.ft) will perform poorly, as the effects of such loci will cancel. For example, consider two associated loci in perfect, but opposite LD, so that the homozygote coded as 2 at the first locus is always found with the 0 homozygote at the second locus and vice versa; these loci are perfectly negatively correlated and cancel completely. Wang and Elston [2007] recommend recoding the genotypes to avoid this (so that in the above we would swap the 0 and 2 labels for the homozygotes at one of the loci), but it is not always possible to find a recoding removing all negative correlations. Table I illustrate such an example, where the correlation between x₁ and x₂ is 0.41 and that between x₁ and x₃ is 0.19 but that there is negative correlation between x₂ and x₃ (-0.31). By switching 0 and 2 for any locus we can change the signs of all correlations between that locus and all others, however, doing this to any subset of (x₁,x₂,x₃) will always lead to one of the correlations having a different sign to the others and we can never produce positive correlations between all three loci. When this occurs, T_1.ft will loose power and in fact this situation arises in the CTLA4 and IL21R datasets considered below.

Table I.

Simple example in which swapping allele codings will never produce positive pairwise correlations between all loci

	Haplotypes
Locus	1	2	3	4	5	6	7	8	9
x 1	2	2	1	1	1	1	1	0	0
x 2	2	1	0	2	1	0	2	1	0
x 3	2	1	2	0	1	0	0	0	2

Since the first Fourier component appears to dominate T_wang.ft, we would expect similar issues arise there also. We will therefore, as suggested in Wang and Elston [2007], also consider the performance of these test statistics in the subset of loci that gives the maximal number of positively correlated loci (i.e. those loci with negative correlation under the maximal coding are dropped), denoting these statistics by T_wang.ft.d, T_li.ft.d and T_1.ft.d.

2.2 Simulation study

We illustrate the relative performance of the methods described using a simulation study. We take sequence data on 96 individuals from two regions, one of 24 Kb surrounding CTLA4 and one of 48 Kb surrounding IL21R, and use these to define population genotype frequencies for the different regions. We did this by first estimating the population haplotype frequencies, using the EM based snphap program [Clayton, 2003], and then assuming Hardy-Weinberg equilibrium (HWE) to generate genotype frequencies. We also consider the region considered by Wang and Elston [2007], CHI3L2. We downloaded estimated haplotype frequencies within the 90 CEU individuals from the hapmap website [The International HapMap Consortium, 2007] and used these to generate population genotype frequencies under HWE. As in Wang and Elston [2007], we selected only those 22 loci with allele frequency above 20%. Details of the three regions are in table II. This table demonstrates that CHI3L2 has high levels of LD and by design also has high allele frequencies and CTLA4 has moderately high levels of LD and relatively high allele frequencies. IL21R, on the other hand, has lower levels of LD and slightly lower allele frequencies. For allele frequencies based upon each region, we also consider the extreme scenario in which there is no LD at all and all loci are independent of one another. This situation is particularly simple to simulate since each genotype is sampled independently based upon the allele frequencies of the observed loci within the region and assuming Hardy-Weinberg equilibrium (HWE).

Table II. Details of DS loci chosen within each region.

The first column shows the number of SNPs within each region. The second gives the average “mean R² value” across all sets of tag SNPs selected. For each set of tag SNPs, this mean R² is the mean population R² between each unobserved locus in the region and the set of selected tag SNPs. Column 3 shows the mean number of tag SNPs selected across all samples and columns 4 and 5 show the mean minor allele frequencies across all loci and the across all sets of tag SNPs respectively

Region	# SNPs	Av. Mean R2	Av. # tag SNPs	Av. MAF	Av. tag SNP MAF
CTLA4	34	0.83	6.662	0.27	0.20
IL21R	38	0.629	18.22	0.24	0.25
CHI3L2 (above 20% af)	22	0.78	3.018	0.34	0.33

We then sample M = 1000 case-control data sets using these frequencies and a disease model in which for each replicate we sample, uniformly at random, one of the loci within this region to be the causal locus and assume that this acts in a multiplicative way with a relative risk of 1.3. Hence the causal locus varies amongst the M data sets, but the relative risk remains fixed. We consider analyses both of each complete data set (including the causal locus) and of reduced data sets based on choosing tag SNPs for each region, using a method based on pairwise LD. The tag SNPs are chosen based upon all loci within the region, including the causal locus, and therefore the causal locus may or may not be included within the set of tagging SNPs. Note that tag SNPs are reselected for each replicate dataset and thus free to vary over replicates.

Since our simulation study needs many replicates we require a quick method of tag SNP selection. For this reason we use a simple cluster analysis to group similar loci and then choose the single locus with highest allele frequency from each group as a tag SNP. Our clustering approach uses Euclidean distance measures and defines distance between clusters according to the average distance between loci. We choose the number of clusters (therefore tag SNPs) to be the smallest number that give a mean R², between all “common” untagged loci and the set of tag SNPs, equal to or less than 0.8. We define “common” to be those loci whose minor allele frequencies are greater than or equal to 0.05. Note that for the IL21R and CHI3L2 regions in table II, the Av. Mean R² are below 0.8. This is due to the fact that the average in the table is taken across all loci rather than across just the “common” loci. Similar tag SNP selection methods have been implemented by many others including Byng et al. [2003].

We sample datasets of 2000 cases and 2000 controls and for each dataset we compute the test statistics described above and calculate their appropriate p-values, either based upon asymptotic distributions or by permutation when these are not available. We can then estimate the power of each test, for a given critical level (α), to be the proportion of datasets for which we find a p-value more extreme than α. We consider α levels of 0.01 and 0.001.

3 Results

Results of the simulation study are given in table III. We see that Goeman’s Bayesian score test T_goeman and the minp statistic T_minp perform consistently well, with T_goeman usually the most powerful test when LD is low (IL21R) or absent. The power of Wang’s test statistic, T_wang.ft, is very similar to that of T_1.ft, highlighting the fact that most of the information in Wang’s test is contained within the first Fourier component. These two tests perform poorly, often having the lowest power of all tests considered. In both cases we can usually increase power slightly by dropping those loci that are negatively correlated with the maximal positively correlated set to give the T_wang.ft.d and T_1.ft.d statistics. Also notice that in general T_li.ft, the multivariate test based upon the linearly independent Fourier transforms has increased power compared to the other Fourier transform based tests and often has power competitive with the other tests. This shows that T_wang.ft.d and T_1.ft.d are discarding/down-weighting substantial useful information by relying so heavily on the first Fourier component, which is not surprising, since the first Fourier component is just the sum of genotypes across all loci included in the test. When the region has low or no LD T_li.ft performs best if the negatively correlated loci are not dropped, otherwise dropping these loci makes little difference and T_li.ft.d has similar power to T_li.ft.

Table III. Power of different test statistics.

“goeman” being the power of T_goeman test statistic, “usual.p” being the power of the usual T_usual test statistic (calculated via permutation). “fisher” gives the power of Fisher’s T_fisher statistic, “minp” that of the minimum p-value test statistic (T_minp). “wang.ft”, “1.ft” and “li.ft” are the power of Wang and Elston’s test statistic (T_wang.ft), the first Fourier transform test (T_1.ft) and the linearly independent Fourier transform test (T_li.ft), respectively. Subscript “.d” denotes the power when the negatively correlated loci are dropped. Power is based upon 1000 simulated samples of 2000 case and 2000 controls and randomly selected causal loci with a relative risk of 1.3. For a given p-value, p, its standard error is estimated by $\sqrt{(\widehat{p}(1-\widehat{p})∕1000)}$

Region	Power for α = 0.01
	goeman	usual.p	fisher	minp	1.ft	wang.ft	li.ft	1.ft.d	wang.ft.d	li.ft.d
CTLA4, all loci	0.73	0.57	0.77	0.79	0.60	0.60	0.68	0.60	0.60	0.70
CTLA4, tag SNPs	0.78	0.77	0.79	0.76	0.40	0.47	0.75	0.61	0.60	0.77
IL21R, all loci	0.331	0.252	0.283	0.312	0.193	0.213	0.282	0.205	0.207	0.269
IL21R, all loci	0.35	0.318	0.320	0.360	0.190	0.216	0.288	0.217	0.221	0.183
IL21R, tag SNPs	0.35	0.318	0.320	0.360	0.190	0.216	0.288	0.217	0.221	0.183
CHI3L2, all loci	0.97	0.96	0.96	1.00	0.89	0.90	0.96	0.89	0.90	0.96
CHI3L2, tag SNPs	0.97	0.95	0.95	0.88	0.89	0.88	0.84	0.85	0.88	0.94
INDEPENDENT CTLA4	0.575	0.587	0.241	0.478	0.055	0.056	0.394	0.084	0.075	0.15
INDEPENDENT IL21R	0.317	0.241	0.13	0.266	0.041	0.038	0.263	0.058	0.052	0.078

Region	Power for α = 0.001
	goeman	usual.p	fisher	minp	1.ft	wang.ft	li.ft	1.ft.d	wang.ft.d	li.ft.d
CTLA4, all loci	0.62	0.38	0.68	0.55	0.53	0.53	0.49	0.49	0.49	0.53
CTLA4, tag SNPs	0.69	0.67	0.70	0.65	0.26	0.30	0.64	0.50	0.52	0.66
IL21R, all loci	0.234	0.131	0.204	0.197	0.121	0.137	0.176	0.147	0.159	0.192
IL21R, tag SNPs	0.283	0.207	0.235	0.270	0.110	0.122	0.196	0.146	0.158	0.105
CHI3L2, all loci	0.88	0.84	0.88	0.94	0.80	0.81	0.84	0.82	0.82	0.86
CHI3L2, tag SNPs	0.88	0.84	0.83	0.66	0.74	0.74	0.67	0.73	0.75	0.82
INDEPENDENT CTLA4	0.411	0.356	0.08	0.281	0.01	0.015	0.193	0.034	0.041	0.117
INDEPENDENT IL21R	0.235	0.125	0.044	0.175	0.009	0.01	0.161	0.037	0.028	0.058

As may be expected [Chapman et al., 2003], T_usual has competitive power when using tag SNPs but has lower power when all loci are included in the test statistic. The other test statistics are much less sensitive to the number of loci included and give similar performance on tag SNPs and on the complete data. Fisher’s combined p-value performs very well, particularly when there are many loci in high LD, but has low power when LD is low or in the region. This should be expected, since when there is high LD within a region all/many of the loci are likely to be highly correlated with the causal allele and therefore all/many are likely to have non-null p-values, whilst, when there is low LD, few are likely to be related to the causal locus and therefore only few of the p-values will be non-null: therefore multiplying together p-values as T_fisher does is not sensible.

Wang and Elston [2007] found their test, T_wang.ft, to outperform several other test statistics, including T_minp using data from the CHI3L2 region, but our results suggest the opposite. The reason for this difference is that within our simulations we randomly sample causal loci and select new tag SNPs for each dataset whereas Wang and Elston [2007] choose a single causal locus, namely “rs2182114”, and use a single “a priori” set of tag SNPs (“rs7366568”, “rs8535”, “rs2477574”, “rs11102221”). When we choose this single causal locus and set of tag SNPs, T_wang.ft does indeed have higher power than T_minp (Table IV). This demonstrates that different tests may be optimal for particular causal loci. However our interest lies in tests which are optimal across all loci within a region and those which perform well in all circumstances. We therefore recommend either Goeman’s test statistic or the minimum p-value test in preference to the Fourier transform based tests.

Table IV. Power of test statistics with fixed causal locus and tag SNPs as in Wang and Elston [2007].

“goeman” being the power of T_goeman test statistic, “usual.p” being the power of the usual T_usual test statistic, with p-values calculated via permutation. “fisher” gives the power of Fisher’s T_fisher statistic, “minp” the power of the minimum p-value test statistic (T_minp). “wang.ft”, “1.ft” and “li.ft” are the power of Wang and Elston’s test statistic (T_wang.ft), the first Fourier transform test (T_1.ft) and the linearly independent Fourier transform test (T_li.ft), respectively. “wang.ft.d”, “1.ft.d” and “li.ft.d” show the power of these test statistics when the negatively correlated loci are dropped. Following Wang and Elston [2007], power is now based upon 1000 simulated samples of 200 case and 200 controls and fixed causal locus with a relative risk of 1.4 and fixed tag SNPs. For a given p-value p, its standard error can again be estimated as $\sqrt{(\widehat{p}(1-\widehat{p})∕1000)}$

Region	Power for α = 0.01
	goeman	usual.p	fisher	minp	1.ft	wang.ft	li.ft	1.ft.d	wang.ft.d	li.ft.d
CHI3L2, all loci	0.39	0.15	0.39	0.24	0.38	0.37	0.15	0.37	0.37	0.16
CHI3L2, tag SNPs	0.32	0.22	0.27	0.26	0.27	0.32	0.29	0.35	0.37	0.29

Region	Power for α = 0.001
	goeman	usual.p	fisher	minp	1.ft	wang.ft	li.ft	1.ft.d	wang.ft.d	li.ft.d
CHI3L2, all loci	0.14	0.04	0.13	0.06	0.13	0.12	0.04	0.12	0.12	0.05
CHI3L2, tag SNPs	0.11	0.07	0.10	0.07	0.10	0.11	0.10	0.12	0.13	0.10

4 Discussion

We have compared the power of a number of multivariate test statistics in a simulation study based on observed patterns of LD and allele frequencies. Our most striking finding is the poor performance of the test statistic recently proposed by Wang and Elston [2007]. We argue above that this to be expected on theoretical grounds, but these results contradict simulation results presented in Wang and Elston [2007], based on artificial LD patterns and on the CHI3L2 region, in which T_wang.ft was found to be more powerful than Bonferroni correction of single SNP tests, permutation correction of single SNP test and a logistic regression based likelihood ratio test, and so are worthy of further discussion.

We show above that Wang and Elston [2007] were fortuitous in their choice of causal SNP in CHI3L2, and that in general other tests have greater power than T_wang.ft on this region. We also believe their results using artificial LD patterns were due to unrealistic features of these simulations. Wang and Elston [2007] consider 4 or 10 markers, with allele frequencies between 0.2 and 0.8 and assume that the causal variant is in the centre of the region studied, with all correlations positive and either equal, given by 0.8^|i-j| where i and j index markers, or sampled uniformly between 0.3 and 0.7. We argue that these assumptions are unrealistic, both with respect to allele frequency and LD pattern: in particular, assuming that correlations are equal and positive is exactly where a statistic based on the correlation between the phenotype and the mean of the genotypes, which is effectively what T_wang.ft is, will perform optimally, and this is what Wang and Elston [2007] find.

Our results show the importance of comparing procedures over a range of realistic scenarios, ideally based on real data: the relative performance of methods can be strongly dependent on setting. For example, Fisher’s method worked very well for CTLA4 where LD is high, but poorly when there was no LD between loci. However, both Goeman’s Bayesian score test and the minimum p-value test consistently obtain high (often the best) power across all scenarios considered, whilst T_wang.ft is constantly the worst performer considered and is for example dominated by T_li.ft, the new Fourier transform based test introduced here. Given its simplicity and good performance here, T_minp seems a good default choice of test statistic. This is particularly encouraging given the wide use of this statistic in the recent analysis of genome wide association studies.