Population-Based Mechanistic Prediction of Oral Drug Absorption

Abstract

The bioavailability of drugs from oral formulations is influenced by many physiological factors including gastrointestinal fluid composition, pH and dynamics, transit and motility, and metabolism and transport, each of which may vary with age, gender, race, food, and disease. Therefore, oral bioavailability, particularly of poorly soluble and/or poorly permeable compounds and those that are extensively metabolized, often exhibits a high degree of inter- and intra-individual variability. While several models and algorithms have been developed to predict bioavailability in an average person, efforts to accommodate intrinsic variability in the component processes are less common. An approach that incorporates such variability for human populations within a mechanistic framework is described together with examples of its application to drug and formulation development.

INTRODUCTION

To the extent that low and variable bioavailability is an undesirable feature of a compound formulated for oral administration, early characterization of the factors that determine the rate and extent of drug release and absorption in the gastrointestinal tract is vital during drug development. Increasingly, attempts are being made to predict outcomes using a variety of approaches. These range from the development of quantitative structure–activity relationships based on physicochemical properties, through extrapolation from animal data to the application of mechanistic physiologically-based pharmacokinetic (PBPK) models of the human system. Of these approaches, only the latter is capable of capturing the likely variability in oral bioavailability as it is conditioned by the age, sex, race, genetics and disease of the patient, and by the intake of food. However, while several PBPK models and algorithms have been described that attempt to simulate and predict oral bioavailability in the “average subject”, less attention has been paid to the incorporation of intrinsic variability in each of the components of the process and their known covariates such that the extremes can be anticipated in patient populations (1,2). This consideration is of particular importance with regard to compounds that are poorly soluble or poorly permeable and those that undergo extensive first-pass metabolism. We will review aspects of the variability of the several processes that affect oral bioavailability in humans, and how such variability has been incorporated into the advanced dissolution, absorption and metabolism (ADAM) model implemented within the Simcyp® Population-based ADME Simulator (3) (Simcyp Ltd, Sheffield, UK, http://www.simcyp.com).

THE COMPONENTS OF ORAL BIOAVAILABILITY

Oral bioavailability (F_oral) is the fraction of a dose of drug that reaches the systemic circulation in an unchanged form, given by the running product of fa, the fraction of dose entering the cellular space of the enterocytes from the gut lumen, F_G, the fraction of the drug entering the enterocytes that escapes first pass gut wall metabolism, and F_H, the fraction of drug entering the liver that escapes first pass hepatic metabolism and biliary secretion (Eq. 1).

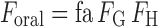1

The prediction of F_H has been discussed elsewhere (1) so the current focus will be on the estimation and variability of fa and F_G as affected by the events in the gut lumen and the gut wall. Factors affecting fa are the characteristics of the formulation (drug particle size and shape, coatings and excipients as they determine disintegration, deaggregation, and dissolution), the physicochemical properties of the drug (solubility and ionization as they influence dissolution and permeability and chemical stability), physiological variables (gastric emptying rate, intestinal transit and mobility, gastrointestinal fluid pH, secretion and reabsorption, intestinal blood flow, bile secretion, enterohepatic recirculation, and intake of food and fluids), and the study design. Factors affecting F_G include the abundance and location of enzymes and transporters down the gastrointestinal tract (GIT). Clearly, all of the physiological factors affecting fa and F_G may also be conditioned by age, sex, race, and disease.

THE ADVANCED DISSOLUTION, ABSORPTION AND METABOLISM (ADAM) MODEL

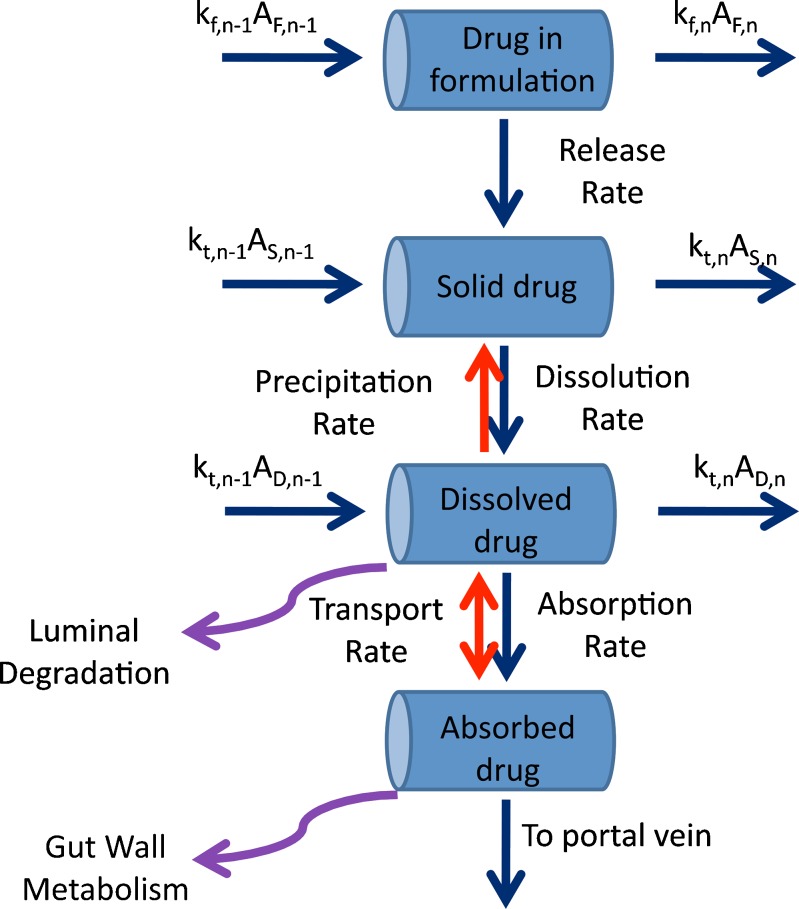
The ADAM model, as implemented in the Simcyp® Population-based ADME Simulator, is a development of a succession of representations of drug absorption from the human GIT—the compartmental absorption and transit (CAT) model (4–10) and the advanced compartmental absorption and transit (ACAT) model (11). It divides the GIT into nine anatomically defined segments from the stomach through the intestine to the colon. Drug absorption from each segment (Fig. 1) is described as a function of release from the formulation, dissolution, precipitation, luminal degradation, permeability, metabolism, transport, and transit from one segment to another.

Fig. 1.

Kinetic processes within each intestinal segment of the ADAM model (see text for explanation of symbols)

It is assumed that absorption from the stomach is insignificant compared with that from the small intestine, and that the movement of liquid and solid drug through each segment of the GIT may be described by first-order kinetics. It is also assumed that drug metabolism in the colon is negligible.

Transit times in the stomach (1/k_st) and colon (1/k_t,8) are defined using gastric and colonic mean resident times, respectively. The transit time in each segment of the small intestine (1/k_t,n) is assigned as a fraction of the total small intestine transit time in proportion to the length of the segment. In the nth segment of the small intestine (n = 1…7), ordinary differential equations are used to describe the dynamics of the amount of solid mass available for dissolution (A_S), the amount of solid mass trapped in the formulation and not available for dissolution (A_F,n) and dissolved drug (A_D; Eqs. 2 and 3, respectively) and the drug concentration in the enterocyte (C_ent; Eq. 4).

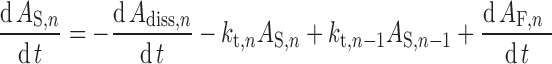2

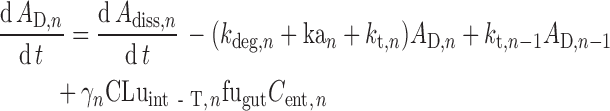3

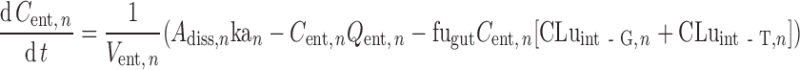4

Where dA_diss,n/dt is the dissolution rate, which can be either entered directly using measured in vitro profiles or calculated using a diffusion layer model (see “Solubility and Dissolution” section). The term dA_F,n/dt indicates the release rate of solid drug from the formulation (by disintegration and deaggregation) in the case where this process is not instantaneous and some solid form is trapped in the formulation and is not available immediately for dissolution; k_deg,n and ka_n are the drug degradation (luminal) and absorption rate constants; γ_n is a unit adjustment factor for the amount of drug transported out of the enterocyte; fu_gut is the fraction of drug unbound in the enterocyte; CLu_int-T,n and CLu_int-G,n are the net efflux clearance from the enterocyte and net metabolic clearance within the enterocyte, respectively; and V_ent,n and Q_ent,n are the volume of enterocytes in the segment and the blood flow to the segment, respectively. The differential equations relating to events in the stomach are simpler in that they do not include any inputs from a previous segment and it is assumed that there is no absorption, metabolism, or transport. The differential equations relating to events in the colon are similar to those for the small intestine segments except that no metabolism is assumed. The Simulator reports, among other details, the time course of A_S, luminal and enterocytic drug concentrations, transporter-mediated clearance, absorption rate, and the fractions of drug absorbed and metabolized in each segment in all individuals within a population.

The outcome of simulations with the model clearly depends on a combination of physiological-, drug- and formulation-related factors. Each of these will be considered briefly, with emphasis on the incorporation of intrinsic variability in gut physiology (12,13).

Physiological Factors

Gastric Emptying

Many factors affect the residence time of solid or dissolved drug in the stomach (14), including the nature of the formulation, the volume of water co-administered, and drug particle size and its distribution, and fed/fasted state (15,16). Although the kinetics of gastric emptying is complex, especially in relation to the fed/fasted state and the composition of food, the process is generally assumed to be first-order. The associated rate constant varies for monolithic and dispersed solids and liquids (16) and is reported to be age- and sex-dependent (17–19). On average, gastric residence time for solutions in the fasted state is 0.25 h (6) with an inter-subject coefficient of variability (CV) of up to 38% (18,20). Within ADAM, known variability in gastric emptying time is implemented in order to assign different values of the gastric emptying rate constant across virtual populations.

For solid dosage forms, further complexity is added by allowing the unit to exit the stomach at discrete times selected at random from a Weibull distribution (Eq. 5).

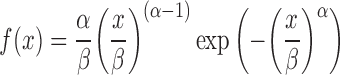5

Where α is a shape factor and β is a scale factor. Davis et al. (16) reported gastric transit times for non-disintegrating single unit systems. These values were used in the “gnlm” (21) routine in the R statistics package (http://www.r-project.org/) and α and β values were found to be 1.66 and 1.44, respectively, giving fasted state mean and standard deviation values of 1.28 and 0.83 h, respectively.

Small Intestine Transit Time

Although the movement of dosage forms down the intestinal tract is discontinuous, sometimes even retrograde, and can be very variable (22,23), net small intestinal transit time is generally, but not exclusively (see below), independent of dosage form and fed/fasted state (16). However, the extent of absorption of sparingly soluble compounds with low lipophilicity (i.e., biopharmaceutic drug classification class 4 drugs) can be limited by residence time in the small intestine (15).

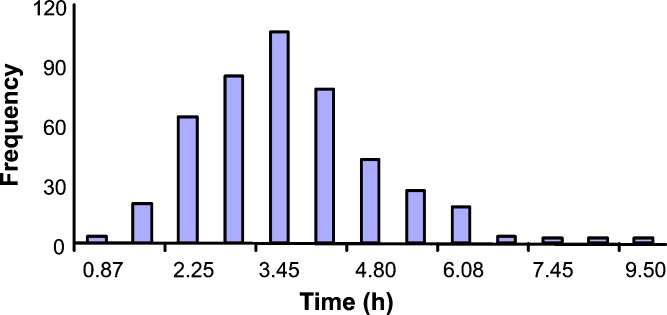
Yu and co-workers reported a mean value of 199 min for net human intestinal transit time from data for over 400 subjects collated from the literature (Fig. 2) (5), a value that was confirmed subsequently in ten subjects by Fadda et al. (24) with median values of 204 and 210 min in fasted and fed states, respectively. The latter authors also observed a significantly shorter mean transit time (141 min) after a pre-feeding dose compared to that in the fed and fasted states (24).

Fig. 2.

The distribution of human small intestinal transit time (5)

Based on these data, ADAM incorporates inter-individual variability in intestinal transit by fitting a Weibull probability distribution function (Eq. 5) to the observed data. Using the “gnlm” routine in the R statistics package values of α and β were found to be 2.92 and 4.04, respectively, giving a mean value of 200 min for net intestinal transit time. Changes in transit as a result of diarrhea and disease can also be accommodated by modifying the Weibull function parameters.

After random assignment of the small intestine transit time for each subject, respective k_t values for intestinal segments are determined in proportion to the lengths of each segment (duodenum, jejunum, and ileum) in each individual. The latter are related to body surface area (BSA) (25) which, in turn, is calculated using the Du Bois and Du Bois equation (Eq. 6) (26).

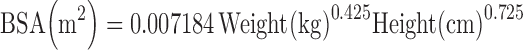6

Thus, segmental transit times are determined based on the assigned small intestine transit time and the weight and height of individuals within a population.

Gastrointestinal pH

Drug solubility and, in some cases, permeability can be affected significantly by pH within different parts of the GIT which, in turn can vary with food, age, and disease (15,27–29). Fallingborg et al. (30) measured pH profiles along the tract in 39 healthy volunteers and observed a range of values up to two pH units at the same site in different subjects. In addition to inter-subject variability, there is also marked inter-occasion variability (31).

Intake of food increases gastric pH followed by a gradual return to its basal value; a change that is significantly dependent on age (28,29). In addition, the impact of hypo/achlorhydria and hypergastrinemia on gastric pH is well documented (32), as is the effect of AIDS (33,34) and of therapeutic intervention with H₂ receptor antagonists (35) and proton pump inhibitors (36).

Feldman and Barnett (37) reported that about 8% of Western populations have a basal (fasted state) gastric pH of 5 to 7. This proportion is traditionally much higher in Japanese and increases with age as a consequence of dietary and lifestyle factors, although with current changes in the latter, the percentage of achlorhydric subjects in the Japanese population is now reducing (38). Clearly, a relatively high gastric pH can have a profound effect on the dissolution and bioavailability of, in particular, sparingly soluble weak basic drugs and can also cause premature release of drugs from enteric-coated formulations (see “Formulation-Related Factors” section) in the stomach instead of the small intestine.

Variability in gastrointestinal pH, including that resulting from age-related changes as a function of fasted/fed state, is incorporated within the population libraries of the Simcyp® Simulator based on meta-analysis of data collated from the literature. During a simulation, GIT pH profiles are assigned to each individual according to the selected population. Hence, drug solubility in each gut segment is computed (see “Solubility and Dissolution” section).

Fluid Dynamics

The extent to which the volume of fluid within the gut lumen (V_lumen,n) changes with time as a result of fluid intake, secretion, and reabsorption can have a significant effect on the dissolution of a drug and hence the concentration presented to enzymes and transporters within the enterocyte. This important consideration is ignored in many models of oral drug absorption by fixing fluid volumes simply at constant values.

Assuming that fluid movement along the GIT is consistent with the rate of gastric emptying and small intestine transit time, Eqs. 7 and 8 define the change in fluid volume in the stomach and each intestinal segment, respectively.

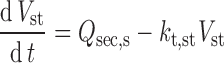7

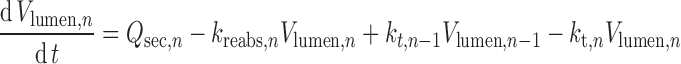8

Where V_st and V_lumen,n are the stomach and nth intestinal segment (n = 1…8) fluid volumes, k_t,st and k_t,n are the gastric emptying and nth segment intestinal transit rate constants, Q_sec,s and Q_sec,n are the stomach and nth segment fluid secretion rates, and k_reabs,n is the fluid reabsorption rate constant in the nth segment. In each segment, the initial volumes are given by basal (steady state) values, but after drug dosing, fluid intake and any inter-individual variability in this are also incorporated.

Fluid volumes along the gastrointestinal tract have been measured by Schiller and co-workers using water-sensitive magnetic resonance imaging in 12 healthy volunteers (six female) (23). Within ADAM, these values, together with data on the variability of fluid secretion and reabsorption rates reported in ICRP (39,40), are used to incorporate variability in gut fluid dynamics and its effects on drug dissolution and absorption.

Gut Wall Enzymes

Human intestinal epithelial cells contain a variety of enzymes involved in phase I and II reactions (41). CYP3A4 and 3A5 are the most prominent cytochrome P450 (CYP) enzymes present in the human enterocyte (42–46), contributing significantly to the first-pass metabolism of many drugs such as cyclosporine (47–49), midazolam (50–52), and verapamil (53,54). Despite the fact that the total content of CYP3A in the entire human small intestine is only 1% of that in the liver (46,55), the intestinal extraction of CYP3A substrates can be significant (49,56,57). The abundances and regional distributions of CYPs 3A4, 3A5, 2C9, 2C19, 2D6, and 2J2 have been documented by Paine et al. (46) together with estimates of their inter-individual variability. Similar but more limited data are available for intestinal UDP-glucuronosyltransferases (UGTs) (58–60). This information together with the frequencies of known genetic polymorphisms is incorporated in the population libraries of the Simcyp® Simulator for use within ADAM simulations.

Gut Transporters

Currently, P-glycoprotein (P-gp) is considered to be the most prominent gut transporter such that drug regulatory bodies recommend that its role in drug–drug interactions be assessed based on in vitro studies (61). As yet, the absolute abundance of P-gp in the human intestinal tract has not been determined. Nevertheless, there is information on its relative distribution down the tract, with evidence that this generally shows an increase from the proximal to the distal small intestine (62,63), although levels of expression in the jejunum appear to exceed those in the ileum (64). Therefore, drugs that are substrates for P-gp but which are relatively permeable by passive diffusion may be relatively well absorbed in the duodenum and proximal jejunum, but if absorption is shifted to more distal parts of the small intestine by a decreased transit time P-gp may play a more significant role in reducing bioavailability (12).

The regional distribution of P-gp along the small intestine and its variability derived from meta-analysis of reported protein and mRNA values are incorporated into the population library of the Simcyp® Simulator. This allows individualized levels of P-gp in each segment to be estimated for simulating the effects of efflux transport on drug absorption across populations (see “Luminal Degradation” section).

Intestinal Blood Flow

The average blood supply to the small intestine (37.2 L/h) is provided by the superior mesenteric artery and constitutes about 10% of the cardiac output in an average adult (25). In the unfed state, mucosal blood flow represents about 80% of the total mesenteric flow (65) while, in turn, about 60% of mucosal blood flow supplies the epithelial cells of the villi (65–67). Hence, average villous blood flow is about 18 L/h. In the Simcyp® Simulator, cardiac index (cardiac output/BSA) is calculated as a function of age (68). This value is then converted to a cardiac output using BSA which, in turn, determines villus blood flow in an individual. The latter is then incorporated with other information on permeability and metabolism to predict F_G. It is worth noting that others have used either total intestinal blood flow (69,70) or mucosal blood flow (71,72) to represent the blood flow relevant to gut wall metabolism. However, since the enzymes are located at the villous tips, it seems more appropriate to use villous blood flow as the reference point (73,74).

For highly permeable drugs, such as midazolam, it has been shown that variability in intestinal blood flow may influence the extent of first-pass gut metabolism (75,76). Accordingly, heterogeneity in the blood supply to different segments of the gut, and its variation (e.g., after food intake) (77), should be incorporated in any model that attempts to replicate the human system. Ideally, dynamic changes with time and variable effects in sub-groups of the population should also be considered (29).

Food Effects

Food can affect drug absorption by several mechanisms including delayed gastric emptying, stimulation of bile flow, alteration of gastrointestinal pH, increased splanchnic blood flow, modulation of intestinal metabolism, and physical or chemical modification of the drug or dosage form (78). Generally, food effects on drug absorption are greatest when a dosage form is administered shortly after a meal. The nutrient and caloric contents of the meal and its volume, and temperature are further potential influences on drug dissolution and permeability and its transit down the gastrointestinal tract. In general, meals that are high in calories and fat content are more likely to affect gut physiology resulting in larger effects on drug absorption (78).

ADAM accommodates the effects of food in slowing gastric emptying, increasing gastric pH (from about 1.3. to about 5), and increasing splanchnic blood flow (by about 30%). It can also incorporate the use of measurements made in biorelevant media such as FaSSIF, FeSSIF (79) where the expectation is that solubility and dissolution more closely mirrors that in vivo. Work is in progress to incorporate the influence of bile secretion and dietary components on drug solubility and dissolution, including the impact of micelle formation (80) (“Solubility and Dissolution” section).

Drug-Related Factors

Drug-related factors affecting oral absorption comprise those relating to solubility and dissolution, luminal degradation, permeability (including transport), and metabolism. In some cases, as already described, these factors are affected by the physiology of the system, e.g., compound solubility can change with environmental pH, bile salt, and counter-ion concentrations, all of which exhibit inter-individual variability and fasted/fed state differences.

Solubility and Dissolution

The ADAM model provides a variety of options for the input of solubility and/or dissolution rate information, both of which may be measured in aqueous buffer or in more biorelevant media. When in vitro dissolution rate profiles are not available, dissolution rate from solid dosage forms can be calculated using diffusion layer models (DLM).

In most models of oral drug absorption, the intrinsic dissolution rate of a drug is described by the classical Noyes–Whitney equation (81) or as modified in versions of the Nernst–Brunner equation (82,83). However, these equations were developed for a planar surface where the concentration gradient in the diffusion layer is linear at steady state. To allow for the fact that the concentration gradient around a spherical particle is not linear under pseudo-steady-state conditions, Wang and Flanagan proposed, and validated experimentally, a general solution of the DLM for dissolution from mono-dispersed spherical particles under sink and non-sink conditions (84,85). This treatment, as defined by Eq. 9, is implemented in ADAM.

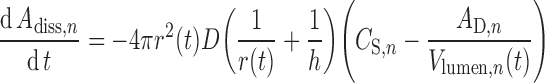9

Where dA_diss,n/dt is the dissolution rate, r(t) is the time-varying particle radius, D is the diffusion coefficient, h is the diffusion layer thickness, C_S,n is the solubility of the drug at the particle surface, A_D,n is the amount of dissolved drug, and V_lumen(t) is the fluid volume, all related to the nth segment of the GIT. Within this formalism, the driving force for dissolution is the concentration gradient given by the second set of brackets in Eq. 9. It should be noted that the pH at the particle surface—the so-called microenvironment pH or pH₀ (86) which can be determined experimentally (87)—and thus C_S,n for ionizable drugs, may be significantly different from that of the bulk solution (88). A free acid will tend to lower pH₀ while a free base will tend to raise pH₀, both of which will tend to limit the extent of pH-dependent solubility (see below) of ionizable drugs. This phenomenon provides both the basis for improvements in dissolution rate that can be obtained where a pharmaceutical salt is used rather than the free acid or base, and the rationale for the use of excipients to modify pH₀ (89).

The diffusion layer thickness of the particles in both mono- and poly-dispersed particle size distributions is a critical parameter. Based on hydrodynamics theory, the apparent diffusion layer thickness of a spherical particle of radius r can be obtained theoretically from Eq. 10 (90).

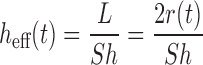10

Where L is the representative length of a particle (the particle diameter for spherical particles) and Sh is the Sherwood number determined using the semi-empirical Ranz–Marshall equation (Eq. 11).

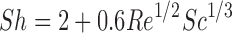11

Where Re is the Reynolds number and Sc is the Schmidt number. Since Re for small particles (<30 μm) floating in a low agitation aqueous medium is negligible, Sh is very close to 2 (91,92) and thus h_eff(t) ≈ r(t). However, as the particle radius increases, h_eff becomes less than the radius, and at low agitation, the h_eff of a large particle is about 30 μm (93). These rules depend upon hydrodynamic factors such as stirring rates and have recently been revisited by Sheng et al. (94). In the ADAM model, the h_eff value is adjusted dynamically for each particle size bin during simulations.

The solubility of ionizable drugs can vary considerably according to luminal gut pH. Thus, by defining the change in pH along the GIT and its inter-individual variability in the fed and fasted states, ADAM adjusts drug solubility for each gut segment in each individual. Where pH-dependent solubility values are to be calculated (rather than extracted from an experimental pH solubility profile), it is assumed that, regardless of the medium, the aqueous pK_a is sufficient to predict the extent of ionization at a given pH and that the Henderson–Hasselbalch equations apply (95) such that the ionized form is completely soluble. Bile salt solubilization effects can also be accounted for in these calculations in a concentration-dependent manner (96), thus enabling the incorporation into simulations of regional, time-dependent and inter-individual differences in bile salt concentrations.

Ionization-enhanced solubility as described by the standard Henderson–Hasselbalch equations does not increase indefinitely but reaches a limit at pH_max (97) beyond which the salt rather than the free acid or base is the equilibrium species. While salt-specific K_sps are not measured routinely (98), non-specific solubility factors (SF) can be used instead. SFs define the ratio between the maximum solubility in the ionized form and the intrinsic solubility and are used to limit solubility and account for drug-counterion precipitation (99,100). If the solubility of a compound has been measured directly (either in aqueous buffer or a biorelevant media) over a range of physiologically relevant pH values (and bile salt and other component concentrations in the case where a biorelevant medium has been used), the ADAM model can use such profiles, with interpolation, to estimate solubility in different segments of the gastrointestinal tract.

As a result of the dissolution process, and particularly if permeation into the enterocyte is slow, the concentration of compound in the bulk luminal solution may reach its equilibrium solubility thus preventing any solubility driven dissolution (Eq. 9) if some of the drug within the formulation is still in solid form (i.e., dissolution can happen only to the limit that permeability and gut wall absorption allows). However, under certain conditions, the luminal concentration of particular compounds may exceed equilibrium solubility. For example, poorly soluble weak bases are expected to have a greater extent of ionization and hence a higher solubility in the acidic milieu of the fasted-state human stomach. Thus, dissolution from an immediate release formulation of such a drug may be partial or complete in the gastric contents, but precipitation may occur upon entering the higher pH conditions of the duodenum. Accordingly, the ability to supersaturate and the kinetics of subsequent equilibration can significantly affect the rate and/or extent of oral absorption (101). The onset of supersaturation may be followed by either immediate or gradual precipitation. The ability to form supersaturated solutions and the rate of precipitation is drug- and medium-specific and cannot be predicted easily (102,103). Furthermore, excipients may be used to stabilize the supersaturated state (104). In the ADAM model, solubility and luminal concentration are monitored continuously, and if saturation solubility is reached or exceeded in any gut segment, precipitation is implemented as a first-order process. In addition, a maximum kinetic solubility (102) can be defined such that drug concentration cannot exceed this value.

The aqueous solubility of sparingly soluble and lipophilic compounds is not always indicative of that in the gastrointestinal milieu. Hence, the use of aqueous solubility to predict oral drug absorption can underestimate oral bioavailability. To obtain more reliable estimates of drug dissolution, it is usually preferable to determine it either in fluids aspirated from the human gastrointestinal tract or in biorelevant media that simulate these fluids (79,105). ADAM has the option of inputting such information to define dissolution within different regions of the gastrointestinal tract.

It should be noted that the extent of increase in solubility in the fed state compared to the fasted state may not translate directly to the same level of increase in dissolution rate (106,107), as might be expected from Eq. 9. In addition, bile salts may decrease the interfacial energy between the drug and the dissolution medium, thereby increasing the effective surface area available for dissolution (80). This improved wetting may facilitate the dissolution of poorly soluble, lipophilic compounds (108), but may have the opposite effect on hydrophilic compounds (109). Overall, the impact of bile salts upon dissolution can be highly variable (110).

As an alternative to the use of the Wang–Flanagan equation (Eq. 9), direct measurements of dissolution as a function of time can be entered in ADAM to represent the first term on the right hand sides of Eqs. 2 and 3. However, in this case, the effects of pH on solubility and of supersaturation are not modeled implicitly.

Luminal Degradation

To account for the possibility of chemical (111) or enzymatic (microbial) (112) degradation of a compound within the gut lumen, ADAM allows this to be defined by a rate constant.

Permeability

The flux (J_AB) of compound across the enterocyte by paracellular and transcellular routes, independent of any metabolism, is defined as follows:

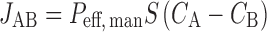12

Where P_eff,man (centimeter per hour) is the effective permeability as affected by all passive and active transport processes, S is the available absorptive surface area, and C_A and C_B are compound concentrations on the apical and basolateral sides of the membrane, respectively.

The value of P_eff,man for a compound may be estimated using relationships between measured values determined for a range of drugs in the human jejunum in vivo (113–116) and permeability measured in various in vitro model systems such as Caco-2 cells (73).

Assuming the absorption rate constant in each gut segment is proportional to P_eff,man, these values can be estimated using Eq. 13 (4).

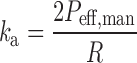13

Where R (centimeter) is the segment radius. Within ADAM, variability in k_a values is accommodated by variability in R as reflected by BSA (25).

Gut Wall Metabolism and Transport

To predict the extent and variability of gut wall metabolism, it is necessary to know the contributions from all of the enzymes involved to net intrinsic metabolic clearance (CLu_int-G). Each contribution may be estimated from the product of the intrinsic unbound clearance per unit of enzyme (CLu_int) and the total abundance of the enzyme in the gut (73). To the extent that variability in the latter is known, this approach facilitates an appreciation of the degree of inter-individual variability in metabolism, including that imposed by genetic polymorphism, race, and disease. Information on the relative abundance of enzymes in different gut regions also allows gradients of metabolism along the gut to be simulated and their implications for relative bioavailability from conventional and modified release dosage forms to be assessed.

While values of CLu_int may be determined using human intestinal microsomes (45,117,118), reasonable predictions may also be made with values obtained using recombinant enzymes or human liver microsomes (73).

Transport-mediated gut absorption of drugs can be described by the Michaelis–Menten equation using the maximal transporter-mediated drug efflux/uptake (J_max) and the related Michaelis constant (or drug-transporter affinity constant; Km) determined in vitro (119). In ADAM, the equivalent net effective transport in vivo is determined by applying scaling factors that include, for instance, allowance for the distribution of transporters along the gut. It has to be said, however, that knowledge of the expression levels of many gut transporters is currently sparse, and consensus on in vitro assays to use in in vitro–in vivo extrapolation is lacking (120).

Formulation-Related Factors

Solid drug within a formulation may not necessarily be available instantly for dissolution, and the rate of its availability will be limited by formulation factors, especially in modified-release dosage forms. This is accommodated within ADAM in two alternative ways. If the dissolution profile of drug from the formulation (and its batch-to-batch variation) has been determined in vitro, this can represent the first term on the right hand sides of Eqs. 2 and 3, with dA_F,n/dt set to zero in Eq. 2. This approach can allow for separate dissolution profiles for gastric and average small intestine pH values (for both the fed and fasted states). Alternatively, if dA_F,n/dt can be defined experimentally (or determined using analytical solutions), the full Wang–Flanagan expression (Eq. 9) embedded in Eqs. 2 and 3 can be used to describe the subsequent dissolution of drug from its solid particles. In this method, the effects of pH on solubility and supersaturation can then be modeled.

A modified release dosage form prior to releasing its content is treated as a single solid object, and its transfer from the stomach to the intestine is treated as a random event (as described in “Gastric Emptying” section). The position of the formulation in the small intestine is then tracked based on the mean residence time in each segment.

The release of drug from enteric-coated formulations is triggered at a critical pH. This is simulated within ADAM as a discrete event dependent on where the formulation is within the gastrointestinal tract, and release can happen at different loci in different individuals depending on variability in local pH. Furthermore, in multiple dosing mode, sequential dosing units can leave the stomach at different times.

The effect of drug particle size on drug absorption has been demonstrated in humans for many drugs including nitrofurantoin (121), benoxaprofen (122,123), digoxin (124), and griseofulvin (125). Within ADAM, Eq. 9 is extended further for poly-dispersed particle size distributions accounting for the number of particles and their radii (90,126). Representative particle size bins and their related mass proportions are constructed based on the observed particle size distribution, and for each bin, a separate set of differential equations is implemented.

SOME APPLICATIONS OF ADAM

The sensitivity of fa to physiological variation in intestinal transit was investigated for a set of passively absorbed virtual compounds assuming instant dissolution (127). Permeability was varied over a broad range of reported P_eff,man values (128). As shown in Fig. 3, fa is relatively invariant with transit time for compounds with high P_eff,man values (>1 cm/h), but changes in transit time can have a marked effect on fa values for low permeability compounds.

Fig. 3.

Theoretical relationship between fraction absorbed (fa), intestinal permeability (P _eff,man), and intestinal transit time (Tsi), assuming rapid dissolution (127)

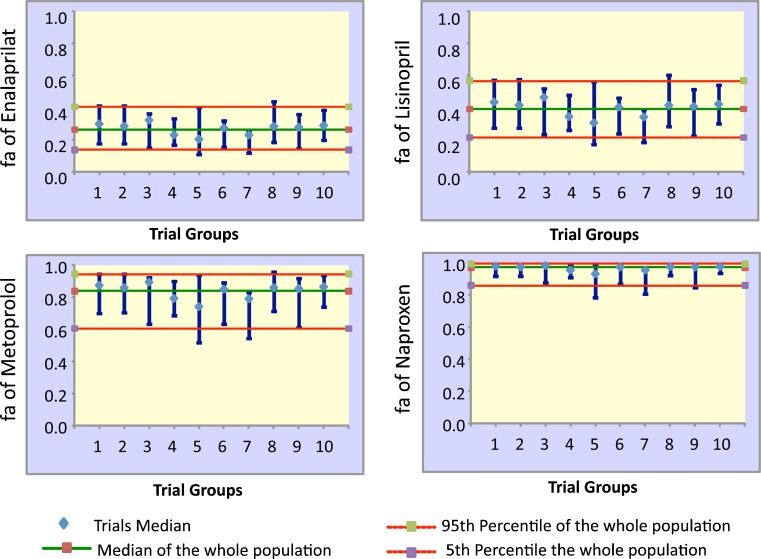
These simulations were extended to investigate variability in the bioavailability of four real drugs covering a wide range of permeabilities (enalaprilat, lisinopril, metoprolol, and naproxen, Table I). A population of 100 virtual healthy subjects was studied, broken down into ten trials with ten subjects in each trial. The predicted median values of fa and their variability for each trial are shown in Fig. 4, and observed (mean) and predicted (mean and range) values are compared in Table I.

Table I.

Observed and Predicted fa Values of Four Drugs Covering a Range of Intestinal Permeability

	P eff,man (cm/h)	BCS class	Observed fa	Predicted fa mean	Minimum	Maximum
Enalaprilat	0.072a	III	0.08a	0.27	0.09	0.46
Lisinopril	0.119a	III	0.35a	0.39	0.15	0.62
Metoprolol	0.482a	I	0.95a	0.81	0.47	0.96
Naproxen	3.06a	I	1.00a	0.96	0.74	1.00

^a(128); the minimum and maximum values are predicted for a population of 100 virtual healthy subjects; BCS biopharmaceutical classification scheme (129)

Fig. 4.

Predicted values of fa and its variability for enalaprilat, lisinopril, metoprolol, and naproxene. Simulations were done for ten trials each with ten subjects selected randomly from a virtual population of 100 subjects (median and 5th and 95th percentiles for the whole population and each trial are shown)

While predicted and observed mean values were similar for the three most permeable compounds, there was a greater discrepancy for enalaprilat, the least permeable drug. This was associated, as expected, with a greater predicted variability in the value of fa of enalaprilat. Thus, inconsistency between point predictions of fa and observed values from small clinical studies may be expected to the extent that the latter may not capture the full extent of inter- and intra-individual variability. Alternatively, this over-prediction could also be the consequence of over-estimation of the in vivo permeability of enalaprilat. The predicted values of fa for naproxen, the most permeable compound, were much less susceptible to variability in physiological parameters, and the predicted medians for trials and the population were very close.

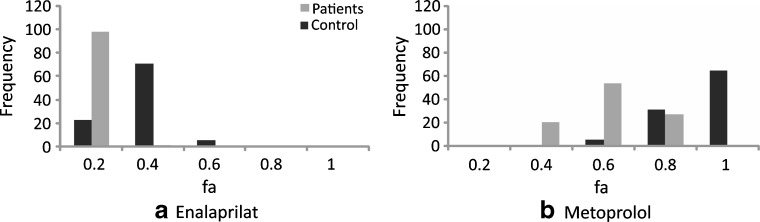
Incorporation of intrinsic variability in physiological parameters also facilitates investigation of the effects of disease on bioavailability. For example, intestinal transit is accelerated in many AIDS patients with cryptosporidiosis (130). This effect was simulated in 100 virtual subjects receiving enalaprilat and metoprolol by decreasing the mean value of intestinal transit by one third while retaining the overall shape of the distribution of transit time (Fig. 5).

Fig. 5.

Simulation of the effect of a decrease in the intestinal transit time secondary to disease on the bioavailability of a enalaprilat and b metoprolol

The simulation indicates a significant decrease in the bioavailability of both drugs, but whereas the variability in the fa of metoprolol is increased, the variability of enalaprilat is somewhat decreased.

Based on its physicochemical properties and in vitro data on its metabolism (68), the intestinal extraction ratio (E_G) of midazolam and its variability were predicted to be 0.41 ± 0.13 SD (131), very close to that determined experimentally in anhepatic patients (0.43 ± 0.18 SD; Fig. 6) (50).

Fig. 6.

Predicted values of the gut extraction ratio (E _G) of midazolam. Simulations were done for ten trials each with five subjects selected randomly from a virtual population of 100 subjects (median and 5th and 95th percentiles for the whole population and each trial are shown) (131)

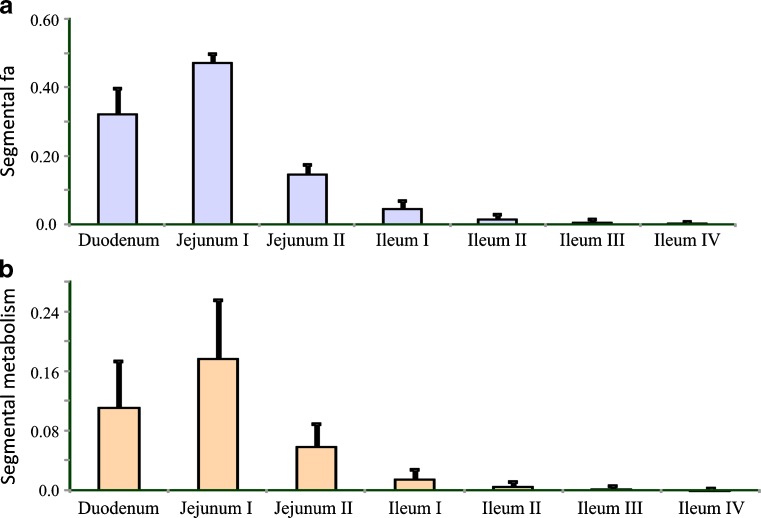
Figure 7 shows the predicted percentages of the dose of midazolam absorbed and metabolized in each segment of the small intestine. Most of the dose is absorbed and metabolized in the proximal part of the small intestine. In addition, the simulation indicated that inter-individual variability in fa is much lower than that in F_G, reflecting the high variability in CYP3A abundance along the gut. Such information can be very helpful when designing modified release formulations of drugs whose oral bioavailability may be affected by CYP3A-mediated gut wall metabolism.

Fig. 7.

Predicted fractions of a dose of midazolam (mean ± SD) a absorbed and b metabolized in different segments of the intestine (131)

In an independent study, Allan et al. (132) predicted human clearance values of UK-453,061, a second-generation non-nucleoside reverse transcriptase inhibitor, using single-species scaling from in vivo data and from in vitro data employing the Simcyp® Simulator. Distribution was estimated using in silico PBPK models and absorption was predicted from measured physicochemical, permeability, and solubility data using the Simcyp® Simulator and GastroPlus™ (Simulations Plus, Inc., Lancaster, CA, USA). Although, the former tended to under predict oral bioavailability at high doses this is speculated to be a result of using an aqueous buffer solubility rather than that in a biorelevant medium and a lack of reliable data on the precipitation rate of the compound. Our in-house simulations (data not shown) indicate the sensitivity of predictions to assumptions regarding the in vivo precipitation rate constant, emphasizing the need for sensitivity analysis when there is insufficient experimental information.

In a last example, the plasma concentration–time profiles of metoprolol given in three formulations (fast, moderate, and slow release) (133) were predicted (134) in a virtual healthy population based on in vitro release profiles, physicochemical properties, and information on the in vitro metabolism of the drug. Table II shows a comparison of predicted and observed mean t_max, C_max, and AUC values. A comparison of the predicted and observed plasma drug concentration–time profiles for the slow-release formulation is shown in Fig. 8. In the original analysis, colonic absorption was not considered. Assuming that the colon permeability is the same as that of the small intestine (135), the t_max, C_max, and AUC values for the slow release formulation in the same virtual population increased to 5.96 h, 0.07 mg/L, and 1.13 mg/L h, respectively.

Table II.

Observed and Predicted Metrics Describing the Plasma Concentration–Time Profile of Metoprolol After Administration in Three Formulations Covering a Range of Release Rates

Formulation	t max (h)		C max (mg/L)		AUC0–24 h (mg/L h)
	Observed	Predicted	Observed	Predicted	Observed	Predicted
Slow	4.86	3.97	0.06 (0.02)	0.06 (0.03)	0.7 (0.17)	0.77 (0.47)
Moderate	3.57	3.88	0.09 (0.03)	0.07 (0.03)	0.81 (0.03)	0.90 (0.56)
Fast	3.14	3.31	0.11 (0.03)	0.09 (0.04)	0.79 (0.02)	1.08 (0.58)

The observed data are from Sirisuth and Eddington (133).

The observed mean and SD values were only reported for C _max and AUC; t _max values were obtained from the graphs in (133).

Fig. 8.

Observed and predicted mean plasma concentrations of metoprolol after administration in a slow-release formulation (observed data are from Sirisuth and Eddington) (133)

CONCLUDING REMARKS

The approach to predicting oral bioavailability implemented in ADAM provides a sophisticated basis for evaluating the impact of inter- and intra-subject variability in gastrointestinal physiology and pathology and genetic and other sources of variability in intestinal gut wall metabolism and transport. Improvements to the currently available software packages should include the incorporation of a fully mechanistic model of enterohepatic cycling, the effects of bile salts on solubility and dissolution (including micellization), the prediction of gastric and colonic drug absorption, and the ability to predict drug–drug interactions at intestinal transporters in addition to those at drug metabolizing enzymes.