Structure-Based Prediction of the Nonspecific Binding of Drugs to Hepatic Microsomes

Abstract

For the accurate prediction of in vivo hepatic clearance or drug–drug interaction potential through in vitro microsomal metabolic data, it is essential to evaluate the fraction unbound in hepatic microsomal incubation media. Here, a structure-based in silico predictive model of the nonspecific binding (fu_mic, fraction unbound in hepatic microsomes) for 86 drugs was successfully developed based on seven selected molecular descriptors. The R² of the predicted and observed log((1 − fu_mic)/fu_mic) for the training set (n = 64) and test set (n = 22) were 0.82 and 0.85, respectively. The average fold error (AFE, calculated by fu_mic rather than log((1 − fu_mic)/fu_mic)) of the in silico model was 1.33 (n = 86). The predictive capability of fu_mic for neutral drugs compared well to that for basic compounds (R² = 0.82, AFE = 1.18 and fold error values were all below 2, except for felodipine and progesterone) in our model. This model appears to perform better for neutral compounds when compared to models previously published in the literature. Therefore, this in silico model may be used as an additional tool to estimate fu_mic and for predicting in vivo hepatic clearance and inhibition potential from in vitro hepatic microsomal studies.

INTRODUCTION

Significant progress have been made recently in the prediction of in vivo hepatic clearance (1–3) and drug–drug interaction potential (4–6). The determination of intrinsic clearance (CL_int) and inhibition constant (K_i) through in vitro microsomal incubation can provide a basis for these predictions. However, lipophilic drugs tended to bind nonspecifically to microsomal phospholipids, resulting in an underestimation of CL_int (7–9) or an overestimation of K_i (10–12). Consequently, in vivo hepatic clearance and the extent of inhibitory drug interactions were often underpredicted.

Investigators have tried to use relative low microsomal protein concentration to avoid the nonspecific binding (13). However, relative high concentrations (1 to 2 mg/mL) were still needed when studying phase II metabolic reactions (14) and in vitro assessment of the time-dependent inhibition potential (15). As such, it is essential to correct the metabolic kinetic parameters (CL_int and K_i) by the unbound fraction to microsomes (fu_mic) in order to ensure accurate pharmacokinetic estimation of potential drug candidates. Unfortunately, currently available experimental methods for measuring the fu_mic are relatively labor- and time-consuming.

In order to avoid these experimental studies, in silico prediction of fu_mic has gained great interest recently. Austin et al. (16) reported a linear relationship between log((1 − fu_mic)/fu_mic) and logP/D (logP for bases, while logD_7.4 for acids and neutrals) of 56 drugs (R² = 0.82). Hallifax and Houston (17) proposed that the relationship between logP/D and log((1 − fu_mic)/fu_mic) was nonlinear. They concluded that the nonlinear empirical equation gave more unbiased predictions of fu_mic for drugs with low binding affinity (fu_mic > 0.9) when compared with the model by Austin et al. Later, Gertz et al. addressed the limitations of these empirical predictive tools and their applicability for fu_mic predictions over a range of lipophilicity and microsomal protein concentrations (18). They concluded that the accuracy of fu_mic predictions for highly lipophilic drugs was poor by both equations, while the Hallifax equation provided more accurate fu_mic predictions on average.

Interestingly, Sykes et al. (19) reanalyzed the data reported by Austin et al. and found that the logP values clearly correlated well with the transformed fu_mic (R² = 0.90) for bases but less predictive for neutrals (R² = 0.34) and acids (R² = 0.10). They obtained good discrimination between drugs classified as strong binders (experimental fu_mic < 0.50) and those with a lower degree of binding (experimental fu_mic > 0.50) by molecular modeling approaches.

Recently, Gao et al. (20) developed a quantitative in silico model correlating fu_mic of 1,223 drug-like molecules with two-dimensional molecular descriptors. These investigators demonstrated that lipophilicity was the most important molecular property contributing to fu_mic in this high performance model. However, the information of the original dataset was not open to the public. Therefore, a model not only with high prediction accuracy but also with open-sourced dataset would be useful for researchers in assessing quantitative structure vs. fu_mic relationships.

In this study, quantitative structure–fu_mic relationship was constructed just based on molecular descriptors for a dataset of 86 drugs covering a large range of molecular properties. Molecular descriptors were calculated using TSAR^TM software version 3.3 (Accelrys Inc.) (21), preADMET (22), and SciFinder Scholar 2007 (23). Then, the feature selection was performed by stepwise regression, and an in silico model was established with multiple linear regression (MLR) method. The principal objectives of the study were, therefore, (1) to develop a quantitative relationship between the molecular structure descriptors and log((1 − fu_mic)/fu_mic); (2) to estimate the predictive accuracy of in silico model, and (3) to understand what structural factors determining fu_mic.

MATERIALS AND METHODS

Data Collection

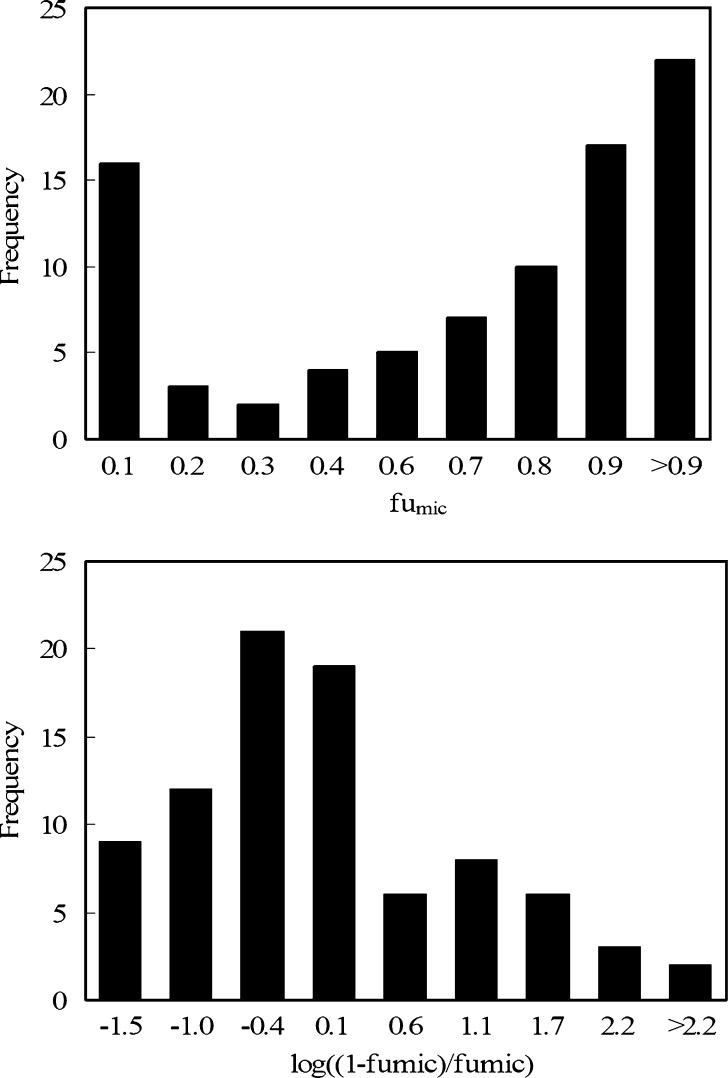
The observed fu_mic values of 86 drugs were obtained from the literatures as described in Table I. These fu_mic values were measured at the microsomal protein concentration of 1 mg/mL or converted to fu_mic values at 1 mg/mL based on the equation proposed by Austin et al. (16). The fu_mic values of each drug were transformed to log((1 − fu_mic)/fu_mic). As shown in Fig. 1, the fu_mic values of 86 drugs did not follow a normal distribution. The transformation of fu_mic to log((1 − fu_mic)/fu_mic) yielded a more desirable distribution and could reduce unequal error variances simultaneously. Therefore, the observed log((1 − fu_mic)/fu_mic) was considered as the dependent variable in the model construction.

Table I.

Characteristics of, and Results Obtained for, the 86 Drugs Studied to Establish the Present In Silico Model

No.	Dataset	Drugs	log((1 − fumic)/fumic)	Chemical class	Observed fumic	Predicted fumic	Fold error	Ref.
1	Training	Bumetanide	−1.0607	A	0.92	0.90	1.02	(16)
2	Training	Cerivastatin	−0.2688	A	0.65	0.75	1.15	(16)
3	Training	Cinoxacin	−1.0607	A	0.92	0.99	1.08	(16)
4	Training	Diclofenac	−1.5097	A	0.97	0.81	1.20	(16)
5	Training	Emodin	0.6297	A	0.19	0.12	1.57	(18)
6	Training	Gemfibrozil	−0.5248	A	0.77	0.67	1.15	(18)
7	Test	Glipizide	−1.3802	A	0.96	0.96	1.00	(16)
8	Training	Glyburide	−0.6585	A	0.82	0.85	1.04	(16)
9	Training	Ibuprofen	−1.0048	A	0.91	0.85	1.07	(16)
10	Test	Indomethacin	−0.6297	A	0.81	0.93	1.15	(16)
11	Test	Ketoprofen	−1.0607	A	0.92	0.92	1.00	(16)
12	Training	Losartan	−0.9542	A	0.9	0.78	1.15	(16)
13	Test	Mycophenolic acid	−0.5754	A	0.79	0.89	1.12	(18)
14	Training	Oxaprozin	−0.8256	A	0.87	0.79	1.10	(16)
15	Test	Piroxicam	−1.0607	A	0.92	0.88	1.04	(16)
16	Training	Repaglinide	−0.4320	A	0.73	0.68	1.08	(18)
17	Test	Rosiglitazone	−0.4102	A	0.72	0.87	1.21	(18)
18	Test	Sulfadoxine	−1.5097	A	0.97	0.98	1.01	(16)
19	Training	Sulindac	−0.7884	A	0.86	0.87	1.01	(16)
20	Training	Tenidap	−0.1581	A	0.59	0.86	1.45	(19)
21	Test	Tenoxicam	−1.5097	A	0.97	0.85	1.14	(19)
22	Training	Tolbutamide	−1.5097	A	0.97	0.97	1.00	(16)
23	Training	Tolmetin	−1.1950	A	0.94	0.99	1.05	(16)
24	Test	Warfarin	−1.1950	A	0.94	0.68	1.38	(16)
25	Test	Amiodarone	2.6981	B	0.002	0.00	1.86	(16)
26	Training	Amitriptyline	1.0548	B	0.081	0.22	2.77	(16)
27	Training	Betaxolol	−0.2126	B	0.62	0.63	1.02	(16)
28	Training	Buspirone	−0.7533	B	0.85	0.40	2.10	(18)
29	Training	Carvedilol	0.9542	B	0.1	0.15	1.53	(18)
30	Test	Chlorpromazine	0.9080	B	0.11	0.11	1.02	(16)
31	Test	Clomipramine	1.4034	B	0.038	0.08	2.07	(16)
32	Training	Clozapine	0.4543	B	0.26	0.51	1.95	(16)
33	Training	Codeine	−1.3802	B	0.96	0.90	1.07	(18)
34	Training	Dextromethorphan	−0.4102	B	0.72	0.38	1.90	(18)
35	Training	Diltiazerm	−0.7884	B	0.86	0.33	2.59	(16)
36	Test	Diphenhydramine	−0.3889	B	0.71	0.48	1.48	(16)
37	Training	Ezlopitant	1.6902	B	0.02	0.01	1.88	(19)
38	Training	Fluvoxamine	0.4320	B	0.27	0.35	1.30	(28)
39	Training	Imipramine	0.7202	B	0.16	0.26	1.61	(16)
40	Training	Ketamine	0.0174	B	0.49	0.56	1.15	(19)
41	Test	Levallorphan	−0.7202	B	0.84	0.37	2.29	(18)
42	Training	Lorcainide	−0.0348	B	0.52	0.24	2.13	(19)
43	Test	Mibefradil	1.5097	B	0.03	0.03	1.09	(18)
44	Training	Miconazole	1.5097	B	0.03	0.08	2.73	(28)
45	Training	Naloxone	−0.8256	B	0.87	0.73	1.19	(18)
46	Test	Nicardipine	1.3802	B	0.04	0.12	3.02	(19)
47	Training	Phenytoin	−0.6297	B	0.81	0.88	1.08	(28)
48	Training	Promethazine	0.9080	B	0.11	0.16	1.46	(16)
49	Training	Propranolol	0.1047	B	0.44	0.58	1.31	(16)
50	Training	Quinidine	−0.3680	B	0.7	0.45	1.57	(16)
51	Training	Quinine	0.2499	B	0.36	0.45	1.25	(28)
52	Training	Tamoxifen	2.5216	B	0.003	0.01	2.52	(16)
53	Training	Terfenadine	1.6902	B	0.02	0.03	1.65	(18)
54	Training	Thioridazine	2.0418	B	0.009	0.03	3.00	(16)
55	Training	Trimeprazine	1.0548	B	0.081	0.12	1.54	(16)
56	Test	Verapamil	0.2311	B	0.37	0.17	2.24	(16)
57	Training	Zolpidem	−0.8653	B	0.88	0.69	1.28	(19)
58	Training	2-Ethoxybenzemide	−1.6902	N	0.98	0.92	1.06	(16)
59	Training	Albendazole	−0.1047	N	0.56	0.68	1.22	(16)
60	Test	Aldosterone	−0.1761	N	0.6	0.85	1.41	(28)
61	Training	Alprazolam	−0.6585	N	0.82	0.77	1.06	(16)
62	Training	Amobarbital	−1.5097	N	0.97	0.94	1.03	(16)
63	Training	Androstenedione	0.0174	N	0.49	0.57	1.17	(28)
64	Training	Caffeine	−1.9956	N	0.99	0.99	1.00	(28)
65	Training	Carbamazepine	−0.8256	N	0.87	0.84	1.04	(16)
66	Training	Colchicine	−1.1950	N	0.94	0.89	1.06	(16)
67	Test	Diazepam	−0.2881	N	0.66	0.55	1.20	(16)
68	Training	Felodipine	1.1950	N	0.06	0.16	2.72	(18)
69	Training	Fluconazole	−1.6902	N	0.98	0.97	1.01	(28)
70	Training	Hexobarbital	−1.3802	N	0.96	0.93	1.03	(16)
71	Test	Isradipine	0.2881	N	0.34	0.38	1.12	(16)
72	Training	Mebendazole	−0.3680	N	0.7	0.76	1.09	(16)
73	Training	Methocarbamol	−0.7202	N	0.84	0.94	1.12	(16)
74	Training	Methohexital	−0.7884	N	0.86	0.89	1.04	(19)
75	Training	Methoxsalen	−0.9080	N	0.89	0.82	1.09	(16)
76	Training	Metyrapone	−1.5097	N	0.97	0.93	1.05	(16)
77	Test	Midazolam	−0.0696	N	0.54	0.47	1.16	(18)
78	Training	Nifedipine	−0.3680	N	0.7	0.71	1.02	(18)
79	Test	Omeprazole	−0.8256	N	0.87	0.73	1.19	(19)
80	Training	Oxazepam	−0.4102	N	0.72	0.66	1.08	(18)
81	Training	Phensuximide	−0.4771	N	0.75	0.97	1.29	(16)
82	Training	Prednisone	−0.1047	N	0.56	0.64	1.15	(16)
83	Training	Progesterone	0.7884	N	0.14	0.30	2.15	(28)
84	Training	Simvastatin	1.1950	N	0.06	0.09	1.49	(18)
85	Training	Testosterone	0.0174	N	0.49	0.42	1.17	(28)
86	Training	Triazolam	−0.5497	N	0.78	0.75	1.04	(16)

Fig. 1.

Distribution of fu_mic and log((1 − fu_mic)/fu_mic) for 86 drugs

Calculation of Molecular Descriptors

The 2D structures of 86 drugs were searched in SciFinder Scholar 2007 and the mol files were saved for further calculation. Then, the molecular descriptors that were known to influence almost all pharmacokinetic properties were selected as original independent variables. A set of 32 descriptors was obtained from TSAR 3.3, preADMET online, and SciFinder Scholar 2007, including: molecular refractivity, cosmic torsional/electrostatic/total energy, number of atoms/halogen atoms/heteroatoms, heat of formation, energy of the lowest unoccupied molecular orbital (LUMO), energy of the highest occupied molecular orbital (HOMO), ΔE (LUMO–HOMO), number of primary/secondary/tertiary amine groups, number of carboxylic acid groups, number of single/double/aromatic bonds, total absolute atomic charge, total/aromatic rings, number of negatively/positively charged groups, rigid/rotable bonds, number of hydrogen bond acceptors/donors, logD₇, logP, molecular weight, mean net charge per molecule of the compounds (f_i) (24), and polar surface area.

Feature Selection

As expected, only some of the 32 descriptors are significantly correlated with log((1 − fu_mic)/fu_mic). Furthermore, many of the descriptors are intercorrelated, which has a negative effect on the accuracy and interpretability of the final quantitative model. Therefore, stepwise regression method was employed to perform the feature selection process in this study.

Model Development and Evaluation

MLR analysis was applied to develop the in silico model. In order to examine the predictive power and robustness of our model, the entire dataset should be subdivided into training and test set. In general, there are three methods for the selection of training and test set: (1) selection based on a random manner; (2) selection based on clusters of the dependent variable; (3) selection based on clusters of factor scores of the descriptor space along with or without the biological activity values. Due to the skew distribution of fu_mic, the entire dataset was categorized into training set (n = 64) and test set (n = 22) by the cluster analysis of log((1 − fu_mic)/fu_mic). The whole range of log((1 − fu_mic)/fu_mic) was divided into bins, and compounds belonging to each bin were randomly assigned to the training or test set. Meanwhile, leave-one-out (LOO) cross-validation was performed. Then, R² and Q² resulted from LOO (Q²_LOO) were calculated to evaluate the model predictability.

Two other commonly employed accuracy test criteria, the fold error and the average fold error (AFE), were used to evaluate the predictive accuracy, as represented by Eqs. 1 and 2, respectively. The percentages of drugs with the fold error more than two (E_2-fold) and three (E_3-fold) were calculated to estimate the accuracy of the model in our study, respectively. A prediction is usually thought to be successful if the value of AFE is less than two (25).

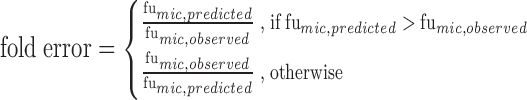1

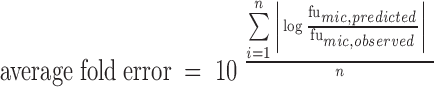2

RESULTS AND DISCUSSION

The Predictive Performance and Accuracy of the Model

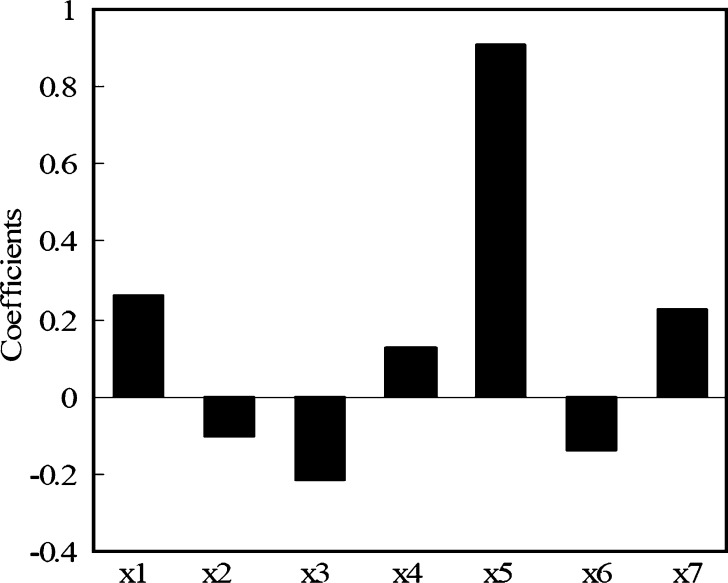
Seven descriptors were chosen via the feature selection to construct the in silico model. Then, the model for the training set was built with 64 drugs, as represented by Eq. 3.

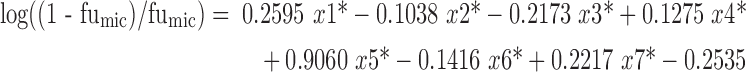3

where x1 is the cosmic electrostatic energy; x2 is the number of aromatic bonds; x3 is the number of negatively charged groups; x4 is the number of positively charged groups; x5 is logP; x6 is the mean net charge per molecule of the compounds; x7 is polar surface area (PSA). All of the selected descriptors, the values of which can be obtained directly from the authors, are standardized to ensure that all descriptors had equally determinant strength affecting log((1 − fu_mic)/fu_mic). The standardized values with a mean value of zero and a variance of unity are represented as “x*” in Eq. 3.

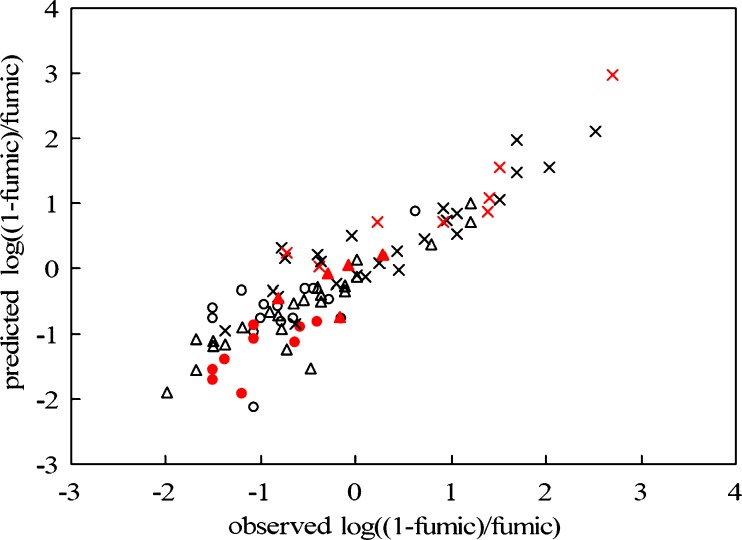
The correlation between predicted log((1 − fu_mic)/fu_mic) and observed log((1 − fu_mic)/fu_mic) from in silico model is shown in Fig. 2. It is seen that the in silico model exhibits high predictive performance: for the training set, n = 64, R² = 0.82 (R² = 0.85 for test set), Q²_LOO = 0.75, RMSE = 0.45, F = 36.31, p < 0.0001, the slope equal to unity and the intercept to zero (the slope is 0.94 and the intercept is −0.08 for test set).

Fig. 2.

Correlation between the predicted and observed log(1 − fu_mic)/ fu_mic) for acidic, basic, and neutral drugs (empty circles acids, n = 24, y = 0.78x − 0.19, R ² = 0.43; multiplication symbols bases, n = 33, y = 0.73x + 0.20, R ² = 0.82; empty triangles neutrals, n = 29, y = 0.76x − 0.14, R ² =  0.82; training set (black symbols): n = 64, y = 1x, R ² = 0.82; test set (red symbols): n = 22, y = 0.94x − 0.08, R ² = 0.85))

The observed and predicted values of fu_mic, and the fold error values of 86 drugs are shown in Table I. As can be seen, 75% of drugs are found with fold error < 2 and only 2% of drugs with fold error > 3 and AFE =  1.33 (Table II) in our model. For training set, 82% of drugs are found with fold error < 2 and only 5% of drugs (one drug) with fold error > 3 and AFE = 1.34. And for test set, 86% of drugs are found with fold error < 2 and only 0% of drugs with fold error > 3 and AFE = 1.33. Therefore, the fu_mic can be predicted accurately by our model.

Table II.

The Predictive Accuracy of the Present In Silico Model vs. Literature Models

Chemical class	No.	Present study				Austin et al. model		Hallifax-Houston model
		E 2-fold (%)	E 3-fold (%)	AFE	R 2	AFE	R 2	AFE	R 2
Total	86	15	2	1.33	0.85	1.47	0.75	1.33	0.79
A	24	0	0	1.12	0.43	1.16	0.49	1.12	0.56
B	33	33	6	1.68	0.82	1.92	0.79	1.68	0.76
N	29	7	0	1.18	0.82	1.34	0.61	1.18	0.66

Predictive Differences among Acids, Bases, and Neutrals

Figure 2 also describes the respective correlations between predicted and observed values of log((1 − fu_mic)/fu_mic) for acids, bases, and neutral compounds. As stated earlier, the good prediction of bases is more easily achieved than neutral compounds and acids. Our model predicted fu_mic for bases well (R² = 0.82, AFE = 1.68). Furthermore, prediction of fu_mic for neutral drugs was comparable (R² = 0.82, AFE = 1.18), which might be a positive feature of this model. Unfortunately, for acids, the correlation between log((1 − fu_mic)/fu_mic) and the seven descriptors was still poor (as shown in Fig. 2; R² = 0.43). However, the fold error values of acids were all below 2 (Table II), indicating that the predictive accuracy of acids in our model might still be useful in some circumstances. The slope of the fitted line (Fig. 2; 0.78) for acids was similar to bases (0.73) and neutral compounds (0.76). These findings indicate that the prediction of fu_mic for acids in our model is still reasonable. In fact, the poor correlation of acids was probably due to the relative narrow distribution of observed fu_mic values (or the log((1 − fu_mic)/fu_mic) values). As can be seen in Table I, except for emodin, the range of the log((1 − fu_mic)/fu_mic) for acids is from −1.5097 to −0.1581, with a log unit span of 1.4, (most of the fu_mic values are within the range of 0.6–0.9). In contrast, for bases and neutral compounds, the log unit spans of the log((1 − fu_mic)/fu_mic) are 4.0 and 3.2, respectively. The relative low nonspecific binding of acids to hepatic microsomes likely results in the skew distribution of the fu_mic and the poor correlation between log((1 − fu_mic)/fu_mic) and the selected seven descriptors.

Identification of Important Molecular Descriptors Affecting Fu_mic

Our results shown in Eq. 3 suggest that the descriptors chosen strongly correlate with fu_mic, thus, allowing some mechanistic interpretations of the model. In general, these molecular descriptors relate to molecular lipophilicity, charge state, flexibility, polarity, and extent of ionization at pH 7.4, as shown in Fig. 3.

Fig. 3.

Coefficients plot of the seven selected molecular descriptors

The molecular mechanism of nonspecific binding is presently unclear, but it is believed to depend on the lipophilicity and the electronic charge. The main binding contributors can be divided into non-electrostatic and electrostatic terms, wherein the non-electrostatic contributions include lipophilic interactions, van der Waals interactions, and translational, rotational, and configurational entropies (26).

As can be expected, the extent of microsomal binding generally increases with increasing lipophilicity of the drug. Especially, as the main structural contributor, logP is positively correlated with fu_mic (Eq. 3), consistent with the above analysis. The cosmic electrostatic energy, parameter x6 (f_i), the number of positively charged groups and the number of negatively charged groups are descriptors representing the above electrostatic term contributing to the nonspecific binding. As shown in Eq. 3 and Fig. 3, the cosmic electrostatic energy is the second important descriptor in our model. It is energy descriptor accounting for the noncovalent interaction potential energy, which determines the binding affinity of a molecule to the pertinent receptor(s). The parameter x6 (f_i) is calculated from the pK_a and pH_7.4, and its value is equal to the ionization fraction for compounds at pH_7.4 (24). Thus, it denotes the contribution of electrostatic interaction to the nonspecific binding based on the ionization of the compounds. However, the basic compounds clearly exhibit enhanced binding over neutral or acidic compounds with similar lipophilicity. This enhanced phospholipid binding of bases is thought to be due to a favorable electrostatic interaction between the protonated base and phosphate groups of the phospholipids (27). The negative charges for acidic drugs at pH 7.4 would likely limit their nonspecific binding. This conclusion can be used to explain the positive effect of the x4 (the number of positively charged groups) on fu_mic, and the negative effect of the x3 (the number of negatively charged groups) on fu_mic (Eq. 3). The PSA and the number of aromatic bonds are two other contributors in our model.

Comparison between In Silico and Published Models

The performance of the present model vs. the models published by Austin et al. and Hallifax-Houston were compared (Table II).

In general, our model compared favorably to these models for basic and neutral compounds but fared equally inadequately for acidic compounds. The present model differs, however, in its approach in that it utilizes more structural specific parameters such as the number of positively or negatively charged groups, the cosmic electrostatic energy and PSA, etc., in addition to log P and log D. The involvement of these parameters provided additional insights into the molecular mechanisms of nonspecific binding of drugs to hepatic microsomes, especially for the electrostatic interaction.

CONCLUSIONS

A structure-based in silico model was developed successfully for the prediction of the nonspecific binding of drugs to hepatic microsomes. Especially, the prediction of fu_mic for neutral drugs demonstrated similar capability to that for basic drugs (R² = 0.82, AFE = 1.18 and fold error values were all below 2, except for felodipine and progesterone). The lipophilicity, charge state, and the extent of ionization at pH 7.4 were identified as important properties affecting fu_mic. One obvious weakness of the present model is the skew distribution of fu_mic in the entire dataset (most of the compounds were in the range of fu_mic > 0.7, especially for the acids). A larger dataset, composed of drugs with uniform distribution of fu_mic values, is necessary for accurate fu_mic prediction and for further reliable evaluation of the free clearance and drug–drug interaction.