Abstract
Although cis-regulatory binding sites (CRBSs) are at least as important as the coding sequences in a genome, our general understanding of them in most sequenced genomes is very limited due to the lack of efficient and accurate experimental and computational methods for their characterization, which has largely hindered our understanding of many important biological processes. In this article, we describe a novel algorithm for genome-wide de novo prediction of CRBSs with high accuracy. We designed our algorithm to circumvent three identified difficulties for CRBS prediction using comparative genomics principles based on a new method for the selection of reference genomes, a new metric for measuring the similarity of CRBSs, and a new graph clustering procedure. When operon structures are correctly predicted, our algorithm can predict 81% of known individual binding sites belonging to 94% of known cis-regulatory motifs in the Escherichia coli K12 genome, while achieving high prediction specificity. Our algorithm has also achieved similar prediction accuracy in the Bacillus subtilis genome, suggesting that it is very robust, and thus can be applied to any other sequenced prokaryotic genome. When compared with the prior state-of-the-art algorithms, our algorithm outperforms them in both prediction sensitivity and specificity.
INTRODUCTION
While a biological function of a cell is the result of specific interactions of a set of gene products—proteins and RNAs expressed in the cell under certain physiological and environmental conditions, the controlling programs that specify when, where, how much, and how fast a specific set of proteins and RNAs should be expressed are mainly defined in the non-coding functional sequences, in particular, the cis-regulatory binding sites (CRBSs) through their interactions with specific transcription factors (TFs). In prokaryotes, several adjacent genes on the same strand of DNA often form an operon and are co-transcribed as a polycistronic mRNA. Genes in an operon generally share the same transcription initiation and termination control signals and machinery. In eubacteria, gene transcription initiation is controlled by the σ-factor of the RNA polymerase together with other specific TFs that respectively bind to the promoter and CRBSs located in the upstream region of an operon. Typically, a genome encodes far fewer TFs than the number of operons, therefore each TF usually regulates multiple operons (for the convenience of this discussion, we also call a singleton gene an operon). The collection of the operons that are regulated by a TF is called the regulon of the TF. As some operons are regulated by more than one TF, an operon can belong to different regulons. The set of similar CRBSs recognized by a TF is called its cis-regulatory motif, or binding site motif.
Although great advances have been made in identifying the coding sequences in prokaryotic genomes using computational methods alone, it remains an unsolved task for both the experimental and computational biology communities to efficiently and accurately identify all the CRBSs in a genome. Therefore, no single organism has so far had most of its cis-regulatory systems characterized; and even for the most well-studied prokaryotic model organism E. coli K12, researchers have only characterized partial CRBSs for 125 of the ∼314 estimated TFs in its genome through decades of research (1). As a result, except for a handful of strains, such as E. coli K12 (1) and B. subtilis (2), we know very little about the cis-regulatory systems in all sequenced prokaryotic genomes (3). The lack of a holistic understanding of the cis-regulatory systems in these organisms has hindered our understanding of many important biological processes such as development, differentiation, evolution, disease and specialized biological functions of many organisms. Hence, there is an urgent need in the biological research community for an efficient and accurate computational method for predicting all possible cis-regulatory systems in sequenced prokaryotic genomes.
Prediction of CRBSs has been a consequence of the development of computational methods for modeling CRBSs over the past almost three decades (4,5). The early attempts to predict new CRBSs started by compiling known binding sites of interest, and then the sequence profile of these known CRBSs was used to search for additional ones in the genome of interest (6,7). With the advent of microarray gene expression profiling technologies and availability of increasing numbers of sequenced genomes, numerous motif-finding algorithms have been developed to identify overrepresented segments of sequences as potential CRBSs from a set of regulatory regions of a few co-regulated genes (8,9). Later, Gelfand et al. introduced the phylogenetic footprinting technique (10) to predict CRBSs of a TF whose regulon members are at least partially known, in a group of related genomes (11,12). This method and its variants have been widely adapted to predict the CRBSs and the regulon of a TF in related bacterial or archaeal species (13–22). However, these methods cannot be scaled up at genome scale for all possible CRBSs because the regulon information is largely unknown for most of sequenced genomes. Structure-based algorithms have also been developed to predict new CRBSs for a TF whose structure is known (23,24); nevertheless, these methods have only had limited application, since accurate structures of most TFs are not available yet. To our knowledge, the first genome-wide CRBS and regulon prediction was carried by van Nimwegen et al. (25). They used Monte Carlo sampling of the putative binding sites to partition thousands of short conserved DNA sequences into clusters, which were identified by phylogenetic footprinting methods and each cluster was predicted as a cis-regulatory motif. However, this approach only predicted ∼100 motifs/regulons in E. coli K12 (25). Later, Qin et al. (26) used a Bayesian clustering algorithm to group similar putative binding sites predicted in E. coli K12 by phylogenetic footprinting in an earlier work (27), and predicted 192 motifs covering only 438 operons. More recently, Alkema et al. (28) proposed yet another phylogenetic footprinting-based algorithm using a rather simple algorithm to cluster putative CRBSs into clusters or motifs which were then used to scan the genome for additional ones. One of the major problems of all these algorithms is that they assume that the input motifs predicted by motif-finding algorithms are true binding sites. However, this assumption may not be valid, as recent studies have shown that, of the surveyed popular motif-finding programs including those used in these studies, the best predicted at most 40% known binding sites in the input intergenic sequences, with high false positive prediction rates (29,30). This would partially explain their generally low prediction accuracy. Although Pritsker et al. (31) have used multiple motifs predicted by a motif-finding tool from pooled orthologous intergenic sequences in fungi strains to predict CRBSs in a genome scale, their coverage was not high either, because a limited number of genomes were used, and a rather simple motif clustering method was employed. In another early study, Li et al. (32) attempted to identify clusters of overrepresented bipartite patterns in the intergenic sequences in E. coli K12 as possible cis-regulatory motifs, but this method is limited as not all binding sites are bipartite, and the power of comparative genomics was not explored. As a result, only one third of known CRBSs were predicted by this method (32). The PhyloNet algorithm is probably the most recent development for genome-wide de novo prediction of CRBSs in simple eukaryotic (33) and prokaryotic (34) genomes. PhyloNet finds binding site motifs through clustering multiple motifs identified by a motif finder in the orthologous intergenic sequences of closely related genomes. However, to speed up the motif comparison process, PhyloNet reduces the continuous motif profile space to a discrete one (33), which would sacrifice the sensitivity to detect highly degenerate CRBSs. Furthermore, sub-motifs of the same TF are not effectively clustered by PhyloNet to form a unique motif (33,34).
In our opinion, the difficulty of genome-wide de novo prediction of CRBSs has three causes. First, CRBSs are short with a length of 6–30 base pairs (bp), and the sequences are degenerate (9), while residing in usually long non-coding sequences where the chance for the random occurrence of a sequence similar to a CRBS is high. Second, there is no general pattern in CRBSs; any segment of a sequence can be potentially a CRBS as long as there is a TF that can specifically bind it. Third, these sequence-based cis-regulatory motif prediction algorithms attempt to model the 3D protein–DNA interaction events with a sequence pattern finding problem, which cannot possibly capture all of the biophysical aspects of the protein–DNA interactions, thus a rather high false positive prediction rate is almost unavoidable. This might explain why all the surveyed motif-finding programs can only predict at most 40% known binding sites, although different algorithms may have complementary predictions (29,30).
In this article, we have developed a novel algorithm called ‘GLECLUBS’ (GLobal Ensemble CLUsters of Binding Sites) for the genome-wide de novo prediction of CRBSs in prokaryotic genomes by circumventing these difficulties. We have applied it to the E. coli K12 and B. subtilis genomes, where a relatively large number of CRBSs are known for validation purposes. The algorithm has achieved rather high prediction accuracy and robustness, and it outperforms the prior algorithms compared. The software package is freely available upon request.
MATERIALS AND METHODS
Materials
The protein sequences, genome sequences and their annotation files of a total of 139 γ-proteobacteria and 124 firmicutes were downloaded from the NCBI RefSeq database at (ftp://ftp.ncbi.nih.gov/genomes). The known CRBSs of E. coli K12 and B. subtilis were downloaded from RegulonDB v6.0 (35) and DBTBS release 5 (2), respectively. Known and predicted TFs were downloaded from the DBD database (36). A compendium of microarray dataset from E. coli K12 collected under 380 experiments using the Affymetrix® platform were downloaded from the M3D database (37).
The design of the algorithm
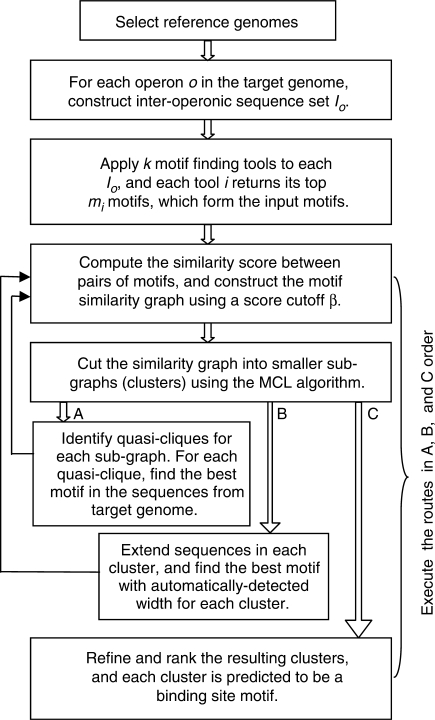
The GLECLUBS algorithm is based on a comparative genomics approach and its flowchart is shown in Figure 1. Given a target genome, e.g. E. coli K12, for which we want to predict all possible CRBSs, we first select a group of closely related reference genomes using a new method (see below). For each operon o in the target genome, we identify its orthologous operons in all the reference genomes, and extract their corresponding upstream inter-operonic sequences to form a sequence set Io. We assume that some sequences in Io share some similar CRBSs for a set of orthologous TFs encoded in the target genome and some of the reference genomes. Based on this assumption, and for the convenience of discussion, we loosely define a cis-regulatory motif as the set or a subset of the binding sites of a TF in the target genome and of its orthologs in the reference genomes. Since the existing motif-finding algorithms can only predict a small fraction of the true CRBSs present in the input intergenic sequences, and different algorithms produce complementary predictions (29,30), we applied multiple (k) complementary motif-finding algorithms to each sequence set Io to harvest as many true binding sites as possible. In addition, since a motif with the highest score returned by a motif-finding algorithm may not necessarily be the true binding motif, a relatively low-ranked prediction can be a true one instead (29,30), we kept the top mi motifs found by the i-th motif-finding algorithm to include even more true binding sites. All these putative motifs are designated the input motifs. In order to separate the correctly predicted motifs from spurious ones in the set of input motifs, we computed the similarity scores between pairs of input motifs using a new metric (see below), and constructed a weighted graph called the motif similarity graph, in which a node represents an input motif, and two nodes are connected by an edge if and only if the similarity score between their corresponding input motifs is greater than a preset cutoff β with the similarity score being the weight of the edge (Figure 2). We reason that a true motif is more likely to be predicted by multiple tools than are spurious ones, when based on the same inter-operonic sequence set associated with an operon in the target genome if its binding sites are conserved beyond a certain level. Furthermore, a true motif is also more likely than a spurious one to have multiple similar motifs predicted in different sets of inter-operonic sequences associated with different operons, simply because all of these operons are regulated by the same TF, and therefore are expected to contain similar CRBSs. In other words, true binding site motifs are more likely to form highly connected sub-graphs with high weights on the edges in the motif similarity graph than are spurious ones, because the probability for multiple similar spurious motifs to occur by chance should be low. Our algorithm was then designed to identify ‘condensed sub-graphs’ as possible true binding site motifs. However, due to the degenerate nature, the similarity between two subsets of a motif may not be significantly high (see below), making our task of ‘separating true motifs from spurious ones’ in a single step not easy. To overcome this difficulty and find the condensed sub-graphs, we designed a graph clustering algorithm that iteratively constructs and clusters graphs to gradually filter out the spurious motifs in the motif similarity graph (Figure 1). We found that only three iterations were needed to asymptotically converge on the optimal prediction accuracy. We then refined the resulting sub-graphs/clusters, and ranked them according to the quality of the best motif that each cluster contains. Each top-ranked cluster is predicted to be a putative cis-regulatory binding motif, and the genes associated with it are predicted to form a regulon.
Figure 1.
Flowchart of the GLECLUBS algorithm for genome-wide de novo CRBS predictions.
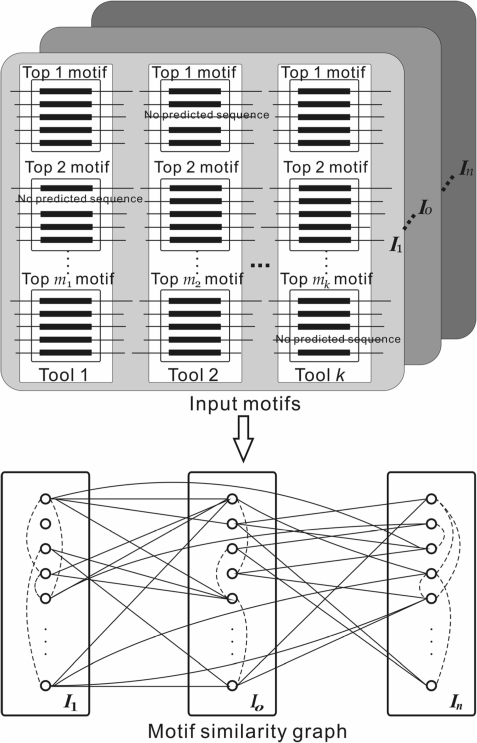
Figure 2.
Construction of the motif similarity graph. Multiple (k) motif-finding tools are used and each predicts multiple motifs in each inter-operonic sequence set Io. All the predicted motifs form the set of input motifs. A node in the motif similarity graph represents a motif. Two nodes are connected if their corresponding motifs have a similarity score ≥β with the score being the weight on the edge (not shown for clarity). A solid line represents an edge between two nodes associated with two different Io, and a dashed line represents an edge between two nodes associated with the same Io.
Predictions of orthologs and operons
Orthologous proteins and their genes between two genomes were predicted by the bidirectional best hits method (38) using the BLASTP algorithm with an E-value cutoff 10–20 for both searches. Operons in each genome were predicted by the algorithm described in (39), which performed best among all other predictors when evaluated by Brouwer et al. (40).
Selection of reference genomes
Since gene transcription regulatory networks tend to evolve very rapidly (41,42), we selected a genome as a reference genome not only based on its evolutionary relationship to the target genome, but also based on its shared gene transcription regulatory networks with the target genome. To this end, we represented the distribution of a total of n known and predicted TFs of the target genome (downloaded from DBD database (36)) in a related genome Gj by a bit vector Gj(b1, b2, …, bi, …, bn), where bi = 1, if the i-th TF of the target genome has an ortholog in Gj, otherwise bi = 0. The Hamming distance between each pair of these TF distribution vectors was used to construct a neighbor-joining tree. We typically selected a monophyletic group including the target genome in this tree as reference genomes with too closely related genomes removed, and each genome has orthologs of at least 25% TFs in the target genome. We have selected this cutoff as it can generally include moderately related genomes according to other phylogenetic information (e.g. 16S RNA genes trees, data not shown), but exclude closely related parasitic genomes that are known to have a simpler gene transcriptional regulatory network due to their tremendous genome reductions. Using this criterion, we selected 55 from 139 sequenced γ-proteobacteria, and 17 and 33 from 124 sequenced firmicutes as the reference genomes for the CRBS predictions in E. coli K12 (Figure S1), B. subtilis (Figure S2) and S. oneidensis (Figure S3) respectively.
Prediction of input motifs
Let Gt be our target genome and GR be the set of m reference genomes G1, G2, … , Gm. Each gene g in Gt and its orthologs in all of the genomes in GR consist of an orthologous group Og. For each Og, we extract up to 800 bases upstream inter-operonic region of each gene in Og to form a sequence set Jg according to the predicted operon structures in Gt and GR, and we say that Jg is associated with gene g. The union of all {jg} associated with each gene g in an operon o of the target genome forms a larger inter-operonic sequence set Io if it contains at least five sequences, and we call that Io is associated with the operon o. That is, Io=∪g ∈ o
Jg. We apply k motif-finding tools to each Io, and the i-th tool returns its top mi predicted motifs. All the tools return the same length motifs at this point. Thus, there are 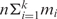 motifs identified from each Io. If there are n operons in the target genome, we will end up with a total of
motifs identified from each Io. If there are n operons in the target genome, we will end up with a total of 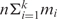 input motifs. In order to distinguish the true motifs from the spurious ones in these input motifs based on the assumption that a true motif is likely to have multiple similar copies in these input motifs, whereas a spurious one will not, we need to compute the similarity between a pair of input motifs. Although several metrics have been developed previously to quantify the similarity of sequence motifs (43–46), none of them resulted in a satisfactory results for our purpose (see ‘Results’ section), therefore we define the following metric.
input motifs. In order to distinguish the true motifs from the spurious ones in these input motifs based on the assumption that a true motif is likely to have multiple similar copies in these input motifs, whereas a spurious one will not, we need to compute the similarity between a pair of input motifs. Although several metrics have been developed previously to quantify the similarity of sequence motifs (43–46), none of them resulted in a satisfactory results for our purpose (see ‘Results’ section), therefore we define the following metric.
Computing the similarity between two sequence motifs
Let M be a sequence motif containing n sequences with length L, andFM = (fM (b, i))4 × L be the base frequency matrix of the motif M. The profile matrix of M is defined as,
where pM(b, i) is the probability of base b appearing at position i of the motif M, and q(b) is the probability of base b appearing in the background sequences. A pseudo-count is added when computing these probabilities.
The information content of column i of the profile matrix PM is defined as,
Let M1 and M2 be two motifs with profile matrices P1 and P2, frequency matrices F1 and F2, and n1 and n2 sequences, respectively. To compare motif M1 and M2, we first scan M2's frequency matrix F2 with M1's profile matrix P1 to find all the optimal alignments without gaps in the middle between the frequency matrix F2 and the profile matrix P1, denoted by the set A1,2. An optimal alignment s ∈ A1, 2, is defined as the alignment of the columns of F2 and P1 that maximize the number of columns {i} satisfying Σb (f2 (b, s(i))Prf1 (b, i) ≥ 0 (Figure S4). We define the likelihood score for P1 to generate F2 as
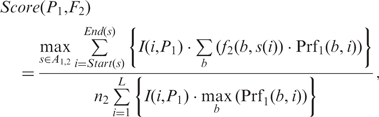 |
Similarly, we define the likelihood score for P2 to generate F1 as,
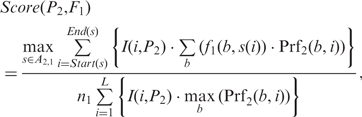 |
Notably, the denominators of the two score functions are the upper bounds of their numerators, which are used to normalize the scores. We then define the (motif-motif) similarity score between M1 and M2 as
Note that we use the information content of each column to attenuate the influence of the low information parts, and to enhance the effect of the high information parts of the profile on the similarity score.
We computed the similarity between any two motifs from different inter-operonic sequence sets. For the motifs from the same inter-operonic sequence set, we only calculated the similarity between the pair of motifs whose sequences from the target genome have a large overlap (≥50%).
To compute the similarity scores between sub-motifs of a known motif that has n known binding sites (we only consider the motifs that have at least three binding sites), we randomly selected (n − k + 1) sub-sets (sub-motifs) of size k with replacement from the n binding sites, k = 1, … , n. Therefore, there are n(n + 1)/2 sub-motifs for each known motif. Pair-wise similarity scores among these sub-motifs were then computed for each known motif.
Prediction of cis-regulatory motifs
We predicted all possible CRBSs in the target genome through the following algorithm.
Step 1. Construct the motif similarity graph
Given the computed similarity scores between pairs of input motifs, we constructed the motif similarity graph using the input motifs as the nodes. We connected any two nodes if the similarity score between their corresponding motifs was greater than a preset cutoff β, and assigned the similarity score as the weight of the edge.
Step 2. Cut the motif similarity graph into smaller subgraphs
The above constructed motif similarity graph was usually very large. To efficiently cut this graph into smaller condensed subgraphs, we applied the Markov clustering (MCL) algorithm (47) to the graph. MCL iteratively computes random walks determined by a Markov chain through alternately executing two operators (expansion and inflation) on a stochastic matrix. We kept the resulting clusters that contained at least three input motifs for further analysis, and discarded the rest.
Step 3. Find cliques from each of the resulting subgraphs obtained by MCL
For each node in a subgraph obtained by MCL, we found a clique associated with it. This can be done by repeatedly deleting its neighbor node with the minimum-degree, until a clique is formed (Figure S5). If at least two nodes have the same minimum degree, we break the tie by deleting the node with the minimum sum of weights of its incident edges. Although finding all the cliques with maximal nodes in a large graph is impossible because the Maximum Clique Problem is NP-hard (48), this greedy algorithm searches for exactly one clique associated with each node, and thus is rather fast (for a node v with degree dv, its time complexity is O(dv2); and since the graph is sparse, v is usually small). We discarded the nodes/motifs that were not included in a clique. Note that a node could appear in multiple different cliques identified by this algorithm.
Step 4. Construct quasi-cliques by merging cliques
We noted that cliques were too strict for clustering the binding sites of the same motif, as many known binding sites of the same motif were separated into different cliques due to their low similarity; therefore we needed to combine them. To this end, we first deleted the redundant cliques, and computed the overlapping rate of two cliques Ca and Cb, defined as
If rab > δ and Rab > ε, where δ and ε are two preset cutoff values, and δ > ε, then we merged Ca and Cb into a so-called quasi-clique Qab (δ = 0.9 and ε = 0.7 in our current applications). Notably, a node could appear in different quasi-cliques due to its appearance in multiple cliques.
Step 5. Construct target genome specific non-overlapping sequence sets
For each quasi-clique, we extracted the sequences from the target genome, and merged the overlapping sequences to form a target genome-specific sequence set.
Step 6. Predict renewed motifs
We applied a motif-finding tool (MEME) to each of the constructed target genome specific sequence sets, and kept the best motif, which we called a renewed motif and discarded the rest of sequences in the set.
Step 7. Cluster the renewed motifs
We computed the similarity scores between pairs of renewed motifs and repeated steps 1 and 2 to group these motifs into new clusters.
Step 8. Merge and extend sequences in each cluster
We first merged the sequences in each new cluster into a new non-overlapping sequence set. To fix the drawbacks of using a fixed length in our motif-finding processes so far, we then extended each sequence on both ends by a fixed length (10 bases) by padding its flanking genome sequences.
Step 9. Repeat Steps 6 and 7
For each extended non-overlapping sequence set, we used the motif-finding tool MEME to find the best motif with motif length being automatically determined in the region 6–22 bp, and then grouped these motifs into clusters by repeating Steps 6 and 7.
Step 10. Refine clusters
We applied MEME again to each cluster obtained in Step 9 with motif length being automatically determined in the region 6–22 bp. The sequences recovered by the top 10 motifs by MEME in each cluster formed our final predicted motifs in that cluster, since we noted that MEME and other motif-finding tools tended to find different parts of the same binding site motif in its different top-ranked predictions.
Step 11. Rank the predicted motifs/clusters
The resulting clusters from Step 10 varied in terms of the quality of the putative motif that each contained, and thus the likelihood of their correspondence to a true cis-regulatory binding motif. In addition, the same sequence could appear in different clusters, we needed to determine the most possible cluster/motif to which it should belong. To this end, we ranked the clusters according to the similarity of the sequences in a cluster. For this purpose, we computed a cluster quality score for each cluster defined as
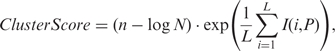 |
where n is the number of sequences in the best L-length motif found by MEME in step 10, I(i, P) is the information content of column i of the profile matrix P of the best motif, and N is the number of sequences in the cluster. A score similar to ClusterScore was also used in the BioProspector algorithm to measure the quality of a motif (49). We assume that a high ClusterScore means high likelihood that the cluster corresponds to a true cis-regulatory binding motif. Therefore, we ranked the clusters/motifs in descending order according to their ClusterScores as the final output of the algorithm, and considered the highest-ranked cluster as the motif to which a sequence belongs if a sequence is assigned to difference clusters. A cutoff T can be used to predict the top T clusters as cis-regulatory motifs encoded in the target genome, according to the total number of TFs encoded in the target genome or the saturation of unique putative binding sites in the top T clusters.
RESULTS
The accuracy of operon predictions is a constraint on phylogenetic footprinting based cis-regulatory motif predictions
To insure the robustness of our algorithm and to popularize it for other less well-studied genomes which usually have no ample experimental data, we did not use the experimentally determined operon structures in E. coli K12. Instead, we predicted a total of 2396 operons including 1556 singleton and 840 multi-gene operons in the E. coli K12 genome, which cover 84.6% of the known operon structures (39). Based on these operon predictions as well as those in the 55 reference genomes, we constructed 2313 inter-operonic sequence sets {Io} associated with the same number of operons in E. coli K12, each contains at least five sequences (see ‘Materials and Methods’ section). To evaluate the effect of the accuracy of operon predictions on the extraction of inter-operonic sequences, and thus, the CRBS predication, we used all of the 1642 known CRBSs (the 30 known binding sites of the RNA genes were excluded for analysis) in RegulonDB (v 6.0) to scan the predicted inter-operonic sequences in the E. coli K12 genome. We found that 1411 (86%) known CRBSs could be mapped to the predicted inter-operonic sequences (Table 1), suggesting that under the current state-of-the-art operon prediction accuracy, about 14% of possible true binding sites will be missed, simply because of incorrect operon predictions. This conclusion is therefore in agreement with the operon prediction accuracy, as well as the finding by a recent survey study that current operon prediction algorithm can only predict about 80% known operon structures in E. coli K12 (40). Therefore, the accuracy of operon predictions is a limiting factor for identifying all possible CRBSs in a prokaryotic genome using phylogenetic footprinting techniques.
Table 1.
Recovery of known binding sites and motifs by GLECLUBS in E. coli K12 and B. subtilis
| Genome | Binding sites or motifs | RegulonDB/DBTBSa | Contained in inter-operonic sequencesb | Recovered by motif-finding tools | Recovered by the top clustersc | Final recovery rate |
|---|---|---|---|---|---|---|
| Escherichia coli K12 | Binding sites | 1642 | 1411 (86%) | 1316 (93%) | 1065 (81%) | 64.8% |
| Motifs | 125 | 122 (98%) | 119 (97%) | 112 (94%) | 89.6% | |
| Bacillus subtilis | Binding sites | 568 | 481 (85%) | 450 (94%) | 357 (79%) | 62.9% |
| Motifs | 99 | 98 (98%) | 98 (100%) | 86 (88%) | 86.9% |
aRedundant binding sites in RegulonDB and DBTBS are removed and binding sites for RNA genes are not considered in this study.
bThe percentage in a brace is the recovery rate at that step of the prediction pipeline based on the previous step.
cThe top 400 and 300 clusters predicted in E. coli K12 and B. subtilis, respectively.
Optimization of the combination and outputs of motif-finding tools
Based on the recent survey studies on the performance of the available motif-finding tools (29,30,50), our preliminary experiments on more than a dozen of these tools for their complementarities and efficiency, as well as the type of algorithm that they are based upon, we selected six well-regarded ones for further evaluation of their performance on recovering the 1411 known binding sites in the extracted 2313 inter-operonic sequence sets {Io} of E. coli K12, including CUBIC (51), BioProspector (49), MotifSampler (52), MEME (53), CONSENSUS (54) and MDscan (55). Although different motifs may have different lengths, most of these tools require specifying the length of motifs to be predicted. To find the optimal motif length used in these programs, we have tested different lengths from 8 to 22 bp with all these programs, and found that the motif length 16 bp performed best in recovering the known CRBSs/motifs in our extracted inter-operonic sequences sets {Io} (Figure S6). However, the other motif lengths 14–22 bp performed almost equally well (Figure S6). Thus, the motif length parameter is rather robust in the range of 14–22 bp. We also noted that the distribution of the motif lengths of the known CRBSs in both RegulonDB and DBTBS were rather similar (Figure S7), with 12–22 bp being the most predominate lengths. We thus selected 16 bp as the fixed motif length for these motif-finding tools in all our applications.
Note that we did not use any more recently developed motif-finding tools that incorporate phylogenetic information of the input inter-operonic sequences, because these algorithms are mainly designed to predict CRBSs in eukaryotic genomes (56–60), and they require multiple sequence alignments or co-regulated genes as the inputs in addition to a phylogenetic tree of the input intergenic sequences. However, all these three pieces of information are not easily obtained for prokaryotes, because orthologous intergenic sequences from most related prokaryotic genomes cannot be reliably aligned, co-regulated genes are usually unknown for most sequenced prokaryotic genomes, and it is difficult to construct a phylogenetic tree that describes the evolution of all the inter-operonic sequences in prokaryotes due to massive horizontal gene transfer events during the course of their evolution.
As shown in the second column of Table 2, of the 1411 known CRBSs that were correctly extracted in the inter-operonic sequences, only 168–355 (12–25%) could be identified by these six programs as their best predictions. However, these programs did show complementary prediction effect, as 731 (52%) of these 1411 CRBSs could be jointly predicted by these six programs as their best predictions, even though this coverage was still not high enough. However, when multiple top motifs found by each tool were considered, the coverage of the 1411 CRBSs increased remarkably (Table 2). For instance, if each tool returned its top 25 motifs, then 1389 (98.4%) of these 1411 CRBSs could be recovered. Clearly, the more predicted motifs each tool returns, the more these 1411 CRBSs can be recovered. Nevertheless, too many motifs returned by each tool would also tremendously increase the spurious predictions, thus complicating the sequential steps of the algorithm. Furthermore, the number of the recovered known CRBSs actually entered a saturation phase when each tool returned more than 15 motifs (Table 2). We also noted that although these tools were in general complementary to one another, they did not perform equally well (Table 2). Considering all of these factors and by comparing different combinations of the number of output motifs for each tool as shown in Table 3, we selected a total of 40 motifs from the outputs of five of the six tools for each inter-operonic sequence set Io, which included the top 15 of MEME, the top 10 of BioProspector, and the top five of CUBIC, MDscan, and MotifSampler, respectively. The results from the CONSENSUS program were not used since almost all of its predictions were covered by other programs (Table 3). Therefore, we had a total of 2313 (Io)× 40 = 92 520 input motifs for the E. coli K12 genome, which contained 1316 (93%) of the 1411 known CRBSs in the extracted inter-operonic sequences (Table 3). These 1316 identified known binding sites belong to 119 motifs (Table 1). Obviously, most of the 92 520 input motifs were spurious predictions; thus, the objective of our algorithm was to identify the true binding sites from the spurious ones. We used these 1316 known CRBSs identified by the five tools in the whole set of 92 520 input motifs containing a very large number of sequences (∼106) to evaluate the performance of our algorithm.
Table 2.
The performance of motif-finding tools on the recovery of known binding sites and motifs in E. coli K12
| Tools | Top 1 | Top 5 | Top 10 | Top 15 | Top 20 | Top 25 |
|---|---|---|---|---|---|---|
| MEME | 298/83 | 877/109 | 1134/115 | 1202/117 | 1233/117 | 1254/117 |
| BioProspector | 354/85 | 743/103 | 953/112 | 1056/112 | 1150/116 | 1181/116 |
| CUBIC | 242/75 | 563/98 | 791/108 | 905/109 | 999/111 | 1062/114 |
| MDscan | 355/82 | 552/96 | 634/99 | 684/102 | 758/107 | 793/109 |
| MotifSampler | 168/61 | 486/92 | 612/102 | 729/102 | 792/107 | 831/108 |
| Consensus | 168/63 | 186/68 | 200/74 | 210/76 | 214/76 | 220/76 |
| Total | 731/106 | 1145/117 | 1301/118 | 1355/119 | 1379/119 | 1389/119 |
A known binding site is considered being recovered if a half length of its sequence is identified (the first number); and a known motif is considered being recovered if more than 20% of its known binding sites are recovered.
Table 3.
Combinatory effects of different motif-finding tools and their outputs on the recovery of known binding sites and motifs
| Combination of the tools and the number of their outputs (in braces) | Total number of motifs returned | Number of binding sites recovered | Number of motifs recovered |
|---|---|---|---|
| ME(5)+BP(5)+CU(5)+MD(5)+MS(5)+CS(5) | 30 | 1145 | 117 |
| ME(5)+BP(5)+CU(5)+MD(5)+MS(5) | 25 | 1144 | 117 |
| ME(10)+BP(10)+CU(5)+MD(5)+MS(5) | 35 | 1284 | 118 |
| ME(10)+BP(10)+CU(10)+MD(10)+MS(10) | 50 | 1300 | 118 |
| ME(10)+BP(10)+CU(10)+MD(10)+MS(10)+CS(10) | 60 | 1301 | 118 |
| ME(10)+BP(10)+CU(10)+MD(5)+MS(5) | 40 | 1292 | 118 |
| ME(10)+BP(15)+CU(5)+MD(5)+MS(5) | 40 | 1305 | 118 |
| ME(15)+BP(10)+CU(5)+MD(5)+MS(5) | 40 | 1316 | 119 |
| ME(15)+BP(15)+CU(5)+MD(5)+MS(5) | 45 | 1333 | 119 |
| ME(15)+BP(20)+CU(5)+MD(5)+MS(5) | 50 | 1342 | 119 |
| ME(20)+BP(15)+CU(5)+MD(5)+MS(5) | 50 | 1345 | 119 |
| ME(20)+BP(20)+CU(5)+MD(5)+MS(5) | 55 | 1353 | 119 |
ME: MEME; BP: BioProspector; CU: CUBIC; MD: MDscan; MS: MotifSampler; CS: CONSENSUS. The combination shown in bold is adapted in our algorithm.
Our motif similarity metric outperforms the exiting metrics in separating relevant motifs from irrelevant ones
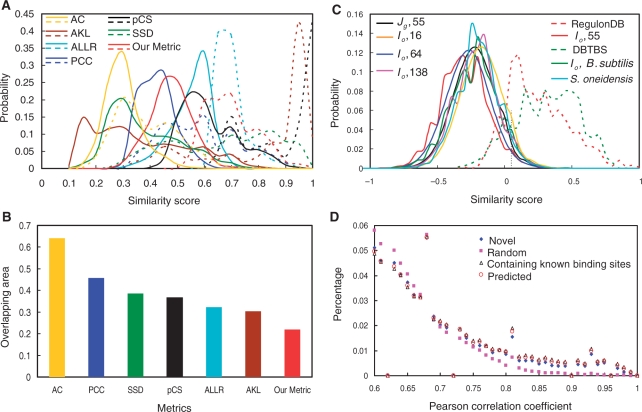
There are typically about 105 putative motifs in the set of input motifs. In order to facilitate the separation of true motifs from spurious ones in the motif similarity graph, we need a motif similarity metric that not only accurately measures the similarity between pairs of input motifs, but also can be efficiently computed. Specifically, we sought for a motif similarity metric that gives a high score for two relevant motifs, i.e. two sub-motifs of the motif of a TF, but a low score for two irrelevant motifs, i.e. two motifs for evolutionarily unrelated TFs or two spurious motifs. To this end, we designed a metric, and have compared it with six existing metrics for their capability of differentiating between relevant motifs and irrelevant ones. These compared existing metrics include Pearson correlation coefficient (PCC), average Kullback–Leibler (AKL, or relative entropy), average log-likelihood ratio (ALLR), 1 −P-value of Chi-square (pCS), sum of squared distances (SSD) [for a survey of these metrics, see (45)] and asymptotic covariance (AC) (46) (see Supplementary Method for the calculation of these metrics). As shown in Figure 3A, we plotted the distribution of the normalized motif similarity scores computed by each of these metrics among the input motifs (solid lines) and that of the normalized scores computed by each of these metrics among randomly selected sub-motifs of a known motif in RegulonDB (dashed lines). Since the majority of the input motifs are irrelevant to one another, a good metric should well-separate the bulk of the distribution of the scores among the input motifs and that of the scores among the sub-motifs of a known motif. As shown in Figure 3A and B, of all the metrics examined, our metric resulted in the smallest overlap between the distribution of the similarity scores among the input motifs and that of the similarity scores among the randomly selected (see ‘Materials and Methods’ section) sub-motifs of a known motif, suggesting that our metric outperforms these existing metrics in separating the relevant motifs from irrelevant ones. In other words, with our metric, a similarity score cutoff β can be chosen, such that as many as possible nodes that represent the sub-motifs of the motif of a TF are connected, while as many as possible nodes that represent sub-motifs of motifs of different TFs or of spurious motifs are disconnected. Therefore, the similarity graph constructed using our metric will have the sparsest edges while the relevant motifs are still likely to be connected. For example, with our metric, 85% of randomly sampled sub-motifs of known motifs had a raw similarity score greater than 0.05, and the graph constructed with this cutoff β = 0.05 contained only 1.6% of all possible edges of the motif similarity graph. In contrast, with the PCC metric, 85% of the sub-motifs of the known motifs have a raw similarity score greater than 0.35, but the graph constructed with this cutoff β = 0.35 contained 6.5% of all possible edges. Therefore, the motif similarity graph constructed using our metric will facilitate the our purpose to separate true motifs from spurious one, as it is easier to identify the highly connected subgraphs as possible true binding site motifs in a sparsely connected graph than in a densely connected one. Notably, although Mahony and coworkers (45) found that PCC and SSD were more efficient than the others to detect the similarities between familiar binding motifs, they are clearly not suitable for our purpose to separate true motifs from the spurious ones. This is because these two metrics in addition to AKL are biased to the correlation between the columns of the two compared motifs, whereas most of our predicted true motifs in the input motifs were partial, thus these metrics tend to score them low.
Figure 3.
The distributions motif similarity scores. (A) Comparison of the distributions of motif similarity scores computed by average Kullback–Leibler (AKL), average log-likelihood ratio (ALLR), Pearson correlation coefficient (PCC), 1 − P-value of Chi-square (pCS), sum of squared distance (SSD), asymptotic covariance (AC), and our metric. The alignment defined by our method (see ‘Materials and Methods’ section) between two motifs was used to compute the similarity scores by all the metrics. The scores computed by each metric were normalized to their maximal values. The solid lines are the distributions of the motif similarity scores among the input motifs in E. coli K12. The dashed lines are the distributions of the motif similarity scores among the sub-motifs of known binding sites in RegulonDB. (B) The overlapping area between the distribution curve of the similarity scores among the input motifs and that of the similarity scores among the sub-motifs of known motifs in RegulonDB. (C) Effects of the selection of reference genomes and the way of grouping inter-operonic sequences on the distribution of the similarity scores among the input motifs. The dashed lines are the distributions of the motif similarity scores among the sub-motifs of the known binding sites in RegulonDB or DBTBS. The vertical dotted line indicates the point of the similarity score cutoff β = 0.05 used for constructing the initial motif similarity graphs. (D) Distributions of the absolute values of Pearson correlation coefficient scores of the expression vectors of each pair of genes in each of the top 400 predicted clusters/regulons in E. coli K12 and that of randomly selected 400 gene groups with the corresponding numbers of genes in the top 400 predicted clusters/regulons.
Our method for selecting reference genomes facilitates the separation of relevant motifs from irrelevant ones
As shown in Figure 3C, the distribution of the motif similarity scores of the input motifs found by using the 55 reference genomes selected by our method is left-shifted compared with that of the input motifs found by using the 64 reference genomes selected by the conventional method, and that of the input motifs found by using all the sequenced 139 γ-proteobacterial genomes. Therefore the bulk of the distribution of the motif similarity scores of the input motifs found by using the 55 reference genomes has least overlap with that of the similarity scores of the sub-motifs of a known motif in RegulonDB, indicating that the reference genomes selected by our method are more likely to facilitate the separation of true CRBSs from the spurious ones than are the reference genomes selected by the conventional method. However, the distribution of the motif similarity scores of the input motifs found by using the more closely related 16 genomes that form a monophyletic group from these 55 genomes (Figure S1) is right-shifted compared with that of the input motifs found by using these 55 reference genomes, suggesting that reference genomes that are too closely related to the target genome does not improve the motif-finding due to their insufficient evolutionary divergence. Taking together, all these results suggest that the inter-operonic sequence sets from the 55 reference genomes are more likely to facilitate the separation of true binding sites from spurious ones than from the 16, 64 and 138 reference genomes tested. Furthermore, the distribution of the similarity scores of the input motifs found in {Io}, each of which is the union of inter-operonic sequence set Jg associated with each gene g in operon o, is also left-shifted compared with that of the input motifs found in {Jg} (Figure 3C), indicating that using Io for input motif discovery is more likely to facilitate the separation of true binding sites from spurious ones than using Jg.
Selection of the motif similarity score cutoff for the construction of motif similarity graphs
However, even using our motif similarity metric and these 55 selected reference genomes, the distribution of the similarity scores among the input motifs for the E. coli K12 genome still has a considerable overlap with that of the similarity scores of the sub-motifs of a known motif (Figure 3C). On other hand, Figure 3C shows that the optimal value of β that maximally separates these two distributions should lie around 0, although such a β value would still lead to a similarity graph in which some spurious motifs were connected, while some true ones were disconnected, suggesting that it is very challenging to separate the true motifs from spurious ones in a single step. Nonetheless, to find the possible optimal value of β, we have tested the β values in the range of [0, 0.5] for their recovering of known CRBSs in E. coli K12 identified by the five motif-finding tools, as we noted that it became impractical to effectively cut the similarity graph using the MCL algorithm (47) when β < 0 due to the too high density of the resulting graph, which is defined as the number of nodes divided by the number of edges in the graph. This observation is not surprising, because as shown in Figure S8, the density of the similarity graph increases rapidly when β becomes less than 0. Nonetheless, our algorithm performed almost equally well with β in the range of [0, 0.1], though the recovered known CRBSs dropped sharply when β > 0.1 (Figure S8), suggesting that the parameter β is also very robust in the range of [0, 0.1]. Accordingly, we chose β = 0.05 in this study to construct the initial motif similarity graph, which is a rather low cutoff, since it includes 99.7% of input motifs with at least one neighbor in the similarity graph of E. coli K12 (Figure S8). However, as mentioned earlier, the graph constructed contains only 1.6% of all possible edges, thus, is rather sparse.
Prediction of CRBSs in E. coli K12—sensitivity and specificity of the algorithm
The final output of our algorithm is a list of ranked clusters of putative CRBSs. Each cluster presumably corresponds to a cis-regulatory motif recognized by a TF encoded in the target genome. Operons that are presumably regulated by the binding sites in each cluster are predicted to form the regulon of the TF. Ideally, the higher the rank of a cluster/motif/regulon, the higher confidence we have for the prediction. Furthermore, if the target genome encodes a total of T TFs, then the top T clusters/motifs of our prediction should largely cover the binding sites of these T TFs. In order to evaluate our algorithm according to these criteria, we first applied it to the E. coli K12 genome using the 55 reference genomes (Figure S1).
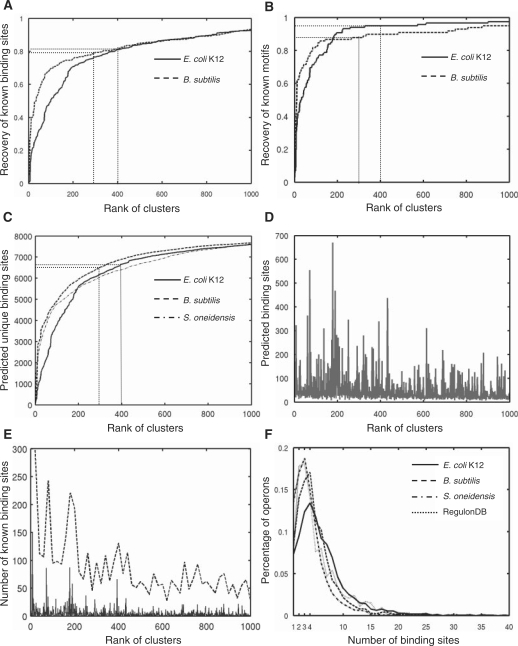
We first computed the recovery of the 1316 known binding sites in the input motifs by our top-ranked clusters. As shown in Figure 4A, with the increase in the number of top-ranked clusters, the cumulative recovery rate by the top-ranked clusters of these known binding sites in the input motifs increased very rapidly for the top 200 clusters, which recovered 71% of the known binding sites in the input motifs, and then it entered a saturation phase with slow linear increase around the top 300–400 clusters. With the top 400 clusters, our algorithm recovered 1065 (81%) of the 1316 known binding sites in the input motifs. We then computed the recovery rate by our top-ranked clusters of the 119 known motifs to which these 1316 known binding sites in the input motifs belong. We considered that a known motif was recovered by our prediction if more than 20% of its known binding sites were included in one of the top-ranked clusters. As shown in Figure 4B, again, with the increase in the number of top-ranked clusters, the cumulative recovery rate of known motifs by our top-ranked clusters increased even more rapidly for the top 200 clusters, which recovered 107 (90%) of the 119 known motifs, and then it entered a saturation phase with little increase around the top 300–400 clusters. With the top 400 clusters, our algorithm recovered 94% (112/119) these 119 known motifs. Therefore, our algorithm achieved rather high sensitivity in predicting the known binding sites as well as the known motifs. Interestingly, the E. coli K12 genome is estimated to encode a total of 271–400 TFs (including predicted and experimentally characterized) (41,61,62), if these 119 known motifs were characterized by experimentalists randomly, then the saturation of the recovery rate of these known motifs around the top 300–400 clusters (Figure 4B) suggests that our top 400 clusters should have covered at least 20% binding sites for almost all of these 271–400 TFs encoded in the E. coli K12 genome. Furthermore, the rapidly increasing phase of the recovery rates of both known binding sites and known motifs in the input motifs suggests that the higher the rank of a cluster, the higher the likelihood that it is a true binding site motif.
Figure 4.
Evaluation of the top-ranked clusters. (A) Cumulative recovery rate of the known binding sites in the input motifs by the top-ranked cluster, computed as the ratio of the number of cumulative known binding sites recovered in top-ranked clusters to the number of known binding sites in the set of input motifs. (B) Cumulative recovery rate of the known motifs that have binding sites in the input motifs by the top-ranked clusters, computed as the ratio of the number of cumulative known motifs recovered in top-ranked clusters to the number of known motifs in the input motifs. (C) The number of cumulative unique putative binding sites in the top ranked clusters as a function of the rank of clusters. (D) The number of predicted binding sites of E. coli K12 in the top 1000 clusters. (E). The number of known binding sites recovered by the top 1000 clusters in E. coli K12 by each cluster (dashed line), and by each 20 consecutively ranked cluster group (solid line). (F). The distribution of the number of putative binding sites of the top 400, 300 and 300 clusters in the inter-operonic regions of E. coli K12, B. subtilis and S. oneidensis, respectively, and the distribution of known binding sites in RegulonDB in the inter-operonic regions in E. coli K12.
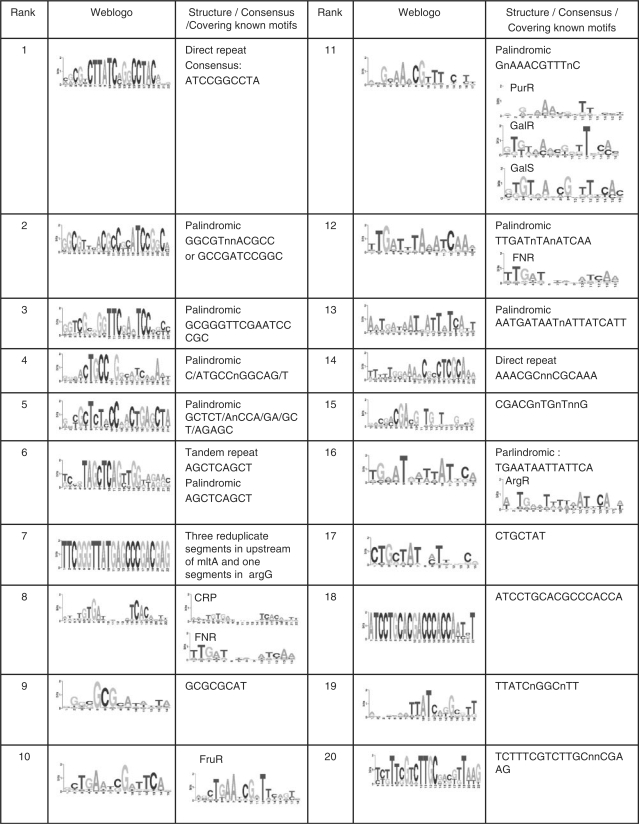
To estimate the specificity of our predictions, we plotted the number of cumulative unique predicted binding sites (the overlap between any two sequences is fewer than eight bases) as a function of the rank of our top 1000 clusters. As shown in Figure 4C, the number of cumulative predicted unique binding sites increased in a way very similar to the cumulative recovery rate of the known binding sites with the increase in the number of top-ranked clusters (Figure 4A), and it saturated at 6662 around the top 400 clusters. This relatively small number (6662) of predicted unique binding sites compared with the 92 520 putative binding sites from the E. coli K12 genome in the input motifs and its saturation indicate that most sequences in our input motifs have been filtered out by our algorithm, and that most of them are likely spurious predictions. Therefore, our algorithm could effectively separate the true binding sites from the spurious ones. Furthermore, the fact that these 6662 unique putative binding sites recovered 1065 of 1316 known binding sites in the 92 520 putative binding site from the E. coli K12 genome (P < 10–13, according to a hyper-geometric distribution) strongly suggests that our algorithm has likely achieved high prediction specificity, although it is difficult to estimate this number accurately. The clusters that were ranked after 400 were generally small in size as shown in Figure 4D, and contained motifs of low quality, and thus were ranked low. The overlap of sequences in differently ranked clusters was caused by the clique finding and quasi-clique construction procedures of our algorithm (see ‘Materials and Methods’ section), in which an input motif can be assigned to multiple quasi-cliques due to ambiguity of motif similarity (Figure 3A). However, it was the clique finding and quasi-clique construction procedures that filtered out most of spurious motifs. Although most of the known binding sites (81%) were located in the top 400 clusters (Figure 4A), some were also located in clusters ranked after 400 due to such overlap. However, the top ranked clusters contained more known binding sites than low-ranked ones (Figure 4E). Thus, we believe that the motif determined by the highest-ranked cluster of a sequence is the most possible motif to which the sequence belongs. Furthermore, since the recovery rate of known binding sites and motifs, and the cumulative unique putative binding sites all became saturated around the top 400 clusters, we consider the top 400 clusters as possible cis-regulatory motifs encoded in the E. coli K12 genome. The top 20 clusters are summarized in Figure 5. As shown in this figure, five of these top 20 clusters are highly enriched for known binding sites for seven TFs. In addition, although neither all of our the motif-finding tools were set, nor our algorithm was designed to identify motifs with special structures, more than half (12) of the top 20 clusters have palindromic, tandem repeat, or direct repeat structures (Figure 5), suggesting that they are highly likely to be true binding sites. The predicted binding sites and the recovery of known binding sites in the top 400 clusters are available at our webpage (http://gleclubs.uncc.edu/pbs).
Figure 5.
The top 20 motifs/clusters predicted in E. coli K12. The logo is for the best motif identified by MEME in each cluster.
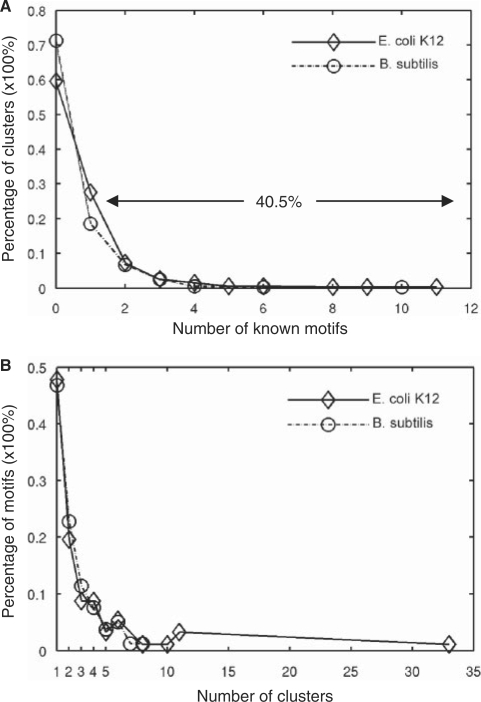
To evaluate the correspondence of the top-ranked clusters and the known binding site motifs, we first counted the number of known motifs that have their binding sites recovered by a top-ranked cluster. As shown in Figure 6A, 162 (40.5%) of the top 400 clusters contained binding sites of the 112 known motifs. Of these 162 clusters, 110 (67.9%) and 29 (17.9%) clusters contained known binding sites of one and two motifs, respectively; and only 23 clusters (14.2%) contained known binding sites of at least three known motifs. Thus, the majority (85.8%) of these 162 clusters corresponded to one or two known motifs. There are two reasons that a portion of our clusters contained binding sites of more than one known motifs. First, the binding sites of some TFs have overlaps. For instance, as shown in Figure 5, the binding sites of CRP and FNR, which are overlapped in some promoters, were clustered in the eighth cluster. Second, the binding sites of some TFs of the same superfamily are very similar to one another (63,64), thus were often clustered together. For example, the binding sites of GalS, GalR and PurR, which belong to the same protein family, formed the 11-th cluster. These phenomena have also been noted by Qin et al. (26). On other hand, the rest 238 (59.5%) of the top 400 clusters did not contain any known binding sites (Figure 6A). Interestingly, if the E. coli K12 genome encodes 314 TFs (61), then there are 314 − 125 = 189 TFs, for which we still do not know the binding sites. Based on the performance of our algorithm on the known binding site motifs, we further argue that the majority of these 238 of the top 400 clusters that contained no known binding sites are likely to correspond to new true binding site motifs, which is supported by gene expression data shown later.
Figure 6.
The correspondence between the clusters and known motifs. (A) Distribution of the number of known motifs in which the sequences of a cluster are located. (B) Distribution of the number of clusters that contain the known binding sites of a motif.
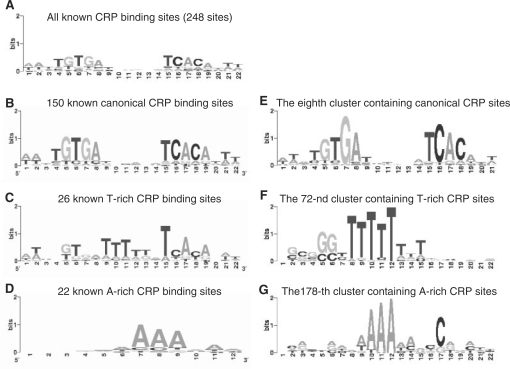
We then counted the number of the top-ranked clusters that contain the binding sites of a known motif. As shown in Figure 6B, the binding sites of 47.8% and 19.5% of the 112 known motifs recovered by our top 400 clusters were clustered into 1, and 2 clusters, respectively. Thus, the majority (67.3%) of known motifs were clustered into less than three clusters in our top 400 clusters. One possible reason that the binding sites of some motifs were split by our algorithm into multiple clusters was that the similarity between some binding sites of the same motif can be very low as indicated by the distribution of the similarity scores among the sub-motifs of a known motif (Figure 3A). For example, even though the 248 known CRP binding sites form a palindromic motif, the information content in even the most conserved columns is not very high (Figure 7A). In fact, these 248 CRP binding sites can be further divided into at least three sub-motifs; i.e., a more information content-rich canonical palindromic sub-motif (Figure 7B), a T-rich sub-motif (Figure 7C), and an A-rich sub-motif (Figure 7D). These 248 known CRP binding sites were mainly distributed in three clusters of the top 400 clusters of our algorithm. Specifically, the eighth (Figure 7E), the 72-th (Figure 7F) and the 178-th clusters (Figure 7G) correspond to the palindromic canonical, T-rich and A-rich CRP binding sub-motifs, respectively. Interestingly, when the sequences of these three clusters were combined, they formed a motif similar to that of the 248 known CRP binding sites (Figure 7A). CRP probably binds these distinct sub-motifs through adapting difference structure configurations. Alternatively, there are might be errors in the ‘known’ CRP binding sites: CRP might recognize the T-rich and A-rich sub-motifs through other regulators. This phenomenon has also been noted by Qin et al. (26).
Figure 7.
Three distinct sub-motifs of the CRP binding sites correspond to three top-ranked clusters. The all known CRP binding sites (A), can be subdivided into a more information-rich canonical palindromic sub-motif (B), a T-rich motif (C) and an A-rich sub-motif (D). Our predicted eighth (E), 72-th (F) and 178-th (G) clusters, largely correspond to the CRP's canonical palindromic sub-motif (B), the T-rich motif (C) and the A-rich sub-motif (D), respectively.
Lastly, we analyzed the distribution of the predicted binding sites of the top 400 clusters in the predicted inter-operonic regions. Figure 4F shows that for the majority of operons, their upstream inter-operonic regions contained putative binding sites from less than 10 clusters of the top 400 clusters. These putative binding sites included the σ-factor binding sites such as the 24-th cluster corresponding to the −10 σ70-factor binding sites, and the 89-th cluster corresponding to the −35 σ70-factor binding sites (Figure S9). This distribution is generally in good agreement with that of the known binding sites (including σ-factor binding sites) in the inter-operonic regions in E. coli K12, where most operons are under control of 1 ∼ 10 different TF binding sites (Figure 4F) except that the latter is left-shifted by one binding site relative to the former. However, these two distributions are likely to become more overlapped as more binding sites of more TFs are characterized. Furthermore, the putative binding sites of the top 400 clusters are distributed in the upstream regions of 2224 (96%) of the 2313 operons, thus we have predicted CRBSs for the most of the predicted operons in the genome, which is the largest coverage of operons achieved so far.
Validation of the CRBS and regulon predictions in E. coli K12 using a compendium of microarray gene expression datasets
To further validate our predicted CRBSs and regulons in E. coli K12, we computed the PCC score between the expression vectors for each pair of genes in each of the top 400 clusters/regulons, as well as for each pair of genes in each randomly selected 400 gene groups with the corresponding number of genes in the top 400 clusters/regulons (see ‘Materials and Methods’ section), using a compendium of 380 microarray gene expression datasets in E. coli K12 (37). As shown in Figure 3D, genes in our predicted top 400 clusters tend to have higher absolute values of PCC scores than do the randomly selected gene groups (P < 10–15, χ2 test). Moreover, the distribution of the absolute values of PCC scores of the genes in the clusters that do not contain known binding sites is almost the same as that of genes in the clusters that contain known binding sites (Figure 3D). These results strongly suggest that we have achieved the same level of prediction accuracy for the clusters that do not contain known binding sites as for those that contain known binding sites. Hence, our algorithm is not biased to the clusters that contain known binding sites, and therefore is very robust. We consider those clusters that do not contain known binding sites as putative new binding site motifs, and the genes associated with them as putative new regulons.
Prediction of CRBSs in B. subtilis—robustness of the algorithm
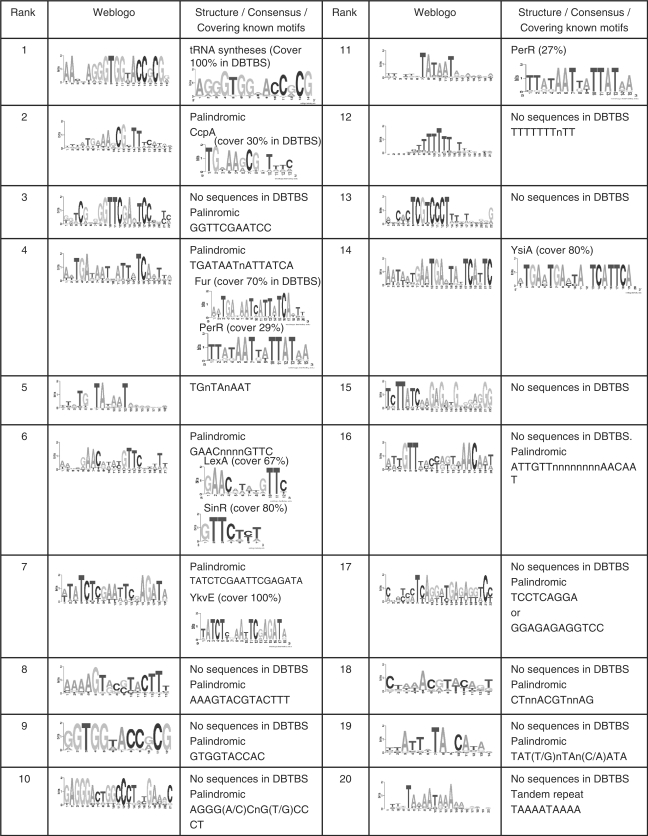
To further test the robustness of our algorithm, we applied it to the B. subtilis genome with exactly the same parameter settings as used for the E. coli K12 genome. In this case, we selected 17 firmicutes as the reference genomes that form a monophyletic clade in the tree of the 124 sequenced firmicutes (Figure S2). There are 568 known CRBSs in B. subtilis as documented in DBTBS (2), belonging to 99 motifs. We extracted a total of 2,400 inter-operonic sequence sets according to the predicted operon structures in B. subtilis and the reference genomes. Of the 568 known binding sites in B. subtilis, 481 (85%) are located in the inter-operonic sequences according to our operon predictions, belonging to 98 motifs; and 450 (94%) of the 481 binding sites were correctly predicted by the motif-finding tools in the 96 000 (2400 × 40) input motifs, belonging to 98 motifs (Table 1). Interestingly, the similarity scores among these 96 000 input motifs and that of the sub-motifs of the known motifs in B. subtilis have similar distributions to those of the input motifs and sub-motifs of the known motifs in E. coli K12, respectively (Figure 3C). In addition, the density of the motif similarity graph as a function of the cutoff β is also similar to that of E. coli K12 (Figure S8). As shown in Figure 4A and B, the recovery rates of both known binding sites and motifs increased very rapidly with the increase in the rank of the clusters, and then entered saturation phases at the top 300 clusters with small linear increase as seen in E. coli K12, suggesting that as in E. coli K12, high sensitivity of the prediction of individual binding sites as well as of motifs was achieved in B. subtilis. Similar to the predictions in E. coli K12, the saturation of the recovery rate of the known binding sites as well as motifs in the top-ranked clusters suggests that the higher the rank of a cluster, the more likely it is a true binding site motif. In addition, as in E. coli K12, the number of cumulative unique putative binding sites saturated at 6300 around the top 300 clusters (Figure 4C), suggesting again that the spurious motifs were largely filtered out by our algorithm. However, note the faster saturation of the recovery rates of binding sites, motifs, and unique putative binding sites in B. subtilis than in E. coli K12, although both genomes encode similar numbers of genes (4105 vs. 4132) and operons (2400 vs. 2313). This might reflect that fewer TFs are possible encoded in the former than in the latter. Indeed, the E. coli K12 genome was estimated to encode 314 TFs (61), while the B. subtilis genome 237 TFs (65). Furthermore, the majority of the top-ranked clusters contain either no known binding sites or known binding sites of one to two motifs (Figure 6A), and the most known motifs are located in one to two clusters (Figure 6B) due to the same reasons discussed earlier. Figure 8 summarizes the top 20 clusters of our predictions in B. subtilis. As in E. coli K12, seven of these top 20 clusters correspond to one or two known motifs, and more than half (12/20) of them contain motifs of palindromic structure, suggesting that they are likely to be true binding motifs (Figure 8). The predicted binding sites and recovery of known binding sites in the top 300 clusters are available at our website (http://gleclubs.uncc.edu/pbs). Similar to E. coli K12, the majority of upstream inter-operonic regions of B. subtilis contained putative binding sites from less than 10 clusters (Figure 4F), and 2334 (97%) of the 2400 predicted operons contained putative binding sites of the top 300 clusters. In summary, our algorithm has achieved similarly high prediction accuracy in B. subtilis as in E. coli K12. Therefore, we conclude that our algorithm is very robust, and can be applied to any sequenced prokaryotic genome as long as a few related reference genomes are available.
Figure 8.
The top 20 motifs/clusters predicted in B. subtilis. The logo is for the best motif identified by MEME in each cluster.
Comparison of our algorithm with other state-of-the-art methods
To further evaluate our algorithm, we have compared the performance of GLECLUBS to other prior state-of-the-art methods that have been applied to E. coli K12 or B. subtilis, where enough CRBSs are known for more objective evaluations. As shown in Table S1 in Supplementary Data, GLECLUBS clearly recovered more known motifs, and covered more operons than any of these algorithms in both the genomes. Furthermore, as we have mentioned earlier, PhyloNet (33), which was designed to predict CRBSs at a genome scale in simple eukaryotic (33) and prokaryotic (34) genomes, is probably the most comparable algorithm to GLECLUBS in terms of the scope of predictions that they both can achieve. However, the outputs of PhyloNet are a set of redundant motifs that need to be further clustered in an ad-hoc manner (33,34), and it has not been applied to either E. coli K12 or B. subtilis by its authors. Therefore, to compare the two algorithms, we applied GLECLUBS to S. oneidensis using 33 reference genomes selected from the 124 sequenced firmicutes (Figure S3). The similarity scores of the 91 000 input motifs from 2275 predicted operons in S. oneidensis have a similar distribution to those of the input motifs from E. coli K12 and B. subtilis (Figure 3C). In addition, the density of the motif similarity graph as a function of the cutoff β is also similar to those of E. coli K12 and B. subtilis (Figure S8).
As shown in Figure 4C, the number of cumulative unique putative binding sites predicted in S. oneidensis by GLECLUBS increased very rapidly with the increase in the rank of motifs, and then saturated at 5900 around the top 300 clusters followed by a small linear increase as seen in B. subtilis and E. coli K12, suggesting that the S. oneidensis genome might contain about 300 motifs. However, the saturation of unique putative binding sites in S. oneidensis was faster than in E. coli K12, but slower than in B. subtilis in the top 200 clusters, although the three genomes encode similar numbers of genes (4467 in S. oneidensis, 4237 in E. coli K12, and 4105 in B. subtilis) and operons (2275 in S. oneidensis, 2313 in E. coli K12, and 2400 in B. subtilis). This might reflect the fact that the number (243) of TFs encoded in S. oneidensis (36) is fewer than that (314) in E. coli K12 (61), but more than that (238) in B. subtilis (65). Furthermore, as seen in E. coli K12 and B. subtilis, the majority of upstream inter-operonic regions of S. oneidensis contained putative binding sites from less than 10 clusters (Figure 4F), and 2147 (94.4%) of the 2275 predicted operons contained putative binding sites of the top 300 clusters. Thus, we have likely achieved similar prediction accuracy in S. oneidensis as in B. subtilis and E. coli K12. In contrast, Liu et al. (34) used two input sequence datasets (I and II) to predict CRBSs in S. oneidensis, and PhyloNet output 203 and 1665 redundant motifs from datasets I and II, respectively. To remove the redundancy, they applied an ad-hoc hierarchical clustering procedure to these predictions, resulting in 194 none-redundant motifs, covering only 849 operons, which clearly underestimated the number of motifs that the S. oneidensis genome may contain given that the genome is predicted to encode at least 238 TFs (36). One possible reason for this under-prediction might be that PhyloNet was aimed to only search for palindromic motifs, but not all CRBSs are palindromic. In addition, since experimentally characterized CRBSs in S. oneidensis are still very limited (34), we followed the practice of Liu et al. (34), and compared our predicted motifs with these 194 motifs for their abilities to recover the top 24 conserved motifs between S. oneidensis and E. coli K12 (the first 24 motifs in Table 2 in Liu et al. (34), 13 of which are palindromic motifs). First, the combined 194 motifs predicted by Liu et al. recovered only nine (69.2%) of the 13 palindromic motifs, though their algorithm was aimed to predict palindromic motifs in this application (34). In contrast, as shown in Figure S10 and Table S1, our top 197 motifs recovered 12 (92.3%) of the 13 palindromic motifs. Second, the 194 motifs predicted by Liu et al. did not recover any non-palindromic motif of the 24 conserved motifs except the 9 palindromic motifs, thus they only predicted 9 (37.5%) of the 24 motifs (34). In contrast, as shown in Figure S10 and Table S1, our top 197 motifs recovered 16 (66.4%) of the 24 motifs, including four non-palindromic motifs. In addition, our top 300 motifs recovered 18 (75%) of the 24 motifs (Table S10). Third, Liu et al. (34) found that their 194 motifs recovered four motifs from an earlier work of Tan et al. (66). In contrast, as shown in Figure S10, our top 197 motifs recovered seven motifs by Tan et al. (66), including the four motifs recovered by Liu et al. (34). Therefore, GLECLUBS outperformed PhyloNet not only in efficiency of clustering motifs, but also in prediction sensitivity and specificity. The top 20 motifs predicted in S. oneidensis by GLECLUBS are shown in Figure S11, which include six of the top 24 conserved motifs between S. oneidensis and E. coli K12 and two possible σ-factor binding site motifs. The top 300 predicted motifs in S. oneidensis are available at our website (http://gleclubs.uncc.edu/pbs/).
DISCUSSION
Our algorithm has achieved high prediction accuracy and robustness
Genome-wide experimental characterization of CRBSs in all the sequenced genomes remains an open problem due to the tedious and laborious work required by even the most high-throughput experimental methods such as the ChIP-chip technique (67). Furthermore, the ChIP-chip technique is also limited by the conditions that allow the TF to bind to its binding sites as well as the low resolution nature of the technique, as it can only locate the possible binding sites in a region of hundreds to thousands bp length sequences. With the availability of increasing numbers of sequenced prokaryotic genomes, comparative genomics-based computational methods will become more and more powerful in deciphering the CRBSs in all the sequenced prokaryotic genomes. In this study, we have developed an algorithm called GLECLUBS for genome-wide de novo prediction of CRBSs in prokaryotic genomes based on the principles of comparative genomics. We have designed several novel features into our algorithm to address the three identified difficulties associated with the CRBS prediction problem as follows.
First, since any sequence segment can be potentially a binding site, motif-finding tools generally work by identifying the overrepresented sequences in a set of input sequences as the possible binding sites. Therefore, the quality of the inter-operonic sequences greatly affects the performance of motif-finding tools. An ideal high quality inter-operonic sequence set should contain as many as possible sequences that contain the binding sites of the orthologous TFs, and these binding sites should be conserved enough yet their flanking sequences should be divergent enough, so that the binding sites can be readily identified. In order to increase the quality of the input inter-operonic sequences for the phylogenetic footprinting procedure, we have designed a new method for selecting reference genomes. When compared with the reference genomes selected by the conventional method, those selected by our method are more likely to facilitate the separation of true CRBSs from spurious ones, as indicated by the left-shifted distribution curve of the similarity scores based on our method (Figure 3C). One possible explanation for this is that our method tends to select reference genomes that have the most similar gene transcription regulatory networks to the target genome, thus the extracted input sequences are more likely to contain similar binding sites of orthologous TFs, yet the flanking sequences are divergent enough to allow the binding sites to stand out. Furthermore, instead of using the inter-operonic sequence set Jg associated with a group of orthologous genes, Og, as the input sequences for the motif-finding tools, we used the union Io of inter-operonic sequence sets {Jg : g ∈ o}, which also facilitates the separation of true binding sites and spurious ones as indicated by the left-shifted distribution curve of the motif similarity scores based on the sets Io} compared to that based on {Jg} (Figure 3C). The reason for this might be that the union operation likely increases the number of sequences containing true binding sites in the input sequences, and thus increases the possibility that the true binding sites can be found by a motif-finding tool. This is reminiscence of the incorporation of co-regulated genes that improves the motif-finding through phylogenetic footprinting (68). Second, in order to overcome the problem that the current sequence-based motif-finding tools can only predict a small fraction of binding sites in the input sequences, we have used multiple motif-finding tools, and have optimized the combination of the tools and the number of outputs that each tool returns based on its performances on predicting the known binding sites and its complementary effect on the others. The total number of motifs returned by the motif-finding tools is also the trade-off of the coverage of known CRBSs and the number of spurious predictions included. Third, due to the short length and degenerate nature of the binding sites, there are many irrelevant sequences in the genome similar to a true binding site; to complicate the problem further, some binding sites of the same TF are not similar to one another at all (Figure 7) (26). Both factors make the task of separating the true binding sites from the spurious ones very challenging. To tackle this problem, we have first introduced a new metric to measure the similarity between two motifs. Although numerous motif similarity metrics have been proposed (43–46), some are based on the frequency matrices of the two compared motifs (such as PCC, pCS, SSD and AC), some are based on the frequency matrices and position weight matrices (PWMs) of the two compared motifs (such as ALLR), and some are based on the relative entropy of two compared columns of the motifs (such as AKL), none of them can achieve a satisfactory result for our purpose of efficiently separating the true motifs from the spurious ones (Figure 1A). Our metric uses not only the frequency matrices and PWMs of the two compared motifs, but also the information content of each column of the motifs. Moreover, our metric is based on the optimal alignment without gaps in the middle between the two compared motifs, and is normalized to the length of compared motifs; therefore, motifs of different lengths can be efficiently compared. Hence, it is not surprising that our metric outperforms all of these existing metrics for our purpose (Figure 3A and B). We then developed a graph-theoretic based algorithm to separate the true motifs from the spurious ones through an iterative motif similarity graph construction and clustering process, with varying stringency in each step of motif similarity graph construction.
When applied to the E. coli K12 and B. subtilis genomes with the same parameter settings, GLECLUBS can rapidly recover by its top-ranked predictions ∼81% known CRBSs in both genomes identified by the five motif-finding tools. More importantly, the recovery rates of known binding sites as well as the number of unique putative CRBSs saturated around the top 400 and 300 motifs for E. coli K12 and B. subtilis, respectively. These saturation points are in excellent agreement with the numbers of TFs possible encoded in the genomes. Further validation of our predictions in E. coli K12 using a compendium of microarray gene expression dataset indicates that we have achieved the same level of accuracy for the predicted new motifs as for those that contain known binding sites. Therefore, GLECLUBS was neither over trained on the known binding sites, nor biased to the E. coli K2 genome. Taking together, our algorithm has achieved high sensitivity as well as high specificity in both genomes in identifying the true binding sites in the input motifs predicted by multiple motif-finding tools and is also very robust, therefore can be applied to any prokaryotic genomes. One possible explanation for the robustness of GLECLUBS is that it only contains two parameters needed to be optimized, i.e. the motif length L as one of the inputs of the motif-finding tools and the motif similarity cutoff β for the construction of motif similarity graphs. However, both the motif length and the similarity between two sub-motifs recognized by the same TF are mainly governed by the physical and chemical principles of protein DNA interactions, and thus they are not likely to be species specific. In other words, the range of motifs length and the level of similarity of binding sites of a motif should be very similar in at least bacterial genomes. This conclusion is strongly supported by the similar distributions of the length of known CRBSs in E. coli K12 and B. subtilis (Figure S7), as well as the similar distributions of the similarity scores of the sub-motifs of the known motifs in E. coli K12 and B. subtilis (Figure 3C). Furthermore, our results showed that both the motif length and similarity cutoff were robust in a range of values in the same genomes (Figure S6 and S8).
When compared with other state-of-the-art genome-wide CRBS prediction algorithms that have been applied to E. coli K12 and/or B. subtilis, GLECLUBS outperformed all of them in terms of the number of known motifs recovered and the number of operons covered in both the genomes (Table S1). In addition, GLECLUBS out-performed the more recently developed PhyloNet algorithm (33) in terms of motif clustering efficiency, and prediction sensitivity and specificity when evaluated on the S. oneidensis genome. Furthermore, PhyloNet seems to require intergenic sequences from very closely related genomes (e.g., genomes from the same genus) for better performance (34); however, such a requirement cannot be always met. Therefore, our algorithm is more applicable, as its output requires no further process, and it only needs moderately related reference genomes for accurate predictions. With the availability of exponentially increasing number of sequenced prokaryotic genomes, it is highly possible to identify enough number of such reference genomes for any sequenced prokaryotic genomes.
The bottlenecks of genome-wide CRBS predictions
The performance of our algorithm depends on two pieces of information: (i) the operon structures in the target genome as well as in the reference genomes; and (ii) the input motifs found by multiple motif-finding tools. In the foreseeable future, operon structures in sequenced genomes will be mainly provided by computational predictions instead of experimental determination due to the enormous work that may incur. Therefore, we did not even use the known operon structures in both E. coli K12 and B. subtilis to make sure that our algorithm is robust enough to be applied to other less well-studied genomes. However, we have found that the accuracy of operon prediction is a major limiting factor for the performance of our algorithm. Even with the most accurate operon prediction algorithm developed so far (39,40), only about 84.6% and 83.3% known operons in E. coli K12 and B. subtilis, respectively, can be correctly predicted (40). Based on such predictions, the location of only 85 ∼ 86% known CRBSs in both genomes are correctly extracted as inter-operonic regions, and thus can be potentially identified by the motif-finding tools in the phylogenetic footprinting procedure (Table 1). The rest 14 ∼ 15% known CRBSs were missed by the procedure simply because they were not in the extracted inter-operonic regions. Further improvement of operon prediction algorithms or the development of other strategies will certainly increase the sensitivity of our algorithm.
Another limiting factor for the performance of our algorithm is the prediction accuracy of the motif-finding tools used in our algorithm to predict the input motifs. Although our algorithm was designed to overcome the problem of the low prediction sensitivity and specificity of current motif-finding tools by using an optimized combination of multiple outputs of multiple tools, for the sake of computational efficiency, the number of the input motifs can not be too large. This requirement affects the performance of our algorithm to some extent. Therefore, improvement of motif-finding tools and their combination in the future are likely to increase the sensitivity of our algorithm further, as our algorithm is very flexible to include any new motif-finding tools.
Furthermore, our graph clustering algorithm also has room for further improvement, although it has achieved ∼81% sensitivity and possibly high specificity to predict true binding sites in a large number of input motifs in both the E. coli K12 and B. subtilis genomes. Therefore, when all of these factors are considered, and the results are evaluated on the all known binding sites, we can only predict ∼64% of them in both E. coli K12 and B. subtilis (Table 1). In order to achieve higher prediction sensitivity and specificity and to identify all possible CRBSs encoded in a genome, all these three bottlenecks in our prediction pipeline need to be well addressed in the future.
Lastly, the binding sites of some different TFs were clustered in the same cluster due to the large overlap or high similarity of these binding sites; on the other hand, some binding sites of the same TF were clustered into different clusters due to the dissimilarity of these distinct sub-motifs. These phenomena had also been noted by an earlier study (26), suggesting that gene regulation is a far more complicated problem than previously imagined in that the same TF can bind to distinct motifs by adapting different configurations, and different TFs of the same family can binding to very similar binding sites. These observations might indicate the limitations of the sequence based genome-wide motif-finding algorithms, which assume that the same TF recognizes similar binding sites, and different TFs recognize distinct motifs. Solving these problems might require additional information such as the 3-dimensional structures of TFs encoded in the genomes.
Biological insights of our predictions into the cis-regulatory systems in E. coli K12 and B. subtilis
E. coli K12 and B. subtilis are the most extensively studied model organisms for Gram-negative and Gram-positive bacteria, respectively, for all aspects of bacterial biology, including gene transcription regulation. Although many important gene transcription machineries have been derived from the studies of these two organisms, so far we only know fewer than half of the cis-regulatory systems in both organisms after decades of research (1–3). Hence, we are still far away from having a holistic view of the gene transcription regulatory networks in any of the studied organisms. In this study, we have provided so far the most extensive lists of high quality candidates of new cis-regulatory binding motifs as well as regulons in both E. coli K12 and B. subtilis for further experimental characterization. Intriguingly, in both the genomes, the predicted new cis-regulatory binding motifs are close to the number of (putative) TFs whose binding sites are unknown. As our algorithm has likely achieved high prediction specificity, it would be reasonable to believe that most of these predictions are likely to be the binding site motifs of these (putative) TFs whose binding sites as well as regulons are largely unknown. Furthermore, since our predictions have tremendously narrowed down the candidates of CRBSs in the voluminous genome sequences, it becomes feasible to experimentally verify these predictions and, at the same time, to map each predicted motif to its cognate binding TF. For instance, one can use a double-stranded oligo-DNA containing the consensus sequence of a predicted motif to pull down the cognate TF from a pooled lysates of bacterial cells cultured under different conditions, presumably at least one of which can activate the TF; and then identify the bound protein using mass spectrometry analysis (69). Thus, combining our predictions with a high throughput DNA affinity capture and a protein identification technique can greatly facilitate the elucidation of the entire gene transcription regulatory networks in these model organisms in particular, and in any other sequenced prokaryotic genome in general.
Implications for current genome annotation efforts
One of the major objectives of current genome annotation is to define all of the functional sequence elements in the sequenced genomes. For practical reasons, this can only be done by highly accurate computational predictions. However, due to the aforementioned reasons, current genome annotation efforts are mainly focused on coding sequences, and little has been achieved on the annotation of CRBSs in most sequenced prokaryotic genomes (3). The relatively high prediction accuracy and robustness of our algorithm imply that it can be used to annotate the CRBSs in any sequenced prokaryotic genome as long as a few moderately related reference genomes are available. With more prokaryote genomes sequenced, this restriction will no longer exist for any sequenced genomes in the near future. Of course, to apply our algorithm to all the sequenced prokaryotic genomes, we need to further improve its computational efficiency, which we believe, is highly doable. First, our current algorithm only focuses on the target genome, the information about the CRBSs in dozens of reference genomes are not fully utilized. Full utilization of this information will possibly lead to the prediction of the CRBSs not only in the target genome, but also in all of the reference genomes as well. This will speed up the algorithm dozens of times. Second, the program can be easily parallelized, which can speed up the algorithm further. We are in the process of constructing a relational database to store our predicted CRBSs from the genomes to which our algorithm has been or will be applied. We hope that the database will become a valuable resource to the community to elucidate the CRBSs in all sequenced prokaryotic genomes.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
University of North Carolina at Charlotte grant and CMC-UNCC Collaborative Research Fund (to Z.S.). Funding for open access charge: The University of Carolina at Charlotte.
Conflict of interest statement. None declared.
Supplementary Material
ACKNOWLEDGEMENTS
We would like to thank Drs. Larry Mays, Dennis Livesay and Michael Hudson for their critical reading of this manuscript and suggestions. We would also like to thank the two anonymous reviewers for their comments and suggestions that greatly improve the quality of this manuscript.
REFERENCES
- 1.Martinez-Antonio A, Collado-Vides J. Identifying global regulators in transcriptional regulatory networks in bacteria. Curr. Opin. Microbiol. 2003;6:482–489. doi: 10.1016/j.mib.2003.09.002. [DOI] [PubMed] [Google Scholar]
- 2.Sierro N, Makita Y, de Hoon M, Nakai K. DBTBS: a database of transcriptional regulation in Bacillus subtilis containing upstream intergenic conservation information. Nucleic Acids Res. 2007;36 (Database issue):D93–96. doi: 10.1093/nar/gkm910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Montgomery SB, Griffith OL, Sleumer MC, Bergman CM, Bilenky M, Pleasance ED, Prychyna Y, Zhang X, Jones SJ. ORegAnno: an open access database and curation system for literature-derived promoters, transcription factor binding sites and regulatory variation. Bioinformatics. 2006;22:637–640. doi: 10.1093/bioinformatics/btk027. [DOI] [PubMed] [Google Scholar]
- 4.Stormo GD, Hartzell GW., III Identifying protein-binding sites from unaligned DNA fragments. Proc. Natl Acad. Sci. USA. 1989;86:1183–1187. doi: 10.1073/pnas.86.4.1183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Stormo GD. DNA binding sites: representation and discovery. Bioinformatics. 2000;16:16–23. doi: 10.1093/bioinformatics/16.1.16. [DOI] [PubMed] [Google Scholar]
- 6.Stormo GD, Schneider TD, Gold LM. Characterization of translational initiation sites in E. coli. Nucleic Acids Res. 1982;10:2971–2996. doi: 10.1093/nar/10.9.2971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Stormo GD, Schneider TD, Gold L, Ehrenfeucht A. Use of the ‘Perceptron’ algorithm to distinguish translational initiation sites in E. coli. Nucleic Acids Res. 1982;10:2997–3011. doi: 10.1093/nar/10.9.2997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Das MK, Dai HK. A survey of DNA motif finding algorithms. BMC Bioinformatics. 2007;8 (Suppl. 7):S21. doi: 10.1186/1471-2105-8-S7-S21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.GuhaThakurta D. Computational identification of transcriptional regulatory elements in DNA sequence. Nucleic Acids Res. 2006;34:3585–3598. doi: 10.1093/nar/gkl372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tagle DA, Koop BF, Goodman M, Slightom JL, Hess DL, Jones RT. Embryonic epsilon and gamma globin genes of a prosimian primate (Galago crassicaudatus). Nucleotide and amino acid sequences, developmental regulation and phylogenetic footprints. J. Mol. Biol. 1988;203:439–455. doi: 10.1016/0022-2836(88)90011-3. [DOI] [PubMed] [Google Scholar]
- 11.Gelfand MS. Recognition of regulatory sites by genomic comparison. Res. Microbiol. 1999;150:755–771. doi: 10.1016/s0923-2508(99)00117-5. [DOI] [PubMed] [Google Scholar]
- 12.Mironov AA, Koonin EV, Roytberg MA, Gelfand MS. Computer analysis of transcription regulatory patterns in completely sequenced bacterial genomes. Nucleic Acids Res. 1999;27:2981–2989. doi: 10.1093/nar/27.14.2981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gerdes SY, Scholle MD, Campbell JW, Balazsi G, Ravasz E, Daugherty MD, Somera AL, Kyrpides NC, Anderson I, Gelfand MS, et al. Experimental determination and system level analysis of essential genes in Escherichia coli MG1655. J. Bacteriol. 2003;185:5673–5684. doi: 10.1128/JB.185.19.5673-5684.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rodionov DA, Vitreschak AG, Mironov AA, Gelfand MS. Comparative genomics of the methionine metabolism in Gram-positive bacteria: a variety of regulatory systems. Nucleic Acids Res. 2004;32:3340–3353. doi: 10.1093/nar/gkh659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Vitreschak AG, Rodionov DA, Mironov AA, Gelfand MS. Regulation of riboflavin biosynthesis and transport genes in bacteria by transcriptional and translational attenuation. Nucleic Acids Res. 2002;30:3141–3151. doi: 10.1093/nar/gkf433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Panina EM, Mironov AA, Gelfand MS. Comparative analysis of FUR regulons in gamma-proteobacteria. Nucleic Acids Res. 2001;29:5195–5206. doi: 10.1093/nar/29.24.5195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Laikova ON, Mironov AA, Gelfand MS. Computational analysis of the transcriptional regulation of pentose utilization systems in the gamma subdivision of Proteobacteria. FEMS Microbiol. Lett. 2001;205:315–322. doi: 10.1111/j.1574-6968.2001.tb10966.x. [DOI] [PubMed] [Google Scholar]
- 18.Rodionov DA, Mironov AA, Gelfand MS. Transcriptional regulation of pentose utilisation systems in the Bacillus/Clostridium group of bacteria. FEMS Microbiol. Lett. 2001;205:305–314. doi: 10.1111/j.1574-6968.2001.tb10965.x. [DOI] [PubMed] [Google Scholar]
- 19.Makarova KS, Mironov AA, Gelfand MS. Conservation of the binding site for the arginine repressor in all bacterial lineages. Genome Biol. 2001;2 doi: 10.1186/gb-2001-2-4-research0013. RESEARCH0013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tan K, Moreno-Hagelsieb G, Collado-Vides J, Stormo GD. A comparative genomics approach to prediction of new members of regulons. Genome Res. 2001;11:566–584. doi: 10.1101/gr.149301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bulyk ML, McGuire AM, Masuda N, Church GM. A motif co-occurrence approach for genome-wide prediction of transcription-factor-binding sites in Escherichia coli. Genome Res. 2004;14:201–208. doi: 10.1101/gr.1448004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.McGuire AM, Hughes JD, Church GM. Conservation of DNA regulatory motifs and discovery of new motifs in microbial genomes. Genome Res. 2000;10:744–757. doi: 10.1101/gr.10.6.744. [DOI] [PubMed] [Google Scholar]
- 23.Kono H, Sarai A. Structure-based prediction of DNA target sites by regulatory proteins. Proteins. 1999;35:114–131. [PubMed] [Google Scholar]
- 24.Robertson TA, Varani G. An all-atom, distance-dependent scoring function for the prediction of protein-DNA interactions from structure. Proteins. 2007;66:359–374. doi: 10.1002/prot.21162. [DOI] [PubMed] [Google Scholar]
- 25.van Nimwegen E, Zavolan M, Rajewsky N, Siggia ED. Probabilistic clustering of sequences: inferring new bacterial regulons by comparative genomics. Proc. Natl Acad. Sci. USA. 2002;99:7323–7328. doi: 10.1073/pnas.112690399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Qin ZS, McCue LA, Thompson W, Mayerhofer L, Lawrence CE, Liu JS. Identification of co-regulated genes through Bayesian clustering of predicted regulatory binding sites. Nat. Biotechnol. 2003;21:435–439. doi: 10.1038/nbt802. [DOI] [PubMed] [Google Scholar]
- 27.McCue L, Thompson W, Carmack C, Ryan MP, Liu JS, Derbyshire V, Lawrence CE. Phylogenetic footprinting of transcription factor binding sites in proteobacterial genomes. Nucleic Acids Res. 2001;29:774–782. doi: 10.1093/nar/29.3.774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Alkema WB, Lenhard B, Wasserman WW. Regulog analysis: detection of conserved regulatory networks across bacteria: application to Staphylococcus aureus. Genome Res. 2004;14:1362–1373. doi: 10.1101/gr.2242604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hu J, Li B, Kihara D. Limitations and potentials of current motif discovery algorithms. Nucleic Acids Res. 2005;33:4899–4913. doi: 10.1093/nar/gki791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Tompa M, Li N, Bailey TL, Church GM, De Moor B, Eskin E, Favorov AV, Frith MC, Fu Y, Kent WJ, et al. Assessing computational tools for the discovery of transcription factor binding sites. Nat. Biotechnol. 2005;23:137–144. doi: 10.1038/nbt1053. [DOI] [PubMed] [Google Scholar]
- 31.Pritsker M, Liu YC, Beer MA, Tavazoie S. Whole-genome discovery of transcription factor binding sites by network-level conservation. Genome Res. 2004;14:99–108. doi: 10.1101/gr.1739204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Li H, Rhodius V, Gross C, Siggia ED. Identification of the binding sites of regulatory proteins in bacterial genomes. Proc. Natl Acad. Sci. USA. 2002;99:11772–11777. doi: 10.1073/pnas.112341999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wang T, Stormo GD. Identifying the conserved network of cis-regulatory sites of a eukaryotic genome. Proc. Natl Acad. Sci. USA. 2005;102:17400–17405. doi: 10.1073/pnas.0505147102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Liu J, Xu X, Stormo GD. The cis-regulatory map of Shewanella genomes. Nucleic Acids Res. 2008;36:5376–5390. doi: 10.1093/nar/gkn515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gama-Castro S, Jimenez-Jacinto V, Peralta-Gil M, Santos-Zavaleta A, Penaloza-Spinola MI, Contreras-Moreira B, Segura-Salazar J, Muniz-Rascado L, Martinez-Flores I, Salgado H, et al. RegulonDB (version 6.0): gene regulation model of Escherichia coli K-12 beyond transcription, active (experimental) annotated promoters and Textpresso navigation. Nucleic Acids Res. 2008;36:D120–124. doi: 10.1093/nar/gkm994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kummerfeld SK, Teichmann SA. DBD: a transcription factor prediction database. Nucleic Acids Res. 2006;34:D74–81. doi: 10.1093/nar/gkj131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Faith JJ, Driscoll ME, Fusaro VA, Cosgrove EJ, Hayete B, Juhn FS, Schneider SJ, Gardner TS. Many Microbe Microarrays Database: uniformly normalized Affymetrix compendia with structured experimental metadata. Nucleic Acids Res. 2008;36:D866–870. doi: 10.1093/nar/gkm815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Mushegian AR, Koonin EV. A minimal gene set for cellular life derived by comparison of complete bacterial genomes. Proc. Natl Acad. Sci. USA. 1996;93:10268–10273. doi: 10.1073/pnas.93.19.10268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Dam P, Olman V, Harris K, Su Z, Xu Y. Operon prediction using both genome-specific and general genomic information. Nucleic Acids Res. 2007;35:288–298. doi: 10.1093/nar/gkl1018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Brouwer RW, Kuipers OP, Hijum SA. The relative value of operon predictions. Brief Bioinform. 2008;9:367–375. doi: 10.1093/bib/bbn019. [DOI] [PubMed] [Google Scholar]
- 41.Madan Babu M, Teichmann SA. Evolution of transcription factors and the gene regulatory network in Escherichia coli. Nucleic Acids Res. 2003;31:1234–1244. doi: 10.1093/nar/gkg210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Lozada-Chavez I, Janga SC, Collado-Vides J. Bacterial regulatory networks are extremely flexible in evolution. Nucleic Acids Res. 2006;34:3434–3445. doi: 10.1093/nar/gkl423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Schones DE, Sumazin P, Zhang MQ. Similarity of position frequency matrices for transcription factor binding sites. Bioinformatics. 2005;21:307–313. doi: 10.1093/bioinformatics/bth480. [DOI] [PubMed] [Google Scholar]
- 44.Gupta S, Stamatoyannopoulos JA, Bailey TL, Noble WS. Quantifying similarity between motifs. Genome Biol. 2007;8:R24. doi: 10.1186/gb-2007-8-2-r24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Mahony S, Auron PE, Benos PV. DNA familial binding profiles made easy: comparison of various motif alignment and clustering strategies. PLoS Comput. Biol. 2007;3:e61. doi: 10.1371/journal.pcbi.0030061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Pape UJ, Rahmann S, Vingron M. Natural similarity measures between position frequency matrices with an application to clustering. Bioinformatics. 2008;24:350–357. doi: 10.1093/bioinformatics/btm610. [DOI] [PubMed] [Google Scholar]
- 47.van Dongen S. 2000. National Research Institute for Mathematics and Computer Science in the Netherlands, Amsterdam. [Google Scholar]
- 48.Garey MR, Johnson DS. Computers and Intractability: A Guide to the Theory of NP-Completeness. Gordonsville, VA: W H Freeman & Co; 1979. A cluster algorithm for graphs. [Google Scholar]
- 49.Liu X, Brutlag DL, Liu JS. BioProspector: discovering conserved DNA motifs in upstream regulatory regions of co-expressed genes. Pac. Symp. Biocomput. 2001:127–138. [PubMed] [Google Scholar]
- 50.Hu J, Yang YD, Kihara D. EMD: an ensemble algorithm for discovering regulatory motifs in DNA sequences. BMC Bioinformatics. 2006;7:342. doi: 10.1186/1471-2105-7-342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Olman V, Xu D, Xu Y. CUBIC: identification of regulatory binding sites through data clustering. J. Bioinform. Comput. Biol. 2003;1:21–40. doi: 10.1142/s0219720003000162. [DOI] [PubMed] [Google Scholar]
- 52.Thijs G, Lescot M, Marchal K, Rombauts S, De Moor B, Rouze P, Moreau Y. A higher-order background model improves the detection of promoter regulatory elements by Gibbs sampling. Bioinformatics. 2001;17:1113–1122. doi: 10.1093/bioinformatics/17.12.1113. [DOI] [PubMed] [Google Scholar]
- 53.Bailey TL, Elkan C. Fitting a mixture model by expectation maximization to discover motifs in biopolymers. Proc. Int. Conf. Intell. Syst. Mol. Biol. 1994;2:28–36. [PubMed] [Google Scholar]
- 54.Hertz GZ, Stormo GD. Identifying DNA and protein patterns with statistically significant alignments of multiple sequences. Bioinformatics. 1999;15:563–577. doi: 10.1093/bioinformatics/15.7.563. [DOI] [PubMed] [Google Scholar]
- 55.Liu XS, Brutlag DL, Liu JS. An algorithm for finding protein-DNA binding sites with applications to chromatin immunoprecipitation microarray experiments. Nat. Biotechnol. 2002;20:835–839. doi: 10.1038/nbt717. [DOI] [PubMed] [Google Scholar]
- 56.Liu Y, Liu XS, Wei L, Altman RB, Batzoglou S. Eukaryotic regulatory element conservation analysis and identification using comparative genomics. Genome Res. 2004;14:451–458. doi: 10.1101/gr.1327604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Sinha S, Blanchette M, Tompa M. PhyME: a probabilistic algorithm for finding motifs in sets of orthologous sequences. BMC Bioinformatics. 2004;5:170. doi: 10.1186/1471-2105-5-170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Li X, Wong WH. Sampling motifs on phylogenetic trees. Proc. Natl Acad. Sci. USA. 2005;102:9481–9486. doi: 10.1073/pnas.0501620102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Siddharthan R, Siggia ED, van Nimwegen E. PhyloGibbs: a Gibbs sampling motif finder that incorporates phylogeny. PLoS Comput. Biol. 2005;1:e67. doi: 10.1371/journal.pcbi.0010067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Newberg LA, Thompson WA, Conlan S, Smith TM, McCue LA, Lawrence CE. A phylogenetic Gibbs sampler that yields centroid solutions for cis-regulatory site prediction. Bioinformatics. 2007;23:1718–1727. doi: 10.1093/bioinformatics/btm241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Perez-Rueda E, Collado-Vides J. The repertoire of DNA-binding transcriptional regulators in Escherichia coli K-12. Nucleic Acids Res. 2000;28:1838–1847. doi: 10.1093/nar/28.8.1838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Shen-Orr SS, Milo R, Mangan S, Alon U. Network motifs in the transcriptional regulation network of Escherichia coli. Nat. Genet. 2002;31:64–68. doi: 10.1038/ng881. [DOI] [PubMed] [Google Scholar]
- 63.Gelfand MS. Evolution of transcriptional regulatory networks in microbial genomes. Curr. Opin. Struct. Biol. 2006;16:420–429. doi: 10.1016/j.sbi.2006.04.001. [DOI] [PubMed] [Google Scholar]
- 64.Sandelin A, Wasserman WW. Constrained binding site diversity within families of transcription factors enhances pattern discovery bioinformatics. J. Mol. Biol. 2004;338:207–215. doi: 10.1016/j.jmb.2004.02.048. [DOI] [PubMed] [Google Scholar]
- 65.Moreno-Campuzano S, Janga SC, Perez-Rueda E. Identification and analysis of DNA-binding transcription factors in Bacillus subtilis and other Firmicutes – a genomic approach. BMC Genomics. 2006;7:147. doi: 10.1186/1471-2164-7-147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Tan K, McCue LA, Stormo GD. Making connections between novel transcription factors and their DNA motifs. Genome Res. 2005;15:312–320. doi: 10.1101/gr.3069205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Ren B, Robert F, Wyrick JJ, Aparicio O, Jennings EG, Simon I, Zeitlinger J, Schreiber J, Hannett N, Kanin E, et al. Genome-wide location and function of DNA binding proteins. Science. 2000;290:2306–2309. doi: 10.1126/science.290.5500.2306. [DOI] [PubMed] [Google Scholar]
- 68.Wang T, Stormo GD. Combining phylogenetic data with co-regulated genes to identify regulatory motifs. Bioinformatics. 2003;19:2369–2380. doi: 10.1093/bioinformatics/btg329. [DOI] [PubMed] [Google Scholar]
- 69.Forde CE, Gonzales AD, Smessaert JM, Murphy GA, Shields SJ, Fitch JP, McCutchen-Maloney SL. A rapid method to capture and screen for transcription factors by SELDI mass spectrometry. Biochem. Biophys. Res. Commun. 2002;290:1328–1335. doi: 10.1006/bbrc.2002.6352. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.