Can Morphing Methods Predict Intermediate Structures?

Abstract

Movement is crucial to the biological function of many proteins, yet crystallographic structures of proteins can give us only a static snapshot. The protein dynamics that are important to biological function often happen on a timescale that is unattainable through detailed simulation methods such as molecular dynamics as they often involve crossing high-energy barriers. To address this coarse-grained motion, several methods have been implemented as web servers in which a set of coordinates is usually linearly interpolated from an initial crystallographic structure to a final crystallographic structure. We present a new morphing method that does not extrapolate linearly and can therefore go around high-energy barriers and which can produce different trajectories between the same two starting points. In this work, we evaluate our method and other established coarse-grained methods according to an objective measure: how close a coarse-grained dynamics method comes to a crystallographically determined intermediate structure when calculating a trajectory between the initial and final crystal protein structure. We test this with a set of five proteins with at least three crystallographically determined on-pathway high-resolution intermediate structures from the Protein Data Bank. For simple hinging motions involving a small conformational change, segmentation of the protein into two rigid sections outperforms other more computationally involved methods. However, large-scale conformational change is best addressed using a nonlinear approach and we suggest that there is merit in further developing such methods.

Introduction

Protein structures are inherently dynamic; movement is crucial to their function as motors, as cellular factories, as regulators, and as messengers in signal transduction. Many proteins have been crystallographically solved in several conformations. In order to understand the biological function of these proteins, we must understand the pathways that a protein follows between conformations. In addition, there may be long-lived intermediate states that we would like to be able to predict given the known crystal structures. Ideally, we would like to study these transitions in as much detail as possible. Molecular dynamics (MD) would allow detailed study of the motion of each atom in the protein. However, biologically relevant motions often happen on a timescale of milliseconds to seconds and involve many tens and hundreds of thousands of atoms, making such a computation infeasible. The high computational burden of MD has prompted an interest in methods that study protein dynamics on a coarse-grained level.

Considerable effort has been invested in creating movies that visualize conformational transitions,^1–4 with an emphasis on creating trajectories that provide physically feasible intermediate structures, but with no claims to actually recreate the biologically relevant pathway. Elsewhere, conformational transitions have been studied to predict the active forms of proteins in solution, for example, for drug design.⁵ Normal modes analysis is often used, alone or in conjunction with low-resolution experimental data.^6–9

Reaction path methods have also been applied to study protein transitions.^10,11 Some examples are the nudged elastic band method and the string method.^12,13 A related field of investigation is the use of motion planning (traditionally used in robotics to steer robots around obstacles) to study protein folding and dynamics.¹⁴ Large-scale protein motions can also be approximated through rigid-body motions, where substructures of the protein are treated as rigid bodies.^15,16

Myosin is one such example of a large protein system for which several crystallographic on-pathway structures exist but for which the active structure is unsolved. Myosin dynamics have been extensively studied through coarse-grained methods.¹⁷

Although the stated purpose of many online servers is to provide an instructive movie, the idea of coarse-grained dynamics to study protein motions is appealing as it is computationally inexpensive and would be especially useful for large protein systems provided that there are high-resolution structures of the protein in the initial and final state. Coarse-grained methods vary in the coordinates along which the motion of the protein system evolves, often through interpolation: Cartesian coordinates,^2,18 internal coordinates,¹⁹ and interresidue distances or a subset of interresidue distances^3,20 are some common examples. Some coarse-grained methods are purely geometric while others take energetics into account.

We have developed Climber, a new morphing method that does not move linearly. In this method, the restraining energy depends linearly on the distance deviation between the current structure and the target structure in a way that allows a great deal of flexibility to the motion of the protein and enables the protein to move around high-energy barriers, rather than over them, in a nonlinear fashion.

We are aware of no objective procedure to test how well coarse-grained dynamics can reconstruct the biologically relevant pathways, and here we propose such a test. We search the Protein Data Bank for proteins for which there are at least three structurally distinct crystallographically solved conformations. Using biological knowledge, we determine which of the three is the intermediate state. We create trajectories using four online servers that represent completely distinct coarse-grained dynamics algorithms and our new method, going from the initial to the final state (with no knowledge of the intermediate state). We then measure how close the coarse-grained trajectory comes to the intermediate crystal structure. Our test set includes five proteins ranging in size from 271 to 994 residues. The conformational changes involved range from a simple hinge bending to complete domain rearrangement. We compare all results to naïve geometric interpolations in Cartesian and internal coordinates, which act as a control. Using coarse-grained methods (especially via web servers) to infer functionally relevant motion between two crystallographic states has become a widespread practice in the community. We therefore feel it is of great importance to perform this objective test and to determine whether further development is merited.

These different methods are in some cases successful in coming near to the known intermediate crystal structure, particularly when the conformational change involves a hinging motion. In the case of a hinging motion, clever segmentation of the protein into a small number of rigid sections (usually two) seems to work well, outperforming more complicated methods. Our results show that the use of interresidue distances as the interpolation coordinate is advantageous and suggest that the use of nonlinear motion, through our new scheme or through normal modes analysis, is useful when studying more complex conformational changes. We believe it will be desirable to continue to develop coarse-grained motion methods, particularly those that use nonlinear motion.

Results

The Climber method

In the Climber method, the interresidue distances of a given conformation are pulled towards the distances in the target final conformation using a set of harmonic restraints that are added to the internal energy function, minimized at each step. Imagine a climber (the current conformation) pulling on a rope to move towards a target point (the target conformation), possibly in an adjacent valley. The set of restraints always involves the same set of distances in the target structure but the force constant is changed so that the climber (conformation) gets to the target destination in approximately N_cycle steps (the user-defined number of steps). Specifically, he moves towards the target by a sufficient amount as measured by the change in coordinate root-mean-square deviation (cRMS) each step to get there in N_cycle steps. If he is not moving fast enough towards the target, he needs to pull harder on the rope. If he is moving too fast, he needs to pull less. When moving too quickly, he may miss the easier path (lowest energy) around the peak. When moving too slowly, he has the chance to follow the easier path but may never get to the target. This self-adjusting method allows for nonlinear movement, moving around high-energy barriers, and trajectories differ as N_cycle is varied.

Trajectory generation servers

We test four online coarse-grained protein trajectory generation servers, our new morphing method Climber, and two naïve geometric interpolations (in Cartesian and internal coordinates), which act as a control. For each of the proteins in our test set, three on-pathway high-resolution crystal structures exist. One structure is designated the intermediate according to experimental biochemical evidence found in the literature, and the trajectory is generated from the initial to final structure with no structural information from the intermediate. We then determine if the calculated trajectory passes through or near the experimentally determined intermediate structure.

The four online servers we test were chosen to represent four completely distinct algorithms for coarse-grained trajectory generation:

1. MolMovDB^{† 21,22}

2. FATCAT^{‡ 23}

3. NOMAD-Ref^{§ 24}

4. MinActionPath^{|| 25}

Particulars of the algorithms can be found in the references and will not be reported here in detail. They are briefly described as follows:

1. The MolMovDB server creates a linear interpolation in Cartesian space after fitting the largest superimposable part of the initial and final structure, minimizing the energy of each structure along the trajectory.

2. The FATCAT server returns an interpolation of rigid-body motions, first finding the optimal structural alignment and the corresponding minimal number of hinge points for that alignment around which rigid fragments are rotated.

3. The NOMAD-Ref server uses elastic normal modes and interpolates interresidue distances using the algorithm of Kim et al.³

4. MinActionPath assumes a harmonic potential at the end states and solves the action minimization problem by solving the equations at each end state and finding the crossing point of these two solutions.

Protein test set results

The different sets of protein structures used here (Table 1) have been carefully chosen and it is important to consider the role that the change in conformation plays in the biological role of each.

Table 1.

The test set used to evaluate all coarse-grained dynamics methods

		Protein Data Bank ID (chain)			rmsd (Å)
Name	Residues	Initial	Intermediate	Final	(AB)	(BC)	(AC)
5′-NT	525	1OID (A)	1OI8 (B)	1HPU (D)	5.42	4.72	9.33
Ca2+-ATPase	994	1SU4 (A)	1VFP (A)	1IWO (A)	13.75	10.10	13.97
Myosin	837	1QVI (A)	1KK7 (A)	1KK8 (A)	16.56	12.01	27.32
RBP	271	1BA2 (A)	1URP (D)	2DRI (A)	2.22	4.20	6.19
RNase III	437	1YYO (AB)	1YZ9 (AB)	1YYW (AB)	7.26	13.15	17.47

Scallop myosin II

Myosin is a motor protein, hydrolyzing ATP to drive muscle contraction. During the myosin power cycle, the protein undergoes a large conformational change involving a rotation of a long helical arm, which essentially hinges. Myosin hydrolyzes ATP to swing to the pre-stroke state, releases ADP and P_i and binds actin in the nucleotide-free actin-binding rigor state, and finally binds ATP to detach from actin and reach the post-stroke state. We define the initial structure as the pre-stroke structure, the intermediate structure as the near-rigor structure, and the final structure as the post-stroke state, which is where they lie sequentially in the power stroke cycle.^26–28 The pre-stroke and post-rigor state have an rmsd of 27 Å, making this the largest conformational change in our set, and the intermediate structure is 16.6 Å from the initial state and 12 Å from the final state. The head domain (residues 1–708) does not undergo any significant conformational change. Most of the movement is in the converter domain (residues 708–775), which results in a large and rigid swing of the lever arm (residues 776–837). The light chains are not included as many online servers accept no more than 1000 C^α atoms.

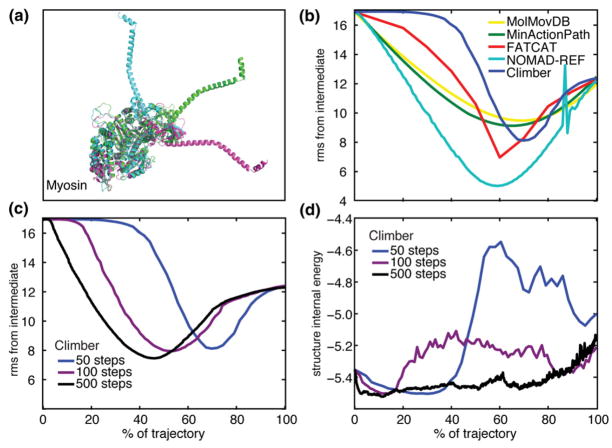
Data for the resulting trajectories of myosin are shown in Fig. 1. We used three different values of the user-defined number of steps N_cycle to run the Climber energy minimization interpolation (50, 100, and 500). The resulting trajectories are different both in the intermediate structures generated and in the internal energy of the intermediate structures. Returning to the mountain climber analogy, taking smaller steps to reach the adjacent valley, the climber is better able to find the easier path around the mountain.

Fig. 1.

(a) The three crystallographic structures of scallop myosin II. (b) The C^α rmsd (in angstroms) of the interpolated myosin structures from the crystallographic intermediate structure is shown for MolMovDB (yellow), MinActionPath (green), FATCAT (red), NOMAD-Ref (cyan), and Climber with N_cycle = 50 (blue). For clarity, the controls are not shown because they never come closer to the intermediate compared to the endpoints. (c) The C^α rmsd from the crystallographic intermediate using N_cycle =50 (blue), 100 (violet), and 500 (black) as input to the Climber morphing method. (d) The internal energy of the intermediate structures using N_cycle =50, 100, and 500 in the Climber method. A longer interpolation with a smaller desired cRMS change per step allows Climber to find the low-energy pathway. An increase in the energy at the end of the morph is due to the difficulty of repacking the side chains into the compact final structure.

We also generated trajectories using a variable number of steps on the other online servers (not shown). For MinActionPath, FATCAT, and Mol-MovDB, the trajectories do not depend on the number of steps. The trajectories generated by NOMAD-Ref with 50 steps and with 500 steps were unfeasible, with structures that “exploded”.

The improvement of the calculated trajectory in predicting the crystallographic intermediate relative to the endpoints was as follows (in ascending order): MolMovDB, 21%; MinActionPath, 24%; Climber, 32%, 34%, and 38% with N_cycle =50, 100, and 500 steps, respectively; FATCAT, 42%; and NOMAD-Ref, 58%. All these were markedly better than both control trajectories, which never came closer to the intermediate crystal structure compared to the endpoints.

Ribonuclease III

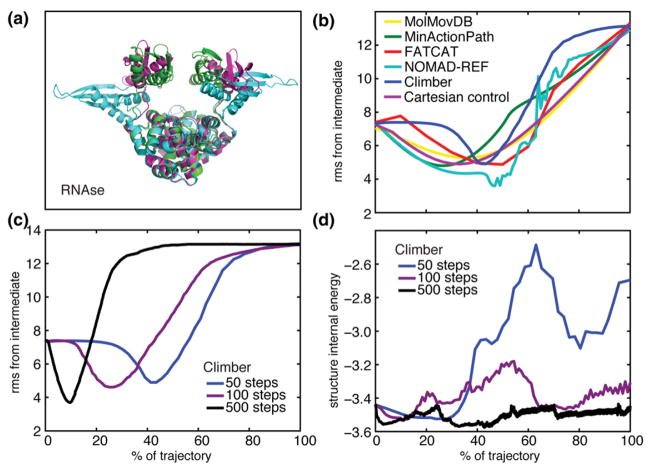
RNase III affects gene expression in two distinct catalytic pathways: through cleavage of double-stranded RNA (dsRNA) or through binding, but not cleaving, dsRNA. The protein is a homodimer, each polypeptide consisting of two domains separated by a flexible linker. The relative orientations of the two domains are changed dramatically from the catalytic (dsRNA cleaving) form to the non-catalytic (dsRNA binding) form. The three crystal structures represent intermediate conformations,²⁹ leading to the two functional forms of RNase III. The rmsd values are 7.26 Å from the initial to the intermediate state, 13.15 Å from the intermediate to the final state, and 17.47 Å from the initial to the final state.

Nonlinear motion is the only way to come closer to the intermediate structure compared to the Cartesian control trajectory (Fig. 2). Specifically, Climber can achieve an improvement of 48% over the endpoints but only when running a very long trajectory with N_cycle =500, and NOMAD-Ref achieves an improvement of 50%, although the trajectory is not smooth, and rerunning under different parameters did not produce a smooth trajectory. All other methods reached an improvement of about 30%, equal to the Cartesian control.

Fig. 2.

(a) The three crystallographic structures of RNase III. (b) The C^α rmsd (in angstroms) of the interpolated structures from the crystallographic intermediate structure; colors are as in Fig. 1. (c) The C^α rmsd from the crystallographic intermediate using N_cycle =50 (blue), 100 (violet), and 500 (black) as input to the Climber method. (d) The internal energy of the intermediate structures using N_cycle =50, 100, and 500 in the Climber method.

Skeletal muscle Ca²⁺-ATPase

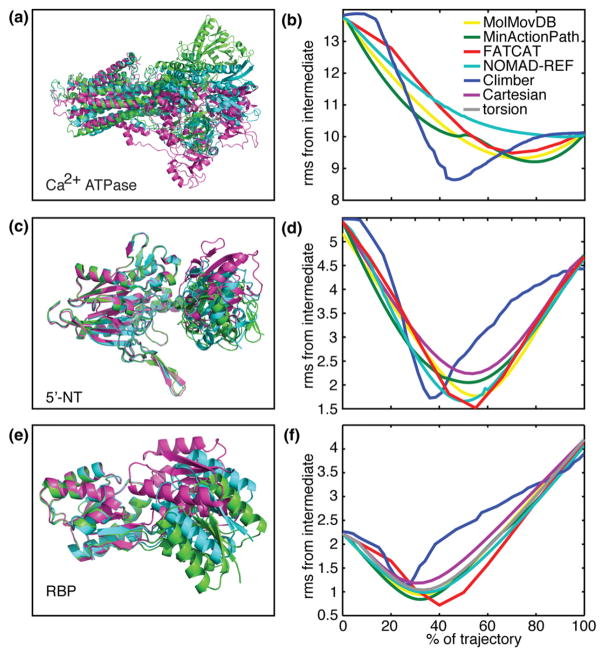
In skeletal muscle, calcium ions are pumped against a concentration gradient by a Ca²⁺-ATPase pump, which couples the hydrolysis of ATP to the translocation of calcium ions across the membrane of the sarcoplasmic reticulum (SR). The enzyme undergoes a large conformational change including the translation and rotation of three domains and a rearrangement within one of those domains.^30–32 Along with the complicated conformational change, the protein itself is also the largest in our test set with 994 residues, making this a very difficult problem. The Ca²⁺-ATPase cycle can be described as follows: The pump exists in two distinct conformations, E1 and E2. In the E1 conformation, the pump is empty and exposes two high-affinity sites for Ca²⁺ binding to the cytoplasm of the SR. Initially, two Ca²⁺ ions are bound (E1-2Ca²⁺ conformation) and ATP is bound (E1-2Ca²⁺-ATP conformation) in the cytoplasm. ATP is then hydrolyzed, driving the calcium transport across the SR membrane (E2-2Ca²⁺ conformation) and releasing two Ca²⁺ ions into the lumen of the SR (E2 empty conformation). We generate interpolations from the E1-2Ca²⁺ state to the E2 empty state. As an intermediate crystallographic state, we have chosen the E1-2Ca²⁺-ATP structure (the protein in the crystal structure is bound to AMPPCP, an ATP analog). The rmsd of the initial (E1-2Ca²⁺) state to the final (E2 empty) state is 14 Å, and the rmsd of the intermediate (E1-2Ca²⁺-ATP) is 13.75 and 10 Å, respectively. In the conformational change, the three widely separated cytoplasmic domains hinge and rotate to come together, and there is a change in the internal structure of one of those domains. The transmembrane helices undergo a large rearrangement. Obviously, this is a tremendously complicated series of conformational changes that involve binding and unbinding, ATP hydrolysis, and translocation events.

In the case of this complicated motion, none of the trajectories came very close to the intermediate structure; however, Climber was the most successful, with an improvement of 11.6%, 14%, and 16% over the endpoints using N_cycle =50, 100, and 500, respectively. The internal and Cartesian control showed no improvement. The improvement from the other methods was 1%, 6.1%, 7.7%, and 8.8% for NOMAD-Ref, FATCAT, MolMovDB, and MinAction-Path, respectively (Fig. 3a and b).

Fig. 3.

(a) The three crystallographic structures of Ca²⁺-ATPase and (b) the C^α rmsd (in angstroms) of the interpolated Ca²⁺-ATPase structures from the crystallographic intermediate structure. The same is shown for (c and d) 5′-NT and (e and f) RBP. Colors are as in Fig. 1. For clarity, the Cartesian control (purple) and internal control (gray) are not shown when they do not come closer to the intermediate compared to the endpoints.

5′-Nucleotidase

The 5′-nucleotidase (5′-NT) protein is a nucleotidase that can hydrolyze mono-, di-, and trinucleotides, as well as nucleotide sugars and bis(5′-nucleosidyl) polyphosphates. It undergoes a large 96° domain rotation, with an intermediate structure at 43.2° rotation. The protein is large with 525 residues, and the conformational changes are also large at 5.4 Å from the initial to the intermediate structure and 4.7 Å from the intermediate to the final structure (9.3 Å total rmsd from the initial to final structure). In this case, the intermediate structure is indeed a conformation that the protein passes through from the initial to the final state, which has been captured by an engineered disulfide bridge.³³ All methods are able to predict the intermediate structure of this hinging motion despite the relatively large size of the protein (Fig. 3c and d). In fact, the rigid-body motion allowed by FATCAT, which identifies just one hinge point for 5′-NT, predicts the intermediate most accurately (improvement of 68% over the endpoints), while the relatively complicated calculation performed by MinAction-Path actually hurts its performance (58% improvement). The other methods all perform almost equally (62–64% improvement), and even a completely naïve Cartesian interpolation predicts the intermediate to 2.6 Å rmsd (48% improvement).

Ribose-binding protein

The ribose-binding protein (RBP) molecule binds its ligand with a hinge-bending motion of its two domains. Crystal structures exist, showing a static pathway of this opening/closing motion with structures opened by 43°, 50°, and 64° with respect to the ligand-bound protein.^34,35 The rmsd values are 2.22 Å from the initial to the intermediate state, 4.20 Å from the intermediate to the final state, and 6.19 Å from the initial to the final state. All intermediates are hypothesized to exist at equilibrium in solution, and the addition of ribose changes the distribution at equilibrium. This protein is in some ways the “easiest” conformational change in our set. It has only 271 residues, the rmsd of the conformations is small, and the motion is a simple hinging. The improvement in predicting the intermediate over the endpoints is therefore high, in ascending order: 47%, 48%, 53%, 56%, 58%, 62%, and 68% for the Cartesian control, Climber, the torsion angle control, NOMAD-Ref, MolMovDB, MinActionPath, and FAT-CAT, respectively (Fig. 3e and f). Interestingly, for this simple hinging motion, the nonlinearity and flexibility allowed by Climber was detrimental, performing more poorly than the internal coordinate control. The best result was obtained by FATCAT.

Comparing trajectories

Are trajectories generated by different interpolation methods similar? Are there some sections of the pathway, particularly at the transition state, that are similar?

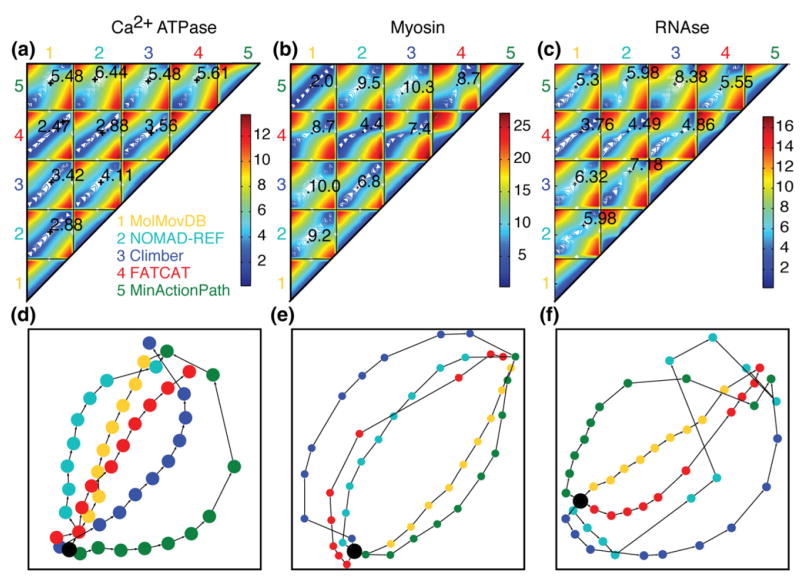
To explore this, we looked more closely at the proteins myosin, RNase III, and Ca²⁺-ATPase. They are large proteins that undergo a large conformational change, which would be difficult to access through MD simulation. Coarse-graining would therefore be a very useful tool for studying the dynamics of these proteins. Figure 4 presents different ways to visualize and compare the coarse-grained trajectories. The top panel shows a contour plot of the between-structure rmsd along the trajectories generated for five methods (MolMovDB, NOMAD-Ref, Climber, FATCAT, and MinActionPath). To generate the contour plot, we measured the rmsd of 10 evenly spaced structures from each trajectory to all other structures. The bottom panel contains the same information but shows a two-dimensional representation of the five interpolated trajectories. The graph has been energy-minimized, and the input distances between nodes are the rmsd values.

Fig. 4.

A comparison of interpolated trajectories. (a) Ca²⁺-ATPase, (b) myosin, and (c) RNase III trajectories, showing a contour plot of the rmsd between the trajectories generated by each of the five interpolation servers: 1, MolMovDB; 2, NOMAD-Ref; 3, Climber; 4, FATCAT; 5, MinActionPath. The value indicated numerically on each subplot is the rmsd between the intermediate structures in each trajectory that are closest to the crystallographic intermediate structure (their position along the two trajectories is marked by “+”). (d) Ca²⁺-ATPase, (e) myosin, and (f) RNase III, showing a two-dimensional representation of the interpolated trajectories. Ten structures were selected at evenly spaced intervals along each trajectory. The graph is energy-minimized, produced by Graphviz, and takes into account all rmsd between structures. Trajectories are colored as follows: Climber, blue; MolMovDB, yellow; MinActionPath, green; NOMAD-Ref, cyan; and FATCAT, red. The starting structure is marked as a black circle.

Interestingly, some trajectories appear to be taking similar paths. The middle panels depict the myosin trajectories. MinActionPath and MolMovDB follow similar trajectories, diverging by only 2 Å at the structure closest to the crystallographic intermediate, indicating that the MolMovDB finds a path through the valley that minimizes the action potential as defined by MinActionPath. The use of completely distinct algorithms to find the intermediate structures indicates that the trajectories may be following a common valley in the energy landscape of the protein. However, both are not very successful at finding the actual intermediate structure—indicating that finding the same valley in high-dimensional space does not guarantee finding the lowest-energy valley. FATCAT and NOMAD-Ref also find pathways that are relatively close, diverging by 4.4 Å at the structure closest to the crystallographic intermediate. Climber follows a completely distinct trajectory in this case.

Ca²⁺-ATPase trajectories shown in the left panel diverge slightly more considering that the endpoints are closer. However, it is still clear that the trajectories may be following similar pathways, except for MinActionPath, which is far from all the others. RNase III in the right panel shows five distinct trajectories evenly spaced from each other. The trajectories do not come together except at the endpoints. In all three examples, FATCAT takes a middle path between the other trajectories, suggesting that a rigid-body rotation is a good first approximation of the other pathways.

How “protein-like” are the structures generated by the interpolation servers? After rebuilding the backbone where only C^α atoms are returned, we use VADAR (Volume, Area, Dihedral Angle Reporter),³⁴ an online server for analyzing protein structures, to assess the feasibility of the calculated intermediate. In general, interpolations produce reasonable structures, with an amount of secondary structure that is similar to the crystallographic intermediate, and with similar (φ, ψ) distributions in the Ramachandran plots.

Discussion

We have presented a test set of proteins each with at least three crystallographically solved structures at high resolution that are on-pathway conformations. The crystal structures used are distinct with at least 2 Å rmsd between them. We believe that this set provides an objective, biologically applicable test of interpolation and other methods for coarse-graining protein dynamics. We quantify how biologically relevant a coarse-grained trajectory is by measuring how close it can come to the intermediate crystallographic state without prior knowledge of that state. We have tested four online servers, our novel morphing method, and two naïve interpolations (in Cartesian and internal coordinates) with our test set.

The high computational burden of atomically resolved MD simulation limits its usefulness in studying large protein systems, particularly over the biologically relevant timescales of milliseconds to seconds. Coarse-grained dynamics are an attractive alternative, and many online servers exist, which make use of very different coarse-grained dynamics, interpolation, and path minimization algorithms. As well as providing biological insight into protein dynamics when two crystal structures are already known, the construction of high-fidelity coarse-grained pathways could be useful for structure prediction of new conformations using lower-resolution experimental data, such as fluorescence resonance energy transfer measurement of interresidue distances or electron microscopy. In addition, it could be used for molecular replacement calculations when solving the crystal structures of new intermediates.³⁶ We found that no coarse-grained method succeeded in correctly predicting the crystallographic intermediate structure. However, several of the methods did move in the direction of the intermediate.

The most successful strategy when the motion is a simple hinging is the use of rigid-body motion, combined with a sophisticated method to find the hinging points (FATCAT). For three of the five proteins, one hinge point was sufficient to describe the protein motion (myosin, RBP, and 5′-NT), and for Ca²⁺-ATPase and RNase III, three hinge points were identified.

The use of normal modes in NOMAD-Ref to predict the intermediate structure was very successful in the case of myosin, where the first 8 normal modes can predict the 17-Å conformational change between the initial and the intermediate state to within 7.6 Å and 100 modes to 4.4 Å (unpublished calculation). In a larger set of test structures, where the protein set included off-pathway structures, NOMAD-Ref was successful in moving in the direction of the off-pathway structure, in many instances more than the other methods (unpublished results). This implies that information about all the possible conformations of the protein and shape of the energy landscape is encoded in the normal modes, which makes this a powerful tool.

Interresidue distances as the restrained quantities (Climber and NOMAD-Ref) were useful particularly for the larger conformational changes in the set (myosin, RNase III and Ca²⁺-ATPase). In cases where the motion was not a straightforward hinging motion involving a small conformational change, the nonlinearity allowed by these methods was required.

The interpolations are calculated using distinct algorithms; however, some interpolations share the same directions of motion and similar transition structures (although this is no guarantee that those motions are the biologically relevant motions of the protein). It is interesting that in the cases we investigated, FATCAT appears to take the “middle way” between the trajectories and is the most representative, indicating that rigid-body motion is a good first approximation of other coarse-grained methods.

We would like to further develop the use of normal modes in interpolation by the use of normal modes in internal coordinates in the implementation of the algorithm of Kim et al.^3,4 This will overcome the problem that, in some cases, combining Cartesian normal modes creates structures that are completely infeasible. We feel that the Climber algorithm is particularly relevant for predicting large nonlinear motions and could be further developed in combination with the interresidue distance interpolations.

Methods

Trajectory generation

We tested seven different coarse-grained methods: the implementation of our new morphing algorithm Climber and four online servers (MolMovDB,^21,22 FATCAT,²³ NOMAD-Ref,²⁴ and MinActionPath²⁵), as well as two controls using LSQMAN³⁷ to generate a simple linear interpolation in Cartesian and internal coordinates. We generated 30 intermediate structures using MolMovDB (this is the maximum allowed); 100 intermediate structures using NOMAD-Ref, LSQMAN, and MinActionPath; and 10 intermediate structures using FATCAT (the maximum allowed). We set N_cycle =50 for Climber unless otherwise indicated. Where a cutoff distance needed to be supplied, we used the cutoff distance of 10 Å for 5′-NTand RBP and a cutoff of 15 Å for RNase III, myosin, and Ca²⁺-ATPase.

The Climber morphing scheme

We use a subset of interatomic distances as the coordinate for interpolation, using the following algorithm:

1. For each conformation, create the set of atom pairs (i,j) that define the restrained distance. For pairs of C^α atoms, i and j must be more than 10 Å apart in both the initial and target structures. For the side-chain atoms, i and j must be less than 10 Å apart in both the initial and target structures. Focusing on distant C^α atom pairs will drive large conformational changes; focusing on close side-chain pairs will, at the same time, provide good local packing.

2. At each step of the morphing, the distance restraint energy is calculated as E_restraint = K_springG [Σ_i Σ_j F(d_ij)], where the function F(d)=(d_ij²-D_ij²)²/(2(d_ij²+D_ij²))

   and the function G[ ] is defined below. The distances d_ij =|r_i − r_j| and D_ij =|r_i − r_j| are between atoms i and j in the moving and target structures, respectively. Note that as we can write (d_ij²-D_ij²)²=(d_ij-D_ij)²(d_ij+D_ij)² and (d_ij+D_ij)² =d_ij²+2d_ijDij+D_ij²≈2(d_ij²+D_ij²) for D_ij ≈ d_ij, we have F(d) ≈ (d_ij − D_ij)². If we define $t=\sqrt{{\sum }_i{\sum }_{j}F(d_{ij})/n}$, which is approxi mately equal to $\sqrt{{\sum }_i{\sum }_j{(d_{ij}-D_{ij})}^2/n}$, then t is in turn approximately equal to dRMS. The function G[t] relates dRMS to the restraint energy as follows: E_restraint = K_spring G[t]= K_spring (t²/(t_L + t)). For t>t_L, E_restraint varies linearly with dRMS, whereas for small t, it varies quadratically. This means that the restraint energy is linearly proportional to the distance deviation between the current and target structures (dRMS).

   3. Minimize the conformation while adding the restraint energy to the internal potential energy function. Specifically, if the internal energy is E₀, then minimize E=E₀ + E_restraint. The internal energy function used is the ENCAD potential energy function.

   4. Measure the cRMS between the current and target structure at the end of the minimization (the structures are first aligned), and if the cRMS between the current and target structures has not decreased by the desired amount, increase the spring constant, K_spring, in the next step. If the cRMS change is sufficient, then decrease the K_spring values. Thus, the spring constant is self-adjusting to ensure that at each step, the conformation moves to the target structure at an approximately constant rate. We initialize the value of K_spring at 5 kcal mol⁻¹ Å⁻¹, a value too small to move the protein structure. We then slowly increase K_spring until the cRMS value begins to drop. Depending on the size of the protein and the distance to the target structure, this requires an initial increase in K_spring by approximately 20- to 50-fold. Note that the target distances remain the same throughout the morphing path. All that changes is the value of K_spring that is adjusted iteratively to cause the cRMS value to drop a constant amount per cycle (specifically, we set ΔcRMS to be 1.5 × cRMS_initial/N_cycle), which is designed to ensure that we can get to the target structure with cRMS less than or equal to some cutoff (0.5 Å) in approximately N_cycle steps.

Repeat steps 1–4, for the user-defined number of cycles (N_cycle). If the cRMS value between current and target structure falls below a cutoff value, the procedure terminates. Note that the actual number of intermediate steps can differ from N_cycle as the value of K_spring may be needed to be increased in several cycles until it is large enough to cause the desired decrease in cRMS. This procedure has a number of virtues all related to having the least possible influence on the path followed during the morphing: (a) the only set of distances are those of the final target structure; (b) the energy function depends linearly on the distance deviation (dRMS) so that there will be no tendency to satisfy large deviations more than small ones; (c) the only thing changed during the morphing is the value of the spring force constant and this is done using the change in the cRMS that is not directly involved in the restraint energy; (d) the distances selected to deform the overall chain path are all between distant pairs of C^α atoms.

Evaluating the coarse-grained dynamics methods

To evaluate the coarse-grained trajectories generated using our objective biological test, we calculated the C^α rmsd between the calculated interpolation intermediates and the crystallographic intermediate. We defined an improvement score for each method as

$$\frac{min[\text{rmsd}(\text{AB}),\text{rmsd}(\text{CB})]-min[\text{rmsd}(\text{iB})]}{min[\text{rmsd}(\text{AB}),\text{rmsd}(\text{CB})]}\times 100$$

where A, B, and C are the initial, intermediate, and final crystal structures, respectively; rmsd(AB) is the rmsd of the initial structure to the crystallographic intermediate; rmsd (CB) is the rmsd of the final structure to the crystallographic intermediate; and rmsd(iB) are the rmsd values of the calculated intermediates to the crystallographic intermediate. Thus, this is a measure of how close the interpolation comes to the crystallographic intermediate, as a fraction of how close the endpoints are to the crystallographic intermediate. We feel that this is more informative as a measure than rmsd as it does take into account the starting points. A higher improvement score indicates greater success at predicting the crystallographic intermediate structure. All rmsd values quoted in this work are C^α rmsd.

Comparing interpolation methods

To compare the trajectories created by the different coarse-grained methods, we calculated the rmsd between the calculated structures in one method and those calculated by all the methods. In this case, if we had M coarse-grained methods with N calculated intermediate structures, this would give us an upper triangular matrix of N×M rmsd values and a value of zero along the diagonal. We expect the rmsd to be low at the corners (the starting points and endpoints) because all trajectories start and end at the same point. However, if we observe other regions of low rmsd in the middle, this is a sign that two trajectories come closer together to visit the same region of structure space. In addition, we create a two-dimensional visualization of the trajectories using the multidimensional scaling package Graphviz³⁸ to account for all rmsd values between all structures. We chose N=10 structures evenly spaced along each trajectory.

Abbreviations

MD

molecular dynamics

cRMS

coordinate root-mean-square deviation

dsRNA

double-stranded RNA

SR

sarcoplasmic reticulum

5′-NT

5′-nucleotidase

RBP

ribose-binding protein