Abstract
We report the largest and most comprehensive comparison of protein structural alignment methods. Specifically, we evaluate six publicly available structure alignment programs: SSAP, STRUCTAL, DALI, LSQMAN, CE and SSM by aligning all 8,581,970 protein structure pairs in a test set of 2930 protein domains specially selected from CATH v.2.4 to ensure sequence diversity.
We consider an alignment good if it matches many residues, and the two substructures are geometrically similar. Even with this definition, evaluating structural alignment methods is not straightforward. At first, we compared the rates of true and false positives using receiver operating characteristic (ROC) curves with the CATH classification taken as a gold standard. This proved unsatisfactory in that the quality of the alignments is not taken into account: sometimes a method that finds less good alignments scores better than a method that finds better alignments. We correct this intrinsic limitation by using four different geometric match measures (SI, MI, SAS, and GSAS) to evaluate the quality of each structural alignment. With this improved analysis we show that there is a wide variation in the performance of different methods; the main reason for this is that it can be difficult to find a good structural alignment between two proteins even when such an alignment exists.
We find that STRUCTAL and SSM perform best, followed by LSQMAN and CE. Our focus on the intrinsic quality of each alignment allows us to propose a new method, called “Best-of-All” that combines the best results of all methods. Many commonly used methods miss 10–50% of the good Best-of-All alignments.
By putting existing structural alignments into proper perspective, our study allows better comparison of protein structures. By highlighting limitations of existing methods, it will spur the further development of better structural alignment methods. This will have significant biological implications now that structural comparison has come to play a central role in the analysis of experimental work on protein structure, protein function and protein evolution.
Keywords: comparison of structural alignment, protein structure alignment, protein structure comparison, geometric measures, ROC curves
Introduction
The problem of aligning, or establishing a correspondence between, residues of two protein structures is fundamental in computational structural biology. In 1960, Perutz et al.1 showed, using structural alignment, that myoglobin and hemoglobin have similar structures even though their sequences differ. Functionally these two proteins are similar and are involved with the storage and transport of oxygen, respectively. Since then, researchers have continued to look for structural similarity in hope of detecting shared functionality. Because structural similarity is conserved more than sequence similarity, it can be used as a more powerful “telescope” to look back to earlier evolutionary history.
Structural alignment is carried out between two known structures, and is typically based on the Euclidean distance between corresponding residues, instead of the distance between amino acid “types” used in sequence alignment. Structural alignment methods are useful for organizing and classifying known structures.2,3 Furthermore, for a newly determined structure, fast methods that correctly identify known structures that align with it are indispensable. Lastly, structural alignment methods provide the gold standard for sequence alignment.4,5 Consequently, many methods for protein structure alignment have been developed, including those described by Taylor & Orengo,6 Subbiah et al.,7 Holm & Sander,8 Holm & Park,9 Kleywegt,10 Shindyalov & Bourne,11 Kedem et al.,12 Yang & Honig,13 Krissinel & Henrick14,44 and those cited in a review by Koehl.15
Many studies compare sequence alignment methods.5,16,17 Given a separable scoring function, the optimal sequence alignment can always be found using dynamic programming.18 Unfortunately, it is not easy to find the parameters of a scoring function that best captures the similarity between amino acid residues. This has led to many studies of substitution matrices that produce biologically meaningful sequence alignments.19,20 A common task of sequence alignment techniques is to scan existing databases of protein sequences in hope of detecting homologs of a newly found protein sequence. The exponential growth in the size of these sequence databases has led to the development of popular programs, such as BLAST21 or FASTA22 that employ faster heuristics yet find sub-optimal alignments. A large body of literature compares the performances of these heuristic sequence alignment methods. To address the underlying difficulty in identifying the best of many sub-optimal sequence alignments, many of these studies use structure similarity as a gold standard. For example, Brenner et al.17 use the hierarchical protein classification SCOP,23 which is based on structural and sequence similarity, as their gold standard for comparing sequence alignment programs. Others5,24,25 also evaluate sequence alignment programs using structural alignment.
When aligning two structures, the situation is reversed: while it is harder to find the optimal alignment, judging which is best among several alignments of a pair of structures is easy. Finding the optimal structural alignment is harder because the rotation and translation of one of the two structures with respect to the other must be found in addition to the alignment itself. Although an approximate optimal solution can be computed,26 it is expensive and all methods available to-date are heuristic. Similarity in structural alignment is geometric and captured by the cRMS deviation of the aligned atoms (generally the CA atoms). Other properties of structural alignments that are likely to be significant are the number of matched residues, and the number and length of alignment gaps. Clearly, better alignments match more residues, have fewer gaps and are more similar (of lower cRMS). Since these alignment properties are not independent (shortening the alignment or introducing many gaps can decrease the cRMS deviation), researchers have devised alignment scores that attempt to balance these values. In this study, we use SAS,7 SI,27 MI27 and GSAS, which is our variant of SAS that penalizes gaps. Deciding which alignment is the most geometrically similar is an easier question than evaluating if an alignment is biologically significant.28,29
Previous evaluations of structural alignment methods use the CATH2 or SCOP23 classifications as a gold standard, and verify that pairs of structures that are classified the same are similar, whereas all other structure pairs are not. Novotny et al.30 assessed the performance of structural alignment methods, as part of their evaluation of structural alignment (or fold comparison) servers. Their study uses CATH as the gold standard, and queries the servers’ databases using approximately 70 query structures. Sierk & Pearson29 compare receiver operating characteristic (ROC) curves31 to evaluate the success of different methods in detecting domains of the same homology or topology, as defined by CATH; they test one query in each of 86 families. Using SCOP as the standard, Leplae & Hubbard32 built a web-server that evaluates structural alignment methods by comparing their ROC curves. Descriptions of structural alignment methods sometimes include evaluations of the methods. For example, Gerstein & Levitt33 evaluated STRUCTAL using SCOP; Shindyalov & Bourne3 compared CE to DALI; Shapiro & Brutlag34 evaluated FoldMiner, VAST and CE by comparing their ROC curves, using SCOP.
In this study we conduct a large-scale computer experiment to compare protein structural alignment methods. We consider a set of 2930 sequence diverse domains from CATH v.2.42 and align all pairs of structures. The methods we test are (listed chronologically): (1) SSAP,6 (2) STRUCTAL,7,33 (3) DALI,8,9 (4) LSQMAN,10 (5) CE,11 and (6) SSM.14 Each alignment has a significance (or native) score assigned by the program that found it and four geometric match measures (SAS, SI, MI, GSAS). We first evaluate the above methods by comparing the ROC curves based on their native score, and the four geometric match measures. We take the view that structural alignment methods are, in effect, optimizers of the geometric match measures, and create a better optimizer, the “Best-of-All” method, which takes the best alignment found by all methods. Using this approach, we evaluate the performance of the programs by directly comparing the geometric match measures of their alignments. We also elaborate on problems in assuming the lack of structural similarity between structures that are classified differently by the gold standard. We end by taking another look at hard cases, i.e. ones where only one of the methods succeeds, and analyzing the behavior of the different methods on the four CATH classes (“Mainly α”, “Mainly β”, “Mixed α/β”, “Few Secondary Structure”). The total computer time used in this experiment is over 20,000 hours on a 2.8 GHz processor.
Our main conclusion is that structural alignment methods should be evaluated by comparing the alignments they find. We show that ROC curves are of limited value and that their ranking of the methods is not consistent with the ranking implied by the quality of the alignments the methods find. We also highlight the problems inherent in comparing similarity of pairs of objects based on a hierarchical classification (namely a tree) of those objects: a classification attempts to group objects that share some property but does not guarantee that pairs of objects in different classes are indeed different. We find that the objective geometric match measures provide more relevant information than the native scores given by each particular method. Of the different measures we use, GSAS and SAS perform best in separating good alignments from less good ones. We consider the set of the pairs that are in the same CATH fold class as well as the set of all pairs and find that certain structural alignment methods consistently outperform other methods. More specifically we find that the Best-of-All method (i.e. a combination of all six methods under study) finds the best results, followed by STRUCTAL and SSM. Finally, we identify a set of structurally similar pairs that are found only by a single method, providing a useful test set that will allow structural alignment methods to be improved.
Results
We compare six structural alignment methods by aligning all 4,290,985 pairs in a set of 2930 sequence-diverse CATH v.2.42 domains (2930×2929/2 pairs as (i,j) and (j,i) are treated once). These methods are implemented in the following programs: (1) SSAP,6 (2) STRUCTAL,7,33 (3) DALI using DaliLite (v.1.8),8,9 (4) LSQMAN,10 (5) CE,11 and (6) SSM.14 The set of structures†, includes 769 fold classes. The programs output the alignment native score, the number of residues matched, and the cRMS deviation. We count the number of gaps in both structures by inspecting the alignment, which is available for all programs except for the standalone version of SSM. Based on these data, we calculate the geometric match measures SI, MI, and SAS for all methods and calculate GSAS for all methods except SSM. Using the geometric match measures we create a seventh method denoted Best-of-All, which returns the best alignment found by all the other methods.
Comparison of methods using ROC curves
We first evaluate the methods (i.e. the six individual programs mentioned above, and the Best-of-All method) by comparing their ROC curves.31 CATH serves as the gold standard: a pair of structures is defined as “positive” (or similar) if both structures have the same CAT classification and “negative” (or not similar) otherwise. For varying thresholds, all pairs below the threshold are assumed positive, and all above it negative: the pairs that agree with the standard are called true positives (TP) while those that do not are false positives (FP). We sort the alignments either by their geometric match measures or by the native scores of the programs. A method that best agrees with the gold standard will have the uppermost curve, or equivalently, the one with the largest area under it. It can be argued that we are more concerned with comparing the agreement of the methods with CATH when the percentage of FPs is low. We do this by plotting the x-axis of the ROC curve in log scale, that is, log10 of fraction of FPs against the fraction of TPs.
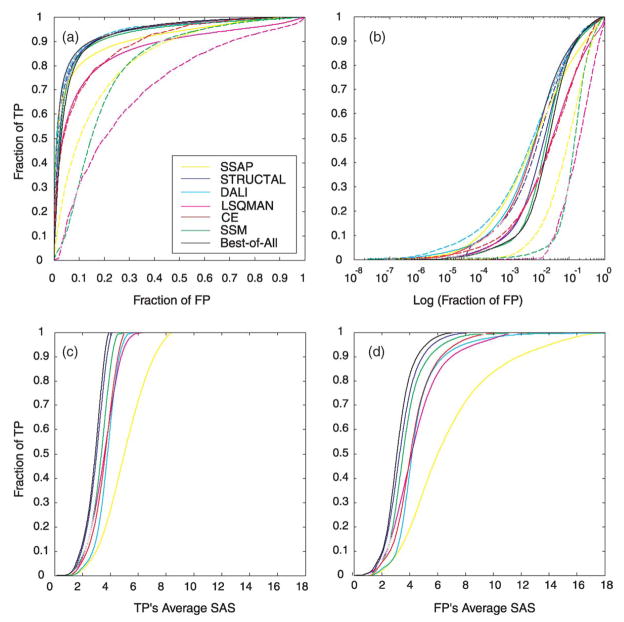
Figure 1(a) shows the ROC curves of all the methods; we sort the alignments either by their native score (broken lines) or by the SAS geometric match measure (continuous lines). Figure 1(b) shows the same ROC curves with log10 (fraction of FP) versus fraction of TPs. Table 1 lists values quantifying these ROC curves: the area under the curve and the number of TPs when the fraction of FPs is 1% (numbering 42,910).
Figure 1.
Receiver operating characteristic (ROC) curves for the structural alignment methods SSAP, STRUCTAL, DALI, LSQMAN, CE, and SSM. A true positive is assumed when the two aligned structures have the same Class/Architecture/Topology CATH classification. We sort all alignments and calculate the fraction of false positives (FP) and fraction of true positives (TP) with values lower than a particular threshold. As the threshold is increased to include less good alignments, we get pairs of FP and TP values that are plotted in the ROC curve. Here the alignments are sorted by their native scores, (those given by the programs and shown as broken lines) or by the geometric match measure SAS (continuous lines). In continuous black, we plot the ROC curve of the Best-of-All method, the best alignments (in terms of SAS) found by all methods. In (a) we plot the fractions of FP against the fractions of TP, and in (b), we plot log10 (fraction FP) against fractions of TP, to better see performance at low rates of false positives. In (c) and (d) we plot for every threshold the average SAS value of the TP and the FP alignments below that threshold. Methods that perform better in terms of their ROC curves climb to high TP values very quickly (i.e. at low FP values). We see that the performance of the methods depends on whether the alignments are sorted by the SAS geometric match measures or the native scores. Furthermore, some of the best methods as judged by the ROC curves (such as DALI and SSAP) do not produce the best alignments as indicated by the average TP SAS value; they seem to do well because they find even worse average FP SAS values.
Table 1.
Score from ROC curves and cumulative distributions distinguish structural alignment methods
| Score with methoda | |||||||
|---|---|---|---|---|---|---|---|
| MEASURE | SSAP | STRUCTAL | DALI | LSQMAN | CE | SSM | Best-of-All |
| ROC area (native score) | 0.83 | 0.94 | 0.94 | 0.70 | 0.89 | 0.80 | NAb |
| ROC area (SAS score) | 0.91 | 0.93 | 0.94 | 0.87 | 0.94 | 0.93 | 0.93 |
| ROC area (GSAS score) | 0.91 | 0.94 | 0.94 | 0.84 | 0.94 | – | 0.93 |
| ROC area (SI score) | 0.80 | 0.79 | 0.84 | 0.72 | 0.81 | 0.79 | 0.76 |
| ROC area (MI score) | 0.80 | 0.78 | 0.84 | 0.72 | 0.79 | 0.82 | 0.78 |
| %TP at 1% FP (native score) | 9 | 42 | 50 | 0.4 | 29 | 3 | NA |
| %TP at 1% FP (SAS score) | 48 | 32 | 47 | 29 | 46 | 25 | 22 |
| %TP at 1% FP (GSAS score) | 48 | 30 | 47 | 20 | 46 | – | 15 |
| %TP at 1% FP (SI score) | 16 | 2 | 16 | 4 | 9 | 0.8 | 1 |
| %TP at 1% FP (MI score) | 16 | 3 | 16 | 7 | 10 | 4 | 3 |
| % CAT–CAT at GSAS=5 Å | 19 | 68 | 37 | 29 | 50 | – | 74.0 |
| % CAT–CAT at SAS=5 Å | 25 | 80 | 62 | 54 | 61 | 73 | 85.7 |
| % CAT–CAT at SI=5 Å | 16 | 56 | 36 | 36 | 37 | 45 | 60.4 |
| % CAT–CAT at MI=0.8 | 26 | 62 | 44 | 28 | 50 | 53 | 65.5 |
| % All pairs at GSAS=5 Å | 0.6 | 5.6 | 1.5 | 2.6 | 2.4 | – | 8.5 |
| % All pairs at SAS=5 Å | 0.8 | 9.4 | 3.5 | 5.6 | 3.5 | 7.1 | 13.5 |
| % All pairs at SI=5 Å | 1.4 | 17.2 | 4.7 | 11.1 | 6.1 | 13.8 | 24.2 |
| % All pairs at MI=0.8 | 2.6 | 21.7 | 7.0 | 6.9 | 12.2 | 13.6 | 25.2 |
A high value is always better. The best scores for each measure are shown in bold, as are the scores for Best-of-All when they are the best.
There is no native score for the Best-of-All method.
When sorting the alignments by their SAS measure, the ROC curve analysis suggests that DALI, CE, STRUCTAL, and SSM are the strongest methods. When sorting the alignments by their native scores, the methods DALI and STRUCTAL are strongest. At low false positives rates (Figure 1(b)), DALI, CE, SSAP and STRUCTAL do well. It is somewhat surprising that the programs CE, SSM, LSQMAN and SSAP do much better when using the geometric measure than when using their own native score. DALI performs similarly when using the two measures, but the geometric score does better in the lower FP rates. STRUCTAL also performs similarly using these two measures, although the STRUCTAL native score, which was specifically designed to be better than the SAS measure,33 does increase the area under the ROC curve from 0.93 to 0.94. Clearly, a program can be successful in finding good alignments and less successful in evaluating them. Another surprising result is that the Best-of-All method does not perform better, in terms of its ROC curve, than the individual methods.
Figure 1(c) and (d) shows the plot of the average SAS measure of the TPs and the FPs below increasing thresholds against the fraction of TPs. This compares directly the quality of the alignments found by different methods in equally sized sets of pairs. Here, successful methods find alignments with lower SAS values, represented by curves that are shifted to the left. The average SAS of the TPs is lower than the average SAS of the FPs. As expected from a list sorted by increasing SAS values, this difference is small and subtle in the parts of the curve corresponding to a low TP fraction. The Best-of-All method finds the best alignments, followed by STRUCTAL and SSM. Surprisingly, the ranking of the structural alignment methods based on their average SAS values differs from that implied by their ROC curves. For example, DALI and CE have almost identical ROC curves ranking them similarly, yet their SAS curves show that CE finds consistently better alignments. Another example is SSAP that performs well by its ROC curve, while its average SAS curve suggests otherwise. This means that the best alignments found by SSAP, although generally not as good as those found by other methods, often correspond to proteins in the same CATH fold class. Clearly, a particular method can seem to be as, or more, successful than another method based on its ROC curve, while the actual alignments it finds are inferior.
We have also plotted the same figures when sorting the alignments by their SI, MI and GSAS measures (data not shown, but available online†). In general the relative performance of the methods is similar when judged by the average values of the four geometric match measures. When examining the curves of average values of SI, MI, and GSAS, we see that similarly to Figure 1(c) and (d) the implied ranking of the methods is different from that suggested by the methods’ ROC curves.
Comparing the methods directly using geometric match measures
We calculate the four geometric match measures (SI, MI, SAS, and GSAS) for all alignments found by all the methods. In all four measures, better alignments correspond to lower values. Using these data, we calculate the cumulative distributions of the geometric measures, over the set of 104,309 structure pairs, that have the same CAT classification (the CAT–CAT set) and over the set of all structure pairs (the full set). In both cases, we normalize to 100% the total number of pairs in the set.
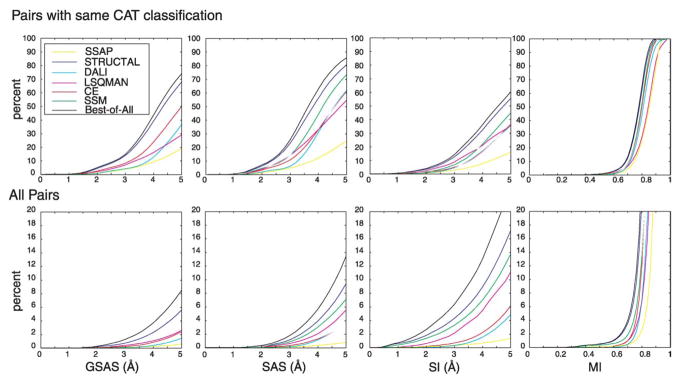
Figure 2 shows the cumulative distributions of the geometric match measures. Here, better performance corresponds to finding more alignments (greater values along the y-axis) with better geometric match measures (lower values along the x-axis). In the case of GSAS, SAS, and SI, we focus on good alignments: the cutoff value is 5 Å in all three cases. Even though all programs were given the same set of pairs, the maximum value on each curve varies, since there are many alignments of match measure greater than 5 Å that are not shown. For each method, Table 1 lists, for both the CAT–CAT set and full set, the number of pairs for which good alignments are found (expressed as a percentage of pairs in the set).
Figure 2.
Comparison of the quality of the alignments produced by the methods SSAP, STRUCTAL, DALI, LSQMAN, CE, and SSM, using four geometric match measures: GSAS, SAS, SI, and MI. For each geometric measure and for each method, we plot a cumulative distribution. This gives the number of alignments (expressed as a percentage of the total number of alignments in the set considered) that is found with a geometric match score better than the particular threshold plotted along the x-axis. A lower value of the geometric match measure is better in all cases. In the upper panels, we consider the set of 104,309 pairs that have the same Class/Architecture/Topology (CAT) classification; in the lower panels we consider all pairs (these number 4,290,985). Better performing methods find more alignments (greater values along the y-axis) with better scores (smaller values on x-axis). The MI measure is always between 0 and 1, whereas the other measures are unbounded. For GSAS, SAS, and SI, we use a cutoff value 5 Å, which allows us to focus on good matches. The Figure also shows the cumulative distribution of the Best-of-All method, a method that returns the best alignment found by any of the above methods. This method is clearly the best performer in all categories. Among the existing methods, for each of the geometric match measures, STRUCTAL is the best performer; the next best method is SSM.
We see that the Best-of-All method finds the greatest number of good alignments, both in the CAT–CAT set and the full set, for all four geometric measures; the second best performer is STRUCTAL in both sets and for all geometric measures; the third best performer is SSM (except when using GSAS). Among the programs compared, SSAP performs the worst. When using GSAS, a version of SAS that penalizes alignment gaps, the relative performance is flipped in two cases: CE versus DALI and CE versus LSQMAN. This implies that CE finds less fragmented alignments than those found by DALI and LSQMAN. We also see that LSQMAN finds more highly similar alignments, and less moderately similar alignments, than all other methods except STRUCTAL.
When using the similarity cutoff value 5 Å, even the best methods find good alignments for no more than 80% of the CAT–CAT pairs. At the same threshold level, there are good alignments for about 10% of all pairs, even though the CAT–CAT pairs account for only 2.5% of these pairs. This shows that there is a significant amount of structural similarity between structures in different fold classes. An alignment’s GSAS measure will generally be larger than its SAS measure because we reduce the denominator (Nmat) by the number of gaps; for this reason the percentage of pairs below the 5 Å threshold is smaller for GSAS than for SAS. Similarly, the relative size of the values of SI and SAS depends on how the typical length of the shorter structure relates to the value 100. We see that the percentage of pairs below the 5 Å threshold is greater for SI than SAS, implying that the typical length of the shorter structure is less than 100 (we estimate 70 residues). This means that SAS is generally larger than SI.
Analysis of the good alignments found by the Best-of-All method
Table 2 lists the proportional contribution of each of the methods to the Best-of-All method, when considering good alignments. In all cases, STRUCTAL is the leading contributor, contributing more than 50%. SSM is the second largest contributor, with more than 15%, followed by LSQMAN with over 7%. SSAP, DALI and CE contribute less to the combined effort; if one of the top contributors were to be omitted these methods could contribute more.
Table 2.
Contributions to Best-of-All method
| Total | SSAP | STRUCTAL | DALI | LSQMAN | CE | SSM | |
|---|---|---|---|---|---|---|---|
| GSAS≤5 Å | 275,547 (100%) | 832 (0.3%) | 189,871 (69%) | 5868 (2.1%) | 54,606 (20%) | 24,370 (8.8%) | – |
| SAS≤5 Å | 539,755 (100%) | 498 (0.09%) | 286,972 (53%) | 15,648 (2.9%) | 103,408 (19.2%) | 15,844 (2.9%) | 117,385 (21.8%) |
| SI≤5 Å | 978,531 (100%) | 3745 (0.4%) | 497,330 (51%) | 24,767 (2.5%) | 201,202 (21%) | 17,142 (1.8%) | 234,345 (24%) |
| MI≤0.8 | 880,503 (100%) | 4579 (0.5%) | 573,542 (65%) | 31,402 (3.6%) | 63,088 (7.2%) | 72,974 (8.3%) | 134,918 (15.3%) |
The absolute number of alignments contributed by each method is listed and the percentage of alignments is given in parentheses. The largest contributor is shown in bold.
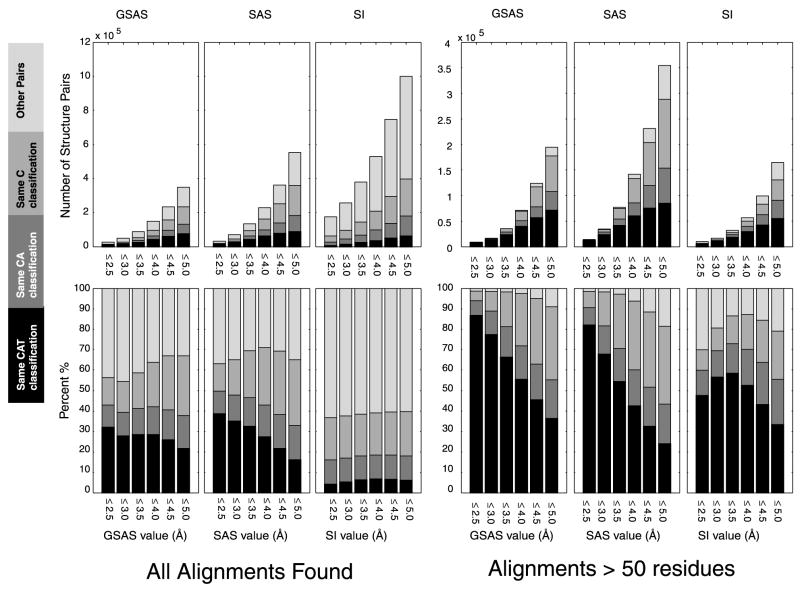
For each pair of structures we find the best structural alignment, as determined by its GSAS, SAS or SI value. This set of structure pairs is partitioned into four sets: (1) pairs that agree on the three CATH classifiers: Classification/Architecture/Topology (the CAT set), (2) pairs that agree only on the first two classifiers (the CA set), (3) pairs that agree only on the first classifier (the C set) and (4) others. In Figure 3 we plot, for several threshold values of the geometric similarity measures (less than 2.5 Å, 3 Å, …, 5 Å), the number of alignments found at that level of similarity (upper panel) as well as the percentage of each of the four sets found at that level (lower panel). The rightmost panels show the same analysis for the subset of long alignments (more than 50 residues matched). The threshold values we consider describe structural alignments that vary from highly similar (less than 2.5 Å) to moderately similar (less than 5 Å).
Figure 3.
The composition of the set of structure pairs that have good alignments demonstrates the significant amount of structural similarity across CATH fold classes. These Best-of-All alignments are divided into four categories depending on the similarity of the CATH classification of the two aligned structures. These four categories (color-coded from black to light gray) are: (1) both structures have the same C, A and T classifiers (CAT set), (2) both structures have only the same C and A classifiers (CA set), (3) both structures have only the same C classifier (C set), and (4) both structures have different C classifiers (other pair set). We consider all good alignments, i.e. of low GSAS, SAS or SI value (left hand six panels), as well as the subset of good alignments with more than 50 matched residues (right hand six panels). The upper panels give the number of good alignments and the lower panels plot the percentage of alignments found at that level of similarity for each category. All methods find many examples of highly similar structures that CATH classifies differently.
Figure 3 shows that there are many cases of very similar structure pairs that are in different CAT classes; in some cases they are even in different C classes. For example, with a GSAS threshold of 5 Å, less than 40% of the pairs of proteins found are in the same CATclass, even when considering only the long alignments (more than 50 residues matched). Note, that at this level of similarity, only 80% of all the pairs of proteins with the same CAT classification are detected by any of the programs (see Figure 2). For both GSAS and SAS, the fraction of the alignments for which both structures are in the same CAT class is biggest for the highly similar pairs (less than 2.5 Å), and lowest for the moderately similar pairs (less than 5 Å). This expected behavior is even more pronounced when we consider only long alignments. Figure 3 also shows that the number of good alignments is greatly reduced (by more than a factor of 2) when restricting our attention to long alignments.
Challenging alignments
For each protein structure alignment method Table 3 lists the total number of pairs of proteins that only the particular method was able to identify as structurally similar. We include only those pairs of structures for which one of the methods found a good alignment (SAS less than 4 Å and more than 35 residues matched), and all other programs found only bad alignments (SAS greater than 6 Å for any length of match). These alignments are by definition challenging for all programs but the successful one. We also present in Table 3 a breakdown of these cases according to the C classification of the structures aligned. The complete list of these pairs, along with the best cRMS, the alignment length and the SAS values for all the programs is available online†. STRUCTAL contributes the largest number of alignments, followed by LSQMAN and SSM. For all three methods, a significant number of the contributed pairs corresponds to similarities between a “Mainly α” protein and a “Mixed α/β” protein. In the case of STRUCTAL, there is also a significant number of pairs involving a “Mainly β” protein and a “Mixed α/β” protein.
Table 3.
Difficult structure pairs with good alignments found just by one method
| Categorya | Total | SSAP | STRUCTAL | DALI | LSQMAN | CE | SSM |
|---|---|---|---|---|---|---|---|
| All α–All α (same CAT)b | 369(8) | 0 | 103 (5) | 2 (0) | 212 (2) | 0 | 52 (1) |
| All α–All β | 61 | 0 | 57 | 0 | 2 | 0 | 2 |
| All α–Mixed α/β | 610 | 0 | 275 | 0 | 243 | 0 | 92 |
| All α–Few Secondary Structure | 13 | 0 | 7 | 1 | 4 | 0 | 1 |
| All β–All β (same CAT)b | 37 (5) | 1 (0) | 24 (4) | 1 (0) | 10 (1) | 0 | 1 (0) |
| All β–Mixed α/β | 318 | 0 | 260 | 1 | 39 | 0 | 18 |
| All β–Few Secondary Structure | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Mixed α/β–Mixed α/β (same CAT)b | 292 (8) | 0 | 130 (4) | 1 (0) | 111 (1) | 0 | 50 (3) |
| Mixed α/β–Few Secondary Structure | 4 | 0 | 2 | 0 | 2 | 0 | 0 |
| Few Secondary Structure–Few Secondary Structure | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Total | 1704 | 1 | 858 | 6 | 623 | 0 | 216 |
Good alignments are defined as those where one of the methods finds a good alignment (SAS<4 Å and matches more than 35 residues), while all other methods find bad alignments (SAS>6 Å for any length of match). We also tested other definitions of difficult alignments (e.g. longer matches, or less stringent SAS values) and found a similar distribution amongst the different methods (data not shown).
We categorize the pairs of aligned structures by their class (C) classifier.
We list in parenthesis the number of difficult alignments found with structures of the same CAT classification.
Table 4 compares the relative success of the methods in detecting alignments of pairs that we know are similar. Here, we consider six test sets of similar structure pairs, and use the Best-of-All method to find the pairs in each test set. A set of similar pairs is parameterized by: (1) an upper bound on the SAS value, (2) a lower bound on the alignment length Nmat and (3) a lower bound on the percent of overlap between the aligned residues and the shorter structure in the pair. The first column lists the parameters for each of the test sets when using Best-of-All, as well as their respective sizes. The test set sizes vary significantly, ranging from 20,000 to 350,000. We then use the methods to find sets of well-aligned pairs. We hold the methods to lower standards than those used to select the test sets: we relax the bounds for good alignments: the upper SAS bound is increased, and the lower bounds of the alignment length and overlap (when applicable) are decreased. Table 4 lists the percentage of the missed good alignments in the test set for each of the methods. In all cases, STRUCTAL, CE and SSM miss fewest alignments.
Table 4.
Percentage of good Best-of-All alignments missed by each method
| Relaxed testa | Best-of-All testa | Test set size | SSAP | STRUCTAL | DALI | LSQMAN | CE | SSM |
|---|---|---|---|---|---|---|---|---|
| SAS<6 Å, Nmat>40, overlap>50% | SAS<3 Å, Nmat>50, overlap>60% | 20,065 | 16.4 | 1.5 | 29.6 | 55 | 4.3 | 3.9 |
| SAS<6 Å, Nmat>35, overlap>0% | SAS<3 Å, Nmat>45, overlap>0% | 33,485 | 32.4 | 0.3 | 12.3 | 8.6 | 6.1 | 1.5 |
| SAS<7 Å, Nmat>40, overlap>50% | SAS<4 Å, Nmat>50, overlap>60% | 66,125 | 29.4 | 4.4 | 22.4 | 74.5 | 7.5 | 9.9 |
| SAS<8 Å, Nmat>40, overlap>50% | SAS<5 Å, Nmat>50, overlap>60% | 138,373 | 41.2 | 7.2 | 22.9 | 85.1 | 11 | 17.6 |
| SAS<7 Å, Nmat>35, overlapa>0% | SAS<4 Å, Nmat>45, overlap>0% | 140,826 | 51.8 | 0.2 | 12.1 | 20.5 | 7.7 | 1.8 |
| SAS<8 Å, Nmat>35, overlap>0% | SAS<5 Å, Nmat>45, overlap>60% | 349,203 | 64.3 | 0.3 | 20 | 44.3 | 10.8 | 3.1 |
A good Best-of-All has a SAS score less than SAS defined in the Best-of-All test, and an alignment missed by a particular method has a SAS score greater than SAS defined in the relaxed test.
Nmat is the size of the alignment. Overlap is defined as the percentage of the shorter structure that is matched.
Analysis of the performance of the methods on different CATH classes
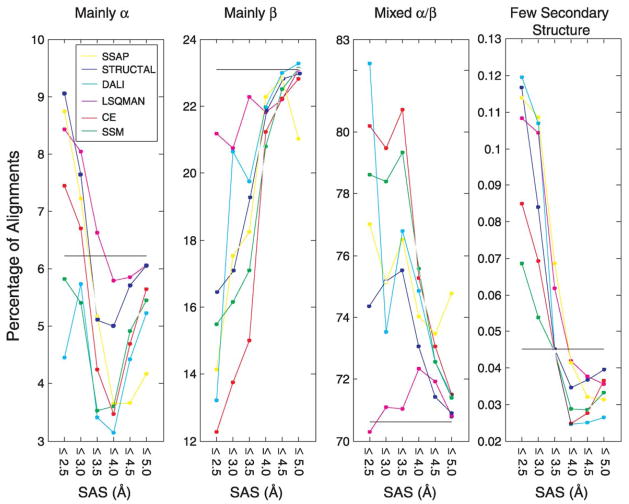
Figure 4 compares the relative success of each structural alignment method on CAT pairs in the four classes of protein structure (level C of CATH hierarchy). This is done for alignments with SAS values between 2.5 Å and 5 Å. We see, that α–α pairs, and α–β pairs are over-represented when the match is good (SAS value less than 3.5 Å), and, consequently, the β–β pairs are under-represented. When the match is less good (SAS value between 4 Å and 5 Å) each method behaves as expected finding different classes of pairs with a frequency that is proportional to the fraction of the pairs in the entire CAT set (shown by the horizontal lines in each panel). Most methods behave similarly in that at a particular SAS value, they detect similar percentages in each of the four classes. Such common behavior is unexpected, as the methods do not necessarily find the same pairs or even similar numbers of pairs. The LSQMAN method is unusual in that it finds more β–β pairs when the match is good (low SAS value) and consequently under-represents α + β pairs. Most of the pairs in CAT are Mixed α/β pairs (71%), followed by Mainly β pairs (23.5%), Mainly α pairs (6.2%) and Few Secondary Structures (0.45%). The fact that most methods detect relatively few β–β pairs of high match quality may mean that matches between β proteins are less good possibly due to the greater deformability of β strands.
Figure 4.
Comparing the performance of the different structural alignment programs when aligning different classes of structures. We consider all 104,309 pairs of the same fold class (i.e. same CAT), and partition them according to their C classification into four classes: Mainly α, Mainly β, Mixed α/β and Few Secondary Structure (from left to right). For each of the programs, and for each SAS threshold value, we plot the percent of alignments found below it. The percentage of pairs of each group, among all pairs, is the horizontal line. We see that Mainly α pairs, and Mixed α/β pairs, are over-represented in the high geometric similarity region, while the Mainly β pairs are under-represented. Generally, all methods have similar behavior, with the exception of LSQMAN, which is less successful, compared to all the other methods at detecting Mixed α/β pair similarity when the geometric similarity is high (this leads to a compensatory increase in recognition of alignments of Mainly α, Mainly β, and Few Secondary Structures pairs).
Running times
Table 5 lists the total amount of central processor unit time (CPU hours) used to compute all the structural alignments for each of the programs. All programs were run under the Linux operating system (RedHat 7.3) on a cluster of dual 2.8 MHz Intel Xeon processor machines, each with one Gigabyte of memory. SSM is the fastest method, followed by LSQMAN; SSAP and DALI are the slowest methods.
Table 5.
Total running time of each program on all pairs
| Program | CPU hours | Relative to SSM |
|---|---|---|
| SSAP | 9042 | 14.3 |
| STRCUTAL | 1906 | 3.0 |
| DALI | 4515 | 7.1 |
| LSQMAN | 1790 | 2.8 |
| CE | 2642 | 4.2 |
| SSM | 633 | 1.00 |
Time is measured in CPU hours on an Intel Xeon 2.8 GHz processor with 512 Mbytes of RAM memory. There are 8,581,970 pairs in all (2930×2929).
Discussion
Reservations about ROC curves
In our opinion, the number of disadvantages of using the ROC curves methodology for comparing structural alignment methods exceeds the number of potential advantages. ROC curves seem like a reasonable way to compare structural alignment methods because each curve evaluates a method with respect to an agreed gold standard (in the case of this study, CATH2); moreover, the methods’ self-evaluation (i.e. their native scores) can be used without needing any additional geometric match measure. The gold standard, however, is based on a classification, rather than a direct reflection of a similarity measure. For use in a ROC curve, the CATH classification must be converted to a binary similarity measure and this only allows two levels of similarity: “similar” if in the same C, A and T class, and “not similar” if not in the same C, A, and T class. Clearly, the scale of structural similarity is far richer, and this binary view introduces a great deal of “noise”. For example, a pair of structures with the same C and A classifiers and another pair with completely different classifiers will both be treated as unrelated structure pairs. More generally, there is a significant amount of similarity between structures that have a different CAT classification; this phenomenon was also observed by Harrison et al.35 and by Kihara & Skolnick.36 However, the ROC curve analysis ignores, and even penalizes, methods that find these similarities.
As pointed out earlier,17,29 the creators of CATH use information from some of the structural alignment methods; this implies that some of the methods under study are influencing the evaluation procedure. In this regard, it is of particular interest that two methods seem to agree best with the CATH classification but do not produce the best geometric matches. Another interesting detail is that one of these methods, SSAP, which was developed by some of those involved in defining the CATH classification, scores very badly when using its native score but does much better when using the SAS geometric match measure. The other method that seems to have influenced the CATH classification is DALI, the most commonly used alignment program, which has been available for many years through its web server.
When comparing two methods, there are cases in which one of the methods performs better and the ROC curve analysis fails to detect it. This can happen when one of the methods consistently finds better alignments, yet both methods order the alignments similarly. Since ROC curves use only the order of the alignments, the performance of these two methods will appear similar. Indeed, when comparing the ROC curves of DALI and CE using SAS to sort the alignments, we observe this phenomenon. Another example of this is that there are methods that perform well by the ROC curve criteria (i.e. the order of their alignments is consistent with the gold standard), yet find relatively poor alignments as evidenced by their geometric match measures. Lastly, although the Best-of-All method finds the best alignments by definition, its ROC curve suggests that it is a poor performer.
Structural alignment as a geometric optimization problem
Here we suggest treating structural alignment as an optimization problem in which alignments with the best geometric match measure are sought. This leads naturally to a definition of a combined effort, or the Best-of-All method. It also suggests a methodology for comparing methods: given several different structural alignments of the same pair of structures, it is easy to evaluate which is best based on the geometric properties of these alignments. Equivalently, when a particular method aligns two structures in such a way that it lines up many residues with a small cRMS deviation, the alignment itself serves as proof of its significance; it cannot be considered as an error or a false positive. A method can only fail to find good alignments that are known to exist.
In this study, we evaluate the quality of the alignments found by the different methods using four different geometric match measures. These match measures, both those previously proposed (SAS, SI and MI) and that suggested here (GSAS), attempt to balance properties of good alignments: cRMS or geometric similarity, Nmat the length of the alignment, the fraction of the shorter structure matched, and number of gaps. Different alignment methods seem to emphasize these same measures, although they may balance the values differently. Clearly, other geometric match measures, which balance these (and possibly additional) values differently, could be used thus changing the definition of a good alignment. For these measures, one could compare the ROC curves of the methods, and even better, compare the overall quality of the alignments directly. For example, one could use SASn=cRMS(100/Nmat)n, a version of SAS that favors longer alignments even at the cost of higher cRMS values. Since different methods have different strengths, shifting the emphasis may alter the evaluation. For most of the different match measures we studied, including SASn, the results were generally similar in that: (a) Best-of-All is better than any of the individual methods; (b) STRUCTAL and SSM produce better alignments. When we use SAS4 (i.e. dramatically emphasizing longer match length), we find that the order is different, and SSAP produces the best alignments.
The main observation of this work is that different alignments of a pair of structures found by different programs can be compared directly and evaluated using geometric match measures. This direct comparison also applies to a set of alignments. Overall quality can be measured via cumulative distributions of the quality of alignments of sets of protein pairs. This also suggests a way to examine cases in which one method succeeds while others fail.
Restricting the evaluation to the alignments
We believe that the principal quality of a structural alignment method is finding a good alignment. Thus, an evaluation of alignment methods should focus on the quality of the alignments. Most notably, the evaluation should not depend on the scoring of the alignments that the programs provide. Indeed, we show that most methods (apart from DALI and STRUCTAL) are better in finding alignments than in scoring them, or equivalently, do not distinguish good alignments from bad ones. This is consistent with the findings of Sierk & Pearson29 that many alignment programs greatly overstate the significance of structural alignments. Similarly, comparing all-against-all structures in a selected set avoids the pitfall of coupling the evaluation of the alignment programs and the database of structures used by a server. Since Novotny et al.30 evaluate the aligners and the databases simultaneously, it is hard to directly compare our results with theirs. Furthermore, using servers rather than the standalone versions can give misleading results in terms of the time performance of the programs, as it depends on many extraneous factors (e.g. the network and server loads and the servers hardware).
Direct comparison of structural alignment methods
Our analysis shows that the combined, Best-of-All, method finds the best alignments. Among existing methods STRUCTAL finds the best alignments. The second best method is SSM, but due to a limitation in the program’s output, we could not evaluate if the alignments found by the latter have many or few gaps. In terms of speed, SSM is the fastest method, followed by LSQMAN. Clearly, the computing time for the Best-of-All method is the sum of computing time of all the methods it uses. When designing a combined structural alignment method, such as Best-of-All, STRUCTAL, SSM and LSQMAN are important contributors, both in terms of quantity, i.e. percent of contribution, and quality, i.e. they excel in finding difficult alignments.
Sierk & Pearson29 evaluate (among others) CE, DALI and LSQMAN; Novotny et al.30 also evaluate SSM. The ranking by Novotny et al. is different from ours; we believe that there are two reasons for this difference: (1) our experiment is significantly larger, and (2) we focus on the structural alignment methods, while their evaluation also depends on the server’s database of structures. Our results confirm the observation by Sierk & Pearson that when considering only the ROC curves and using CATH as a gold standard, DALI appears to be the best performer. We also confirm the observation by Shindyalov & Bourne3 that CE produces alignments with fewer gaps compared to DALI.
In Methods, we summarize the main features of the six methods used here. It is notable that three of the methods, SSAP, DALI and CE, find correspondences by matching features in the distance matrices of each structure. This approach was first introduced in SSAP.6 The other three methods, STRUCTAL, LSQMAN and SSM all start with an alignment, superimpose the structures, deduce a new alignment from the superposition and iterate. This approach was first introduced by Satow et al.43 in the context of antibody structural alignment. Neither approach is guaranteed to converge to the best structural alignment. It has been shown26 that exhaustive exploration of the space of rigid body transformations guarantees finding all optimal (approximate) alignments in polynomial time (O(n8)). The methods STRUCTAL, LSQMAN, and SSM explore this same space using a faster heuristic search rather than exhaustive exploration. The methods SSAP, DALI and CE work by selecting similar subsets of two internal distance matrices. This is an NP-hard problem, which is as difficult as finding a maximal clique in a graph. It is possible that relying on the fact that these distance matrices describe objects in three-dimensional space will reveal a polynomial time algorithm, which compares the matrices directly. At present, we see no way in which this can be done.
Future directions
Understanding protein function and protein evolution are key aims in structural biology. Both are furthered by detecting all known protein structures that are geometrically similar to a given query structure. The straightforward way of doing this is to maintain a database of all (representative) structures, and compare the query structure to each of the structures in the database, using a structural alignment method. In this study, we evaluate the structural alignment methods that can be “plugged” into this procedure. Following homology modeling37 one can construct a method that calls different structural alignment methods, and selects the best alignment(s). The geometric match measures are reasonable criteria for this selection. Unfortunately, as the database is fairly large, this is computationally expensive. Ideally, we would like a fast filter that rules out some of the structures. Many approaches are currently tested in order to design such filters, including methods that consider geometric properties of protein backbone,38 as well as probabilistic methods based on contact maps describing protein structures.39 Certifying that a structure cannot be structurally aligned to another structure is a hard because the certifier must prove that no alignment can be found (for reasons other than the failure of the heuristic search). Designing such filters remains an important area of research.
This work touches upon the fundamental difference between classification of protein structures and measuring the similarities amongst them. In particular, we argue that converting a classification gold standard to a binary gold standard similarity measure is too crude of an approximation. We plan further investigation in this area. Specifically, we plan to study similarities among structures that are classified differently. In addition, we hope to study cases in which the classification is the same, yet all methods indicate that there is no similarity. This can be due to classification errors, or, more interestingly, due to protein structures that are intrinsically hard for structural alignment methods.
Methods
Geometric match measures of structural alignments
We aim to compare different structural alignments of pairs of structures by comparing their geometric match measures. There are two types of comparisons: (1) alignments found by different programs for the same pair(s) of structures. Here, the match measures must depend on the geometric and other properties of the particular alignments (cRMS, number of matched residues, number of gaps, and length of the proteins). (2) Alignments found by the same program. Here, we compare different alignments for the same pair of protein structures, as well as different alignments for different pairs of structures. In the second case, the geometric match measures can be used in addition to the native score provided by the particular protein structure alignment program. Native scores cannot be used when comparing alignments found by different programs as the scores may be in different units and on different scales.
Consider an alignment of two structures that have been optimally superimposed with respect to one another. The number of residues in each of the two structures is denoted by L1 and L2. The number of matches (aligned residue pairs) is denoted by Nmat. The coordinate root means square (in Å), between the aligned pairs of α-carbon (CA) atoms, is denoted cRMS. A gap opening is every instance of an aligned residue whose previous residue is not aligned. The number of gaps, denoted by Ngap, is the total number of gap openings in both structures. Note that here we have assumed that we compare structures using one atom per residue, generally but not necessarily, the CA atom. This simplifies things, making the unit of comparison (a CA atom) correspond to a unit of sequence (a residue).
Intuitively, a match measure based on the geometric properties of an alignment should favor alignments with many matched residues, low cRMS deviations, and few gaps. Unfortunately, these properties are not independent. For example, a lower cRMS deviation can always be achieved by selecting a shorter match; given the fixed inter-CA distance there is the extreme case of many alignments of just two residues that have cRMS deviation of 0 Å. Also, by allowing additional gaps, the alignment can be lengthened without necessarily increasing the cRMS deviation. Different match measures attempt to balance these values in different ways. In this work, we consider four geometric match measures: similarity index (SI),27 match index (MI),27 structural alignment score (SAS)7 and gapped SAS (GSAS). The original match index (OMI),27 has values between 0 and 1, with better alignments having higher values; instead we take MI = 1–OMI, so that lower values always imply better alignments. GSAS is introduced here as a variant of SAS that penalizes gap openings. MI includes a normalizing factor w0=1.5 (following Krissinel’s suggestion†). All measures are defined explicitly in terms of cRMS, Nmat, L1, L2 and Ngap as follows:
| (1) |
| (2) |
| (3) |
| (4) |
A GSAS value of 99.9 denotes worst possible value. The number “100” used above is in units of number of aligned residues. Thus, the units of SI, SAS and GSAS are Å.
Data set of structures to be aligned
The set of structures aligned in this study consists of 2930 sequence-diverse CATH2 v.2.4 domains, each with a CATH classification. As we focus on three-dimensional structures, we consider only the top three levels of CATH, Class, Architecture, and Topology to give a CAT classification. We refer to a set of structures with the same CAT classification as a fold class. There are 769 fold classes in the set that fit the Class categories as follows: 218 Mainly α class, 132 Mainly β class, 345 Mixed α/β class and 74 Few Secondary Structures class. The Supplementary Material to this work, presented online†, lists the names of the CATH domain of all these structures.
Using a set of structures with sufficient sequence diversity ensures that the set is duplicate-free and that the problem of structural alignment is non-trivial for all pairs. Here, we select the structures as follows: (1) sort all 34,287 CATH v.2.4 domains by their SPACI score.40 (2) Select the domains from the list, starting with the one with the best SPACI score (most accurately determined). (3) Remove from the list the selected one and all domains that share significant sequence similarity with it (FASTA22 E-value <1×10−4). (4) Continue until there are no domains left for selection. This is the same method used by Brenner et al.17 to produce the sequence-diverse set of SCOP structures.
The protein structure superposition programs
The structural alignment methods that we evaluate, listed chronologically from date of first publication, include: (1) SSAP,6 (2) STRUCTAL,7 (3) DALI,8 more specifically DaliLite (v.1.8),9 (4) LSQMAN,10 (5) CE,11 and (6) SSM.14 The common goal of all methods is to identify a set of residue pairs from each protein that are structurally similar. There are two general strategies for finding such good alignments: (1) search for transformations that optimally position the two structures with respect to one another, and then use the transformation to find the best alignment, and (2) directly search for a good alignment. STRUCTAL, LSQMAN, and SSM belong to the first group, whereas SSAP, DALI, and CE belong to the second. Most methods also rely on a structure superposition procedure (such as that due to Kabsch41), which finds the transformation (i.e. rotation and translation) to optimally match the aligned pairs, in terms of their cRMS deviation.
Each method scores a good alignment differently, which can impact the perceived performance of the method. For example, if a method defines an alignment as good only by its length, while ignoring the cRMS, it will find alignments with high values of the geometric match measures, and therefore will score badly in our analysis. Some of the methods report as a score the final value of the function optimized to find a good alignment. Others report a Z-score, or significance score calculated by comparing a particular score to the distribution of scores expected by chance. In general, the different methods judge the quality of an alignment by the number of matched residues (longer is better), the number of gaps (fewer is better), the geometric similarity value (either cRMS or dRMS), and the length of the shorter of the two structures min(L1,L2) (used to estimate the fraction of the structure matched). Below, we briefly describe the six methods with an emphasis on how they calculate the native score of a structural alignment.
SSAP6 searches for an optimal alignment of two protein structures using dynamic programming (DP). The DP algorithm requires a similarity measure for all pairs of residues, one from each structure to find the optimal alignment. For SSAP, the residue similarity is the overlap of the “views” from each of the two residues, where the “view” is the list of distances from the particular residue to all other residues in the same structure. SSAP also uses dynamic programming to optimize the overlap of distances in the two distance lists. The procedure is thus dubbed double dynamic programming. Gaps are allowed, but their lengths are limited to improve speed. The native score of SSAP is a normalized logarithm of a measure which combines the similarity of the aligned residues (accounting for the length of the alignment) and the number of residues in the smaller protein, min(L1,L2).
STRUCTAL7‡ assumes an initial alignment (a correspondence of residues in the two structures), and gets the rigid-body transformation that superimposes the corresponding residues. It then finds an optimal alignment for this superposition. The new alignment is used to superimpose the structures again and the procedure is repeated till it converges to a local optimum that depends on the initial alignment. In an attempt to reach the global optimum, STRUCTAL starts with several different correspondences. For a given correspondence, the optimal transformation is the one with minimal cRMS and STRUCTAL uses the procedure by Kabsch41 to find it. For a given transformation, the optimal correspondence is the one with a maximal STRUCTAL score, and STRUCTAL uses DP to find it. The STRUCTAL score of a correspondence is Σi∈correspondence(20/(1+5 dist(ai, bi)2)) − 10 × Ngap, where dist(ai,bi) is the distance in space between the α-carbon (CA) atoms of the ith residue pair in the correspondence. Three of the initial correspondences are: aligning the beginnings, the ends and the midpoints of the two structure chains without allowing any gaps. The fourth initial correspondence maximizes the sequence identity of the chains and the fifth is based on similarity of α-carbon torsion angles between the two chains.
DALI8 constructs an alignment by joining well aligned fragment pairs (which are six-residue backbone fragments). The similarity score is calculated from the pair-wise differences of all equivalent elements of the two distance matrices. DALI uses the Monte Carlo method to search for the best consistent set of similar fragment pairs joined into an alignment. The basic step in the Monte Carlo search is addition or deletion of residue equivalence assignments. The native score of DALI is a sum, over all aligned residue pairs in both structures, of a bonus score that is maximal when the inter-residue distances in both structures are equal. DALI uses many initial alignments, and searches for the best one in parallel, using the total score to select the best one. It reports the similarity score, and a normalized Z-score; we use the former as the DALI native score.
CE10 constructs an alignment by successively joining well aligned fragment pairs (denoted as AFPs). The AFPs are pairs of eight-residue fragment, which are considered similar if their corresponding internal distances are similar (of low dRMS). Gaps are allowed between neighboring AFPs, but their length is limited (less than 30 residues) to improve speed. CE constructs the alignment by choosing an initial AFP and extending it; the heuristic algorithm is greedy but it does consider AFPs that are not the very best to widen and improve the search. Finally, CE has an optimization step, which lengthens the alignment without compromising its cRMS. The native score of CE is a Z-score that evaluates the statistical significance of the alignment by considering the probability of finding an alignment of the same length (Nmat), with the same (or less) gaps (Ngaps) and geometrical distance (dRMS).
LSQMAN11 iteratively searches for a rigid body transformation (i.e. rotation and translation) that superimposes the structures. The initial transformation is calculated by optimally superimposing41 the first residues of the secondary structure elements (SSEs) in the two structures. Once the structures are superimposed, LSQMAN starts by searching for a long alignment, where matching residues are within 6 Å of each other, and the minimum fragment length is four residues. Given the alignment, an optimal transformation is calculated, starting a new iteration. The distance cutoff is slowly increased in the later optimization cycles. LSQMAN uses the similarity index (SI), which is defined above, as its optimization criterion. LSQMAN also calculates a Z-score, as defined by Levitt & Gerstein42 for its native score.
Secondary Structure Matching (SSM)14 iteratively searches for a rigid body transformation (i.e. rotation and translation) that superimposes the structures; it then finds an optimal alignment for this transformation. The initial transformations are found by matching substructures in the three-dimensional graphs that describe the structures in terms of secondary structure elements (SSEs) and their relative position and orientation. SSM then iteratively finds a correspondence of nearby α-carbon (CA) atom pairs, one from each structure, and optimally superimposes41 the corresponding sets. The procedure for finding the correspondence is greedy in nature. First it matches nearby residues of matched SSEs, then nearby residues of non-matched SSEs, and then more nearby residues that are not part of SSEs. The correspondence is further refined by removing some of the pairs. SSM uses a geometric quality measure Q, which balances the cRMS, the alignment length Nmat, and the length of the structures L1, L2: Q = (Nmat)2/((1+(cRMS/R0)2)L1L2). The refinement of the alignment tries to maximize the value of Q. Q is also used for the evaluation of the significance of the alignment with a P value and a Z-score. We use the latter as the native score of SSM.
Setting up the large scale protein structure comparison experiment
Each of the programs compared in this study aligned all 8,581,970 pairs of structures from the above set (i.e. 2930×2929=8,581,970 pairs). As our focus is evaluating the performance of the structural alignment methods, and due to the scope of the test, we ran the standalone Linux versions of the programs that implement the methods in-house using i386 Intel processors. Unless otherwise noted, each structural alignment program took as input the coordinates for all atoms (all lines starting with ATOM, TER or END in the PDB file). All the programs were run using default parameters, and no efforts were made to adjust these parameters to specific cases, such as low sequence or structure similarity. Doing so, we are aware that the individual results of each program may not be optimal, and that an expert of one of the methods tested here would certainly get better results than we do. Our goal however is to test these programs on large-scale comparisons, for which fine-tuning is not always possible. This also allows us to treat all six programs equally.
Each of the programs tested output the alignments, their cRMS values, and their scores, according to the method implemented in the program. The only exception is SSAP which provides the alignment and the score; in this case, the (optimal) cRMS was computed from the alignment and the PDB structures, using in-house software. From the alignment, we then calculated the number of matched residues and the total number of gaps (for SSM we could not derive the number of gaps). We stored the values of the geometric properties of the alignment together with the native score for further analysis. Each pair of structures has two alignments and we consider the one with the better native score (i.e. we use only 4,290,985 alignments). In cases where a particular method finds more than one alignment for a given pair of proteins, we consider the alignment with the best native score. Lastly, we recorded the computing times.
In CE, we change the source code so that the z-threshold value is 0 rather than 3.5, to ensure that the optimization block is always invoked. For CE, we also add the SEQRES fields to the input files to insure proper parsing of multi fragment chains. Since the ROC curve of CE based on SAS was significantly better than the one based on the native score, we select the best alignment for a pair of structures based on the one with highest SAS score. In LSQMAN, we use “Brute_force” mode, following the O macro procedure published in align2.omac†.
Comparison of methods using ROC curves
The traditional method of evaluating the performance of structural alignment programs is by comparing their receiver operating characteristic (ROC) curves.31 ROC curves quantify how much a scoring scheme agrees with a gold standard; the gold standard indicates for every pair if it is similar or not. Here, we derive a binary (similar or not similar) gold standard from the CATH hierarchy: we consider a structure pair to be a positive if both structures have the same CAT classification, and to be a negative otherwise. The alignments found by each program are sorted according to a quality measure, either one of the four geometric measures or the program’s native score. This order, along with a threshold value, marks all structure pairs with values below it as positives. We denote structure pairs that are also marked as positives by the gold standard as true positives (TPs) and pairs that are not marked by the gold standard as positives as false positives (FPs). For a particular measure, the ROC curve plots the fraction of FPs (1 – specificity) against the fraction of TPs (sensitivity). These fractions are calculated at every increasing threshold of the measure, starting from the most significant in the pair list sorted by the measure. A perfect predictor will have a ROC curve that moves up the y-axis turning right at the left-topmost corner, with area 1 below it; a completely random predictor will have a curve that follows the diagonal, with area 0.5 below it.
Acknowledgments
This work was supported by the National Institutes of Health (GM063817) and National Science Foundation (CCR-00-86013). M.L. was also supported by the Fondation de l’Ecole Normale Supérieure Chaires de Blaise Pascal. We are grateful to the authors of the structural alignment methods for making their programs available.
Abbreviations
- ROC
receiver operating characteristic
- TP
true positives
- FP
false positives
- DP
dynamic programming
- SSEs
secondary structure elements
- SSM
secondary structure matching
Footnotes
Available online at http://csb.stanford.edu/levitt/structal.html
Note added in proof: Dr Taylor informs us that SSAP is an obsolete program, which has been superceded by SAP (Taylor, W. R. (1999). Protein structure alignment using iterated double dynamic programming. Prot. Sci., 8, 654–665).
References
- 1.Perutz MF, Rossmann MG, Cullis AF, Muirhead H, Will G, North ACT. Structure of myoglobin: a three-dimensional Fourier synthesis at 5.5 Angstrom resolution, obtained by X-ray analysis. Nature. 1960;185:416–422. doi: 10.1038/185416a0. [DOI] [PubMed] [Google Scholar]
- 2.Orengo CA, Michie AD, Jones S, Jones DT, Swindells MB, Thornton JM. CATH—a hierarchic classification of protein domain structures. Structure. 1997;5:1093–1108. doi: 10.1016/s0969-2126(97)00260-8. [DOI] [PubMed] [Google Scholar]
- 3.Shindyalov IN, Bourne PE. An alternative view of protein fold space. Proteins: Struct Funct Genet. 2000;38:247–260. [PubMed] [Google Scholar]
- 4.Thompson JD, Plewniak F, Poch O. BAliBASE: a benchmark alignment database for the evaluation of multiple alignment programs. Bioinformatics. 1999;15:87–88. doi: 10.1093/bioinformatics/15.1.87. [DOI] [PubMed] [Google Scholar]
- 5.Sauder JM, Arthur JW, Dunbrack RL. Large scale comparison of protein sequence alignment algorithms with structure alignments. Proteins: Struct Funct Genet. 2000;40:6–22. doi: 10.1002/(sici)1097-0134(20000701)40:1<6::aid-prot30>3.0.co;2-7. [DOI] [PubMed] [Google Scholar]
- 6.Taylor WR, Orengo CA. Protein structure alignment. J Mol Biol. 1989;208:1–22. doi: 10.1016/0022-2836(89)90084-3. [DOI] [PubMed] [Google Scholar]
- 7.Subbiah S, Laurents DV, Levitt M. Structural similarity of DNA-binding domains of bacteriophage repressors and the globin core. Curr Biol. 1993;3:141–148. doi: 10.1016/0960-9822(93)90255-m. [DOI] [PubMed] [Google Scholar]
- 8.Holm L, Sander C. Protein structure comparison by alignment of distance matrices. J Mol Biol. 1993;233:123–138. doi: 10.1006/jmbi.1993.1489. [DOI] [PubMed] [Google Scholar]
- 9.Holm L, Park J. DaliLite workbench for protein structure comparison. Bionformatics. 2000;16:566–567. doi: 10.1093/bioinformatics/16.6.566. [DOI] [PubMed] [Google Scholar]
- 10.Kleywegt GJ. Use of non-crystallographic symmetry in protein structure refinement. Acta Crystallog sect D. 1996;52:842–857. doi: 10.1107/S0907444995016477. [DOI] [PubMed] [Google Scholar]
- 11.Shindyalov IN, Bourne PE. Protein structure alignment by incremental combinatorial extension (CE) of the optimal path. Protein Eng. 1998;1:739–747. doi: 10.1093/protein/11.9.739. [DOI] [PubMed] [Google Scholar]
- 12.Kedem K, Chew LP, Elber R. Unit-vector RMS(URMS) as a tool to analyze molecular dynamics trajectories. Proteins: Struct Funct Genet. 1999;37:554–564. [PubMed] [Google Scholar]
- 13.Yang AS, Honig B. An integrated approach to the analysis and modeling of protein sequences and structures. I Protein structure alignment and quantitative measure for protein structural distance. J Mol Biol. 2000;301:665–678. doi: 10.1006/jmbi.2000.3973. [DOI] [PubMed] [Google Scholar]
- 14.Krissinel E, Henrick K. In: Kungl AJ, Kungl PJ, editors. Protein structure comparison in 3D based on secondary structure matching (SSM) followed by C-alpha alignment, scored by a new structural similarity function; Proceedings of the Fifth international Conference on Molecular Structural Biology; Vienna. September 3–7.2003. [Google Scholar]
- 15.Koehl P. Protein structure similarities. Curr Opin Struct Biol. 2001;11:348–353. doi: 10.1016/s0959-440x(00)00214-1. [DOI] [PubMed] [Google Scholar]
- 16.Pearson WR. Comparison of methods for searching protein sequence databases. Protein Sci. 1995;4:1145–1160. doi: 10.1002/pro.5560040613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Brenner SE, Chothia C, Hubbard TJ. Assessing sequence comparison methods with reliable structurally-identified distant evolutionary relationships. Proc Natl Acad Sci USA. 1998;95:6073–6078. doi: 10.1073/pnas.95.11.6073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Needleman SB, Wunsch CD. A general method applicable to the search for similarities in the amino acid sequence of two proteins. J Mol Biol. 1970;48:443–453. doi: 10.1016/0022-2836(70)90057-4. [DOI] [PubMed] [Google Scholar]
- 19.Dayhoff MO. Atlas of Protein Sequence and Structure. Vol. 5. National Biomedical Research Foundation; 1978. [Google Scholar]
- 20.Henikoff S, Henikoff JG. Amino acid substitution matrices from protein blocks. Proc Natl Acad Sci USA. 1992;89:100915–100919. doi: 10.1073/pnas.89.22.10915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Altschul S, Gish W, Miller W, Myers E, Lipman D. Basic local alignment search tool. J Mol Biol. 1990;215:403–410. doi: 10.1016/S0022-2836(05)80360-2. [DOI] [PubMed] [Google Scholar]
- 22.Pearson W, Lipman D. Improved tools for biological sequence comparison. Proc Natl Acad Sci USA. 1988;85:2444–2448. doi: 10.1073/pnas.85.8.2444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Murzin AG, Brenner SE, Hubbard T, Chothia C. SCOP: a structural classification of proteins database for the investigation of sequences and structures. J Mol Biol. 1995;247:536–540. doi: 10.1006/jmbi.1995.0159. [DOI] [PubMed] [Google Scholar]
- 24.Domingues F, Lackner P, Andreeva A, Sippl M. Structure-based evaluation of sequence comparison and fold recognition alignment accuracy. J Mol Biol. 2000;297:1003–1013. doi: 10.1006/jmbi.2000.3615. [DOI] [PubMed] [Google Scholar]
- 25.Friedberg I, Kaplan T, Margalit H. Evaluation of PSI-BLAST alignment: accuracy in comparison to structural alignments. Protein Sci. 2000;9:2278–2284. doi: 10.1110/ps.9.11.2278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kolodny R, Linial N. Approximate protein structural alignment in polynomial time. Proc Natl Acad Sci USA. 2004;101:12201–12206. doi: 10.1073/pnas.0404383101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kleywegt GJ, Jones A. Superposition. CCP4/ESF-EACBM Newsletter Protein Crystallog. 1994;31:9–14. [Google Scholar]
- 28.Stark A, Sunyaev S, Russel RB. A model for statistical significance of local similarities in structure. J Mol Biol. 2003;326:1307–1316. doi: 10.1016/s0022-2836(03)00045-7. [DOI] [PubMed] [Google Scholar]
- 29.Sierk ML, Pearson WR. Sensitivity and selectivity in protein structure comparison. Protein Sci. 2004;13:773–785. doi: 10.1110/ps.03328504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Novotny M, Madsen D, Kleywegt GJ. Evaluation of protein-fold-comparison servers. Proteins: Struct Funct Genet. 2004;54:260–270. doi: 10.1002/prot.10553. [DOI] [PubMed] [Google Scholar]
- 31.Gribskov M, Robinson NL. Use of receiver operating characteristic (ROC) analysis to evaluate sequence matching. Comput Chem. 1996;20:25–33. doi: 10.1016/s0097-8485(96)80004-0. [DOI] [PubMed] [Google Scholar]
- 32.Leplae R, Hubbard TJP. MaxBench: evaluation of sequence and structure comparison methods. Bioinformatics. 2002;18:494–495. doi: 10.1093/bioinformatics/18.3.494. [DOI] [PubMed] [Google Scholar]
- 33.Gerstein M, Levitt M. Comprehensive assessment of automatic structural alignment against a manual standard, the Scop classification of proteins. Protein Sci. 1998;7:445–456. doi: 10.1002/pro.5560070226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Shapiro J, Brutlag D. FoldMiner: structural motif discovery using an improved superposition algorithm. Protein Sci. 2004;13:278–294. doi: 10.1110/ps.03239404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Harrison A, Pearl F, Mott R, Thornton J, Orengo C. Quantifying the similarities within fold space. J Mol Biol. 2002;323:909–926. doi: 10.1016/s0022-2836(02)00992-0. [DOI] [PubMed] [Google Scholar]
- 36.Kihara D, Skolnick J. The PDB is a covering set of small protein structures. J Mol Biol. 2003;334:793–802. doi: 10.1016/j.jmb.2003.10.027. [DOI] [PubMed] [Google Scholar]
- 37.Ginalski K, Elofsson A, Fischer D, Rychlewski L. 3D-Jury: a simple approach to improve protein structure predictions. Bioinformatics. 2003;19:1015–1018. doi: 10.1093/bioinformatics/btg124. [DOI] [PubMed] [Google Scholar]
- 38.Rogen P, Fain B. Automatic classification of protein structure by using Gauss integrals. Proc Natl Acad Sci USA. 2003;100:119–124. doi: 10.1073/pnas.2636460100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Choi I, Kwon J, Kim SH. Local feature frequency profile: a method to measure structural similarity in proteins. Proc Natl Acad Sci USA. 2004;101:3797–3802. doi: 10.1073/pnas.0308656100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Brenner SE, Koehl P, Levitt M. The ASTRAL compendium for protein structure and sequence analysis. Nucl Acids Res. 2000;28:254–256. doi: 10.1093/nar/28.1.254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kabsch W. A discussion of the solution for the best rotation to relate two sets of vectors. Acta Crystallog sect A. 1978;34:827–828. [Google Scholar]
- 42.Levitt M, Gerstein M. A unified statistical framework for sequence comparison and structure comparison. Proc Natl Acad Sci USA. 1998;95:5913–5920. doi: 10.1073/pnas.95.11.5913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Satow Y, Cohen GH, Padlan EA, Davies DR. Phosphocholine binding immunoglobulin Fab McPC603. J Mol Biol. 1986;190:593–604. doi: 10.1016/0022-2836(86)90245-7. [DOI] [PubMed] [Google Scholar]
- 44.Krissinel E, Henrick K. Secondary-structure matching (SSM), a new tool for fast protein structure alignment in three dimensions. Acta Crystallog sect D. 2004;60:2256–2268. doi: 10.1107/S0907444904026460. [DOI] [PubMed] [Google Scholar]