Abstract
Background
Heart attack and stroke are often caused by atherosclerotic plaque rupture which happens without warning most of the time. MRI-based atherosclerotic plaque models with fluid-structure interactions (FSI) have been introduced to perform flow and stress/strain analysis and identify possible mechanical and morphological indices for accurate plaque vulnerability assessment. For coronary arteries, cyclic bending associated with heart motion and anisotropy of the vessel walls may have significant influence on flow and stress/strain distributions in the plaque. FSI models with cyclic bending and anisotropic vessel properties for coronary plaques are lacking in the current literature.
Method of Approach
In this paper, cyclic bending and anisotropic vessel properties were added to 3D FSI coronary plaque models so that the models would be more realistic for more accurate computational flow and stress/strain predictions. Six computational models using one ex vivo MRI human coronary plaque specimen data were constructed to assess the effects of cyclic bending, anisotropic vessel properties, pulsating pressure, plaque structure, and axial stretch on plaque stress/strain distributions.
Results
Our results indicate that cyclic bending and anisotropic properties may cause 50%–800% increase in maximum principal stress (Stress-P1) values at selected locations. The stress increase varies with location and is higher when bending is coupled with axial stretch, non-smooth plaque structure, and resonant pressure conditions (zero phase angle shift). Effects of cyclic bending on flow behaviors are more modest (9.8% decrease in maximum velocity, 2.5% decrease in flow rate, 15% increase in maximum flow shear stress).
Conclusions
Inclusion of cyclic bending, anisotropic vessel material properties, accurate plaque structure, and axial stretch in computational FSI models should lead to considerable improvement of accuracy of computational stress/strain predictions for coronary plaque vulnerability assessment. Further studies incorporating additional mechanical property data and in vivo MRI data are needed to obtain more complete and accurate knowledge about flow and stress/strain behaviors in coronary plaques and to identify critical indicators for better plaque assessment and possible rupture predictions.
Keywords: Coronary artery, cardiovascular, cyclic bending, fluid-structure interaction, blood flow, atherosclerotic plaque rupture
1. Introduction
Assessing atherosclerotic plaque vulnerability is important because many cardiovascular clinical events such as heart attack and stroke are caused by plaque rupture which often happens without any warning signal [1–6. “Every year, nearly half of heart attack victims (over 650,000 only in the United States) are unaware of their vulnerability to a near future heart attack until it happens. And more than 220,000 of them die within an hour. Essentially, they each are a walking time bomb and completely unaware.” said Dr. Morteza Naghavi, chairman of the SHAPE (Screening for Heart Attack Prevention and Education) Task Force who founded the Association for Eradication of Heart Attack (AEHA) [7].
Plaque rupture is believed to be related to plaque morphology, mechanical forces, vessel remodeling, blood conditions (cholesterol, sugar, etc.), chemical environment, and lumen surface conditions (inflammation) [2–3, 8–13]. However, mechanisms causing plaque rupture are not fully understood [5–6, 12–15]. Some studies indicated that the following factors appear to be closely associated with plaque ruptures [2,8–9,11,16]: a) a large atheromatous lipid-rich core; b) a thin fibrous cap; c) weakening of the plaque cap, superficial plaque inflammation, and erosion. MRI techniques have been developed to non-invasively quantify plaque size, shape, components (fibrous, lipid, calcification/ inflammation) and flow characteristics [17–19]. Attempts of using ultrasound and intravascular ultrasound (IVUS) techniques have been made to quantify vessel motion, mechanical properties, and vessel wall structure, even to predict rupture locations [12–13,20]. Liang, Zhu and Friedman developed techniques to estimate transverse strain tensors in the artery wall using IVUS image registration [21]. In McCord and Ku’s experiments, fresh human artery rings were cyclically bent for 500,000 cycles. The cyclic bending stresses induced intimal rupture that may mimic artery fatigue and plaque rupture [22–23].
It has been proposed that mechanical forces play an important role in the complex plaque progression and rupture process and that adding mechanical analysis to the current morphology-based plaque assessment may lead to more accurate predictions of possible future rupture events. Image-based computational models for atherosclerotic plaques have been introduced to perform flow and stress/strain analysis and identify possible mechanical and morphological indices for plaque vulnerability assessment [18, 24–34]. Fluid-structure interactions (FSI) were introduced in our previous papers for carotid atherosclerotic plaques [18, 31–33,35]. However, 3D multi-component FSI models based on MRI data for human coronary plaques with cyclic bending and anisotropic material properties are still lacking in the literature [18, 35–37].
In this paper, we are adding cyclic bending and anisotropic vessel properties to 3D FSI coronary plaque models for more realistic models and more accurate computational predictions. It is known that coronary plaques are more likely to rupture compared to carotid plaques under comparable conditions (such as stenosis severity at about 50% by diameter). One possible reason is that coronary arteries are under cyclic bending caused by heart motion and compression. We hypothesize that cyclic bending of coronary atherosclerotic plaques may be a major contributor to critical stress conditions in coronary plaques leading to increased plaque rupture risk. By including both cyclic bending and vessel anisotropic material properties in 3D multi-component FSI models for coronary plaques, we hope to capture the major factors affecting critical flow and mechanical conditions and improve the accuracy of computational predictions for plaque vulnerability assessment. One coronary plaque sample re-constructed from a 3D ex vivo MRI data set was used for this investigation. Anisotropic material properties were measured from a human coronary plaque sample. Physiological pressure and curvature variations of human coronary arteries were obtained from available literature and used in the model [17,29,35,38]. Details are given below.
2. Data Acquisition, Models and Methods
2.1. Mechanical testing of vessel material properties
A coronary artery was obtained from Washington University Medical School with consent obtained. After the connective tissue was removed, the artery was cut to open. Dumbbell-shaped strips of 2mm width were cut in the axial and radial directions. The strips were cut from areas without obvious plaque blocks to avoid the disturbance to the experimental data. Pieces of water-proof sand paper were attached on the ends of each strip with cyanoacrylate adhesive. Then two black markers were put in the central area for non-contact deformation measurement. Samples were submerged in a 37°C thermostatic saline bath and mounted on a custom-designed device to perform uniaxial tests [39]. For each test, after 5 pre-conditioning cycles to a stretch ratio of 1.3, the sample was cycled three times with stretch ratio varying from 1.0 to 1.3 at a rate of 10% per minute. Force was measured using an isometric torque transducer (.15 N-m, Futek) attached to the sample via a 7.6 cm plexiglass arm extending out of the bath yielding ± 4 mN accuracy. Engineering stress was calculated by dividing force by the initial cross-sectional area of the sample measured with a micrometer (± 10 µm). Measured circumferential and axial stress-stretch experimental data will be plotted in Section 2.3 together with the stress-stretch curves derived from the anisotropic and isotropic material models.
2.2 MRI data acquisition
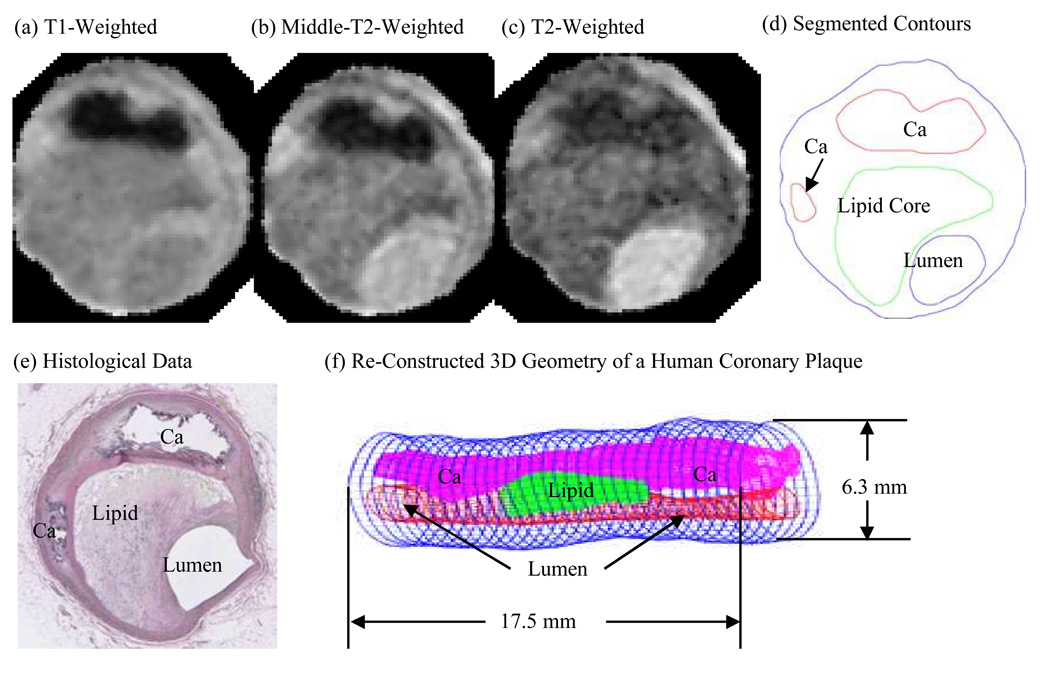
A 3D MRI data set obtained from a human coronary plaque ex vivo consisting of 36 slices with a relatively high resolution (0.25mm × 0.23mm × 0.5mm) was used as the baseline case to develop the computational model [31]. The specimen was fixed in a 10% buffered formalin solution and placed in a polyethylene tube and then stored at 4°C within 12 hours after removal from the heart. MRI imaging was taken within 2 days at room temperature. Multi-contrast (T1, middle-T2, T2, and proton density-weighting) MRI imaging was performed to better differentiate different components in the plaque (Fig. 1). Our individual contour plots show that T1-weighting is better to assess calcification, T2-weighting is better to assess the lumen and outer boundary, and the middle-T2 weighting is better for lipid core assessment. The MR system is 3T Siemens Allegra clinical system (Siemens Medical Solutions, Malvern, PA). A single-loop volume coil (Nova Medical, Inc, Wilmington, MA) with a diameter of 3.5 cm was used as a transmitter and receiver. After completion of MR study, the transverse sections with a thickness of 10 µm were obtained at 1 mm intervals from each specimen. These paraffin-embedded sections were stained with hematoxylin and eosin (H&E), Masson’s trichrome, and elastin van Gieson’s (EVG) stains to identify major plaque components: calcification (Ca), lipid rich necrotic core (LRNC), and fibrotic plaques (FP). Plaque vulnerability of these samples was assessed pathologically to serve as bench mark to validate computational findings. The 3D ex vivo MRI data were read by a self-developed software package Atherosclerotic Plaque Imaging Analysis (APIA) written in Matlab (Math Works, MATLAB, Natick, MA) and also validated by histological analysis [31].
Figure 1.
A human coronary atherosclerotic plaque sample: Multi-contract MR images and re-constructed 3D geometry. (a)–(c), MR images with T1, middle-T2, and T2-weighted images. (d) Contour plot of the segmented image using a multi-contrast algorithm; (e) Histological data. The location and shape of each major plaque component correlated very well with histological data; (f) 3D plaque geometry re-constructed from a 36-slice ex vivo MRI data set.
All segmented 2D slices were read into ADINA input file. 3D plaque geometry was re-constructed following the procedure described in Tang et al. [33]. Figure 1 shows one slice selected from a 36-slice data set of a human coronary plaque sample, plaque component contour plots based on histological segmentation data, and the re-constructed 3D geometry. Our individual contour plots show that T1w is better to get the two Ca pools, T2w is better to get the lumen and outer boundary, the middle-T2w is better for lipid core. The diameter of the vessel is about 5–6 mm. Some smoothing (third-order spline) was applied to correct numerical and MR artifacts, as well as overly unsmooth spots that affect the convergence of the model. Smoothing was kept to minimum only to remove data artifacts and extreme sharp angles which affect code convergence. Critical morphological features (such as plaque cap thickness) were carefully kept unchanged so that the accuracy of computational predictions will not be affected. The vessel was extended uniformly at both ends by 3 cm and 6 cm for the no-bending case to avoid flow entrance and end effects. For cases with cyclic bending, the vessel was extended at both ends by 4 mm to keep vessel length reasonable for implementing cyclic bending conditions.
2.3. A component-fitting mesh generation technique
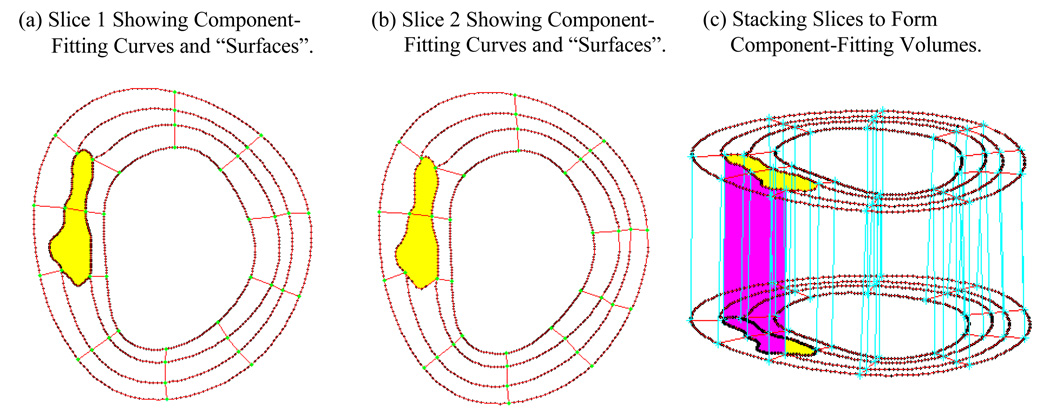
Because plaques have complex irregular geometries with component inclusions which are challenging for mesh generation, we have developed a component-fitting mesh generation technique to generate mesh for our models. Figure 2 gives a simple illustration of the method. Using this technique, the 3D plaque domain was divided into hundreds of small “volumes” to curve-fit the irregular plaque geometry with plaque component inclusions. 3D surfaces, volumes and computational mesh were made under ADINA computing environment. For the plaque sample given in Fig. 1, the finite element ADINA FSI solid model has 804 volumes, 59360 elements (8-nodes brick element), 64050 nodes. The fluid part has 216 volumes, 71481 elements (4-nodes tetrahedral element), 14803 nodes. Mesh analysis was performed by decreasing mesh size by 10% (in each dimension) until solution differences were less than 2%. The mesh was then chosen for our simulations.
Figure 2.
The component-fitting mesh generation process. (a)–(b): two slices with a lipid core inclusion (yellow) and numerically-generated component-fitting curves and “surfaces” to form “volumes”; (c) component-fitting volumes formed by connection corresponding areas from stacking adjacent slices. Distance between the two slices was enlarged for better viewing.
2.4. The anisotropic and isotropic multi-component FSI models with cyclic bending
3D anisotropic and isotropic multi-component FSI models were introduced to evaluate the effects of cyclic bending and anisotropic properties on stress/strain distributions in coronary plaques using the plaque sample re-constructed in 2.2 (Fig. 1). Blood flow was assumed to be laminar, Newtonian, and incompressible. The Navier-Stokes equations with arbitrary Lagrangian Eulerian (ALE) formulation were used as the governing equations. Physiological pressure conditions were prescribed at both inlet and outlet (Fig. 3). No-slip conditions and natural traction equilibrium conditions are assumed at all interfaces. Putting these together, we have (summation convention is used):
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
where u and p are fluid velocity and pressure, ug is mesh velocity, µ is the dynamic viscosity, ρ is density, Γ stands for vessel inner boundary, f •,j stands for derivative of f with respect to the jth variable, σ is stress tensor (superscripts indicate different materials), ε is strain tensor, v is solid displacement vector, superscript letters “r” and “s” were used to indicate different materials (fluid, or different plaque components). For simplicity, all material densities were set to 1 in this paper. Details of material models and other boundary conditions are further explained below.
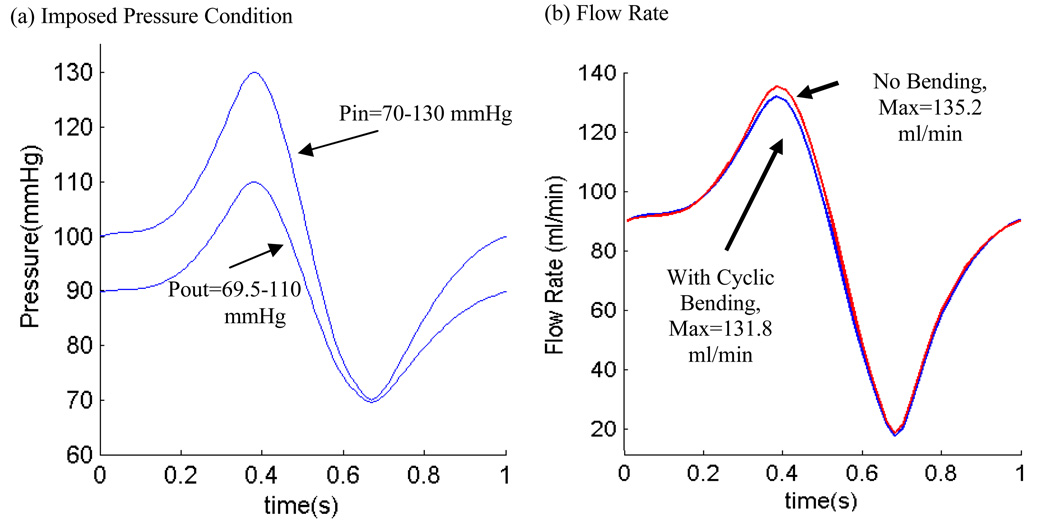
Figure 3.
Prescribed pressure conditions for the baseline model and corresponding flow rates. (a) A simplified pressure profile for human coronary artery was scaled to 70–130 mmHg and used as the upstream pressure (Pin). Down stream pressure was chosen so that flow rate was within physiological range; (b) Flow rate corresponding to the prescribed pressure conditions with and without cyclic bending. Cyclic bending reduced max flow rate by about 2.5%.
To get the constitutive stress-strain relationship for the isotropic model, both artery vessel material and plaque components in the plaque were assumed to be hyperelastic, isotropic, incompressible and homogeneous. The 3D nonlinear modified Mooney-Rivlin (M-R) model was used to describe the material properties of the vessel wall and plaque components [31–34,40–44]. The strain energy function for M-R model is given by,
| (9) |
| (10) |
where I1 and I2 are the first and second strain invariants, C =[Cij] = XTX is the right Cauchy-Green deformation tensor, X=[Xij] = [∂xi/∂aj], (xi) is current position, (ai) is original position [40–41], ci and Di for i=1,2 are material parameters chosen to match our own experimental measurements for fibrous tissue and data in the current literature for lipid pool and calcifications [26,36,45–46]. 3D stress/strain relations can be obtained by finding various partial derivatives of the strain energy function with respect to proper variables (strain/stretch components). In particular, setting material density ρ= 1 g • cm−3 and assuming incompressibility,
| (11) |
where λ1, λ2 and λ3 are stretch ratios in the (x,y,z) directions respectively, the uni-axial stress/stretch relation for an isotropic material is obtained from Eq. (9) [31–33],
| (12) |
Using the modified Mooney-Rivlin model available in ADINA and adding an additional anisotropic term to Eq. (9), we have the anisotropic (transversely isotropic) strain energy density function for our anisotropic FSI model [40, 41 (Section 3.8.4), 25]:
| (13) |
where I4 =Cij (nc)i (nc)j, Cij is the Cauchy-Green deformation tensor, nc is the circumferential direction of the vessel, K1 and K2 are material constants [41]. A two-step least-squares method was used to determine the parameter values in Eq. (13) to fit our experimental circumferential and axial stress-stretch data. Step 1. By choosing the principal axes as local coordinate axes, calculations are simplified. Noticing that λr λc λz =1, λr=λz (there are radial and axial directions, respectively), σ = J−1FTFT where σ is Cauchy stress, T is the second Piola-Kirchhoff stress, and Tcc = ∂W/∂Ecc,Tzz = ∂W/∂Ezz we obtain from Eq. (13):
| (14) |
| (15) |
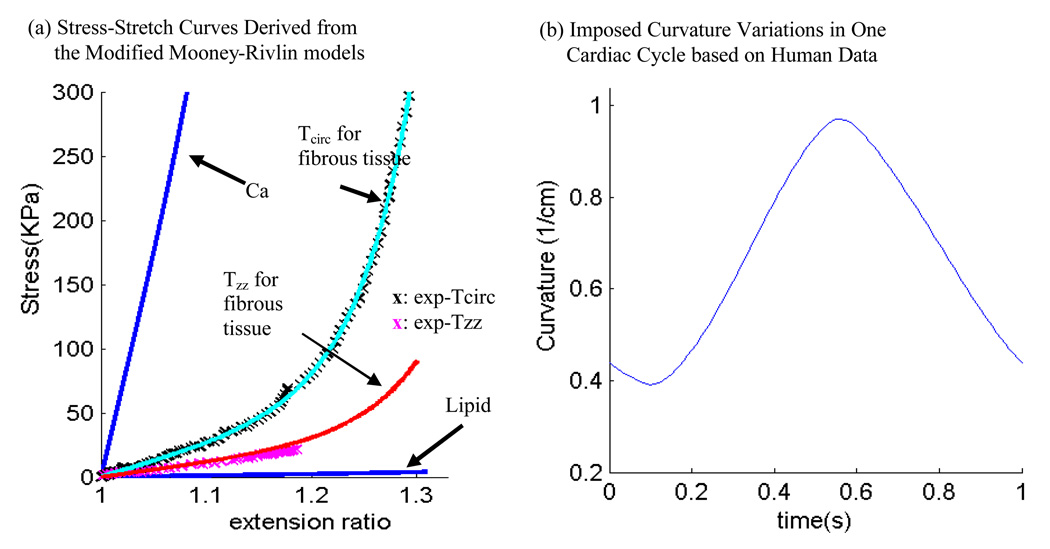
where cz=(C)zz=(FT F)zz, , c c = (C) cc = (FT F) cc are components of the right Cauchy-Green deformation tensor. Using stress-stretch values obtained from our measurements (Fig. 4) and with D2 and K2 fixed, a least square approximation technique was used to obtain C1, D1, K1 (all functions of D2 ,K2). Step 2. Let D2 and K2 change from −100 to100, Step 1 was performed for all (D2, K2) combinations with initial increment=10 to get the corresponding C1, D1, K1 values and the least squares fitting errors. Optimal (D2, K2) and the associated C1, D1, K1 values are determined by choosing the pair corresponding to a minimum fitting error. Searching increment for (D2, K2) started from 10 for [−100,100] and then refined to 1, and 0.1 when search domain was reduced. Fig. 3 (a) shows that our model with parameters selected with this procedure fits very well with the measured experimental data. Parameter values numerically determined from this optimization process are: anisotropic model for fibrous tissue: C1 =8.2917 KPa, D1 =0.9072 KPa, D2 =3.1, K1 = 8.8240 KPa, K2 =3.7000; corresponding isotropic models: circumferential (used for isotropic fibrous tissue): C1=28.1443KPa, D1=1.3101KPa, D2=11.5; axial: C1=14.0722KPa, D1=0.6551KPa, D2=9.2. Our measurements are consistent with data available in the literature [25,47–48].
Figure 4.
Material stress-stretch curves and imposed curvature conditions. (a) Axial and circumferential stress-stretch data (marked by x) measured from a human coronary specimen and stress-stretch matching curves derived from the modified anisotropic Mooney-Rivlin models for fibrous tissue (vessel). Stress-stretch curves for lipid pool and calcification models were also included. Parameter values are given in the main text; (b) Imposed curvature conditions based on human coronary curvature variation data [29].
Isotropic models were used for calcification (Ca) and necrotic lipid-rich pool. Because calcification is much stiffer than fibrous tissue, and lipid core is much softer than fibrous tissue, the following parameter values were used: Ca, C1= 281.443KPa, D1=13.101KPa (C1 and D1 are 10 times of the corresponding values for normal tissue), D2=11.5; lipid pool: C1=0.5KPa, D1=0.5KPa, D2=0.5 (these small numbers were chosen so that lipid would be very soft). Parameter analyses were performed in our previous paper [45].
Cyclic arterial bending secondary to cardiac motion was introduced into the computational model by specifying cyclic nonuniform 3D displacement function d(x,y,z,t) on the lower edge of the outer surface of the vessel. The displacement function could be adjusted to achieve desirable curvature changes [29,38,49]. The imposed curvature variation is given in Fig. 4(b) using the data of a human left anterior descending (LAD) coronary curvature variation data given in [29]. The displacement function was set to zero at the two ends of the vessel together with some additional neighboring nodes so that a small portion of the vessel inlet/outlet was fixed when the vessel was bent. This should be taken into consideration when interpreting computational results from the near-end portion of the vessel. Additional length (4 mm at each end) was added to the vessel to avoid this computational artifact.
2.5. Solution method
The coupled FSI models were solved by a commercial finite-element package ADINA (ADINA R & D, Inc., Watertown, MA, USA). ADINA uses unstructured finite element methods for both fluid and solid models. Nonlinear incremental iterative procedures were used to handle fluid-structure interactions. Proper mesh was chosen to fit the shape of each component, the vessel, and the fluid domain. Finer mesh was used for thin plaque cap and components with sharp angles to get better resolution and handle high stress concentration behaviors. The governing finite element equations for both the solid and fluid models were solved by the Newton-Raphson iteration method. Details of the computational models and solution methods are given in [31–35,40–44,50].
3. Results
Computational simulations were conducted using the coronary plaque sample to quantify effects of anisotropic properties, cyclic bending and their combined effects with pressure (phase angle shift), plaque components, and axial stretch on flow and stress/strain distributions. Six models were used in the simulation: Model 1, Baseline anisotropic model with plaque components, cyclic bending and pulsating pressure as prescribed in Section 2; Model 2, same as Model 1, but no bending; Model 3, same as Model 1, but no plaque components, i.e., the same material properties were assigned to Ca and lipid core components; Model 4 is the same as Model 1, but with no phase angle between cyclic bending and pressure. Maximum pressure occurs with maximum bending; Model 5 has 10% axial pre-stretch added to Model 1; Model 6, same as Model 1, but isotropic model (matching circumferential stress-stretch curve) was used for the normal tissue. Because of that, it should be noted that vessel material in Model 6 is much stiffer than that in Model 1. For Model 5, the vessel was stretched (10% axial stretch) and pressurized first. Then the inlet and outlet were fixed and cyclic bending was applied.
3.1 Cyclic bending leads to considerable stress/strain variations in the plaque
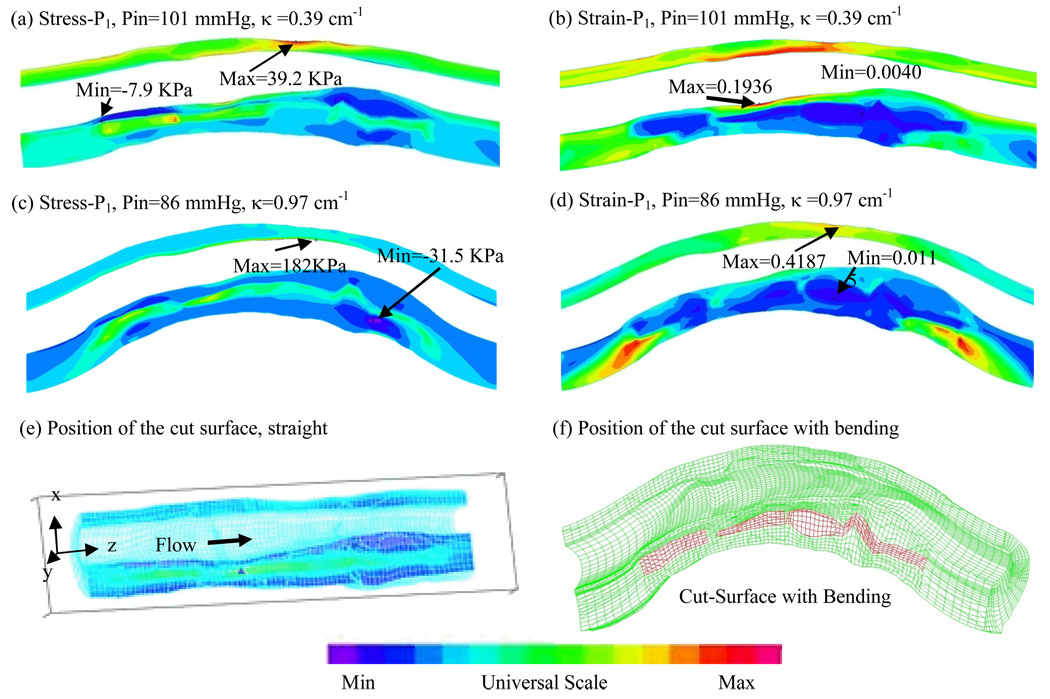
Figure 5 & Figure 6 give maximum principal stress (Stress-P1) and maximum principal strain (Strain-P1) plots from Model 1 (with cyclic bending) and Model 2 (without cyclic bending), corresponding to maximum and minimum curvature conditions in one cardiac cycle.
Figure 5.
Cyclic bending leads to large stress/strain variations: Stress-P1/Strain-P1 distributions from Model 1 (with cyclic bending) corresponding to maximum and minimum curvature conditions. Position of the cut-surface is shown.
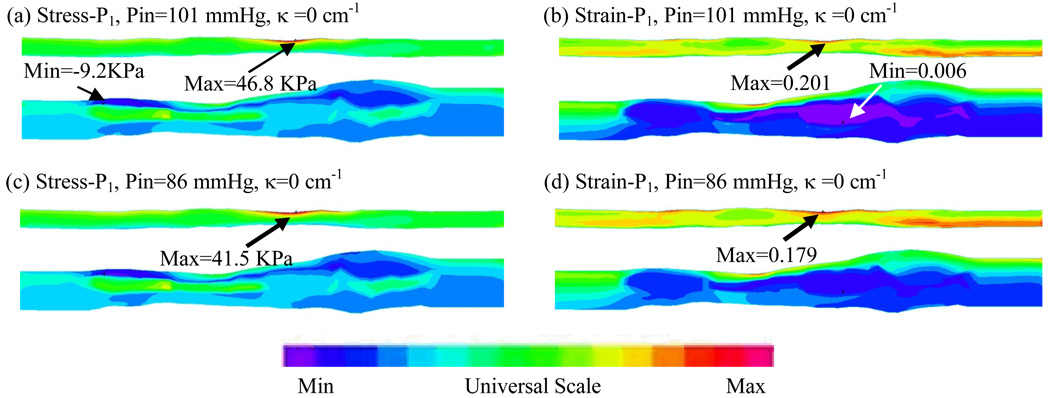
Figure 6.
Stress-P1/Strain-P1 distributions from Model 2 (no cyclic bending) show only modest variations caused by imposed pulsating pressure conditions.
For Model 1, Maximum Stress-P1 from Fig. 5(c) (maximum curvature) was 360% higher than that from Fig. 5(a) (minimum curvature) even though pressure was lower in (c). Maximum Stress-P1 value from Fig. 5(c) (the bending case) was also 340% higher than that from the no-bending case (Fig. 6(c)). Maximum Strain-P1 value from Fig. 5(d) (the bending case) was also 134% higher than that from the no-bending case (Fig. 6(d)). Fig. 6 shows that stress/strain variations are dominated by pressure changes when no cyclic bending is imposed. Strain distributions in the plaque showed similar behaviors. These results show very clearly that cyclic bending leads to large stress/strain increases (100–360%) in the plaque and must be included in computational models for coronary plaques for accurate stress/strain predictions. Two significant figures were used percentage calculations.
3.2 Cyclic bending caused only modest flow velocity and shear stress changes
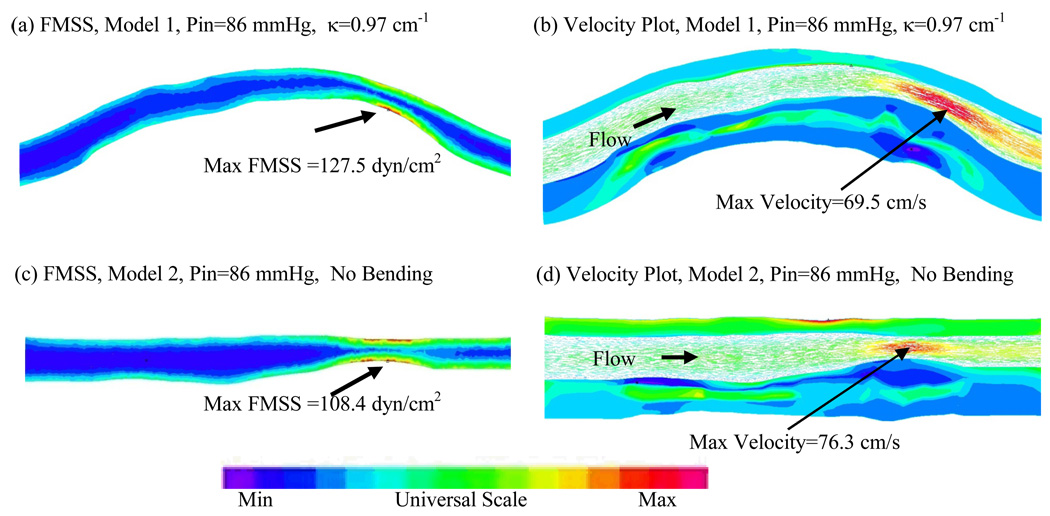
Effects of cyclic bending on flow behaviors are more modest because flow is more closely related to pressure drop across the plaque segment which was kept the same for both bending and no-bending models. Cyclic bending does increase flow resistant because of the increased curvature. Figure 7 compares flow maximum shear stress (FMSS) and velocity for the bending and no-bending cases corresponding to the time step with maximum curvature. Table 1 lists the maximum FMSS and velocity values for three curvature conditions. Maximum velocity from Model 1 corresponding to maximum curvature was 69.5 cm/s, which increased to 76.3 cm/s for the no-bending case, a 9.8 % increase. FMSS actually decreased from 127.5 dyn/cm2 for the bending case to 108.4 dyn/cm2 (15%) for the non-bending case. It should be noted that computational maximum values were observed at only one or a few computational nodal points, while experimental data measured by medical devices are often averaged values of the selected region of interest (ROI). A second effect of bending may be seen in the overall flow rate during the cardiac cycle (see Fig. 3). Maximum flow rates were 131.8 ml/min with bending, and 135.2 ml/min (2.5% increase) without bending, respectively, likely due to additional viscous losses associated with the changing curvatures.
Figure 7.
Comparison of flow maximum shear stress (FMSS) and velocity plots from Model 1 (with bending) and Model 2 (no bending) shows that cyclic bending has modest effects (<15%) on flow velocity and maximum shear stress.
Table 1.
Comparison of maximum flow maximum shear stress (FMSS) and velocity values from Model 1 (with bending) and Model 2 (no bending) shows that cyclic bending has modest effects (<15%) on flow velocity and maximum shear stress.
| Cases | Max Velocity | Max FMSS | Max Velocity | Max FMSS | Max Velocity | Max FMSS |
|---|---|---|---|---|---|---|
| Model 1 | κ=0.39 1/cm, Pin=101 | κ=0.78 1/cm, Pin=130 | κ=0.97 1/cm, Pin=86 | |||
| Baseline | 98.7 | 147.5 | 133.6 | 236.1 | 69.5 | 127.5 |
| Model 2 | κ=0, Pin=101 | κ=0, Pin=130 | κ=0, Pin=86 | |||
| No Bending | 99.1 | 140.9 | 135.1 | 195.7 | 76.3 | 108.4 |
3.3 Combined effects of bending with plaque components, phase angle and axial stretch
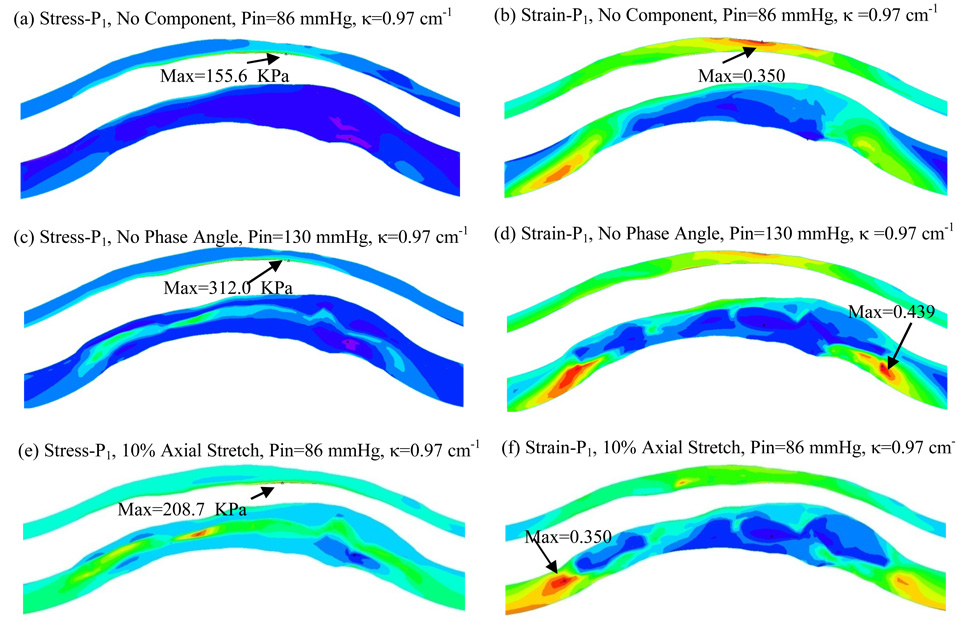
Our previous papers investigated the effects of major contributing factors for stress-strain distributions in the plaque [31–34,42–44,50]. Those factors included plaque morphology, plaque structure with components, pressure condition, material properties, and axial stretch. Figure 8 gives Stress-P1 and Strain-P1 plots from Model 3 (no plaque components), Model 4 (no phase angle) and Model 5 (with 10 axial stretch) to show the patterns of stress/strain distributions. Table 2 lists the maximum Stress-P1/Strain-P1 from Models 1–5 corresponding to maximum and minimum curvature/pressure conditions. Maximum Stress-P1 and Strain-P1 from Model 1 at minimum curvature were used as the base numbers for comparison purpose. Overall, cyclic bending led to 300%–800% higher maximum stress values and 80%–185% higher maximum strain values. Models without plaque components led to slightly less stress/strain variations because stress/strain distributions were more uniform (Fig. 8 (a)–(b)). When maximum pressure and maximum bending occurred simultaneously (α=0, α is the phase angle between maximum curvature and maximum pressure), maximum stress value was 696% higher than the base stress value. With a 10% axial stretch added to Model 1, maximum Stress-P1 value for κ=0.39 1/cm, Pin=101 mmHg increased to 133.4 KPa, a 240% increase from that of Model 1. However, effects of each contributing factor on stress/strain distributions were of localized nature, and were not uniform for the cardiac cycle. Localized stress/strain behaviors will be tracked at selected sites and results will be presented in 3.5.
Figure 8.
Combined effects of plaque components, pressure/curvature phase angle and axial stretch with cyclic bending on stress/strain distributions.
Table 2.
Summary of maximum Stress-P1 and Strain-P1 values from five models showing that cyclic bending has large effects on stress/strain values in coronary plaques.
| Cases | Max Stress-P1 (KPa) | Max Strain-P1 | Max Stress-P1 (KPa) | Max Strain-P1 |
|---|---|---|---|---|
| κ=0.39 1/cm, Pin=101 | κ=0.97 1/cm, Pin=86 | |||
| Model 1 | 39.2 (100%) | 0.194 (100%) | 182 (464%) | 0.419 (216%) |
| Model 2 | 46.8 (119%) | 0.201 (104%) | 41.5 (106%) | 0.179 (92.2%) |
| Model 3 | 38.1 (97.1%) | 0.187 (96.4%) | 155.6 (397%) | 0.350 (180%) |
| Model 5 | 133.4 (340%) | 0.372 (192%) | 208.7 (532%) | 0.553 (285%) |
| Model 4 | κ=0.39 1/cm, Pin=96.4 | κ=0.97 1/cm, Pin=130 | ||
| 37.4 (95.4%) | 0.185 (95.3%) | 312.0 (796%) | 0.439 (226%) | |
3.4. Comparison of anisotropic and isotropic models
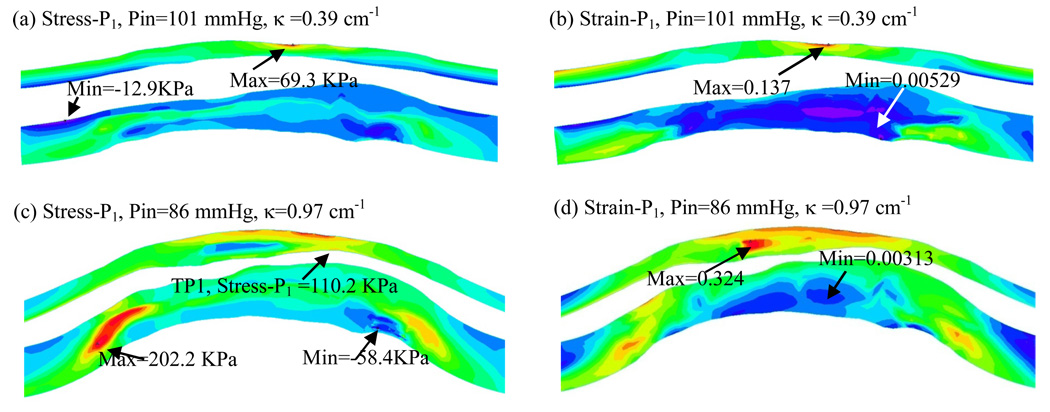
The measured circumferential stress-stretch data from the human coronary specimen was used to construct an isotropic model with cyclic bending to quantify the differences between the anisotropic and isotropic models. It should be noted that the normal tissue in the isotropic model is stiffer compared to that in the anisotropic model because circumferential stress-stretch data was used. Figure 9 presents Stress-P1 and Strain-P1 plots from Model 6 (isotropic with cyclic bending) corresponding to maximum and minimum curvature conditions. Strain values from Model 6 are noticeably lower because the material used is stiffer. Location of maximum Stress-P1 is different for the maximum curvature case (Fig. 9(c)). Using the same location at Tracking Point 1 (TP1), Stress-P1 value (110.2 KPa) from Model 6 is 65% lower than that from Model 1 (182KPa). Stress differences caused by the calcification block is more noticeable in Fig. 5(c) than that in Fig. 9(c) because of the stiffer normal tissue material in Model 6. Clearer comparisons will be shown by tracking stress/strain behaviors at selected sites in next section.
Figure 9.
Stress/Strain plots from the isotropic model (Model 6) with cyclic bending showing different stress/strain distribution patterns.
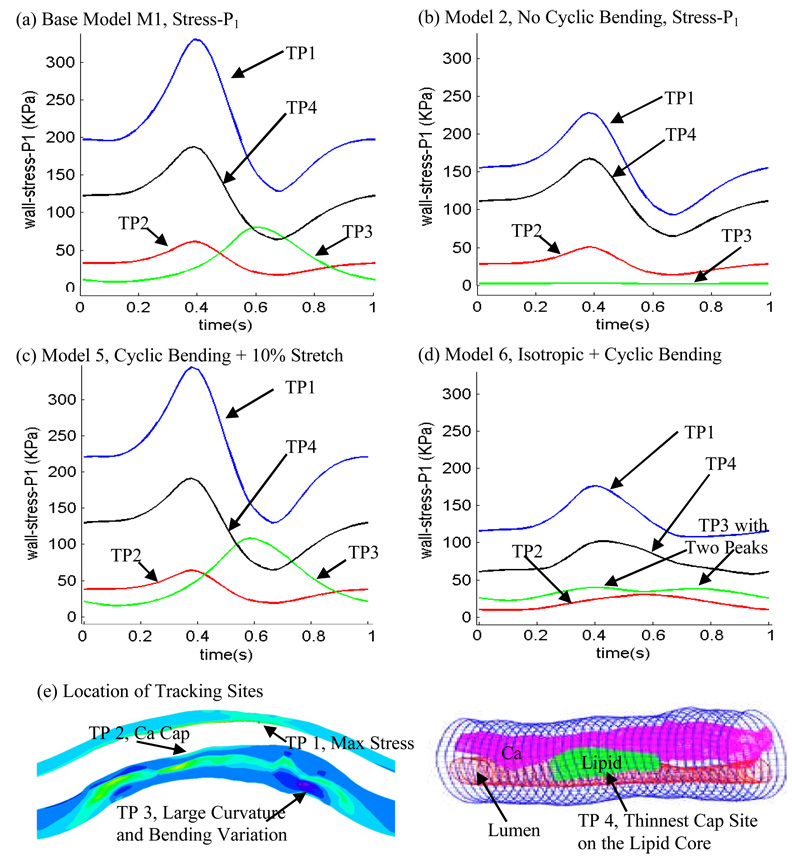
3.5. Local stress/strain behaviors tracked at selected critical sites
With so many factors involved, it is hard to compare the differences of 4D (time + 3D space) stress/strain distributions from different models. It has also been reported that plaque vulnerability may be more closely associated with local stress/strain behaviors than with global maximum stress/strain values [32]. With those in mind, Fig. 10 shows Stress-P1 variations from 4 models tracked at four selected sites. Track Point 1 (TP1) is the location where global maximum Stress-P1 was found under maximum curvature for Models 1, 3–5. Track Point 2 (TP2) is located at the plaque cap (thinnest site) over the calcification block. Track Point 3 (TP3) is at a location where the plaque has a large local curvature. Track Point 4 (TP4) is located at the plaque cap (thinnest site) over the lipid pool (Fig. 10(e)). Maximum and minimum values of all tracking curves from the 6 models are summarized in Table 3. Several observations can be made from the curves in Fig. 10: a) Effects of cyclic bending and pulsating pressure depends heavily on the location of the tracking sites. TP1, TP2 and TP4 are on lumen surface and Stress-P1 was affected by the pulsating pressure most. TP3 is located at the outer surface of the vessel which is affected the least by pressure. Being on the bending side, Stress-P1 is affected the most by cyclic bending, reaching its maximum at maximum bending. Overall, effect of cyclic bending is the strongest on the bending side (the lower edge of the vessel), and becomes weaker as the location moves further away from the bending side. Effect of pulsating pressure becomes less as we move towards the outer surface of the vessel; b) Stress-P1 variations are greater at the cap on lipid pool than that on the cap on the calcification block; c) Peak Stress-P1 values from Model 1 at TP1, TP2 and TP4 are 44.5%, 21.6, 11.2% higher from Model 2. More noticeably, peak Stress-P1 value (80.3) at TP3 is 26.7 times higher than that from the near-zero stress values (peak value = 2.90 KPa) from Model 2; d) In general, Stress-P1 values from the anisotropic models tracked at TP1-TP4 were about 80%–100% higher than those from the isotropic model (Model 6). The peaking time showed some delay at TP1, TP2 and TP4. TP3 curve has two peaks, indicating that the bending and pressure effects were at a balancing point. Table 3 offers maximum and minimum values for the 4 tracking points from 6 models.
Figure 10.
Local Stress-P1 variations tracked at four selected locations from four models showing cyclic bending causes large stress variations in the coronary plaque. TP1: a location where global maximum Stress-P1 was found; TP2: calcification plaque cap (thinnest site); TP3: a location on the bending side with a large local curvature; TP4: lipid pool plaque cap.
Table 3.
Summary of maximum and minimum Stress-P1 and Strain-P1 values in one cardiac cycle at four tracking sites from six models showing that cyclic bending and anisotropic properties have large effects on critical stress/strain values in coronary plaques. Track point definitions were given in the paper.
| Model | TP1 Max Stress-P1 (KPa) |
TP2 Max Stress-P1 (KPa) |
TP3 Max Stress-P1 (KPa) |
TP4 Max Stress-P1 (KPa) |
TP1 Max Strain-P1 |
TP2 Max Strain-P1 |
TP3 Max Strain-P1 |
TP4 Max Strain-P1 |
|---|---|---|---|---|---|---|---|---|
| Model 1 | 329.9 | 61.4 | 80.3 | 187.9 | 0.5019 | 0.2446 | 0.3955 | 0.3382 |
| Model 2 | 228.3 | 50.5 | 2.89 | 167.4 | 0.5251 | 0.2318 | 0.0420 | 0.3329 |
| Model 3 | 309.7 | 51.8 | 22.41 | 136.8 | 0.4719 | 0.2184 | 0.1857 | 0.3188 |
| Model 4 | 343.5 | 61.5 | 66.67 | 183.2 | 0.4942 | 0.2449 | 0.3816 | 0.3352 |
| Model 5 | 344.7 | 64.2 | 108.3 | 191.1 | 0.4933 | 0.2481 | 0.4168 | 0.3423 |
| Model 6 | 176.3 | 30.2 | 39.72 | 102.0 | 0.2231 | 0.1063 | 0.1268 | 0.2025 |
| Model | TP1 Min Stress-P1 (KPa) |
TP2 Min Stress-P1 (KPa) |
TP3 Min Stress-P1 (KPa) |
TP4 Min Stress-P1 (KPa) |
TP1 Min Strain-P1 |
TP2 Min Strain-P1 |
TP3 Min Strain-P1 |
TP4 Min Strain-P1 |
| Model 1 | 128.4 | 16.86 | 7.56 | 64.16 | 0.3786 | 0.1318 | 0.1012 | 0.2387 |
| Model 2 | 93.3 | 13.63 | 1.63 | 64.89 | 0.3937 | 0.1228 | 0.0192 | 0.2460 |
| Model 3 | 126.3 | 13.32 | 6.14 | 41.52 | 0.3604 | 0.1063 | 0.0627 | 0.2070 |
| Model 4 | 123.4 | 16.80 | 7.82 | 67.76 | 0.3851 | 0.1304 | 0.1041 | 0.2431 |
| Model 5 | 129.8 | 18.90 | 15.23 | 64.67 | 0.3722 | 0.1623 | 0.1063 | 0.2723 |
| Model 6 | 107.8 | 9.41 | 22.18 | 57.70 | 0.1670 | 0.0479 | 0.0935 | 0.1049 |
These results indicate that cyclic bending, anisotropic properties, pressure, plaque components, and axial stretch are major contributing factors to stress conditions in coronary plaques. Their effects on stress distributions can be in the order of 50% – 800% depending on location and contributing factors. Combined effects may lead to complex stress/strain behavior changes. Our localized tracking technique may be the right approach to reveal critical stress/strain information at rupture-prone sites for better plaque assessment.
4. Discussion
4.1 Critical site tracking (CST) method to study complex flow and stress/strain behaviors
It can be seen clearly that 3D flow and stress/strain behaviors in the plaque are very complex. It is hard to quantify the effect of the contributing factors (five considered in this paper: cyclic bending, anisotropic material properties, pulsating pressure, plaque structure, and axial stretch) in the time-dependent full 3D setting, especially when several factors are combined at the same time. Our critical site tracking (CST) method reduces the full 3D investigation to site-tracking at selected locations and helps to identify the useful and relevant information much more clearly with less effort. Our results presented in Section 3.5 demonstrate the effectiveness of the CST method. It has been shown that plaque vulnerability may correlate more closely with stress/strain values at certain critical sites which are prone to rupture. This suggests that CST method could be used in atherosclerotic plaque assessment and other investigations where localized information are critical to the problem being investigated.
4.2 Benchmark model for coronary plaques: major contributing factors to plaque stress/strain distributions
It is of vital importance to choose a coronary plaque model with proper model assumptions and initial and boundary conditions so that accurate flow and stress/strain information can be obtained for rupture risk assessment. The model should be as simple as possible so that cost and effort could be minimized, yet “complete” enough to include all major factors contributing to the problem (plaque mechanical analysis and vulnerability assessment) under investigation. We have demonstrated that blood pressure, material properties, plaque structure and components, fluid-structure interactions, initial pressurization and axial stretch are important and should be included in plaque models. In this paper, anisotropic vessel properties and cyclic bending are added into the “major factor” list. Our results indicate that each of the five major factors (pulsating pressure, cyclic bending, material properties, plaque structure, and axial stretch) may affect critical stress and strain conditions from 50% to 800% or even more. It should be understood that results presented here were from one plaque sample. More patient studies (including healthy volunteers) are needed to generate a database for benchmark ranges of biological parameters and critical flow and stress/strain values. The order of importance of high blood pressure, plaque components and structure, cyclic bending, material properties, and axial stretch should be carefully evaluated using more plaque samples with a wide range of combinations of various components, especially large lipid pools and thin caps.
The current model did not include turbulence, lumen surface weakening and inflammation, vessel viscoelastic properties, and non-Newtonian flow properties. Turbulence may be present for severe stenosis and may be considered in our future effort. Our guess is that effect of turbulence will be more to the flow side, and limited to the structure side. Lumen surface condition will be very important for plaque vulnerability analysis and will be included in our model by adjusting the stiffness of the area affected when such data becomes available. It is known that vessel viscoelastic properties and non-Newtonian flow properties have very limited effects (< 5%) on flow and stress/strain values and could be omitted for cost saving [34,42].
4.3 Adding cyclic bending to coronary plaque models with more realistic heart motion
Our results demonstrated that adding cyclic bending to coronary plaque models will change stress predictions up to 100% or more which makes cyclic bending a necessary modeling addition to have accurate stress-strain predictions and stress-based vulnerability assessment. It should be noted that cyclic bending was added in this paper by imposing a cyclic displacement at the lower edge of the vessel. It would be more realistic if the vessel could be combined with a heart model or at least placed on a sphere so that the bending and stretching would be more realistic [29]. It is possible that an atherosclerotic artery, which might be rigidified by fibrotic and calcified components, may exhibit smaller amplitude of curvature variations.
4.4 More accurate material property measurements
The anisotropic vessel material property used in this paper was obtained from one human coronary plaque sample. It is only an illustration of potential systematic approach where MRI data and mechanical testing could be from the same plaque samples. Material properties of human coronary atherosclerotic plaques are not available in the current literature. While our measurements were consistent with results in [48] in which material properties of 107 tissue samples from 9 human iliac high grade stenotic plaques were reported, more samples and patient-specific material data (when possible) should be obtained for our model to get more accurate predictions. It is also desirable to have direct measurements of material properties of plaque components such as calcifications, lipid pool (special technique needed since it is very soft), and other tissue types. Those will be the focus of our future efforts.
4.5. Limitations on available in vivo human data
The plaque model was constructed based on ex vivo MRI data. It is known that there are considerable differences between ex vivo and in vivo MR images [36,50]. Artery samples show considerable shrinkage from in vivo to ex vivo conditions [50]. Lipid contents often leak out. There may be vessel deformation without supporting tissue tethers. It would be very desirable to have in vivo plaque images. At the same time, in vivo material properties, pressure and curvature conditions would also make computational plaque models more realistic. Our computational prediction may be greatly improved when the model can be constructed based on in vivo plaque morphology, pressure and curvature conditions. Those are our future challenges.
5. Conclusion
Our modeling study indicates that each of the five major contributing factors, i.e., cyclic bending, anisotropic material properties, pulsating pressure, plaque structure and axial stretch may affect critical stress/strain values in coronary plaques from 50% to 800% or more depending on locations and contributing factors. Critical site tracking (CST) method provides an efficient way for plaque mechanical analysis identifying critical stress/strain conditions in the full 3D data mining process. Peak wall stresses with bending may exceed critical ultimate strength values for the plaque cap suggesting induced rupture. Computational FSI models including cyclic bending, anisotropic material properties, plaque components and structure and axial stretch and accurate in vivo measurements of pressure and curvature variations should lead to significant improvement on stress-based plaque mechanical analysis and more accurate coronary plaque vulnerability assessment.
Acknowledgement
This research was supported in part by NSF/NIGMS DMS-0540684 and NIH R01 EB004759. Professor Yang was supported in part by a priority discipline grant of Beijing Normal University. Advice and guidance from Professor Morton Friedman at Duke University and Professor Roger Kamm at MIT are happily acknowledged.
REFERENCES
- 1.American Heart Association. Heart Disease and Stroke Statistics – 2003 Update. Dallas Tex: American Heart Association; 2003. [Google Scholar]
- 2.Fuster V, Cornhill JF, Dinsmore RE, Fallon JT, Insull W, Libby P, Nissen S, Rosenfeld ME, Wagner WD, editors. The Vulnerable Atherosclerotic Plaque: Understanding, Identification, and Modification. Armonk NY: Futura Publishing; 1998. [Google Scholar]
- 3.Fuster V, Stein B, Ambrose JA, Badimon L, Badimon JJ, Chesebro JH. Atherosclerotic Plaque Rupture and Thrombosis, Evolving Concept. Circulation. 1990;82 Supplement II:II-47–II-59. [PubMed] [Google Scholar]
- 4.Giddens DP, Zarins CK, Glagov S. The Role of Fluid Mechanics in the Localization and Detection of Atherosclerosis. J. Biomech. Engng. 1993;115:588–594. doi: 10.1115/1.2895545. [DOI] [PubMed] [Google Scholar]
- 5.Naghavi M, Libby P, Falk E, Casscells SW, Litovsky S, Rumberger J, Badimon JJ, Stefanadis C, Moreno P, Pasterkamp G, Fayad Z, Stone PH, Waxman S, Raggi P, Madjid M, Zarrabi A, Burke A, Yuan C, Fitzgerald PJ, Siscovick DS, de Korte CL, Aikawa M, Juhani Airaksinen KE, Assmann G, Becker CR, Chesebro JH, Farb A, Galis ZS, Jackson C, Jang IK, Koenig W, Lodder RA, March K, Demirovic J, Navab M, Priori SG, Rekhter MD, Bahr R, Grundy SM, Mehran R, Colombo A, Boerwinkle E, Ballantyne C, Insull W, Jr, Schwartz RS, Vogel R, Serruys PW, Hansson GK, Faxon DP, Kaul S, Drexler H, Greenland P, Muller JE, Virmani R, Ridker PM, Zipes DP, Shah PK, Willerson JT. From Vulnerable Plaque to Vulnerable Patient: a Call for New Definitions and Risk Assessment Strategies: I. Circulation. 2003;108(14):1664–1672. doi: 10.1161/01.CIR.0000087480.94275.97. [DOI] [PubMed] [Google Scholar]
- 6.Naghavi M, Libby P, Falk E, Casscells SW, Litovsky S, Rumberger J, Badimon JJ, Stefanadis C, Moreno P, Pasterkamp G, Fayad Z, Stone PH, Waxman S, Raggi P, Madjid M, Zarrabi A, Burke A, Yuan C, Fitzgerald PJ, Siscovick DS, de Korte CL, Aikawa M, Juhani Airaksinen KE, Assmann G, Becker CR, Chesebro JH, Farb A, Galis ZS, Jackson C, Jang IK, Koenig W, Lodder RA, March K, Demirovic J, Navab M, Priori SG, Rekhter MD, Bahr R, Grundy SM, Mehran R, Colombo A, Boerwinkle E, Ballantyne C, Insull W, Jr, Schwartz RS, Vogel R, Serruys PW, Hansson GK, Faxon DP, Kaul S, Drexler H, Greenland P, Muller JE, Virmani R, Ridker PM, Zipes DP, Shah PK, Willerson JT. From Vulnerable Plaque to Vulnerable Patient: a Call for New Definitions and Risk Assessment Strategies: Part II. Circulation. 2003;108(15):1772–1778. doi: 10.1161/01.CIR.0000087481.55887.C9. [DOI] [PubMed] [Google Scholar]
- 7.Association for Eradication of Heart Attack (AEHA) Leaders in Cardiology from AEHA’s National SHAPE Task Force Propose New. AEHA Press Release, BusinessWire; 2005. http://www.businesswire.com/cgi-bin/mmg.cgi?eid=4835722. [Google Scholar]
- 8.Bock RW, Gray-Weale AC, Mock FP, Stats MA, Robinson DA, Irwig L, Lusby RJ. The Natural History of Asymptomatic Carotid Artery Disease. J. Vasc Surg. 1993;17:160–171. doi: 10.1067/mva.1993.43142. [DOI] [PubMed] [Google Scholar]
- 9.Boyle JJ. Association of Coronary Plaque Rupture and Atherosclerotic Inflammation. J. Pathology. 1997;181:93–99. doi: 10.1002/(SICI)1096-9896(199701)181:1<93::AID-PATH696>3.0.CO;2-H. [DOI] [PubMed] [Google Scholar]
- 10.Burke AP, Farb A, Malcom GT, Liang YH, Smialek JE, Virmani R. Plaque Rupture and Sudden Death Related to Exertion in Men with Coronary Artery Disease. JAMA: J. of American Medical Association. 1999;281:921–926. doi: 10.1001/jama.281.10.921. [DOI] [PubMed] [Google Scholar]
- 11.Falk E, Shah PK, Fuster V. Coronary Plaque Disruption. Circulation. 1995;92:657–671. doi: 10.1161/01.cir.92.3.657. [DOI] [PubMed] [Google Scholar]
- 12.Ohayon J, Pierre T, Finet G, Rioufol G. In-Vivo Prediction of Human Coronary Plaque Rupture Location Using Intravascular Ultrasound and the Finite Element Method. Coronary Artery Disease. 2001;12:655–663. doi: 10.1097/00019501-200112000-00009. [DOI] [PubMed] [Google Scholar]
- 13.Park JBR, Tobis JM. Spontaneous Plaque Rupture and Thrombus Formation in the Left Main Coronary Artery Documented by Intravascular Ultrasound. Catheterization and Cardiovascular Diagnosis. 1997;40:358–360. doi: 10.1002/(sici)1097-0304(199704)40:4<358::aid-ccd7>3.0.co;2-8. [DOI] [PubMed] [Google Scholar]
- 14.Shah PK. Pathophysiology of Coronary Thrombosis: Role of Plaque Rupture and Plaque Erosion. Prog. Cardiovasc. Dis. 2002;44(5):357–368. doi: 10.1053/pcad.2002.123473. [DOI] [PubMed] [Google Scholar]
- 15.Virmani R, Kolodgie FD, Burke AP, Farb A, Schwartz SM. Lessons from Sudden Coronary Death: a Comprehensive Morphological Classification Scheme for Atherosclerotic Lesions. Arterioscler Thromb Vasc Biol. 2000;20(5):1262–1275. doi: 10.1161/01.atv.20.5.1262. [DOI] [PubMed] [Google Scholar]
- 16.van der Wal AC, Becker AE, van der Loos CM, Das PK. Site of Intimal Rupture or Erosion of Thrombosed Coronary Atherosclerotic Plaques Is Characterized by an Inflammatory Process Irrespective of the Dominant Plaque Morphology. Circulation. 1994;89:36–44. doi: 10.1161/01.cir.89.1.36. [DOI] [PubMed] [Google Scholar]
- 17.Gatehouse PD, Keegan J, Crowe LA, Masood S, Mohiaddin RH, Kreitner KF, Firmin DN. Applications of Phase-Contrast Flow and Velocity Imaging in Cardiovascular MRI. Eur Radiol. 2005;15(10):2172–2184. doi: 10.1007/s00330-005-2829-3. [DOI] [PubMed] [Google Scholar]
- 18.Tang D, Yang C, Yuan C. Mechanical Image Analysis Using Finite Element Method. In: Gillard JH, Hatsukami TS, Graves M, Yuan C, editors. Carotid Disease: The Role of Imaging in Diagnosis and Management. Cambridge, England: Cambridge University Press; 2006. pp. 323–339. [Google Scholar]
- 19.Yuan C, Mitsumori LM, Beach KW, Maravilla KR. Special Review: Carotid Atherosclerotic Plaque: Noninvasive MR Characterization and Identification of Vulnerable Lesions. Radiology. 2001;221:285–299. doi: 10.1148/radiol.2212001612. [DOI] [PubMed] [Google Scholar]
- 20.Pedersen PC, Chakareski J, Lara-Montalvo R. Proc. for the 2003 SPIE Med Imaging Symposium. San Diego: 2003. Ultrasound Characterization of Arterial Wall Structures Based on Integrated Backscatter Profiles; pp. 115–126. [Google Scholar]
- 21.Liang Y, Zhu H, Friedman MH. Estimation of the Transverse Strain Tensor in the Arterial Wall Using IVUS Image Registration. Ultrasound Med Biol. 2008 doi: 10.1016/j.ultrasmedbio.2008.04.005. In press. [DOI] [PubMed] [Google Scholar]
- 22.McCord BN. Ph.D Thesis. Georgia Inst. of Tech. 1992. Fatigue of Atherosclerotic Plaque. [Google Scholar]
- 23.McCord BN, Ku DN. Mechanical Rupture of the Atherosclerostic Plaque Fibrous Cap; Proceedings of 1993 Bioengineering Conference; Colorado: BED; 1993. pp. 324–327. [Google Scholar]
- 24.Cheng GC, Loree HM, Kamm RD, Fishbein MC, Lee RT. Distribution of Circumferential Stress in Ruptured and Stable Atherosclerotic Lesions, a Structural Analysis with Histopathological Correlation. Circulation. 1993;87:1179–1187. doi: 10.1161/01.cir.87.4.1179. [DOI] [PubMed] [Google Scholar]
- 25.Holzapfel GA, Gasser TC, Ogden RW. A New Constitutive Framework for Arterial Wall Mechanics and a Comparative Study of Material Models. J. Elasticity. 2000;61:1–48. [Google Scholar]
- 26.Huang H, Virmani R, Younis H, Burke AP, Kamm RD, Lee RT. The Impact of Calcification on the Biomechanical Stability of Atherosclerotic Plaques. Circulation. 2001;103:1051–1056. doi: 10.1161/01.cir.103.8.1051. [DOI] [PubMed] [Google Scholar]
- 27.Kaazempur-Mofrad MR, Isasi AG, Younis HF, Chan RC, Hinton DP, Sukhova G, Lamuraglia GM, Lee RT, Kamm RD. Characterization of the Atherosclerotic Carotid Bifurcation Using MRI, Finite Element Modeling, and Histology. Annals of Biomedical Engineering. 2004;32(7):932–946. doi: 10.1023/b:abme.0000032456.16097.e0. [DOI] [PubMed] [Google Scholar]
- 28.Long Q, Xu XY, Ariff B, Thom SA, Hughes AD, Stanton AV. Reconstruction of Blood Flow Patterns in a Human Carotid Bifurcation: A Combined CFD and MRI Study. J. Magn. Reson. Imaging. 2000;11:299–311. doi: 10.1002/(sici)1522-2586(200003)11:3<299::aid-jmri9>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
- 29.Prosi M, Perktold K, Ding Z, Friedman MH. Influence of Curvature Dynamics on Pulsatile Coronary Artery Flow in a Realistic Bifurcation Model. J. Biomech. 2004;37:1767–1775. doi: 10.1016/j.jbiomech.2004.01.021. [DOI] [PubMed] [Google Scholar]
- 30.Steinman DA. Image-Based Computational Fluid Dynamics Modeling in Realistic Arterial Geometries. Ann. Biomed. Eng. 2002;30(4):483–497. doi: 10.1114/1.1467679. [DOI] [PubMed] [Google Scholar]
- 31.Tang D, Yang C, Zheng J, Woodard PK, Saffitz JE, Sicard GA, Pilgram TK, Yuan C. Quantifying Effects of Plaque Structure and Material Properties on Stress Behaviors in Human Atherosclerotic Plaques Using 3D FSI Models. J. Biomech. Eng. 2005;127(7):1185–1194. doi: 10.1115/1.2073668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tang D, Yang C, Zheng J, Woodard PK, Saffitz JE, Petruccelli JD, Sicard GA, Yuan C. Local Maximal Stress Hypothesis and Computational Plaque Vulnerability Index for Atherosclerotic Plaque Assessment. Ann. Biomed. Eng. 2005;33(12):1789–1801. doi: 10.1007/s10439-005-8267-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Tang D, Yang C, Zheng J, Woodard OK, Sicard GA, Saffitz JE, Yuan C. 3D MRI-Based Multi-Component FSI Models for Atherosclerotic Plaques a 3-D FSI model. Ann. Biomed. Eng. 2004;32(7):947–960. doi: 10.1023/b:abme.0000032457.10191.e0. [DOI] [PubMed] [Google Scholar]
- 34.Yang C, Tang D, Yuan C, Hatsukami TS, Zheng J, Woodard PK. In Vivo/Ex Vivo MRI-Based 3D Models with Fluid-Structure Interactions for Human Atherosclerotic Plaques Compared with Fluid/Wall-Only Models. CMES: Comput. Model. Eng. Sci. 2007;19(3):233–245. [PMC free article] [PubMed] [Google Scholar]
- 35.Tang D. Wiley Encyclopedia of Biomedical Engineering, Article 1525. New Jersey: John Wiley & Sons, Inc.; 2006. Flow in Healthy and Stenosed Arteries; pp. 1–16. [Google Scholar]
- 36.Humphrey JD. Cardiovascular Solid Mechanics. New York: Springer-Verlag; 2002. [Google Scholar]
- 37.Ku DN. Blood flow in arteries. Annu. Rev. Fluid Mech. 1997;29:399–434. [Google Scholar]
- 38.Moore JE, Jr, Weydahl ES, Santamarina A. Frequency Dependence of Dynamic Curvature Effects on Flow through Coronary Arteries. J Biomech Eng. 2001;123(2):129–133. doi: 10.1115/1.1351806. [DOI] [PubMed] [Google Scholar]
- 39.Balestrini J, Billiar KL. Magnitude and duration of Stretch Modulates Fibroblast Remodeling of Fibrin Gels. J. Biomech. Eng. doi: 10.1115/1.3049527. In Press. [DOI] [PubMed] [Google Scholar]
- 40.Bathe KJ. Finite Element Procedures. New Jersey: Prentice Hall, Inc.; 1996. [Google Scholar]
- 41.Bathe KJ, editor. ADINA and ADINA-F. Vol I & II. Watertown: ADINA R & D, Inc.; 2007. Theory and Modeling Guide. [Google Scholar]
- 42.Tang D, Chen X, Yang C, Kobayashi S, Ku DN. A Viscoelastic Model and Meshless GFD Method for Blood Flow in Collapsible Stenotic Arteries. Advances in Computational Engineering & Sciences, Chap. 11; International Conference on Computational Engineering and Sciences; Norcross, GA: Tech Science Press.; 2002. [Google Scholar]
- 43.Tang D, Yang C, Kobayashi S, Zheng J, Vito RP. Effects of Stenosis Asymmetry on Blood Flow and Artery Compression: a 3-D FSI Model. Ann. Biomed. Eng. 2003;31:1182–1193. doi: 10.1114/1.1615577. [DOI] [PubMed] [Google Scholar]
- 44.Tang D, Yang C, Kobayashi S, Ku DN. Effect of a Lipid Pool on Stress/Strain Distributions in Stenotic Arteries: 3D FSI Models. J. Biomech. Eng. 2004;126:363–370. doi: 10.1115/1.1762898. [DOI] [PubMed] [Google Scholar]
- 45.Kobayashi S, Tsunoda D, Fukuzawa Y, Morikawa H, Tang D, Ku DN. Flow and Compression in Arterial Models of Stenosis with Lipid Core; Proceedings of 2003 ASME Summer Bioengineering Conference; 2003. pp. 497–498. [Google Scholar]
- 46.Kobayashi S, Fukuzawa Y, Ayama Y, Morikawa H, Tang D, Ku DN. Pulsatile Flow And Deformation In Curved Stenosis Models Of Arterial Disease - Influence Of Cyclic Change Of Curvature On Flow And Deformation; Proceedings of ASME 2005 Summer Bioengineering Conference, paper #: b0062819.2005. [Google Scholar]
- 47.Holzapfel GA, Stadler M, Schulze-Bause CAJ. A Layer-Specific Three-Dimensional Model for the Simulation of Balloon Angioplasty Using Magnetic Resonance Imaging and Mechanical Testing. Ann. Biomed. Eng. 2002;30(6):753–767. doi: 10.1114/1.1492812. [DOI] [PubMed] [Google Scholar]
- 48.Holzapfel GA, Sommer G, Regitnig P. Anisotropic Mechanical Properties of Tissue Components in Human Atherosclerotic Plaques. J. Biomech. Eng. 2004;126(5):657–665. doi: 10.1115/1.1800557. [DOI] [PubMed] [Google Scholar]
- 49.Friedman MH, Bargeron CB, Deters OJ, Hutchins GM, Mark FF. Correlation between Wall Shear and Intimal Thickness at a Coronary Artery Branch. Atherosclerosis. 1987;68:27–33. doi: 10.1016/0021-9150(87)90090-6. [DOI] [PubMed] [Google Scholar]
- 50.Huang X, Yang C, Yuan C, Liu F, Canton G, Zheng J, Woodard PK, Sicard GA, Tang D. Patient-Specific Artery Shrinkage and 3D Zero-Stress State in Multi-Component 3D FSI Models for Carotid Atherosclerotic Plaques Based on In Vivo MRI Data. Journal of Molecular & Cellular Biomechanics, Special Volume dedicated to Y. C. Fung’s 90th birthday. 2008:337–350. [PMC free article] [PubMed] [Google Scholar]