Registration-based estimates of local lung tissue expansion compared to xenon-CT measures of specific ventilation

Abstract

The main function of the respiratory system is gas exchange. Since many disease or injury conditions can cause biomechanical or material property changes that can alter lung function, there is a great interest in measuring regional lung ventilation and regional specific volume change. We describe a registration-based technique for estimating local lung expansion from multiple respiratory-gated CT images of the thorax. The degree of regional lung expansion is measured using the Jacobian (a function of local partial derivatives) of the registration displacement field, which we show is directly related to specific volume change. We compare the ventral-dorsal patterns of lung expansion estimated across five pressure changes to a xenon CT based measure of specific ventilation in five anesthetized sheep studied in the supine orientation. Using 3D image registration to match images acquired at 10 cm H²O and 15 H²O airway pressures gave the best match between the average Jacobian and the xenon CT specific ventilation (linear regression, average r² = 0.73).

1 Introduction

The main function of the respiratory system is gas exchange. Regional ventilation depends on the mechanical relationships between the lungs, rib cage, diaphragm, and abdomen, which work together to generate expansile forces. Since many disease or injury conditions can change lung material properties, lung mechanics, and lung function, it is useful to understand both the global and local functional behavior of lungs.

Regional ventilation and regional lung strain have been measured directly and indirectly with a variety of invasive techniques (Hoffman et al., 1983a; Hubmayr et al., 1983; Robertson et al., 1997), with radioisotope imaging (Milic-Emili et al., 1966; Bunow et al., 1979; van der Mark et al., 1984), with X-ray computed tomography (CT) (Hoffman et al., 1983b, 1995; Hoffman and Ritman, 1985; Tajik et al., 2002; Chon et al., 2005, 2007), and with hyperpolarized gas magnetic resonance (MR) imaging (Wild et al., 2003; Woodhouse et al., 2005; Altes et al., 2006; Patz et al., 2007). Invasive methods, such as percutaneously or surgically implanted parenchymal markers or inhaled fluorescent microspheres are not possible to translate to humans. Radioisotope imaging, such as scintigraphy, single photon emission CT (SPECT), and positron emission tomography (PET), can provide a direct functional assessment of ventilation, but nuclear medicine imaging has low spatial resolution, and to obtain reasonable signal to noise ratios, one must usually image across many respiratory cycles, further reducing imaging resolution. Hyperpolarized gas MR imaging can image ventilation with sufficient temporal resolution so that the dynamics of gas flow patterns through the lung can be observed. Lung microstructure, such as alveolar size, can also be indirectly assessed using MR through the use of the so-called “apparent diffusion coefficient.” However, lung MR is currently only partially quantitative, does not depict much anatomic detail, and requires special equipment to hyperpolarize the gas used during imaging. CT imaging can provide high-resolution images of the lung, but this high spatial resolution usually comes at the cost of low temporal resolution (relative to the speed of gas transport in the airspaces) and/or limited spatial coverage. And while CT can produce excellent anatomic images, standard CT imaging does not typically provide for functional assessment.

Xenon-enhanced CT (Xe-CT) is a non-invasive method for the measurement of regional pulmonary ventilation. With Xe-CT, radiodense, non-radioactive xenon gas is inhaled and exhaled during imaging, and local ventilation time constants are calculated by observing the gas wash-in and wash-out rates on serial CT images (Simon and Marcucci, 1998; Marcucci et al., 2001; Tajik et al., 2002; Chon et al., 2005, 2007). Xenon gas provides enhancement on the CT proportional to the concentration of xenon in the region being imaged; enhancements as much as 150 to 200 Hounsfield units (HU) are possible with high concentrations of xenon (Marcucci et al., 2001; Tajik et al., 2002; Chon et al., 2005, 2007). Xe-CT is not without shortcomings. Xe-CT requires the use of expensive xenon gas and the associated hardware to control gas delivery. Additional hardware is needed if one wishes to harvest the expired gas for recycling during a re-breathing study. In addition, it is known that xenon gas has a strong anesthetic effect that must be carefully monitored. Finally, Xe-CT imaging protocols require high temporal resolution imaging, so axial coverage is usually limited. Z-axis coverage with modern multi-detector scanners currently ranges from about 2.5 to 12 cm, but the typical z-axis extent of the human lung is on the order of 25 cm. Nonetheless, recent work with the Xe-CT technique has re-established the interest in these methods for measuring regional ventilation. When combined with the unique capability of CT to describe lung anatomic detail, Xe-CT can provide detailed information on lung structure and respiratory function (Hoffman et al., 2003).

Imaging has long been used to study lung mechanics, and some investigators have studied the linkage between estimates of regional lung expansion and local lung ventilation (Hoffman et al., 1983a; Rodarte et al., 1985; Hoffman et al., 1986; Hubmayr et al., 1987; Guerrero et al., 2005; Sundaram and Gee, 2005; Guerrero et al., 2006). Sundaram and Gee have applied serial magnetic resonance imaging to the problem of studying lung mechanics. Using static breath-hold imaging they acquired a single sagittal cross-section of the lung at different inflations (Sundaram and Gee, 2005). Using non-linear image registration, they estimated a dense displacement field from one image to the other, and from the displacement field they computed regional lung strain. Guerrero et al. used two CT images, acquired at different lung inflations, and optical flow image registration to estimate regional ventilation to identify functioning vs. non-functioning lung tissue for radiotherapy treatment planning (Guerrero et al., 2005, 2006). While they were able to show a close correlation with global measurements of lung ventilation, their experimental methods did not allow them to compare local estimates of lung expansion with regional lung ventilation. Christensen et al. used image registration to match images across cine-CT sequences, and estimate rates of local tissue expansion and contraction (Christensen et al., 2007). Their measurements matched well with spirometry data, but they were not able to compare the registration-based measurements to local measures of regional tissue ventilation.

We describe a technique that uses multiple respiratory-gated CT images of the lung acquired at different levels of inflation, along with 3D image registration, to make local estimates of lung tissue expansion. We compare these lung expansion estimates to Xe-CT derived measures of regional ventilation to validate our measurements and establish their physiological significance. The ability to estimate regional ventilation maps for the entire lung from quickly and easily obtained respiratory-gated images is a significant contribution to functional lung imaging because of the potential increase in resolution, and large reductions in imaging time, radiation, and contrast agent exposure. The image registration also provides estimates of directional tissue strains, which may yield insights into the mechanics of regional ventilation.

2 Methods

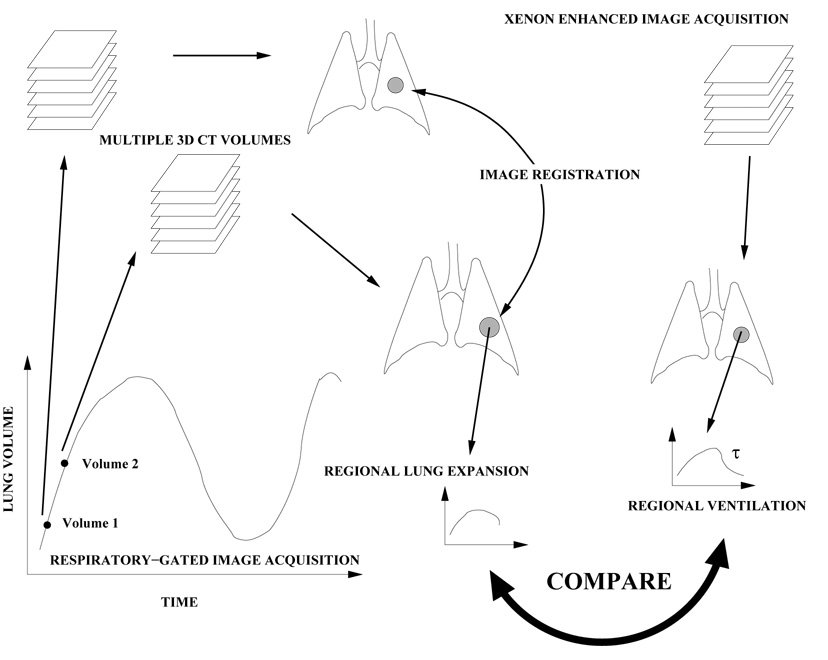
Figure 1 shows a block diagram of the entire process. Two or more respiratory-gated data sets are gathered at different points in the respiratory cycle, reflecting the state of the lung at two different volumes (and therefore, pressures). 3D image registration is used to create a voxel-by-voxel displacement map that shows the motion of the lung tissue as a function of respiratory state. The Jacobian of the displacement field is calculated for each voxel in the lung and is used to represent local tissue expansion. This index of tissue expansion is compared to Xe-CT based measures of lung ventilation.

Fig. 1.

Multiple volumetric CT images (in this case images at volume 1 and volume 2) are acquired at two different points in the respiratory cycle and analyzed to compute a voxel-by-voxel transformation from one image to another. The Jacobian of the transformation is used to estimate regional lung expansion. Xenon-enhanced CT imaging is used to estimate local time constants associated with ventilation. We compare the registration-derived measure of lung expansion with the xenon-based estimate of regional ventilation.

2.1 Data Sets and Image Acquisition

Appropriate animal ethics approval was obtained for these protocols from the University of Iowa Animal Care and Use Committee and the study adhered to NIH guidelines for animal experimentation. Five adult sheep were used for these experiments. All images were acquired with the animals in the supine orientation on a Siemens Sensation 64 multi-detector CT scanner (MDCT) (Siemens Medical Solutions; Erlangen, Germany). The animals were anesthetized using intravenous pentobarbital (2 cc of 50 mg/ml bolus, 2.5–5 mg/kg/hr maintenance), intubated, monitored for ECG and arterial pressure, and mechanically ventilated during the experiments.

2.1.1 Respiratory-Gated Volumetric CT

Volumetric CT scans covering the thorax are acquired at 0, 5, 10, 15, 20, and 25 cm H₂O (herein denoted as the P0, P5, P10, P15, P20, and P25 images) airway pressures with the animal held apneic. The scanning protocol uses a tube current of 100 mAs, a tube voltage 120 kVp, slice collimation of 0.6 mm, an effective slice thickness of 0.75 mm, a slice separation of 0.5 mm, a pitch of 1, a 360° rotation, a rotation time of 0.5 sec, a 512 by 512 reconstruction matrix, and a field of view selected to fit the lungs. Image reconstruction used a Siemens B30f kernel. All of the images are acquired without moving the animal between scans, so after acquisition the data sets are in rigid alignment.

2.1.2 Xenon CT

The axial locations for the Xe-CT studies are selected from the whole lung volumetric scan performed near end-expiration. Images are acquired with the scanner set in ventilation triggering mode, typically using 80 keV energy (for higher Xe signal enhancement), 160 mAs tube current, a 360° rotation, a 0.33 sec scan time, a 512 by 512 reconstruction matrix, and a field of view adjusted to fit the lung field of interest. The Xe-CT slice thickness is approximately 2.4 mm thick, or about 3.4 times thicker than the volumetric CT slices. Twelve contiguous xenon slices are acquired and provide approximately 3 cm of coverage along the axial direction. Respiratory gating during image acquisition is achieved by replacing the standard ECG gating signal with a trigger signal from a LabView program. Images were acquired at the end expiratory point during the respiratory cycle. A respiratory tidal volume of 8 cc/kg was used for the Xe-CT acquisition.

The image acquisition sequence is as follows. Acquisition starts and images are gathered as the animal breathes six to eight breaths of room air. Next, the xenon delivery system is turned on and approximately 40 breaths of pure xenon are delivered while imaging, and then the air source is switched back to room air for another 40 breaths. Thus, axial images are acquired for approximately 90 breaths as the xenon gas washes in and out of the lungs.

2.2 Image Registration

The volumetric images are registered pairwise according to airway pressure. We consider two methods of choosing the images that make up each pair. In the first method, we form pairs using a fixed pressure change of 5 cm H₂O, so that we register images P0 to P5, P5 to P10, etc., up to P20 to P25. In the second method, we consider different pressure changes from P0, so that we register images P0 to P5, P0 to P10, etc., up to P0 to P25. Both methods result in five pairs of registered images.

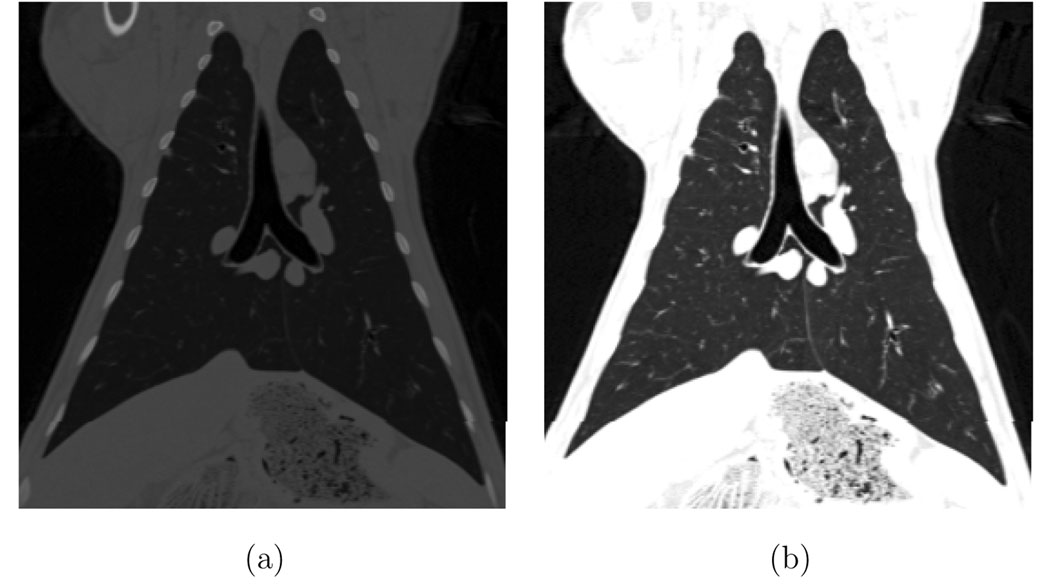
For this discussion we shall refer to the images under consideration as I₀ and I₁, where I₀ is the image from the image pair acquired at the lower pressure (i.e., P₀ from the pair P₀–P₅) and I₁ refers to the image acquired at the higher pressure (i.e., P5). The I₀ and I₁ volumetric images are registered using an intensity-based inverse consistent image registration algorithm (Christensen and Johnson, 2001; Johnson and Christensen, 2002). In this approach, the forward and reverse transformations between the two images are jointly estimated subject to the constraints that minimize the inverse consistency error, the intensity mismatch error, and the smoothness of the image transformation function. Before registration, we transform the CT values to 8-bit unsigned character voxels by mapping the range from [−1024, 0] HU to [0, 255]. CT values below −1024 HU are set to 0 and values above 0 HU are set to 255. This grayscale transformation highlights the intensity differences between the lung tissue and the surrounding chest wall, and between the lung tissue and the blood vessels and airway walls. An example coronal slice before and after this graylevel transformation is shown in Figure 2. No rigid alignment was required prior to registration since the animals were not moved between scans.

Fig. 2.

A grayscale window and level transformation maps the CT values in Hounsfield units to 8-bit unsigned integers prior to registration. (a) Original CT data. (b) After conversion to 8-bit.

The inverse consistent intensity registration is accomplished by minimizing this cost function:

$$\begin{array}{ll}C=\hfill & \sigma [C_{SIM}(I_0\circ h,I_1)+C_{SIM}(I_1\circ g,I_0)]+\hfill \\ \hfill & \chi [C_{ICC}(u,\tilde{w})+C_{ICC}(w,\tilde{u})]+\hfill \\ \hfill & \rho [C_{REG}(u)+C_{REG}(w)],\hfill \end{array}$$ (1)

where C_SIM, C_ICC, and C_REG are cost functions defined below. The functions u, w, u͂, w͂ are voxel displacement fields and are related to the forward and reverse transformations by the equations: h(x) = x + u(x), g(x) = x + w(x), h⁻¹(x) = x + u͂(x), g⁻¹(x) = x + w͂ (x).

The forward transformation h is used to deform the image I₀ into the shape of the image I₁, and the reverse transformation g is used to deform the shape of I₁ into that of I₀. The deformed template and target images are denoted by (I₀ ∘ h) and (I₁ ∘ g), respectively.

The cost functions in (1) are as defined in Christensen and Johnson (2001); Johnson and Christensen (2002). The C_SIM term of the cost function in equation 1 defines the symmetric intensity similarity. This term is designed to minimize the squared error intensity differences between the images. The C_ICC term is the inverse consistency constraint or inverse consistency error cost and is minimized when the forward and reverse transformations are inverses of each other. The C_REG term is a linear-elastic operator that is used to regularize the forward and reverse displacement fields. This term forces the displacement fields to be smooth and continuous. The constants σ χ and ρ are used to enforce/balance the constraints. In our registrations, we set the weighting constants σ = 1, χ = 600, and ρ = 0.00125. A multiresolution procedure is used to perform the full resolution registration of the images. We start at one-eighth resolution, and increase the resolution scale by a factor of two until we reach full resolution. The number of iterations used during the minimization of (1) is 500 iterations for the one-eighth and one-quarter scale steps, 100 iterations for one-half scale step, and 20 iterations for the full resolution step. When the registration process is complete, the displacement fields u and w (and u͂ and w͂) are voxel-by-voxel displacements between images I₀ and image I₁ that can be used to track arbitrary regions of interest across the portion of the respiratory cycle represented by the transition from I₀ to I₁.

2.3 Xenon CT Ventilation Analysis

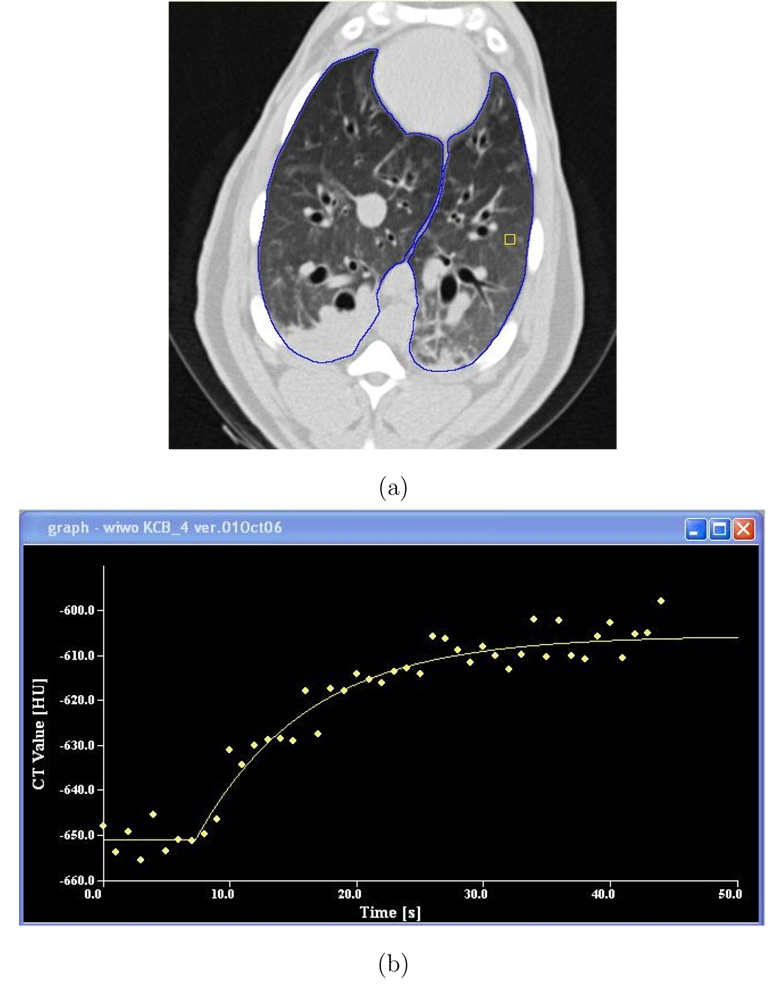
Prior to Xe-CT data analysis, the lung region was defined using the method from Hu et al. (2001), followed, when necessary, by manual editing. Figure 4a shows an example Xe-CT slice with the lung segmentation overlaid. After lung segmentation, non-overlapping 8×8 pixel regions of interest (ROIs) were defined in the lung region on each 2D slice.

Fig. 4.

Time series data from Xe-CT study. (a) shows the Xe-CT image of the lungs, with the lung boundaries marked in blue and a rectangular region of interest in yellow. (b) shows the raw time series data for this region of interest (wash-in phase) and the associated exponential model fit.

The Xe-CT time series data shows an exponential rise and fall in lung density during the wash-in and wash-out phases of image acquisition. To quantify regional ventilation, a single-compartment exponential model is fit to the rise and decay portions of the data using a least-squares fit. For each ROI to be analyzed, the mean region density, D(t), is calculated versus time (or equivalently, image number). For the wash-in phase, the compartment model gives (Simon and Marcucci, 1998):

$$D(t)=\{\begin{array}{ll}{D}_0\hfill & 0\le t<t_0\hfill \\ D_0+(D_f-D_0)(1-e^{-\frac{t-t_0}{\tau }})\hfill & t\ge t_0,\hfill \end{array}$$ (2)

where D₀ is the baseline density in the ROI prior to switching to xenon gas, D_f is the density that would be observed if xenon was inspired until equilibrium, t₀ is the start time of the switchover from room air to xenon, and τ is the model time constant. Thus, using this model, the D_f − D₀ term represents the enhancement due to the inspired xenon. The model gives a similar expression for the wash-out phase:

$$D(t)=\{\begin{array}{ll}{D}_f\hfill & 0\le t<t_0\hfill \\ D_0+(D_f-D_0)e^{-\frac{t-t_0}{\tau }}\hfill & t\ge t_0,\hfill \end{array}$$ (3)

where for the wash-out phase t₀ denotes the time of switchover from xenon back to room air. Figure 3 shows the density–time variation predicted by the model. As discussed by Chon et al. (2005), the time constants of the rising and falling phases of the curves may be fitted separately or may be forced to be equal. In our analysis, only the wash-in phase of the Xe protocol was analyzed. To reduce aberrations in the time series data due to the ROIs overlapping with large blood vessels or regions of atelectasis (see, for example, the bottom left side of the lungs shown in Figure 4a), we eliminated from consideration any ROI that had more than 40% of its pixels above −300 HU. Time series data was measured and analyzed for the remaining ROIs. Specific ventilation (sV, ventilation per unit lung air volume in min⁻¹) for each ROI was calculated as the inverse of the time constant τ.

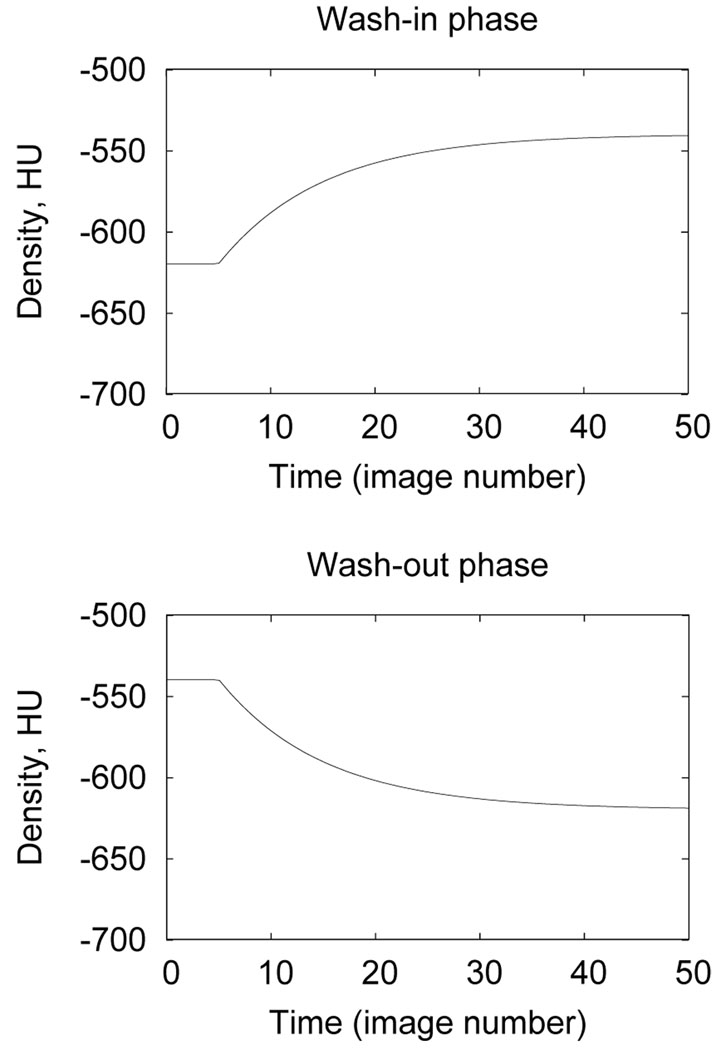
Fig. 3.

Wash-in and wash-out behaviors predicted by compartment model for t₀ = 5 seconds, τ = 10 seconds, D₀= −620 HU, and D_f = −540 HU.

Figures 4a–b shows screen shots from the software tool used to analyze the Xe-CT data (Chon et al., 2005). This tool facilitates lung segmentation, region of interest specification, and allows control over the curve fitting parameters during the exponential fits.

2.4 Assessment of Image Registration Accuracy

To assess the accuracy of the image registration, 9 to 15 anatomic landmarks were manually selected and matched between all six volume images for each animal. These landmarks were selected as recognizable branchpoints of the vascular and airway branches. For each image pair, the manually-defined landmarks in the lower pressure image were mapped to the higher pressure image using the transformation determined during the image registration step. The actual landmark position was compared to the registration-predicted landmark position and the landmark positioning error was calculated.

2.5 Comparing Lung Expansion to Xe-CT Estimates of sV

Local lung volume change is calculated using the Jacobian of the transformation that maps image I₀ to image I₁. Consider the vector displacement function h (with x, y, and z components) that transforms a voxel from image I₀ into its corresponding location in image I₁, so that the voxel at location (x, y, z) in image I₀ is displaced by a vector function u to map it to its corresponding location in image I₁. The Jacobian J(x, y, z) of u is

$$J(x,y,z)=\left|\begin{array}{ccc}\hfill 1+\frac{\partial u_x(x,y,z)}{\partial x}\hfill & \hfill \frac{\partial u_x(x,y,z)}{\partial y}\hfill & \hfill \frac{\partial u_x(x,y,z)}{\partial z}\hfill \\ \hfill \frac{\partial u_y(x,y,z)}{\partial x}\hfill & 1+\frac{\partial u_y(x,y,z)}{\partial y}\hfill & \hfill \frac{\partial u_y(x,y,z)}{\partial z}\hfill \\ \hfill \frac{\partial u_z(x,y,z)}{\partial x}\hfill & \hfill \frac{\partial u_z(x,y,z)}{\partial y}\hfill & \hfill 1+\frac{\partial u_z(x,y,z)}{\partial z}\hfill \end{array}\right|,$$

where u_x(x, y, z) is the x component of u(x, y, z), u_y(x, y, z) is the y component of u(x, y, z), and u_z(x, y, z) is the z component of u(x, y, z). The Jacobian measures the differential expansion at position (x, y, z) in the image. If the Jacobian is unity, there is no expansion or contraction in the function u at location (x, y, z) in I₀. If the Jacobian is greater than one, there is local tissue expansion; if the Jacobian is less than one, there is local tissue contraction.

If we consider a small volume V₀ at point (x, y, z) in I₀ and the corresponding volume V₁ in I₁, the specific volume change is (V₁ − V₀)/V₀. If V₀ is small and the transformation from I₀ to I₁ is continuous, V₁ = J(x, y, z)V₀, i.e., the Jacobian tells us the local volume expansion (or contraction). Thus, specific volume change can be calculated from the Jacobian as J(x, y, z) − 1.

To compare the Xe-CT ventilation measurements to the Jacobian from the image registration transformation, for each animal we manually registered the Xe-CT slices to a 3D rectangular region in the P0 image by using a rigid transformation to match major anatomic landmarks (locations of the ribs, blood vessels, and airways). Within the 3D rectangular region, we define 30 to 39 4 mm thick subregions equally spaced along the y (ventral-dorsal) direction. An example of this spatial encoding is shown in Figure 5a. Then, using the image registration deformation field, we track the deformation of the 3D rectangular region and the spatially-encoded subregions across the P5, P10, P15, P20, and P25 images. Figures 5b–f shows how the subregions deform as a function of increasing pressure. Within each of the 4 mm thick subregions, we compute the mean and standard deviation of the Jacobian as a function of lung height (y coordinate, or ventral-dorsal direction) by averaging over all lung voxels in the x–z region of interest that contain between 30% and 90% air. In the Xe-CT data, we compute the mean and standard deviation of the Xe-CT sV parameter for the same 4 mm thick subregions. We define the most dependent lung region (region closest to the direction of gravity) as y = 0 cm. A scatter plot showing mean sV and mean Jacobian is created and general Deming regression is used to fit a linear model to this data (Martin, 2000; Analyse-It, 2008).

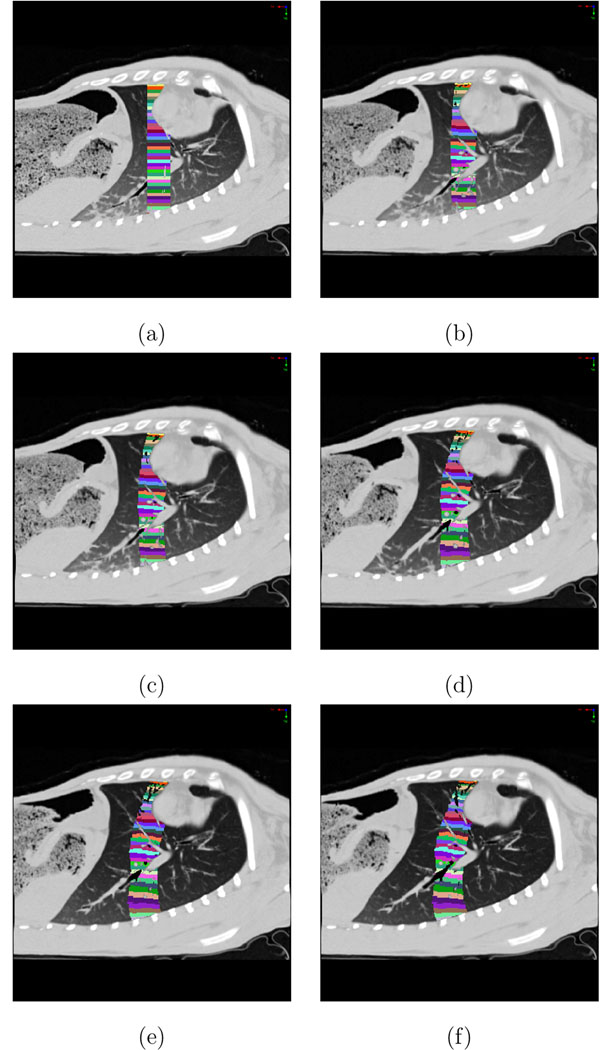
Fig. 5.

Definition of the 3D region of interest for the Jacobian analysis. Image shows a sagittal slice with spatially-encoded color map that defines ventral-dorsal regions of interest. (a) P0 image shows the initial 3D rectangular region of interest. Subsequent images show how the region deforms as the lung expands. (b) P5 image; (c) P10 image; (d) P15 image; (e) P20 image; (f) P25 image.

3 Results

3.1 Registration Accuracy

Registration accuracy was first visually assessed by examining anatomic land-marks in the registered images. Figures 6a–b shows coronal slices from the P0 and P25 images for one animal. Figure 6c shows a coronal view of the P0 image transformed to match the P25 image, and shows good anatomic correspondence. The differences in grayscale intensity between Figures 6b and 6c are due to the increased air content (and hence, decreased CT density) at the 25 cm H₂O pressure.

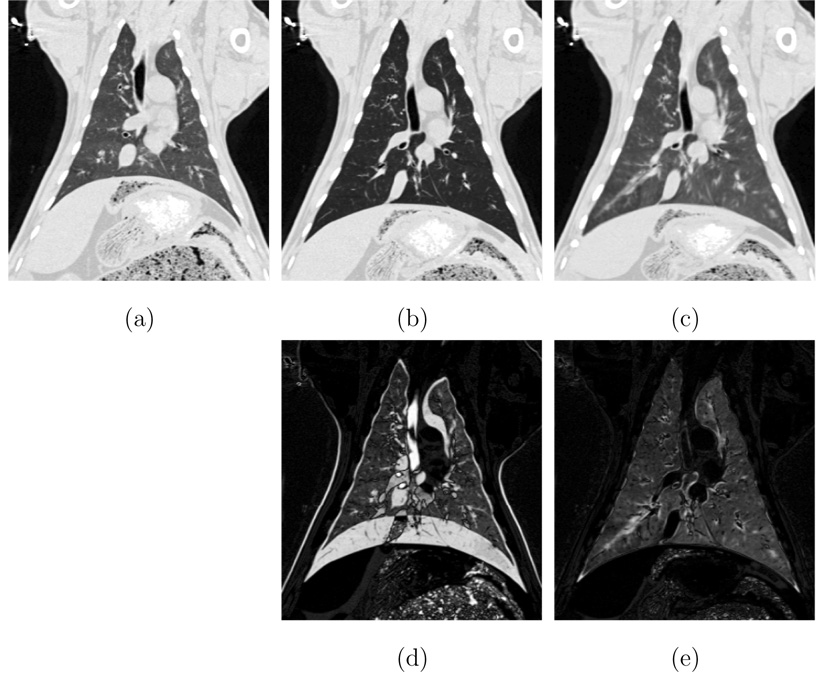
Fig. 6.

Visual assessment of registration accuracy. (a) P0 image. (b) P25 image. (c) P0 image transformed to match the P25 image. (d) difference between P0 and P25 images. (e) difference between P25 and P0 transformed to match P25. Note that since (a) and (b) have different percent air content, the difference image (e) will never be exactly zero.

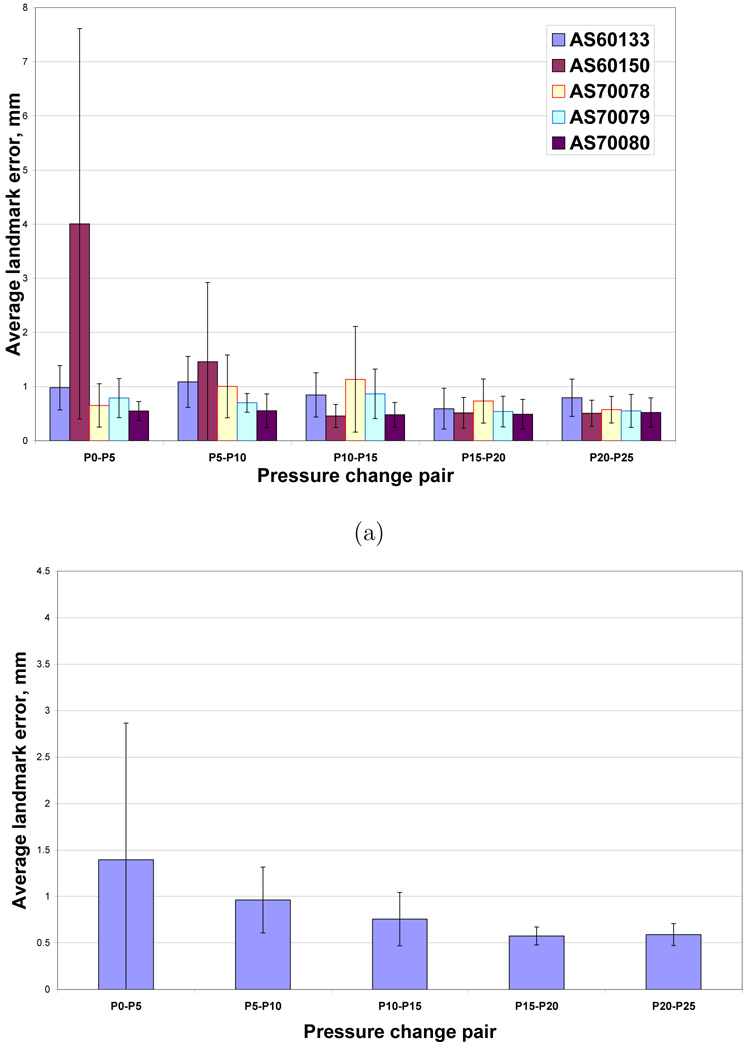
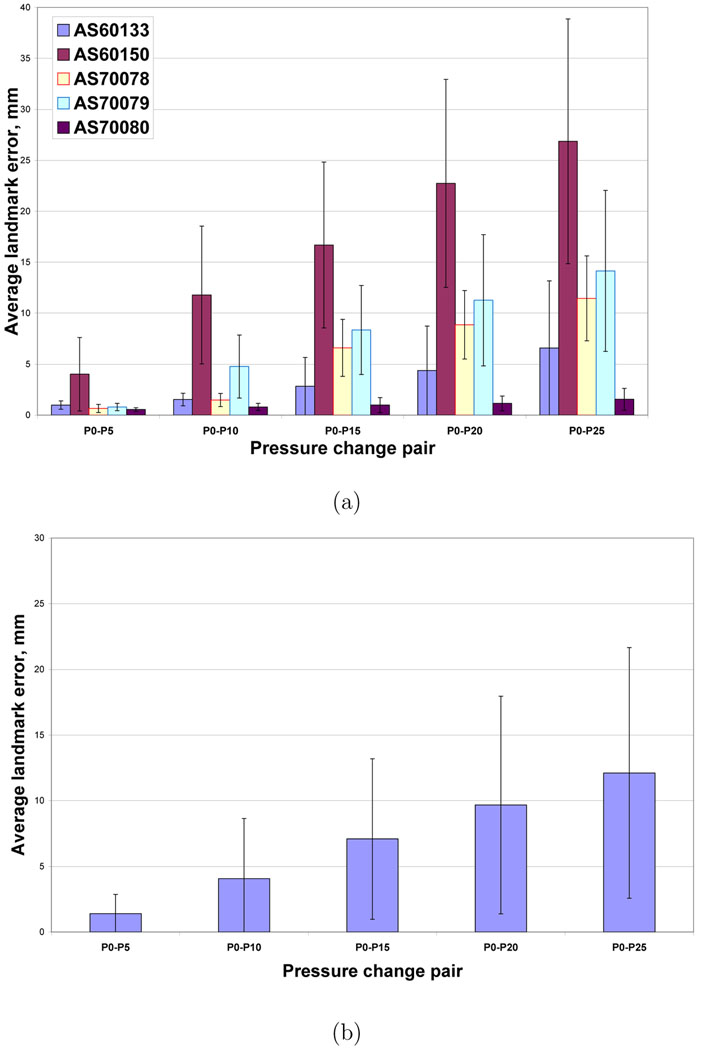
Figure 7a–b shows the projection of the manually-selected landmark locations onto coronal and sagittal slices for one animal. This figure shows that most of the landmarks are centrally located, with no landmarks in the apices or near the costophrenic angles. Figure 8a shows the registration accuracy as assessed by predicting the motion of the manually-defined landmarks across the five 5 cm H₂O pressure pairs P0–P5, P5–P10, P10–P15, P15–P20, and P20–P25 for each of the five animals. Figure 8b shows registration accuracy calculated by averaging the marker registration errors across all five animals. As discussed later, the average marker registration error is on the order of 1.5 mm or less in four of the five animals.

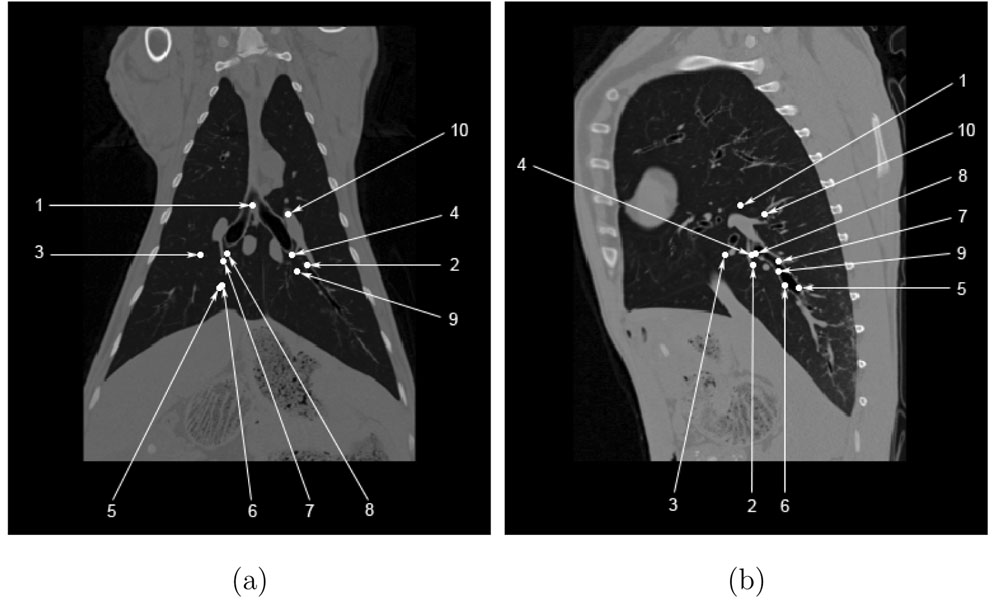
Fig. 7.

Manually-selected landmark locations projected onto (a) a coronal slice and (b) a sagittal slice for one animal at 25 cm H₂O airway pressure.

Fig. 8.

Registration accuracy for the 5 cm H₂O pressure change pairs. (a) Mean of landmark errors for each of the animals for each of the pressure change pairs. (b) Mean ± standard deviation of landmark errors for each of the pressure change pairs averaged across all animals.

Figure 9a shows the registration accuracy as assessed by predicting the motion of the manually-defined landmarks in each of the five animals across increasing pressure steps in registration pairs P0–P5, P0–P10, P0–P15, P0–P20, and P0–P25. Figure 9b shows landmark registration error for these experiments by averaging across all five animals.

Fig. 9.

Registration accuracy vs. increasing pressure change step size. (a) Mean of landmark errors for each of the animals for each of the pressure change pairs. (b) Mean ± standard deviation of landmark errors for each of the pressure change pairs averaged across all animals.

3.2 Lung Expansion and Xe-CT Estimates of sV

We are interested in establishing the linkage between the Jacobian of the registration deformation field, and the functional measurements from the Xe-CT scan. Since the Xe-CT measures ventilation, and the Jacobian measures local expansion (contraction) due to the movement of air into (out of) the lung tissue, there should be a direct relationship between these two parameters.

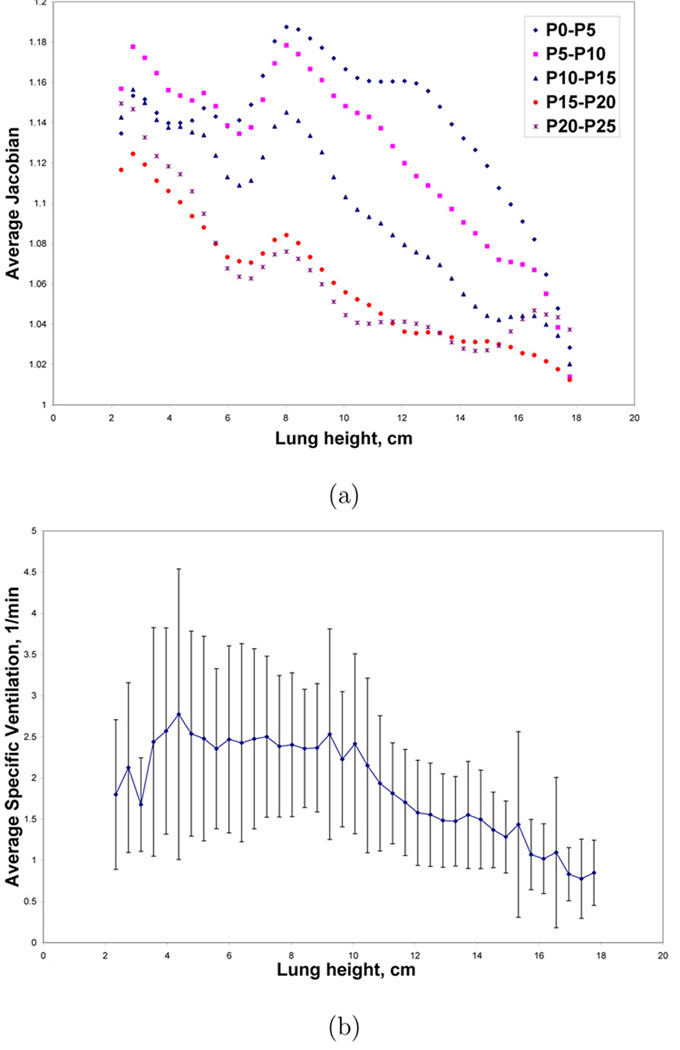
Figures 10a–b show color-coded maps of the Xe-CT specific ventilation, sV, and the Jacobian of the registration transformation at approximately the same anatomic axial location for one animal. Recall from Section 2.5 that the Jacobian map is proportional to specific volume change, with local specific volume change equal to J(x, y, z)−1, so Figure 10b is essentially a voxel-by-voxel map of tissue specific volume change. Figure 11a shows the average Jacobian vs. lung height for all pressure change pairs for one animal, and for comparison, Figure 11b shows the average sV vs. lung height calculated from the xenon study for the same animal.

Fig. 10.

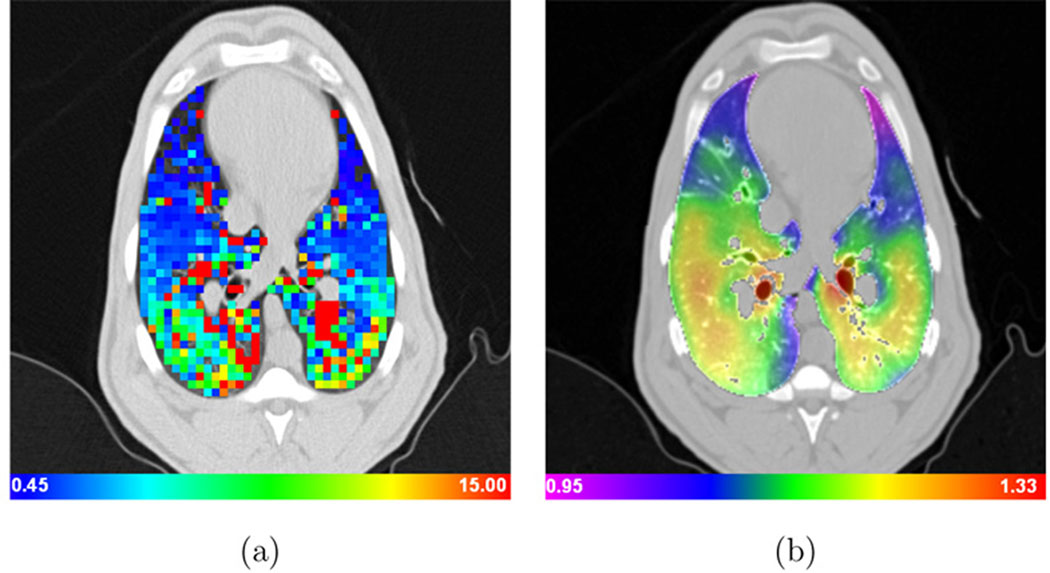
Color-coded maps showing (a) specific ventilation (1/min) and (b) the Jacobian of the image registration transformation (unitless) for approximately the same anatomic slice computed from the P5–P10 image pair. Note that the physical units and color scales are different for (a) and (b). Dark blue regions on the specific ventilation image (a) are regions that have low ventilation while green and yellow regions have higher ventilation; Bright red and orange regions on the Jacobian image (b) have large lung deformation while blue and purple regions are deforming less.

Fig. 11.

Example Jacobian and sV measurements vs. lung height for one animal. (a) Average Jacobian values for all pressure pairs vs. lung height; and (b) average ± standard deviation of sV vs. lung height. Error bars are not shown for the Jacobian data, however, the coefficient of variation is less than 10% of the average value.

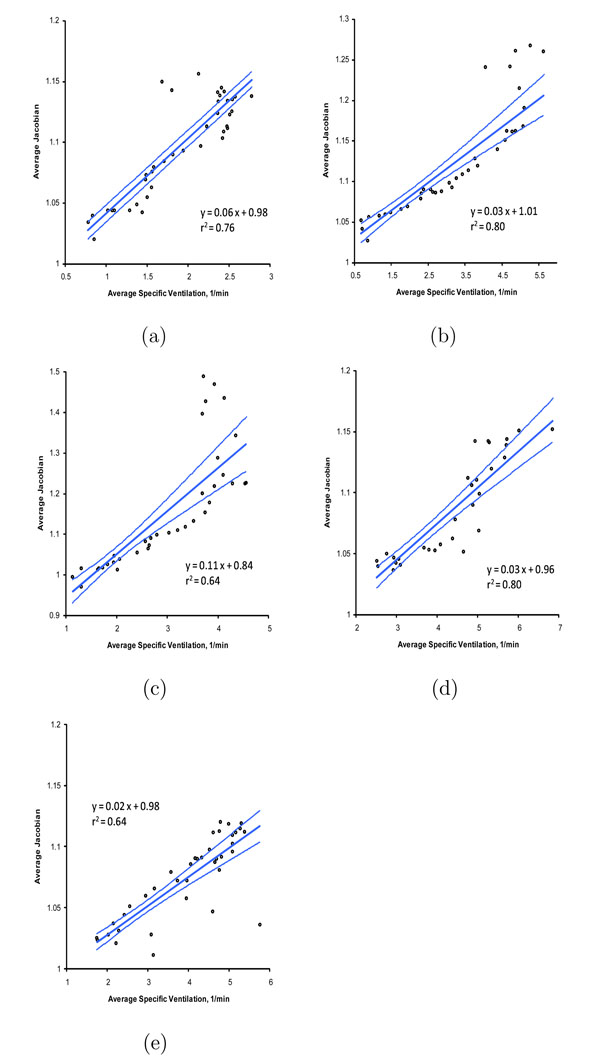
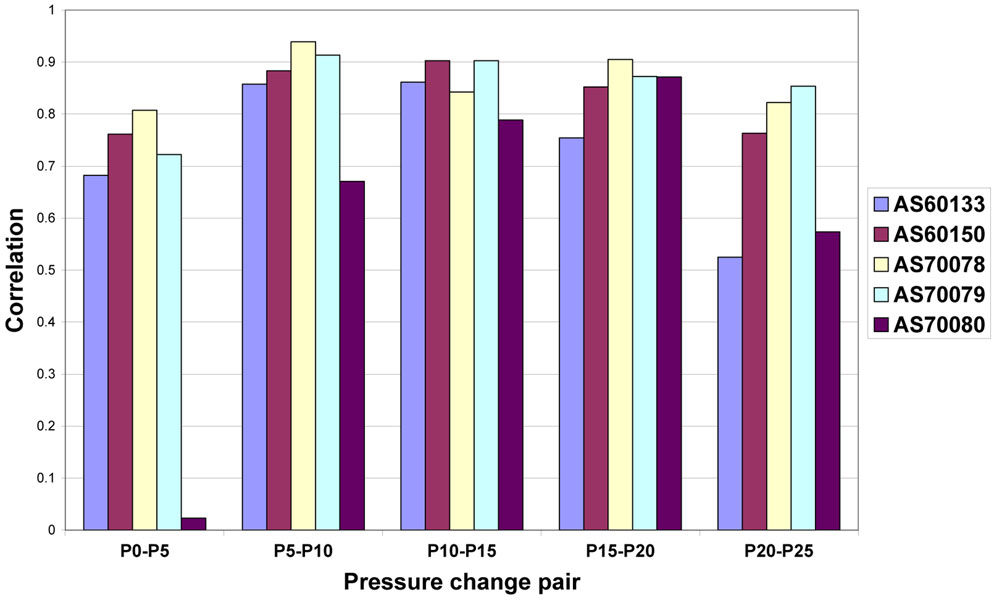
Figure 12 shows the average sV vs. average Jacobian for the P10 to P15 pressure transition in all animals. Similar linear relationships exist at the other pressure change pairs (e.g., for the P15 to P20 pressure change pair), however, on average the correlation coefficients are closest to unity for the P10 to P15 pressure change pair. Figure 13 shows the correlation coefficients r obtained from the linear regression of the average Jacobian vs. sV for each of the animals and each of the 5 cm H₂O pressure change pairs.

Fig. 12.

Scatter plots of average sV and average Jacobian for the P10 to P15 pressure change pair for (a) animal AS60133; (b) animal AS60150; (c) animal AS70078; (d) animal AS70079; (e) animal AS70080. Linear regression lines and 95% confidence bands are shown. Regression parameters are given in Table 1.

Fig. 13.

Correlation coefficients r from the linear regression of average Jacobian and sV for each 5 cm H₂O pressure change pair and for each animal.

4 Discussion

Figures 8a–b show that for four of the five animals, the average marker registration error for the 5 cm H₂O step size pairs was small (less than 1.5 mm) as assessed by the manually-defined landmarks. The outlier, animal AS60150, shows large registration errors when matching the P0 image to P5 image. Upon further inspection, it was determined that the AS60150 case had significant edema and atelectasis in the most dorsal lung regions, greatly reducing the contrast between the vessels, airway walls, and surrounding parenchyma. Since the registration is based on intensity matching, the loss of contrast in the P0 image was the likely cause of the increased registration errors for AS60150. For the P5 through P25 images, the increased airway pressure would force more air into the airways and parenchyma, thus decreasing the average graylevel in the parenchyma and increasing the overall contrast and providing better local structure information for registration. In general, we see from Figure 8b that there is a decreasing registration error with increasing lung pressure, again due likely to the fact that more and more of the lung parenchyma is expanded at the higher pressures, leading to better contrast between the vessels, airways, and surrounding parenchyma.

For the landmark registration errors measured across increasing pressure steps (Figures 9a–b), the results show increasing registration errors with increasing pressure differences (corresponding to increasing volume differences). These increasing errors are likely caused by the larger anatomic deformations that occur as the pressure step size is increased. Again, animal AS60150 shows larger errors than the other animals, and this is almost certainly caused by the poor registrations due to the low contrast in the P0 image for this animal.

Our registration optimization is based minimizing the sum of the squared intensity differences; however, there are natural intensity changes in the breathing lung as air moves in and out of the alveoli. We attempted to compensate for this by using a graylevel transformation that emphasized the tissue–chest wall and tissue–vessel boundaries, but other registration similarity functions, such as mutual information, may produce similar or better results.

Figures 10a–b shows an example of the color-coded maps of sV from the Xe-CT and the Jacobian of the registration displacement field. While these images show different physical parameters and have different underlying resolution, it is easy to see there are similar ventral-dorsal gradients in both images. These gradients are consistent with known physiology, which predicts increased ventilation in the more dependent regions of the lung (zones of the lung closest to the direction of the force of gravity). Because of limitations in the Xe-CT acquisition protocol, images such as those shown in Figures 10a are available over only a very narrow wedge of anatomy; however, the expansion map shown in Figure 10b can be calculated voxel-by-voxel using the techniques described in Section 2. In addition, since the Jacobian map is proportional to specific volume change, Figure 10b can be interpreted as a voxel-by-voxel map of specific volume change.

Figure 11b shows that the sV measurements have large coefficients of variation (almost 50%) during the wash-in phase. The reasons for this are unclear; it could be that the Xe-CT images have low signal to noise ratio, that the curve-fitting and ROI processing is noisy, or it could be an indication that the underlying physiology is not homogeneous. In comparison, the coefficients of variation for the Jacobian measurements are less than 10% of the average value, but this smoothness might be artificially induced by the model constraints used during the registration process. Both Figures 11a–b show the expected ventral-dorsal gradient in lung expansion; and as expected, Figure 11a shows that there is increased expansion (higher Jacobian values) at lower lung pressures (lower lung volumes), and less expansion at higher lung volumes. Figure 11a also shows that the gradient in the average Jacobian is not monotonic, and in fact shows an unusual deviation from the expected gradient between 6 and 8 cm of lung height. It is unknown whether this represents true differences in the amount of lung expansion in these regions, or increased systematic registration errors in the most dorsal regions of the lung due to edema and atelectasis, but we note that similar patterns of lung expansion were observed in the data from some of the other animals. We further note that no such marked change in sV is observed in the 6 cm to 8 cm region in Figure 11b.

Figure 12 shows the linear regression relationship between the sV and Jacobian measurements for the P10 to P15 pressure change pair for all animals. This pressure change pair gave the best linear regression correlations. Figure 13 shows that the r values obtained with other pressure change pairs varied from almost zero (case AS70080 for P0 to P5 has r = 0.08, which may be a case where the registration failed at the lowest lung volumes) to 0.94; however, it is clear from Figure 13 that there is a reasonably strong linear relationship between sV and Jacobian over a fairly wide range of pressures. Figure 12 also shows that there is much variation in the amount of lung expansion and ventilation across the different animals; for some animals (e.g., AS60133) there is little variation in the amount of expansion and ventilation, while for others (e.g., AS70079) there is a wide range of variation in these parameters. We suspect these differences are due to natural anatomic variation and the condition of the lungs at the time of the scanning.

Additional studies are needed before this work can be translated to humans. Since our study uses multiple CT scans to track tissue deformation, radiation dose may be a concern for normal subjects. It would be interesting to determine if low-dose scanning could be used to obtain the two or more lung volumes needed for the biomechanical analysis. Further, since the animals in this study were mechanically ventilated, and we used low pitch, slow rotation time scanning to acquire high-resolution, low-noise images, more research is required to determine how the image acquisition protocol can be modified for use in humans and how the increased noise might affect the image registration.

In addition, since some hardware now allows retrospectively-respiratory-gated images to be reconstructed from continuous scanning during free breathing, work needs to be done to compare the results obtained using static image acquisitions to the results from dynamic image acquisition. While it seems likely that the results from the dynamic acquisition will more accurately reflect the true biomechanical conditions of the breathing lung, this assertion needs to be thoroughly tested. One area in which the methods in this paper might have immediate application is the detection and evaluation of air trapping in the lung for subjects with chronic obstructive pulmonary disease (COPD). The registration Jacobian map can be used to identify tissue regions that are not expanding or contracting during respiration. The amount of trapped air and the relationship between the trapped air and nearby airways can be evaluated from the 3D CT scan. Follow-up scans can be be used to track the progression of the disease in an longitudinal study.

5 Summary and Conclusions

We have described a registration-based technique for estimating local lung expansion from multiple respiratory-gated CT images of the thorax. The degree of lung expansion is measured using the Jacobian of the registration displacement field. The Jacobian map is shown to be proportional to local specific volume change, a physiologically meaningful parameter that can be used to assess the functional capacity of lung tissue.

Our registration results show that in four of the five animals we have average registration errors on the order of 1.5 mm, as assessed by manually-selected landmarks located mainly near the central airways. In the fifth animal, we observed much larger registration errors at the lowest lung volume due to a marked amount of edema and atelectasis that reduced image contrast in the parenchyma. However, as the lung expanded at higher pressures, the registration performance for the fifth animal was similar to that of the other four animals.

We have compared the Jacobian-based lung expansion measures estimated across five pressure changes to a xenon CT based measure of specific ventilation, and have shown good agreement in five animals. Both the Xe-CT data and the Jacobian maps show the expected ventral-dorsal gradient in lung function. The P10 to P15 pressure change pair was found to correlate best with the Xe-CT data.

Xe-CT can provide highly detailed structure-function information, but is currently limited to assessing select slabs of lung tissue. A significant strength is Xe-CT imaging is that it can, if appropriately applied, reveal evidence of collateral ventilation and provide measures of regional time constants that characterize the dynamic properties of lung tissue. Xenon is a fairly expensive, requires special equipment for administration, is an anesthetic, and requires a physician’s investigational new device (IND) approval prior to use in the United States. In contrast, a registration-based Jacobian analysis of lung expansion uses just two easy-to-acquire volumetric images of the lung acquired at different lung volumes to produce a useful, high-resolution map of lung expansion. This map is easy to compute, but questions remain concerning the spatial resolution and sensitivity of these maps. Since the registration deformation field provides directional information, measurements such as the lung tissue strain tensor, which provides estimates of tissue expansion and the direction of expansion, may give a more complete assessment lung tissue function.

Table 1.

Linear regression parameters and 95% confidence intervals for each of animals. Scatter plots and regression lines are shown in Figure 12.

Animal	Slope	95% CI	Intercept	95% CI
AS60133	0.06	0.05–0.07	0.98	0.96–0.99
AS60150	0.03	0.03–0.04	1.01	1.00–1.03
AS70078	0.11	0.08–0.13	0.84	0.78–0.89
AS70079	0.03	0.02–0.03	0.96	0.94–0.98
AS70080	0.02	0.02–0.03	0.98	0.97–0.99