Psychophysical spectro-temporal receptive fields in an auditory task

Abstract

Psychophysical relative weighting functions, which provide information about the importance of different regions of a stimulus in forming decisions, are traditionally estimated using trial-based procedures, where a single stimulus is presented and a single response is recorded. Everyday listening is much more “free-running” in that we often must detect randomly occurring signals in the presence of a continuous background. Psychophysical relative weighting functions have not been measured with free-running paradigms. Here, we combine a free-running paradigm with the reverse correlation technique used to estimate physiological spectro-temporal receptive fields (STRFs) to generate psychophysical relative weighting functions that are analogous to physiological STRFs. The psychophysical task required the detection of a fixed target signal (a sequence of spectro-temporally coherent tone pips with a known frequency) in the presence of a continuously presented informational masker (spectro-temporally random tone pips). A comparison of psychophysical relative weighting functions estimated with the current free-running paradigm and trial-based paradigms, suggests that in informational masking tasks subjects’ decision strategies are similar in both free-running and trial-based paradigms. For more cognitively challenging tasks there may be differences in the decision strategies with free-running and trial-based paradigms.

I. INTRODUCTION

The “method of free response”, where a target signal is added to a continuous masker at random times and subjects respond with a button press when they detect the target signal, was developed to better reflect the continuous nature of sound in everyday listening situations (Egan et al., 1961). The method of free response has not been widely used in psychophysics because there are no explicitly defined trials, which makes characterizing the decision processes in terms of the index of sensitivity d′ and bias β difficult (Egan et al., 1961; Watson and Nichols, 1976). Here, we explore a technique in which the decision process, associated with the method of free response, is characterized in terms of the relationship between the stimulus and the responses.

Ahumada (2002) formalized a method to describe the relationship between the stimulus and the responses in traditional “trial-based” psychophysical tasks. In Ahumada’s method, all the trials for which the response was “No” (i.e., misses and correct rejections) are combined and all the trials for which the response was “Yes” (i.e., hits and false alarms) are separately combined. The classification image is then formed by differencing the “Yes” and “No” trials. The classification image is a psychophysical weighting function that indicates regions in which increasing the magnitude of the stimulus will increase the likelihood of a Yes response and regions in which increasing the magnitude of the stimulus will decrease the likelihood of a Yes response. Other methods for estimating psychophysical weighting functions include linear regression (Ahumada and Lovell, 1971; Lutfi, 1995; Richards and Zhu, 1994) and logistic regression (Alexander and Lutfi, 2004; Berg, 1989; Dye et al., 2005).

The method developed by Ahumada (2002) to estimate psychophysical weighting functions is similar to methods used to estimate neural spectro-temporal receptive fields (STRFs). The physiological STRF is in essence a relative weighting function that indicates spectro-temporal regions in which increasing the magnitude of the stimulus will increase the likelihood of a neural response (often an action potential) as well as regions in which increasing the magnitude of the stimulus will decrease the likelihood of a neural response. The physiological STRF can be estimated by continuously presenting a stimulus and averaging a spectrographic representation of the stimulus relative to the times at which neuronal responses occur (e.g., de Boer and Kuyper, 1968; Theunissen et al., 2000; Wu et al., 2006). By equating the button presses by the subjects in the method of free response with neural responses a “psychophysical STRF” that is analogous to the physiological STRF can be estimated.

The methods used to estimate the physiological STRF often lack a component that is critical for the method of free response. The method of free response, like many other psychophysical paradigms, revolves around the detection of a target signal. In awake and behaving physiological preparations there is often the requisite target signal, but the analysis often does not take into account the timing of the behavioral response (e.g., Fritz et al., 2005; Gutschalk et al., 2008). Similarly, psychophysical weighting patterns estimated with trial-based paradigms do not incorporate the relative timing of the behavioral response of the subject. It is possible that a method could be developed to allow psychophysical weighting patterns that incorporate the relative timing of the behavioral response of the subject to be estimated with trial-based paradigms. The psychophysical STRF, estimated with the method of free response, is desirable since it incorporates the relative timing of the behavioral response when the stimulus is presented in a more realistic free-running manner.

Incorporating the relative timing of the behavioral response into a psychophysical weighting function with the method of free response may be difficult due to two potential sources of variability. The first potential source of variability is that the relative timing of the behavioral responses of the subjects varies on the order of 50 ms across trials in auditory detection tasks (Pfingst et al., 1975). This variability in the reaction time may blur interesting aspects of the psychophysical STRF. The second potential source of variability is that the continuous stimulus presentation used in the method of free response may increase the likelihood that the psychophysical weighting function will vary over time. The method of free response is in essence a vigilance task where performance may wax and wane over time. Additionally, the decision strategy of the subject may be influenced by recent segments of the continuous stimulus.

As a proof of concept, the psychophysical STRF is estimated here in an auditory informational-masking task. Informational masking was chosen because estimates of psychophysical weighting functions, obtained with trial-based methods, show that spectro-temporal regions that are distant from the signal can influence the decisions of the subjects (Alexander and Lutfi, 2004; Richards and Tang, 2006; Huang and Richards, 2008). In the current task, subjects were asked to press a response button whenever they detected a signal (four temporally abutted short tone pips of a fixed, known, frequency) in the presence of a continuous masker of multiple random-frequency short duration tone pips.

II. MATERIALS AND METHODS

A.Subjects and Apparatus

Testing was conducted following standard psychoacoustic procedures approved by the University of Pennsylvania Institutional Review Board. Three subjects (S1, S2, and S3) received reimbursement for their participation in the experiment. All subjects had pure tone thresholds below 15 dB HL at frequencies of 250, 500, 1000, 2000, 3000, 4000, 6000, and 8000 Hz in both ears. Subjects were between 23 and 25 years old. Subjects S1 and S3 had previously participated in psychoacoustic experiments.

The stimuli were presented monaurally over headphones (Sennheiser HD 410 SL) at the left ear of a subject who was seated in a single-walled sound attenuating booth situated in a quiet room. An LCD monitor and a response box were located inside the booth and outside the booth was a computer running MATLAB connected to Tucker-Davis Technology system three hardware (RP2 and HB7 modules). The hardware generated the stimuli at a sampling rate of 48828.125 Hz and digital attenuation was used to achieve the desired stimulus levels.

B. Stimuli

The masker was composed of 50-ms tone-pips gated on and off with 5-ms cosine squared ramps. The level of each pip was 76 dB SPL. The masker tone pips were distributed independently in time and frequency. Unlike many informational masking studies, the masker did not include a “protected” region; i.e., the masker could contain pips with the same frequency as the signal. The logarithmic frequencies of these masker pips were chosen from a uniform distribution between 250 and 4000 Hz and the phases, relative to the onset of the ramp, were chosen from a uniform distribution between ±π radians. The masker was presented continuously for 307.2 s.

The signal consisted of a temporal series of four identical-frequency tone pips that were temporally abutted. The pips that comprised the signal were identical to those of the masker (50-ms duration, 5-ms cosine squared ramps, and a level of 76 dB SPL). Unlike the masker, each pip of the signal was temporally aligned with its neighbors such that the total duration was 200 ms. Signal frequencies of 1000 Hz and 2431 Hz were tested separately. The phases of the signal pips, relative to the onset of the ramp, were zero. The rate of occurrences of the signal followed a dead-time modified Poisson process. The time between consecutive signal onsets were drawn from a geometric distribution with an expected rate of 1 s and an enforced dead time of 2.2 s (the minimum time between the offset of one signal and the onset of the next was two seconds).

The difficulty of detecting the signal depended on the rate parameter of the Poisson distribution that determined the number of masker pips to be turned on every 20.48 μs. The rate parameter was chosen individually for each subject to yield approximately equal performance. For subjects S1 and S2 on average one masker pip was turned on every 8.33 ms and for subject S3 on average one masker pip was turned on every 12.5 ms; alternatively, the expected number of masker pips, at any instant in time, was either six (subjects S1 and S2) or four (subject S3). Although on average there would be six (or four for subject S3) masker pips playing at any particular time, given the distribution of the masker pips in time and frequency the probability that the masker would contain multiple temporally abutted pips at a single frequency was zero.

C.Paradigm

The experimental paradigm required subjects to detect a signal (coherent series of four tone pips of a known frequency) presented in a continuous masker of tone pips which are distributed independently in time and frequency. The subjects were instructed to press the response button as soon as the signal was detected. Unlike traditional trial-based psychophysics, the masker was continuous and the signal was presented at random times. Subjects rested between the approximately 5 minute long blocks and they completed approximately 10 blocks in a two-hour session. Data analyses are based on 90 blocks during which the signal frequency and the expected number of masker pips was held fixed.

Subject S1 was tested with the 1000-Hz target followed by the 2431-Hz target. Subject S2 was tested with only the 1000-Hz target and subject S3 was tested with only the 2431-Hz target. Practice preceded data collection. Initially the signal was presented without the masker (i.e., in quiet). Then, the masker was introduced with an expected number of masker pips equal to two. In the subsequent training blocks the number of coherent tone pips in the signal and the expected number of masker pips were adjusted depending on subjects’ performance and their reported confidence on the task. Most subjects reliably detected the signal in the presence of the masker after a few training blocks. Notably, the only subject to be tested with both frequencies (S1) had difficulties learning to detect the second signal frequency that was tested.

During training and testing, subjects were provided with feedback by way of a graphical display that was updated approximately every 10 s. The information in the graphical display was delayed by approximately 10 to 20 s, so it provided no direct information for the detection of a recent signal. The display showed the times at which the signal occurred and the times at which the subject responded. The feedback also provided information about the number of hits, misses, and false alarms; refer to Section II.D.1 for how hits, misses, and false alarms were classified with the free-running paradigm.

At the end of each block, two histograms were displayed. One displayed the times between adjacent responses. The second histogram showed the times between each response and the nearest preceding signal. This histogram helped subjects track their response times so they could respond as quickly as possible. The subjects were also instructed to utilize a liberal response criterion to maximize the percentage of hits at the expense of an increase in the number of false alarms.

D.Data Analysis

1. Classification Scheme

In traditional trial-based psychophysics, each trial results in a hit, a miss, a false alarm, or a correct rejection. For paradigms in which there are no clearly defined trials, such as the one under study here, it is still desirable to label each signal presentation as either a hit or a miss and to label each response as either a hit or a false alarm (Egan et al., 1961). By using the relative timing between the signals and the responses of the subjects in the method of free response, hits, misses, and false alarms can be identified (identifying correct rejections is more difficult since there is neither a signal nor a response in this case).

Based on the analysis of the distribution of times between each response and the closest preceding signal onset, a 1.7 s long classification window, starting 0.3 s after every signal onset, is used to sort the signals and responses. By this classification scheme, all responses that occur 2 s after the signal onset, or alternatively 1.8 s after the signal offset, are classified as false alarms. A hit occurs when there is a response within the 1.7 s long classification window, and a miss occurs when there is neither a response within the classification window nor a response within the 300 ms between the onset of the signal and the onset of the classification window. Responses which occur within 300 ms of the signal onset are not classified. In some cases, there are two (or possibly more) responses in the classification window. When multiple responses occurred within the classification window, none of the responses were included in the analysis due to the ambiguity as to which response to code.

2. Spectrogram Generation

In the method of free response, subjects indicate the presence of a signal, which is embedded within an ongoing masker, by pressing a response button. Only a portion of the 5-minute stimulus is analyzed. The analyses focus on segments of the ongoing stimulus in which the signal is present and/or a response occurs. When false alarms and hits occur, average spectrograms of the stimulus relative to the time of the response (i.e., response triggered) are calculated. Similarly, when hits and misses occur, average spectrograms of the stimulus relative to the time of the signal (i.e., signal triggered) are calculated. Since there is no response when a miss occurs, a response-triggered spectrogram for misses cannot be estimated and since there is no signal when a false alarm occurs, the signal-triggered spectrogram for false alarms cannot be calculated.

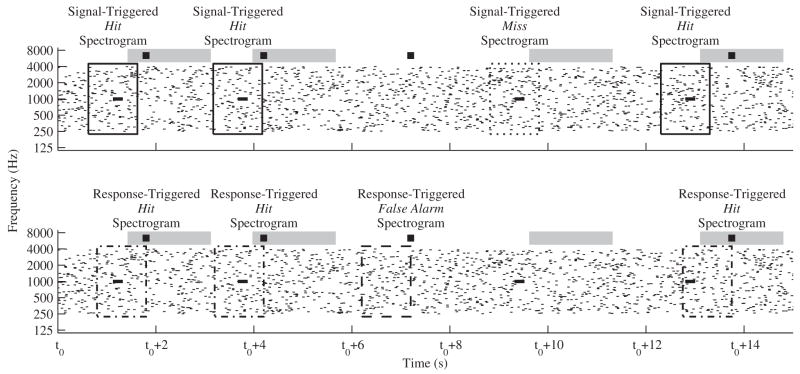
Figure 1 is a schematic of the temporal relationship between the signals, responses, and the segments of stimuli used to construct the signal-triggered averaged spectrograms for the hits and misses (top panel) and the the response-triggered average spectrogram for hits and false alarms (bottom panel). For each subject and signal frequency, averaged spectrograms are each calculated by averaging together, in linear units of power, spectrograms of 1-s segments of the stimulus. For the signal-triggered spectrograms, the onset of the signal is located at the temporal center of the segment. For the response-triggered spectrograms, the response occurs at the end of the segment.

Figure 1.

Schematic showing the segments of the stimuli used to generate the signal-triggered average spectrograms for hits and misses (top panel) and response-triggered average spectrograms for hits and false alarms (bottom panel). Both panels show a cartoon spectrogram of the same 15 second segment of the stimulus with a signal frequency of 1000 Hz. For clarity the signals are drawn using thicker lines. At the top of each panel the classification window associated with each signal is shown using a grey rectangle and the responses of the subjects are shown as black squares. In the top panel, the large open rectangles enclose the segments of the stimulus used in the calculations of the signal-triggered averaged spectrogram for hits (solid) and misses (dotted); note that the rectangles are centered at the signal onset. In the bottom panel, the large open rectangles enclose the segments of the stimulus used in the calculations of the response-triggered averaged spectrogram for hits (dash-dot) and false alarms (dashed); note that the rectangles end at the time at which the subject responded.

The spectrograms of the 1-s segments of the stimulus are based on the discrete short-time Fourier transform. The segment of the stimulus is first windowed in time with 1024-sample Hamming windows (approximately 21 ms in duration) with 50 percent overlap. These 1024-sample windowed temporal segments are zero padded and transformed to the frequency domain with a 65536-sample discrete Fourier transform (spectral density of approximately ¾ Hz). Then, the spectrogram is smoothed in frequency with a one-third octave filter. Specifically, the power within a one-third octave band is calculated at 200 frequencies which are logarithmically space between approximately 250 and 4000 Hz (the bandwidth of the masker).

The resulting spectrogram calculated with the smoothed discrete short-time Fourier transform is desirable for two reasons. The discrete short-time Fourier transform accurately represents stimuli in which multiple tone pips are close in time and frequency by accounting for the spectral splatter associated with the gating of the tone pips and the relative phases of each tone pip. The second reason is that the smoothing results in the spectrogram having uniform spacing in both time and logarithmic frequency (traditional spectrograms are uniform in time and linear frequency and wavelet-based transforms are uniform in logarithmic frequency, but not in time). Although spectrograms with uniform spacing in both time and logarithmic frequency can be achieved using narrower smoothing filters, one-third octave filtering was used because it provides a first-order approximation of cochlear processing.

The response-triggered averaged spectrogram of the false alarms shares many similarities with the physiological STRF. The response-triggered averaged spectrogram of the false alarms, as well as the response-triggered averaged spectrogram of the hits, incorporates the relative timing of the behavioral responses. The response-triggered averaged spectrogram of the false alarms, unlike the response-triggered averaged spectrogram of the hits, is free from the “corruption” of the signal since false alarms are defined as responses that occur 1.8 s or more after the signal offset and the response-triggered spectrogram only utilizes 1 s of the stimulus prior to the response. Therefore, the psychophysical STRF is defined as the response-triggered averaged spectrogram of the false alarms.

3. Characterization of Spectrograms

A post-hoc investigation of the signal- and response-triggered spectrograms revealed that regions of above-average amounts of energy were concentrated into a single spectro-temporal region located near the signal frequency. The characteristics of each of these regions of high level are estimated by enclosing the region of high level with a contour of equal level. The initial contour is calculated with the contourc function of MATLAB. The level at which the contour is calculated is adjusted for each spectrogram individually. Since the function relating regions of high level and the background are very steep, the properties of the contour are largely invariant to the level at which the contour is calculated. The initial contour is then manipulated to remove “outliers” and seemingly spurious peaks. Bootstrap simulations indicate that this procedure did not “miss” regions of statistical significance relative to the background.

The contours are characterized in terms of their center frequency (spectral center of mass of the contour), bandwidth (spectral extent of the contour), latency (temporal center of mass of the contour), and duration (temporal extent of the contour). Notably, the levels of the contours are not characterized; we do note, however, three aspects about the levels at the signal frequency in the signal- and response-triggered averaged spectrograms. First, the level at the signal frequency for hits must be greater than the level for false alarms since the signal is always present when hits occur and is never present when false alarms occur. Second, the level at the signal frequency will be greater for the signal-triggered hits than for the response-triggered hits, due to the temporal smearing associated with the variability in the reaction time of the subjects that is captured in the response-triggered hits but absent in the signal-triggered hits. Third, the level at the signal frequency for false alarms depends on the criterion of the subject. For example, a conservative criterion (few false alarms) means that more energy is required at the signal frequency in order to generate a “signal” response and should lead to a larger average level at the signal frequency in the response-triggered averaged spectrogram for the false alarms.

The signal-triggered averaged spectrogram of the signal-plus-masker stimulus, regardless of whether a hit or a miss occurs, is dominated by the signal since the spectrogram of every segment used to generate the averaged spectrograms contains an identical copy of the signal. Differencing the hit and miss spectrograms on a logarithmic (decibel) scale removes the effects of common elements, in this case the signal, from the visual representation making it easier to investigate the masker characteristics affecting detection. The variability in the stimulus, which is crucial for estimating weighting functions, however, is decreased because the signal is always present when hits and misses occur and the effects of this decreased stimulus variability is not eliminated by differencing the spectrograms. To counter this decreased variability in the stimulus the hit-minus-miss signal-triggered spectrograms are averaged across both subjects and signal frequencies after aligning the spectrograms on the signal frequency.

III. RESULTS

Hits and false alarms are sorted/classified by considering the time between the response and the onset of the nearest preceding signal. Figure 2 shows a histogram of the times between the response and the onset of the nearest preceding signal for each subject and condition tested. Responses that occur “soon after” the onset of the signal are classified as hits while responses that occur “long after” the most recent signal offset are classified as false alarms. The particular values of “soon after” and “long after” were chosen based on the pattern of the data shown in Fig. 2. The gray bar at the top of Fig. 2 provides a graphical depiction of the classification window relative to the signal-response time histogram. For each subject the histogram has a marked peak and a long tail. The tails, which indicate the occurrence of false alarms, are not flat but slope downward. This is because the probability of having a long time interval between signals is small, thereby reducing the likelihood of having a long duration between a response and the nearest preceding signal.

Figure 2.

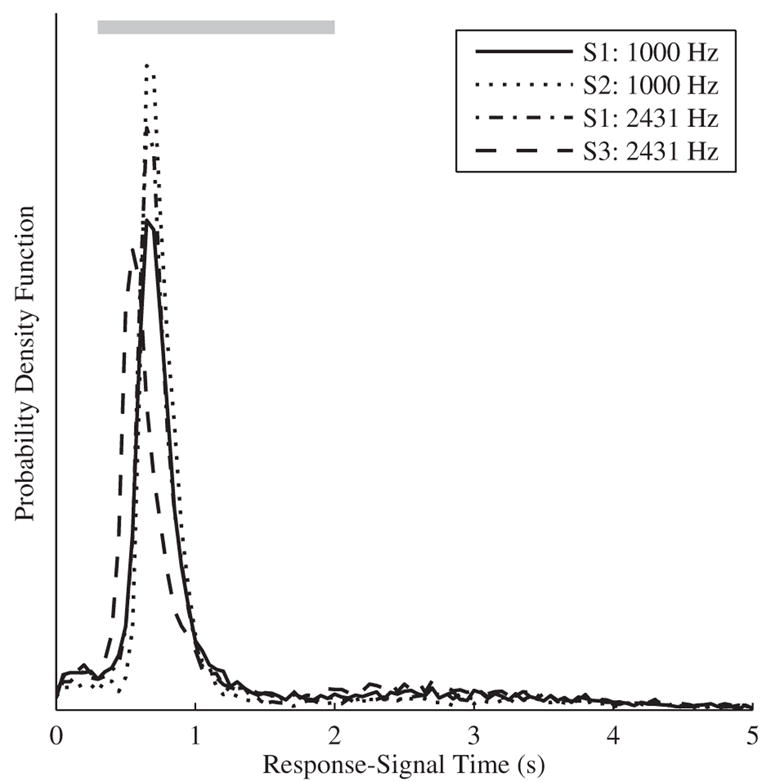
The probability density functions of the time difference between the responses and the onset of the nearest preceding signal for the three subjects and two conditions are shown. The gray shaded region at the top of the figure represents the ultimately chosen classification window. Signals which have at least one response within this window are classified as hits and responses that occur after this window are classified as false alarms.

The temporal location of the peak in the histogram provides information about the reaction time of the subject. For subjects S1 and S2 the peak is at approximately 700 ms, while subject S3 is slightly “faster” with a peak in the histogram at 500 ms. These reaction times are far longer than the 200–300 ms typically reported for the detection of tonal signals (Emmerich et al., 1976; Pfingst et al., 1975). Some of the increase in the reaction time may be due to the similarity of the signal and masker; in order to accurately differentiate between signal and masker in the current task the observer needs to process the stimulus across at least 200 ms (the signal duration). Consistent with this hypothesis is that reaction times decrease by approximately 300 ms (data not shown) when the masker is not present and the task is to detect a clearly audible sound in quiet. The width of the peak in the histogram spans about 500 ms. The variability in the reaction times of the subjects is therefore an order of magnitude larger than previous reports of variability in reaction time (Pfingst et al., 1975). This large variability in reaction time of the subjects may potentially blur interesting aspects of the psychophysical STRF.

Since the main peak of the signal-response histogram is relatively constrained in time, hits, misses, and false alarms are reliably classified. That is, “misclassifications” (e.g., delayed responses to the signal being classified as false alarms) are rare. Table 1 shows the results of the classification. For each subject, approximately 8600 signals were presented over the approximately seven hours of stimulus presentation. The low probability of a miss (between 0.07 and 0.19) is not surprising since the subjects were encouraged to use a liberal criterion that minimized misses at the expense of increased false alarms. Analyses of the hit rate, over the course of the 5-minute stimulus presentation, the testing session, and across days, were unable to confirm changes in performance across any of these three time scales and suggested that performance was in fact stable.

Table 1.

Summary of response classification.

Subject	Signal Freq.	Signals	Misses		Hits		Responses		False Alarms
	(Hz)	#	#	Pmiss	#	Phit	#	per second	#	per second
S1	1000	8591	1173	0.14	7028	0.82	9070	0.33	1531	0.06
	2431	8571	1139	0.13	7095	0.83	8972	0.32	1431	0.05
S2	1000	8534	605	0.07	7851	0.92	9720	0.35	1132	0.04
S3	2431	8548	1581	0.19	6562	0.77	9010	0.33	1861	0.07

All signals for which there was at least one response within the 1.7 second classification window are hits and signals for which there was no response are misses. Signals for which the only response was within 300 ms of the onset of the signal are not classified and were excluded from the analysis. Responses which occurred more than 2 seconds after the nearest preceding signal are false alarms. The difference between the number of responses and the sum of the false alarms and hits is attributable to early responses and multiple responses falling within the classification window, both of which were excluded from the analysis.

If subjects were performing near chance, than the classification procedure would result in approximately 38 percent of the responses being false alarms. In actuality, only 16 percent of the responses are false alarms. Even though the expected number of masker pips was smallest for subject S3, subject S3 still had the lowest hit rate and highest false alarm rate. Although d′ cannot be unambiguously estimated, any plausible classification of false alarms and hits would suggest that the signal is well above threshold for all the subjects and signal frequencies.

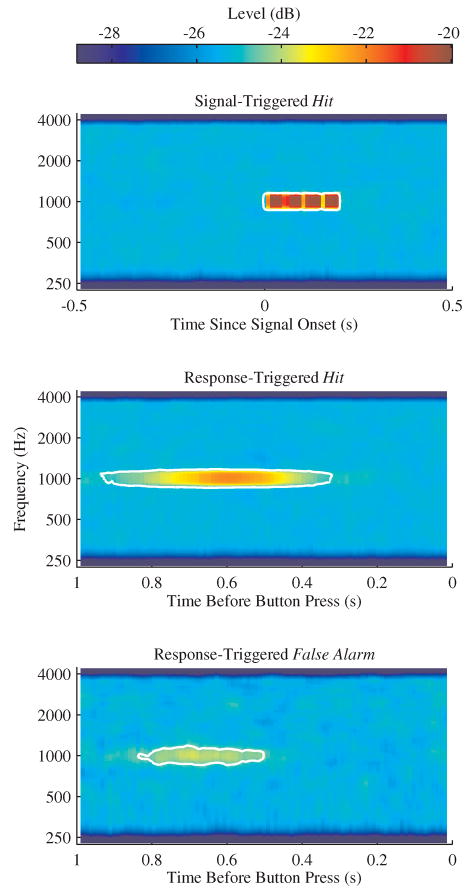
Insight into the mechanisms underlying performance can be gained by averaging spectrographic representations of the stimuli. Each of the three panels of Fig. 3 shows an averaged spectrogram of the stimulus presented to a representative subject (S1) with a signal frequency of 1000 Hz. The top panel of Fig. 3 shows the signal-triggered averaged spectrogram of the signal-plus-masker stimulus, from 0.5 s before to 0.5 s after the onset of the signal, given a hit occurred. The other two panels of Fig. 3 show spectrograms that are relative to the time of the response. The response-triggered averaged spectrogram for the hits is shown in the middle panel and the response-triggered averaged spectrogram for the false alarms is shown in the bottom panel. In each of the three panels, there is a single pronounced region of high stimulus level at the signal frequency. The contour of equal level that encloses the region of high level is indicated using white lines. Table 2 lists the properties of the contours of equal level for the three spectrogram types shown in Fig. 3 for all the subjects and conditions tested.

Figure 3.

The signal-triggered averaged spectrogram for the hits (top panel), the response-triggered averaged spectrogram for the hits (middle panel) and the response-triggered averaged spectrogram for the false alarms (bottom panel) are shown for subject S1 in the 1000-Hz condition. Spectro-temporal regions with high levels are red and regions with low levels are blue. The white contours of equal level enclose the regions of high level.

Table 2.

Summary of equal-level contours that enclose regions of high level.

				Equal Level Contour Properties
		Subject	Signal Freq. (Hz)	Center Freq. (Hz)	Bandwidth (Octaves)	Latency (ms)	Duration (ms)
Signal-Triggered	Hit	S1	1000	989	0.43	92	204
			2431	2426	0.38	93	205
		S2	1000	989	0.42	92	205
		S3	2431	2400	0.36	92	200
Response-Triggered	Hit	S1	1000	1003	0.46	624	618
			2431	2454	0.42	623	714
		S2	1000	1001	0.47	667	528
		S3	2431	2428	0.38	574	712
	False alarm	S1	1000	984	0.48	665	335
			2431	2423	0.49	685	358
		S2	1000	999	0.38	704	334
		S3	2431	2439	0.71	497	263

The level at which the contours were calculated varies with the “signal-to-noise ratio” of the spectrogram. The contours were manipulated to capture the region of high level and to avoid the inclusion of spurious noise. The latency for the signal-triggered hit contour is the temporal center of the contour relative to the signal onset, while for the response-triggered hit and false alarm contours the latencies are the temporal centers relative to the time of the response.

The region of high level in the signal-triggered averaged spectrogram of the stimulus for the hits (Fig. 3 top panel) has four temporal “bands.” This is consistent with the signal being four temporally-abutted, but gated (5 ms rise/fall times), 50-ms tone pips. The level at the signal frequency is approximately 4.8 dB above the background, which is consistent with the properties of the signal and masker. Since the signal-triggered averaged spectrogram of the stimulus for the hits is dominated by the signal, there is little variability across the subjects in the properties of the contours of equal level. As shown in Table 2, for the signal-triggered hits the center frequencies, durations, and temporal centers (latency) of the regions of high level are consistent with the signal properties. Further, the bandwidths are consistent with the one-third octave smoothing used in the calculation of the spectrogram. The slightly larger estimated bandwidth for the 1000-Hz signal than for the 2431-Hz signal reflects the (linear) spectral splatter associated with the brief tone pip stimuli, and is not related to decision processes of the subjects. Due to the large number (approximately 7000) of hits the variability in the masker is nearly imperceptible in the spectrogram. The presence of the masker, however, is still noticeable as the level of the spectrogram drops for frequencies outside the masker bandwidth (250–4000 Hz).

The middle panel of Fig. 3 shows the average spectrogram of the stimulus relative to when a hit response occurred. The temporal location and duration of the region of high level reflects the latency and temporal blurring associated with variability in the reaction time of the subject (cf. Fig. 2). The level at the signal frequency of the average spectrogram of the stimulus relative to when a hit response occurred is slightly lower than the level at the signal frequency in the signal-triggered averaged spectrogram; this decreased level is a result of the temporal blurring associated with capturing the variability in the reaction time of the subject. Comparing the signal-triggered and response-triggered equal-level contour properties for hits (Table 2), the variability in the reaction times of the subjects influences the temporal properties of the region of high level, as expected, but not the spectral properties. As was the case with the signal-triggered averaged spectrograms, for each subject and signal frequency, the center frequency of the region of high level is nearly equal to the signal frequency and the bandwidth is consistent with the spectral splatter of the short duration tone-pips and the one-third octave smoothing included in the spectrogram processing.

The bottom panel of Fig. 3 shows the response-triggered averaged spectrogram for the false alarms, the psychophysical STRF, for subject S1. The psychophysical STRF reflects only the attributes of the masker, since when a false alarm occurs the signal is absent. The similarity between the regions of high level for the psychophysical STRF and the response-triggered hit spectrogram indicates that false alarms occur when the masker, due to its random nature, has properties that mimic the signal. The similarity is quantified in Table 2; the bandwidth and center frequency of the region of high level in the psychophysical STRF (response-triggered false alarm spectrogram) are nearly indistinguishable from the bandwidth and center frequency of the region of high level in the response-triggered averaged spectrogram for the hits. The duration of the region of high level in the psychophysical STRF is shorter than for the response-triggered averaged spectrogram for the hits. This may reflect the substantial difference in the number of hits and false alarms or it may reflect the decision process of the subjects. The subjects may respond that they heard the “signal” when “tone pip streams” with fewer pips than the 4-pip signal occurred. As expected, the level at the signal frequency in the response-triggered false alarm spectrogram is lower than the level at the signal frequency in response the response-triggered hit spectrogram. On average, responses occur when the level at the signal frequency is at least 1 or 2 dB above the background level.

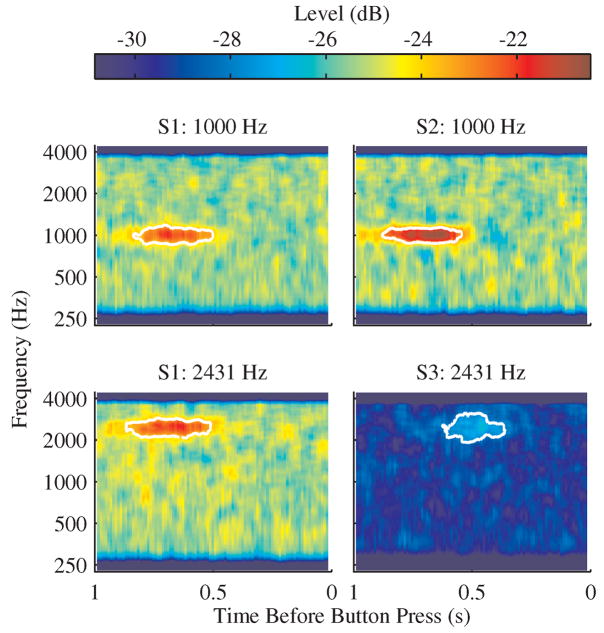
Figure 4 shows the psychophysical STRF for all the subjects and conditions. The four psychophysical STRFs are shown using a common color mapping. Recall that the expected number of masker pips for subject S3 was lower than for the other subjects resulting in the psychophysical STRF having a lower average level. Each psychophysical STRF shown in Fig. 4 has a single region of high level near the signal frequency. Each region of high level is enclosed with a contour of equal level that was computed with an individualized color mapping that maximized the visual contrast. As quantified in Table 2, the regions of high level are similar across the subjects and conditions. The similarities in the psychophysical STRFs demonstrate that it is possible to estimate a psychophysical weighting function with the method of free response that incorporates the relative timing of the behavioral responses.

Figure 4.

The response-triggered averaged spectrograms for the false alarms are plotted for subject S1 with a signal frequency of 1000 and 2431 Hz (left column) and subject S2 with a signal frequency of 1000 Hz (top right panel) and subject S3 with a signal frequency of 2431 Hz (bottom right panel). The expected number of masker pips (see methods) was lower for subject S3 resulting in a lower overall level of the average spectrogram. The contour of equal level that encloses the region of high level located near the signal frequency is shown in white.

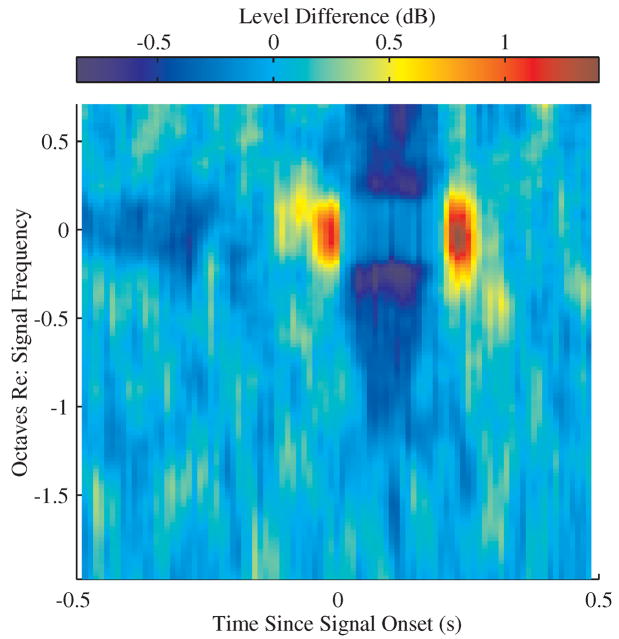
Figure 5 presents the averaged difference between the signal-triggered averaged spectrogram of hits and misses. The ordinate for this spectrogram is normalized frequency, where zero corresponds to the signal frequency. Because the spectral locations of the 1000- and 2431-Hz signals, relative to the masker bandwidth, were different, there is an asymmetry in the frequency axis of Fig. 5. The color map of Fig. 5 corresponds to the magnitude of the differences between the signal-triggered averaged spectrogram of hits and misses. Spectral-temporal regions with relatively low levels (blue) indicate a reduced likelihood of a response when the masker has power in that spectro-temporal region, whereas areas with relatively high levels (red) indicate an increased likelihood of a response. These regions are akin to the spectral-temporal regions of “inhibition” and “excitation,” respectively, in physiological STRFs.

Figure 5.

The difference in the signal-triggered averaged spectrograms for the hits and misses averaged across subjects and signal frequencies. Positive values (red) indicate a hit is more likely when the stimulus has energy in that spectro-temporal region and negative values (blue) indicate that a hit is less likely.

There are three spectro-temporal regions of interest in the hit-minus-miss signal-triggered spectrogram. First, masker energy near the signal frequency just prior to and just after the signal increases the likelihood of a signal response, suggesting that increasing the number of temporally abutting tone pips in the signal increases the likelihood of a response. Second, increased energy in frequency regions above and below the signal frequency that co-occur with the signal decrease the likelihood of a response and suggest that masker energy in frequency regions flanking the signal frequency results in masking. Alternatively, this might reflect a use of the spectral contrast between the energy at the signal and nearby frequencies (Green 1988). Third, masker energy near the signal frequency that precedes the signal onset by a few tenths of a second decreases the likelihood of a response. One possible interpretation is that this “early” masker energy masks the signal. Another possibility is that this “early” masker energy may illicit a response from the subjects and therefore briefly decrease the likelihood of the subjects responding again (Egan et al., 1961).

Notably, masker power near the signal frequency, at the time at which the signal is presented, has almost no influence on the likelihood of a response. This suggests that when the signal is present, the probability of a response is only weakly influenced by masker power at the signal frequency. This is consistent with the fact that the signal, when present, dominates the overall level at the signal frequency. Therefore, the effect of the masker on the combined signal-plus-masker stimulus is much reduced when the signal is present.

IV. DISCUSSION

The continuous stimulus presentation used in the method of free response, as Egan et al. (1961) noted, better reflects everyday listening situations than traditional trial-based paradigms. The method comes with a cost, however, in that traditional summary statistics, such as d′ and β, are not unambiguously defined. Here, we demonstrated that within the framework of the method of free response a psychophysical weighting function, analogous to the physiological STRF, can be estimated. The psychophysical STRF, like all psychophysical weighting patterns, provides information about inefficiencies in the decision strategies of subjects (Berg, 2004). Finally, there is the potential that psychophysical and physiological STRFs can be obtained in parallel in awake and behaving physiological experiments.

The goal of this study was to determine if a psychophysical STRF can be reliably estimated. In order to estimate a psychophysical weighting function the decision strategy of the subject must be relatively stable over time. Further, the variability in the reaction times of the subject must be small enough as to not obscure the interesting aspects of the psychophysical STRF. As discussed below, in the current informational-masking task both the weighting functions were stable enough and the variability in the reaction times was small enough that a meaningful psychophysical STRF could be estimated.

The psychophysical STRFs shown in Fig. 4 demonstrate that psychophysical weighting functions that incorporate the relative timing of responses can be measured with the method of free response. The variability in the reaction times of the subject may pose a problem for analyses in which better temporal resolution is required, but in the current task the variability in the reaction time does not obscure interesting aspects of the psychophysical STRF. The decision strategies of the subjects appear to be stable since each psychophysical STRF resembles the expected psychophysical weighting function, once reaction time variability is accounted for. Overall, the similarities in the psychophysical STRFs across the subjects and signal frequencies demonstrate that reliable psychophysical weighting functions can be obtained with the method of free response in an informational-masking task.

The task required subjects to detect a simple target in the presence of a spectro-temporally complex masker, the paradigm is general enough that it is likely that psychophysical STRFs may be estimated in any detection task where subjects decide, on a moment-to-moment basis, to respond or not. It is also likely that the paradigm could be expanded to discrimination paradigms by providing subjects with two response buttons or to identification paradigms by proving a means of multiple responses. The advantage of using a simple target signal is that the psychophysical weighting functions (both the psychophysical STRF and the hit-minus-miss signal-triggered spectrogram) measured with the method of free response can be compared qualitatively to psychophysical weighting functions measured with trial-based paradigms.

The comparison between the current psychophysical weighting functions that were measured with the method of free response and previously measured trial-based psychophysical weighting functions focuses on four prominent features of the psychophysical weighting functions that were measured in the current study. First, as indicated by the center frequency of the equal-level contour that enclosed the region of high level (cf. Table 2), subjects predominately relied on information at the signal frequency in making their detection decision. Second, the bandwidth of the equal-level contour that enclosed the region of high level is the same when the signal is present (hits) and absent (false alarms). Third, there are negative weights at frequencies above and below the signal frequency when the signal is present (cf. Fig. 5), but not when the signal is absent (cf. Fig. 4). Fourth, when the signal is present there are positive weights immediately before and after the signal (cf. Fig. 5).

Three of the four basic findings using the psychophysical weights estimated with the method of free response qualitatively agree with previous measurements of psychophysical weights estimated using trial-based paradigms and a multi-pip tonal signal and an informational masker (Richards and Tang, 2006; Huang and Richards, 2008). Specifically, in the psychophysical weighting functions measured in those studies (1) the most weight is given to the signal frequency, (2) there are negative weights at frequencies above and below the signal frequency when the signal is present but not when the signal is absent and (3) there are positive weights immediately before and after the signal. Due to the methods used to compute the psychophysical weights with trial-based paradigms, it is not possible to determine if the bandwidth is the same when the signal is present and absent.

There are also fundamental similarities between the psychophysical weights estimated with the method of free response in an informational-masking task and the psychophysical weights estimated with trial-based procedures in a tone-in-noise detection task (Ahumada et al., 1975). In the tone-in-noise detection task, like the informational-masking task, the most weight is given to the signal frequency and there are negative weights at frequencies above and below the signal frequency when the signal is present but not when the signal is absent. There are, however, two qualitative discrepancies between the psychophysical weights estimated with the method of free response in an informational-masking task and the psychophysical weights estimated with trial-based procedures in a tone-in-noise detection task. These differences are considered in detail in the next two paragraphs.

Ahumada et al. (1975) measured differences in the bandwidth across which subjects integrate information when the signal is present and absent in a trial-based tone-in-noise detection task. This result is not obtained in the current free-running informational-masking task. This discrepancy may reflect differences in the decision processes associated with free-running and trial-based paradigms. Alternatively, it may be that the one-third octave filter used to estimate the spectrograms in the current procedure obscures potential differences in bandwidth. Most probable is that this discrepancy reflects differences in the decision processes with informational maskers, where the effective bandwidth is relatively large, and noise maskers, where the effective bandwidth is relatively narrow (Oh and Lutfi, 1998).

The second qualitative difference is that Ahumada et al. (1975) found that when a signal is presented in the presence of a noise masker there are negative weights immediately before the signal whereas in the current task, as well as other informational-masking tasks (e.g., Richards and Tang, 2006; Huang and Richards, 2008), there are positive weights prior to the signal onset. Potentially this difference reflects the fact that the informational masker is composed of the same elements as the signals while the noise masker is different than the signal. With the informational masker, if there happen to be five tone pips in a row at the signal frequency, it is reasonable that the subject would be more likely to indicate that the four-pip signal was presented. With the noise masker, it seems less likely that the subjects would confuse the noise masker with tonal target signal. Therefore it seems that this difference between the psychophysical weights estimated with the method of free response in an informational-masking task and the psychophysical weights estimated with trial-based procedures in a tone-in-noise detection task is not associated with the free-running nature of the stimulus in the method of free response.

Overall, the similarities in the psychophysical weights estimated with free-running and trial-based paradigms suggest that the current free-running paradigm can be used to investigate the decision process of listeners using more naturalistic stimulus presentation schemes. Critically, the continuous nature of the stimulus presentation does not appear to drastically alter the way in which subjects form their decisions. For more cognitively demanding tasks, however, the additional burden of vigilance and the increased temporal uncertainty in a free-running paradigm may result in systematic changes in detection strategies, and given the current data, these changes are likely to be measurable.

LIST OF ABBREVIATIONS

STRF

spectro-temporal receptive field