Abstract
Purpose
To evaluate an algorithm based on algebraic estimation of T1 values (three-point estimation) in comparison with computational curve-fitting for the postprocessing of quantitative cerebral perfusion scans.
Materials and Methods
Computer simulations were performed to quantify the magnitude of the expected error on T1 and consequently cerebral perfusion using the three-point estimation technique on a Look-Locker (LL) EPI scan. In 50 patients, quantitative cerebral perfusion was calculated using the bookend method with three-point estimation and curve-fitting. The bookend method, a novel approach for calculating quantitative cerebral perfusion based on changes in T1 values after a contrast injection, is currently being validated. The number of computations was used as a measure of computation speed for each method. Student’s paired t-test, Bland-Altman, and correlation analyses were performed to evaluate the accuracy of estimation.
Results
There was a 99.65% reduction in the number of computations with three-point estimation. Student’s t-test showed no significant difference in cerebral perfusion (P = 0.80, 0.49, paired t-test N = 50, quantitative cerebral blood flow-white matter [qCBF-WM], qCBF-gray matter [qCBF-GM]) when compared to curve-fitting. The results of the two techniques were strongly correlated in patients (slope = 0.99, intercept = 1.58 mL/(100 g/minute), r = 0.86) with a small systemic bias of -0.97 mL/(100 g/minute) in Bland-Altman analysis.
Conclusion
The three-point estimation technique is adequate for rapid calculation of qCBF. The estimation scheme drastically reduces processing time, thus making the method feasible for clinical use.
Keywords: quantitative CBF, MR perfusion, T1 mapping, LL-EPI, acute stroke
THE IMAGING OF PHYSIOLOGIC PARAMETERS related to cerebral perfusion, such as mean transit time (MTT), cerebral blood volume (CBV), and cerebral blood flow (CBF), is possible with MRI (1-5). In its current clinical implementation, MR-based perfusion images report relative, rather than quantitative perfusion. The ease of use and widespread availability of MRI based cerebral perfusion is becoming increasingly important in determining the underlying pathophysiology of several diseases (6-8). A method for obtaining quantitative CBF (qCBF), called the “bookend technique,” which is based on T1 changes after injection of gadolinium-based contrast, has been reported (9-11). The bookend approach has not been fully validated to the reference standard, [15O]-H2 positron emission tomography (PET); however, the bookend approach has produced values that are consistent with historical reference values and has been shown to be highly reproducible in a clinical setting (9-11). A major impediment to the dissemination and more widespread evaluation of this technology is the need for specialized software for image postprocessing.
The goal of this report is to evaluate an algorithm for the postprocessing of bookend perfusion scans. We present an approach to approximate T1 values using three-point estimation fitting. We propose that this three-point estimation approach is adequate for the purpose of quantifying cerebral perfusion.
MATERIALS AND METHODS
This Health Insurance Portability and Accountability Act (HIPAA)-compliant study was approved by the institutional review board at our institute. Our approach is a modification to the postprocessing used in the bookend method, which has been proved to be accurate, reliable, and reproducible (9-11). All image post-processing and analyses were performed using commercially available software (MATLAB R2006a; The MathWorks, Inc., Natick, MA, USA). Currently, post-processing of bookend perfusion images can take over an hour, hindering the adaptation of MR cerebral perfusion into the diagnostic algorithm. The rate-limiting step for quantitative MR perfusion using the bookend technique is currently the mapping of longitudinal relaxation (T1) values. Obtaining the quantitative CBV (qCBV) is the first step in obtaining the qCBF, based on the ratio of differences in inverse T1 in blood and tissue after a gadolinium injection as shown by Eq. [1]. The bookend equation takes into account intravascular water exchange correction (WCF), the brain density (ρ), and the hematocrit levels (Hct) in large and small vessels (LV and SV) (9,10,12):
| [1] |
To calculate qCBF, relative CBV and CBF (rCBV and rCBF) have to be determined next. rCBV is determined from a ratio of integrals of tissue concentration (C) and arterial input function (AIF) as shown in Eq. [2], taking into account the brain density (ρ) and Hct in LV and SV (9,10):
| [2] |
rCBF is found by deconvolution of the tissue concentration and AIF by singular value decomposition of a reformulation of Eq. [3], where R(t) is the residue function (9).
| [3] |
Since the ratio qCBV/rCBV is the same as the ratio qCBF/rCBF, qCBF is determined by Eq. [4] (9):
| [4] |
The T1 maps for qCBV determination are derived from signal data acquired with a Look-Locker echo-planar imaging (LL-EPI) sequence by fitting the signal data to a relaxation curve for each voxel using a Levenberg-Marquardt (L-M) least-squares approach (13). L-M curve fitting is a well-established iterative technique for curve-fitting that has been proven to have high accuracy and convergence properties but can be prohibitively slow.
THEORY
Our analysis is based on the LL signal relaxation equation (Eq. [5]), where M0 is the initial magnetization, InvF is the inversion factor, and T1* is the apparent T1. T1* is used to determine longitudinal T1 relaxation values using Eq. [6] (10,13):
| [5] |
| [6] |
We simplified the signal equation using three parameters to characterize the signal as shown in Eq. [7], where X1 is equal to M0, X2 is equal to InvF times M0, and X3 is equal to T1*, similar to Deichmann et al (14):
| [7] |
In the L-M fit, X1, X2, and X3 are free parameters and are used in determining T1:
| [8] |
To mitigate the time-intensive least-squares fit to determine the parameters X1, X2, and X3 of the signal relaxation equation, we implemented a three-point estimate of T1, obtained from three points of the signal curve: 1) the initial magnetization point (M0) where we approximate S(t = 0) in Eq. [6], 2) the null point (tnull) (S(t) = 0), and 3) the signal at t > T1, called “infinity point” (t∞):
| [9] |
| [10] |
| [11] |
Figure 1 shows a plot of a short and long T1 relaxation curves and the points used for determining the fit parameters. For the purposes of this study, we approximated the infinity point (X1) as t∞ = 2520 msec, which corresponds to the last image acquired in the LL scan, that is, the last time point sampled on the regrowth curve. We calculated X2 by using the initial magnetization point since at time zero the exponential term is equal to one and thus initial magnetization is the absolute difference between X1 and X2. The initial magnetization point was estimated as the signal from the first sampled time point. Lastly, X3 is calculated from X1 and X2 using the fact that at the null point (tnull) the signal value is zero as shown in Eq. [11]. We estimated the null point as the point of minimum signal intensity in the T1 regrowth curve. Once the parameters had been estimated, T1 values were calculated using Eq. [8].
Figure 1.
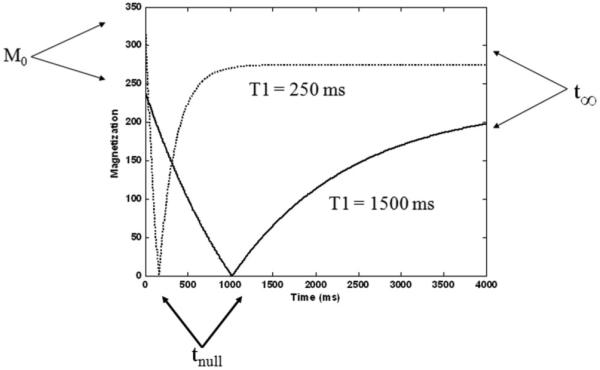
T1 relaxation curves shows the three-point estimation parameters used for estimating the fit of the longitudinal relaxation signal equation. Note that for long T1 species, the approximation that the last acquired data point corresponds to t = ∞ breaks down.
Simulations
Computer simulations were performed in MATLAB to quantify the magnitude of the expected error on T1 from the three-point estimation technique. This simulation was designed to determine the range of T1 values over which the three-point estimation would be valid for the calculation of CBF. A signal was simulated using the Bloch equation with parameters for the existing scanning sequence (LL-EPI) (13). Noise was generated using Eq. [12], where M is the magnetization without noise, normalized so M0 = 1, n1,2 are random numbers from a Gaussian distribution with zero mean and unit variance. The value of the signal-to-noise ratio (SNR) was set to 110, based on measurement of signal and noise regions of interest (ROIs) from an LL image at the first time point (15). In the simulations, we set a T1 value (true T1 value), and then generated a signal with noise using that T1 value. We then used both the curve-fitting technique and our three-point estimation technique to measure experimental T1:
| [12] |
Data Analysis
Simulation results were used in a correlation analysis to determine the relative error introduced in the quantification of cerebral perfusion. Because there is a linear dependence between qCBV measurement in white matter (WM) and the global qCBF values (9-11, 16-18), we determined the resulting error on qCBF analytically as the relative error in qCBV in WM. We assume a 2% blood volume, for WM, a single dose (0.1 mmol/kg body weight) gadolinium injection and an initial WM T1 of 650 msec. Under these assumptions: T1 WM pre = 650 msec, T1 WM post = 625 msec, T1 blood precontrast = 1200 msec, T1 blood postcontrast = 250 msec. These values yield a qCBVTRUTH value of 1.94 mL/100 g. This was compared with the same value calculated from the T1 values calculated from the three-point estimate. To get an estimate of the error calculated as:
| [13] |
Patient Study
The MRI perfusion examinations of 50 consecutive patients (male: 23, female: 27, ages 54 ± 17 years) with a wide range of pathologies: stroke (N = 9), tumor (N = 21), or intracranial arteriovenous malformation (AVM) (N = 10) were retrospectively reviewed. Patients were excluded if there was severe motion during the perfusion scans or if they had undergone contrast-enhanced MRI within 24 hours of the perfusion scan.
MRI
All 50 patients were scanned in a 1.5T scanner (Avanto: N = 19, Espree: N = 3, Sonata: N = 6, Symphony: N = 22; Siemens Medical Solutions, Erlangen, Germany). In the bookend perfusion protocol, three scans are required. First, a segmented inversion-recovery (IR) LL-EPI (nonselective inversion pulse, 20° excitation flip angle, TR = 21 msec, TE = 9.9 msec, TI = 15 msec, 128 × 128 matrix, 220 mm field of view (FOV), 21 lines in k-space per an acquisition, 5 mm thickness, 120 time points) scan was performed. A delay time between the data acquisition at the last time point and another inversion pulse is 2 seconds, leading to a total scan time of 45 seconds. This sequence was designed with 4400 msec between inversion pulses to allow full regrowth. This LL-EPI scan was used to estimate the initial T1 values. The LL-EPI sequence was designed without regard to scanner-specific parameters and falls within specifications of all of the scanners used in the data accrual. Next, a perfusion-weighted imaging (PWI; gradient echo, TR/TE = 1500 msec/40 msec, matrix size = 128 × 128, FOV = 220 mm, slice thickness = 5 mm, slices = 13, 50 measurements on each slice) scan consisting of single-shot EPI acquisitions was performed. A single-dose injection of a gadolinium-based contrast agent (0.1 mmol/kg; Magnevist; Berlex, Princeton, NJ, USA) was injected during PWI at a rate of 5 mL/second by a power injector. The last scan is another segmented IR LL-EPI scan with same specifications as the first scan. This LL-EPI scan was used to estimate the final T1 values, shortened by contrast injection. The slice for LL-EPI is usually one of the 13 slices of the PWI containing a major WM region. In the event that the slices did not match between LL-EPI and PWI, coregistration was performed using Statistical Parametric Mapping (SPM) software package (SPM5; Wellcome Department of Cognitive Neurology, London, England).
Image Postprocessing
qCBF values were calculated according to the bookend method (Eqs. [1]-[4]) using the three-point estimation approach for determining T1 values. As Eq. [1] shows, qCBV calculation is based on the ratio of differences in inverse T1 values in WM (tissue) and blood before and after gadolinium-based contrast (9-11). WM was automatically chosen from the estimated T1 distribution by selecting the full width of half the maximum of T1 distribution (9,10). Thus, T1 of WM results directly from WM segmentation (10). The sagittal sinus was used for obtaining blood T1 values and was chosen by an automatic algorithm without user input (9,10). First, a ΔR1 map was obtained from the difference of inverse T1 values before and after gadolinium-based contrast injection as shown by Eq. [14]:
| [14] |
Maximum ΔR1 occurs in blood, specifically the sagittal sinus (9,10). To create a mask of the sagittal sinus, we empirically determined that raising ΔR1 to the sixth power creates a large enough separation between blood and tissue ΔR1 values to allow for efficient segmentation of the sagittal sinus. After filtering out values for which ΔR1 < 0.80 × (ΔR1)6, the only values left corresponded to voxels for the sagittal sinus. We found the cutoff by finding a ratio between an ROI of the sagittal sinus and the rest of the brain. Contrast acts as a T1 shortening agent, and thus T1 of blood before contrast injection is much higher (about 1200 msec at 1.5T) than T1 of blood after contrast (about 250 msec at 1.5T) for a signal dose injection (9,10). Since qCBV calculation involves the inverse of these T1 values (i.e., R1), the R1 of blood precontrast is very close to zero; hence, we approximated 1/T1 blood precontrast to be zero. This step reduced the systematic error on qCBV from the poor performance of our estimation for long T1 species. The T1 of blood postcontrast value was calculated from the average T1 value from all voxels covering the sagittal sinus.
Data Analysis
The three-point estimation technique was evaluated based on its computational efficiency, accuracy in determining T1 values, and accuracy in quantifying CBF. A simple computation of time measurement between the three-point estimation and fitting methods was not sufficient because processing time varies depending on the computer, processor, and background processes running. Even when the background processes are controlled by disconnecting the computer from the network, operating system processes can change between trials; hence, a better measure of processing time is a record of the number of computational operations each method utilizes. This was measured by using a built-in MATLAB function. All measurements were performed on the same computer (Lenovo T60, Intel Core2 Duo T5500, 1.66 GHz, 1.00 GB RAM). A paired t-test for difference in number of operations for all 50 patients was performed to determine whether observed differences were statistically significant.
A comparison of the three-point estimation and the fitting methods was performed using paired Student’s t-tests for qCBF in WM and gray matter (GM). WM and GM regions were chosen by drawing ROIs in qCBF images calculated by the fitting method, and same ROIs were used for comparison of qCBF values calculated using the three-point estimation method. A Bland-Altman analysis of the L-M fitting and three-point estimated qCBF values was performed to elucidate any trends that depend on the value of perfusion.
RESULTS
Simulations
Figure 2 shows the correlation between T1 determined from the three-point estimate and the L-M fitting of the full regrowth curve. The unity line shows that the L-M fitting method correlates well with true T1 values, but the three-point estimation correlates only for values less than 1000 msec. Based on these simulations, we determined that the percentage error of 10.5% was present in the three-point estimate of qCBF. For WM this corresponds to 2.2 mL/(100 g/minute).
Figure 2.
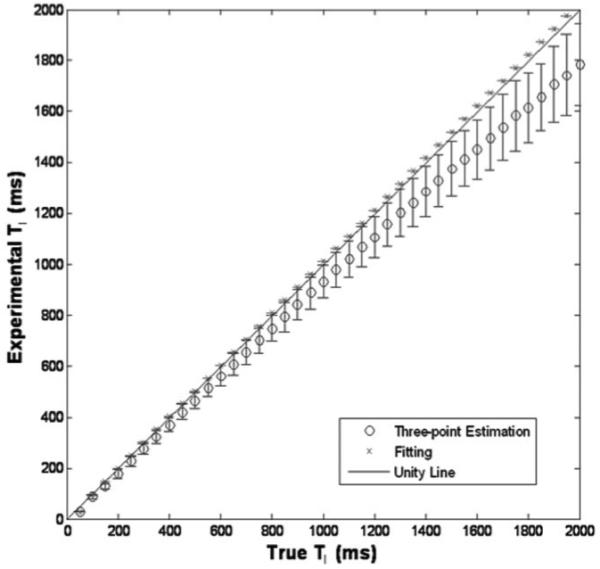
Simulation results of three-point estimation and fitting compared to true T1 values. The fitting method shows a good correlation and three-point estimation correlates for T1 values less than 1000 msec.
Patient Study
Examinations and postprocessing were performed successfully in all 50 patients. Figure 3 shows a direct comparison between images in a stroke patient reconstructed with the L-M fitting and three-point estimation methods. The parametric images show quantitative perfusion on a scale from 0 to 120 mL/(100 g/minute), with the red-green-blue (RGB) scaling that is used clinically at our institution. Quantitatively, the two approaches to image reconstruction are identical, and qualitatively right hemispheric hypoperfusion is evident in both images.
Figure 3.
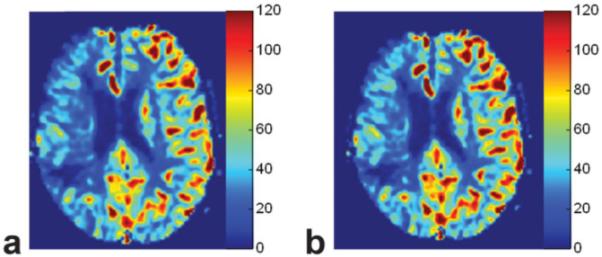
Parametric images from a stroke patient of CBF reconstructed using the bookend technique with (a) L-M fitting and (b) the three-point estimation. Note the areas of hypoperfusion in the right hemisphere that are equally represented by both approaches to image reconstruction.
Results of the ROI analysis of measured T1 values are shown in Fig. 4. These plots show that linearity exists for T1 values less than 1000 msec and nonlinearity increases for higher T1 values because of higher variability. The results of the correlation analysis for T1 values up to 2400 msec (twice the expected T1 of unenhanced blood) yield a slope of 1.11, intercept of 177 msec and r-value of 0.991. The Bland-Altman analysis shows good agreement between the L-M fitted and estimated T1 with a mean bias of 85.34 msec.
Figure 4.
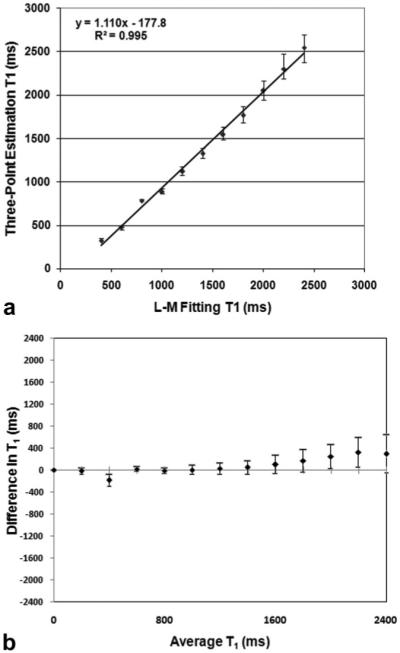
a: Voxel-by-voxel comparison of T1 values measure in patients (N = 50) between the three-point estimation and L-M fitting methods. The line of unity shows correlation between the methods at low values of longitudinal relaxation (T1 < 1000 ms). b: Bland-Altman analysis of voxel-by-voxel comparison of the same data.
We found the mean qCBF-WM, and qCBF-GM values for the fitting method are 26.03 ± 11.46 mL/(100 g/minute), and 69.68 ± 27.30 mL/(100 g/minute), respectively. The mean qCBF-WM and qCBF-GM values for the three-point estimation method are 25.69 ± 11.90 mL/(100 g/minute) and 71.96 ± 34.64 mL/(100 g/minute), respectively. Paired t-tests for qCBF show no significant difference between the fitting and three-point estimation methods (P = 0.80, 0.49, paired t-test N = 50, qCBF-WM, qCBF-GM, respectively). Figure 5a shows a correlation plot of qCBF values in both WM and GM between the three-point estimation and fitting methods. A good correlation (slope = 0.99, intercept = 1.58 mL/(100 g/minute), r = 0.86) is observed. A Bland-Altman analysis (shown in Fig. 5b) yielded a systematic bias of -0.97 mL/(100 g/minute) in the determination of qCBF.
Figure 5.
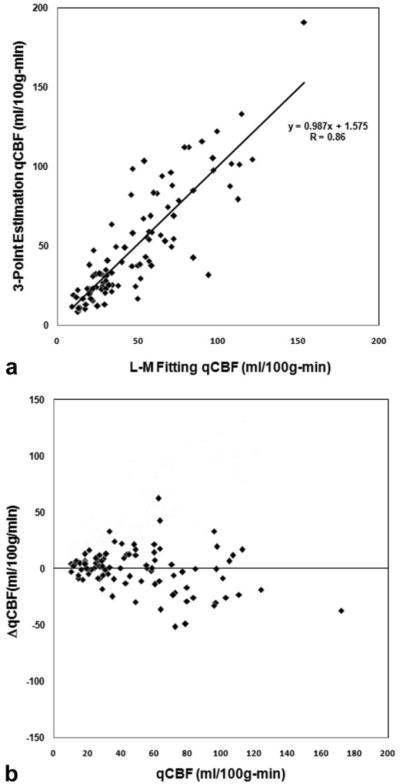
a: Correlation of qCBF values between the three-point estimation and fitting methods. Good correlation is seen with slope = 0.99, intercept = 1.58 mL/100 g/minute, and correlation coefficient of r = 0.86. b: Bland-Altman analysis of qCBF values shows no systematic bias.
The number of computational operations for T1 mapping did not change at different times of day or with/without network activity. The average number of operations was 6,934,582 ± 697,661 operations for the fitting method, and 24,284 ± 1914 operations for the three-point estimation technique.
DISCUSSION
We have found that using the three-point T1 estimation method in the calculation can reduce the postprocessing of quantitative perfusion images by two orders of magnitude. Despite systematic errors on our three-point estimation at long T1s, the error on the quantification of cerebral perfusion is negligible. The results indicate the analytical and curve-fitting approaches are comparable. This novel approach to accelerating perfusion quantification has the potential to reduce the complexity of image processing of quantitative perfusion images, a recognized limitation in the bookend technique. The bookend method has been shown to produce accurate and reproducible results (11), but has not been fully validated. We are currently focusing on validating the bookend technique to the reference standard [15O]-H2 PET.
Several MR approaches toward absolute quantification of CBF exist. Arterial spin labeling (ASL) consists of inverting the magnetization of flowing blood upstream of the desired region for perfusion measurement. The inverting magnetization is transferred to tissue as blood flows into imaging regions, altering local magnetization in proportion to CBF. Consequently, CBF can be calculated by measuring change in local magnetization (19). The accuracy of CBF depends on the time it takes for blood to flow from the labeling region to the readout slice. Some ASL techniques can minimize this dependence when transit times are in the normal range, but in patients with severely altered hemodynamics, the transit time can confound accurate CBF determination (20). Accordingly, the utility of ASL has not been established, since label-to-tissue transit times cannot be predicted.
The strongest correlation between MRI and the reference standard, radiolabeled [15O]-H2 PET, was found in an MR approach that applies a scale factor to rCBF images, accounting for errors in AIF (16). However, in this approach the correction factor relies on population-based, average venous efflux. Similarly, Ostergaard et al (18) have shown that it is possible to accurately determine qCBF by applying an empirically determined scale factor from a concurrent PET measurement. These population-based methods, nevertheless, do not account for the observed age-dependent reductions in qCBF (21,22) or vasoreactive hemodynamic responses seen in a disease state such as stroke that can alter the value of CBF in presumably normal tissue (17). The bookend method is a patient-based approach for determining the scale factor.
The three-point estimation technique for the bookend method introduces errors at three stages. First, as shown in Fig. 1, for a longer relaxation time, the signal curve does not reach steady state as fast as the signal for a short relaxation time. When we estimate the infinity point at t = 2520 msec, we assume the signal has reached steady state, but this assumption is a limitation at higher relaxation times. The next error is introduced when estimating M0. The first measured point of the signal is not the true initial magnetization point because of delay between signal readout and start of the scan, TI (initial time-point). The last source of error in estimation results from measurement of tnull. Since the LL-EPI signal is not continuous and is measured at 120 discrete time points, the true null point could possibly occur between the measured time points. Thus an error is introduced when using the minimum of LL-EPI signal as the null point. Because relatively short TR and TI (TR = 21 msec, TI = 15 msec) are used in our protocol, the error in null point estimations is minimized, and most error probably results mainly from infinity point estimation at higher true T1 values. Simulation and in vivo results (Figs. 2 and 4) support the conclusion that three-point estimation is adequate at T1 values less than 1000 msec.
Since WM T1 values are in the range of 500-700 msec, three-point estimation is valid for WM segmentation. The higher T1 values occur in cerebrospinal fluid and unenhanced blood. Thus we can only apply the same reasoning for T1 blood postcontrast, since contrast is a T1 shortening agent. However, the estimation scheme is not valid for T1 blood precontrast, as those values typically exceed 1200 msec. Since qCBV calculation involves the inverse of these T1 values (Eq. [1]), the R1 blood precontrast is very close to zero; hence, we approximate 1/T1 blood precontrast to be zero by setting T1 blood precontrast to infinity. For the purpose of whole-brain T1 mapping, we may be able to extend LL-EPI scanning to include more time points to allow longer relaxation signals to reach steady state, consequently improving the range for which estimation is adequate.
No difference occurs in the number of computational operations throughout the day, whereas network traffic fluctuates, and thus the number of computations is a better measure of reconstruction efficiency than absolute reconstruction time. A significant difference in speed exists between the methods (reduction by 99.65% in operations used). The average computationaloperations were 6,934,582 ± 697,661 operations for the fitting method and 24,284 ± 1,914 operations for the three-point estimation technique. In addition, MATLAB functions are compiled right before being used and remain in memory for the duration of the program. Thus, when a program calls a function numerous times, the function is executed faster after the first call. This is a major disadvantage for using MATLAB in the clinical setting. The final algorithm will be coded in C/C++, in which the code is precompiled; as a result, the speed of these programs is much faster. Thus, by coding our quantification analysis in C/C++ for use on the MRI console, we anticipate a further reduction in postprocessing time. We can also expect to see a decrease in time for curve-fitting, but curve-fitting will always be slower due to the iterative process, even if fully optimized.
As shown by paired t-tests, no significant difference exists between the fitting and three-point estimation methods (P = 0.80, 0.49, paired t-test N = 50, qCBF-WM, qCBF-GM, respectively) in patients. This means that our three-point estimation technique was adequate for qCBF calculation. Figure 3 yields visual evidence of the similarity of the two methods, showing that both perfusion images have the same voxel-to-voxel perfusion values. This agreement between the results demonstrates that there are no systematic shifts (up or down) in the parameters related to quantification of perfusion. Figure 5a supports the results by showing a good correlation (slope = 0.99, intercept = 1.58 mL/(100 g/minute), r = 0.86) in qCBF values in both GM and WM between the three-point estimation and fitting methods. This means that in a clinical setting, in cases where qCBF scans would be advantageous (e.g., stroke, AVM, and tumors), qCBF can be quickly and adequately determined using the three-point T1 estimation scheme. Using LL for T1 measurement in flowing blood has the potential confounding effect that the blood is flowing. This could result in differences in signal saturation, which depends on the velocity of the flowing blood. We did not find this effect to be a problem in these exams due to the fact that T1 measurement enters the quantification analysis as differences and ratios of T1. Therefore, the error introduced by systematic effects, such as signal saturation, is small. Figure 5b shows the Bland-Altman analysis of qCBF values between the fitting and three-point estimation methods. Higher variation is seen at higher qCBF values of 50-100 mL/(100 g/minute). This is due to blood-vessel blooming and partial volume averaging effects in qCBF images. These errors can potentially be minimized in the future by using spin-echo sequences instead of gradient-echo sequences (23).
This approach to qCBF quantification is not without limitations. Of primary concern is the lack of agreement for T1 values exceeding 1000 msec. This poor agreement results from insufficient regrowth of the magnetization within the echo train of the LL scan. Although these effects do not adversely affect our results when scanning at 1.5T, we anticipate that 3.0T scans, where T1 values are 30% longer, may be affected. This would require a retuning of the pulse sequence. Requiring a longer delay time between inversion pulses has the potential to mitigate these effects, at the expense of prolonged scan times. A second limitation is that the L-M fitting routines were not fully optimized prior to the comparison with the three-point method. However, it is unlikely that software optimization of an iterative fitting algorithm will ever be more efficient than simply extracting single data points from a vector. Last, the LL pulse sequence is a sequence we developed in-house, which can hinder clinical availability. We hope that if there is a need for widespread dissemination of the technology, productization would include a vendor-supplied pulse sequence.
In conclusion, we have found that our three-point estimation technique is adequate for rapid calculation of qCBF. However, the T1 estimation technique does not meet the need for rapid T1 measurement because estimation variability increases at high T1 relaxation times. Our estimation scheme drastically reduces processing time, thus making the method feasible for clinical use.
REFERENCES
- 1.Ostergaard L, Sorensen AG, Kwong KK, Weisskoff RM, Gyldensted C, Rosen BR. High resolution measurement of cerebral blood flow using intravascular tracer bolus passages. Part II: experimental comparison and preliminary results. Magn Reson Med. 1996;36:726–736. doi: 10.1002/mrm.1910360511. [DOI] [PubMed] [Google Scholar]
- 2.Ostergaard L, Weisskoff RM, Chesler DA, Gyldensted C, Rosen BR. High resolution measurement of cerebral blood flow using intravascular tracer bolus passages. Part I: Mathematical approach and statistical analysis. Magn Reson Med. 1996;36:715–725. doi: 10.1002/mrm.1910360510. [DOI] [PubMed] [Google Scholar]
- 3.Rosen BR, Belliveau JW, Aronen HJ, et al. Susceptibility contrast imaging of cerebral blood volume: human experience. Magn Reson Med. 1991;22:293–299. doi: 10.1002/mrm.1910220227. discussion 300-303. [DOI] [PubMed] [Google Scholar]
- 4.Rosen BR, Belliveau JW, Buchbinder BR, et al. Contrast agents and cerebral hemodynamics. Magn Reson Med. 1991;19:285–292. doi: 10.1002/mrm.1910190216. [DOI] [PubMed] [Google Scholar]
- 5.Rosen BR, Belliveau JW, Vevea JM, Brady TJ. Perfusion imaging with NMR contrast agents. Magn Reson Med. 1990;14:249–265. doi: 10.1002/mrm.1910140211. [DOI] [PubMed] [Google Scholar]
- 6.Baron JC, Marchal G. Ischemic core and penumbra in human stroke. Stroke. 1999;30:1150–1153. [PubMed] [Google Scholar]
- 7.Francis ST, Pears JA, Butterworth S, Bowtell RW, Gowland PA. Measuring the change in CBV upon cortical activation with high temporal resolution using Look-Locker EPI and Gd-DTPA. Magn Reson Med. 2003;50:483–492. doi: 10.1002/mrm.10547. [DOI] [PubMed] [Google Scholar]
- 8.Harris GJ, Lewis RF, Satlin A, et al. Dynamic susceptibility contrast MR imaging of regional cerebral blood volume in Alzheimer disease: a promising alternative to nuclear medicine. AJNR Am J Neuroradiol. 1998;19:1727–1732. [PMC free article] [PubMed] [Google Scholar]
- 9.Sakaie KE, Shin W, Curtin KR, McCarthy RM, Cashen TA, Carroll TJ. A method for improving the accuracy of quantitative cerebral perfusion imaging. J Magn Reson Imaging. 2005;21:512–519. doi: 10.1002/jmri.20305. [DOI] [PubMed] [Google Scholar]
- 10.Shin W, Cashen TA, Horowitz SW, Sawlani R, Carroll TJ. Quantitative CBV measurement from static T1 changes in tissue and correction for intravascular water exchange. Magn Reson Med. 2006;56:138–145. doi: 10.1002/mrm.20937. [DOI] [PubMed] [Google Scholar]
- 11.Shin W, Horowitz SW, Ragin A, Chen Y, Walker MT, Carroll TJ. Quantitative cerebral perfusion using dynamic susceptibility contrast MRI: evaluation of reproducibility and age- and gender-dependence with fully automatic image postprocessing algorithm. Magn Reson Med. 2007;58:1232–1241. doi: 10.1002/mrm.21420. [DOI] [PubMed] [Google Scholar]
- 12.Rempp KA, Brix G, Wenz F, Becker CR, Guckel F, Lorenz WJ. Quantification of regional cerebral blood flow and volume with dynamic susceptibility contrast-enhanced MR imaging. Radiology. 1994;193:637–641. doi: 10.1148/radiology.193.3.7972800. [DOI] [PubMed] [Google Scholar]
- 13.Look DC, Locker DR. Time saving in measurement of NMR and EPR relaxation times. Rev Sci Instrum. 1970:250–251. [Google Scholar]
- 14.Deichmann R, Hahn D, Haase A. Fast T1 mapping on a whole-body scanner. Magn Reson Med. 1999;42:206–209. doi: 10.1002/(sici)1522-2594(199907)42:1<206::aid-mrm28>3.0.co;2-q. [DOI] [PubMed] [Google Scholar]
- 15.Donahue KM, Weisskoff RM, Chesler DA, et al. Improving MR quantification of regional blood volume with intravascular T1 contrast agents: accuracy, precision, and water exchange. Magn Reson Med. 1996;36:858–867. doi: 10.1002/mrm.1910360608. [DOI] [PubMed] [Google Scholar]
- 16.Lin W, Celik A, Derdeyn C, et al. Quantitative measurements of cerebral blood flow in patients with unilateral carotid artery occlusion: a PET and MR study. J Magn Reson Imaging. 2001;14:659–667. doi: 10.1002/jmri.10021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mukherjee P, Kang HC, Videen TO, McKinstry RC, Powers WJ, Derdeyn CP. Measurement of cerebral blood flow in chronic carotid occlusive disease: comparison of dynamic susceptibility contrast perfusion MR imaging with positron emission tomography. AJNR Am J Neuroradiol. 2003;24:862–871. [PMC free article] [PubMed] [Google Scholar]
- 18.Ostergaard L, Johannsen P, Host-Poulsen P, et al. Cerebral blood flow measurements by magnetic resonance imaging bolus tracking: comparison with [(15)O]H2O positron emission tomography in humans. J Cereb Blood Flow Metab. 1998;18:935–940. doi: 10.1097/00004647-199809000-00002. [DOI] [PubMed] [Google Scholar]
- 19.Wong EC, Buxton RB, Frank LR. Quantitative perfusion imaging using arterial spin labeling. Neuroimaging Clin N Am. 1999;9:333–342. [PubMed] [Google Scholar]
- 20.Chalela JA, Alsop DC, Gonzalez-Atavales JB, Maldjian JA, Kasner SE, Detre JA. Magnetic resonance perfusion imaging in acute ischemic stroke using continuous arterial spin labeling. Stroke. 2000;31:680–687. doi: 10.1161/01.str.31.3.680. [DOI] [PubMed] [Google Scholar]
- 21.Frackowiak RS, Lenzi GL, Jones T, Heather JD. Quantitative measurement of regional cerebral blood flow and oxygen metabolism in man using 15O and positron emission tomography: theory, procedure, and normal values. J Comput Assist Tomogr. 1980;4:727–736. doi: 10.1097/00004728-198012000-00001. [DOI] [PubMed] [Google Scholar]
- 22.Pantano P, Baron JC, Lebrun-Grandie P, Duquesnoy N, Bousser MG, Comar D. Regional cerebral blood flow and oxygen consumption in human aging. Stroke. 1984;15:635–641. doi: 10.1161/01.str.15.4.635. [DOI] [PubMed] [Google Scholar]
- 23.Carroll TJ, Horowitz SW, Shin W, et al. Quantification of cerebral perfusion using the “bookend technique”: an evaluation in CNS tumors. Magn Reson Imaging. doi: 10.1016/j.mri.2008.04.010. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]


