Abstract
Subject-specific computational and experimental models of hemodynamics in cerebral aneurysms require the specification of physiologic flow conditions. Because patient-specific flow data is not always available, researchers have used “typical” or population average flow rates and waveforms. However, in order to be able to compare the magnitude of hemodynamic variables between different aneurysms or groups of aneurysms (e.g. ruptured vs. unruptured) it is necessary to scale the flow rates to the area of the inflow artery. In this work, a relationship between flow rates and vessel areas is derived from phase-contrast magnetic resonance measurements in the internal carotid arteries and vertebral arteries of normal subjects.
Keywords: Blood flow, carotid artery, vertebral artery, cerebral aneurysm, magnetic resonance imaging, wall shear stress
1. Introduction
Intracranial aneurysms are focalized dilatations of the cerebral arteries, typically located in the major vessels of the circle of Willis (Stehbens, 1972; Weir, 2002; Foutrakis et al., 1999). Cerebral aneurysm rupture is a major cause of hemorrhagic stroke and has high mortality and morbidity rates (Tomasello et al., 1998; Winn et al., 2002; Linn et al., 1996; Kaminogo et al., 2003). The initiation, growth and rupture of cerebral aneurysms are complex multi-factorial processes that are not well understood. However, it is widely believed that hemodynamics plays a fundamental role since it has been linked to mechano-biological processes such as growth, remodeling and degeneration of the arterial wall (Kayembe et al., 1984). The hemodynamics in the major cerebral arteries has recently been studied using 4D phasecontrast magnetic resonance techniques (Wetzel et al., 2007; Bammer et al., 2007; Yamashita et al., 2007). In addition, many researchers have used computational and experimental models constructed from patient-specific anatomical images to study the hemodynamics of cerebral aneurysms (Cebral et al., 2005; Steinman et al., 2003; Jou et al., 2003; Tateshima et al., 2003a; Shojima et al., 2004).
The two main ingredients required for realistic modeling of the hemodynamics in cerebral aneurysms are the patient-specific geometry and the physiologic flow conditions. Subject-specific geometrical models can be constructed from 3D anatomical images. Both computational and in vitro models have been constructed from different imaging modalities such as rotational angiography (3DRA), computed tomography angiography (CTA) or magnetic resonance angiography (MRA). Models of intracranial aneurysms have used patient-specific flow conditions derived from phase-contrast magnetic resonance (PC-MR) measurements of flow rates (Jou et al., 2003). Unfortunately, patient-specific flow conditions are not always available because they are not part of the routine clinical examinations. Thus, authors have used “typical” flow conditions for computational (Shojima et al., 2004; Cebral et al., 2005) and experimental models (Tateshima et al., 2001; Tateshima et al., 2003a; Tateshima et al., 2003b). These “typical” flow conditions were derived from measurements performed on normal subjects in different arteries. In order to assign flow rates for an individual patient specific model, the differences between the arterial anatomy of the normal volunteer and patient/subject must be considered. Sizes of arteries vary between individual and therefore flow rates are affected. To compare hemodynamic variables such as wall shear stress between different patients, it is necessary to use the appropriate flow rates for each individual.
The internal carotid arteries (ICAs) and vertebral arteries (VAs) are the major arteries feeding the circle of Willis. Therefore, most models of intracranial aneurysms have their inlet boundaries along these arteries, requiring knowledge about the flow conditions in these arteries. ICAs and VAs vary in size between individuals because of developmental, age related and disease conditions. The size and geometry of these vessels can be accurately determined with imaging techniques. Thus, the aim of this work was to quantify the flow rates and areas of ICAs and VAs, and to establish an empirical relationship between area and flow that can be used to estimate the flow rate for a given patient when flow measurements are not available. To the best of our knowledge, such relationship has not been presented.
2. Methods
2.1 Subjects and Imaging
A total of 11 normal subjects were imaged with phase-contrast magnetic resonance (PC-MR) using 1.5 T (7 subjects) and 3.0 T (4 subjects) scanners (GE Healthcare, Waukesha, WI) to study the relationship between cerebral blood flow and intracranial pressure (Alperin et al., 2005). The imaging protocol was approved by the institutional review board and informed consent was obtained from all subjects. A measurement slice was placed above the carotid bifurcation at about mid-C2 level and oriented perpendicularly to the nominal flow direction. Both left and right internal carotid arteries (ICA) and left and right vertebral arteries (VA) were imaged simultaneously with the same slice plane. The images were acquired with a field of view of 14 cm, a 256×128 matrix, a 6 mm slice thickness, a 15° flip angle and a 70-80 cm/s velocity encoding. For each 2D cine phase-contrast sequence, a total of 32 frames during the cardiac cycle were obtained.
2.2 Flow and Area Quantification
Volumetric flow waveforms and cross-sectional areas were quantified in both ICAs and VAs of each subject (Ford et al., 2005). For each of the 44 arteries, the time-dependent flow rate was obtained by integrating the through-plane velocity over the lumen cross-sectional area at every frame. An automated lumen segmentation technique called pulsatility-based segmentation or PUBS was used to delineate the boundary of the lumens for improved accuracy and reproducibility (Alperin and Lee, 2003). Assuming a constant cardiac output for each patient, the flow rates (Q) of all subjects were scaled to a nominal heart rate (HR) of 60 beats per minute: Qscaled = Qmeasured (HRMno min al/HRmeasured) in order to compare flows at the same hear rate.
2.3 Data Analysis
According to Poiseuille law (steady flow of a Newtonian fluid in a rigid straight cylinder of circular cross section), the flow rate and the area are related by the following formula (Kundu and Cohen, 2004):
| (1) |
where Q is the volumetric flow rate, A is the cross-sectional area, μ is the viscosity, and τ is the wall shear stress (WSS). This formula was used to estimate the wall shear stress for given values of the flow rate and vessel area.
Motivated by the fact that a Poiseuille flow implies a power law relationship between the flow rate Q and the cross-sectional area A, a curve of the form:
| (2) |
was fitted to the data using a Least Squares Method (Press et al., 1992). This was carried out for both the mean flow rate (time average over the cardiac cycle) as well as for the peak flow rate (flow rate at peak systole).
3. Results
The cross-sectional areas as well as the mean and peak volumetric flow rates were computed for each artery of each patient. The mean and standard deviations of these variables for each artery group and the entire sample are listed in Table 1. This table lists both the measured and scaled mean and peak flow rates.
Table 1.
Mean values and standard deviations of the cross sectional area, mean and peak flow rate (measured and scaled), for each artery group and the entire sample.
| Artery | A (cm2) | Measured |
Scaled |
||
|---|---|---|---|---|---|
| Qmean (cm3/sec) | Qpeak (cm3/sec) | Qmean (cm3/sec) | Qpeak (cm3/sec) | ||
| ALL | 0.19 ± 0.06 | 2.73 ± 1.55 | 4.91 ± 2.62 | 2.44 ± 1.46 | 4.40 ± 2.50 |
| VA | 0.14 ± 0.05 | 1.40 ± 0.75 | 2.66 ± 1.28 | 1.25 ± 0.67 | 2.38 ± 1.18 |
| ICA | 0.23 ± 0.03 | 4.05 ± 0.82 | 7.17 ± 1.32 | 3.63 ± 0.97 | 6.43 ± 1.65 |
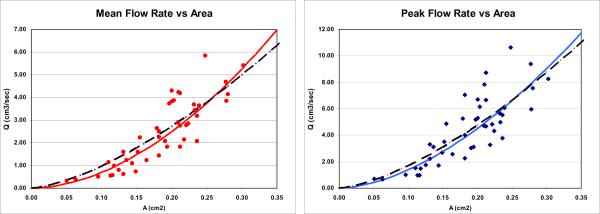
Using the Least Square Method, a curve of the form (2) was fitted to both the mean and peak flow rates for all arteries. The optimum values of n and k together with the correlation coefficients (R) are listed in the top row of Table 2. Assuming a Poiseuille flow (fixing n=1.5), the Least Squares Method yields the values of k and correlation coefficients (R) listed in the bottom row of Table 2.
Table 2.
Values of parameters and correlation coefficients found using the Least Squares Method.
| Curve | Mean flow |
Peak flow |
||||
|---|---|---|---|---|---|---|
| n | k | R | n | k | R | |
| Q = k · An | 1.84 | 48.21 | 0.9053 | 1.70 | 70.80 | 0.9110 |
| Q = k · A1.5 | 1.5 | 30.40 | 0.8074 | 1.5 | 53.82 | 0.8558 |
The mean and peak flow rates for all arteries are plotted against the cross-sectional area in Figure 1, left and right panels, respectively. The corresponding optimal curves (top row of Table 2) are plotted with solid lines and the curves corresponding to Poiseuille flows (n=1.5, bottom row of Table 2) are shown with dashed lines.
Figure 1.
Plots of mean (left panel) and peak (right panel) flow rate against area. The dots represent the measurement data for each artery, the solid lines the optimal curves (top row of Table 2) and the dashed lines the n=1.5 lines (bottom row of Table 2).
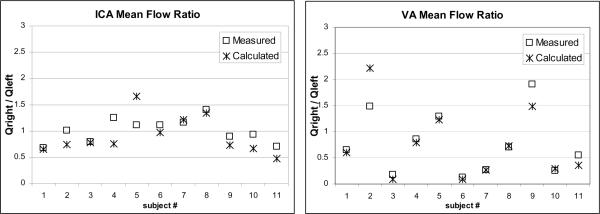
The ratios between measured mean flow rates in the right and left ICA's and right and left VA's of each subject were computed and plotted in Figure 2 (open squares). These ratios were also calculated from the corresponding areas using the formula Q = k · An (with n=1.84 and k=48.21) and plotted in Figure 2 (crosses). The average relative error between the predicted and the measured ratios was 20% and the maximum relative error reached 50% for both the ICA's and the VA's. Although dispersion in the predicted ratios is large, for the majority of the subjects the fitted curve yields a flow asymmetry ratio close to the actual ratio (relative difference less than 10%), especially for the vertebral arteries.
Figure 2.
Plots of the ratio between left and right mean flow rates in the ICA's (left panel) and VA's (right panel) of each subject.
Finally, the wall shear stress was calculated for each vessel using Equation (1), for both the mean flow and peak flow rates. The blood viscosity was set to μ=0.04 dyne sec/cm. The average values of WSS for each artery group and the entire sample are presented in Table 3 along with their standard deviations.
Table 3.
Values of wall shear stress computed for each artery group for both the mean and peak flow rates.
| Artery | Mean flow WSS (dyne/cm2) | Peak flow WSS (dyne/cm2) |
|---|---|---|
| ALL | 7.98 ± 2.66 | 16.46 ± 4.84 |
| VA | 6.35 ± 1.94 | 13.65 ± 3.44 |
| ICA | 9.61 ± 2.28 | 19.26 ± 4.42 |
4. Discussion
Previous studies have focused on measuring blood flow rates and wall shear stress in different arteries using Doppler ultrasound (DUS) and PC-MR techniques. Several researchers have reported on blood flow rates measured on normal subjects in common carotid arteries (Reneman et al., 2006; Shaaban and Duerinckx, 2000; Gnasso et al., 1996; Hoeks et al., 1995; Oyre et al., 1998; Shamijo et al., 1997) and internal carotid arteries (Marshall et al., 2004; Deane and Markus, 1997). Flow waveforms have been characterized in common carotid arteries from DUS measurements (Holdsworth et al., 1999) and in internal carotid arteries and vertebral arteries from PC-MR measurements (Ford et al., 2005). Others have calculated WSS from measurements of flow and area in common carotid arteries (Wu et al., 2004; Oshinski et al., 2006), brachial arteries (Dammers et al., 2003) and internal carotid arteries (Box et al., 2007).
In this paper the average mean flow rate measured in the ICA was 4.05 ml/s or 243 ml/min (see Table 1). This value is consistent with the measurements of 4.14 ml/s and 4.25 ml/s reported by Marshall et al. and Deane and Markus, respectively (Marshall et al., 2004; Deane and Markus, 1997). This value is also slightly higher than the 3.2 ml/s reported by Box et al. (Box et al., 2007) for elder subjects, and in between the values reported by Buijs et al. (Buijs et al., 1998) for elder subjects (215 ml/min) and younger subjects (290 ml/min). It must also be noted that most subjects in our sample had heart rates higher than 60 bpm, therefore the flow rates were in general reduced by the scaling to 60 bpm.
The mean wall shear stress in the ICA presented in Table 3 is slightly higher than the value reported by Box et al. (Box et al., 2007) for elderly patients. This is to be expected since elderly patients tend to have lower flow rates and thus lower wall shear stress. The peak WSS was computed using the area measurements obtained with the PUBS method. This technique yields the diastolic area, therefore the peak WSS values reported may be overestimations of the actual WSS at peak systole when the area is expected to enlarge as the vessels distend.
These previous studies did not investigate the relationship between flow rate and vessel area. A relationship between flow rate and vessel area is to be expected because alterations in wall shear stress values secondary to increased or decreased blood flow velocity elicit acute and long-term compensatory responses in arteries that ultimately result in normalization of the WSS, which in turn results in normalization of blood flow (Kamiya et al., 1988). In the short term, vessels either dilate or constrict in order to accommodate changes in blood flow velocity, usually owing to the local release of vasoactive peptides. However, in the case of a persistent increase or decrease in blood flow, a different process occurs involving the adaptive remodeling of the vessel wall with concomitant reorganization of cellular and extra-cellular components. Indeed, clinical findings indicate that chronic changes in blood flow rates through larger arteries induce corresponding adjustments of arterial diameter, and this has been confirmed in a number of in vivo experimental studies (Tronc et al., 2000; Tronc et al., 1996; Tulis et al., 1998).
To the best of our knowledge, this relationship has not been reported for ICA or VAs. The relation between flow rate and vessel area in 64 retinal arteries has been investigated using a combination of Laser Doppler Velocimeter (LDV) and monochromatic fundus photographs (Riva et al., 1985). In this study, the flow rate correlated with area to a power 1.38. The authors concluded that these values were in close agreement with Murray's law, which states that an optimal arterial network that achieves flow with the minimum biological work should have a constant wall shear stress throughout the whole vascular system (Sherman, 1981). Assuming a Poiseuille flow, this implies a power-law relation between flow rate and area with n=1.5.
In this paper, a power-law function was fitted to flow rate and cross-sectional PC-MR measurements performed on 44 intracranial arteries (22 internal carotids and 22 vertebral arteries) of 11 subjects. The optimal correlation coefficients for the mean flow and peak flow rate against area were both above 0.9. The optimal curves fitted to the data slightly deviated from the n=1.5 value predicted by Murray's law at n=1.84 for the mean flow and n=1.70 for the peak flow. However, the difference between these curves is smaller than the dispersion in the data, suggesting that the difference between the optimal curves and n=1.5 is not significant. In fact, an F-test can be used to test whether the two formulas produce significantly different results (Lomax, 2007). The measured data and the two curves (statistical models) yield an F-value of 1.255 which is smaller than the critical value of the F distribution at 5% significance level. Therefore, this test shows that the difference between the two formulas is not statistically significant. A significant difference would imply that the in vivo conditions are different from an idealized Poiseuille flow. This would be understandable since cerebral arteries have curved geometries, non-uniform cross sections, blood flow is pulsatile and non-Newtonian, and vessel walls are compliant (Reneman et al., 2006). The wall shear stress is a complex function of the arterial geometry, blood rheology, vessel compliance and flow conditions. The distribution of WSS along a cerebral artery typically exhibits zones of elevated and decreased WSS near arterial bifurcations and in regions of high vessel curvature (Cebral et al., 2003; Ferrandez et al., 2000; Alnaes et al., 2007; Oshima et al., 2001). Therefore, the estimations of wall shear stress from Poiseuille's formula may differ from the in vivo values. In spite of this fact, the flow rates and areas follow a relationship remarkably close to the ideal relation predicted by Murray's law and Poiseuille flows (see Figure 1). This suggests that most likely, the arterial system is designed to transport blood with the least amount of work.
Holdsworth et al. showed a strong and significant correlation between the mean and peak flow rates in the ICA and VA (Holdsworth et al., 1999), therefore it is not surprising that both the mean and peak flows correlate with the vessel area. The difference between the optimal curves fitted to the mean and peak flow rates may be due to the fact that a single value of the vessel area was used for both fittings, the diastolic area given by the PUBS method.
Interestingly, the values of the average wall shear stress computed for the ICA and VA groups differ by a small amount (see Table 3). In a previous study, Dammers et al. (Dammers et al., 2003) presented data showing that carotid arteries and brachial arteries have different wall shear stress values. They suggested that although both systems are likely at an optimal design point (similar to Murray's principle) their structures may be different because of the different characteristics of the brain and peripheral vascular beds fed by these arteries. According to this argument the ICA and VA systems are expected to have similar wall shear stress values since they are feeding vascular beds with similar characteristics. The small differences we observe may be related to inaccuracies in the flow rate and area estimations or from deviations of the in vivo conditions from the idealized Poiseuille flow. Therefore, we cannot conclude that the two systems have adapted to a different baseline values of wall shear stress.
In most subject-specific computational and experimental models of cerebral hemodynamics, data about the physiologic flow conditions necessary to prescribe inflow boundary conditions is not available. Therefore, researchers have used “typical” or “average” flow waveforms and flow rates derived from population studies. There is a large variability in sizes of arteries between individuals. Because arteries remodel to accommodate flow (Reneman et al., 2006), it is to be expected that larger arteries will have larger flows and vice versa. The question is then, how to scale these “typical” flow rates for a given artery cross-sectional area. This study provides an empirical relationship that allows scaling of flow rates from cross-sectional areas of internal carotid arteries and vertebral arteries, which are the main vessels supplying blood to the circle of Willis. A recent study showed that modeling a long segment of the parent artery is important for a realistic representation of the hemodynamics in cerebral aneurysms (Castro et al., 2006). For most models of intracranial aneurysms their inlet boundaries will therefore be either in the cervical internal carotid arteries or in the vertebral arteries, depending on whether the aneurysm is located in the anterior or posterior circulation. Thus this study provides a relationship between vessel area and flow rate that can be used as a guideline to derive flow boundary conditions for these models. However, different patients can have a significant deviation from these baseline conditions and sensitivity analyses around these values should be conducted in order to properly characterize the aneurysmal hemodynamics. With reasonable inflow conditions, researchers can move from a qualitative to a more quantitative analysis of hemodynamic variables and compare the variability of these variables across different populations (e.g. ruptured vs. unruptured aneurysms, etc.). This will further improve our ability to link hemodynamics data to clinical information and consequently may enhance our understanding of the processes which cause aneurysms to grow and rupture.
This study has several limitations. First, the measurements of flow rates and vessel luminal area are affected by imaging parameters and resolution. A recent study by Jiang et al. (Jiang et al., 2007) showed that when the ratio of vessel diameter to the resolution of MR images is about 8 the cross-sectional areas have an error less than 5%. The flow measurements reported by Alperin et al. (Alperin et al., 2005; Alperin and Lee, 2003) indicate that a resolution ratio of 8 mm vessel diameter to 0.78 mm pixel size provides a 3% accuracy for lumen area and flow, and a 5/0.78 ratio translates to about 5%. This translates to a vessel diameter of about 3mm in the current case, thus, except for small vessels the measurements should be well within 3% accuracy and possibly within 10% accuracy for smaller ones (less than 6 mm2 area). The second limitation is the use of data from young healthy volunteers. The flow-area relationship presented in this paper was derived from direct measurements of both area and flow rates in normal subjects using PC-MR techniques. However, this relationship may be affected by other physiological factors such as systemic blood pressure or heart rate. In diseased arteries these factors can influence the vessel area (e.g. modifying the arterial lumen or its compliance) or the blood flow rate (e.g. changing the resistance of the artery and its vascular bed). In addition, daily variations of the physiologic conditions with subject activity can also cause changes in the flow conditions and deviation from the flow-area relation derived in this study. Thus, the flow-area relation described in this study can be used to scale flow rate curves to individual vessel areas for CFD simulation, but it is recommended that sensitivity or variability analysis of the CFD results should be conducted in order to account for daily variations in the physiologic conditions and deviations from the flow-area relation and properly characterize the hemodynamic patterns. The third limitation is the use of the Poiseuille flow to estimate wall shear stresses. As discussed before, the WSS in arteries depends on geometrical and physiologic parameters and differs from Poiseuille's formula. However, the estimations of WSS presented in this study were used only to discuss the implications of the empirical relationship between flow rate and vessel area, namely that this relationship seems to imply that the arterial systems obeys the principle of optimal work described by Murray's law.
5. Conclusions
An empirical relation between mean flow rate and peak flow rate with the cross-sectional area of internal carotid arteries and vertebral arteries was derived from flow and area measurements performed with phase-contrast magnetic resonance techniques in normal subjects. This relationship can be used to scale flow rate waveforms with vessel areas in order to guide computational and experimental models of hemodynamics. In the case of cerebral aneurysms, this is useful, for instance, to compare hemodynamic variables such as the wall shear stress between ruptured and unruptured aneurysms in order to search for rupture risk indices.
Acknowledgements
We thank Philips Medical Systems and the American Heart Association for financial support.
References
- Alnaes MS, Isaksen J, Mardal KE, Rommer B, Morgan MK, Ingebritsen T. Computation of hemodynamics in the circle of Willis. Stroke. 2007;38:2500–5. doi: 10.1161/STROKEAHA.107.482471. [DOI] [PubMed] [Google Scholar]
- Alperin N, Lee SH. PUBS: Pulsatility-based segmentation of lumens conducting non-steady flow. Magn Reson Med. 2003;49:934–44. doi: 10.1002/mrm.10455. [DOI] [PubMed] [Google Scholar]
- Alperin N, Lee SH, Sivaramakrishnan A, Lichtor T. Relationship between total cerebral blood flow and ICP measured noninvasively with dynamic MRI technique in healthy subjects. Acta Neurchir (Wein) 2005;Suppl. 95:191–3. doi: 10.1007/3-211-32318-x_40. [DOI] [PubMed] [Google Scholar]
- Bammer R, Hope TA, Aksoy M, Alley MT. Time-resolved 3D quantitative flow MRI of the major intracranial vessels: initial experience and comparative evaluation at 1.5T and 3.0T in combination with parallel imaging. Magn Reson Med. 2007;57:127–40. doi: 10.1002/mrm.21109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Box FMA, van der Grond J, de Craen AJM, Palm-Meinders IH, van der Geest RJ, Jukema JW, Reiber JH, van Buchem MA, Blauw GJ. Paravastatin decreases wall shear stress and blood velocity in the internal carotid artery without affecting flow volume. Results from the PROSPER MRI study. Stroke. 2007;38:1374–6. doi: 10.1161/01.STR.0000260206.56774.aa. [DOI] [PubMed] [Google Scholar]
- Buijs PC, Krabbe-Hartkamp MJ, Bakker CJG, de Lange EE, Ramos LM, Breteler MM, Mali WPTM. Effect of age on cerebral blood flow: measurement with ungated two-dimensional phase-contrast MR angiography in 250 adults. Radiology. 1998;209:667–74. doi: 10.1148/radiology.209.3.9844657. [DOI] [PubMed] [Google Scholar]
- Castro MA, Putman CM, Cebral JR. Computational fluid dynamics modeling of intracranial aneurysms: effects of parent artery segmentation on intra-aneurysmal hemodynamcis. AJNR Am J Neuroradiol. 2006;27:1703–9. [PMC free article] [PubMed] [Google Scholar]
- Cebral JR, Castro MA, Burgess JE, Pergolizzi R, Sheridan MJ, Putman CM. Characterization of cerebral aneurysm for assessing risk of rupture using patient-specific computational hemodynamics models. AJNR Am J Neuroradiol. 2005;26:2550–9. [PMC free article] [PubMed] [Google Scholar]
- Cebral JR, Castro MA, Soto O, Löhner R, Alperin N. Blood flow models of the circle of Willis from magnetic resonance data. J Eng Math. 2003;47:369–86. [Google Scholar]
- Dammers R, Stifft F, Tordoir JHM, Hameleers JMM, Hoeks APG, Kitslaar P. Shear stress depends on vascular territory: comparison between common carotid and brachial artery. J Appl Physiol. 2003;94:485–9. doi: 10.1152/japplphysiol.00823.2002. [DOI] [PubMed] [Google Scholar]
- Deane CR, Markus HS. Colour velocity flow measurement: in vitro validation and application to human carotid arteries. Ultrasound Med Biol. 1997;23:447–52. doi: 10.1016/s0301-5629(96)00224-4. [DOI] [PubMed] [Google Scholar]
- Ferrandez A, David T, Bamford J, Scott J, Guthrie A. Computational models of blood flow in the circle of Willis. Computer Methods in Biomechanics and Biomedical Engineering. 2000;4:1–26. doi: 10.1080/10255840008907996. [DOI] [PubMed] [Google Scholar]
- Ford MD, Alperin N, Lee SH, Holdsworth DW, Steinman DA. Characterization of volumetric flow rate waveforms in the normal internal carotid and vertebral arteries. Physiol Meas. 2005;26:477–88. doi: 10.1088/0967-3334/26/4/013. [DOI] [PubMed] [Google Scholar]
- Foutrakis GN, Yonas H, Sclabassi RJ. Saccular aneurysm formation in curved and bifurcation arteries. AJNR Am J Neuroradiol. 1999;20:1309–17. [PMC free article] [PubMed] [Google Scholar]
- Gnasso A, Carallo C, Irace C, Spagnuollo V, De Novara G, Mattiolo PL, Pujia A. Association between intima-media thickeness and wall shear stress in common carotid arteries in healthy male subjects. Circulation. 1996;94:3257–62. doi: 10.1161/01.cir.94.12.3257. [DOI] [PubMed] [Google Scholar]
- Hoeks APG, Samijo SK, Brands PJ, Reneman RS. Noninvasive determination of shear-rate distribution across the arterial lumen. Hypertension. 1995;26:26–33. doi: 10.1161/01.hyp.26.1.26. [DOI] [PubMed] [Google Scholar]
- Holdsworth DW, Norley CJ, Frayne R, Steinman DA, Rutt BK. Characterization of common carotid artery blood-flow waveforms in normal human subjects. Physiol Meas. 1999;20:219–40. doi: 10.1088/0967-3334/20/3/301. [DOI] [PubMed] [Google Scholar]
- Jiang J, Haacke EM, Dong M. Dependence of vessel area accuracy and precision as a function of MR imaging parameters and boundary detection algorithm. J Mag Res Imaging. 2007;25:1226–34. doi: 10.1002/jmri.20918. [DOI] [PubMed] [Google Scholar]
- Jou LD, Quick CM, Young WL, Lawton MT, Higashida R, Martin A, Saloner D. Computational approach to quantifying hemodynamic forces in giant cerebral aneurysms. AJNR Am J Neuroradiol. 2003;24:1804–10. [PMC free article] [PubMed] [Google Scholar]
- Kaminogo M, Yonekura M, Shibata S. Incidence and outcome of multiple intracranial aneurysms in a defined population. Stroke. 2003;34:16–21. doi: 10.1161/01.str.0000046763.48330.ad. [DOI] [PubMed] [Google Scholar]
- Kamiya A, Ando J, Shibata S, Matsuda H. Roles of fluid shear stress in physiological regulation of vascular structure and function. Biorheology. 1988;25:271–8. doi: 10.3233/bir-1988-251-236. [DOI] [PubMed] [Google Scholar]
- Kayembe KNT, Sasahara M, Hazama F. Cerebral aneurysms and variations of the circle of Willis. Stroke. 1984;15:846–50. doi: 10.1161/01.str.15.5.846. [DOI] [PubMed] [Google Scholar]
- Kundu PK, Cohen IM. Fluid mechanics. Elsevier; 2004. [Google Scholar]
- Linn FH, Rinkel GJ, Algra A, van Gijn J. Incidence of subarachnoid hemorrhage: role of region, year, and rate of computed Tomography: a meta-analysis. Stroke. 1996;27:625–9. doi: 10.1161/01.str.27.4.625. [DOI] [PubMed] [Google Scholar]
- Lomax RG. Statistical concepts: a second course. Lawrence Erlbaum Associates, Inc.; New Jersey: 2007. [Google Scholar]
- Marshall I, Papathanasopoulou P, Wartolowska K. Carotid flow rates and flow division at the bifurcation in healthy volunteers. Physiol Meas. 2004;25:691–7. doi: 10.1088/0967-3334/25/3/009. [DOI] [PubMed] [Google Scholar]
- Oshima M, Torii R, Kobayashi T, Taniguchi N, Takagi K. Finite element simulation of blood flow in the cerebral artery. Comp Methods Appl Mech Eng. 2001;191:661–71. [Google Scholar]
- Oshinski JN, Curtin JL, Loth F. Mean-average wall shear stress measurements in the common carotid artery. Journal of Cardiovascular Magnetic Resonance. 2006;8:1–6. doi: 10.1080/10976640600723839. [DOI] [PubMed] [Google Scholar]
- Oyre S, Ringgaard S, Kozerke S. Accurate noninvasive quantitation of blood flow, cross-sectional lumen vessel area and wall shear stress by three-dimensional paraboloid modeling of magnetic resonance imaging velocity data. J Am Coll Cardiol. 1998;32:128–34. doi: 10.1016/s0735-1097(98)00207-1. [DOI] [PubMed] [Google Scholar]
- Press WH, Flanney BP, Teukolsky SA, Vetterling WT. Numerical Recipes in C: The art of scientific computing. Cambridge University Press; New York: 1992. [Google Scholar]
- Reneman RS, Arts T, Hoeks APG. Wall Shear Stress - an Important Determination of Endothelial Cell Function and Structure - in Arterial System in vivo. J Vasc Res. 2006;43:251–69. doi: 10.1159/000091648. [DOI] [PubMed] [Google Scholar]
- Riva CE, Grunwald JE, Sinclair SH, Petrig BL. Blood velocity and volumetric flow rate in human retinal vessels. Investigative Ophthalmology. 1985;26:1124–32. [PubMed] [Google Scholar]
- Shaaban AM, Duerinckx AJ. Wall shear stress and early atherosclerosis: a review. AJR. 2000;174:1657–65. doi: 10.2214/ajr.174.6.1741657. [DOI] [PubMed] [Google Scholar]
- Shamijo SK, Willigers JM, Brands PJ, Barkhuysen R, Reneman RS, Kitslaar P. Reproducibility of shear rate and shear stress assessment by means of ultrasound in the common carotid artery of young human males and females. Ultrasound Med Biol. 1997;23:583–90. doi: 10.1016/s0301-5629(97)00044-6. [DOI] [PubMed] [Google Scholar]
- Sherman TF. On connecting large vessels to small. The meaning of Murray's law. J Gen Physiol. 1981;78:431–53. doi: 10.1085/jgp.78.4.431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shojima M, Oshima M, Takagi K, Torii R, Hayakawa M, Katada K, Morita A, Kirino T. Magnitude and role of wall shear stress on cerebral aneurysm: computational fluid dynamic study of 20 middle cerebral artery aneurysms. Stroke. 2004;35:2500–5. doi: 10.1161/01.STR.0000144648.89172.0f. [DOI] [PubMed] [Google Scholar]
- Stehbens WE. Intracranial aneurysms. Pathology of the Cerebral Blood Vessels. 1972:351–470. [Google Scholar]
- Steinman DA, Milner JS, Norley CJ, Lownie SP, Holdworth DW. Image-based computational simulation of flow dynamics in a giant intracranial aneurysm. AJNR Am J Neuroradiol. 2003;24:559–66. [PMC free article] [PubMed] [Google Scholar]
- Tateshima S, Murayama Y, Villablanca JP. Intraaneurysmal flow dynamics study featuring an acrylic aneurysm model manufactured using computerized tomography angiogram as a mold. J Neurosurg. 2001;95:1020–7. doi: 10.3171/jns.2001.95.6.1020. [DOI] [PubMed] [Google Scholar]
- Tateshima S, Murayama Y, Villablanca JP, Morino T, Nomura K, Tanishita K, Vinuela F. In vitro measurement of fluid-induced wall shear stress in unruptured cerebral aneurysms harboring blebs. Stroke. 2003a;34:187–92. doi: 10.1161/01.str.0000046456.26587.8b. [DOI] [PubMed] [Google Scholar]
- Tateshima S, Vinuela F, Villablanca JP, Murayama Y, Morino T, Nomura K, Tanishita K. Three-dimensional blood flow analysis in a wide-necked internal carotid artery-ophthalmic artery aneurysm. J Neurosurg. 2003b;99:526–33. doi: 10.3171/jns.2003.99.3.0526. [DOI] [PubMed] [Google Scholar]
- Tomasello F, D'Avella D, Salpietro FM, Longo M. Asymptomatic aneurysms. Literature meta-analysis and indications for treatment. J Neurosurg Sci. 1998;42:47–51. [PubMed] [Google Scholar]
- Tronc F, Mallat Z, Lehoux S, Wassef M, Esposito B, Tedgui A. Role of matrix metalloproteinases in blood flow-induced arterial enlargement. Arteriosclerosis, Thrombosis & Vasc Biology. 2000;20:e120–e6. doi: 10.1161/01.atv.20.12.e120. [DOI] [PubMed] [Google Scholar]
- Tronc F, Wassef M, Esposito B, Henrion D, Glagov S, Tedgui A. Role of NO in flow-induced remodeling of the rabbit common carotid artery. Arteriosclerosis, Thrombosis & Vasc Biology. 1996;16:1256–62. doi: 10.1161/01.atv.16.10.1256. [DOI] [PubMed] [Google Scholar]
- Tulis DA, Unthank JL, Prewitt RL. Flow-induced arterial remodeling in rat mesentric vasculature. Am J Physiol. 1998;274:H874–H82. doi: 10.1152/ajpheart.1998.274.3.H874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weir B. Unruptured intracranial aneurysms: a review. J Neurosurg. 2002;96:3–42. doi: 10.3171/jns.2002.96.1.0003. [DOI] [PubMed] [Google Scholar]
- Wetzel S, Meckel S, Frydrychowicz A, Bonati L, Radue EW, Scheffler K, Hennig J, Markl M. In vivo assessment and visualization of intracranial arterial hemodynamics with flow-sensitized 4D MR imaging at 3T. AJNR Am J Neuroradiol. 2007;28:433–8. [PMC free article] [PubMed] [Google Scholar]
- Winn HR, Jane JA, Taylor J, Kaiser D, Britz GW. Prevalence of asymptomatic incidental aneurysms: review of 4568 arteriograms. J Neurosurg. 2002;96:43–9. doi: 10.3171/jns.2002.96.1.0043. [DOI] [PubMed] [Google Scholar]
- Wu SP, Ringgaard S, Pedersen EM. Three-dimensional phase contrast velocity mapping acquisition improves wall shear stress estimation in vivo. Magn Reson Med. 2004;22:345–51. doi: 10.1016/j.mri.2004.01.002. [DOI] [PubMed] [Google Scholar]
- Yamashita T, Isoda H, Hirano M, Takeda H, Inagawa S, Takehara Y, Alley MT, Markl M, Pelc NJ, Sakahara H. Visualization of hemodynamics in intracranial arteries using time-resolved three-dimensional phase-contrast MRI. J Mag Res Imaging. 2007;25:473–8. doi: 10.1002/jmri.20828. [DOI] [PubMed] [Google Scholar]