The Response-Signal Method Reveals Age-Related Changes in Object Working Memory

Abstract

Sixteen healthy young adults (ages 18–32) and 16 healthy older adults (ages 67–81) completed a delayed response task in which they saw the following visual sequence: memory stimuli (2 abstract shapes; 3,000 ms), a blank delay (5,000 ms), a probe stimulus of variable duration (one abstract shape; 125, 250, 500, 1,000, or 2,000 ms), and a mask (500 ms). Subjects decided whether the probe stimulus matched either of the memory stimuli; they were instructed to respond during the mask, placing greater emphasis on speed than accuracy. The authors used D. L. Hintzman & T. Curran’s (1994) 3-parameter compound bounded exponential model of speed–accuracy tradeoff to describe changes in discriminability associated with total processing time. Group-level analysis revealed a higher rate parameter and a higher asymptote parameter for the young adult group, but no difference across groups in x-intercept. Proxy measures of cognitive reserve (Y. Stern et al., 2005) predicted the rate parameter value, particularly in older adults. Results suggest that in working memory, aging impairs both the maximum capacity for discriminability and the rate of information accumulation, but not the temporal threshold for discriminability.

Healthy aging impairs human memory in general and working memory in particular (Grady & Craik, 2000). The present study seeks to characterize the specific attributes of working memory (WM) that deteriorate with age. In a delayed-response task, we used the response-signal method to compare the tradeoff between processing time and recognition memory discriminability in young and older adults.

Working memory suffers an age-related loss of both efficiency (Salthouse & Babcock, 1991) and capacity (Zacks & Hasher, 1993). Previous aging literature has extrapolated from simple measures of task performance to theorize about these broader elements of WM. Efficiency is often measured by reaction time (e.g., Anders, Fozard, & Lillyquist, 1972; Salthouse, 1992), and capacity is often described by the number of items remembered (e.g., Holtzer, Stern, & Rakitin, 2004; Oberauer, 2001). In the present study, we mathematically modeled subjects’ task performance to derive quantitative measures of WM retrieval dynamics. These measures characterize broad components of WM and are more directly related to the ideas of efficiency and capacity than simpler measures like reaction time. Our methodology also helps relate theories of WM and aging to the notion of individual differences in reserve against memory loss. Below, we discuss models of WM and how our experimental paradigm relates to these models and to cognitive reserve.

WM consists of three distinct processes: encoding, rehearsal, and retrieval (Awh et al., 1996; Jonides, Lacey, & Nee, 2005). Neuroimaging studies have revealed differences between the neural substrates of these processes (e.g., J. R. Anderson, Qin, Jung, & Carter, 2007; Habeck et al., 2005; Rypma, Prabhakaran, Desmond, & Gabrieli, 2001). A particularly useful behavioral paradigm for investigating WM along these divisions is a delayed-response task (DRT; Habeck et al., 2005; Holtzer et al., 2004; Holtzer, Stern, & Rakitin, 2005; Rypma & D’Esposito, 1999; Sternberg, 1966; Wager & Smith, 2003; Zarahn, Rakitin, Abela, Flynn, & Stern, 2005, 2006). In a DRT, subjects are presented with a set of stimuli (often visual, such as letters, shapes, or spatial locations), followed by a delay and then a probe stimulus. Subjects must determine whether the probe stimulus was included in the presentation set. DRTs are advantageous because they allow the experimental procedure to be temporally divided into periods of encoding, rehearsal, and retrieval (Holtzer et al., 2004; Rypma & D’Esposito, 1999), reducing the overlap between ongoing processes. One can manipulate the extrinsic difficulty of a DRT by varying presentation set size (Habeck et al., 2005; Rypma, Eldreth, & Rebbechi, 2007; Zarahn et al., 2006) or by varying the duration of the probe stimulus (Corbett & Wickelgren, 1978; Dosher, 1984; Dosher, McElree, Hood, & Rosedale, 1989; Hintzman, Caulton, & Curran, 1994; McElree & Dosher, 1993; Reed, 1973, 1976; Wickelgren, 1977). Moreover, DRTs allow manipulation of extrinsic difficulty without the use of dual-task methods (e.g., N. D. Anderson, Craik, & Naveh-Benjamin, 1998) and without any temporal overlap of task elements, as in the n-back task (e.g., Jonides et al., 1997).

Previous experiments have used Rypma and D’Esposito’s (1999) variant of the DRT with letters of the Latin alphabet as stimuli (e.g., Habeck et al., 2005; Holtzer et al., 2004, 2005; Zarahn et al., 2005, 2006). These studies characterized the aural component of the Baddeley and Hitch (1974) model of WM—the phonological loop—which was theorized to support the retention of letter stimuli. The present study addresses the analogous visual component of the Baddeley and Hitch model—the visuospatial sketchpad. We employed unfamiliar, abstract (i.e., difficult to name) shape stimuli, which we assumed would require use of the visuospatial sketchpad, to provide information about WM in aging that complements the previous studies. In a prior DRT experiment, these shape stimuli were used along with letter stimuli to compare the parallel processing of the phonological loop and the visuospatial sketchpad (Holtzer et al., 2004, 2005).

In the present study, we manipulated the extrinsic difficulty of a DRT by varying the probe duration and eliciting the recognition response promptly after termination of the probe. This technique, known as the response-signal method (RSM), varies the duration of the retrieval process and usually results in a speed—accuracy tradeoff (Reed, 1973). That is, as the processing time allowed for retrieval increases (slower speed), accuracy on a memory task improves, and vice versa. We assessed accuracy with the signal detection measure d_L (Snodgrass & Corwin, 1988), following the example of Hintzman and Curran (1994). Previous studies have used the RSM to investigate how subjects discriminate between semantic and episodic associations (Dosher, 1984) and to study the dynamics of recognition memory (Dosher et al., 1989; Hintzman & Caulton, 1997; Hintzman & Curran, 1994; Reed, 1973). Boldini, Russo, and Avons (2004) used the RSM to distinguish between single- and dual-process accounts of recognition memory via mathematical modeling similar to that used in the present study. To our knowledge, this paradigm has not been used to study WM in the context of aging.

When processing time is systematically varied to affect recognition memory discriminability, mathematical modeling can describe the speed—accuracy tradeoff (SAT) in terms of a three-parameter compound bounded exponential curve (Hintzman & Curran, 1994). The fit parameters that define this curve quantitatively describe three characteristics of WM. The curve’s x-intercept represents the time at which retained information first becomes available to guide recognition memory decisions beyond random guessing. The curve’s asymptote represents the maximum level of accuracy that can be attained and thus the maximum amount of mnemonic information an individual can process without time constraints. The rate of change of the curve’s slope represents the rate at which information becomes available for decision making. In these ways, the x-intercept and rate parameters describe how efficiently WM retrieves information, and the asymptote parameter describes WM capacity.

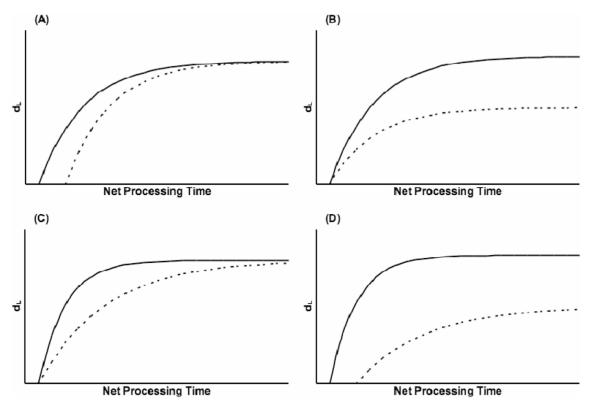
Aging is known to impair the speed of encoding new information in WM (Salthouse, 1992; Salthouse & Babcock, 1991), and older adults have longer reaction times than young adults in delayed item recognition (Anders et al., 1972; Eriksen, Hamlin, & Daye, 1973; Holtzer et al., 2004; Zarahn, Rakitin, Abela, Flynn, & Stern, 2007). We therefore predicted a more acute tradeoff for older adults than for young adults. In terms of our mathematical model, we hypothesized that older adults would show a higher x-intercept and a lower rate parameter (both indicating slower performance) because these two measures relate specifically to the speed of information processing. The asymptote parameter is not speed related; it is associated with the maximum capacity for information processing in WM, which is also known to deteriorate with age (Zacks & Hasher, 1993). Thus, we similarly predicted that older adults would have a lower asymptote (smaller capacity) than young adults would. Because we modeled performance using a compound bounded exponential curve, we could predict how the resultant curves for the two age groups would look on the basis of our various hypotheses. Figure 1 presents hypothetical resultant curves showing a group difference for each individual fit parameter, as well as for all three. Our hypotheses predicted that the actual resultant curves would resemble those in Figure 1D.

Figure 1.

Hypothetical sets of exponential curves for modeling speed—accuracy tradeoff across two groups of subjects. Young adults (solid lines) always show better performance than older adults (dotted lines). A: Young adults have a lower x-intercept than older adults; asymptote and rate are the same across groups. B: Young adults have a higher asymptote than older adults; x-intercept and rate are the same across groups. C: Young adults have a higher rate than older adults; x-intercept and asymptote are the same across groups. D: Young adults have a lower x-intercept, higher asymptote, and higher rate than older adults. d_L = discriminability measure.

Previous studies have shown that individuals differ greatly in their susceptibility to age-related changes in cognitive function (Gold et al., 1995; Hultsch, Hertzog, Small, & Dixon, 1999; Manly, Touradji, Tang, & Stern, 2003; Scarmeas, Levy, Tang, Manly, & Stern, 2001; Schaie, 1984; Stern et al., 1994; Wilson et al., 2000, 2002). Cognitive reserve (CR) theory posits that individual differences in task performance give some individuals greater resilience than others against age-related neural change (Stern, 2002; Stern et al., 2005). That is, if the neural network underlying task performance is the same in young and old, individuals can still differ in how quickly they must increase activation with the rising demands of a task (efficiency) or in the maximum level of activation they can achieve (capacity; neural reserve is the overall term for differential efficiency and/or capacity of a network). CR theory also posits that some older adults develop more effective compensatory mechanisms than others against age-related changes, recruiting brain networks not used by young adults (neural compensation). Differential efficiency and capacity of the same network, as well as recruitment of compensatory networks, have been observed in the neural activation associated with different phases of WM tasks (Stern et al., 2008; Zarahn et al., 2006). Individual differences in the use of these networks may be reflected in behavioral measures of WM ability.

In the present study, we used estimated verbal IQ, vocabulary, and years of education as proxy measures of CR to investigate the relationship between WM and CR. Premorbid IQ and vocabulary have proven to be strong proxies for CR, in that they are associated with slower rates of cognitive decline in normal aging and reduced risk of developing dementia (e.g., S. M. Albert & Teresi, 1999; Alexander et al., 1997; Corral, Rodríguez, Amenedo, Sánchez, & Díaz, 2006; Solé-Padullés et al., 2007). Similarly, education has been shown to impart reserve over an individual’s lifetime (Evans et al., 1993; Mortel, Meyer, Herod, & Thornby, 1995; Rocca et al., 1990; Stern et al., 1994), and individuals with higher levels of education demonstrate slower cognitive and functional decline during normal aging (M. S. Albert et al., 1995; Butler, Ashford, & Snowdon, 1996; Chodosh, Reuben, Albert, & Seeman, 2002; Christensen et al., 1997; Colsher & Wallace, 1991; Farmer, Kittner, Rae, Bartko, & Regier, 1995; Lyketsos, Chen, & Anthony, 1999; Snowdon, Ostwald, & Kane, 1989). Moreover, we have successfully used IQ, vocabulary, and education as proxies for CR in previous behavioral and neuroimaging studies (e.g., Habeck et al., 2005; Scarmeas et al., 2004; Stern et al., 2005, 2008). Thus, we believe these measures serve as meaningful indicators of individual differences in susceptibility to age-related cognitive impairment.

Our statistical analysis addressed the question of whether CR mediates retrieval dynamics in object working memory. If CR does not modulate the aspects of WM characterized by our SAT model, our CR measures should not statistically predict the fit parameter values across age groups. If CR does modulate WM, our CR measures should predict the fit parameter values either in the same way for both age groups (e.g., high IQ is associated with a higher rate parameter in young and older adults) or differently for each group (e.g., high IQ is associated with a higher rate parameter in older adults but not in young adults). To address the relationship between CR and behavior, and to allow for these various possibilities, we included CR variables and their interactions with age group as covariates in our statistical model.

Because CR accumulates over one’s lifetime and provides resilience against age-related memory loss, we hypothesized that CR is more likely to modulate behavioral performance in older adults. That is, we anticipated CR × Group interaction effects on the fit parameters such that our CR measures would predict the fit parameter values in older adults but not in young adults.

Method

Participants

Sixteen healthy young adults and 16 healthy older adults participated in this study. Young adults were recruited via fliers or Internet ads, and older adults were recruited from senior day centers located in Manhattan, New York. Table 1 provides descriptive demographics for each group. All participants were right-handed, spoke English, and had normal or corrected-to-normal vision. Participants had no past or current medical, neurological, or psychiatric disorders, were not being treated with psychoactive drugs, and were screened to ensure the absence of dementia. Given the age range of participants, subjects had to score 133 or higher on the Mattis Dementia Rating Scale (Mattis, 1988) to be included in the study (cf. Mayo’s Older Americans Normative Studies scaled scores; Lucas et al., 1998). All study participants met this criterion, and no recruits were excluded from the study. We obtained informed consent from all participants in accordance with the procedures of Columbia University Medical Center.

Table 1.

Participant Demographics and Neuropsychological Test Results

Variable	Older	Young
Age range	67-81	18-32
Age*	72.8 ± 5.1	24.6 ± 3.7
%Female	68.75	50.00
Education	14.3 ± 2.4	15.9 ± 2.5
NART IQ	110.515 ± 9.583	116.383 ± 8.610
Vocabulary	46.3 ± 12.8	54.5 ± 8.8
DRS	140.1 ± 3.7	141.9 ± 2.0

Note. Values for age, education, National Adult Reading Test (NART) IQ, Vocabulary, and Mattis Dementia Rating Scale (DRS) are the mean ± 1 standard deviation. Education is measured in years. All t tests assume equal variances, except DRS, where Levene’s test for equality of variances indicates equal variances should not be assumed.

^*p < .05, 2-tailed t test.

Apparatus

Participants completed the experiment on a Macintosh G3 iBook computer with a 12-in. LCD color monitor. Testing occurred in a well-lit room where the subject was approximately 25 in. from the screen. The task was programmed and run using PsyScope software (Version 1.2.5; Cohen, MacWhinney, Flatt, & Provost, 1993), and subjects entered responses on the computer keyboard.

Procedure

Participants completed the study in a single session. After providing informed consent, they completed a pretraining task, the DRT, and a brief neuropsychological battery.

Pretraining was administered to ensure that subjects could meet the demands of the RSM experiment. Pretraining consisted of a two-alternative forced-choice (2-AFC) object discrimination task, divided into 10-trial blocks. Participants completed at least 5 blocks of the 2-AFC task and continued until they were able to respond accurately during the mask on at least 9 out of 10 trials within a block. Subjects who could not meet this criterion after 50 blocks would have been excluded from the study. However, all participants met criteria; young participants completed an average of 5.56 ± 0.22 blocks of pretraining, and older participants completed an average of 14.00 ± 2.60 blocks.

The DRT consisted of 11 blocks of 30 trials each, divided into three training phases and 1 test phase. In Training Phase 1 (2 blocks), subjects received feedback after each trial about their speed and their accuracy. At the end of each block, a summary displayed the number of trials on which the subject responded both correctly and on time, as well as the number of trials when the response was on time (regardless of choice accuracy). Training Phase 2 (3 blocks) provided only speed feedback after each trial, and the summary for each block displayed only the number of on-time responses. In Training Phase 3 (1 block), no feedback was provided. Participants then completed 5 test blocks with no feedback, the results of which we used for statistical analysis.

Participants were administered the Mattis Dementia Rating Scale test (DRS; Mattis, 1988) for neuropsychological screening. With the exception of two subjects, young and older participants also completed the vocabulary subtest of the revised Wechsler Adult Intelligence Scale (Wechsler, 1981) and the National Adult Reading Test (NART; Grober & Sliwinsky, 1991) as proxy measures of CR.

The entire protocol lasted about 2.5 hr: 70 min for pretraining and training, 50 min for testing, and 30 min for the neuropsychological evaluation.

Tasks

In each trial of the pretraining 2-AFC task, participants were presented with one out of a fixed set of two abstract shapes (described below), followed by the same mask used in the DRT. To reduce the task’s memory demands, the same set of two shapes was used across all the pretraining trials and blocks. The single shape was presented for a variable duration (similar to the DRT probe item, described below), and during the mask, subjects had to identify which of the two shapes they saw via computer key-press (the X key or the period key, depending on the stimulus). After each response, they received speed and accuracy feedback. If the participant responded before or after the mask, the feedback read, “Sorry, response made too soon …” or “Sorry, time ran out …,” respectively. If the subject responded during the mask, the feedback read either “Correct!” or “Fast enough, but wrong,” depending on response accuracy. At the end of each block, a summary displayed the number of trials on which the subject responded both on time and correctly.

Each DRT trial consisted of encoding, retention, and probe phases. The encoding phase presented two shape stimuli (visual angle for the two-shape stimulus = 4° vertical × 26° horizontal) for 3 s, followed by a 5-s retention interval during which the computer screen was blank. Subjects then saw a single probe item (visual angle = 4° ± 4°) that either matched one of the stimuli from the study set (true positive) or was completely different from both of them (true negative). The probe item was presented for either 125, 250, 500, 1,000, or 2,000 ms and was followed immediately by a 500-ms mask (gray square, visual angle = 4° × 4°), during which subjects were instructed to respond. The current task differs from previous implementations of the response-signal method in its use of a relatively long response window following the removal of the probe stimulus. Our mask was 500 ms in duration, compared to more typical values around 300 ms (Hintzman & Curran, 1994; Reed, 1973). On the basis of extensive pilot data, we made this modification to accommodate slower reaction times in older adults.

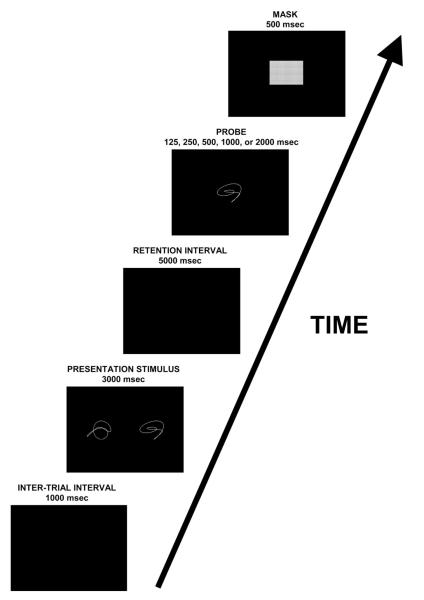
Subjects responded during the mask by indicating whether the probe stimulus matched either of the memory stimuli via computer key-press (X key or period key). Assignment of response keys to the true positive and true negative conditions was counterbalanced across participants within each age group. Participants were instructed to place greater emphasis on speed than accuracy in responding and to guess rather than delay their response on trials when they felt unsure. In training, the mask was followed by a 250-ms delay and a 1,750-ms feedback display. Training Phase 1 provided speed and accuracy feedback identical to the feedback in the 2-AFC task. Training Phase 2 provided only speed feedback, so the display for any on-time response read ON TIME regardless of choice accuracy; the display for early or late responses was the same as in the 2-AFC task. Figure 2 illustrates the visual sequence for a single test phase trial.

Figure 2.

Schematic representation of the delayed response task. After a 1,000-ms intertrial interval, presentation stimuli were shown for 3,000 ms, followed by a 5,000-ms blank retention period. Next, the probe shape was shown for a variable amount of time (five different probe durations), and a 500-ms mask immediately followed the probe. Subjects were instructed to respond during the mask.

Each DRT block consisted of 30 trials. The crossing of two probe types (positive or negative) and five probe durations yielded 10 conditions, which were repeated three times within a block. Analyses included five testing phase blocks, so that from each participant we obtained a total of 15 trials for each of the 10 conditions.

Within each block of 30 trials, there were 70 blank, 2,000-ms intervals, randomly interspersed. When added to the minimum 3-s intertrial interval (ITI) preceding each trial, these intervals resulted in a mean ITI of 9,119 ms (SD = 5,265 ms). This design element staggered the timing of trial presentation so that subjects could not anticipate the onset of the next trial. The exact duration of the ITI was determined to maximize statistical power in an ongoing functional neuroimaging study.

Visual stimuli were selected from a set of 420 computer-generated closed-curve shapes (Holtzer et al., 2004). These shapes were abstract and did not correspond to or intuitively relate to real words or objects (see Figure 3). The mean pixel ratio of the shapes (white) to the background (black) provided an estimate of their complexity, which was comparable among encoding and probe stimuli within a single trial. Positive and negative trials were also matched for complexity, and the overall complexity of the shapes was counterbalanced across all five probe durations. At most, each individual shape appeared once across the three training phases and once within the testing phase. Within training 228 shapes appeared twice, and in testing 120 shapes appeared twice. However, each combination of 3 shapes within a single trial (two encoding stimuli plus one probe stimulus) was unique across the entire experiment. Additionally, no shape occupied the same position (e.g., left side of the encoding stimulus) more than once.

Figure 3.

Examples of the experimental shapes. Each row is a given trial: The first two columns are the presentation shapes, and the last column is the probe shape. The three shapes of each trial (row) are matched for complexity by mean pixel ratio. True negative trials are represented in Rows 1 and 3. True positive trials are represented in Rows 2 and 4. From “Age-related differences in executive control of working memory,” R. Holtzer, Y. Stern, and B. C. Rakitin, 2004, Memory & Cognition, 32, Appendix, p. 1345. Copyright 2004 by the Psychonomic Society.

Statistical Analysis

We used a repeated-measures analysis of variance (ANOVA) to analyze reaction time (RT; measured from the onset of the mask) with probe duration (five-level) as the within-subjects variable and age group (two-level) as the between-subjects factor. We conducted a similar analysis for the proportion of time-out trials (pTO), defined as the number of trials on which subjects did not respond during the mask, divided by 15 (the total number of trials per condition). CR covariates were not included in either of these models.

Proficiency at the task was calculated in terms of the discriminability measure d_L, given by the formula d_L = ln{[H(1 - FA)]/[(1 – H) FA)]} where H = hits (correct true-positive probe trials), FA = false alarms (incorrect true-positive probe trials), and ln is the natural logarithm function. Response bias was calculated as C_L, given by the formula C_L = 0.5[ln{[(1 - FA)(1 - H)]/[(H)(FA)]}] (Snodgrass & Corwin, 1988). With the same design used for RT, we conducted repeated-measures ANOVAs to analyze both signal detection parameters. CR covariates were not included in these models. Planned comparisons between levels of the probe duration were conducted using polynomial contrasts with one degree of freedom.

Last, to determine whether RT or pTO account for any of the variability in signal detection measures, we conducted separate repeated-measure ANCOVAs on d_L and C_L with probe duration as a five-level within-subjects variable and age group as a two-level between-subjects factor. We included RT and pTO as covariates, and we included the interactions between these continuous variables and the fixed effects as tests of homogenous slopes across fixed-effects levels.

For all standard parametric tests involving probe duration, we report the actual degrees of freedom, measuring statistical significance at the p = .05 level after Huynh-Feldt epsilon correction for violations of the assumptions of the ANOVA.

We modeled the SAT between discriminability and total processing time (probe duration plus reaction time) using a three-parameter bounded exponential curve (Hintzman & Curran, 1994). Each such curve is defined in terms of its x-intercept, asymptote, and slope, using the compound equation: For x ≤ x-intercept, d_L = 0; for x > x-intercept, d_L = asymptote × {1 - exp[-slope × (probe duration - intercept)]}, where x is the total processing time.

We derived best-fit curves for each individual’s performance in three steps: First, for each age group and at each probe duration, we calculated the between-subject mean d_L and the between-subject mean total processing time, generating a SAT function for each age group. Second, we fitted a three-parameter best-fit curve to these group-average SAT functions. We completed this step simultaneously for both age groups to identify a set of fit parameters that optimizes both best-fit curves at once (six parameters altogether, three for each group curve). Third, we fitted similar curves to each individual’s SAT function: Using the intercepts, asymptotes, and slopes of the group-average best-fit curves (from Step 2) as starting points, we carried out a simple gradient descent procedure to estimate the parameter values for each individual’s best-fit curve (Step 3), minimizing the residual to each subject’s data for each fit parameter. Each subject’s unique parameter values served as the dependent variables in our statistical analysis.

For each of the three fit parameters (intercept, asymptote, and rate), we built a general linear model (GLM) that proceeded in stages (method of heterogeneous slopes; Siegel, 1956). In the first stage (full model), the following independent variables were used as predictors: age group, years of education, NART IQ estimate, and age-scaled vocabulary score. We also added interaction terms by multiplying the group-membership predictor with each of the subject-specific predictors. Thus, the full model comprised seven predictors: group, education, NART IQ, vocabulary, Group × Education, Group × NART IQ, and Group × Vocabulary. Including these interaction terms allowed for formal tests of group heterogeneity of the slope of the relation between the CR measures and the model fit parameters. After performing the full-model analysis, we retained the covariate main effects and only those interaction terms that yielded statistically significant regression weights. The results of the linear regression with the reduced set of predictors are reported as the reduced model. The simple model contains only the fixed effect and is relevant when none of the covariate terms are significant in the reduced model.

Because we used group-average fit parameters to begin to estimate each individual’s fit parameters in Step 3, our GLMs violated the assumption of independent errors, and so we could not rely on standard parametric assumptions to determine the probabilities associated with test statistics. Instead, we employed a nonparametric permutation procedure to generate the null-hypothesis distribution of regression weights from the data itself. This was achieved by randomly sampling from the data 10,000 times without replacement, destroying the subject-to-group assignment. For each such permuted data set, we performed our fitting routine to generate the three fit parameters anew. The fit parameters obtained from the permuted data sets were then used as dependent variables for general linear modeling (see above), while the subject-to-group assignment for the independent variables was left intact. This generated a null-hypothesis distribution for each regression weight. This process was repeated as needed for the full, reduced, and simple GLMs.

To assess statistical significance, we empirically estimated the percentile location of the unpermuted data set’s regression weight in relation to the computed null-hypothesis distribution. Our significance test was two-tailed: the p level equaled the fraction of absolute values in the null-hypothesis distribution that lay beyond the absolute value of the unpermuted data set’s regression weight. Therefore, a p level of 0.05 meant the absolute value of the unpermuted data set’s regression weight was larger than at least 95% of the absolute-valued regression weights produced by the permutation procedure. Although we derived p values from two-tailed t distributions, our hypotheses about the effects of age group on the fit parameters are unidirectional (see Introduction). So for main effects of age group, we present one-tailed p values derived by halving the permutation test p levels. For the effects of CR covariates, about which we do not offer directional hypotheses, we report two-tailed p values.

For comparison, we used standard parametric methods to test the same statistical models submitted to permutation testing. Univariate ANCOVA was performed for each of the individual fit parameters—intercept, asymptote, and rate—with age group (two-level) as the between-subjects factor and with proxy measures of CR—education, NART IQ, and vocabulary—as covariates. As in our nonparametric reduced model, we retained only those interaction terms that yielded statistically significant regression weights.

Results

Neuropsychological Measures

Table 1 shows participant demographics and neuropsychological test results for each age group. Young and older adults performed comparably on the DRS, vocabulary, and NART tests; they had equal (and high) levels of education; and they were equivalent in terms of sex distribution.

Analysis of Reaction Time and Proportion of Time-Out Trials

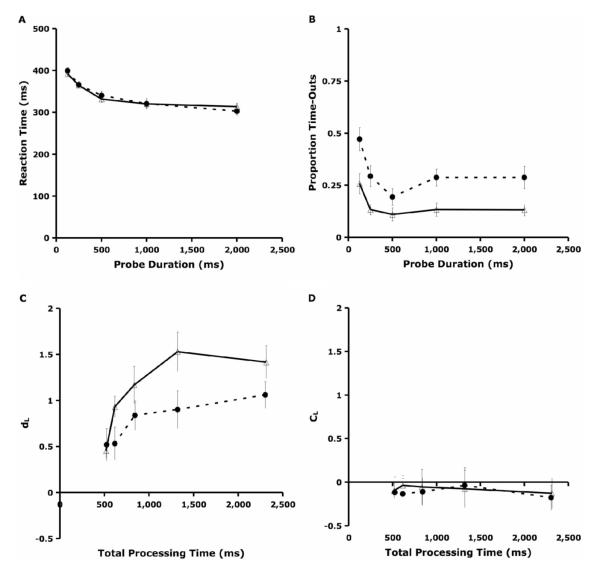
The analysis of SAT using the RSM is predicated on controlling a participant’s total time for processing the probe item. The response window in the current task is longer than in previous implementations of the RSM (Hintzman & Curran, 1994; Reed, 1973), allowing for greater within- and between-group variability in processing time that could complicate the interpretation of the SAT analyses. Thus, we analyzed reaction time from the mask onset as a function of age group and probe duration to determine, for example, whether young adults had more processing time than older adults had and whether this difference was comparable across probe duration levels. For the same reasons, we also analyzed the proportion of trials on which subjects timed out (pTO), defining time-outs as trials with no response recorded during the mask. Figures 4A and 4B show the relationships between RT and probe duration and between pTO and probe duration, respectively.

Figure 4.

Data for reaction time, proportion of time-out trials, and signal detection measures. A: reaction time versus probe duration. B: pTO versus probe duration. C: d_L vs. total processing time. D: C_L versus total processing time. Data shown for 16 young adults (unfilled triangles, solid lines) and 16 older adults (filled circles, dotted lines). Error bars represent standard errors. d_L = discriminability measure; C_L = response bias.

Results of the RT analysis indicated no effect of age group on RT, F(1, 30) = 0.04, ns, nor any interaction between age group and probe duration, F(4, 120) = 0.636, ns. However, RT did vary as a function of probe duration, F(4, 120) = 56.22, p < .001, such that subjects had longer RTs for shorter probes. This variability in RT across conditions indicates that we did not control perfectly for total processing time, so there may be a bias in analysis of the discriminability measures. For this reason, we include RT as a covariate in the d_L analyses reported in the next section. The inverse relationship between RT and probe duration may indicate that the probe was serving as a warning signal for the presentation of the mask, much like the warning signal effect on RT shown in variable foreperiod experiments (e.g., Niemi & Naatanen, 1981). Because our SAT model is fit to functions of d_L with respect to total processing time (probe duration + RT), analysis of the fit parameters accounts for the differences in RT across conditions.

ANOVA of pTO showed an effect of age group such that older adults failed to respond on more trials than younger adults, F(1, 30) = 13.56, p < .001, and both age groups’ pTO varied as a function of probe duration, F(4, 120) = 17.20, p < .001. The effects of group and probe duration on pTO also demonstrate the experiment’s imperfect control of processing time, motivating inclusion of pTO as a covariate in the d_L analyses reported in the next section. Post hoc review of the data found responses recorded on TO trials during the ITIs following these trials. That is, older participants rarely failed to respond but rather made the occasional response with latency greater than the mask duration. These responses did not contribute to the mean RT, explaining the absence of an age group difference in RT. Overall, it appears that older participants have an RT distribution similar to that of the young participants but with a longer right tail.

Signal Detection Measures

We plotted d_L and C_L against total processing time to depict the relationship between speed and accuracy (Figures 4C and 4D). Effects of probe duration on C_L were not significant, F(1, 30) = 2.84, ns, indicating no response bias across all probe duration conditions. There was a significant effect of probe duration on d_L, F(1, 30) = 90.25, p < .001, including both a linear trend, F(1, 30) = 41.34, p < .001, and a quadratic trend, F(1, 30) = 14.29, p < .001. The linear characteristic of the curve shows that discriminability increases with processing time, and the quadratic characteristic shows that this increase decelerates as processing time increases. These results are consistent with the hypothesis that there is an SAT between processing time and discriminability.

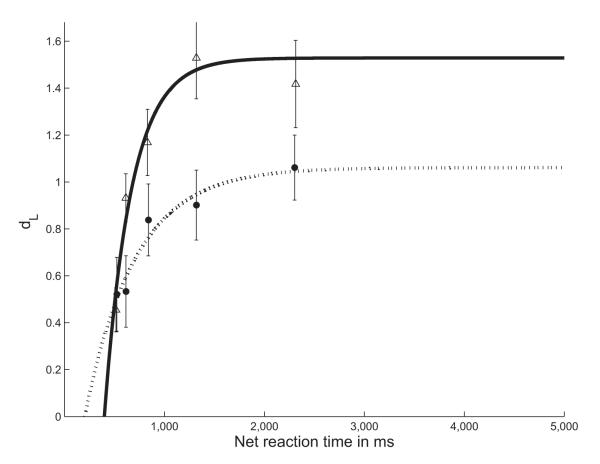
In addition, polynomial planned contrasts with the ANOVA probe duration effect also revealed a significant interaction between group and probe duration in the quadratic effect, F(1, 30) = 4.22, p < .05, and in the fourth-order effect, F(1, 30) = 4.73, p < .05, with group mean d_L increasing to a level of 1.42 for young adults and 1.06 for older adults at a probe duration of 2,000 ms. This demonstrates that the degree of SAT depends upon age group, with a more acute tradeoff for older adults. That is, with the successive increases in probe duration, older adults showed a slower improvement in performance than young adults (Figure 4C). Also, maximum recognition memory discriminability for these abstract visual stimuli was lower than in previous experiments that used letter stimuli and a 3-s probe duration (Habeck et al., 2005; Holtzer et al., 2004).

As noted in the previous section, the variability in RT and pTO across conditions implies a failure to control perfectly for probe processing time, which may be reflected in initial analyses of the discriminability data. To determine whether the effects of interest were independent of potential processing time confounds, we conducted analyses of covariance (ANCOVAs) for d_L and C_L.

The ANCOVA for d_L, with RT and pTO as covariates, revealed three-way interactions among age group, probe duration, and RT, F(5, 159) = 5.15, p < .001, and among age group, probe duration, and pTO, F(5, 159) = 3.87, p < .05. These effects show that RT and pTO predicted discriminability differently for each age group and at each probe duration, indicating that in the simple ANOVA for discriminability, the effects of probe duration were biased. However, the effects of probe duration persisted in the ANCOVA: There was still an independent effect of probe duration on d_L, F(4,159) = 21.15, p < .001, and there was still an independent interaction between probe duration and group, F(4, 159) = 3.18, p < .05. Thus, the ANCOVA corroborated the results of the ANOVA, and also like the ANOVA, it yielded no significant effects of age group alone.

The ANCOVA for C_L, with RT and pTO as covariates, yielded similar results for RT. A three-way interaction among group, probe duration, and RT, F(5, 159) = 4.75, p < .001, shows that RT predicted response bias differently for each age group and at each probe duration, indicating a bias in the simple ANOVA for C_L. Nonetheless, the ANCOVA for C_L, like the ANOVA for C_L, showed neither an effect of group, F(1, 159) = 0.12, ns, nor an effect of probe duration, F(4, 159) = 0.62, ns, on response bias.

Analysis of Model Fit Parameters

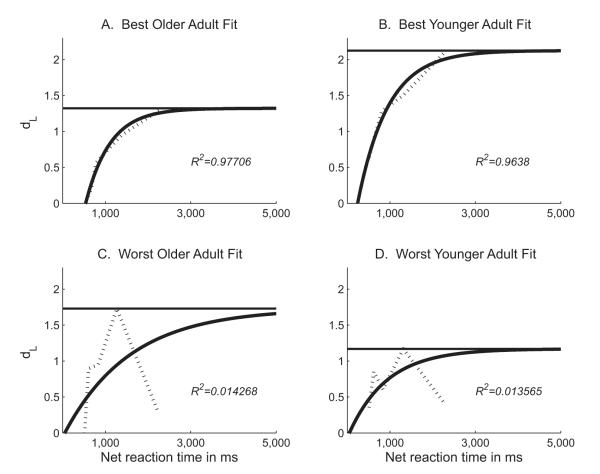
We transformed the discriminability data into a best-fit curve for each subject, collapsing across probe durations. The three unique fit parameters for each individual’s curve were the dependent variables in separate statistical analyses. Figure 5 shows some examples of model fits to individuals’ SAT functions. Figure 6 shows the group averages of the individual best-fit curves. Goodness of fit for each regression was measured in terms of R², where R(X, Y) = [Cov(X, Y)]/[StdDev(X) × StdDev(Y)] for any set of data points (x, y). Mean R² was .6074 ± .0840 for the young adults group and .4945 ± .0788 for the older adults group. The age groups did not differ significantly in the quality of their fits, t(1, 30) = 0.980, ns.

Figure 5.

Sample individual data for two young adults and two older adults. Dotted lines represent individual discriminability data at the five levels of processing time; solid lines represent best-fit curves. Because each individual fit is estimated from a best-fit curve for the relevant age group, some curves fit the discriminability data better than others. A and B show the most exact fits for a young adult and an older adult, respectively; C and D show the least exact fits. R² values indicate the quality of each best-fit curve regressed to the actual data set.

Figure 6.

Best-fit curves for each age group. The older adult group is represented by filled circles and the young adult group is represented by the unfilled triangles. The fit parameter values that define these two curves are the averages of the parameter values for each individual in the relevant group. Error bars represent standard errors.

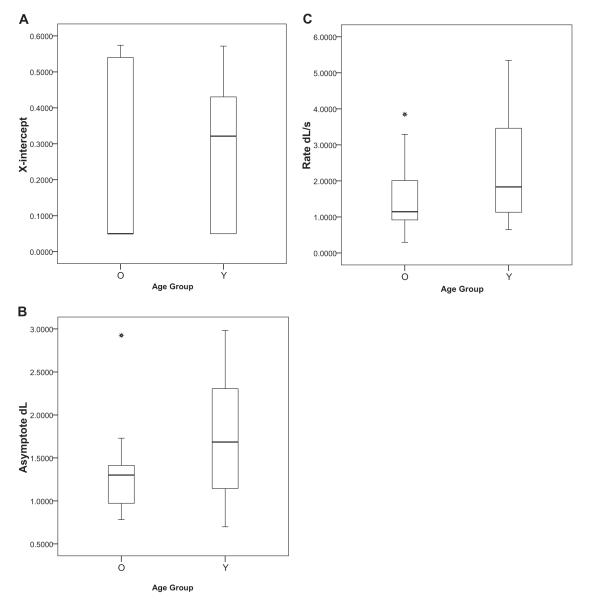
Figure 7 compares the distributions of numerical values for each fit parameter (x-intercept, asymptote, and rate) between age groups. Table 2 shows the correlations among the three fit parameters for each age group. The only significant correlation was between rate and x-intercept in the young adults group, but this observation likely results from the restricted range of x-intercept values in our mathematical model (floor effect in the older adults group; see Figure 7A). The absence of other correlations shows that each fit parameter represents a separate component of task performance.

Figure 7.

Box plot distributions for fit parameter values by age group. A: x-intercept for older adults (M = 0.259 ± 0.062 s, Mdn = 0.050 s) and young adults (M = 0.282 ± 0.047 s, Mdn = 0.321 s). B: Asymptote for older adults (M = 1.304 ± 0.127 d_L, Mdn = 1.300 d_L) and young adults (M = 1.769 ± 0.190 d_L, Mdn = 1.685 d_L). C: Rate for older adults (M = 1.543 ± 0.250 d_L/s, Mdn = 1.143 d_L/s) and young adults (MN = 2.276 ± 0.362 d_L/s, Mdn = .832 d_L/s). The horizontal lines in each box plot show median fit parameter values. Error bars represent standard errors. Asterisks represent outliers. O = older adults; Y = young adults; d_L = discriminability measure.

Table 2.

Correlations Among the Three Fit Parameters

Variable	x-intercept	Asymptote	Rate
	Young adult group
x-intercept	1.000	0.086	0.771*
Asymptote	0.086	1.000	0.019
Rate	0.771*	0.019	1.000
	Older adult group
x-intercept	1.000	-0.124	0.308
Asymptote	-0.124	1.000	0.622
Rate	0.308	0.622	1.000

Note. Table shows Pearson correlation values.

^*p < .05.

For each of the three parameters, we built three GLMs: a full model, a reduced model, and a simple model. The full model included all CR variables as covariates, as well as the interactions of these variables with age group. The full model allowed for the possibility that age group, every covariate, and every interaction term predicts the value of a given fit parameter. If any interactions did not predict a fit parameter (i.e., not significant at the α = .05 level, two-tailed), these terms were dropped from the model. The GLM with the CR covariates and remaining interactions (if any) was considered the reduced model. If no covariates or interactions reached statistical significance even in the reduced model, we concluded that CR does not modulate that fit parameter. In this case, we built a simple model with age group as the sole predictor, because this is the fixed factor—the independent variable of interest. The mathematical logic behind this process (known as the heterogeneous slopes method; Siegel, 1956) is described in detail in the Method section. Table 3 gives a quantitative summary of the successive GLMs for each fit parameter.

Table 3.

General Linear Models Predicting Each of the Three Fit Parameters

Variable	Full	Reduced	Simple
	x-intercept
Group	0.72	0.77	0.96
Education	0.22	0.23
NART IQ	0.44	0.47
Vocabulary	0.96	0.47
Group × Education	0.25
Group × NART IQ	0.94
Group × Vocabulary	0.91
	Asymptote
Group	0.78	0.31	0.07
Education	0.44	0.41
NART IQ	0.42	0.40
Vocabulary	0.87	0.66
Group × Education	0.63
Group × NART IQ	0.48
Group × Vocabulary	0.21
	Rate
Group	0.62	0.00
Education	0.05	0.06
NART IQ	0.02	0.01
Vocabulary	0.16	0.19
Group × Education	0.00	0.01
Group × NART IQ	0.13
Group × Vocabulary	0.59

Note. Cells show p values for each predictor’s significance in the corresponding model. The full model includes all covariates and interactions. The reduced model drops all nonsignificant interactions but maintains all covariates. The simple model measures only the effect of age group, without any covariates. All probabilities were determined nonparametrically via the method of permutations (see Method section). The simple model is the final model for the x-intercept and asymptote parameters, and the reduced model is the final model for the rate parameter. NART = National Adult Reading Test

In the full model, x-intercept did not differ across age groups, nor did the reduced model show any significant effects of CR covariates or interactions ( p > .2 for all predictors). Because CR did not modulate age-related differences in x-intercept, we built a simple model without any covariates or interactions; even here, we observed no difference in performance across age groups. This suggests that the earliest time at which information becomes available to WM remains the same across a person’s lifetime.

Neither the full model nor the reduced model for asymptote yielded any significant effects of the covariates or of interactions between the covariates and age group ( p > .3 for all predictors). Because group differences in asymptote could not be attributed to CR, we ran a simple GLM for asymptote with age group as the sole predictor variable. Here, asymptote was higher for young adults than for older adults ( p < .05, one-tailed). This suggests that aging impairs the maximum capacity for information processing in WM, but the extent of impairment is not mitigated by CR.

In the full model for the rate parameter, only NART IQ, education, and the Group × Education interaction were significant, so the other interaction terms were dropped in the subsequent GLM. The reduced model showed an effect of group on rate ( p < .05) such that young adults had a higher rate parameter than older adults (Figure 7C), which agrees with the previous observation that young adults had a more quickly rising SAT function (Figure 4C). Thus, aging impairs the rate at which information for the recognition decision accumulates over time. The reduced model also showed an effect of education on rate ( p < .05) and an education by group interaction ( p < .05) such that high levels of education predicted a higher rate for older adults and a lower rate for young adults. In other words, education level mitigated the effect of age on rate, and the degree to which education improved rate was itself age-dependent. NART IQ also predicted the value of the rate parameter ( p < .05), such that high IQs were associated with higher rates for both age groups. Because the reduced model showed CR to modulate group differences in rate, there was no need to build a simple model for the rate parameter.

We verified these nonparametric analyses using standard parametric statistics. Individual GLMs for each fit parameter, including the CR covariates, showed identical results to those of the nonparametric method, except that the reduced rate parameter model showed no effect of education alone, F(1, 25) = 2.642, ns.

Discussion

On the basis of our prior understanding of the relationships between aging, WM, and CR, we hypothesized that: (a) there would be a tradeoff between processing time and accuracy in the DRT, with a more acute tradeoff for older adults; (b) older adults’ more acute speed—accuracy tradeoff would be evident in higher x-intercept, lower asymptote, and lower rate parameters from the SAT model compared to young adults; and (c) proxy measures of CR would predict WM ability (in terms of the fit parameters), particularly for older adults.

In keeping with Hypothesis 1, discriminability measures revealed a clear tradeoff between processing time and proficiency at the DRT, with discriminability reaching its maximum at the 2,000 ms probe duration. Also as predicted, older adults showed a more acute tradeoff than young adults did. When we modeled each subject’s SAT data as a three-parameter compound bounded exponential curve, we found age-related differences in some but not all aspects of retrieval dynamics. Hypothesis 2 predicted that all three parameters would differ across groups, so that the resultant curves would look like Figure 1D. In fact, both age groups showed comparable x-intercepts, whereas young adults approached a greater maximum level of recognition memory discriminability at a greater rate than older adults (Figure 6). Finally, in regard to Hypothesis 3, CR modulated the effect of age on rate but not on x-intercept or asymptote. Below we discuss the results for each individual fit parameter.

Intercept

The curve’s x-intercept represents the time at which information in WM first becomes available for decision making and discriminability rises above chance. This value was comparable across age groups, and CR measures did not predict the value of the x-intercept. These results disaffirm parts of Hypotheses 1 and 3, respectively. The lack of a group difference in intercept may be due to the large variability in intercept parameter values (young adults: M = 0.282, SD = 0.189; older adults: M = 0.259, SD = 0.248; see Figure 7A), as well as a floor effect in estimates of the x-intercepts for the older group. Both the variability and the floor effect indicate that the x-intercept term was underdetermined, most likely because discriminability was not zero at the shortest probe duration (see Figure 4C). It is possible that our data obscure a real age-related difference in the temporal threshold for discriminability; but from the present analyses we must conclude that intercept does not vary, either with age or with CR. A future experiment using the RSM should include a shorter probe duration or increase the overall difficulty of the task, so that the obtained SAT functions actually reach floor at the shortest processing times.

Asymptote

The maximum value at which the curve tapers off represents the maximum level of discriminability that can be attained in WM. Our results support Hypothesis 2 that young adults have a higher asymptote than older adults do and that aging impairs maximum discriminability. Because the broader statistical model including measures of CR showed no significant effects, we further conclude that CR does not mediate this age-related impairment, partially disaffirming Hypothesis 3.

Rate

The rate of change of the exponential curve represents the rate at which information becomes available for decision making. Young adults had higher rates than older adults did, showing that aging impairs the rate of information accumulation in WM. With respect to the CR measures, high IQ predicted a higher rate for all participants, and high levels of education predicted a higher rate for older adults only. The interaction of age and education in predicting the rate parameter is largely due to an association between education and rate in the older adults and the absence of such an association in the young adults, who have little variability in education. Overall, the rate parameter differs from intercept and asymptote in that it changes with CR variables, which are known to predict behavioral resistance to age-related pathology (Stern, 2002). Below we discuss some of the limitations of this experiment and then the implications of our findings for theories of WM and CR.

A methodological limitation of the current study is that the long time course of our delayed-response task (DRT; 8–10-s trials with a 5-s delay) may have resulted in a temporal overlap between short-term and long-term memory processes. Given the assumption that WM is divided into encoding, rehearsal, and retrieval phases, and given the additional assumptions of the compound bounded exponential model, we could not avoid this overlap in our experimental paradigm. Additionally, DRTs of comparable length, with delay periods ranging from 6.5–10 s, have been used reliably in previous studies of WM (e.g., Gazzaley, Sheridan, Cooney, & D’Esposito, 2007; Holtzer et al., 2004).

A further theoretical limitation of this experiment concerns the model from which we derived the fit parameters. We based our approach on a model used to characterize retrieval in verbal episodic memory for a single age group (Hintzman & Curran, 1994), but the present study focuses on object working memory across two different age groups. Moreover, our experimental design is quite different from that of Hintzman and Curran’s (1994) study. Our subjects received significantly less training (hours as opposed to days), and their window for responding in the task was larger (500 ms as opposed to 300 ms). Nevertheless, the compound bounded exponential model is a rather general model of the threshold for use and the exhaustion of a limited resource over time because it makes only three assumptions: first, that accuracy is at chance until a certain minimum level of information accumulates; second, that memory has a limited capacity; and third, that this capacity is reached with decreasing efficiency over time. We believe our assumptions are as valid for working memory as for long-term verbal episodic memory, and that young and older adults differ only quantitatively in their WM dynamics. Thus, given the model’s formulation, its use here is appropriate.

Although our mathematical model is a general one, we focused on a very specific memory process, manipulating only the retrieval phase of WM for two abstract objects in a visual paradigm. This limits the generalizability of our findings in that we cannot extrapolate our results either to memory for verbal or semantic information or to other sense modalities besides vision. It is also difficult to relate our conclusions to the encoding and rehearsal processes in WM. However, it may be possible to apply our methodology to encoding and rehearsal dynamics (see below). Our methodology can also be easily adapted to study memory for heavier and smaller workloads and perhaps to study different sense modalities.

The present study is important because it successfully applies the RSM in the context of healthy aging. The RSM, together with Hintzman and Curran’s (1994) modeling method, provides quantitative measures of components of WM that, until now, have been discussed in mainly qualitative terms as they relate to aging. Previous experiments have used simple measures (reaction time, number of items retained, etc.) to describe age-related differences in retrieval ability, allowing for only qualitative discussions of concepts like WM efficiency and capacity. The fit parameters derived from our mathematical model provide quantitative measures that relate directly to these concepts: x-intercept and rate characterize the efficiency of WM retrieval (how soon information can be accessed and how quickly it accumulates), whereas asymptote characterizes capacity (how much information can accumulate) in units of discriminability. Below we discuss how the rate and asymptote parameters inform past research.

The rate parameter may be a better measure of WM speed than reaction time because it avoids the conflation of efficiency and capacity. For example, Holtzer et al. (2004) measured retrieval efficiency in terms of reaction time and found that when the memory set size gets large (e.g., six letters), response accuracy drops in older adults but not in young adults. This finding reveals a difference in WM capacity that complicates estimates of WM efficiency in terms of speed (Stern et al., 2008; Zarahn et al., 2005). The rate parameter derived in the present study explicitly accounts for SAT, encompassing the relationship between the duration and the effectiveness of the retrieval process. Moreover, this parameter is computed simultaneously with estimates of the fastest effective memory processing (x-intercept) and the maximum efficacy of WM (asymptote). So the process for estimating the rate parameter takes into account the important distinction between the amount of information that is immediately available to WM and the amount of information that can be recalled at all (cf. Sternberg, 1966). In addition to providing a good quantitative measure of WM efficiency, the age-related impairment of rate affirms previous studies that have shown aging to specifically impair the speed of WM retrieval (e.g., Holtzer et al., 2004; Salthouse, 1992; Salthouse & Babcock, 1991).

The asymptote effect affirms previous assertions that aging limits the capacity of WM (e.g., Zacks & Hasher, 1993); and like rate, the asymptote parameter provides an improved characterization of capacity. Although previous aging research has commonly measured capacity as the quantity of information (e.g., number of items) that can be processed before memory failure occurs (e.g., Anders et al., 1972; Holtzer et al., 2004), asymptote measures one’s maximum ability to use available information. Age-related impairment may involve similar mechanisms for both concepts of capacity. That is, if aging impairs a cognitive function that is relevant to a variety of tasks, such as attention (e.g., Greenwood & Parasuraman, 2004; West, 2004), this could result in decreased WM capacity regardless of how capacity is measured. But because asymptote quantifies the accuracy of WM, it is more broadly applicable to theoretical assertions about capacity.

In these ways, characterizing the retrieval process with the SAT model parameters has conceptual advantages over previous approaches that have used individual, direct measures of performance. The present method for modeling SAT may also prove useful in manipulations of the encoding and rehearsal processes. For example, an experiment similar to the current study in which the timing of the presentation stimulus is manipulated instead of the probe could provide similarly meaningful measures of WM encoding dynamics, demonstrating the specific effects of aging on encoding ability.

A quantitative characterization of WM efficiency and capacity also provides a useful bridge to understanding cognitive reserve. CR insulates aging individuals from the cognitive consequences of degenerative neuropathology (Stern, 2002; Stern et al., 2005). We tested proxies of CR as predictors for our fit parameters, and we found that CR provides resistance against age-related impairments in WM efficiency (rate) but not WM capacity (asymptote). To whatever extent the efficiency of WM retrieval decreases over one’s lifetime, individual differences in IQ, vocabulary, and education modulate the degree of natural memory loss. Other factors that have been shown to impart reserve, such as occupational attainment and leisure activity (Evans et al., 1993; Stern et al., 1994), are likely to temper the loss of efficiency as well. On the other hand, the extent to which aging impairs the capacity of WM retrieval is independent of these reserve-related factors.

Prior research has shown a relationship between measures of CR and the activation of individual brain regions or brain-wide networks (Habeck et al., 2005; Stern et al., 2003, 2005). Stern (2002) has hypothesized that one aspect of the implementation of CR is neural reserve, which involves individual differences in unimpaired cognitive networks (those used by young, healthy individuals), particularly with respect to the efficiency and capacity of functional memory networks. The modulating effect of CR on WM retrieval efficiency observed in the present study may also extend to neural efficiency, in that individuals with greater CR can ramp up neural activation more quickly as task demands increase. Similarly, the absence of a CR effect on WM retrieval capacity may also extend to neural capacity, in that the degree of neural activation an individual can achieve is only a function of age and not of CR. We cannot definitively address these issues in a behavioral paradigm. Future neuroimaging studies that employ the RSM along with CR measures will clarify how reserve modulates neural activation associated with WM, while providing a quantitative characterization of WM retrieval dynamics.