Sizing Subcellular Organelles and Nanoparticles Confined within Aqueous Droplets

Abstract

This paper describes two complementary techniques, single-particle tracking and correlation spectroscopy, for accurately sizing nanoparticles confined within picoliter-volume aqueous droplets. Single-particle tracking works well with bright particles that can be continuously illuminated and imaged, and we demonstrated this approach for sizing single fluorescent beads. Fluorescence correlation spectroscopy detects small intensity bursts from particles or molecules diffusing through the confocal probe volume, which works well with dim and rapidly diffusing particles or molecules; we demonstrated FCS for sizing synaptic vesicles confined in aqueous droplets. In combination with recent advances in droplet manipulations and analysis, we anticipate this capability to size single nanoparticles and molecules in free solution will complement existing tools for probing cellular systems, subcellular organelles, and nanoparticles.

INTRODUCTION

Few methods exist currently to size single subdiffraction-limited particles in free solution. Scanning probe microscopies (e.g. atomic force microscopy) and electron microscopies require immobilization of the particle on a surface or in a matrix. This requirement makes subsequent solution-phase analysis or transport difficult to perform. Light scattering measurements can size particles in solution, but lacks sufficient sensitivity to size single or a small group of particles, and typically requires high concentrations of particles for accurate measurement.¹ Correlation spectroscopy^2,3 and particle tracking⁴ have the potential to size single particles in free solution, but currently it is difficult to achieve this feat because the particle can diffuse away from the interrogation region before its diffusion coefficient can be accurately measured, especially for small nanoparticles or macromolecules. To address this issue, this paper describes the use of single aqueous droplets to spatially confine single or a small group of nanoparticles so their diffusion coefficient and size can be measured.

Droplet microfluidics have emerged in recent years as an attractive platform for conducting small-scale chemistries and for parallel assays.^5-17 For example, we have developed techniques for the selective encapsulation of single subcellular organelles into a single femtoliter-picoliter volume droplet⁷, methods for the transport and fusion of two droplets to initiate a chemical reaction^8,11, and single-molecule capillary-electrophoresis techniques to separate and detect the contents of single droplets.^9,18 Here, we describe the use of aqueous droplets to confine the diffusion of single or a small group of nanoparticles so their diffusion coefficient and thus hydrodynamic size can be measured. We are particularly interested in the ability to size subdiffraction-limited subcellular organelles prior to the analysis and quantification of their molecular contents.

This paper describes two methods that offer complementary advantages for accurately measuring diameters of nanoscale particles in aqueous droplets. The first method is based on imaging and particle tracking^19-22, where the diffusive trajectories of a droplet-confined particle is first imaged then analyzed to extract the diffusion coefficient and size. This method is easy to apply and can be adapted for the parallel tracking and measurement on particles confined in an array of droplets. The second method is based on confocal correlation spectroscopy (CCS)^2,3 and fluorescence correlation spectroscopy (FCS) ^23-25, which are capable of accurately sizing both fluorescent and non-fluorescent particles in small sample volumes. FCS is particularly suited for measuring “dim” biological particles or ones that are easily photodamaged, because the confocal detection geometry illuminates only a small region of the droplet and thus the particle is illuminated only for short periods of time (versus continuous excitation in particle tracking).

With either method, it is important to be aware of issues unique to confined volumes and droplets that may affect accurate diffusion measurements. We categorize these potential issues into two categories, ones that are hydrodynamic in origin and those that arise from interfacial/surface interactions. Once these variables are accounted for, it is a relatively simple process to size biological particles such as synaptic vesicles or polymer nanoparticles accurately in droplets. In combination with recent advancements in droplet microfluidics, we anticipate these sizing techniques will offer new ways to probe single nanoparticles and biological molecules in solution.

MATERIALS AND METHODS

Materials

AR20, AS4, Span 80 and polyethylene glycol (avg. mol. wt. 8000 Da) were obtained from Sigma Aldrich (St. Louis, MO). Light mineral oil was purchased from Fischer Scientific (Hampton, NH). Sulfate-modified and amine-modified beads were 290nm and 200nm diameter, respectively, and were acquired from Invitrogen Corporation (Carlsbad, CA).

Synaptic Vesicle Preparation

Synaptic vesicles were isolated from rat brains with a modified procedure from Hell et al.²⁶ Frozen rat brains (Pel-Freeze, Rogers, AR) were blended with liquid nitrogen until a fine powder formed and then suspended in 85-ml homogenization buffer (2 mM EGTA, 50 mM HEPES, pH 7.2, 0.3 M sucrose). A Teflon-glass homogenizer was used to homogenize the solution. A synaptic vesicle rich supernatant was obtained by centrifuging the homogenate in a MLA-80 rotor (Beckman Coulter, Fullerton, CA) at 100 000 g for 28 min at 4°C. The supernatant was suspended on a 1.5 M/0.6 M sucrose step gradient before centrifuging at 250 000 g for 72 min at 4°C. The isolated synaptic vesicles were collected from the 1.5 M/0.6 M sucrose interface then frozen and stored at -80°C for up to 4 months.

Droplet Preparation

Droplets were generated by vigorously mixing 200 μL of a 10^-10-10^-12 M bead/synaptic vesicle aqueous solution with 800 μL of oil. The vigorous mixing provided a relatively heterogeneous population of droplet sizes and number of particles contained within. A pipette was used to transfer ∼100 μL of oil/water mixture onto the glass substrate. After ∼3 minutes, all of the droplets settled and absorbed to the coverslip leaving a droplet container as shown in Figure 1B. To measure the diffusion of particles, we searched the substrate to find a suitable droplet containing 1-5 particles for measurement. To minimize any hydrodynamic biasing due to the small size of a droplet, droplets used for measurement were typically greater than 10μm in diameter. Furthermore, we focused at a plane near the middle of the droplet so that surface effects would also be minimized.

Figure 1.

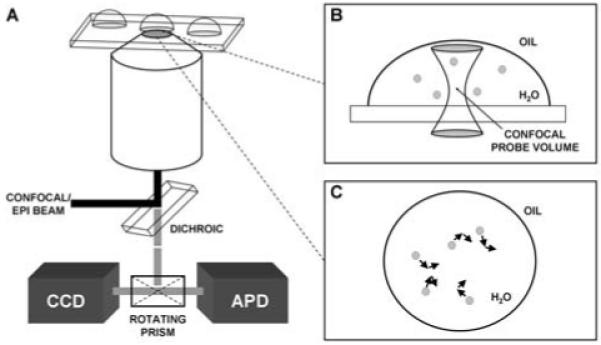
A) Schematic of the experimental setup used to excite and collect signals from particles encapsulated within microdroplets. B) With fluorescence correlation spectroscopy, which used point detection with an avalanche photodiode (APD), the confocal probe volume was placed at the center of the water droplet to detect burst events from the contained particles, thus measuring the diffusion time and size of the particles. C) For particle tracking, which used imaging with a sensitive CCD camera, each particle was tracked individually and the associated Δx and Δy values were recorded and used to calculate the diffusion time for each particle in the droplet.

Experimental Setup for FCS and Particle Tracking

Excitation and collection of the fluorescence from particles encapsulated in droplets was performed on a Nikon TE2000 microscope using a high numerical aperture objective (NA 1.45). A laser emitting at 488nm (Coherent Sapphire, Santa Clara, CA) or 633nm (Coherent HeNe laser, Santa Clara, CA) was split into two independent beams and recombined to provide both confocal and epifluorescence illumination. Shutters were placed in front of either beam depending on which mode was being used. For confocal, the beam was expanded to fill the back aperture and collimated before being directed off a dichroic mirror (Chroma Tech. Corp., Rockingham, VT), which was designed to reflect both 488nm and 633nm, into the objective. For epifluorescence, the beam was focused at the back aperture of the objective, so the beam exited at the object plane in a collimated form offering even illumination throughout the sample. Fluorescence from the encapsulated particles was collected using the same objective and filtered with the dichroic and bandpass filters (Chroma Tech. Corp., Rockingham, VT), which were specific whether 488nm or 633nm excitation light was employed, before the detectors to remove any excess laser radiation. A rotating prism, stock in the microscope assembly, was used to select the mode of imaging. For particle tracking, we used a highly sensitive CCD camera (Cascade 512B, Roper Scientific, Tuscon, AZ). For FCS, the fluorescence from the confocal probe volume was spatially filtered through a 50-μm pinhole and then focused onto an avalanche photodiode (AQR-14, Perkin Elmer, CA), after which the signal was correlated using a Flex02-12D multiple-tau autocorrelator from correlator.com (Bridgewater, NJ). For particle tracking, the recorded trajectories were analyzed using the MetaMorph software from Molecular Devices (Sunnyvale, CA).

Simulations of Particle Diffusion in a Confined Volume

The calculation of the friction factor of a bead inside a spherical droplet has been discussed previously. Cunningham²⁷ derived an expression for the special case of a bead at the center of the droplet. Allison²⁸ performed calculations similar to what is performed here for a small bead (4nm diameter) inside a small spherical vesicle (100nm diameter) using well established procedures.^29,30 In this work, as in Allison’s, the translational friction factor of a spherical bead inside a droplet is modeled by replacing the droplet interface by a rigid array of N spheres (shell beads) whose centers lie on the interface (Supplemental Figure 1A). Including the sphere for the bead inside yields a set of N+1 spheres. The hydrodynamic properties of these spheres can be calculated using the procedures described by Garcia de la Torre et al.³⁰ and Allison.²⁸ In particular, it is possible to calculate the force necessary to maintain the bead inside at a constant velocity while the shell beads are stationary, and from that to obtain the average friction factor, f, for the bead inside the droplet. The diffusion factor of the bead, D, is related to the friction factor by

$$D=\frac{kT}{f}$$ (1)

where k is Boltzmann’s constant and T is the temperature. In general the friction factor for a bead inside of a droplet will be larger than the unperturbed friction factor, f₀, for the same particle in bulk solution. In bulk solution

$$f_0=3\pi \eta d$$ (2)

where η is the viscosity of the solution and d is the diameter of the spherical particle. In this work, the hydrodynamic interactions are modeled using the Rotne-Prager tensor³¹ for non-overlapping spheres of different sizes as was done by Allison.²⁸ Due to the increase in computing power since 1988, the approximations used by Allison to reduce the computer time required for the calculation were not necessary.

For each position of a bead inside a droplet, the calculation of the bead’s friction factor is performed several times using successively more and smaller shell beads to model the droplet surface. For nearly all of the calculations, the friction factor converges in the sense that the difference between the values calculated using the smallest and next smallest shell bead sizes is less than 0.1%. For the smallest spherical droplet the differences were all less than 0.5%. In the results below, only the value calculated using the smallest sizes of shell beads to model the droplet interface are reported.

For each droplet it was necessary to calculate the coordinates of the N different shell beads used to model the droplet surface. For the spherical droplets, the center of a single shell bead is placed at each of the two points where the droplet surface intersects the z axis. The coordinates of a series of circles on the surface of the droplet are then calculated. The circles are positioned so that the closest distance between adjacent circles and the distance between the intersection of the droplet with the z axis and the circle closest to it are all identical. A radius for the shell beads is chosen that will fill in as much of the droplet surface as possible without allowing shell beads on adjacent circles to overlap. The coordinates of the shell beads, evenly spaced on each circle, are calculated and the entire set of coordinates constitutes the array of spheres used to represent the droplet wall. The size of the droplet and the number of circles determine the size of the shell bead used. The calculation was repeated with 11, 19, 29, 39, and 49 circles. The number of shell beads used to represent the droplet was 124, 502, 1129, 2016, and 3153, respectively. Since the number of circles used is odd, one of the circles lies in the equator (xy-plane) of the droplet. The coordinates of one more sphere, which represents the particle inside the droplet, is added to the set of coordinates, which is then used to calculate the friction factor of the particle inside the spherical droplet.

For the hemispherical droplet, the procedure is similar to that for the spherical droplet. For the curved portion of the surface, the procedure is the same as for the spherical droplet, except that only those shell beads whose z coordinate is greater than or equal to zero are used. The base is formed by the circle of shell beads in the xy-plane (corresponding to the equator of the spherical droplet), a shell bead placed at the center of the base, and a set of concentric circles. The spacing between the concentric circles is chosen to allow the use of shell beads whose size is as close as possible to the ones in the curved wall of the droplet while still filling in as much as possible of the hemisphere’s base (Supplemental Figure 1B). The calculation was repeated using 5, 10, 15, 20, 25, 28, and 30 circles on the curved surface of the hemisphere. The corresponding numbers of concentric circles added to fill out the base of the hemispheres were 2, 5, 8, 10, 13, 16, and 18, respectively. The total number of shell beads was 92, 370, 831, 1483, 2322, 2925, and 3408, respectively. As before, these are the coordinates of the shell beads used to represent the droplet wall. One more sphere, used to represent the particle inside the droplet, is added to the set of coordinates, which is then used to calculate the friction factor of the particle inside the hemispherical droplet.

RESULTS AND DISCUSSION

We have explored two complementary methods for measuring the diffusion times of nanoparticles confined in an aqueous droplet. The first method is to use single-particle tracking, and the second technique is based on confocal correlation spectroscopy.^2,3 Single-particle tracking works well with large (e.g. > 100nm) and bright particles, because these particles diffuse slowly, which facilitates tracking, and are less prone to photobleaching or photodamage as they are continuously illuminated during tracking. The advantage of single-particle tracking is the ability to use imaging to sample most of the trajectories of the particle in the droplet as well as the ability to monitor many droplets simultaneously for parallel measurements. Single-particle tracking, however, tends to work less well with small particles (e.g. < 100nm) that diffuse rapidly or fragile particles that are easily photodamaged. For these small and fragile particles, confocal or fluorescence correlation spectroscopy is more suitable. In fact, rapid diffusion of small particles facilitates correlation measurements because of the higher rate of sampling of the trajectories of the particle per unit time. Furthermore, the sensitivity of confocal fluorescence measurements in free solution is orders of magnitude higher than epi-fluoresence imaging. We have demonstrated these two approaches to sizing particles using fluorescence measurements, owing to the wide-spread use of fluorescence labeling in biological samples, but these approaches may be extended to non-fluorescent particles, such as with the use of back scattering² or dark-field imaging for metallic particles.³²

Measuring Diffusion Coefficient in a Droplet with Single-Particle Tracking

During particle tracking, the probability of the displacement, P(Δx), of a particle during Brownian motion is

$$P\left(\Delta x\right)=\frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{\frac{-\Delta x^2}{2{\sigma }^2}}$$ (3)

and

$${\sigma }^2=2D\Delta t$$ (4)

were D is the diffusion coefficient and Δt is the time between frames. The displacement of a particle was determined using one of two tracking algorithms, template matching or threshold. Both algorithms identify the particle in the current image by comparing it to a preceding image, typically the initial frame of the video. The template matching algorithm filters the current image using a convolution mask generated from the initial frame. An object is defined as the particle if the peak intensity in the current convolved image is greater than a minimum percentage of the peak intensity in the initial frame. The displacement, Δx and Δy, is the distance between the intensity maximum in the preceding convolved image and the intensity maximum in the current convolved image. This algorithm is ideal for particles where the centroid is best represented by the brightest pixel in the image. However, contamination, such as dust, causes image artifacts that can interfere with tracking when using this algorithm.

Alternatively, with the threshold algorithm a detected object is identified as the particle if the object’s size is greater than a defined percentage of the total size of the particle in the initial frame. The displacement is then defined as the Δx and Δy from the center of the object in the preceding frame to the center of the object in the current frame. This threshold algorithm is not easily affected by contamination as is the template matching algorithm. The major limitation to this algorithm is its inability to accurately determine the centroid of a particle that is not symmetric in appearance, but this limitation can be overcome. After experimental investigation of both algorithms, we found the threshold algorithm to be the most applicable to our system due to its tolerance for dust particles or other imperfections in our images.

With either tracking algorithm, the Δx and Δy obtained were binned into histograms and the probability was fit with equation 3. We found the diffusion coefficient extracted from the probability-displacement curve is greatly affected by two factors: (1) The appearance of the particle in the image (particle symmetry), which affects the threshold tracking algorithm, and (2) The exposure time, frame rate, and lag time of the CCD camera used for imaging.

Particle-image symmetry

Over the exposure time, the particle is continually moving. As a result, for longer exposure times and faster diffusing particles, the image of the particle will represent the entire path taken by the particle during the exposure time instead of an instant representation of the position of the particle. The resulting image then becomes a non-resolved, asymmetric representation of the particle. This problem can be addressed by increasing the viscosity of the aqueous solution or by decreasing the exposure time. By increasing the viscosity with sucrose in our experiments, a reduced diffusion coefficient was observed. The reduced diffusion coefficient minimized blurring of the particle over the exposure time. This approach, however, increases the complexity of the experiment and can place undesirable constraints on the system under study. Decreasing the exposure time provided a sharper image and a better representation of the instant position of the particle in our experiments. There are, however, two considerations when implementing this approach: (1) To ensure sufficient displacement of the particle between successive frames, a delay time between frames is usually needed, and (2) Using an overly short exposure time will decrease the signal integration time of a given CCD pixel, and thus the sensitivity of detection. Therefore, there is an optimal exposure time that both preserves detection sensitivity and minimizes blurring of the particle.

Exposure time and frame rate

It has been shown that the measured diffusion of particles in a confined space will decrease as the exposure time increases.³³ An analytical expression relating the exposure time and frame rate to the apparent diffusion coefficient was presented by Montiel et al.⁴ It was shown that the true diffusion coefficient could be approximated with

$$\frac{D_{\mathrm{app}}}{D}\approx 1-\frac{1}{3}\left(\frac{T_{\text{exposure}}}{T_{\text{frame}}}\right)$$ (5)

where D_app is the apparent diffusion coefficient, T_exposure is the exposure time, and T_frame is the frame rate. By taking the above factors into consideration, we have measured the diffusion coefficient and the particle size for single 290nm-diameter (from manufacturer) beads confined in aqueous droplets (Figure 2); at 21°C with an exposure time of 100 msec, 155 msec frame rate, and 800 acquired frames, the average measured diffusion coefficient was 1.68 ± 0.55 μm²/sec. This corresponds to an average bead diameter of ∼272nm which compares well to the measured bulk diffusion coefficient of 1.69 ± 0.22 μm²/sec at 22°C, which is equivalent to ∼279nm average diameter.

Figure 2.

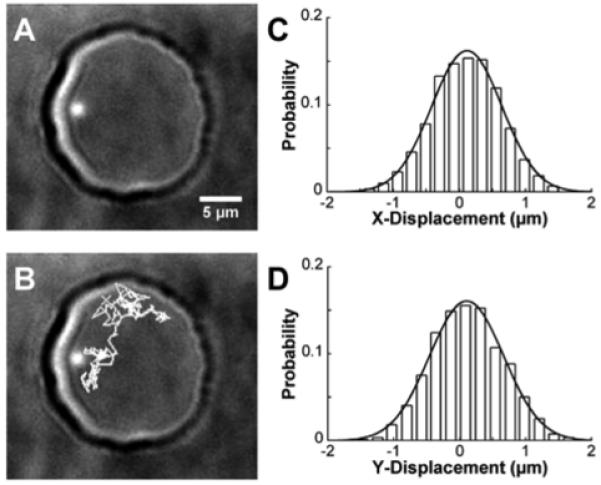
A) Single, 290nm-diameter fluorescent bead encapsulated within a hemispherical, water droplet (∼20μm diameter). B) Particle tracking (gray lines) showed the diffusion path of the bead inside the droplet over 200 frames. For each displacement, the displacement corresponding to Δx (C) and Δy (D) were recorded, binned into histograms, and fit with equation 3 to determine the diffusion coefficient in each dimension. In this example, integration time for the camera was 100 msec, frame rate was 155 msec, and 800 images were acquired.

Accurate Sizing of Synaptic Vesicles in Droplets with Fluorescence Correlation Spectroscopy(FCS)

It has been hypothesized that the concentration of neurotransmitters contained within synaptic vesicles remains relatively constant and the sizes of synaptic vesicles vary depending on the number of contained neurotransmitters.³⁴ Therefore, we are particularly interested in the ability to size synaptic vesicles in free solution, followed by quantification of the neurotransmitter contents of the vesicles. Figure 3 shows the sizing of synaptic vesicles confined to an aqueous droplet with FCS; the measured size of synaptic vesicles in a droplet compares well with bulk measurements. A number of factors can affect the ability of FCS to accurately measure the size of nanoparticles,^{2, 35-37} which we have described and analyzed in a previous publication.³ In this experiment, we first coated the glass surface with 1 mg/mL solution of dried milk, which contained mostly casein protein to prevent adsorption of the synaptic vesicles to the glass surface. The coating was highly hydrophilic and thus the water droplets wetted the surface much more than compared to unmodified glass substrate. The shape of the droplet then became much more pancake like instead of the hemispherical shape exhibited on the unmodified surface. This shape change, however, will not affect the diffusion coefficient of the synaptic vesicles within the droplet, as will be discussed later.

Figure 3.

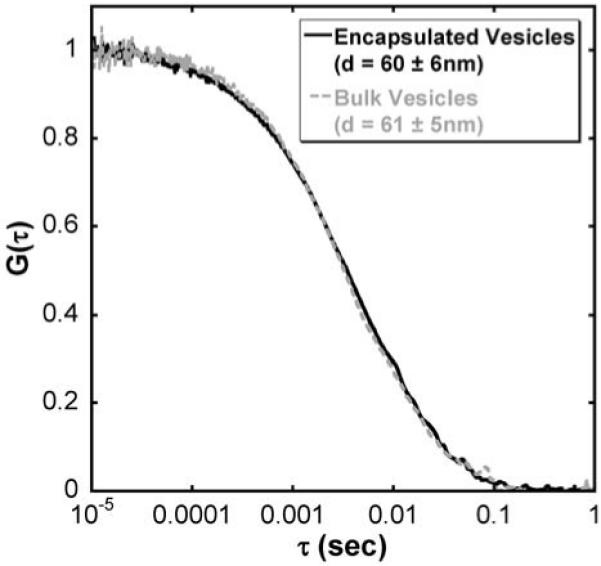
Normalized fluorescence correlation curves of synaptic vesicles encapsulated within a droplet (solid dark grey) and in the bulk solution (dashed light grey). Measured diameters of the synaptic vesicles in each sample agreed well within error (encapsulated, d=60 ± 6nm and bulk, d=61 ± 5nm).

Using electron microscopy, the average diameter of synaptic vesicles is typically reported to be 40-50nm.³⁸ In free solution, however, few examples exist that describe the hydrodynamic radius of these organelles. With dynamic light scattering, the size of the synaptic vesicles is larger than that reported using EM and has been shown to be between 50-60nm in diameter.³⁹ Here, we recorded with FCS the size of the synaptic vesicles in unconfined, bulk solution and found a similar diameter of 61 ± 5nm. The recorded diameter from vesicles within the droplet is 60 ± 6nm (Figure 3), which matches both the reported diameters from light scattering measurements and our FCS measurement on bulk samples. With the convenient incorporation of droplets into separations on chip,⁹ the ability to size single particles is an important step towards determining concentrations within nanometer-scale subcellular organelles.

Factors that affect accurate sizing in droplets

In comparison to bulk measurements in free solution, a number of factors unique to confined volumes can influence the ability to conduct accurate measurements of diffusion coefficients and sizing of nanoparticles. We divide these factors into two groups, those that are hydrodynamic in origin and those caused by interfacial/surface interactions.

Hydrodynamic factors

The accurate sizing of particles in droplets requires accounting for the hydrodynamic interactions between the particle and droplet wall. The magnitude of the hydrodynamic interactions is a function of size of the particle and the droplet as well as the droplet’s shape. As the particle moves inside the droplet, it creates a fluid flow field, or wake, around it. The fluid flow field transfers momentum between the moving particle and the stationary droplet wall which increases the friction factor of the particle above what it would have been if the particle was in a dilute bulk solution. To investigate this effect further, we performed calculations to investigate how size and shape affected the measured diffusion coefficient of the particle within the droplet. Figure 4 shows a comparison between spherical and hemispherical droplets by plotting the ratio f/f₀, where f is the calculated friction factor and f₀ is the friction factor of the particle in bulk solution. The relationship between the actual diameter of the particle and the value measured in the droplet (the apparent diameter) is

$$\frac{f}{f_0}=\frac{d_{\text{apparent}}}{d_{\text{actual}}}$$ (6)

Figure 4.

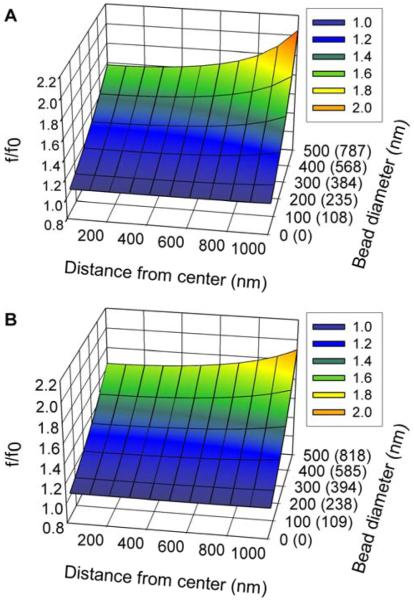
f/f₀ for a spherical bead inside of a droplet as a function of droplet shape, distance from the droplet center, and the actual and apparent bead diameters. The unparenthesized tic labels on the Bead-diameter axis are the actual bead diameters. The numbers in parentheses are the apparent bead diameters which were calculated from the actual bead diameters using equation (6) and the value of f/f₀ at the center of the droplet. (A) f/f₀ for a bead inside of a 3μm-diameter spherical droplet. (B) f/f₀ for a bead inside of a hemispherical droplet whose base has a diameter of 4μm. For the hemispherical droplet, the bead is always positioned 1μm above the hemisphere’s base, and the distance is the horizontal distance to the symmetry axis of the droplet.

Fig. 4 shows the ratio (f/f₀) as a function of position from the center of the droplet and particle size. Similar surfaces calculated for larger droplets showed that as the droplet size was increased, the f/f₀ surface flattened out and tended towards f/f₀=1 as the droplet became large. The magnitude of hydrodynamic interactions increases as the distance between objects in fluids decreases. Therefore, as expected, the ratio f/f₀ increases as the bead moves closer to the droplet wall. Furthermore, the effect of the hydrodynamic interactions increases as the size of the particle in the droplet increases. Both of these effects can be seen in Fig. 4.

The apparent particle diameter is a weak function of the droplet’s shape. For instance, the 3μm-diameter spherical droplet in Fig. 4A has a volume which is approximately 15% smaller than the 4μm-diameter hemispherical droplet in Fig. 4B. When the particle is close to the center of the droplet, the smallest distance from the particle’s center to the droplet wall is 1μm for the hemisphere versus 1.5μm for the sphere. As expected, the f/f₀ ratio is slightly larger for the hemisphere, with the largest differences occurring for the largest particle (500nm diameter). The horizontal distance to the nearest droplet wall is larger in the hemisphere than the sphere, but this does not become a factor until the particle is more than 700nm away from the center. Beyond that point, the f/f₀ ratio is slightly larger (less than 7%) for the spherical droplet than the hemispherical droplet. A similarly modest shape dependence is observed when comparing the f/f₀ ratios in a 5μm spherical droplet with those in a 6μm hemispherical droplet. In this second case, the hemisphere is approximately 15% larger than the sphere, and the f/f₀ ratio in the hemisphere is always slightly larger (less than 6% for the 500nm particle, results not shown). As a result, accurate modeling of the friction factor in a small droplet does not appear to require an extremely accurate description of the droplet’s shape. While any small errors introduced by an approximate description of the droplets shape would be systematic, they would be swamped by the random measurement errors. The results of the calculations show that for large droplets, such as the 20μm droplet in Fig. 2, f/f₀ is nearly equal to one over a fairly substantial region of the droplet’s interior. As a result, for such large droplets, any errors introduced into the analysis by ignoring the hydrodynamic interactions will be small compared to other experimental errors and can be ignored.

For smaller droplets, a figure similar to those in Fig. 4 can be used to account for the effect of hydrodynamic interactions and to correct the experimentally determined particle diameter. The figure can be used to define a region within the droplet where f/f₀ is relatively constant to be used for particle tracking. For all of the displacements included in the analysis, f/f₀ is approximately equal to its value at the center of the droplet because the region where f/f₀ is least sensitive to position will include the center of the droplet. In Fig. 4 the bead diameter axis is labeled both with the actual diameter of the particle for which the friction factor was calculated, but also (in parentheses) the apparent diameter, obtained by multiplying the actual diameter by the ratio f/f₀. If the droplet is small enough that f/f₀ is not approximately equal to 1, then the diameter obtained by the particle tracking analysis is the apparent diameter. The appropriate value of f/f₀ can be obtained from the apparent diameter and the ratio can then be used to convert the apparent diameter into an actual diameter. So even for small droplets where the effect of the droplet wall on the particle diffusion is significant, it is possible to correct for the droplet size and shape and accurately size particles in small droplets.

Correcting for the effect of the droplet on the diffusion of a particle becomes easier as the droplet becomes larger. The magnitude of the effect becomes smaller, which means the required accuracy to which the shape and size of the droplet must be described is relaxed. Furthermore, the region over which the ratio f/f₀ is relatively constant becomes larger, which might allow for more of the particle’s trajectory to be used. There is, however, one difficulty encountered with particle tracking as the droplet becomes larger, namely that the particle will spend more time out of the plane of focus as the droplet becomes taller, which will reduce the amount of the particle’s trajectory that is visible.

In the FCS measurement of the diffusion coefficient, the particle’s fluorescence is measured as it crosses an approximately ellipsoidal volume defined by the focusing of the laser and the confocal pin hole in front of the detector. The effect of the droplet wall on the diffusion can be approximated by averaging the calculated f/f₀ ratio over a cylindrical volume which is 2.2μm tall and 490nm in diameter. This volume, which is the same size as the volume defined by the typical height and width of the probe volume in our FCS measurements,³ is aligned with the symmetry axis of the droplet and has its center at the center of the droplet. The results of this averaging for different sizes of droplets and particles are shown in Fig. 5.

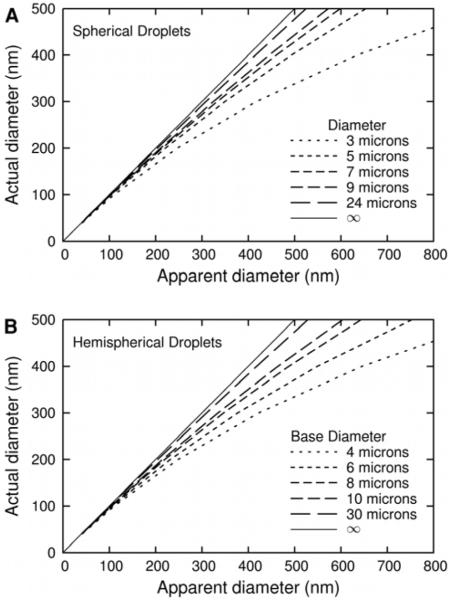
Figure 5.

Actual diameter vs. Apparent diameter from FCS measurements for spherical particles in droplets. In both panels, the thin solid line is for equal actual and apparent FCS diameter (infinite size droplet). The relationship was calculated by averaging the ratio f/f₀ over a cylinder with a diameter of 490nm and a length of 2.2μm, which is aligned with the symmetry axis of the droplet and whose center is at the center of the droplet. (A) Results for a spherical droplet. The five dashed lines represent the effect on the diameter as measured by FCS of (left to right) 24, 9, 7, 5 and 3μm-diameter spherical droplets. (B) Results for a hemispherical droplet. The five dashed lines represent the effect on the radius as measured by FCS of (left to right) 30, 10, 8, 6 and 4μm-diameter hemispherical droplet. For the 4μm hemisphere, f/f₀ is averaged over a cylinder with a diameter of 490nm and a length of 1.4μm. The results for the 4μm hemisphere are presented only for comparison with the results for a 3μm spherical droplet, as its short height (2μm) would cause problems with an FCS experiment, which would have a sample volume exceeding 2μm in height.

The results in Fig. 5 are averages over the FCS volume, so the apparent diameter (as measured by FCS) can be directly converted to the actual diameter using Fig. 5. Due to the height of the FCS probe volume, a somewhat larger dependence on droplet shape is observed in Fig. 5, but only for the smallest droplet sizes. As the droplet become larger, the overall effect of the droplet as well as the shape dependence becomes small. From Fig. 5 it appears that once the droplet size is increased over 20μm in diameter, the effect of hydrodynamic interactions with the droplet wall has a very small effect on the measured friction factor of the particle. It is also important to note that as the particle becomes smaller (e.g. <150nm), this hydrodynamic interaction becomes negligible, even for the smallest droplet (e.g. 3μm).

During our FCS measurements of the synaptic vesicles, the droplets were not the spherical or hemispherical shape we typically observe. Instead a pancake shaped droplet is observed due to the hydrophilic surface used during the measurements. A model of a pancake droplet can be obtained from a model of a hemispherical droplet of the same height by expanding its base while keeping the height fixed. For any given location in the droplet, this increase in size results in an f/f₀ ratio which is closer to 1 for a pancake droplet than for a hemispherical droplet of the same height. Therefore, a shape change from a hemispherical to a pancake droplet of the same height will not affect the diffusion of a particle in regions where f/f₀ is already close to 1, as is the case for our measurements of synaptic vesicles encapsulated in a droplet.

Interfacial/Surface Interactions

In addition to hydrodynamic affects that depend on the size and shape of the aqueous droplet, there are other physical factors that can impact the measurements of the diffusion of particles in droplets. These factors include the surface charge of the particle, ionic/buffer strength of the solution, surface property of the glass substrate (if it were a hemispherical droplet), property of the immiscible phase, and whether any surfactants are used to coat the beads or the oil/water interface. We have studied the effects these factors can have on diffusion measurements in droplets; for example, a variety of oils (AS4 and AR20 silicone oil, and mineral oil), particles (sulfate-modified beads, amine-modified beads, and synaptic vesicles), aqueous solutions (DI water and phosphate buffered saline), and surfactants (1% wt Span 80 and 16 mg/mL PEG [MW 8000 Da]) were examined while we developed a model system for sizing particles in droplets. In these experiments, we found it was important to prevent permanent absorption of the particles to the droplet interface or glass surface, but it was not critical to eliminate biasing of the particle’s diffusion near such interfaces as long as only the particle’s trajectories in the center of the droplet were used. We satisfied these criteria in FCS by “parking” the probe volume in the center of the droplet, and in particle tracking by only using trajectories localized to the middle two thirds of the droplet. Even if the particle eventually becomes attached to droplet interface/glass surface, we were still able to make accurate diffusion measurements if there was sufficient time (typically a few minutes) to record enough trajectories of the particle near the center of the droplet before the particle becomes irreversibly absorbed to the interface/surface.

CONCLUSION

We demonstrated here the ability of single-particle tracking and correlation spectroscopy to measure the diffusion coefficient and to determine the size of nanoparticles encapsulated within femtoliter to picoliter-volume aqueous droplets. These two techniques are complementary. Particle tracking works best with bright particles that diffuse slowly, but has the advantage of imaging and can measure multiple single nanoparticles confined in multiple droplets in parallel. Correlation spectroscopy, such as FCS, is a point-detection technique, but it offers high sensitivity (e.g. diffusion coefficients of single dye molecules have been measured using FCS) and works best with small, dim, and rapidly diffusing particles. Currently, few techniques are capable of sizing single nanoparticles in free solution, and we anticipate our approach to sizing single particles and molecules in droplets complements existing methods, such as light scattering, scanning probe methodologies, and electron microscopy imaging. We are particularly interested in combining this capability to size biological nanoscale objects and subcellular organelles with our droplet manipulation and analysis techniques for addressing a wide range of biological questions, such as the concentration of neurotransmitters contained within single synaptic vesicles or the level of metabolites and proteins contained in single mitochondria.