Mitochondrial Oscillations in Physiology and Pathophysiology

Abstract

Oscillations in chemical reactions and metabolic pathways have historically served as prototypes for understanding the dynamics of complex nonlinear systems. This chapter reviews the oscillatory behavior of mitochondria, with a focus on the mitochondrial oscillator dependent on reactive oxygen species (ROS), as first described in heart cells. Experimental and theoretical evidence now indicates that mitochondrial energetic variables oscillate autonomously as part of a network of coupled oscillators under both physiological and pathological conditions. The physiological domain is characterized by small-amplitude oscillations in mitochondrial membrane potential (ΔΨ_m) showing correlated behavior over a wide range of frequencies, as determined using Power Spectral Analysis and Relative Dispersion Analysis of long term recordings of ΔΨ_m. Under metabolic stress, when the balance between ROS generation and ROS scavenging is perturbed, the mitochondrial network throughout the cell locks to one main low-frequency, high-amplitude oscillatory mode. This behavior has major pathological implications because the energy dissipation and cellular redox changes that occur during ΔΨ_m depolarization result in suppression of electrical excitability and Ca²⁺ handling, the two main functions of the cardiac cell. In an ischemia/reperfusion scenario these alterations scale up to the level of the whole organ, giving rise to fatal arrhythmias.

Introduction

The study of oscillatory phenomena in physics, chemistry and biology has fascinated scientists for centuries. For example, the synchronization of pendulum clocks as coupled oscillators was described by Huygens in 1665, and in biological systems, Kaempfler wrote of the synchronized blinking of fireflies that he had observed on a visit to Siam in 1680 (see refs. ^1,2 for historical reviews). In the 20th century, Van der Pol modeled the electrophysiological properties of the heart as collection of coupled relaxation oscillators³ and other examples of electrical, biochemical, and ionic oscillators in physiology abound.^4-7

The Russian scientist B.P. Belousov demonstrated that complex temporal and spatial dynamics can be observed in the simple chemical reaction of citric acid/bromate/cerium. He had difficulty publishing the work when first submitted in 1951,⁸ but after Zhabotinsky repeated Belousov’s experiments,⁹ the Belousov-Zhabotinsky reaction grew to became a prototype for the theoretical and experimental study of oscillators. In the same era, oscillations in enzyme-catalyzed biochemical pathways were reported. Duysens and Amesz¹⁰ published the first observation of biochemical oscillations of reduced pyridine nucleotides in intact cells and these findings were followed by the elucidation of a glycolytic oscillator in yeast^11,12 and in cell-free extracts from various sources.^13-18 This triggered an explosion of interest in the elucidation of the mechanism(s) of biological oscillators (see refs. ⁴ and ¹⁹ for early reviews, see Lloyd, D, this volume). In yeast, this interest has continued throughout the years with new exciting findings.^7,20-22

Oscillations in ion fluxes, respiration, and mitochondrial volume were noted 40 years ago in several laboratories^23-25 and Chance and Yoshioka²⁶ demonstrated that they could be sustained over many cycles. Others have also observed mitochondrial oscillations triggered by divalent cations.^27-30 In these earlier studies, the oscillations were typically induced by an increase in cation cycling (e.g., by adding valinomycin) in isolated energized mitochondria and usually took the form of damped sinusoidal oscillations, the damping corresponding to a loss of synchrony among mitochondria in the population over time.^31-33

In 1994, our laboratory reported that substrate deprivation could induce spontaneous low frequency oscillations in sarcolemmal K⁺ currents, action potential duration and excitation-contraction coupling in adult cardiomyocytes.³⁴ These oscillations were associated with cycles of oxidation and reduction of the intracellular NADH pool. At the time, we proposed that the mechanism could involve the well-known glycolytic oscillator, which could entrain oxidative phosphorylation, but we could not exclude mitochondria as the source of oscillation. Subsequent investigations revealed that the oscillations were associated with mitochondrial flavoprotein redox transients and waves of mitochondrial membrane potential (ΔΨ_m) depolarization,³⁵ which shifted our view to a mitochondrial mechanism. More recently, we have investigated in detail the mechanisms involved in triggering and maintaining synchronized, self-sustaining oscillations of bioenergetics in the mitochondrial network of intact cardiac cells, aided by the discovery that they could be reproducibly triggered by laser-induced depolarization of just a few mitochondria in the cell.³⁶

Here, we review the properties of mitochondrial oscillators described previously and present a comprehensive account of our theoretical and experimental studies of the reactive oxygen species (ROS)-dependent mitochondrial oscillator induced by metabolic stress in heart cells. Moreover, we put forward the idea, based on relative dispersion and power spectral analysis that coupled oscillation is an inherent property of the mitochondrial network under physiological conditions as well. Understanding the basic mechanism of mitochondrial oscillation is shown to provide fundamental new insights into the origins of post-ischemic electrical and contractile dysfunction in the whole heart and also suggests a novel frequency- and amplitude-encoded ROS signalling function for mitochondria.

Early Descriptions of Mitochondrial Ionic Oscillations

Oscillations in ion flux across the inner membrane of isolated liver or heart mitochondria have been known since the 1960s (reviewed in ref. 32). Chance and Yoshioka reported persistent sinusoidal oscillations of H⁺ and K⁺ induced by valinomycin in the presence of oxygen, monitored with ion-selective glass electrodes.²⁶ Initially, K⁺ is taken up by the mitochondria (seen as a decrease of K⁺ in the medium) and this is then accompanied by H⁺ extrusion. The K⁺ uptake results in mitochondrial swelling, as judged photometrically and by electron microscopy.³¹ Oscillations come to a halt after oxygen in the medium depletes and the ionic changes reverse, i.e., H⁺ concentration outside the mitochondria decreases and the K⁺ concentration increases.^26,31 The damping of the ionic oscillations in isolated mitochondria is a function of the external pH, the K⁺/H⁺ ratio, and ADP, and the F₁F_o ATPase is required, since oligomycin blunts the oscillations.^26,31

Subsequent work on mitochondrial suspensions showed that the addition of a pulse of Sr²⁺ (a Ca²⁺ analogue that is efficiently transported across mitochondrial membranes) could trigger sustained oscillations in fluxes of divalent ions (reviewed in ref. 27). The shape, amplitude and frequency of oscillation were sensitive to the type of substrate. The oscillatory period ranged from 20 s up to 3 min, depending on the substrate, or from 15 s up to 10 min as a function of the amount of Ca²⁺ or Sr²⁺ added.²⁷ Further experimentation demonstrated the existence of mitochondrial Ca²⁺-induced oscillations in permeabilized protozoa³⁷ and in Erhlich ascites tumor cells.³⁸

Mitochondrial Oscillations in Intact Cells and Tissues

While the phenomena described above clearly show the potential for autonomous synchronized oscillation of mitochondria in suspension, only recently have oscillations in mitochondrial parameters been observed in intact cells, and it becomes more difficult to determine whether the oscillatory mechanism is intrinsic or extrinsic to the mitochondrial network. For example, mitochondria have been shown to respond to oscillatory Ca²⁺ signals evoked by signal transduction pathways³⁹ and have been implicated in the mechanism of bursting patterns of insulin release in pancreatic cells^40-42 and ultradian rhythms in yeast.⁴³ However, it is still not clear whether the mitochondria are a fundamental component of the oscillatory mechanism or are entrained by extramitochondrial factors, including cyclical changes in the plasma membrane electrical potential or Ca²⁺.

In excitable cells, in which cyclical changes in plasmalemmal membrane potential and Ca²⁺ handling may occur, it becomes even more difficult to separate cause and effect when oscillatory behavior is observed. For instance, oscillations in mitochondrial variables in neurons from the brainstem respiratory center have been reported.⁴⁴ Measurements of FAD and NADH autofluorescence, ΔΨ_m (Rhodamine 123) and mitochondrial Ca²⁺, Ca²⁺_m (Rhod-2), were performed in slice preparations of the preBötzinger complex (pBC) and in the hypoglossal (XII) nucleus. The neural activity of the pBC is essential for maintaining rhythmic respiratory activity in brainstem neurons in vivo and in vitro. Rhythmic respiration was functionally correlated with oscillations in NADH, FAD, ΔΨ_m and Ca²⁺_m. These oscillations in mitochondrial variables were reversibly abolished by brief hypoxia (2-4 min) and, in parallel, ATP-sensitive K⁺ channels were activated and respiratory output was depressed. These authors proposed that respiratory function was modulated by spontaneous activity in the mitochondrial network.

Adult cardiac ventricular myocytes are a good example of a cell-type containing multiple oscillators. However, since an external pacemaker normally entrains them, their mitochondria can be studied in the quiescent (noncontracting) state. Under such conditions, individual mitochondria have been observed to undergo spontaneous transient depolarization-repolarization cycles. This was first observed in 1982 by Berns et al⁴⁵ in myocytes loaded with fluorescent ΔΨ_m sensors using focal laser excitation. Again, cause and effect become blurred when the mitochondrial depolarization is associated with the spontaneous local discharge of the intracellular Ca²⁺ store, as was reported for mitochondrial “flickers” in cardiac myocytes.⁴⁶ Similar transient mitochondrial depolarizations were also observed in cultured neurons^47,48 and in smooth muscle cells;⁴⁹ in the latter case, they were found to be independent of sarcoplasmic reticular Ca²⁺ release.⁵⁰ In addition, spontaneous ΔΨ_m fluctuations can be observed in individual isolated mitochondria.^51-54 With respect to Ca²⁺-induced ionic oscillations in mitochondria, a Ca²⁺-induced Ca²⁺-release mechanism³⁰ involving the permeability transition pore (PTP) has been proposed^46,51,52 and may be responsible for fast mitochondrial Ca²⁺ release in cells;⁵⁵ however, in many of the examples mentioned above, the phenomenon is insensitive to cyclosporin A, calling into question the conclusion that the PTP is involved.^48,53

Another important consideration is whether or not the method of observation of ΔΨ_m depolarization is actually contributing to the perceived “spontaneous” event. In the original work of Berns et al,⁴⁵ the fluorescence oscillations depended on the type of dye used, suggesting that photosensitization played a role, and it is now well-recognized that even low levels of fluorescence excitation can generate enough free radicals to cause mitochondrial depolarization. This effect of laser-induced radical generation was used to great advantage by Zorov and Sollott^56,57 in describing mitochondrial ROS-induced ROS release in rat cardiomyocytes.

Metabolic Oscillations in Substrate-Deprived Heart Cells

We previously observed that cardiomyocytes subjected to energetic stress by substrate deprivation display spontaneous oscillations (period ∼ 1-3 min) in sarcolemmal currents that were attributed to the cyclical activation and deactivation of ATP-sensitive potassium current (I_K,ATP).³⁴ The activation of I_K,ATP was correlated with, and slightly preceded by, oxidation of the intracellular NADH/NAD⁺ redox couple (Fig. 1A), indicating that large changes in energy metabolism were occurring. In addition to I_K,ATP activation, the amplitude of the Ca²⁺ transient was suppressed, highlighting the global effects of metabolic oscillation on the integrated function of the cell. This was also illustrated by the shortening and suppression of the action potential of myocytes undergoing oscillations in I_K,ATP (Fig. 1B), leading us to propose that this mechanism may be of pathophysiological relevance as a trigger of arrhythmias related to ischemia-reperfusion injury (refs. ^34,58 and see discussion below).

Figure 1.

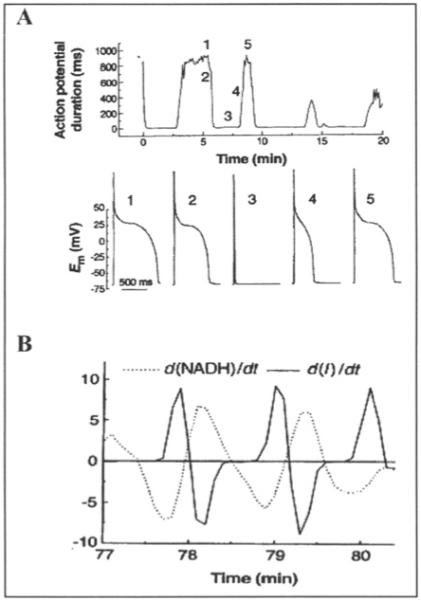
Oscillations of membrane current, excitability and redox pool in substrate-deprived isolated cardiomyocytes. A) Effects of metabolic oscillations on electrical excitability. Upper panel, the action potential duration (90% repolarization time) for a series of action potentials (APs) evoked by brief current injections in a current-clamped cardiomyocyte. Lower panel, selected APs recorded at the time points indicated by the numbers on the upper panel. The brief depolarization in 3 is the stimulus artifact. E_m is the cell membrane potential. B) Phase shift between the first derivative plots of NADH (dashed line) and membrane current (solid line). Reprinted with permission from O’Rourke, Ramza and Marban. Oscillations of membrane current and excitability driven by metabolic oscillations in heart cells. Science 1994; 265(5174):962-966. Copyright © 1994 AAAS.

Since the period and amplitude of the I_K,ATP oscillations were the same in electrically-stimulated or quiescent cells, a Ca²⁺- or plasma membrane potential-dependent source of oscillation was ruled out. On the other hand, manipulation of substrate supply (by increasing glucose availability or inhibiting glycolysis), temporarily uncoupling mitochondria, or photolytically releasing ADP within the cell, strongly influenced the oscillator, suggesting that the underlying driver was metabolism itself. Hence, we proposed that the well-studied glycolytic oscillator, previously demonstrated in cell-free heart extracts, could be the source of oscillation;⁵⁹ however, we could not rule out a mitochondrial origin.

The evidence for the mitochondria being the source of oscillation was subsequently reinforced by demonstrating that the redox potential of mitochondrial flavoproteins rapidly cycles between the oxidized and reduced state in association with depolarization and repolarization of ΔΨ_m.³⁵ Confocal imaging experiments revealed that flavoprotein oxidation could either involve the entire cell or clusters of mitochondria, and that redox waves could propagate from one myocyte to another through the intercalated disc,^35,59 emphasizing the role of synchronization of the mitochondrial network in the response. Moreover, the findings suggested the presence of a putative low molecular weight messenger responsible for the propagation of redox waves. Importantly, it was shown that neither Ca²⁺, nor the permeability transition pore were likely to be involved in the mechanism of the oscillator in substrate-deprived cells. Alternatively, a mechanism involving the mitochondrial benzodiazepine receptor and the inner membrane anion channel (IMAC) was proposed.⁵⁸

The Mitochondrial Oscillator of Heart Cells: The Pathophysiological Domain

Focal Oxidative Stress as a Trigger

Since it was difficult to predict when or how the oscillations in metabolism could be initiated in substrate-deprived cells, the detailed study of the oscillatory mechanism was greatly facilitated by the discovery that they could be triggered by oxidative stress.³⁶ Unlike the earlier studies of direct laser-induced mitochondrial depolarization mentioned in the introduction, we found that focal excitation of a small portion of the mitochondrial network of an adult cardiomyocyte can induce autonomous oscillations in ΔΨ_m and mitochondrial redox potential in the whole cell. This provided a tool for studying the mitochondrial oscillator under controlled and highly reproducible conditions, allowing us to elucidate the mechanism in the context of pathophysiology.³⁶

ΔΨ_m depolarization and local mitochondrial ROS generation were initiated using a two-photon laser to generate free radicals in a small volume of the cell (a “flash”), affecting only a few mitochondria (∼50; Fig. 2A). In contrast to the rapid and sustained effect of the laser within the flashed region (Fig. 2A), the remainder of the mitochondrial network was initially unaffected; however, after a variable latency period (43 seconds on average), ROS levels abruptly increased and Δψ_m collapsed throughout the cell (Fig. 2A, top right). This was followed by synchronized and self-sustained mitochondrial oscillations in ΔΨ_m, NADH, ROS (Fig. 2B),³⁶ as well as reduced glutathione.⁶⁰

Figure 2.

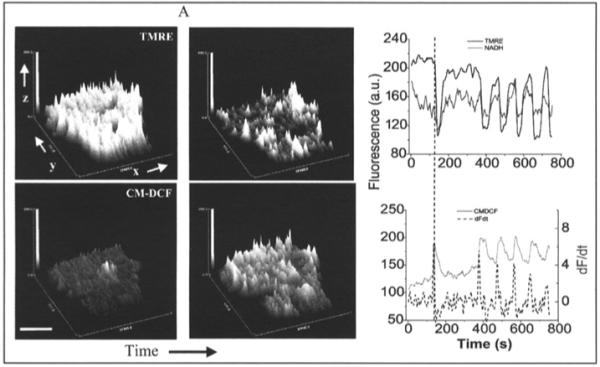
Whole-cell oscillations in mitochondrial metabolism triggered by a local perturbation. A) Top panels, surface plot of mitochondrial membrane potential (ΔΨ_m) in a TMRE-loaded cardiomyocyte during the flash (white arrow, top left panel) showing the local ΔΨ_m depolarization, and the cell-wide ΔΨ_m collapse (top right panel) ∼40s (on average) after the flash. Bottom panels, surface plot of the fluorescence intensity of the ROS-sensitive fluorophore CM-H₂DCF during the flash showing the local (bottom left panel) and the cell-wide (bottom right panel) increase in ROS generation associated with the ΔΨ_m collapse. x,y,z, in the axes of the surface plot correspond to the transversal and longitudinal axes of the cell, respectively, and the fluorescence intensity of TMRE (top panels) or CM-DCF (bottom panels). Bar ∼ 20μm. B) The first cell-wide ΔΨ_m collapse was followed by synchronized oscillations in mitochondrial energetics. Simultaneous recordings of the time course of average whole-cell fluorescence of TMRE and NADH (top panel) and CM-DCF and the derivative of CM-DCF signals (dF/dt, dashed line) (bottom panel). The precise phase relationship between all signals can be clearly appreciated from the vertical reference line drawn. (Panel B is reproduced from Aon, Cortassa, Marban and O’Rourke. J Biol Chem 2003; 278, 44735, with permission of the American Society for Biochemistry and Molecular Biology).

The important role of intracellular ROS in the mechanism of cell-wide oscillations was suggested by the observation that cells showing the oscillatory behavior always had ROS levels exceeding a threshold of ∼20% above baseline. In addition, scavenging ROS with TMPyP (Mn(III)tetrakis (1-methyl-4-pyridil)porphyrin pentachloride), a superoxide dismutase mimetic, or N-acetyl cysteine (NAC), a thiol modifier, decreased ROS levels below threshold and prevented oscillations (Figs. 3C,D).

Figure 3.

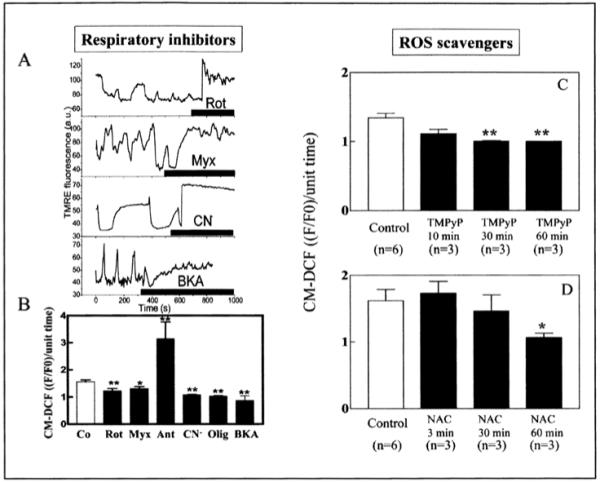
Effect of respiratory inhibitors and ROS scavengers on mitochondrial oscillations. A) TMRE traces of myocytes showing cell-wide mitochondrial oscillations after a laser flash and, subsequently, being subjected to an acute addition of rotenone (15 μM, Rot) (see also B), myxothiazol (5 μM, Myx), NaCN (5 mM, CN^-) or bongkrekic acid (25 μM, BKA) while the image acquisition was briefly paused. After imaging resumed (within ∼3 min of inhibitor addition), the oscillations were abolished. Thick line in each panel indicates presence of inhibitor. B) The effect of the different inhibitors on ROS production as measured by the normalized CM-DCF signal per unit time. Antimycin (Ant) and oligomycin (Olig) concentrations were 6 μM and 10 μg/ml whereas the other inhibitor concentrations were as described in (A). ROS production following a flash was quantified for cells preincubated in the presence of each inhibitor. Under these conditions, the cells did not exhibit oscillations after the laser flash. *p < 0.05, **p < 0.01 vs. control. C) The SOD mimetic TMPyP (250 or 500 μM) or (D) the ROS scavenger N-acetyl-L-cysteine (NAC, 4 mM) was acutely added to myocytes. Prolonged incubation (1 h) with the scavengers completely suppressed the synchronized oscillations.³⁶ The control corresponds to cells exhibiting cell-wide mitochondrial oscillations before addition of the scavenger. The time-dependent effect of TMPyP and NAC to suppress oscillations correlated with a significant decrease of ROS production to basal levels. Panels A and B are reproduced from Aon, Cortassa, Marban and O’Rourke (2003) J. BioI. Chem. 278, 44735, with permission of the American Society for Biochemistry and Molecular Biology © 2003).

Mitochondrial Respiration as the Source of ROS Production

Acute application of mitochondrial electron transport inhibitors could immediately stop the oscillations in ΔΨ_m and could also prevent the accumulation of ROS to the threshold for depolarization (Fig. 3A,B). This experimental evidence directly implicated mitochondrial respiration as the source of ROS in the oscillatory mechanism. Thus, we next addressed the question of which site(s) of the electron transport chain were responsible for the ROS produced. Our findings, obtained in living cardiomyocytes under quiescent conditions and unrestricted access to oxygen, pointed to complex III as the source of superoxide anion (O₂^.-). Our attempts to halt respiration with inhibitors of complex I (rotenone) and complex IV (cyanide) caused a reduction in ROS, indicating that ROS generation did not correspond to a highly reduced, high ΔΨ_m state, which can cause ROS prodution in isolated mitochondria. At the level of complex III, O₂^.- production was enhanced only when ubisemiquinone accumulated in the presence of antimycin A, but not when the oxidation of ubiquinol to ubisemiquinone and electron transfer to the FeSIII center of complex III was prevented with myxothiazol.³⁶

The main site of ROS production in the respiratory chain of living cells is unclear see also Appendix in (ref. ⁶⁰) for a detailed discussion of this topic); however, in isolated mitochondria, there is evidence for ROS production by several different sites. Depending upon conditions, superoxide can be generated either at complex I or complex III (from the Q cycle). ROS production from complex I appears to be favored at high ΔΨ_m and highly reduced redox potentials (>-390mV), usually achieved when respiration is inhibited (e.g., with rotenone). ROS production from complex III in isolated mitochondria is promoted by treatment with antimycin A, which promotes the accumulation of ubisemiquinone on the outer aspect of the mitochondrial inner membrane. We showed that this treatment can cause massive ROS accumulation and the collapse of Δψ_m in myoeytes subjected to the flash protocol, complementing the evidence using inhibitors that complex III is the main source of ROS in intact cells. This model would be consistent with the proportionality between complex III-derived ROS production and respiration reported previously.

The key question is whether ROS production is mainly controlled by ΔΨ_m or flux through the electron transport chain. Cyanide inhibition of the respiratory flux and, concomitantly, of ROS levels, suggested that electron transport was necessary for mitochondrial ROS production. Taking mitochondria to state 4 and slowing down the electron flux should also decrease ROS production. This was done in our experimental system by inhibiting the F₁F₀ ATPase with oligomycin, or the adenine nucleotide translocator with bongkrekic acid (BKA). Both inhibitors decreased ROS levels below threshold and suppressed oscillations pointing out that mitochondrial electron transport is necessary for ROS production and, consequently, oscillations.

The Role of Mitochondrial Ion Channels in the Oscillatory Mechanism

The asymmetry of the ΔΨ_m depolarization-repolarization cycle is consistent with the behavior exhibited by relaxation oscillators that possess slow and fast components.⁶⁰ The sudden depolarization phase of ΔΨ_m during the oscillations suggests that an energy dissipating ion channel is opening, causing rapid uncoupling of oxidative phosphorylation.

An obvious candidate for rapid depolarization of ΔΨ_m was the PTP, which can be activated by various toxic agents or metabolic changes associated with necrosis and/or apoptosis. Ca²⁺ overload is one cofactor in the opening of the PTP (see ref. 61,62 for reviews) and a model of Ca²⁺-induced Ca²⁺ release from the mitochondrial matrix through the PTP has been proposed.

We investigated whether or not the PTP and/or Ca²⁺ was involved in the mechanism of whole-cell ΔΨ_m oscillation. Several lines of evidence ruled out both the PTP and Ca²⁺ as playing a role in the mitochondrial oscillations observed in heart cells. With regard to Ca²⁺, as we have previously reported: (i) the myocytes were studied under quiescent, minimally Ca²⁺-loaded conditions, and no sarcomere shortening was evident; (ii) suppression of sarcoplasmic reticulum (SR) or mitochondrial Ca²⁺ handling did not influence flash-induced mitochondrial oscillations; (iii) extensive buffering of intracellular Ca²⁺ with 1 mM EGTA did not affect flash-induced oscillations. The possible contribution of the PTP was ruled out by the following evidence: (i) cyclosporin A (CsA) did not block the transitions, and (ii) small (600 MW) fluorophores were not lost from the mitochondrial matrix upon depolarization. Bongkrekic acid inhibited the oscillations and stabilized ΔΨ_m. This compound is often used as a PTP blocker because it is assumed that the adenine nucleotide translocase is a component of the PTP. However, since the effects of BKA were similar to those of other inhibitors of electron transport such as cyanide, our interpretation was that this compound’s main effect, to inhibit the distal electron transport chain, causes a decrease in mitochondrial ROS production by putting the mitochondria in state 4.³⁶

Other ion channels have been described on the mitochondrial inner membrane, and could be candidates for fast mitochondrial depolarization. An IMAC was described in isolated mitochondria and was shown to be inhibited by cationic amphiphiles including peripheral (mitochondrial) benzodiazepine receptor (mBzR) ligands.^63-65 Subsequently, single channel patch-clamp studies of mitoplasts have provided evidence that anion channels are present on the inner membrane, the most common being the outwardly rectifying 108 pS (or “centum-picosiemen”) anion channel which is inhibited by mBzR antagonists. We showed that PK11195, an isoquinoline carboxamide mBzR ligand, could acutely inhibit mitochondrial ΔΨ_m oscillations, initiated either by substrate deprivation or laser flash, in a reversible manner. Mitochondrial oscillations were also abolished by a structurally different mBzR ligand, 4′-chlorodiazepam (4′Cl-DZP) (Ro5-4864) or by the anion transport inhibitor DIDS.^36,58 These inhibitors prevented ROS accumulation in the mitochondrial network, but actually potentiated ROS accumulation in the small laser-flashed region of the cell, leading to the proposal that IMAC might also be an efflux pathway for superoxide anion from the matrix, since O₂^.- is membrane impermeable. Moreover, induction of mitochondrial ΔΨ_m depolarization by FGIN-1-27, an agonist that binds selectively to the mBzR, reinforced the idea that this receptor, which is thought to be present on the mitochondrial outer membrane, may be modulating IMAC. Taken together, the data are consistent with a role for IMAC, rather than PTP, in both ΔΨ_m depolarization and O₂ efflux, forming the mechanistic basis for our theoretical model of the mitochondrial oscillator.

The Theoretical Approach

An Integrated Computational Model of the Mitochondrial Oscillator

An integrated model of mitochondrial energetics and Ca²⁺ handling was extended to describe the key features of the proposed mechanism of mitochondrial oscillations based on our experimental findings.³⁶ These included incorporating a shunt of electrons of the respiratory chain toward the generation of O₂^.-, a ROS scavenging system, and an outwardly rectifying IMAC modeled after the centum pS channel. The normal anion permeability of IMAC would permit the passage of O₂^.- from the matrix to the cytoplasmic side of the inner membrane. In addition, the IMAC opening probability was assumed to be increased by O₂^.- at an external site. The scheme of the integrated model is shown in (Fig. 4A).

Figure 4.

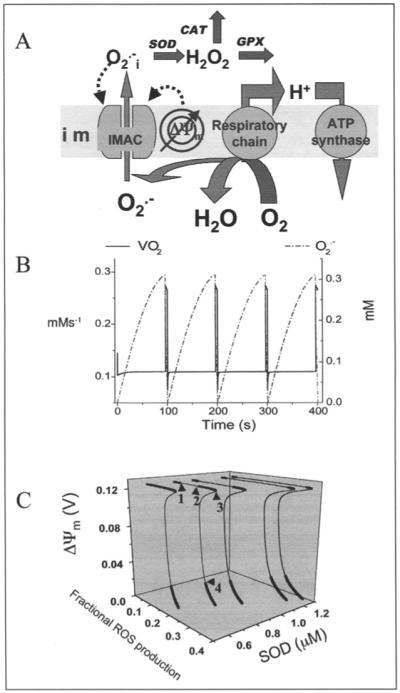
Model of mitochondrial energetics coupled to ROS production, transport, and scavenging. A) The IMAC and the ROS scavenging system were incorporated into an integrated model of mitochondrial energetics and Ca²⁺ handling.⁶⁰,⁷³ The model postulates that superoxide anion in the mitochondrial matrix (O₂^.-_m) is transported through the IMAC whose opening probability is activated by cytoplasmic (intermembrane) superoxide anion (O₂^.-_i). The integrated computational model of mitochondrial energetics incorporates IMAC, ROS production, and ROS scavenging. See (ref. ⁶⁰) for a description of the parameters utilized in the simulations. B) Simulation of the 100s period oscillations observed experimentally (see Fig. 2) using the integrated computational model of mitochondrial energetics with incorporated IMAC, ROS production, and ROS scavenging (panel A). Represented are the oscillations in O₂^.-_m, and the O₂ consumption flux. See (ref. ⁶⁰) for a description of the parameters utilized in the simulations. C) Bifurcation diagram of ΔΨ_m as a function of ROS production and scavenging. The dynamic behavior of the computational model shows an upper branch of steady states in which ΔΨ_m is predominantly polarized, and a lower branch, in which ΔΨ_m is mainly depolarized. Transitions between both branches happen at arrowheads 3 and 4. Thick lines indicate domains of stable steady-state behavior whereas thin lines denote either unstable or oscillatory states. A stable oscillatory domain, embedded within the upper branch, emerges as SOD concentration increases. Arrowheads 1 and 2 in the upper branch indicate Hopf bifurcations delimiting the oscillatory region (thin line). Key to abbreviations: im, inner mitochondrial membrane; IMAC, inner membrane anion channel; CAT, catalase; SOD, Cu,Zn superoxide dismutase; GPX, glutathione peroxidase. (Panels A and C are reproduced from Cortassa, Aon, Winslow and O’Rourke (2004) Biophys. J. 87, 2060, with permission of the Biophysical Society © 2004).

Model simulations show the ability to reproduce the oscillatory period and the phase relationship between ΔΨ_m and NADH observed experimentally (see Fig. 2B). According to the model, a burst in cytoplasmic ROS accompanies ΔΨ_m depolarization as a result of a mixed process of accelerated O₂^.- production (due to an increase in the rate of mitochondrial respiration during uncoupling) and a transient increase in O₂^.- release (as a result of the self-amplifying effect of IMAC opening on anion transport (Fig. 4B)). Thus, a pulse of cytoplasmic O₂^.-_i is released when the buffering capacity of superoxide dismutase (SOD) is exceeded. This pulse subsides because of several factors, including (i) a decrease in O₂^.- efflux when the electrochemical driving force for anions is diminished by ΔΨ_m depolarization, (ii) an increase in SOD-mediated O₂^.-removal, and (iii) a decrease in respiration as the NADH is consumed.

The model was able to reproduce the major experimental findings, including the requirement for ROS to cross a threshold to trigger fast ΔΨ_m depolarization, the suppressive effect of inhibitors of the electron transport chain, ANT and the F₁F_O ATPase on ROS production and ΔΨ_m oscillation, the effects of anion channel inhibitors, and the sensitivity of the oscillator to the levels of ROS scavengers. The model also predicted oscillations in reduced glutathione that could be demonstrated experimentally.⁶⁰

Predicting the High Frequency Domain of the Mitochondrial Oscillator

Stability analysis of the model confirmed the presence of Hopf bifurcations, a signature of the existence of limit cycles, visualized as sustained oscillations (Fig. 4C). The bifurcation diagrams have the typical S-shape that describes the behavior of systems exhibiting bistability, and show an unstable region (thin lines) between the upper (polarized) and lower (depolarized) branches of steady states (thick lines in Fig. 4C). This diagram illustrates the importance of the balance between mitochondrial ROS generation and ROS buffering since the oscillatory domain, flanked by Hopf bifurcations, appears within the upper branch of the curve as the concentration of ROS scavenger increases. This domain gradually expands at higher SOD concentrations (from left to right in Fig. 4C) until the limit between the upper or lower branch, where the model behavior changes precipitously and ΔΨ_m jumps from polarized to depolarized steady states or vice versa (see Fig. 4C).

At each oscillatory cycle, the computational model predicts a burst of respiration (Fig. 4B) triggered by the rapid membrane uncoupling and the concomitant oxidation of the mitochondrial NADH pool together with the rapid release of O₂^.- to the mitochondrial intermembrane space (Fig. 4B).

An intriguing finding in the model simulations was that the frequency and amplitude of the stable oscillations could be modulated over several orders of magnitude (milliseconds to hours) by simply changing (as little as) one parameter, e.g., the SOD concentration. From the physiological point of view, the observation that fast oscillations in ROS could be generated by the mitochondria with minimal energetic consequences (i.e., only μV to mV changes in ΔΨ_m) led us to propose that the ROS-dependent mitochondrial oscillator could represent a frequency- and/or amplitude-modulated signaling mechanism that could connect bioenergetics to ROS-activated signal transduction pathways, including those responsible for regulating gene transcription.⁶⁶

These computational studies motivated experiments to determine if small amplitude fluctuations in ΔΨ_m could be detected in cardiomyocytes under physiological conditions, described in the next section.

The Mitochondrial Oscillator in the Physiological Domain

As mentioned in the Introduction, mitochondria in various cell types, including neurons, smooth muscle cells and cardiomyocytes, have been observed to undergo spontaneous transient depolarizations or flickers of ΔΨ_m. These observations suggest that individual, or small clusters of mitochondria may be able to oscillate autonomously in intact cells. However, the results discussed above indicate that pathological conditions appear to induce synchronized, coupled oscillations across the mitochondrial network of the cardiac myocyte. The computational studies of the mitochondrial oscillator suggested two fundamentally different views to explain this self-organization process for large amplitude oscillations in ΔΨ_m. The first possibility was that mitochondria in the “normal” state are in a dynamic steady-state and metabolic stress pushes the system towards a bifurcation point and oscillation. The second possibility was suggested by the parametric analysis, which showed that low-amplitude, high-frequency oscillations were possible. We hypothesized that if mitochondria behaved as high-frequency oscillators under physiological conditions, small fluctuations in ΔΨ_m may be detectable by correlation analysis of long time series recording of ΔΨ_m.

In the absence of metabolic stress, cardiomyocytes loaded with tetramethylrhodamine methyl esther (TMRM), a fluorescent reporter of mitochondrial membrane potential, display stable ΔΨ_m for more than an hour. Using two-photon laser scanning fluorescence microscopy, cells were imaged every ∼100ms and the average fluorescence for the whole cell was calculated (Fig. 5). By applying Relative Dispersional Analysis (RDA) and Power Spectral Analysis (PSA) to the data, we found that collectively, cardiac mitochondria behave as a highly correlated network of oscillators.⁶⁶ According to RDA, the fluorescence time series exhibit long-term memory quantitatively characterized by an inverse power law with a fractal dimension, D_f, of approximately 1.0. This behavior, characteristic of self-similar fractal processes, is distinct from processes without memory that show completely random behavior (white or brown noise), which are characterized by an exponential (Poisson) law with a slope corresponding to D_f=1.5.

Figure 5.

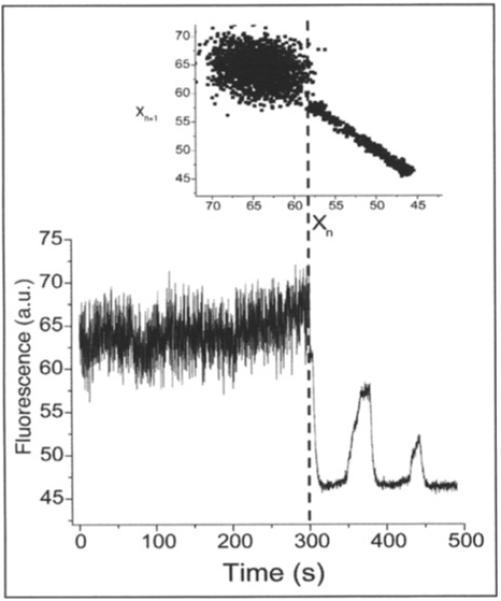
Physiological and pathophysiological behaviors of the mitochondrial network in heart cells in the presence of glucose. The main panel shows the time series of TMRM fluorescence of a freshly isolated ventricular cardiomyocyte, imaged by two photon microscopy (150ms time resolution). Before the mitochondrial network reaches criticality,⁷⁴-⁷⁶ the ΔΨ_m (as measured by TMRM) oscillates at high frequencies and small amplitudes. After criticality, the network behavior evolves into “pathophysiological” behavior characterized by low-frequency, high-amplitude oscillations.³⁶,⁶⁰ The inset shows a return plot of the time series, the dashed line separating the richness of high frequency-low amplitude oscillations present in the physiological as opposed to the low frequency-high amplitude oscillations present in the pathophysiological regime. (Reproduced from Aon, Cortassa and O’Rourke (2006) Biophys. J. 91, 4317-4327, with permission of the Biophysical Society © 2006).

Self-similar scaling was also revealed by PSA after applying Fast Fourier Transform (FFT) to the TMRM fluorescence time series. The power spectrum followed an homogenous inverse power law of the form 1/f^β with with β∼ 1.7. These results pointed out that mitochondrial oscillations exhibit a broad frequency distribution spanning at least three orders of magnitude (from milliseconds to a few minutes).

The results indicate that collective behavior of the mitochondrial network is a statistically fractal, self-similar, process characterized by a large number of frequencies in multiple time scales, rather than an inherent “characteristic” frequency. We propose that these mitochondrial oscillators are weakly coupled by low levels of mitochondrial ROS in the physiological state but that an increase in ROS production under metabolic stress can reach a threshold that results in strong coupling through mitochondrial ROS-induced ROS release, and organization of the network into a synchronized cluster spanning the whole cell. A dominant low-frequency high-amplitude oscillation ensues.

Spatial Aspects: ROS and Mitochondrial Criticality

The transition between the physiological and pathophysiological domains of mitochondrial oscillation is a clear example of emergent self-organization in both time (limit cycle oscillation) and space (synchronization across the mitochondrial network) (Fig. 5). With respect to the spatial organization, we have applied percolation theory to explain how a local interaction among mitochondria organized in a lattice can lead to a widespread change in the state of energization of the system. The mitochondria of the heart cell are particularly amenable to this analysis because they are organized almost as a cubic lattice, with a spacing of ∼0.2-1 μm between elements. In two-dimensional images of a single focal plane of the myocyte, we measured ΔΨ_m and ROS accumulation after a local laser flash, and determined the percentage of the mitochondria showing a ROS signal above a certain threshold level (20% above baseline fluorescence) as a function of time after the flash (Fig. 6A). At the point in time just before the first cell-wide collapse of ΔΨ_m, which we referred to as “criticality”, we found that ∼60% of the mitochondrial network had ROS levels at or near threshold (Fig. 6A), and this cluster of mitochondria spanned the whole cell (i.e., a “spanning cluster” was evident) (Fig. 6B). This number is very close to the theoretical prediction for systems at a percolation threshold (p_c = 0.59).^67,68 Moreover, fractal analysis of the shape of the spanning cluster was also consistent with percolation theory.⁶⁹

Figure 6.

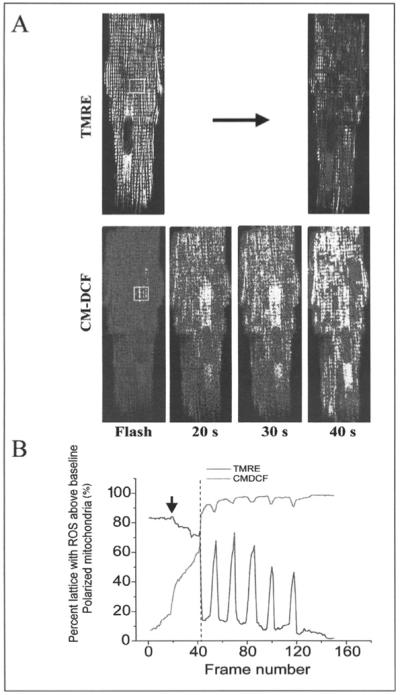
Time course of the mitochondrial cluster formation. A) Sustained oscillations in ΔΨ_m happening beyond criticality are depicted. Arrow indicates the timing of the flash. B) At criticality, a cell-wide ΔΨ_m depolarization (TMRE, top right) occurs in a cluster encompassing about 60% of the mitochondria with ROS levels above baseline (CM-DCF, bottom). Adapted from Aon, Cortassa and O’Rourke (2004) Proc Natl Acad Sci USA 1018, 4447).

The significance of this characterization of the mitochondrial network as a percolation process is that it helps to explain why ΔΨ_m depolarization occurs in a synchronized manner throughout the cell and where it will occur. Only those mitochondria belonging to the spanning cluster take part in the global limit cycle oscillation, explaining why some mitochondria appear to resist oscillation even though they are surrounded by depolarized mitochondria (Fig. 2A). Furthermore, it explains why there does not seem to be a single point in the cluster (for example, the flashed area) from which each cycle originates—the system at criticality is susceptible to small perturbations anywhere in the spanning cluster to initiate a transition.

With faster time resolution, or by slowing the kinetics of the oscillator (e.g., with submaximal oligomycin concentrations), the ΔΨ_m depolarization wave can often be resolved. This wave travels at a speed of 22 μm/s, corresponding to a total time for global depolarization of about 4s (see Fig. 6B) (considering an average myocyte length of 100 μm), in agreement with the experimental data. Although the ΔΨ_m depolarization is global (Fig. 6B), the interaction between mitochondria is local. The short lifetime of the O₂^.- radical and the presence of fast scavenger systems prevents long range diffusion, but in our mechanistic model, O₂^.- liberated from a mitochondrion in the spanning cluster must only diffuse to its neighbors. The second criterion is that the neighbor must also be a member of the spanning cluster (i.e., be close to the threshold for depolarization). According to percolation theory, a p_c of 0.59 corresponds to a coordination number of four, again emphasizing that each mitochondrion is influencing its nearest neighbors in the network. These results also explain why the speed of the depolarization wave is faster than it would be if sustained by diffusion of the chemical messenger (O₂^.-) alone.

From Mitochondrial Dynamics to Whole Heart Arrhythmias

Coupling of Mitochondrial Oscillations to Cellular Electrical Excitability

The early studies of cardiac metabolic oscillations showed that they have a profound effect on the excitability and Ca²⁺ handling properties of the cardiac cell. The oscillatory uncoupling of mitochondria depletes cellular ATP levels and drives the activation of ATP-sensitive K⁺ (K_ATP) channels in the sarcolemma. This will, in turn, produce cyclical changes in the action potential of the cardiomyocyte (Fig. 1A) and this heterogeneity was proposed to be a possible source of ischemia-related arhythmias.

Using the laser flash-induced oscillation, we demonstrated that the action potential duration was tightly coupled to the mitochondrial energetic state. At the onset of ΔΨ_m depolarization, the action potential rapidly shortens and the cell quickly becomes inexcitable; this is followed by the parallel recovery of both the metabolic and electrical signals (Fig. 7).^36,70 Stabilizing ΔΨ_m by the abovementioned interventions, such as inhibition of the mBzR, not only inhibits the oscillations in mitochondrial variables, but also stabilizes the action potential (Fig. 7). Action potentials were strongly affected only during the synchronized whole-cell mitochondrial oscillations and not when single, or small clusters of, mitochondria were depolarized.

Figure 7.

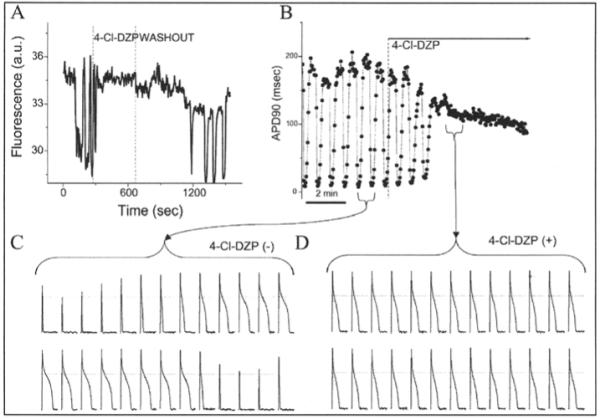
Blockade of mitochondrial oscillations and stabilization of the cellular action potential (AP) by 4′-Cl-DZP. Freshly isolated cardiomyocytes loaded with TMRM (100 nM) at 37°C, where patched and APs were recorded under whole-cell current-clamp conditions on the stage of the microscope. A) This panel shows the reversible effect of acutely added 4′-Cl-DZP (32 μM; between dashed lines) on mitochondrial ΔΨm oscillations that resume after washout of the MBzR antagonist. B) Mitochondrial oscillations in ΔΨm and the sarcolemmal action potential duration (APD) were triggered after a highly localized laser flash (3 min before the train of oscillating APDs shown in this panel). APs evoked by brief current injections were recorded during the oscillations. During a synchronized cell-wide depolarization-repolarization cycle, the AP shortens in synchrony with fast mitochondrial depolarization.³⁶ C) During the APD oscillations, the cell becomes inexcitable when ΔΨm is fully depolarized (remaining upward spikes are from the stimulus only). D) After addition of 64μM 4′-Cl-DZP, a stable AP is restored and ΔΨm oscillations are suppressed. (Reproduced from Akar, Aon, Tomaselli and O’Rourke (2005) J. Clin. Invest. 115, 3527, with permission of the American Society for Clinical Investigation © 2005).

The Mitochondrial Origin of Post-Ischemic Arrhythmias

We have described how the failure of individual mitochondria can scale to involve whole-cell bioenergetics and the integrated function of the cardiac myocyte. Next, we tested if a similar mechanism can occur in the whole heart and contributes to ischemia-related arrhythmias.

After ischemic injury, the early reperfusion phase would be expected to favor mitochondrial criticality since a burst of ROS production and antioxidant depletion are known to occur.⁷¹ Optical mapping studies of isolated perfused guinea-pig hearts subjected to 30 minutes of ischemia demonstrated that persistent ventricular tachycardia and/or fibrillation occurs within minutes of reperfusion (Fig. 8). We used this experimental system to determine if the mBzR antagonist 4′Cl-DZP could prevent post-ischemic arrhythmias, presumably by stabilizing ΔΨ_m. 4′Cl-DZP had no effect on epicardial action potentials or myocardial conduction velocity in normoxic hearts. Global ischemia induced, within minutes, shortening of the action potential and eventual failure of excitability in untreated controls, but this effect was blunted dose-dependently in hearts perfused with μM concentrations of 4′Cl-DZP.⁷⁰ Most dramatically, the tachyarrhythmias upon reperfusion were prevented (Fig. 8). By comparison, CsA, the PTP inhibitor, had no effect on ischemic electrical parameters, and a delayed and incomplete effect on reperfusion arrhythmias (Fig. 8).

Figure 8.

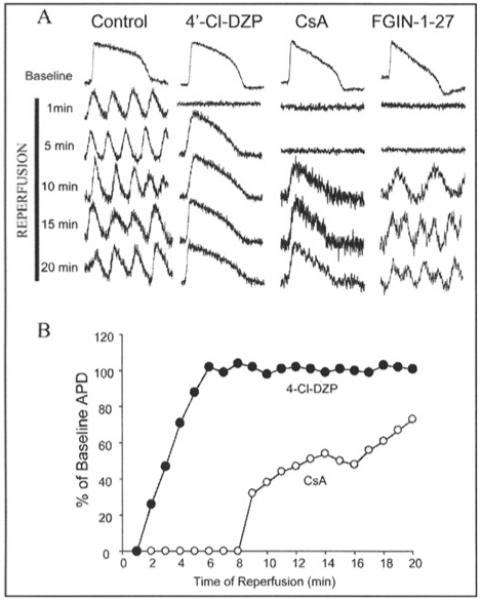
Post-ischemic AP recovery and arrhythmias. A) Representative APs during recovery upon reperfusion in control, 4′-Cl-DZP-, CsA-, and FGIN-1-27-treated hearts. B) Plot of the recovery of APD upon reperfusion normalized to the baseline APD before ischemia in 4′-Cl-DZP- and CsA-treated hearts. (Reproduced from Akar, Aon, Tomaselli and O’Rourke (2005) J. Clin. Invest. 115, 3527, with permission of the American Society for Clinical Investigation © 2005).

The mBzR ligand FGIN-1-27, which enhanced mitochondrial depolarization in single cell studies, shortened the time to inexcitability and conduction block in ischemic hearts, but had no effect in normoxic hearts.

Taken together, the findings supported the idea that loss of ΔΨ_m during ischemia and early upon reperfusion, is due to the opening of IMAC, and can be inhibited by mBzR antagonists.⁷⁰ This event is coupled with activation of sarcolemmal K_ATP channels, creating spatial and perhaps temporal action potential heterogeneity that can be a substrate of ventricular reentry.³⁶ PTP activation, on the other hand, occurs with some delay after reperfusion.

From these results, we have postulated that the failure of mitochondrial energetics can create “metabolic sinks” in the reperfused myocardium that may constitute sites of functional conduction block. This mechanism is distinct from (but could be occurring in parallel with) blocks caused by the closure of gap junctions between cells, in that the current supporting a wave of depolarization would be annihilated by the metabolic sink; whereas with gap junctional block, an increase in voltage at the wave front could result in propagation via a bypass path (i.e., propagation has a high safety factor ref. 72).

Conclusions

Mitochondria are capable of synchronized oscillations in a number of variables (e.g., volume, ΔΨ_m, redox, etc.) when studied in suspension or when they are organized as a network in intact cells. In part, this stems from the fact that oxidative phosphorylation is a complex nonlinear system which involves ion movements, stored electrochemical gradients, and a semi-permeable membrane barrier to carry out energy transduction. The possibility for charging and discharging the storage element is a common feature of relaxation oscillators in electrical circuits (e.g., a resistor-capacitor circuit) and in biological oscillators such as pacemaker cells in the heart and brain, but the mitochondrial oscillator is unique in terms of its inherent frequency response and amplitude modulation.

A primary ROS-dependent mitochondrial oscillator in intact cardiac cells has been characterized using an integrated experimental and theoretical approach. The mechanism fundamentally determines the cell’s response to metabolic stress (whether in a steady polarized or depolarized parametric domain or an oscillatory domain) that scales from the mitochondrion to the whole heart. Moreover, we show that under physiological conditions cardiac mitochondria function as a network of coupled oscillators with a broad range of frequencies. ROS weakly couples mitochondria under normal conditions but becomes a strong coupling messenger when, under oxidative stress, the mitochondrial network attains criticality. Mitochondrial criticality is achieved when a threshold of ROS is overcome and a certain density of mitochondria forms a cluster that spans the whole cell. Under these conditions, the slightest perturbation triggers a depolarization wave throughout the cell. Although locally, mitochondria depolarize in response to a ROS-induced ROS release mechanism, the fact that mitochondria outside the spanning cluster resist depolarization argues against a simple regenerative wave. The mitochondria are also required to be near threshold and belong to a percolation cluster. This requirement means that the spatial organization of mitochondria, which is very different in various cell types, will play a major role in the group dynamics of mitochondrial function. Neighbor-neighbor interaction of mitochondria, and thus functional synchronization, will be most prevalent in closely packed networks and less likely in cells with elongated and widely-spaced mitochondria.

While the focus of this chapter has been on the ROS-dependent mitochondrial oscillator, other mitochondrial oscillatory mechanisms are possible, and may coexist in excitable cells like the cardiomyocyte that contain multiple oscillatory mechanisms. Spontaneous pacemaker firing and oscillations in sarcoplasmic reticulum Ca²⁺ release could also entrain oscillation in mitochondrial function, and a divalent cation-activated intrinsic mitochondrial oscillator may also exist, although it has not been demonstrated in intact cells. Cause and effect is often hard to determine when multiple oscillators are present—this is one reason why the mechanism of oscillatory insulin release from pancreatic β cells has still not been completely resolved, although a clear contribution from glycolysis and Ca²⁺ handling has been proven. Similarly, neonatal cardiac myocytes display alternating periods with and without action potentials, in association with oscillations in ΔΨ_m. These oscillations were correlated with the intermittent activation of K_ATP channels; however, no clear evidence of an intrinsic metabolic oscillator was established.

A connection between the ROS-dependent mitochondrial oscillator and earlier oscillators triggered by enhanced ionic flux across the inner membrane has not been made. Interestingly, in the initial description of oscillations in mitochondrial ionic fluxes by Chance and Yoshioka, these investigators added 1.5-3 mM H₂O₂ and catalase to their mitochondrial suspensions in order to keep a constant supply of oxygen. These conditions could have contributed to oxidative stress in the preparation that could be related to the mitochondrial oscillations observed in living heart cells. Similarly, the role of ROS in divalent-mediated mitochondrial oscillation has not been explored, although the uncoupling effect of Ca²⁺ could, in theory, enhance mitochondrial ROS production according to our view of the relationship between respiration and mitochondrial ROS production at complex III. ROS-independent mitochondrial oscillations have also been described in isolated mitochondria, but this mechanism has not been demonstrated in intact cells.

The evidence that the mitochondria of the cardiac cell behave as a network of oscillators under physiological conditions raises a number of interesting questions to pursue in future investigations. First, while many control systems that are required to respond quickly to changing conditions have been noted to operate close to instability, the emergence of a dominant low-frequency mode associated with pathology in the myocyte begs the question of how close to this instability the network normally operates. Second, the accepted evidence that many signal transduction pathways are ROS-dependent has led us to propose that frequency- and/or amplitude-modulated mitochondrial ROS signals could link the bioenergetic state to acute or long-term (transcriptional) responses in the normal course of energy supply and demand matching in the cell. Mitochondrial ROS bursting during ischemia could also be relevant to the mechanism of ischemic preconditioning or cell injury in the reperfused heart.

Another speculative role for mitochondrial oscillation is the possibility that it serves as a potential intracellular timekeeper. This notion is encouraged by the computational studies that show that the period of the oscillator could be modulated over a broad range of time scales from milliseconds to hours by varying only one parameter. This observation, together with the long-term temporal correlation and power law dependence exhibited by the mitochondrial network could, theoretically, allow a change in one time scale to be felt across the whole frequency range.