Kinetic modeling of Toxoplasma gondii invasion

Abstract

The phylum Apicomplexa includes parasites responsible for global scourges such as malaria, cryptosporidiosis, and toxoplasmosis. Parasites in this phylum reproduce inside the cells of their hosts, making invasion of host cells an essential step of their life cycle. Characterizing the stages of host-cell invasion, has traditionally involved tedious microscopic observations of individual parasites over time. As an alternative, we introduce the use of compartment models for interpreting data collected from snapshots of synchronized populations of invading parasites. Parameters of the model are estimated via a maximum negative log-likelihood principle. Estimated parameter values and their 95% confidence intervals (95% CI), are consistent with reported observations of individual parasites. For RH-strain parasites, our model yields that: 1) penetration of the host cell plasma membrane takes 26 sec (95% CI: 22-30 sec), 2) parasites that ultimately invade, remained attached 3 times longer than parasites that eventually detach from the host cells, and 3) 25% (95% CI: 19-33%) of parasites invade while 75% (95% CI: 67-81%) eventually detach from their host cells without progressing to invasion. A key feature of the model is the incorporation of invastion stages that cannot be directly observed. This allows us to characterize the phenomenon, of parasite detachment from host cells. The properties of this phenomenon would be difficult to quantify without a mathematical model. We conclude that mathematical modeling provides a powerful new tool for characterizing the stages of host-cell invasion by intracellular parasites.

1. Introduction

We present a model for characterizing invasion by the fast-replicating tachyzoite stage of the obligate intracellular parasite Toxoplasma gondii. Obligate intracellular parasites are organisms that must reproduce inside the cells of their hosts. The rewards of this lifestyle include access to host cell machinery, evasion of the immune system, and scavenging of nutrients and energy. Organisms that exploit this lifestyle are found among all major groups of pathogens, including viruses, bacteria, protozoa, fungi and helminthes (Andrade & Andrews, 2005, Despommier, 1998, Mendes-Giannini et al, 2005, Pizarro-Cerda & Cossart, 2006, Sibley, 2004, Sieczkarski & Whittaker, 2005). To gain access to intracellular resources obligate intracellular pathogens cross their host cell's plasma membrane using a variety of pathogen-specific mechanisms (Andrade & Andrews, 2005, Carruthers & Boothroyd, 2007, Pizarro-Cerda & Cossart, 2006, Sieczkarski & Whittaker, 2005, Sieczkarski & Whittaker, 2005, Soldati et al, 2004).

T. gondii is a protozoan of the phylum Apicomplexa, which includes the agents of numerous diseases of significant medical and veterinary importance such as malaria (Plasmodium spp.), cryptosporidiosis (Cryptosporidium spp.), and toxoplasmosis (T. gondii). A detailed understanding of the invasion mechanism used by apicomplexan parasites could lead to improved methods for controlling or treating these diseases.

Invasion by apicomplexan parasites is a complex, multi-stage process involving initial attachment to a host cell, followed by sequential discharge of specialized secretory organelles, leading to penetration and traversal of the host's plasma membrane, culminating in formation of the parasitophorous vacuole and resealing of the plasma membrane (Carruthers & Boothroyd, 2007). T. gondii is a particularly useful model organism for the Apicomplexa due to its genetic and biochemical tractability (Kim & Weiss, 2004), its well-defined cellular structure (Dubey et al, 1998), and the ability to achieve synchronous invasion (Kafsack et al, 2004).

T. gondii invasion involves a series of highly coordinated events. Initial attachment through one or more of the parasite's abundant surface proteins (Dzierszinski et al, 2000, Jacquet et al, 2001) leads to tighter apical attachment upon release of proteins from secretory granules called micronemes. At least one of these microneme proteins associates with other proteins released from the neck of a second set of secretory organelles, the rhoptries, to the form of a structure called the moving junction (Alexander et al, 2005, Mital et al, 2005). During penetration this specialized ring of tight adhesion is translocated distally from its site of formation at the parasite's apex, thereby propelling the parasite into the host cell through the ring (Carruthers & Boothroyd, 2007). Simultaneously, rhoptry bulb contents are secreted and the parasitophorous vacuole forms, enveloping the invading parasite in a non-fusogenic membrane, thereby separating it from the host cell cytosol (Mordue et al, 1999a, Mordue et al, 1999b).

While a detailed qualitative molecular model has been proposed (Carruthers & Boothroyd, 2007), the complexity of the molecular processes involved has so far precluded the development of a quantitative model. A more tractable approach, which we take here, is to divide the invasion processes into phenomenologically defined stages, and transitions between the stages.

2. Materials and Methods

In this section we describe an experimental protocol and a mathematical technique for interpreting the experimental results in terms of transition rates between distinct stages of invasion. Essentially, we monitor in parallel, synchronized populations of invading parasites. Invasion is halted in each population at end points that are sequential in time. At each end-point, a two-color staining protocol permits us to make a census of the number of parasites that are inside, outside, or penetrating the host plasma membrane. These measurements are combined with the aid of the model, to obtain values for the transition rates between invasion stages.

2.1. Synchronized Invasion Kinetics Experiments

A synchronized invasion kinetics experiment uses a multi-well plate format to probe the kinetics of a synchronized population of invading parasites. Each well generates data for a single time-point. Invasion is halted in different wells at successive times. Normalized measurements from successive invasion times are subsequently assembled into a single time series. Figure 1 illustrates the protocol required to process a single well. Six steps are required to process each well.

Figure 1.

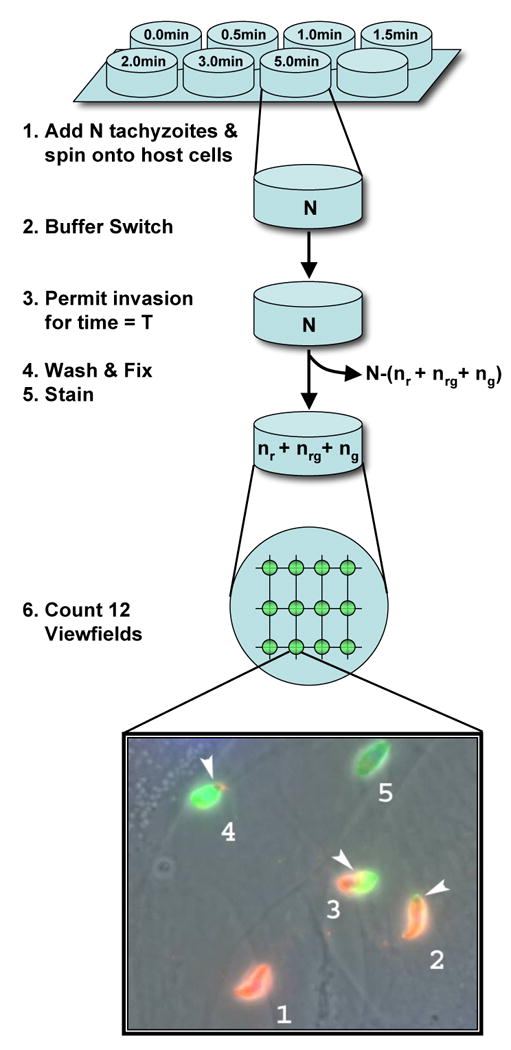
Schematic of well processing. Initially N parasites are placed in a well in a non-permissive buffer. Invasion is initiated at time t=0 by exchanging non-permissive buffer for permissive buffer. The number of parasites removed with the non-permissive buffer (ΔN) is counted and the number of parasites remaining in the well is estimated (N-ΔN). Parasites are allowed to invade for an interval T. At time t=T, the well is washed (removing unattached parasites). The well is fixed and stained. The number of parasites stained red (n_r), green (n_g), and red/green (n_rg) is counted in 12 view-fields and recorded. The number of parasites attached to well walls was microscopically determined to be negligible.

Step 1 Well preparation

Host cells and parasites (tachyzoites) are cultured as described by Morisaki et al. (Morisaki et al, 1995). Wells in 8-well chamber slides are prepared by first growing a monolayer of human foreskin fibroblasts (HFF) to confluence in DMEM containing 10% FBS and 2mM glutamine on LabTek 8-well chamber slides (Nalge NUNC, Rochester, NY).

RH strain (Boothroyd and Grigg, 2002) tachyzoites are cultured separately by serial passage through HFF cells. Following complete lysis of host cells, tachyzoites are recovered using a 3-micron filter, washed and resuspended to 5×10⁶ parasites/ml in an invasion non-permissive buffer, Endo Buffer (44.7 mM K₂SO₄, 10 mM MgSO₄, 106 mM sucrose, 5 mM glucose, 20 mM Tris–H₂SO₄, 3.5 mg/ml BSA, pH 8.2) (Endo et al, 1987).

200 μL of 5×10⁶ parasites/ml in Endo buffer are added to each of the eight wells (N= 10⁶ parasites/well). Chamber slides are spun at 500 g for 2 min at RT to ensure parasite contact with the monolayer, and placed at 37°C in a water bath.

Step 2 Buffer Switch

At time t=0, parasites in a given well are induced to invade synchronously, by replacing the Endo buffer with 500 μL of permissive invasion medium (DMEM + 10 mM HEPES buffer, pH 7.4, and 3% FBS). Tachyzoites in the removed Endo Buffer (ΔN) are determined using a hemocytometer. The total number of parasites in each well at t=0 is estimated by subtracting ΔN from the initial N=10⁶ parasites.

Step 3 Invasion

Tachyozoites are allowed to invade for a different time in each well. A 7-point time series is assembled from the initial data using 7 different time intervals (T₁, T₂, T₃, T₄, T₅, T₆, T₇) in each of seven wells. (8 replicates are obtained for each time-point).

Step 4 Wash and fix

After the appropriate time interval, the cells in a given well are rinsed thoroughly, by pipetting the medium across the host-cell monolayer four times. The medium is completely removed after the last rinse, and invasion is halted immediately by fixation with 2.5% formaldehyde/0.02% gluteraldehyde in PBS for 20 min followed by three washes in PBS for 5 min each.

Step 5 Stain

The staining process exploits the fact that parasites membranes are rich in SAG1 membrane proteins and that SAG1 proteins inside the host cell membrane are masked against anti-SAG1 antibodies until after the host cell membrane is made permeable.

Briefly, slides are blocked with 10% fetal bovine serum for 30 min at RT before staining with rabbit anti-SAG1 (anti-P30) antibodies (1:1000) for 60 min at RT. Host cells are then permeabilized for 10 min in 0.1% Triton X-100 and exposed to mouse anti-SAG (monoclonal G11-9) antibodies (1:500; Argene) at RT for 60 min.

Finally, to differentially stain extracellular parasites red and intracellular parasites green, the slide is exposed to a mixture of goat anti-rabbit IgG (1:500) conjugated to Alexa 594 (Molecular Probes) fluorophore (green), and goat anti-mouse IgG (1:500) conjugated to Alexa 488 fluorophore (red) for 60 min at RT.

Step 6 Counting

After staining, slides are mounted in mowiol. Twelve view fields of 21,760 μm² each are captured (at identical grid points) in each well using an Olympus BX60 microscope equipped with a Olympus DP70 camera at 1000× total magnification. The number of parasites stained red (n_r), green (n_g), or red/green (n_rg) is then counted manually in all twelve images.

2.1 Mathematical Modeling

The model incorporates five invasion stages: detached, contact, attached, penetrating and invaded. The state of the system is represented by a normalized (L₁ norm) state vector

$$\text{x}=(x_d,x_c,x_a,x_p,x_i),$$ (1)

whose components represent the fraction of parasites in each of the invasion stages. In addition to the invasion stages, the system is defined by a set of allowed transitions between the stages. The stages and the allowed transitions are illustrated in Figure 2.

Figure 2.

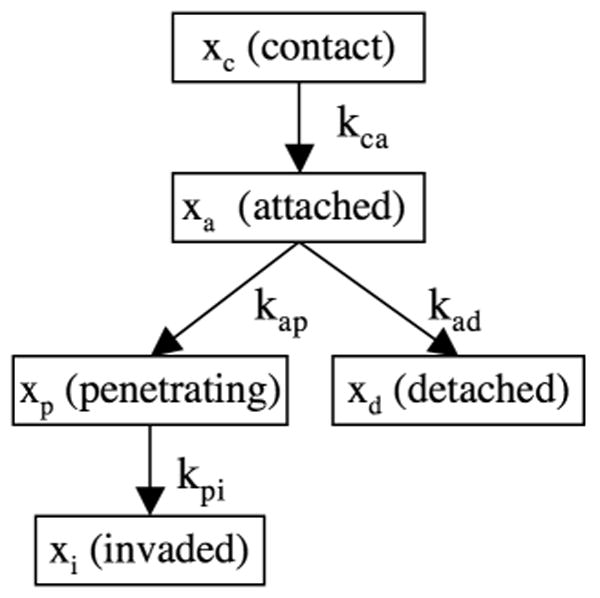
A graphical representation of the causal relationship between the stages of host-cell invasion measured by a synchronized invasion kinetics experiment. The fraction of the parasite population found in the i-th stage is represented by a variable x_i. Similarly, the transition rate from the i-th stage to the j-th stage is represented by the parameter k_ij.

In the contact stage, a parasite binds to the host cell with low affinity. Interactions with the host cell at this stage may involve parasite surface antigens (SAGs) as well as basal levels of micronemal adhesins. (Jacquet et al, 2001) By definition, parasites in the contact stage, are well enough attached to the host that they are not dislodged during the buffer switch at t=0, but fail to bind tightly enough to resist the wash at t=T.

The attached stage is characterized by the ability of a parasite to remain attached by withstanding the shear forces during both the buffer switch at t=0 and the rinse at t=T thus staining red under IFA microscopy. We hypothesize that this increase in attachment strength is due to high affinity binding following the burst of microneme secretion releasing high levels of adhesins (MICs) onto the parasite surface (Huynh et al, 2003, Huynh & Carruthers, 2006).

If attachment strength increases, the parasite progresses to the penetrating stage after becoming apically attached and initiating formation of the moving junction (MJ). The parasite traverses the host cell plasma membrane via distal translocation of the moving junction. Simultaneously rhoptry proteins (ROPs) are secreted and the parasitophorous vacuole forms around the intracellular portion of the parasite (Alexander et al, 2005). The penetrating stage is characterized by parasites staining green and red at their apical and distal ends, respectively.

Conversely, if attachment is not sustained, a parasite enters the detached stage rather than the penetrating stage. Parasites in the detached stage, cannot be directly distinguished from parasites in the contact stage since parasites removed during the wash at t=T contain parasites in both stages. Nevertheless, as we shall demonstrate, our modeling and estimation methods allow us to infer the fraction of parasites that attached and then detached. It has been suggested that detached parasites cannot reattach until sufficient microneme proteins can be newly synthesized over several hours (Carruthers et al, 1999). Hence, the short duration of our experiments allows us to make the simplifying assumption that a parasite never leaves the detached stage, once it has entered it.

Finally, a parasite that has completed penetration and is visually completely intracellular is said to be in the invaded stage. It should be noted that electrophysiological studies indicate that resealing of the host cell plasma membrane does not occur immediately after invasion, but may take up to 5 min (Ward et al, 1993).

The dynamics of invasion are modeled deterministically with a compartment modeling approach. The resulting system of linear ordinary differential equations is expressed compactly in matrix form as

$$\frac{d\text{x}}{dt}=\text{Ax}$$ (2.1)

where

$$\text{A}=\left(\begin{array}{ccccc}0& 0& k_{ad}& 0& 0\\ 0& -k_{ac}& 0& 0& 0\\ 0& k_{ca}& -k_{ap}-k_{ad}& 0& 0\\ 0& 0& k_{ap}& -k_{pi}& 0\\ 0& 0& 0& k_{pi}& 0\end{array}\right),$$ (2.2)

is the matrix of transitions. Referring to figure 2, each positive off-diagonal term in the A matrix corresponds to parasites flowing into a stage, e.g. the matrix element A_ad = k_ad accounts for parasites flowing from the attached stage (a) to the detached stage (d). Similarly the negative diagonal terms represents parasites flowing out of a stage, e.g. the matrix element A_aa = −k_ap − k_ad represents parasites flowing out of the attached stage (a), into the penetrating (p) and detached (d) stages.

The state vector of the system that is propagated by equations (2), is not directly observable. In particular, the parasites in the contact and detached stages are removed together in the wash at t=T and cannot be distinguished. Only the sum of their counts is observable, e.g., by counting the number of parasites in the wash at t=T. We account for this fact by introducing a measurement processes, which transforms the five-dimensional state vector of the system, into a 4-dimensional vector of measurements. y = (y_w, y_r, y_rg, y_g). The components of y represent the only four quantities that are directly observable with our current protocols, i.e. the fraction of parasites removed in the second wash (y_w), stained red (y_w), stained green (y_g), and stained red/green (y_rg). More formally, we model the measurement process compactly, as the linear transformation

$$\text{y}=\text{Bx},$$ (3)

where the matrix B is given by

$$\text{B}=\left(\begin{array}{ccccc}1& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\\ 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 1\end{array}\right).$$ (4)

Thus, for example, from (3) and (4) it can be seen that the predicted fraction of parasites removed in the wash is y_w = x_c+x_d which is just the sum of the fractions of parasites in contact and detached stages plus some measurement error.

To estimate the parameters of the model, it is necessary to compare the predicted fractions of parasites, y, to the corresponding experimentally determined fractions of parasites, z. The components of z are the observed fractions of parasites that are stained in a particular manner. Experimentally determined counts are N, ΔN, n_r, n_g, and n_rg, (see figure 1. for details). The components of z are calculated as follows:

$$\begin{array}{l}{z}_r=\frac{n_r}{N-\Delta N}\\ z_{rg}=\frac{n_{rg}}{N-\Delta N}\\ z_g=\frac{n_g}{N-\Delta N}\end{array}$$ (5)

where N-ΔN is the total number of parasites in the well at t=0, while n_r, n_g, and n_rg are the total number of parasites that are stained red, green, and red/green, respectively. The latter are determined at time t=T. As previously noted, parasites in the contact and detached stages are removed together in the second wash. Only the sum of their counts is observable. In practice, we did not actually count the number of parasites in the second wash (although we could have), instead we calculated n_c + n_d by subtracting the total number of stained parasites (n_r + n_g + n_rg), from the initial number of parasites in a well (N-ΔN). Thus the experimentally observed fraction of parasites that are removed in the second wash is

$$z_w=\frac{(N-\Delta N)-(n_r+n_g+n_{rg})}{N-\Delta N}.$$ (6)

Numerical integration and parameter estimation

The solution of (2.1) depends on the initial state. The choice of initial state influences the details of the solution, but not the general conclusions (see supplement). Ideally, the non-permissive medium would prevent all parasites from attaching and invading, but in practice, some parasites attach, and a smaller number proceed to penetration, even in the permissive buffer. Thus a realistic initial state has the form

$${(x_d,x_c,x_a,x_p,x_i)|}_{t=0}=(0,1-\alpha -\beta -\gamma ,\alpha ,\beta ,\gamma )$$ (7)

Where α is the initial fraction of attached parasites, β is the initial fraction of penetrating parasites and γ is the initial fraction of invaded parasites. This initial state assumes that no parasites have detached at time t=0, i.e. ${x_d|}_{t=0}=0$.

2.3 Numerical methods

All numerical procedures were carried out within the R statistical programming language (R Core Development Team, 2006). In particular, numerical integration was carried out with the lsoda() interface to the FORTRAN 1^st order ordinary differential equation solver of the same name (Setzer, 2006). To enforce positivity of the numerical solution, we numerically integrated an equivalent system of nonlinear equations that we obtained by logarithmically transforming the state space.

To estimate the transition rate vector, k, from the data, we minimize a weighted least squares objective function

$$E\left(\text{k}\right)=\sum _i{w}_i{(z_i-y_i(\text{k}\left)\right)}^2,$$ (8)

where w_i are suitably chosen weights. A principled approach for choosing weight values, is to use the inverse squares of the measurement errors in the corresponding fraction z_i This choice corresponds to maximizing the log-likelihood function of the transition rates, under an assumption of Gaussian errors (McDonough and Whalen, 1995). A parsimonious and robust approach for calculating the weights is to use the inverse square of the median (over time points) of the sample standard deviations of the measurements (see discussion section). A single synchronized invasion experiment yields one replicate of the vector, z along each of 7 time points. If there are M, experiments, the transition rates are estimated from the set of M experiments.

To enforce positive transition rates during parameter estimation, we perform an additional logarithmic transformation of the transition rates, i.e. θ = log(k), and minimize the corresponding objective function E(ϑ) in the transformed space. We minimized with the optim() function using a the quasi-Newtonian L-BFGS-B method without specified boundary conditions (R Core Development Team, 2006).

To calculate 95% confidence intervals (95% CI) requires a distribution for the estimated parameters. We use the bootstrap to generate this distribution (see e.g. (Henderson, 2005) for a practical introduction to bootstrap methodology). In particular, we consider each replicate experiment (7 time-series points) as an event, and we resample the original set of 8 replicate experiments, to create new sets of 8 “resampled” experiments, which are in turn, used to repeatedly refit the parameters, thereby yielding histograms of parameter values, which are used to calculate the confidence intervals. Finally, since M is small (eight in our case), it is possible to enumerate all possible sets, rather than sampling randomly.

Results

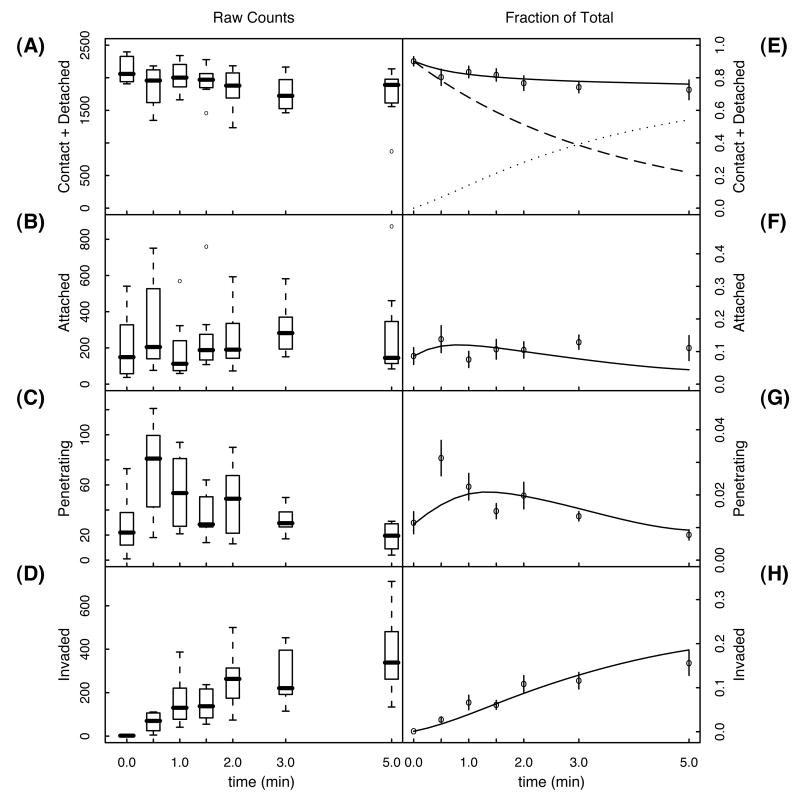
Eight replicate pulse invasion experiments were performed with T. gondii RH strain and HFF cells, as described in the methods section. We used invasion intervals of 0, 0.5, 1, 1.5, 2, 3, and 5 min. The total number of parasites counted over 12 view fields, 7 wells and 8 replicates, was 14352 attached, 2315 penetrating, and 10263 invaded. We solved (equation 2.1) using the realistic initial state (0,1–α–β–γ,α,β,y)), with α = 0.086, β = 0.011, and γ = 0.001. The results of the parameter estimation are summarized in Table 1. The corresponding solutions are shown in Figure 3.

Table 1.

Estimated invasion parameters and 95% confidence intervals using the realistic initial state.

rate (min-1)	fit	95% confidence interval
kca	0.28	0.063-0.53
kad	1.3	0.54-3.0
kap	0.42	0.28-0.79
kpi	2.3	1.8-2.8

Figure 3.

The left hand column (A-D) shows box plots of the raw counts for each of the four observable classes of parasites. The median, 1^st and 3^rd quartiles, and the range of the data over all eight replicates is shown for each time point and each class. Outlier counts are indicated as open circles. The right hand column (E-H) shows the normalized mean number of counts and the error in the mean. Solid curves are the solution to the model using the parameters in Table 1 (realistic initial state). The solid curve in (E) is the predicted fraction of parasites washed away, i.e., the fraction of parasites in the combined contact and detached stages. The dashed curve is the fraction of parasites in the contact stage, while the dotted curve is the fraction of parasites in the detached stage.

3. Discussion

The role of a hidden state

Although it may at first appear that the separation of the model into a kinematic equation (equation 2) and a measurement process (equation 3) adds complexity, this viewpoint is actually a simplifying assumption since it allows us to account for experimental observations with a minimum of assumptions. In particular, pilot studies with a variety of parasite strains and conditions (unpublished), revealed that the fraction of parasites coming off in the second wash (step 4 of Figure 1.) would, in some cases, increase after an initial decrease. A kinematic model such as that described in equation (2) can reproduce this nonmonotonic behavior only if there is some form of nonlinearity, feedback, or biological interaction between invasion stages. This would require us to invoke novel biological processes, for which there is no evidence. Instead, we explain non-monotonic behavior, by making the much simpler assumption, that the underlying state of the system is hidden from direct observation, and must be observed via a measurement process that confounds the contributions from two stages (contacted & detached). The idea of separating a model into a kinematic part that propagates a state vector, and a measurement part that creates a set of observations, yields a framework that can be systematically extended to incorporate either new biology or new experimental protocols. The idea of separating kinematic and measurement processes is powerful and widely exploited in all kinds of models and simulations; perhaps most famously in the class of models known as Hidden Markov Models (Rabiner and Juang, 1986).

Detachment and invasion initiation

The model indicates that approximately 55% of the parasites detach within 5 min of initial attachment (see Figure 3E.). A more formal estimate of affinity is obtained by calculating the asymptotic detachment rate, which can be obtained by solving system (2.1) for the fraction of detached parasites, x_d, at t=∞ under the assumption that all parasites start in the attached stage (i.e., using the ideal initial state). The solution is

$$g=\frac{k_{ad}}{k_{ap}+k_{ad}}$$ (9)

The model predicts that 75% (95% CI: 67 – 81%) of the parasites ultimately detach without proceeding to membrane penetration. Referring to Figure 2, it is evident that f=1-g can be interpreted as a conditional invasion efficiency, which is just the expected fraction of parasites that invade, given that they are already attached.

Attached parasites transition to a penetrating stage, with a time scale determined by $k_{ap}^{-1}$. This corresponds to 2.3 min (95% CI: 1.5-3.3 min). Similarly attached parasites transition to a detached state, with a time scale determined by $k_{ad}^{-1}$. This corresponds to 48 sec (95% CI: 24 – 83 sec). Thus, parasites that managed to invade remained attached about three times longer than parasites that eventually detached from the host cell. This may be due to a general defect in the detaching parasites but recent findings (Alexander et al, 2005, Mital et al, 2005) suggest attachment to be a multi-step process, of increasing strength rather than a binary process. Thus, the success of early attachment events may lead to longer and higher affinity interactions resulting in a longer attachment period.

Finally, we note that one should take care not to over-interpret asymptotic quantities. In this case, our model is designed to account for phenomena that occur over several minutes. Therefore, we do not account for parasites that reattach after detaching -- despite the fact that observations suggest that at least some parasites are able reattach after a period of several hours (Carruthers et al, 1999) But while the conditional invasion efficiency may not accurately reflect the level of invasion after periods considerably longer than those used here, it may be a useful measurement for comparison of different parasite or host strains.

Host plasma membrane penetration

How long does it take for a parasite to traverse the host's plasma membrane? 1/e of attached parasites traverse the plasma membrane of the host, in a time equal to the inverse transition rate $k_{pi}^{-1}$. For RH parasites, our median estimated transition rate implies a characteristic penetration time of 26 sec (95% CI: 22-30 sec). This value is consistent with microscopic observations of individual parasites (Morisaki et al, 1995).

The model predicts that the time at which the greatest fraction of parasites are in the penetration stage is 1.5 min (see figure 3G). This is consistent with the prediction that parasites in the contact stage should experience a delay, allowing attachment before initiating penetration. This delay is just the inverse transition rate $k_{ca}^{-1}=3.5\text{min}$ (95% CI: 2.2 – 7 min). However, the peak in the raw and normalized data occurs at 30 sec. What accounts for this discrepancy? The simplest explanation is that our penetration data is too noisy (the 30 sec data in Figure 3 A-C has the largest variance). Another possible explanation takes into account the fact that about 10% of the parasites are already in the attached stage at t=0. It is conceivable that this population, which has sat attached for as long as 2 min, is primed and initiates penetration immediately upon introduction of permissive conditions. This is not accounted for, in the current model, and could explain the peak in the data at 30 seconds.

Robustness

The maximum negative log-likelihood principle implies that each measurement should contribute to the objective function, in proportion to the inverse square of its error. However, due to the limited number of replicates that are available for calculating the required sample variances, the sample variances for each data point are underestimated, and lead to estimated rates that are dominated by, whichever individual measurement happens to have the most underestimated variance. To mitigate this problem, we calculated one weight for each time series, from the median of the variances along the given time-series. This heuristic yields four weights (one for each time-series), excellent fits, and robust estimates of the rates.

The estimated rates also depend on the choice of initial state. The reader may question how sensitive our predictions are to our choice of initial state. To characterize this dependence, we estimated the parameters using the ideal (rather than realistic) initial state, ${(x_d,x_c,x_a,x_p,x_i)|}_{t=0}=(0,1,0,0,0)$. All the estimated parameters are different from table 1, but they tend to change within the 95% confidence intervals of table 1 (except for k_ca, which was just outside the lower limit). We find that our conclusions are not altered by these changes, although the precise quantities do change (see supplement). The reader may well ask, why we didn't just fit the parameters (α,β,γ) of the initial state? The urge to do this was tempered by the realization that the resulting model would possess a total of 7 free parameters (three more than the model we actually used). Estimating this many parameters with our limited number of replicates and time points, would certainly risk over-fitting, thereby bringing into question the validity of the estimated transition rates. Certainly, something along these lines may be useful in future applications, but in this initial report our objective is to present the principles of the modeling approach.

Applications

Our phenomenological approach provides robust estimates as well as error estimates of Toxoplasma gondii invasion parameters. Estimation of these parameters not only provides quantitative rates that can be used to characterize differences between strains according to their invasion characteristics, but also a powerful tool for gaining a insights into the host-pathogen interplay that takes place during invasion.

First, naturally occurring Toxoplasma infections in Europe and North America are predominantly caused by three near-clonal strains with pronounced differences in virulence between the separate strains. Strain differences in invasion kinetics may explain a component of the observed difference in virulence. Furthermore, differences in specific transition rates will provide insight into which invasion step is particularly important for contributor to virulence.

Second, Toxoplasma exploits an exceedingly large number of species as intermediate hosts, and can invade numerous cell types within a single host. This implies that the parasite is employing one of two mechanisms. Either it is utilizing a wide variety of in-host cell receptors. Or, it is using one or more widely expressed and conserved host cell surface receptors. Yet surprisingly little is known about Toxoplasma's receptors and their role at different steps of invasion. By combining expression profiling of several host cell types with modeling of the respective invasion kinetics by a single Toxoplasma strain, it may be possible to identify a group of receptor candidates for each step of the invasion process.

Third, it would be desirable to connect estimated transition rates to events and rates at the molecular level by comparing invasion gene deletion mutants to their wild-type equivalent parental strains and thus determining the contributions of single genes at separate steps of invasion.

Fourth, our approach could be applied to any intracellular pathogen for which invasion can be synchronized and that can be stained to separate different stages of invasion. Indeed, recent experiments have show that a non-permissive buffer similar to the one used in our toxoplasma synchronized invasion experiments, is effective at reducing invasion of hepatocytes by malaria sporozoites (Kumar et al., 2007). An immunofluorescence assay based on the circumsporozoite surface antigen could be adapted to differentiate various invasion stages.

Finally, we note that the data used in this analysis was counted by hand, but counting stained parasites is simpler (from an image processing point of view) than inferring the invasion stage of individual parasites from microscopic observations. Thus the model-based approach presented here provides a possible avenue for high-throughput analysis of parasite phenotypes, provided that suitable image processing algorithms are used to count the stained parasites.