Experimental and theoretical characterization of implantable neural microelectrodes modified with conducting polymer nanotubes

Abstract

Neural prostheses transduce bioelectric signals to electronic signals at the interface between neural tissue and neural microelectrodes. A low impedance electrode-tissue interface is important for the quality of signal during recording as well as quantity of applied charge density during stimulation. However, neural microelectrode sites exhibit high impedance because of their small geometric surface area. Here we analyze nanostructured-conducting polymers that can be used to significantly decrease the impedance of microelectrode typically by about two orders of magnitude and increase the charge transfer capacity of microelectrodes by three orders of magnitude. In this study poly(pyrrole) (PPy) and poly(3, 4- ethylenedioxythiophene) (PEDOT) nanotubes were electrochemically polymerized on the surface of neural microelectrode sites (1250 μm²). An equivalent circuit model comprising a coating capacitance in parallel with a pore resistance and interface impedance in series was developed and fitted to experimental results to characterize the physical and electrical properties of the interface. To confirm that the fitting parameters correlate with physical quantities of interface, theoretical equations were used to calculate the parameter values thereby validating the proposed model. Finally, an apparent diffusion coefficient was calculated for PPy film (29.2 ± 1.1 cm²/s), PPy nanotubes (72.4 ± 3.3 cm²/s), PEDOT film (7.4 ± 2.1 cm²/s), and PEDOT nanotubes (13.0 ± 1.8 cm²/s). The apparent diffusion coefficient of conducting polymer nanotubes was larger than the corresponding conducting polymer films.

1. Introduction

Impedance characterization of microelectrode-electrolyte interface is important for the application of biosensors and bioelectronics such as neural prostheses, where low impedance small microelectrodes are required for high-resolution stimulation and recording [1, 2]. Microfabricated neural prosthetic devices facilitate the functional stimulation and recording from neurons of the peripheral and central nervous system. In the physiologic environment, bioelectric potentials are carried in electrolyte media in the form of ionic current and the purpose of the neural electrode is to transduce these bioelectric signals to and from electronic signals [3]. The interface between microfabricated neural microelectrodes and neural tissue plays a significant role in the long-term performance of these devices.

A certain charge density is required to generate neural activity during stimulation using microelectrode arrays (i.e. 0.08-1.91 mC/cm² for human retina) [4, 5]. High impedance electrodes would result in a large applied electrode potential leading to undesirable electrochemical reactions that may be harmful to the tissue. During recording, the extracellular signals are low, on the order of microvolts for neurons [1, 3] so the neural signals will be lost in the noisy, ion-based electric fluctuations of the surrounding electrolyte media if the electrode impedance is not low enough. Therefore, a low impedance electrode-electrolyte interface is critical in the design of bioelectrodes. In order to design an optimized low impedance interface a detailed understanding of the physical processes contributing to the impedance is required.

Conducting polymers (CPs) have been widely used for biosensors and biomedical applications [6-13]. The main characteristic of a conducting polymer (CP) is a conjugated backbone with a high degree of π-orbital overlap that can be subjected to oxidation or reduction by electron acceptors or donors, resulting in p-type or n-type doped materials (mostly p-type), respectively. Electrical conductivities can be varied by as much as 15 orders of magnitude by changing dopant concentrations so that control is feasible over the entire range from insulator to semiconductor and then to metal [14]. This makes CPs good candidates for coating the electrodes in order to minimize the impedance of electrode-electrolyte interface.

Among the known CPs, we have been interested in the electrochemical polymerization of PPy, PEDOT, and PEDOT derivatives because of their promising electrical properties and biocompatibility [12, 15]. PEDOT has exhibited some very interesting properties. In addition to high conductivity (ca. 300 S/cm), PEDOT was found to be almost transparent in thin film and showed high chemical stability in the oxidized state [16-18]. We have found that soft, low impedance, and biologically active coatings can be prepared by the electrochemical deposition of these CPs on neural microelectrode arrays [10, 19, 20].

Equivalent circuit models have long been used to model the electrode-electrolyte interface impedance. In 1899 Warburg first proposed that a polarization resistance in series with a polarization capacitor could represent that interface [21]. Randle's model consisted of an interface capacitance shunted by a reaction impedance, in series with a solution resistance [22]. As the use of electrodes in medical applications became more extensive, research was dedicated to the understanding of the electrode physiological solution interface [23, 24]. Kovacs presented an equivalent circuit model based on Randle's model, with an additional Warburg impedance due to the diffusion of faradaic current [3].

Several equivalent circuits have been evaluated in order to model electrode-electrolyte interfaces coated with organic films [25-27] and CPs [28-30]. Cui and co-workers used a simple model of interface that was proposed by Bobacka et al. [28] for a neural electrode coated with PEDOT. This model consisted of a double layer capacitance (interface capacitance) in series with a Warburg impedance and the solution resistance [29]. Yang et al. used Kovacs's model for evaluating the microporous PEDOT coatings interface on the neural electrode [30]. One of the most important challenges required in the analysis of these models is to relate the parameters to chemical physical characteristics of the films themselves.

In the work presented here, PPy and PEDOT were electrochemically polymerized on the neural electrode sites in form of film and nanotubes. Neural electrodes were assembled at the Center for Neural Communication Technology at The University of Michigan (Figure 1). The fabrication process of CP nanotubes is illustrated in Figure 2 and has been described previously [10]. Electrochemical impedance spectroscopy (EIS) has been used to characterize the electrode-electrolyte interface of the modified neural microelectrodes. A new equivalent circuit model has been developed and used where each parameter represents a macroscopic physical quantity contributing to CP-modified electrode interface. The model consists of a coating capacitance in parallel with a pore resistance and interface impedance in series (Figure 3). The model parameters have been fitted to the experimental results by using a nonlinear least-squares method. To confirm that the model parameters represent reasonable physical quantities, theoretical equations have been used to calculate the parameter values thereby validating the model. The effect of the initial interface conditions on the charge transfer resistance has also been determined. We have already shown that PEDOT nanotubes can improve the signal quality of recording sites and improves the long term performance of chronically implanted neural microelectrodes in rats out to seven weeks [31].

Figure 1.

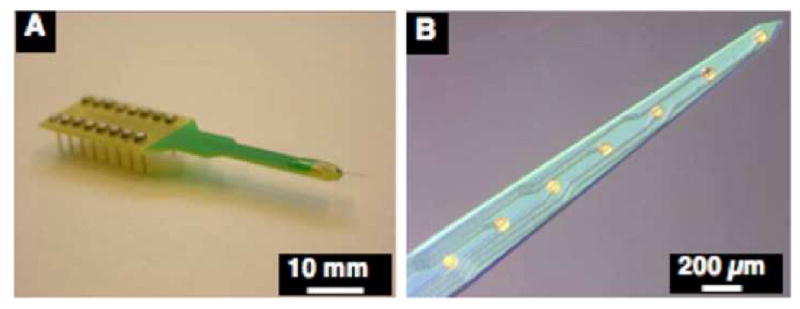
Optical micrographs of stimulating/recording microelectrodes arrays that were fabricated in CNCT and assembled in our laboratory. The probe tip will be inserted in motor cortex or auditory cortex and the rest of the probe will be tethered to the skull: (A) 8 channel silicon substrate acute probe, (B) High magnification image of acute tip probe demonstrates the silicon substrate and gold electrode sites with surface area of 1250 μm².

Figure 2.

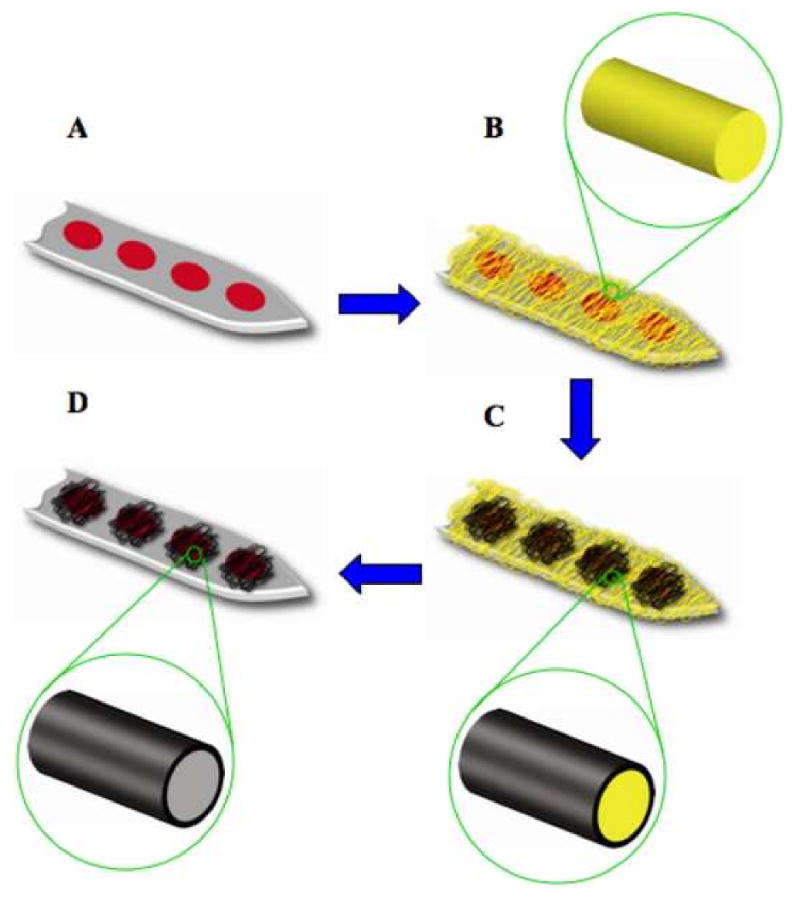
Procedure of surface modification of neural microelectrodes in order to create CP nanotubes: (A) Neural microelectrode before surface modification. (B) Electrospinning of biodegradable polymer nanofibers templates (PLLA) on the neural microelectrode. (C) Electrochemical polymerization of CPs around the electrospun nanofibers (D) Removing of electrospun core fibers to create nanotubular-CPs.

Figure 3.

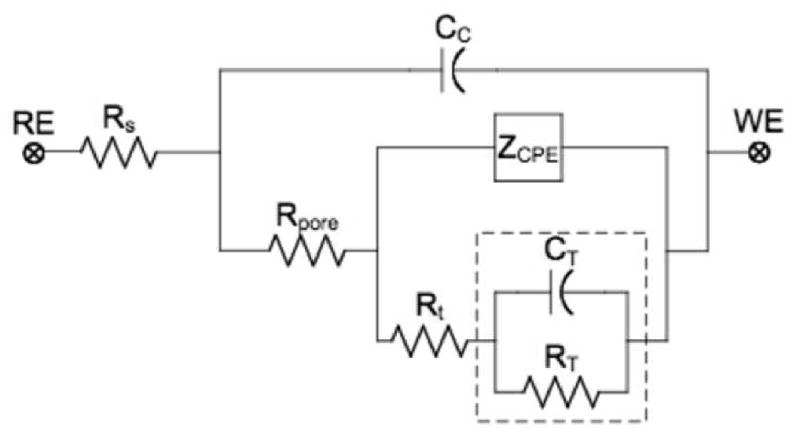
Equivalent circuit model of electrode-CP-electrolyte interface. The circuit elements are: solution resistance (R_S), coating capacitance (C_C), pore resistance (R_pore), double layer interface impedance Z_CPE, charge transfer resistance R_t, and finite diffusion impedance Z_T (including C_T and R_T).

2. Materials & Methods

2.1. Materials

Poly (L-lactide) (PLLA, RESOMER^® L 210) with inherent viscosity 3.3-4.3 dl/g was purchased from Boehringer Ingelheim Pharma GmbH & Co. (KG, Germany). 3, 4-ethylenedioxythiophene (EDOT, BAYTRON^® M) with molecular weight 142.17 g/mol was received from H.C. Starck Inc. (Newton, MA). The pyrrole monomer (Py) and lithium perchlorate (LiClO₄) were purchased and used as received from Sigma-Aldrich.

2.2. Neural microelectrode arrays

The microfabricated neural arrays were provided by the University of Michigan Center for Neural Communication Technology (CNCT) (Figure 1). The silicon substrate supports an array of thin film conductors that are insulated above and below by deposited dielectrics of silicon dioxide and silicon nitride. Openings in the upper dielectrics along the probe define vertical connections to underlying polysilicon traces that are then sputtered with gold over regions of the top dielectrics for interfacing to the tissue. At the rear of the probe, gold bond pads facilitate connections with off-chip instrumentation. Single neural probes were used in our research with gold-coated electrode sites (1250 μm² in area).

2.3. Electrochemical deposition of conducting polymers

The electrochemical process was performed for chronic neural probes on each electrode site by an Autolab PGSTAT 12 (EcoChemie, Utrecht, Netherlands) in galvanostatic mode with a conventional four-electrode configuration at room temperature. CP deposition was carried out under galvanostatic conditions in a 0.01 M 3, 4-ethylenedioxythiophene monomer and 0.1 M LiClO₄ or in a 0.1 M pyrrole monomer and 0.1 M LiClO₄ aqueous solution at a current density of 0.5 mA/cm². The amount of polymer coated on the electrode site was controlled by the total charge passed during polymerization. The working and sensing electrodes were connected to the electrode site. The reference and counter electrode were connected to a platinum wire within the EDOT/LiClO₄ and Py/LiClO₄ solutions.

2.4. Fabrication of electrospun nanofiber template

PLLA solution was prepared by dissolving 0.72 g PLLA in 10 ml of chloroform at a temperature of 50° C for 10 hr in order to have a homogenous solution with PLLA concentration of 4% (w/v). PLLA was directly deposited on the 15 microfabricated neural electrodes by electrospinning (Figure 2B) in an electrical field of 0.6 kV/cm with flow rate of 0.25 ml/h for 30s. The neural probes were held at a distance of 15 cm from the syringe needle.

2.5. Fabrication of conducting polymer nanotubes

PEDOT and PPy were deposited on the surface of gold electrode sites that were coated with electrospun PLLA nanofibers (Figure 2C). PEDOT and PPy were grown on the sites and around the PLLA nanofibers. After electrochemical deposition was completed, the PLLA core fibers were removed by soaking the probe tips in dichloromethane for 10min (Figure 2D).

2.6. Electrochemical impedance spectroscopy (EIS)

An Autolab PGSTAT 12 and Frequency Response Analyzer software (Eco Chemie B.V., Netherlands) were used to record impedance spectra of electrode sites for 15 neural probes. A solution of 0.1 M phosphate buffer solution (PBS, pH = 7) was used as an electrolyte in a three-electrode cell configuration. The working electrode was connected to electrode site through a connector. The counter electrode was connected to a platinum foil that was placed in a glass container. An Ag/AgCl reference electrode and the neural microelectrode tip were immersed in glass container of electrolyte. An AC sinusoidal signal of 5 mV in amplitude was used to record the impedance over a frequency range of 1-10⁵ Hz.

2.7. Cyclic voltammetry

Cyclic voltammetry (CV) was performed using an Autolab 12 instrument in a four-electrode configuration as described earlier. A scan rate of 100 mV/s was used and the potential on the working electrode was swept between −0.9 V to 0.5 V. Before each CV curve was recorded, several cycles were swept to insure that the film had reached a stable state.

2.8. Scanning electron microscopy (SEM)

Information about the surface morphology and microstructure of the coatings were obtained using a FEI Nova 200 Nanolab Dualbeam Focused Ion Beam (FIB) and SEM. SEM images were taken with a typical voltage of 5 kV. A thin film of gold (5nm) was sputtered onto the surface of samples using a Hummer-600 sputtering system.

2.9. Equivalent circuit modeling

As discussed earlier, a number of previous studies have used equivalent circuit modeling to interpret the impedance response of bioelectrodes and CPs [28-30, 32, 33]. In this study, a more in details equivalent circuit model is proposed to characterize impedance of the electrode-CP-electrolyte interface. The equivalent circuit model presented in this work is comprised of a solution resistance R_S, a CP coating capacitance C_C, a pore resistance R_Pore, a double layer interface capacitance CPE, a charge transfer resistance R_t, and a finite diffusion impedance Z_T as shown in Figure 3 (see Table S1 in supplementary data for details).

2.10. Solution resistance

For a planar disk electrode, R_s is expected to be given by [3]:

$$R_s=\frac{\rho }{4r}$$ (1)

where ρ is the solution resistivity (72Ω.cm for physiological saline) [3] and r is the radius (see supplementary material for details).

2.11. Coating capacitance

Theoretically, the capacitance per unit area of a dielectric material is given by:

$$C=\frac{{\epsilon }_0{\epsilon }_r}{d}$$ (2)

where ε₀ is the dielectric permittivity of free space (8.85419 × 10^-12 F/m), ε_r is the relative dielectric permittivity of the medium between the two plates, and d is the distance between them.

2.12. Interface capacitance

The Gouy-Chapman-Stern model [34] gives a theoretical derivation of the interface capacitance. The interface capacitance is taken to be the series combination of the double layer capacitance, termed the Helmholz capacitance, and the diffuse layer capacitance, the Gouy-Chapman capacitance, and is given by the following formula:

$$\frac{1}{C_I}=\frac{1}{C_H}+\frac{1}{C_G}=\frac{d_{\text{OHP}}}{{\epsilon }_0{\epsilon }_r}+\frac{L_D}{{\epsilon }_0{\epsilon }_{r}cosh(\frac{z{V}_0}{2V_t})}$$ (3)

where d_OHP is the thickness of the double-layer, ε₀ is the permittivity of free space, ε_r is the permittivity of the double layer, z is the charge on the ion in solution, V₀ is the applied electrode potential, and V_t is the thermal voltage. The Debye length, L_D, is given by

$${\text{L}}_{\text{D}}=\sqrt{\frac{{\epsilon }_0{\epsilon }_r{V}_t}{2n_0{z}^{2}q}}$$ (4)

$$V_t=\frac{kT}{q}$$ (5)

where n₀ is the bulk number concentration of ions in solution, q is the elementary charge, and k is Boltzmann's constant (1.38066×10⁻²¹ J/K). The values of constants are shown in Table S2 in supplementary material.

2.13. Charge transfer resistance

Charge transfer resistance R_t is given by:

$$R_t=\frac{V_t}{J_{0}z}$$ (6)

The magnitude of these currents is termed the equilibrium exchange current density J₀ (generally given in units of A/cm²) and V_t thermal voltage (see supplementary material for details).

where $V_t=\frac{kT}{q}=0.0259V$

Under the low-field approximation, the Butler-Volmer equation reduces to Ohm's law. A plot of the current versus potential yields a straight line and the slope gives the charge transfer resistance. Finally, exchange current density can be calculated from (6).

Cyclic voltammetry was used to determine J₀. With the assumption of charge transfer arises from the electrolysis of H₂O and reduction of O₂ according to 2H₂O ↔ O₂ + 4H⁺ + 4e⁻, the value of z has assumed to be 4 [3].

2.14. Diffusional impedance

The Warburg circuit element is a good place to start thinking about diffusion but often semi-infinite diffusion is not a reasonable model. Finite diffusions are important when a thin film is involved [35]. The finite diffusion element Z_T is characterized by the diffusional time constant τ_T (τ_T = R_TC_T), the diffusional pseudocapacitance C_T and the diffusion resistance R_T.

$$Z_T=(\frac{{\tau }_T/C_T}{\sqrt{i\omega {\tau }_T}})\text{coth}(\sqrt{i\omega {\tau }_T})$$ (7)

3. Results and Discussion

3.1. Surface characterization of conducting polymer nanostructures

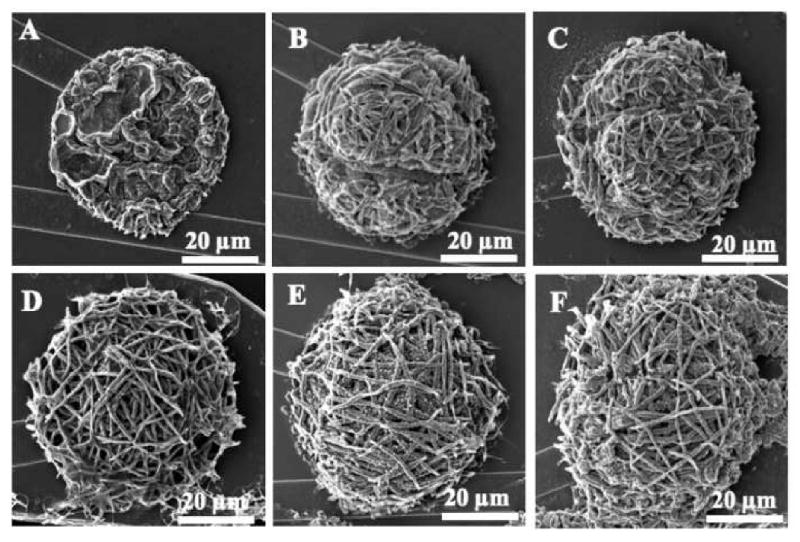
CPs (PPy and PEDOT) doped with LiClO₄ were electrochemically polymerizated on the microelectrode arrays with and without nanofiber templates in galvanostatic (constant current) mode. After PPy and PEDOT deposition, the PLLA fibers were removed by soaking in dichloromethane for 10 minutes. The wall thickness of the PEDOT nanotubes varied from 50-100 nm, and the nanotube diameter ranged from 100-600 nm. By controlling the polymerization time, we could reproducibly prepare tubular structures with thin walls or thick walls [10]. Figures 4A, 4B, 4C, and 4D show scanning electron micrographs of CPs PPy and PEDOT nanotubes on the neural probe sites. The total applied charge density during electrochemical deposition was 1.44 C/cm² (applied current 20 nA for 900 s) for all samples. This corresponded to the charge density needed to give the minimum impedance at 1 kHz, which is the relevant frequency typical of neuronal action potentials [36]. Although electrochemical deposition was done on the individual electrode sites, PEDOT nanotubes grew off the electrode sites, creating more surface area (Figure 4C, Figure 4D). This is presumably due to the fact that the current distribution on the electrode surface is uneven and PEDOT is more conductive than PPy [20].

Figure 4.

Scanning electron micrographs of electropolymerized PPy and PEDOT nanotubes on neural microelectrode sites. (A) Top view of PPy nanotubes, (B) three-dimensional view of PPy nanotubes, (C) Top view PEDOT nanotubes, and (D) three-dimensional view of PEDOT nanotubes. PPy nanotubes with deposition charge density 1.44 C/cm².

The overall thickness of PPy and PEDOT nanotube coatings depends upon the layer thickness of the nanofibers and CP deposition charge density. Figures 5A, 5B, 5C, 5D, 5E, and 5F show surface morphologies of nanotubular PPy doped with LiClO₄ electrochemically polymerized on the electrode sites as a function of applied charge density from 0.48 C/cm² to 2.88 C/cm². The current density was controlled during the deposition at 0.16 mA/cm². The overall thickness of PPy nanotubes increased from 2.0 μm to 8.3 μm by the increasing the deposition charge from 0.48 C/cm² to 2.88 C/cm² respectively. (See Figure S1 in supplementary data). Since Martin and co-workers showed that there was a correlation between the surface topography of CP film and impedance of electrode sites, further investigation can be done using Atomic Force Microscopy (AFM) in order to characterize the surface roughness of CP nanotubes [11]. However scanned-probe techniques such as AFM are of limited utility on extremely rough fibrillar and fuzzy films. In particular, they cannot image inside the nanotubular structures or the films used in this study.

Figure 5.

Scanning electron micrographs of electropolymerized PPy nanotubes on neural microelectrode sites as a function of deposition charge. (A) 6 μC, (B) 9 μC, (G) 12 μC, (H) 18 μC, (I) 24 μC, and (J) 36 μC.

3.2. Electrochemical impedance spectroscopy (EIS)

Figure 6A shows EIS results from neural microelectrode sites before and after surface modification with CP nanotubes. PPy nanotubes and PEDOT nanotubes were electrochemically deposited on the neural electrodes using an applied charge density of 1.44 C/cm² (18μC). It was found that the impedance of both bare gold and modified electrode sites decreased with increasing frequencies, while the impedance of coated electrodes was significantly lower than that of the uncoated gold electrodes over the whole range of frequencies (10⁰ to 10⁴ Hz) as has been seen previously for other CP films [10, 19, 30, 37]. This can be explained by significantly increasing the effective surface area with formation of CP nanotubes on the gold electrodes. The impedance spectroscopy also showed that the uncoated electrode acted as a pure capacitor while the CP nanotube- coated electrode acted as a capacitor in frequencies less than100 Hz and a resistor in frequencies more than 100 Hz. As seen in Figure 6A, the lowest impedance and largest change was observed for PEDOT nanotubes. The magnitude of impedance was decreased from 800 ± 20 kΩ for uncoated sites to 80 ± 6 kΩ (about one-order of magnitude) for PPy nanotubes and 4 ±2 kΩ (about two-orders of magnitude) for PEDOT nanotubes (at 1 kHz). These extremely low values of electrode impedance have been shown significantly enhance the performance of these probes in vivo [31, 38]. This method, coating with CP nanotubes, has resulted in the largest decrease of the 1 kHz impedance multiplied by electrode area (5MΩ×μm²) of any coating design developed to date in our laboratory or reported in literature [30, 37].

Figure 6.

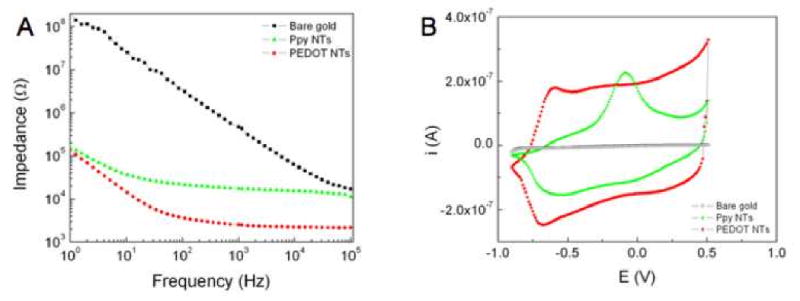
Electrical properties of neural microelectrodes modified with conducting polymer nanotubes. (A) Impedance spectroscopy over a frequency range of 1-10⁵ Hz: bare gold (black squares), PPy nanotubes (green triangles), and PEDOT nanotubes (red circles). (B) Cyclic voltammetry: bare gold (black squares), PPy nanotubes (green triangles), and PEDOT nanotubes (red circles). Deposition charge density = 1.44 C/cm², Scan rate = 0.1V/s.

3.3. Cyclic voltammetry (CV)

CV was used to explore the capacity of charge transfer density for PPy nanotubes and PEDOT nanotubes that were deposited with applied charge density of 1.44 C/cm². The integrated surface area of CV graph corresponds to the capacity of charge transfer through the polymeric film. As can be seen from Figure 6B, the capacity of charge transfer increased significantly using CPs. However, CV results showed that PEDOT nanotubes could transfer even more charge than PPy nanotubes. The charge capacity increased from 0.001 ± 10^-4 μC for bare gold electrodes to 2.3 ± 0.5 μC for PPy nanotubes and 4.9 ± 0.6 μC for PEDOT nanotubes.

3.4. Equivalent circuit modeling of electrode-conducting polymer-electrolyte interface

Equivalent circuit modeling was performed for EIS measurement results according to the proposed circuit model in Figure 3 using ZSimpWin software. Table 1 gives a summary of the averaged, fitted parameter values with corresponding standard deviations for PPy film, PPy nanotubes, PEDOT film, and PEDOT nanotubes.

Table 1.

EIS parameters of electrodeposited PPy, PPy NTs, PEDOT, and PEDOT NTs doped by LiClO₄ on the electrode obtained by fitting experimental data to the equivalent circuit model. Data are shown for ± standard deviation (N = 10 for each case)

	Rs (mΩ.cm2)	CC (μF/cm2)	RP (mΩ.cm2)	Q−Y0 (μS.secˆn/c m2)	n	Rt (Ω.cm2)	T−Y0 (S.secˆn/cm2)	B (secˆ.5)	χ2×10-4
PPy film	111 ± 5	3.2 ± 0.2	2922 ± 128	45 ± 5.5	0.55	1.4 ± 0.3	0.14 ± 0.07	0.185	1.9 ± 0.4
PPy NTs	82 ± 3	6.6 ± 0.2	1181 ± 84	56 ± 4.1	0.59	0.6 ± 0.2	0.26 ± 0.05	0.141	2.9 ± 0.2
PEDOT film	70 ± 4	7.5 ± 0.3	1305 ± 79	51± 2.9	0.91	0.7 ± 0.2	0.92 ± 0.11	0.147	1.1 ± 0.3
PEDOT NTs	53 ± 3	13.8 ± 0.1	618 ± 43	48 ± 8.2	0.93	1.0 ± 0.3	0.42 ± 0.13	0.125	1.7 ± 0.2

As shown in Table 1, the pore resistance (R_P) reduced for both PPy and PEDOT using nanofiber templating. The CP nanotubes showed less pore resistivity due to their increasing porosity. The capacitance of the coating (C_C) increased from 3.2 ± 0.2 μF/cm² for PPy film to 6.6 ± 0.2 μF/cm² for PPy nanotubes and from 7.5 ± 0.3 μF/cm² for PEDOT film to 13.8 ± 0.1 μF/cm² for PEDOT nanotubes. The charge transfer capacities were also calculated from the integrated area of the CV graph. This value increased for both PPy nanotubes and PEDOT nanotubes with respect to PPy and PEDOT film. As expected, an increase of the coating capacitance (C_C) for the nanotubes correlated with an increase of the charge transfer capacity. Therefore, CV results confirmed the results of coating capacitance (C_C) that were achieved from circuit modeling.

Several equivalent circuits have been evaluated in order to model electrode-electrolyte interfaces coated with organic films [25-27] and CPs [28-30]. Although our proposed model (Figure 3) has more elements, but we believe that this model can describe better the electrode-coating-electrolyte interface in details. A comparison of experimental and calculated (fitted) EIS data in the form of Nyquist plot and Bode plot are shown in Figure 7A and 7B for PEDOT nanotubes. As can be seen from Figures 7A, 7B, and the calculated χ² value (χ² = 1.74×10⁻⁴), the equivalent circuit model presented in Figure 3 is a reasonable model for the electrode-PEDOT nanotubes-electrolyte interface on neural microelectrodes.

Figure 7.

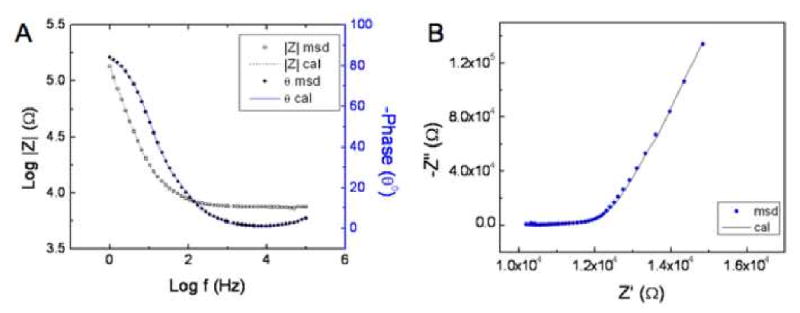
Impedance data of measured and calculated PEDOT nanotubes with applied charge density of 1.44 C/cm² (C) Bode plot, (D) Nyquist plot. The calculated data were obtained by fitting of the experimental.

3.5. Verification of equivalent circuit model parameters

In order to confirm the validity of the proposed equivalent circuit model (Figure 3), the calculated model parameters (R_S, R_t, and Z_CPE) from curve fitting have been compared to the calculated parameters based on the theoretical principles which were described before through the equations (1) to (6). The projected surface area of CP-coated electrodes was measured using MetaMorph 7 software (Molecular Devices Corporation, Sunnyvale, CA) from SEM images (A_PPy = 1384 ± 34 μm², A_{PPy NTs} = 2826 ± 25 μm², A_PEDOT = 4299 ± 41 μm², and A_{PEDOT NTs} = 6644 ± 47 μm²). The resistance of solution (R_S) was calculated using equation (1). Using equations (3) and (4) (see Table S2 in supplementary data for constant values) the theoretical interface capacitance (C_I) was found to be 0.547 F/m. The impedance of the interface capacitance was calculated using:

$$Z_{\text{CPEth}}=\frac{1}{i\omega C_I}$$ (8)

With the angular frequency of ω = 1 rad/s, the magnitude of theoretical interface capacitance of |Z_CPEth| is 18.5 kΩ.cm². As mentioned, under the low-field approximation, the Butler-Volmer equation reduces to Ohm's law (see supplementary data for details). A plot of the current versus potential yields a straight line and the theoretical charge transfer resistance (R_tth) is given by the slope. Therefore, cyclic voltammetry was used to determine R_tth under the following conditions: 5 mV perturbation signal with respect to the open circuit potential, 0.1 mV/s scan rate, averaged over 20 scans.

Table 2 shows the fitting parameter of resistance of solution (R_s) differs and for PPy > PPyNTs > PEDOT > PEDOTNTs due to increasing surface area (A_PEDOTNTs > A_PEDOT> A_PPyNTs >A_PPy). However, the difference between R_sth and R_s represents a maximum 13% deviation from the experimental value, which is evidence that the equivalent circuit model describes the resistance of solution well. The impedance of the interface capacitance showed a maximum 15% deviation between theoretical (Z_CPEth) and experimental (Z_CPE) parameters that is also an acceptable result. The difference between the fitted and calculated theoretical values could be a result of impurities at the interface that are not accounted for in the equivalent circuit model or a result of sensitivities, in both the EIS and the cyclic voltammetry measurements, to the interface conditions [3].

Table 2.

Fitting parameters (R_s, Z_CPE, R_t) and theoretical parameters (R_sth, Z_CPEth, R_tth, J_0th) of PPy, PPy NTs, PEDOT, and PEDOT NTs. They were electropolymerized on the neural microelectrodes with applied charge density of 1.44 C/cm². Data are shown for ± standard deviation (N = 10 for each case)

	Fitting parameters			Theoretical parameters
	Rs (k Ω)	Z CPE (kΩ.cm2)	Rt (k Ω)	Rsth (k Ω)	Z CPEth (kΩ.cm2)	Rtth (kΩ)	J0th (mA/cm2)
PPy	8.9 ± 0.4	20.2 ± 1.2	129.4 ± 3.7	8.7	18.5	145.5	3.57
PPy NTs	6.6 ± 0.1	17.9 ± 1.5	48.8 ± 1.4	6.4	18.5	62.3	8.31
PEDOT	5.6 ± 0.5	19.6 ± 1.1	60 ± 2.6	5.3	18.5	51.3	10.1
PEDOT NTs	4.2 ± 0.3	20.8 ± 0.7	79.2 ± 1.8	3.9	18.5	92.7	5.59

The dielectric constant of PPy film, PPy nanotubes, PEDOT film, and PEDOT nanotubes were calculated in Table 3 from:

Table 3.

Diffusional parameters for PPy film, PPy NTs, PEDOT film, and PEDOT NTs were electropolymerized on the neural microelectrodes with applied charge density of 1.44 C/cm² by fitting experimental EIS data to the model in Figure 3. Data are shown for ± standard deviation (N = 10 for each case).

	L (μm)	τT (ms)	RT (kΩ)	CT (μF)	D ×10-6 (cm2/s)	εr
PPy film	10 ± 0.5	34.2 ± 2.6	108.3 ± 5.0	0.32 ± 0.06	29.2 ± 1.1	3.6 ± 0.3
PPy NTs	12 ± 0.4	19.9 ± 1.5	43.9 ± 5.0	0.45 ± 0.12	72.4 ± 3.3	8.6 ± 0.4
PEDOT film	4 ± 0.3	21.6 ± 2.8	23.6 ± 3.6	0.91 ± 0.17	7.4 ± 2.1	3.5 ± 0.3
PEDOT NTs	4.5 ± 0.4	15.6 ± 2.0	12.9 ± 2.5	1.21 ± 0.32	13.0 ± 1.8	7.0 ± 1.5

$${\epsilon }_r=\frac{C_{c}L}{A{\epsilon }_0}$$ (0.9)

where C_c, L, A, ε₀ are coating capacitance, thickness of coating, surface area of coating, and permittivity of free space, respectively. As indicated in Table 3, the dielectric constant of PPy and PEDOT increased with formation of nanotubes presumably due to increasing of porosity inside the CP structure.

3.6. Determination of apparent diffusion coefficient

The diffusional time constant τ_T is related to the diffusion coefficient D and the diffusion length L as follows [39]:

$${\tau }_T=\frac{L^2}{D}$$ (10)

According to equation (10), with constant D, τ_T is directly proportional to L². The proposed equivalent circuit model was also applied to the EIS data of PPy nanotubes that were electrochemically deposited on neural electrode sites with different applied charge density. As discussed earlier and shown in Table 4 the overall thickness of PPy nanotubes increased (2.0 − 8.3 μm) as the charge deposition increased (6 - 36 μC). Also, the diffusional time constant decreased (30.98 - 9.6 ms) as the charge deposition increased. Consequently, diffusion coefficient D increased about one order of magnitude (1.29 – 71.76 ×10^-6 cm²/s) (Table 4 and Figure 8). An increase of the apparent diffusion coefficient with film thickness was also reported for PPy film [40, 41] The impedance of finite diffusion element T is given by:

Table 4.

EIS and diffusional parameters for PPy, PPy NTs, PEDOT, and PEDOT NTs were electropolymerized on the neural microelectrodes as a function of applied charge by fitting experimental EIS data to the model in Figure 3.

QA (μC)	QA/A (μc/cm2)	T−Y0 (μS.secˆn)	B (secˆ.5)	χ2×10-4	L (μm)	τT (ms)	RT (KΩ)	CT (μF)	D ×10-6 (cm2/s)
6	0.48	2.19	0.176	1.818	2.0	30.98	84.2	0.37	1.29
9	0.72	4.24	0.151	2.636	3.5	22.8	35.61	0.64	5.37
12	0.96	5.52	0.128	1.730	5.0	16.38	23.21	0.71	15.26
18	1.44	7.86	0.124	2.862	6.5	15.38	15.78	0.97	27.47
24	1.92	9.11	0.115	1.662	7.5	13.23	11.84	1.12	42.51
36	2.88	9.87	0.098	2.619	8.3	9.6	9.93	1.23	71.76

Figure 8.

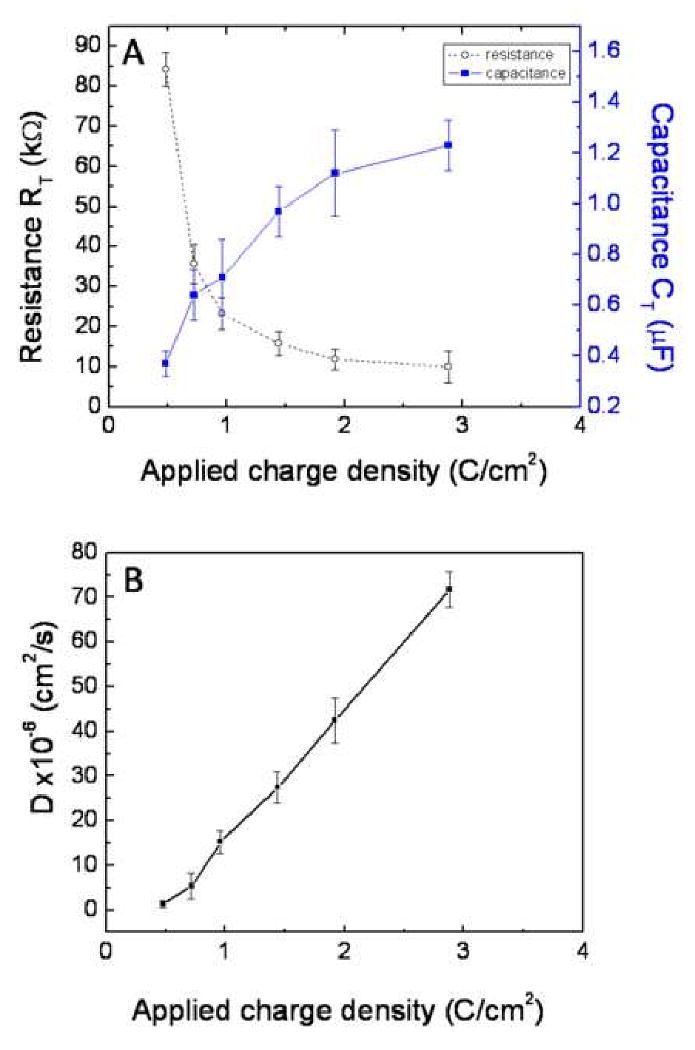
(A) Diffusional pseudocapacitance (CT) and diffusional resistance (RT) for PPy NTs as a function of applied charge density. (B) Diffusion coefficient of PPy NTs as a function of applied charge density.

$$Z_T=\frac{1}{Y_0\sqrt{i\omega }}coth[B\sqrt{i\omega }]$$ (11)

On the other hand, the theoretical impedance of finite diffusion can be calculated from Eq. (7). Therefore, the diffusional time constant τ_T (τ_T = R_TC_T), the diffusional pseudocapacitance C_T and the diffusion resistance R_T are:

$${\tau }_T=B^2$$ (12)

$$R_T=\frac{B}{Y_0}$$ (13)

Since PEDOT tended to grow more off the gold site (Figure 4C), PPy film and PPy nanotubes were thicker than PEDOT film and PEDOT nanotubes with the same applied charge density (1.44 C/cm²) during electrochemical deposition (Table 3). As discussed and shown in Table 3, CP nanotubes (PPy and PEDOT) are thicker than CP films because of the overall thickness of template electrospun nanofibers. PPy and PEDOT nanotubes also had a smaller diffusional time constants (diffusional resistance and pseudocapacitance) in comparison with PPy and PEDOT film. Consequently, the apparent diffusion coefficient of CP nanotubes (72.4 ± 3.3 cm²/s for PPy nanotubes and 13.0 ± 1.8 cm²/s for PEDOT nanotubes) was larger than the corresponding CP film (29.2 ± 1.1cm²/s for PPy film and 7.4 ± 2.1 cm²/s for PEDOT film). Such an open nanotubular structure with a high effective surface area filled with supporting electrolyte allows faster ion diffusion and exchange with the electrolyte. Berggren and colleagues demonstrated that transport of ions using CP devices could also be used to control signaling in cells [42]. Therefore, CP nanotubes are good candidates for surface modification of implantable neural prosthetic devices to facilitate transportation of ions at the interface between electrode and living tissue.

4. Conclusions

We have developed a method for fabrication of extremely low impedance and high charge transfer capacity CP nanotubes on the surface of neural microelectrodes. We have quantified the electrode-CP-electrolyte interface on the neural microelectrodes using measurement techniques, equivalent circuit modeling and theoretical analysis. Equations describing the physical properties occurring at the interface were presented and calculated values from the equations were in good agreement with the fitted parameter values. The impedance spectroscopy results showed that PEDOT nanotubes on the electrode site decreased the impedance magnitude by almost two-orders of magnitude at a frequency of 1 kHz, while there was only a one-order of magnitude decrease with PPy nanotubes. The charge transfer capacity of electrode sites modified with PEDOT nanotubes increased significantly by about three orders of magnitude. Future work would include an investigation on the influence of surface roughness and effective surface area of nanostructured CPs on the coating impedance and diffusion of ions though the polymer structure. The study presented here is expected to help facilitate a better understanding and interpretation of signal transduction and microscopic mechanisms of ion diffusion at the electrode-living tissue interface of biosensors and biomedical devices.