Abstract
Regulation of gene expression occurs largely through the binding of sequence-specific transcription factors (TFs) to genomic binding sites (BSs). We present a rigorous scoring scheme, implemented as a C program termed “ModuleFinder”, that evaluates the likelihood that a given genomic region is a cis regulatory module (CRM) for an input set of TFs according to its degree of: (1) homotypic site clustering; (2) heterotypic sie clustering; and (3) evolutionary conservation across multiple genomes. Importantly, ModuleFinder obtains all parameters needed to appropriately weight the relative contributions of these sequence features directly from the input sequences and TFBS motifs, and does not need to first be trained. Using two previously described collections of experimentally verified CRMs in mammals and in fly as validation datasets, we show that ModuleFinder is able to identify CRMs with great sensitivity and specificity.
1. Introduction
Recent technological advances have enabled both the sequencing of a large number of genomes and the generation of expansive gene expression datasets. Still, little is known about how these gene expression patterns are precisely regulated through the binding of sequence-specific transcription factors (TFs) to their DNA binding sites (BSs). Of particular interest is the organization of TF binding sites (TFBSs) into cis regulatory modules (CRMs) that coordinate the complex spatio-temporal patterns of gene expression, and to use that information to identify the CRMs themselves. Mapping TFs to their target CRMs, however, is significantly complicated in higher eukaryotic genomes by the large proportion of non-protein-coding sequence. Since a typical TFBS can be as short as ∼5 base pairs (bp), matches to its motif occur frequently by chance alone, with many of these occurrences presumably not acting to modulate gene expression. Therefore, a central challenge that must be overcome is distinguishing functional TFBSs from spurious motif matches.
To date, three indicators have been used to identify functional TFBSs. First, functional BSs for some TFs tend to occur in clusters, with multiple BSs occurring in close proximity (homotypic clustering). Second, searching for clusters containing BSs for 2 or more TFs that are believed to co-regulate can enrich for likely CRMs (heterotypic clustering). Finally, functional TFBSs are frequently conserved across evolutionarily divergent organisms1. Cross-species sequence conservation in particular has enormous potential for filtering sequence space, as many genomes have recently been sequenced, and many more are slated to be sequenced (http://www.genome.gov/10002154). The discriminatory power of phylogenetic footprinting for identifying cis regulatory elements is therefore expected to continue to increase through the use of more genomes2-6. In order to appropriately incorporate information on conservation across multiple genomes, however, a measure of TFBS conservation is required that weights each alignment genome according to its evolutionary distance not only from the query genome, but also relative to the other alignment genomes. For example, given a candidate TFBS in the human genome, observing conservation in chicken should be weighted more heavily than conservation in mouse, as mouse is evolutionarily closer to human. Moreover, if the candidate site were also conserved in rat, then this additional conservation should be weighted only slightly, given the evolutionary proximity of mouse and rat.
While numerous groups have developed approaches for the prediction of CRMs, none is optimized for practical applications. Specifically, many approaches7-9 have been based on binary scoring schemes, wherein all regions containing a threshold number of occurrences for a given combination of TFBSs are returned. These approaches suffer from the limitation that they do not prioritize among the predictions, an important feature for experimentalists as only a limited number of candidate CRMs can feasibly be validated. Additionally, the threshold value determined in any given biological system is unlikely to be generalizeable from one set of TFs and CRM type to another; thus, the appropriate discriminatory criterion must be re-discovered with each application. Alternatively, among existing continuous scoring schemes, many require large training sets10,11. Such approaches cannot be applied to a system in which there are only a handful of known examples, as is frequently the case in practical applications. Finally, among approaches that employ continuous scoring schemes and do not require training12-15, most do not systematically integrate BS clustering and conservation. We are aware of only one other approach that combines all three indicators16, but it is computationally rather slow and requires the user to specify a single sequence window size for the search. Since CRMs are known to vary greatly in size, a scoring scheme is needed that evaluates clustering and conservation over windows of varying sizes15.
We have developed a statistically rigorous scoring scheme that for any given genomic region integrates into a single score the degree of: (1) homotypic clustering; (2) heterotypic clustering; and (3) evolutionary conservation across multiple genomes. Similar to programs such as BLAST17, our score is an objective measure of the statistical significance of the observed degree of clustering and conservation that is independent of the genome and TFBSs under consideration. Thus, the scoring scheme obtains all parameters needed to appropriately weight the relative contribution of each input alignment and TFBS motif directly from the sequences and motifs themselves, and so does not need to first be trained. We have implemented this scoring scheme as a C program called “ModuleFinder,” that is algorithmically efficient and has an intuitive interface. Using two previously described collections of experimentally verified CRMs (mammalian skeletal muscle18 and D. melanogaster segmentation genes7), we show that ModuleFinder is able to identify CRMs with ∼95% sensitivity and ∼95% specificity.
2. Methods
Methods that evaluate the overall degree of conservation for a given region have been successful in identifying cis regulatory elements in metazoan genomes2,6; they do not, however, necessarily identify the CRMs through which a given set of TFs exert their regulatory roles (i.e., the TFs’ “target” CRMs). Since our ultimate goal is to identify candidate CRMs that are bound by a given set of TFs, we have developed a scoring scheme that specifically considers the conservation of a particular set of TFBSs comprising a given transcriptional regulatory model. For this, we developed a novel statistical framework that builds on earlier work. Blanchette et al. stated the substring parsimony problem and presented a rigorous and efficient algorithmic procedure for solving it19; this model was applied to the identification of candidate DNA motifs. Moses et al. used mixture models to evaluate conservation within a tree, and applied it to the identification of candidate DNA motifs from sets of co-expressed genes20; this was similar to an approach given by Prakash et al.21 Here we present a related approach for identifying candidate CRMs from input TFBS motifs.
2.1. Scoring Scheme
We define a word to be a short sequence on the DNA alphabet {A,C,G,T}, and a motif to be a collection of words all of the same length. ModuleFinder takes as input a collection of arbitrarily many motifs {m1…mm}, where each motif mi is composed of arbitrarily many words of length li. It also takes as input a set of sequences G = {g1,…gn} corresponding to genomic regions that are to be searched for instances of these motifs, as well as two sets of genomic sequences, A = {a1,…,an} and B = {b1,…,bn}, extracted from evolutionarily divergent organisms and then aligned to the sequences of G. Here, we primarily illustrate the scoring scheme for the case of two alignment genomes, but include comments on the extension to fewer or more alignments. For any gj, let gj,k denote the base at the kth position and (gj,k…gj,k+l) denote the subsequence of length l beginning at position k. If there is a match to a given motif mi at position k of sequence gj, we define it to be conserved in A (respectively, B), if it is true that the subsequence (aj,k…aj,k+l) (respectively, (bj,k…bj,k+l)) is also a word in motif mi. Note that we are not assuming that gj,k…gj,k+l = aj,k…aj,k+l, but merely that they are both words in mi.
Our basic approach is to scan each sequence in G with a series of nested windows (i.e., overlapping windows of differing sizes). In each window we count the number of occurrences of each motif and the number of these that are conserved in A and B. We then evaluate the likelihood of observing this number of matches and conserved matches under the appropriate null hypothesis, and return those windows that are statistically significant. Specifically, let X = (X1,…,Xm) be the vector whose components indicate the number of occurrences for each motif individually in a given window, and let Y = ( Y1,…, Ym) and Z = ( Z1,…, Zm) be the corresponding vectors indicating that Yi and Zi out of Xi occurrences are conserved in A and B, respectively. The window score is obtained by finding the probability of observing (X,Y,Z). This quantity will vary according to the likelihood of conservation in A and/or B, the motif frequency, and the window width. Thus, this probability can be represented by:
| (1) |
where Γ parameterizes conservation likelihood, α parameterizes motif frequencies, and w is the window width. Observe that:
| (2) |
where the relevant parameters can be split between terms in the Markov decomposition, as Pα,w(X) is unaffected by conservation likelihood, and PΓ(Y, Z | X) is unaffected by motif frequency and window size.
For a single motif mi, the term Pαi,w(Xi) of Eq. (2) is the likelihood of observing Xi occurrences under the null hypothesis that the motif matches are distributed at random. This has been proved to be well-approximated by a Poisson distribution, provided the motif occurs infrequently and the words comprising it do not exhibit extensive self-overlap.22 Thus, Pαi,w(Xi)= e-λi(λiXi/ Xi!), where λi=αi*w. The value of αi will itself be determined by both the words comprising mi, as well as genomic word frequencies. To obtain it, we estimate the frequency of each word in mi by a seventh order Markov approximation based on genomic word frequencies, and then sum these frequencies for all words in the motif.
For multiple motifs, the joint probability is given by assuming independence:
This is a simplifying assumption to make the computation tractable; the error in this approximation has, however, been proved to be bounded22.
The computation of the second term of Eq. (2), PΓ(Y , Z | X), is complicated by two factors. First, the score must reflect not only the evolutionary distances of A and B to G, but also the distances of A and B to each other. Thus, Γ must re-parameterize PΓ(Y ,Z | X) so that it becomes smaller as A and B grow more distant from G, and as the correlation between A and B decreases. Second, the quantity PΓ(Y ,Z | X) will depend not only on the phylogeny of A, B and G, but also on the degeneracy of the motifs mi. Since we have defined a given motif match to be conserved in A or B if there is a motif occurrence (but not necessarily an exact word match) at the same position in these aligned sequences, a more degenerate motif has a greater likelihood of being conserved.
We account for these difficulties as follows. Define to be the covariance matrix representing the relative proportions of A and B that can be aligned against G; thus, gives the proportion of sequence in G for which neither A nor B could be aligned, and and give the proportion for which either A or B (but not both) could be aligned, and gives the proportion for which both A and B could be aligned. Similarly, for each motif mi, define to be the covariance matrix representing the relative likelihoods of exact conservation of li positions (i.e., (gj,k…gj,k+l) = (aj,k…aj,k+l)) in A and/or B. Here, we have observed non-independence of exact conservation likelihood between adjacent positions, so we model it as a first order Markov chain.
Conservation of a completely degenerate motif is parameterized by , and conservation of a motif composed of a single word is parameterized by . The parameterization of a generic motif is between these extremes; for this, let Pi,j,k be the matrix giving the frequency of nucleotide j∈{A,C,G,T} at position k∈{1,…,li} in motif mi, and let Ei be the average entropy of the motif:
Hence, Ei=1 for a completely degenerate motif, Ei=0 for a motif composed of a single word, and Ei increases monotonically and smoothly between these extremes as the motif degeneracy increases. Therefore, we take our parameterization of Γi for mi to be a weighted average of and :
We then use Γi to compute PΓi(Yi, Zi | Xi). In a sequence window containing Xi matches to motif mi, let ai be the number that are not conserved in either A or B, let bi and ci be the number conserved in either A or B (but not both), and let di be the number that are conserved in both A and B. The following equations hold:
| (3) |
| (4) |
| (5) |
P(Yi,Zi|Xi) is therefore given by the following multinomial:
| (6) |
where the summation is performed over all values of ai, bi, ci and di satisfying Eqs. (3)-(5). To achieve computational efficiency, we make use of the following 1-dimensional parameterization, where Xi, Yi and Zi remain fixed as di is varied:
| (7) |
| (8) |
| (9) |
Thus, the summation of Eq. (6) can be performed by simply taking each value of di in the range 0 ≤ di ≤ min(Yi, Zi).
If one desires to only input one genome, it is sufficient to set A=B. The relevant parameters then simplify, and the preceding multinomial distribution collapses to a binomial distribution with parameter :
This parameterization can also be easily generalized to more than 2 alignment genomes by replacing the matrix Γi with an appropriate tensor.
This derived value of PΓ,α,w(X,Y,Z) alone is insufficient for determining statistical significance, since a measurement of distance into the appropriate tail of the distribution is also required. Therefore, we perform a summation of PΓ,α,w (X,Y,Z) extending from the observed value of (X,Y,Z) and including all values of (X,Y,Z) with an increased degree of clustering and conservation (we use log values to simplify the numerical analysis):
| (10) |
Therefore, the output score SΓ,α,w(X,Y,Z) for a given window is the linear sum of scores for the input motifs, SΓi,αi,w(Xi,Yi,Zi) , where each such term has been i automatically weighted so that more degenerate motifs contribute less. Observe also that SΓi,αi,w(Xi,Yi,Zi)=0 if and only if Xi=0, and that SΓi,αi,w(Xi,Yi,Zi) increases monotonically with increasing values of (Xi,Yi,Zi), as desired.
2.2. Implementation and Availability
ModuleFinder has been implemented in C. To minimize runtime, we pre-process each sequence of G with suffix arrays23 for efficient searching; additionally, as the algorithm proceeds, a look-up table is kept that contains a list of scores for all observed window sizes w and motif matches (X,Y,Z). ModuleFinder can scan ∼120 Mb/hr using window sizes of 300-700 bp with an increment size of 50 bp and one alignment genome on a Pentium 4 computer. The compiled code, along with README files and appropriately formatted genomes and alignments for human, mouse, rat, fly, worm and yeast based on the latest UCSC assemblies24 are available for download at our website (http://the_brain.bwh.harvard.edu).
Two additional features were included for improved practical applicability. First, it is known that TFs frequently bind to DNA as homo- and hetero-dimers. We have added to ModuleFinder the ability to take pairs of TFBSs as input, along with minimum and maximum spacer lengths between sites. The score of the dimer is computed by evaluating the probability of each component motif as in Eq. (1), then taking the product of these probabilities and summing them over all input spacings. Second, ModuleFinder allows a certain amount of ‘wiggle room’ to compensate for the potential existence of local misalignments. Specifically, given an input value r, a motif match (gj,k….gj,k+l) is considered conserved in A if there is any subsequence of (aj,k-r…aj,k+r+l) that is a word in mi. Although this does increase the likelihood of conservation, the effect is miniscule for small values of r (1≤ r ≤ 5) and has frequently identified potentially conserved sites that would have been missed otherwise.
3. Results
3.1 Validation of ModuleFinder on human skeletal muscle CRMs
In order to evaluate ModuleFinder, we used a set of positive control regions previously compiled by Wasserman et al.18 This test dataset comprises 27a skeletal muscle CRMs that have been demonstrated to direct transcription in skeletal muscle or a suitable cell-culture model system18. Each region contains a validated BS for at least one of the following 5 TFs: the Myf family (total of 39 TFBSs in the positive control set), Mef2 (26 TFBSs), SRF (20 TFBSs), Tef (12 TFBSs) and Sp1 (13 TFBSs). Of these 27 regions, 23 are located within 5 kb upstream of translational Start, and 2 within introns. As negative controls, 1000 regions of size 200 bp were randomly selected to positionally match the positive control regions: 852 (=(23/27)*1000) regions were within 5 kb of translational Start for a randomly chosen RefGene24 gene, and the remaining 148 were within introns. This matching of chromosomal locations was performed as ModuleFinder accounts for local word frequencies, which vary throughout the genome; in particular, promoter regions are known to be GC-rich.
We ran ModuleFinder on the positive and negative control regions with window sizes of 100-200 bp (increment size = 10 bp), using human sequence alone, human/mouse/rat (H/M/R) alignments and human/mouse/chicken alignments (H/M/C) obtained from UCSC Genome Browser (hg16, mm3, rn3, galGal2)24. Currently, two alternative strategies for representing TFBSs have been used by various groups in computational searches for CRMs: exact word matches to known BSs9,15, and position weight matrices (PWMs)7,10-13, which allow for extrapolation to additional BSs. To determine which of these representations had greater discriminatory power, we performed our searches both ways, using a PWM threshold value of 1 standard deviation (SD) below the motif average25. We used a “jack-knife” strategy11 for these searches, whereby the BSs for each CRM were excluded from the construction of the PWM used to search that CRM, and similarly the exact word matches from each CRM were excluded in the search of that CRM. In addition, since in vitro binding experiments had been performed for Mef226 and SRF27, we also added those BSs to both searches.
The results of these evaluations are shown in Table 1. Here, we have reported those values for sensitivity and specificity which maximally discriminate between the positive and negative control sets (i.e., using the threshold score such that the difference between the sensitivity and specificity is minimized). Since there was great variability in score among the positive control regions (see Figure 1; i.e., the top positive control region received a score of -11.23 and the worst positive control region scored only -1.22 (positive controls: mean = -4.69, SD = 2.24; negative controls: mean = -0.42, SD = 0.81)), we also performed a t-test on the positive and negative control region means, in order to measure the effectiveness of ModuleFinder on regions falling far from the threshold score.
Table 1.
ModuleFinder was run on a human skeletal muscle dataset using both exact word matches and PWMs. The searches were done using no alignments, mouse/rat alignments, and mouse/chicken alignments. For each search, sensitivity (“Sens.”), specificity (“Spec.”), and a t-test on the means (“p-val”) were computed, as compared to matched random regions.
| Human Alone | Human/Mouse/Rat | Human/Mouse/Chicken | ||||
|---|---|---|---|---|---|---|
|
| ||||||
| Exact | PWM | Exact | PWM | Exact | PWM | |
|
| ||||||
| Sens. | 88.9% | 92.6% | 92.6% | 96.3% | 92.6% | 92.6% |
| Spec. | 90.1% | 89.2% | 88.8% | 94.4% | 87.4% | 94.4% |
| p-val | 1.19×10-8 | 6.5×10-10 | 2.5×10-10 | 1.4×10-10 | 4.5×10-10 | 7.1×10-10 |
Figure 1.
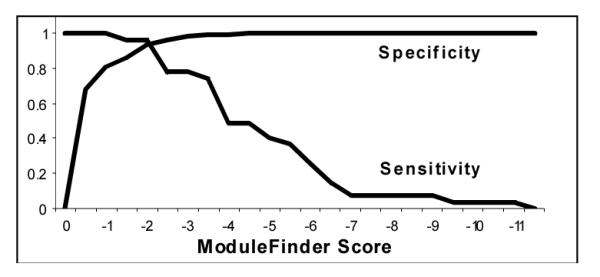
Sensitivity and specificity of ModuleFinder on skeletal muscle test regions, versus randomly selected control regions.
On this dataset, ModuleFinder achieved a maximum sensitivity of 96.3% and specificity of 94.4% on the H/M/R PWM searches. Moreover, the PWM approach consistently gave better discrimination than exact word matches. Much of this improved discrimination, however, is an artifact of the jack-knife procedure, which has a stronger effect on exact match searches. Here, using the complete set of BSs (i.e., without the jack-knife), exact word matching achieves 100% sensitivity and 95.1% specificity (we removed degenerate flanking sequences for all searches with exact words). In addition, these results indicate that the H/M/R searches reliably outperformed the H/M/C searches. There are two possible explanations for this: 1) the chicken genome is not yet complete, and the appropriate alignment regions may not have been sequenced yet; 2) the underlying mechanisms of transcriptional regulation are not actually conserved in an organism as distant as chicken. Neither of these hypotheses can be ruled out until the completion of the chicken genome.
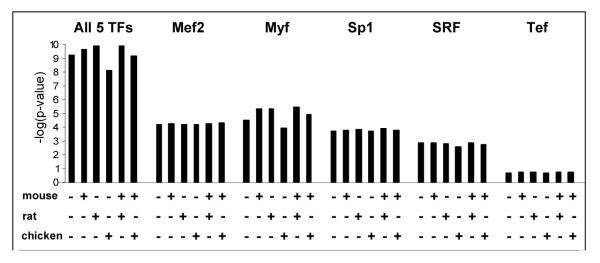
Since ModuleFinder was specifically developed to integrate homotypic clustering, heterotypic clustering, and conservation, we wanted to determine which of these features were most contributory to discriminatory power. In order to assess this, we ran ModuleFinder on the positive and negative control regions using no alignments, one alignment (each of mouse, rat and chicken), and two alignments (H/M/R and H/M/C). These searches were repeated with each TF individually, as well as with all 5 TFs together. In Figure 2, we show the negative logarithm of the p-values obtained from t-tests on the positive versus negative control regions for each of these searches. Here the mouse and rat alignments improved discriminatory power, but little was gained by using both genomes, because of their evolutionary proximity. Somewhat surprisingly, using chicken actually reduced discrimination relative to human alone. This was unexpected, as it implies that our negative controls are more likely to be conserved than these 27 regions. However, this effect could be an artifact of the small size of the positive controls and gaps in the chicken genome (only 13/27 positive controls had any alignable chicken sequence).
Figure 2.
Negative log of p-values obtained from t-test on means between positive and negative controls. ModuleFinder was run with various combinations of mouse, rat, and chicken alignments (indicated by +/-), using all 5 TFs together, and each TF alone.
Finally, at least four other algorithms have used overlapping subsets of this dataset as positive controls11-13,28, achieving sensitivities between 59% and 66%, and specificities between 95.3% and 97.1% (see Table 2). Thus, ModuleFinder appears to have comparable specificity but greater sensitivity. However, note the following caveats for this comparison. First, because ModuleFinder uses evolutionary conservation as a central component and because few vertebrate genomes have been sequenced, we limited our searches to the subset of the original compilation for which human/rodent alignments were available18. The other algorithms tested on this dataset did not consider conservation, and thus used the original, larger compilation that included CRMs obtained from diverse organisms including chicken, hamster, rabbit, pig and cow11. Frith et al.12,13 trimmed this larger set11 to a subset of 27 regions, but their subset overlapped with ours by only 15 genes. Second, each group used a different set of negative controls. The original paper by Wasserman et al.11 used a set of negative control regions similar to our set; it was composed of 200 bp regions selected from the Eukaryotic Promoter Database. Comet and Cister were each tested on 300 bp regions that were selected to overlap well-characterized transcriptional Starts12,13. Finally, MSCAN28 measured specificity by looking at the “hit rate” in contiguous stretches of the Fugu genome.
Table 2.
Relative performance of ModuleFinder: Sensitivities and specificities, as reported by groups using overlapping subsets of the skeletal muscle dataset. Logistic regression, Cister, Comet and ModuleFinder specificities refer to 200-300bp portions of the human genome; the MSCAN specificity was ascertained using large stretches of Fugu sequence.
3.2 Other validations of ModuleFinder
In addition to the mammalian skeletal muscle set, we have also tested ModuleFinder on a D. melanogaster dataset that comprises 20 transcriptional enhancers from 9 genes known to be co-regulated during anterior-posterior segmentation of fly embryos7. Using the D. melanogaster/D. pseudoobscura alignments and a protocol similar to that described in Section 2.1, ModuleFinder was able to discriminate this collection of CRMs from randomly chosen noncoding regions with 95% sensitivity and 95% specificity (Philippakis et al., manuscript in preparation). In addition to these in silico confirmations, we have also successfully applied ModuleFinder to predict CRMs in three biological systems: (1) development of the fly pericardium (Michaud et al., manuscript in preparation), (2) development of fly muscle founder cells (Philippakis et al., manuscript in preparation), and (3) mammalian myogenesis (Warner et al., manuscript in preparation). For mammalian myogenesis, we applied the same 5 TFs and their BSs as described above; indeed much of the work presented here was done for the explicit purpose of selecting optimized BSs and sequence alignments before attempting to predict novel mammalian CRMs.
4. Discussion and Future Directions
We have presented a statistically rigorous approach for scoring windows of genomic sequence according to their likelihood of containing BSs for a collection of input TFs. The approach systematically integrates homotypic clustering, heterotypic clustering and evolutionary conservation across multiple genomes into a single, objective scoring scheme that does not require training. Additionally, our algorithm, implemented as a C program called “ModuleFinder,” is publicly available for download, along with pre-processed genomes and alignments for yeast, worm, fly, mouse, rat, and human, at our lab website (http://the_brain.bwh.harvard.edu). The current version of ModuleFinder considers up to two alignment genomes as input, and we are currently expanding it to accept arbitrarily many genomes.
We have tested ModuleFinder on a set of human skeletal muscle CRMs using a variety of genome alignments and TFBSs, and have achieved a maximum sensitivity and specificity of 96% and 94%. On this dataset, improved sensitivity and specificity were achieved by using mouse and rat alignments in the searches, whereas chicken alignments actually decreased sensitivity and specificity. Furthermore, PWMs resulted in improved sensitivity and specificity over exact TFBS matches. Preliminary results indicate that ModuleFinder can successfully predict novel CRMs in human myoblasts (Warner et al., manuscript in preparation). In addition, on a D. melanogaster segmentation gene dataset with D. pseudoobscura as the alignment genome, ModuleFinder achieved sensitivity and specificity of 95% and 95%. We have also predicted and experimentally validated several novel CRMs in the developing fly mesoderm (Philippakis et al., manuscript in preparation). We expect that in the future we and others will use ModuleFinder to further refine transcriptional regulatory models for CRMs in particular biological systems and thus discover how the associated TFBSs are organized to confer specific gene expression patterns.
5. Acknowledgments
The authors thank Bertrand Huber and Jason Warner for helpful discussion, and Mike Berger, Mark Umbarger, and Roman Yelensky for critical reading of the manuscript. This work was funded in part by a PhRMA Foundation Informatics Research Starter Grant (M.L.B.), a William F. Milton Fund Award (M.L.B.), and NIH/NHGRI R01 HG02966-01 (M.L.B.). A.A.P. was supported in part by a National Defense Science and Engineering Graduate Fellowship from the Department of Defense, and an Athinoula Martinos Fellowship from HST.
Footnotes
The original collection gave 28 genes, but we removed the gene Rb1 as there were no confirmed TFBSs for the listed TFs.
References
- 1.Bulyk ML. Genome Biol. 2003;5:201. doi: 10.1186/gb-2003-5-1-201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Boffelli D, et al. Science. 2003;299:1391–4. doi: 10.1126/science.1081331. [DOI] [PubMed] [Google Scholar]
- 3.Cliften P, et al. Science. 2003;301:71–6. doi: 10.1126/science.1084337. [DOI] [PubMed] [Google Scholar]
- 4.Kellis M, Patterson N, Endrizzi M, Birren B, Lander ES. Nature. 2003;423:241–54. doi: 10.1038/nature01644. [DOI] [PubMed] [Google Scholar]
- 5.McGuire AM, Hughes JD, Church GM. Genome Res. 2000;10:744–57. doi: 10.1101/gr.10.6.744. [DOI] [PubMed] [Google Scholar]
- 6.Thomas JW, et al. Nature. 2003;424:788–93. doi: 10.1038/nature01858. [DOI] [PubMed] [Google Scholar]
- 7.Berman BP, et al. Proc. Natl. Acad. Sci. USA. 2002;99:757–62. doi: 10.1073/pnas.231608898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Halfon MS, Grad Y, Church GM, Michelson AM. Genome Res. 2002;12:1019–28. doi: 10.1101/gr.228902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Markstein M, Markstein P, Markstein V, Levine MS. Proc. Natl. Acad. Sci. USA. 2002;99:763–8. doi: 10.1073/pnas.012591199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Krivan W, Wasserman WW. Genome Res. 2001;11:1559–66. doi: 10.1101/gr.180601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wasserman WW, Fickett JW. J. Mol. Biol. 1998;278:167–81. doi: 10.1006/jmbi.1998.1700. [DOI] [PubMed] [Google Scholar]
- 12.Frith MC, Hansen U, Weng Z. Bioinformatics. 2001;17:878–89. doi: 10.1093/bioinformatics/17.10.878. [DOI] [PubMed] [Google Scholar]
- 13.Frith MC, Spouge JL, Hansen U, Weng Z. Nucleic Acids Res. 2002;30:3214–24. doi: 10.1093/nar/gkf438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rajewsky N, Vergassola M, Gaul U, Siggia ED. BMC Bioinformatics. 2002;3:30. doi: 10.1186/1471-2105-3-30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rebeiz M, Reeves NL, Posakony JW. Proc. Natl. Acad. Sci. USA. 2002;99:9888–93. doi: 10.1073/pnas.152320899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sinha S, van Nimwegen E, Siggia ED. Bioinformatics. 2003;19(Suppl 1):i292–301. doi: 10.1093/bioinformatics/btg1040. [DOI] [PubMed] [Google Scholar]
- 17.Altschul SF, Gish W, Miller W, Myers EW, Lipman DJ. J. Mol. Biol. 1990;215:403–10. doi: 10.1016/S0022-2836(05)80360-2. [DOI] [PubMed] [Google Scholar]
- 18.Wasserman WW, Palumbo M, Thompson W, Fickett JW, Lawrence CE. Nat. Genet. 2000;26:225–8. doi: 10.1038/79965. [DOI] [PubMed] [Google Scholar]
- 19.Blanchette M, Schwikowski B, Tompa M. J. Comput. Biol. 2002;9:211–23. doi: 10.1089/10665270252935421. [DOI] [PubMed] [Google Scholar]
- 20.Moses AM, Chiang DY, Eisen MB. Pac. Symp. Biocomput. 2004:324–35. doi: 10.1142/9789812704856_0031. [DOI] [PubMed] [Google Scholar]
- 21.Prakash A, Blanchette M, Sinha S, Tompa M. Pac. Symp. Biocomput. 2004:348–59. doi: 10.1142/9789812704856_0033. [DOI] [PubMed] [Google Scholar]
- 22.Reinert G, Schbath S, Waterman MS. J. Comput. Biol. 2000;7:1–46. doi: 10.1089/10665270050081360. [DOI] [PubMed] [Google Scholar]
- 23.Irving RW, Love L. Technical Report no. TR-2001082 of the Computing Science Department of Glasgow University. 2001. [Google Scholar]
- 24. http://www.genome.ucsc.edu.
- 25.Stormo GD. Bioinformatics. 2000;16:16–23. doi: 10.1093/bioinformatics/16.1.16. [DOI] [PubMed] [Google Scholar]
- 26.Andres V, Cervera M, Mahdavi V. J. Biol. Chem. 1995;270:23246–9. doi: 10.1074/jbc.270.40.23246. [DOI] [PubMed] [Google Scholar]
- 27. http://www.cognia.com.
- 28.Johansson O, Alkema W, Wasserman WW, Lagergren J. Bioinformatics. 2003;19(Suppl 1):i169–76. doi: 10.1093/bioinformatics/btg1021. [DOI] [PubMed] [Google Scholar]