Abstract
The byssal threads of the California mussel, Mytilus californianus, are highly hysteretic, elastomeric fibers that collectively perform a holdfast function in wave-swept rocky seashore habitats. Following cyclic loading past the mechanical yield point, threads exhibit a damage-dependent reduction in mechanical performance. However, the distal portion of the byssal thread is capable of recovering initial material properties through a time-dependent healing process in the absence of active cellular metabolism. Byssal threads are composed almost exclusively of multi-domain hybrid collagens known as preCols, which largely determine the mechanical properties of the thread. Here, the structure-property relationships that govern thread mechanical performance are further probed. The molecular rearrangements that occur during yield and damage repair were investigated using time-resolved in situ wide angle X-ray diffraction (WAXD) coupled with cyclic tensile loading of threads and through thermally enhanced damage-repair studies. Results indicate that the collagen domains in byssal preCols are mechanically protected by the unfolding of sacrificial non-collagenous domains that refold on a slower time-scale. Time-dependent healing is primarily attributed to stochastic recoupling of broken histidine-metal coordination complexes.
Keywords: self-healing, collagen, mussel, byssus, histidine
1. Introduction
Nature has evolved a variety of damage-tolerant and even self-healing materials (Smith et al., 1999; Keckes et al., 2003; Fantner et al., 2005; Holten-Andersen et al., 2007; Rapoport and Shadwick, 2007). Understanding the mechanisms underlying natural damage-repair processes will aid ongoing efforts to engineer this desirable property into synthetic materials (Chen et al., 2002; Zwaag, 2007). The byssal threads of marine mussel species are shock-absorbing guy-lines that secure the organism to rocks in wave-swept seashore habitats and exhibit remarkable self-repair properties (Carrington and Gosline, 2004; Harrington and Waite, 2008a). Threads from the California mussel, Mytilus californianus are ∼200 μm in diameter, 2-5 cm in length and as can be seen in Fig. 1, are divided morphologically into two distinct regions known respectively as the proximal (closer to the organism) and the distal portions (closer to the substrate) (Harrington and Waite, 2008a). These two regions of the thread are also mechanically and compositionally distinct, with a gradual transition from one to the other (Bell and Gosline, 1996; Harrington and Waite, 2008a). The proximal region of the thread has quite unique and interesting mechanical properties (Bell and Gosline, 1996); however, the focus of this study is the distal region.
Figure 1. Mussel byssal threads.
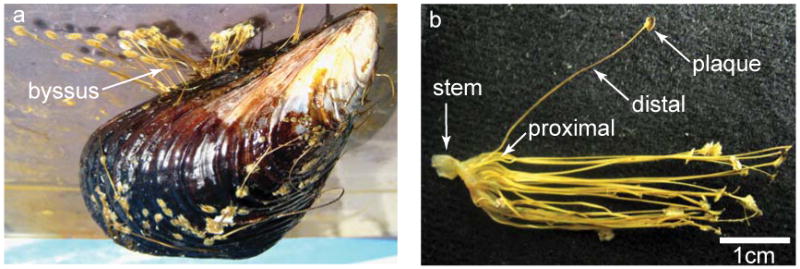
a) Marine mussels attach to available surfaces in rocky seashore habitats with a fibrous holdfast known as a byssus. b) Each byssal thread is individually formed from a mesogenic protein secretion and merged with the growing stem, which provides the linkage between the soft mussel tissue and the byssus. The threads adhere to surfaces via an adhesive plaque made up of numerous dopa-containing proteins. The thread itself is further divided into two morphologically, mechanically, and compositionally distinct regions known as the proximal and distal portions, with a gradual transition from one to the other.
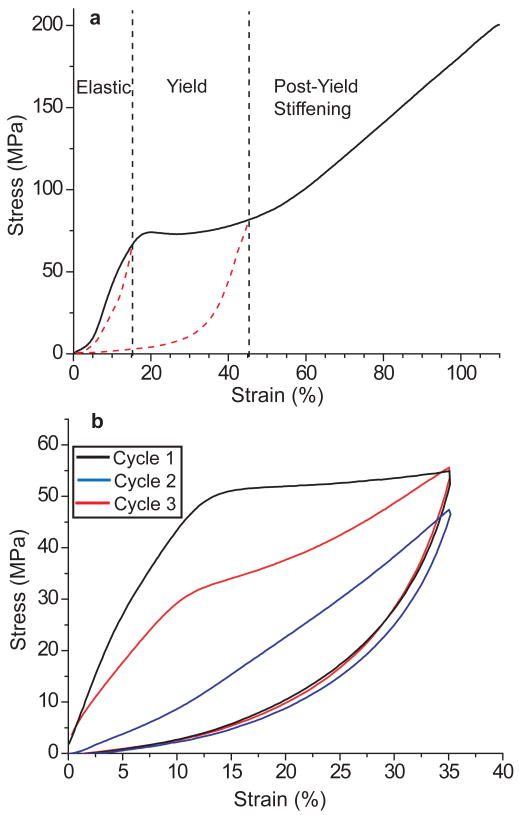
At low strains the distal portion of each thread behaves as a stiff and resilient elastomer similar to tendon; however, whereas tendon fails between 10-15% strain, byssal threads yield and extend as far as 100% strain, providing an energy-to-break comparable to Kevlar (Fig. 2a) (Gosline et al., 2002; Carrington and Gosline, 2004). When re-loaded immediately after being pulled beyond the yield point, thread stiffness and strain energy are significantly decreased (Fig. 2b) (Carrington and Gosline, 2004). While mechanical yield is typically associated with the point at which engineered polymers incur irreversible damage, the distal portion of the mussel byssal thread recovers to pre-yield conditions through a time-dependent damage repair process (Carrington and Gosline, 2004) (Fig. 2b). Notably, recovery proceeds in the absence of active metabolism since threads are completely acellular, making the byssus a particularly attractive biomimetic model for natural self-healing.
Figure 2. Mechanical performance of the distal portion of byssal threads under tensile load.
a) Threads exhibit three well-defined mechanical regimes during loading. At low strain (<15%), threads behave quasi-elastically, similar to tendon, with a Young's modulus of 500-900 MPa and a resilience of nearly 90%. Between ∼15-45% strain, threads undergo mechanical yield at nearly constant load. After yield, stress increases dramatically until catastrophic failure at ∼100% strain. Red dashed lines represent typical return curves of threads cycled within the elastic and yield regimes. b) A single thread cyclically loaded three times with no rest after the first cycle and 1 h rest after the second. The second cycle illustrates the loss of stiffness and strain energy associated with yield, and the third cycle depicts the time-dependent self-healing of byssal threads.
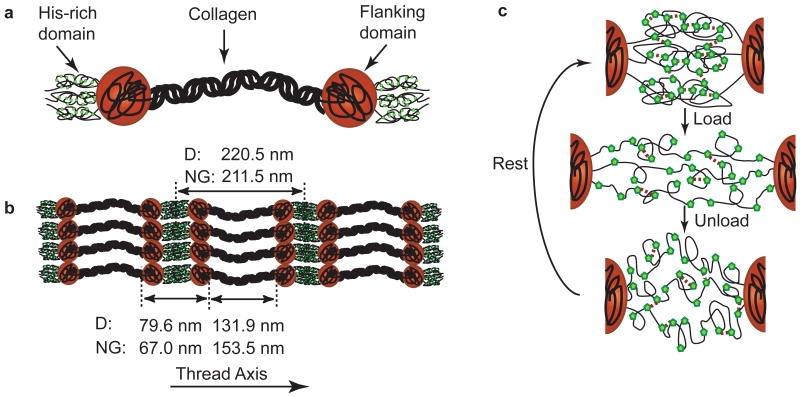
The principal protein components of byssal threads are block co-polymer-like hybrid collagens known as preCols (Harrington and Waite, 2008a) (Fig. 3). Two variants of preCol (denoted preCol-D and -NG) compose ∼96% of the distal region of byssal threads by dry weight (Waite et al., 2002), and thus their nanoscale structural and biochemical properties are directly coupled to thread mechanics (Hassenkam et al., 2004). AFM studies of threads show preCols aligned in a smectic array parallel to the thread axis (Fig 3b) (Hassenkam et al., 2004). As previously determined through biochemical studies, the block domains of preCols include a central collagen domain, variable flanking domains, and histidine-rich terminal domains (Fig. 3a). The collagen domain is a rigid, triple helical rod-like region virtually homologous to that found in tendon and bone (Waite et al., 2002; Hassenkam et al., 2004). The variable flanking domains surrounding the collagen differ between preCol-D and -NG and the protein sequences resemble known load-bearing protein motifs; namely dragline silk and Gly-rich plant cell wall protein, respectively (Harrington and Waite, 2007). The His-rich domains at the N- and C-termini resemble motifs known to coordinate with transition metal ions (Auld, 2001) and demonstrated to confer important structural and mechanical consequences (Schmitt et al., 2000; Vaccaro and Waite, 2001; Broomell et al., 2006; Harrington and Waite, 2007; Harrington and Waite, 2008b; Srivastava et al., 2008). The presence of elevated levels of zinc and copper ions has been detected previously in byssal threads, and reversible breaking and reforming of His-metal complexes have been implicated in byssal thread yield and healing (Fig. 3c) (Coombs and Keller, 1981; Vaccaro and Waite, 2001; Harrington and Waite, 2007). Here, the role of the preCols and their distinct domains in the molecular mechanism of yield and self-healing was further investigated in byssal threads of the California mussel, Mytilus californianus utilizing in situ wide-angle X-ray diffraction and studies probing the temperature-dependence of the rate of damage-repair.
Figure 3. Schematic of preCol morphology, assembly, and behavior under load.
a) PreCols are block co-polymer-like proteins with clearly defined modules including a central bent-core collagen domain, adjacent flanking domains, and terminal histidine-rich domains. The rigid rod-like collagen domains have a well-defined triple helical structure and make up about half of the protein by amino acid quantity. The flanking domains of preCol-D are reminiscent of dragline-silk and are likely more tightly folded than the glycine-rich domains of preCol-NG. His-rich domains at the N- and C-termini of preCols form coordination complexes with transition metals, which are believed to stabilize the domains. PreCol-D and -NG domain lengths were calculated based on sequence data and AFM measurements. b) PreCols are observed to assemble into highly ordered smectic arrays in series with C2 symmetry (Hassenkam et al., 2004). When tensile load is applied to threads, it is transferred along the long axial filaments of preCol. (c) illustrates a molecular level schematic model of His-dependent healing in threads. Green pentagons represent “sticky” His residues interspersed in the amorphous chains of the His-rich domains between two adjacent preCol triple helices. For simplicity of representation in the schematic, a cross-link is formed between two His residues; however, in reality a coordination cross-link would require 3-4 histidines as ligands. In the virgin state prior to applied yield, the His-rich domains are folded in such a way as to supply the largest amount of resistance under tensile load (highest stiffness). When extended past yield, many of the cross-links are ruptured, allowing the folded chains to extend and reveal hidden contour length. The sacrificial breaking of these bonds prevents catastrophic failure of the thread and provides the characteristic hysteretic behavior of the distal portion of byssal threads. When the load is removed, the His-rich domain returns to its initial length, but is not immediately refolded to the “ideal” state. Through stochastic vibrations of the His-rich chains, the His-residues eventually form stable cross-links and over time will recover to a stiff conformation.
2. Materials and Methods
2.1 Specimen preparation
M. californianus mussels maintained in mariculture at 12-15°C were arranged to form threads on a polyacrylic surface from which the threads could be easily harvested without pre-loading them. The distal portion of freshly grown threads (3-5 days old) was carefully removed and placed in seawater at 20°C for at least 1 week prior to testing. Threads obtained in this fashion were used for both X-ray studies and studies on self-repair.
2.2 Synchrotron X-ray measurements
Time-resolved wide-angle X-ray diffraction (WAXD) combined with in-situ tensile testing of byssal threads was carried out on the MuSpot beamline at the synchrotron source BESSY (Berlin Elektronenspeicherring Gesellschaft m.b.H., Berlin, Germany), (Paris et al., 2007) with an X-ray wavelength of 0.999873 Å and a beam size of 30 μm. A 2D CCD detector (MarMosaic 225, Mar USA, Evanston, USA) with pixel size of 73.24 μm and resolution of 3072 × 3072 pixels was used to acquire the WAXD frames. Calibration was carried out with a corundum (Al2O3) standard, giving a sample to detector distance of 297.3 mm. A specially designed tensile test apparatus, applied previously for in-situ measurements on bone and tendon (Gupta et al., 2006), was used to test the fibers. The mechanical test apparatus was controlled using custom programs written in Labview version 7 (National Instruments Germany GmbH, München, Germany) (Gupta et al., 2006). During a typical tensile test (described below), WAXD images were acquired by the CCD detector with an exposure time of 30 s per frame. Between each image acquisition, the tensile stage was moved vertically by 60 μm, so as not to overexpose any particular region of the fiber to the direct X-ray beam.
2.3 Mechanical testing of byssal threads
For mechanical testing, the distal regions of threads were secured between two pieces of cardstock at both ends with cyanoacrylate glue. Cardstock loaded threads were carefully secured in the grips of the tensile tester and were kept in seawater (pH ∼8.0) until just prior to testing. Hydration was maintained during the testing period with a fine mist of distilled water sprayed from a nebulizer (Invacare, Elyria, OH USA). Threads were loaded at an extension rate of 2.4 mm min-1 until they began to exhibit post-yield stiffening behavior (between 60-70% strain) and were then cycled back until load reached 0 MPa (∼5-15% strain). They were then rested for 1 min prior to beginning a second cycle to the same final strain as the first cycle. The diameter of each thread was measured with an optical microscope as in previous studies in order to determine cross-sectional area and calculate stress values from the load data. (Harrington and Waite, 2007)
2.4 X-ray data analysis
The strain experienced by the collagen domain was extracted from in situ time-resolved wide angle x-ray measurements during tensile strain of the threads. Using the analysis program Fit2D, (Hammersley, 1997) the intensity around the collagen WAXD reflection at 0.287 nm was integrated radially using the CAKE command, and the shift and change in peak position was tracked as a function of externally applied stress and strain. Due to Ewald sphere geometry effects, the measured peak profile was not symmetric about the maximum, and hence an asymmetric Gaussian function (Galat and Goldberg, 1987) combined with a linear background term was used for fitting the measured peak profile. Percentage changes of the peak position relative to the unstressed case were used as a marker for the molecular strain in the collagen helix. Background (empty beam) intensities were at least an order of magnitude smaller than the intensity from the sample at the wavevectors corresponding to the collagen 0.287 nm reflection, and hence were not subtracted separately but were included in the linear background term. Custom scripts were written in the Perl programming language for batch file processing and fitting using Gnuplot for Windows (www.gnuplot.info).
2.5 Thermally-enhanced self-repair studies
As in the x-ray studies, threads were prepared for mechanical testing by sandwiching them between cardstock at both ends with cyanoacrylate glue. Immediately prior to testing, threads were submerged in seawater at room temperature and were kept hydrated during the brief testing period with a fine mist of distilled water sprayed from a nebulizer (Invacare). All mechanical tests were performed at room temperature. Threads were secured in mechanical grips and using a Bionix 200 tensile tester (MTS, Eden Prarie, USA), were cycled twice to 35% strain with no rest interval between cycles. Load and extension data were recorded with the Testworks 4 software (MTS) and were converted to engineering stress and strain. After the two cycles, threads were carefully removed from the grips and placed in seawater baths at the following temperatures (4°C, 17°C and 37°C) and were rested for the following time intervals (1 h, 24 h and 168 h). The glass transition temperature of byssal threads was previously measured to be 6°C and the “operational” temperature range was found to be 10-50°C, (Aldred et al., 2007) suggesting that molecular motion will be especially inhibited during the 4°C treatment and that no lasting damage is done by the 37°C treatment. Another set of threads was rested in 50 mM citrate buffer, pH 4.0 at 37°C for the same time intervals. By treating threads at pH 4, it is believed, based on a previous study, that one is primarily disrupting His-metal cross-linking, with minimal effect on the other preCol domains. (Harrington and Waite, 2007) After resting, each thread was re-acclimated briefly in seawater or citrate buffer at room temperature, carefully placed back in the grips, and again cycled twice to 35% strain. The second cycles before and after resting should be nearly identical, (Carrington and Gosline, 2004) and this was used as a quality control when analyzing data. Stiffness was calculated for each cycle as the maximum slope of the stress-strain curve using the Testworks 4 software (MTS). Strain energy was determined with Origin 7.5 graphing software (OriginLab, Northampton, MA USA) as the area enclosed in a stress-strain cycle. Healing efficiency (η) was determined using both strain energy and stiffness, with the following equation:
One-way analysis of variance (ANOVA) with a post-hoc Scheffé test for pairwise comparisons was performed to determine the statistical significance of healing efficiencies during different temperature/pH treatments. The null hypothesis was rejected at a significance level (P) of 0.05.
3. Results
3.1 in situ X-ray measurements
Time-resolved wide angle X-ray diffraction (WAXD) using a synchrotron source was performed on the distal portion of byssal threads during tensile stress-strain cycles to ∼70% strain, enabling direct examination of molecular scale deformation in real time. WAXD patterns obtained from the distal portion of threads at rest are consistent with earlier studies (Mercer, 1952; Rudall, 1955), but offer much improved resolution (Fig. 4). Several prominent features are apparent including faint peaks characteristic of silk-like beta-sheet structure (Geddes et al., 1968), two equatorial peaks in the low angle regime corresponding to the lateral collagen packing and the beta sheet micellar unit (Geddes et al., 1968; Misof et al., 1997), respectively, and a third order layer line associated with collagen triple helical structure. Silk-like structures in threads were previously attributed to a loosely packed beta-sheet arrangement of the preCol-D flanking domains (Mercer, 1952; Rudall, 1955). Due to the diffuse diffraction and weak signal, however, it was not possible to follow the changes in beta sheet structure during cyclic loading of threads. In collagenous materials, the third order layer line indicates the spacing between adjacent amino acid residues on the backbone of the triple helix. At rest in the threads, this peak is measured at 0.2868±0.0007 nm, which is consistent with previously measured values from tendon (Sasaki and Odajima, 1996).
Figure 4. Typical WAXD pattern of thread at rest.
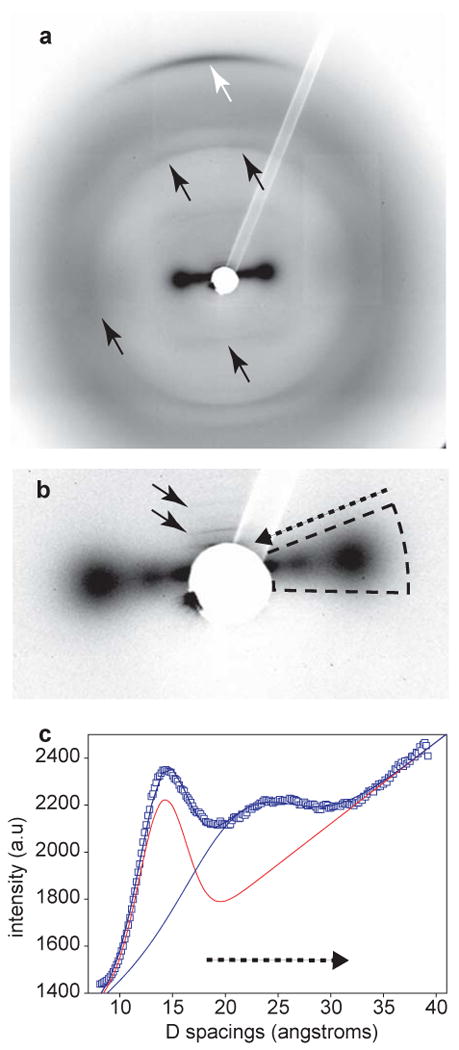
a) 2D CCD X-ray image showing the helical reflection due to collagen (white arrow) and the reflections due to silk-like β-sheet structure (black arrows). To show the contributions from both collagen and silk-like structure more clearly, the small angle region is magnified in (b), where two distinct reflections along the equatorial (horizontal) direction are seen in the indicated sector. Solid black arrows indicate the meridional small angle X-ray scattering (SAXS) reflections. The equatorial features are shown quantitatively in (c), where integrated intensity profiles in the sector show two distinct peaks, one due to the intermolecular (wet) collagen spacing at ∼ 14 Å (Misof et al., 1997), and a second, broader one at ∼ 21 Å, which we tentatively identify as corresponding to the width of the micellar units in the silk like structure (Geddes et al., 1968).
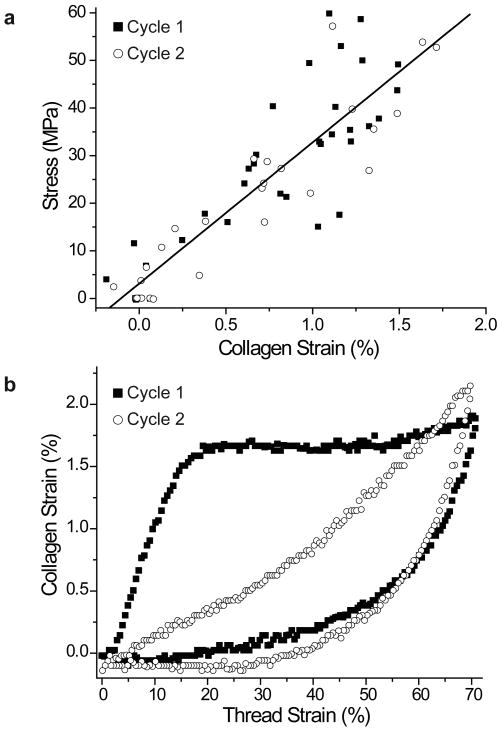
Changes observed in the position of the third order layer line during cyclic thread loading were used to determine the molecular strain of the preCol collagen domains during two consecutive cycles with no rest between. Plotting thread stress vs. molecular strain reveals that the collagen domain behaves essentially elastically with a Young's modulus of 2.97±0.19 GPa (mean ± s.e.m., n=65 data points) during both cycles up to thread strain values of ∼70% (Fig 5a). The experimentally determined modulus was used to convert thread stress values to derived instantaneous molecular strain of the collagen domain for thread specimens. Fig. 5b shows the derived molecular strain plotted vs. the thread strain for a representative specimen from this study. In the first cycle of Fig. 5b, there is an immediate increase in the collagen strain to a value of ∼1.7% which peaks at the yield point and stays more or less constant throughout yield. Collagen strain begins to increase again during the post-yield region, but even at >60% thread strain never exceeds 2% (Fig. 5b). Derived collagen strain values for the second loading cycle are lower for a given thread strain than in the first cycle up to threads strains of ∼50% (Fig. 5b).
Figure 5. Collagen molecular strain during cyclic loading of byssal threads.
a) Collagen strain values from both cycles of five thread specimens are plotted against thread stress. The black line indicates a linear regression curve of the data points (N=65, R2=0.80) and reveals that the collagen behaves elastically at thread strain values up to 70%. The Young's modulus of the collagen domain was determined from this plot to be 2.97±0.19 GPa (mean±s.e.m), and this value was used to convert thread stress values to derived instantaneous collagen strain values as seen in the representative sample in (b). Cycle 2 follows cycle 1 with little rest between.
The lengths of Mytilus galloprovincialis preCols were measured in a previous investigation by atomic force microscopy (Hassenkam et al., 2004). Based on these values, the resting lengths of preCol-NG and -D from M. californianus are estimated to be 211.5 nm and 220.5 nm, respectively. Using the rise-per-residue of the preCol collagen domains obtained in this study from WAXD, it is possible to calculate the length of the preCol collagen domains at rest (NG=131.9 nm, D=153.5 nm) because the number of amino acids in each is known from the cDNA deduced protein sequence (GenBank accession numbers: EU120661 and EU120662 for -D and -NG, respectively). When the calculated lengths of the collagen domains are subtracted from the estimated length of the entire unstrained preCol molecule, the net result represents the resting length of the non-collagen domains, i.e. the combined length of the flanking and His-rich domains at rest (NG=79.6 nm, D=67.0 nm) (Fig. 3b).
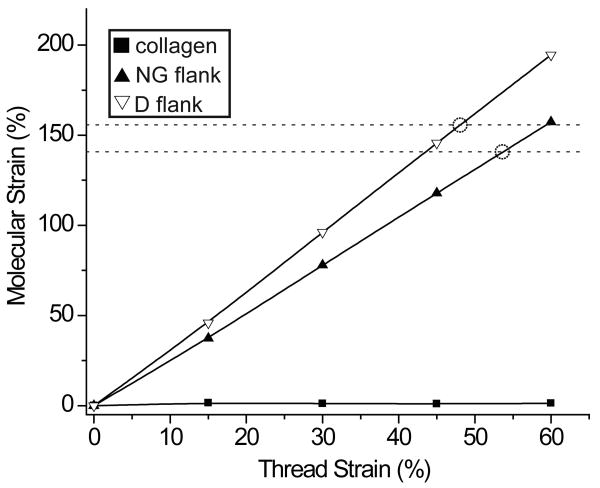
The number of amino acid residues in the non-collagen domains is known, so by using a maximum allowable bond length value of 0.38 nm between residues, it is possible to calculate the maximum length to which these collective domains can be unraveled (NG= 191.1 nm, D= 169.9 nm). Taking the calculated resting and stretched lengths of the non-collagen domains of preCol-D and -NG and assuming a series model of preCol alignment, it was determined that the unraveling of this “hidden” contour length could account for approximately half of the macroscopic breaking strain of the thread which is observed to occur at ∼100% strain (Bell and Gosline, 1996). The results of these calculations are illustrated in Fig. 6.
Figure 6. Calculated strain of preCol domains during thread elongation.
This graph illustrates the predicted strain of the combined flanking and His-rich domains of a single preCol-NG or -D molecule during thread extension assuming a series model of preCol alignment and based on the calculated resting length of each. Horizontal dashed lines represent calculated maximal extension strains for the flanking/His-rich domains of preCol-NG and -D. The thread strain value at which the calculated molecular strain crosses the respective dashed line (indicated by a dashed circle) denotes the maximum possible thread strain following unraveling of the folded flank/His-rich domain of each particular preCol variant. Since threads are extensible to ∼100% strain, these calculations indicate that the extension of preCol domains can account half of this value. This suggests that higher order hierarchical structures must also play a role. The collagen strain calculated from the WAXD results is also included in the figure.
3.2 Thermally-enhanced self-repair studies
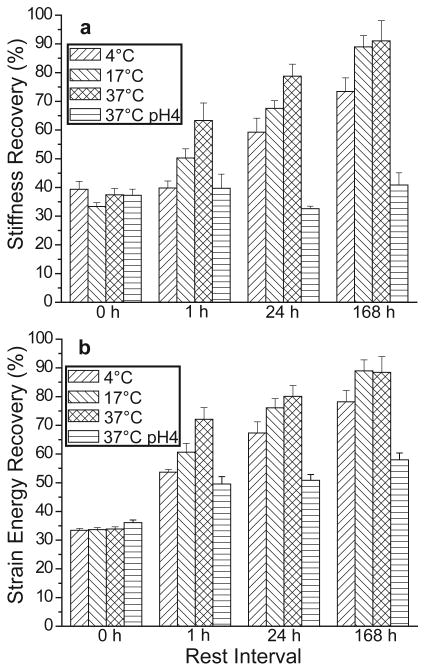
Because byssal thread damage repair is believed to be a consequence of stochastic reformation of broken His-metal cross-links (Vaccaro and Waite, 2001; Harrington and Waite, 2007), the effect of temperature on healing rate was investigated. Threads were cyclically loaded twice to 35% strain, rested at specific temperatures (4°C, 17°C, and 37°C) for set time intervals (1 h, 24 h, and 168 h), and were loaded again at room temperature in order to determine healing efficiency (Fig. 7). The first time point (0 h) is taken from the second cycle prior to any rest, and immediate recovery was found to be 34.2±0.5% for strain energy and 35.8±1.1% for stiffness (mean±s.e.m., n=57). One-way analysis of variance (ANOVA) performed on specimens from each time point reveals statistically significant differences in healing efficiency at 1 h, but not at later time points (P=0.003, n=14 threads; P=0.008, n=14 threads for strain energy and stiffness, respectively) Post hoc Scheffé pairwise analysis showed that increased temperature was associated with faster healing in both stiffness (P<0.05) and strain energy (P<0.03) when the 4°C and 37°C treatments were compared (Fig. 7).
Figure 7. Percent recovery of stiffness and strain energy in threads rested at different temperatures/pH and different time intervals.
Temperature has a significant effect on (a) stiffness and (b) strain energy healing rates after 1 h of rest that becomes less apparent at later time points. Treatment of threads at pH 4 largely inhibits recovery. (Values represent mean ± s.e.m.; n ranged from 17-20 threads for each time point).
Previous studies have demonstrated that treating threads at acidic pH primarily affects mechanical function by disrupting His-metal cross-linking (Harrington and Waite, 2007). This is because at acidic pH the imidazole group of histidine is protonated and unable to bind metal ions. ANOVA revealed significant differences in healing efficiency between seawater (∼ pH 8) and citrate buffer (pH 4) treated threads (P<0.005 at all time points past 0 h, n ranged from 17-20 threads per time point). Notably, Scheffé analysis showed that recovery of threads rested at 37°C in citrate buffer was significantly lower than that of threads rested in seawater at 37°C for both stiffness (P<0.02) and strain energy (P<0.001) (Fig. 7). ANOVA with Scheffé analysis was also used to compare healing efficiencies at different time points for threads treated at pH 4. While a small amount of strain energy recovery is seen after 1 h at pH 4 (P<0.001), no significant recovery is seen past that point (P=0.06, n=14 threads). There is no significant recovery of stiffness at pH 4 at any point (P=0.55, n=32 threads).
Discussion
Byssal threads repair damage incurred during mechanical yield in a time-dependent healing process in the absence of active metabolism. In this study, in situ WAXD studies were performed on threads during cyclic mechanical loading in order to better understand the molecular-level mechanisms underlying byssal yield and healing behavior. It was observed that despite stretching threads to strains of more than 70%, the preCol collagen domain strained disproportionately and did not exceed 2% (Fig. 5b). Assuming the series model of preCol assembly previously observed with AFM (Hassenkam et al., 2004) (Fig. 3b), these data indicate that a pliant non-collagen component must be producing the inelastic behavior of the thread and providing the necessary molecular contour length during elongation. Previous studies showing that thread modulus is strain rate-dependent are consistent with this hypothesis (Carrington and Gosline, 2004). Unfolding of the flanking/His-rich domains is the obvious candidate for the sacrificial hidden lengths in byssal threads. This is supported by AFM studies in which the initially globular regions between rod-like collagen domains appear as taut extended interconnecting strands when threads are strained (Hassenkam et al., 2004). However, the calculations summarized in Fig. 6 indicate that while the flanking/His-rich domains may provide a significant amount of the hidden length, there are clearly other sources present. The implications of this will be amplified later in the discussion.
The nearly identical elastic response observed in the collagen domain during the first and second loading cycle (Fig. 5a) indicates that no lasting damage is sustained by the collagen domain during the first cycle; however, the derived collagen strain values are consistently lower in the second cycle at a given thread strain (Fig. 5b). These observations imply that damage is being sustained elsewhere in the thread and suggest that structural cross-links that previously transferred load to the collagen domain are ruptured during yield and not reformed during short (∼1 min) rest intervals. Time-dependent reformation of these sacrificial cross-links is likely to be the rate limiting factor in byssal thread healing and identifying them will reveal much about the mechanism of thread yield and recovery.
As suggested by previous studies, metal ion coordination between the highly conserved histidine residues in the termini of adjacent preCols is implicated as the reversibly breakable cross-link in byssal threads (Vaccaro and Waite, 2001; Harrington and Waite, 2007). These bonds, in which histidine residues act as soft ligands by donating a pair of electrons each to empty d-orbitals of a transition metal ion, have been shown by AFM pulling studies to rupture and reform reversibly with a breaking force of 20 to 60 pN/mole metal (Schmitt et al., 2000). The preCols of M. californianus have between 16-23 histidine residues per preCol chain concentrated near both the N- and C-terminal ends (Harrington and Waite, 2007). Evidence for the presence of coordination cross-links in byssal threads is provided by studies that showed that transition metals (primarily zinc and copper) are actively concentrated in byssal threads (Coombs and Keller, 1981; Vaccaro and Waite, 2001) and that thread treatments aimed at disrupting His-metal interactions result in loss of stiffness and perturbation of yield, self-healing, and preCol assembly (Vaccaro and Waite, 2001; Harrington and Waite, 2007, Harrington and Waite, 2008b).
The positive correlation between temperature and recovery rate (Fig. 7) suggests that reformation of cross-links is a stochastic process dependent on molecular vibrations bringing cross-linking partners into the proximity of one another. It was also observed that damage repair is significantly impaired in low pH treated threads (Fig. 7). An earlier study monitored changes in the initial modulus of threads treated at different pHs ranging from pH 3-8 (Harrington and Waite, 2007). It was found that stiffness was significantly reduced from a maximum of ∼800 MPa at pH 8 to a minimum of ∼450MPa around pH 4 in a sigmoidal fashion with a halfway point at pH 6.6. This is significant because it follows nearly exactly the titration of a solvent accessible histidyl residue (pKa ∼6.5), and suggests strongly that low pH treatment of threads primarily targets the protonation state of His residues and prevents their ability to cross-link preCols by forming multi-ligand coordination complexes with metal. The apparent pH-dependent reduction in damage repair is also consistent with another study in which thread self-repair was perturbed by chelating out some of the metal ions with EDTA (Vaccaro and Waite, 2001) and further supports the role of His-metal cross-links in yield and self-healing.
Approaching these observations from a molecular perspective allows one to envision the His-rich domains at rest as amorphous tangled chains with “sticky” spots in which some conformations of folding would provide more resistance to tension than others (Fig. 3c). In this model, when these moderately strong bonds are broken during yield they dissipate the applied energy as hysteresis preventing catastrophic failure of the thread. However, when the load is removed, on average they do not immediately revert to the conformation providing the highest stiffness. Recovery to a stiffer conformation requires an optimal partnering of His residues. Since this is a stochastic process dependent on the random motion of the amorphous chains of the His-rich domains, it exhibits both time- and temperature-dependence. When His-metal bonds are broken during yield there is increased freedom of movement for the chains; however, as bonds begin to reform, the stability of the domain increases and chain mobility decreases. This may explain why temperature makes less difference at later time points and why a saturation point is evident at ∼80-90% recovery (Fig. 7). These data reinforce the role of His-metal bonds in thread yield and repair; however, the small amount of strain energy recovery in pH 4 treated threads that peaks at <1 h suggests that some healing is due to other mechanisms. Previous studies have implicated the flanking domains of preCol-NG and -D in hydrophobically-driven reversible unfolding, which could provide this short-term recovery (Harrington and Waite, 2007), but clearly further study is required.
The preCol collagen modulus measured in this study is consistent with a previously measured value for molecular collagen from bovine tendon (Sasaki and Odajima, 1996; but is about half the expected value for a triple-helical molecule (Buehler, 2008; Silver et al., 2008). Notably, this observation is consistent with our calculations showing that the fully stretched preCol can only contribute ∼50% of the required contour length needed to account for a thread breaking strain of ∼100% (Fig. 6) (Gosline et al., 2002). This indicates that the previously proposed series model of load transfer cannot hold for the whole system and suggests the presence of a higher order hierarchical organization as observed in tendon (Buehler, 2008; Silver et al., 2008) that reduces the load on individual preCol filaments. Possible candidates for hierarchical structures suggested by previous studies include closing of voids between the preCol filaments (Bairati and Zuccarello, 1976), loss of the preCol bend and tilt (Hassenkam et al., 2004), and rearrangement of non-preCol matrix proteins (Sagert et al., 2006). Preliminary small angle x-ray scattering (SAXS) results also indicate the presence of an as of yet unidentified, higher order, and possibly super-coiled component that strains proportionally to the thread (Fig. 4b) (unpublished data). Sources of additional hidden length must be investigated further.
5. Conclusion
This study provides the first in situ evidence of molecular strain in byssal threads and supports the role of sacrificial preCol domains that protect both the collagen core and the thread from catastrophic failure. Collagen is a ubiquitous structural motif found in a diverse assortment of biological load-bearing materials (Ricard-Blum et al., 2005; Harrington and Waite, 2008a). Tendon is the archetypal collagenous fiber and is characterized by high stiffness, high resilience, and low extensibility (Gosline et al., 2002). By inserting moderately stiff sacrificial domains in series with stiff collagen domains, mussels transform their tendon-like fibers into tougher, significantly more extensible tethers with an intrinsic capacity to heal. The unfolding of sacrificial domains to reveal hidden length is a toughening mechanism featured in other protein-based biological load-bearing materials, including muscle, bone and nacre (Marszalek et al., 1999; Smith et al., 1999; Fantner et al., 2005); however, preCols are innovative in their use of metal ion coordination complexes that stabilize the His-rich domains and that break and reform reversibly during cyclic tensile loading. Armed with a more mechanistic understanding of healing in byssus, it may be possible to exploit metal ion coordination chemistry to biomimetically tailor yield and recovery into engineered polymeric fibers.
Acknowledgments
This work was supported in part by the NASA University Research, Engineering and Technology Institutes on Bio-inspired Materials under award No. NCC-1-02037, by the National Institutes of Health Grant R01 DE 014672, and through a travel award from the International Conference on Self Healing Materials. HSG and PF thank the Max Planck Society for financial support. We thank Stefan Siegel, Chenghao Li and Ivo Zizak at the Mu-Spot beamline (BESSY, Adlershof-Berlin, Germany) for scientific and technical support.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Aldred N, Wills T, Williams DN, Clare AS. Tensile and dynamic mechanical analysis of the distal portion of mussel (Mytilus edulis) byssal threads. J Roy Soc Interface. 2007;4:1159–1167. doi: 10.1098/rsif.2007.1026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auld DS. Zinc coordination sphere in biochemical zinc sites. Biometals. 2001;14:271–313. doi: 10.1023/a:1012976615056. [DOI] [PubMed] [Google Scholar]
- Bairati A, Zuccarello LV. The ultrastructure of the byssal apparatus of Mytilus galloprovincialis IV. Observation by transmission elctron microscopy. Cell Tiss Res. 1976;166:219–234. doi: 10.1007/BF00227043. [DOI] [PubMed] [Google Scholar]
- Bell E, Gosline J. Mechanical design of mussel byssus: material yield enhances attachment strength. J Exp Biol. 1996;199:1005–1017. doi: 10.1242/jeb.199.4.1005. [DOI] [PubMed] [Google Scholar]
- Broomell CC, Mattoni MA, Zok FW, Waite JH. Critical role of zinc in hardening of Nereis jaws. J Exp Biol. 2006;209:3219–3225. doi: 10.1242/jeb.02373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buehler MJ. Hierarchical nanomechanics of collagen fibrils: atomistic and molecular modeling. In: Fratzl P, editor. Collagen: Structure and Mechanics. Springer; New York: 2008. pp. 175–247. [Google Scholar]
- Carrington E, Gosline J. Mechanical design of mussel byssus: load cycle and strain rate dependence. Amer Malacol Bull. 2004;18:135–142. [Google Scholar]
- Chen X, Dam MA, Ono K, Mal A, Shen H, Nutt SR, Sheran K, Wudl F. A thermally re-mendable cross-linked polymeric material. Science. 2002;295:1698–1702. doi: 10.1126/science.1065879. [DOI] [PubMed] [Google Scholar]
- Coombs TL, Keller PJ. Mytilus byssal threads as an environmental marker for metals. Aquatic Toxicology. 1981;1:291–300. [Google Scholar]
- Fantner GE, Hassenkam T, Kindt JH, Weaver JC, Birkedal H, Pechenik L, Cutroni JA, Cidade GAG, Stucky GD, Morse DE, Hansma PK. Sacrificial bonds and hidden length dissipate energy as mineralized fibrils separate during bone fracture. Nat Mater. 2005;4:612–616. doi: 10.1038/nmat1428. [DOI] [PubMed] [Google Scholar]
- Galat A, Goldberg IH. Analysis of microdensitometric data in terms of probability of cleavage of DNA. CABIOS. 1987;3:333–338. doi: 10.1093/bioinformatics/3.4.333. [DOI] [PubMed] [Google Scholar]
- Geddes AJ, Parker KD, Atkins EDT, Beighton E. Cross-Beta Conformation In Proteins. J Molec Biol. 1968;32:343–358. doi: 10.1016/0022-2836(68)90014-4. [DOI] [PubMed] [Google Scholar]
- Gosline J, Lillie M, Carrington E, Guerette P, Ortlepp C, Savage K. Elastic proteins: biological roles and mechanical properties. (B).Philos Trans R Soc London. 2002;357:121–132. doi: 10.1098/rstb.2001.1022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta HS, Seto J, Wagermaier W, Zaslansky P, Boesecke P, Fratzl P. Cooperative deformation of mineral and collagen in bone at the nanoscale. Proc Natl Acad Sci USA. 2006;103:17741–17746. doi: 10.1073/pnas.0604237103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammersley A. FIT2D: an introduction and overview. ESRF Internal Report ESRF97HA02T 1997 [Google Scholar]
- Harrington MJ, Waite JH. Holdfast heroics: comparing the molecular and mechanical properties of Mytilus californianus byssal threads. J Exp Biol. 2007;210:4307–4318. doi: 10.1242/jeb.009753. [DOI] [PubMed] [Google Scholar]
- Harrington MJ, Waite JH. Short-order tendons: liquid crystal mesophases, metal-complexation and protein gradients in the externalized collagens of mussel byssal threads. In: Scheibel T, editor. Fibrous Proteins. Landes Bioscience; Austin: 2008a. pp. 30–45. [Google Scholar]
- Harrington MJ, Waite JH. pH-dependent locking of giant mesogens in fibers drawn from mussel byssal collagens. Biomacromolecules. 2008b;9:1480–1486. doi: 10.1021/bm8000827. [DOI] [PubMed] [Google Scholar]
- Hassenkam T, Gutsmann T, Hansma P, Sagert J, Waite JH. Giant bent-core mesogens in the thread forming process of marine mussels. Biomacromolecules. 2004;5:1351–1354. doi: 10.1021/bm049899t. [DOI] [PubMed] [Google Scholar]
- Holten-Andersen N, Fantner GE, Hohlbauch S, Waite JH, Zok FW. Protective coatings on extensible biofibres. Nat Mater. 2007;6:669–672. doi: 10.1038/nmat1956. [DOI] [PubMed] [Google Scholar]
- Keckes J, Burgert I, Fruhmann K, Muller M, Kolln K, Hamilton M, Burghammer M, Roth SV, Stanzl-Tschegg S, Fratzl P. Cell-wall recovery after irreversible deformation of wood. Nat Mater. 2003;2:810–813. doi: 10.1038/nmat1019. [DOI] [PubMed] [Google Scholar]
- Marszalek PE, Lu H, Li HB, Carrion-Vazquez M, Oberhauser AF, Schulten K, Fernandez JM. Mechanical unfolding intermediates in titin modules. Nature. 1999;402:100–103. doi: 10.1038/47083. [DOI] [PubMed] [Google Scholar]
- Mercer EH. Observations on the molecular structure of byssus fibres. Aust J Mar Freshwat Res. 1952;3:199–205. [Google Scholar]
- Misof K, Rapp G, Fratzl P. A new molecular model for collagen elasticity based on synchrotron x-ray scattering evidence. Biophys J. 1997;72:1376–1381. doi: 10.1016/S0006-3495(97)78783-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paris O, Li CH, Siegel S, Weseloh G, Emmerling F, Riesemeier H, Erko A, Fratzl P. A new experimental station for simultaneous X-ray microbeam scanning for small- and wide-angle scattering and fluorescence at BESSY II. J Appl Crystallogr. 2007;40:S466–S470. [Google Scholar]
- Rapoport HS, Shadwick RE. Reversibly labile, sclerotization-induced elastic properties in a keratin analog from marine snails: whelk egg capsule biopolymer (WECB) J Exp Biol. 2007;210:12–26. doi: 10.1242/jeb.02613. [DOI] [PubMed] [Google Scholar]
- Ricard-Blum S, Ruggiero F, van der Rest M. The collagen superfamily. Springer-Verlag; Berlin Heidelberg: 2005. [Google Scholar]
- Rudall KM. The distribution of collagen and chitin. Symp Soc Exp Biol. 1955;9:49–71. [Google Scholar]
- Sagert J, Sun CJ, Waite JH. Chemical subtlties of mussel and polychaete holdfasts. In: Smith AM, Callow JA, editors. Biological Adhesives. Springer-Verlag; Berlin Heidelberg: 2006. pp. 125–140. [Google Scholar]
- Sasaki N, Odajima S. Stress-strain curve and Young's modulus of a collagen molecule as determined by the X-ray diffraction technique. J Biomech. 1996;29:655–658. doi: 10.1016/0021-9290(95)00110-7. [DOI] [PubMed] [Google Scholar]
- Schmitt L, Ludwig M, Gaub HE, Tampe R. A metal-chelating microscopy tip as a new toolbox for single-molecule experiments by atomic force microscopy. Biophys J. 2000;78:3275–3285. doi: 10.1016/S0006-3495(00)76863-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silver FH, Landis WJ. Viscoelasticity, energy storage and transmission and dissipation by extracellular matrices in vertebrates. In: Fratzl P, editor. Collagen: Structure and Mechanics. Springer; New York: 2008. pp. 133–153. [Google Scholar]
- Smith BL, Schaffer TE, Viani M, Thompson JB, Frederick NA, Kindt J, Belcher A, Stucky GD, Morse DE, Hansma PK. Molecular mechanistic origin of the toughness of natural adhesives, fibres and composites. Nature. 1999;399:761. [Google Scholar]
- Srivastava A, Holten-Andersen N, Stucky GD, Waite JH. Ragworm jaw-inspired metal ion cross-linking for improved mechanical properties of polymer blends. Biomacromolecules. 2008;9:2873–2880. doi: 10.1021/bm8006659. [DOI] [PubMed] [Google Scholar]
- Vaccaro E, Waite JH. Yield and post-yield behavior of mussel byssal thread: a self-healing biomolecular material. Biomacromolecules. 2001;2:906–911. doi: 10.1021/bm0100514. [DOI] [PubMed] [Google Scholar]
- Waite J, Vaccaro E, Sun C, Lucas J. Elastomeric gradients: a hedge against stress concentration in marine holdfasts? (B).Philos Trans R Soc London. 2002;357:143–153. doi: 10.1098/rstb.2001.1025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zwaag Svd. Self Healing Materials: An Alternative Approach to 20 Centuries of Materials Science. Springer-Verlag; New York: 2007. [Google Scholar]