A skeletal muscle model of extreme hypertrophic growth reveals the influence of diffusion on cellular design

Abstract

Muscle fibers that power swimming in the blue crab Callinectes sapidus are <80 μm in diameter in juveniles but grow hypertrophically, exceeding 600 μm in adults. Therefore, intracellular diffusion distances become progressively greater as the animals grow and, in adults, vastly exceed those in most cells. This developmental trajectory makes C. sapidus an excellent model for characterization of the influence of diffusion on fiber structure. The anaerobic light fibers, which power burst swimming, undergo a prominent shift in organelle distribution with growth. Mitochondria, which require O₂ and rely on the transport of small, rapidly diffusing metabolites, are evenly distributed throughout the small fibers of juveniles, but in the large fibers of adults they are located almost exclusively at the fiber periphery where O₂ concentrations are high. Nuclei, which do not require O₂, but rely on the transport of large, slow-moving macromolecules, have the inverse pattern: they are distributed peripherally in small fibers but are evenly distributed across the large fibers, thereby reducing diffusion path lengths for large macromolecules. The aerobic dark fibers, which power endurance swimming, have evolved an intricate network of cytoplasmically isolated, highly perfused subdivisions that create the short diffusion distances needed to meet the high aerobic ATP turnover demands of sustained contraction. However, fiber innervation patterns are the same in the dark and light fibers. Thus the dark fibers appear to have disparate functional units for metabolism (fiber subdivision) and contraction (entire fiber). Reaction-diffusion mathematical models demonstrate that diffusion would greatly constrain the rate of metabolic processes without these developmental changes in fiber structure.

cellular metabolism is carried out through a network of reactions with individual rates that depend on the relationship between catalytic capacity and molecular diffusion (71). Across the animal kingdom intracellular reaction rates and diffusion distances vary over several orders of magnitude, and diffusion would be expected to play a more critical role as either of these properties increases (35, 41, 42, 72). In muscle cells, growth often occurs hypertrophically (increase in fiber size, rather than fiber number), and diffusive flux may progressively exert more control as intracellular diffusion path lengths increase and the fiber surface area-to-volume ratio decreases with growth. For example, increasing fiber size may compromise aerobic metabolism by reducing the rate of O₂ transport to the mitochondria and increasing diffusion distances for small metabolites (e.g., ADP, ATP, and phosphagens). It may be expected that, during fiber growth, the cellular distribution of mitochondria is governed by the need for sufficiently short diffusive path lengths between the blood and the mitochondria and between adjacent mitochondria (6, 14, 26, 32). Similarly, fiber hypertrophy may impede net protein synthesis and turnover, since these processes rely on diffusive transport of large, slow-moving macromolecules (e.g., tRNA, mRNA, rRNA, nuclear proteins, and ribosomal subunits) (22, 60). Thus diffusion may play a major role in shaping the evolution of basic cellular design and function.

Since the influence of diffusion on aerobic processes becomes greater as reaction fluxes increase (24, 35, 47, 72), diverse muscle fiber types may be impacted differently based on their metabolic demands and ATP turnover rates. For instance, burst locomotor fibers power contraction anaerobically, and maximal aerobic metabolic rates are important only during postcontractile recovery, which is often associated with relatively low ATP demand (16, 40). In contrast, aerobic fibers rely on mitochondrial ATP production to support the high rates of ATP turnover associated with sustained contractile activity (15, 39). Anaerobic fibers may therefore tolerate comparatively long intracellular diffusion distances (38), which is consistent with the observation that anaerobic fibers tend to be larger than aerobic fibers. This argument is supported by reaction-diffusion model analyses of experimental data, which indicated that the low rate of postcontractile phosphocreatine or arginine phosphate recovery in large anaerobic fibers is not substantially limited by diffusion, despite the presence of extremely large diffusion distances (29, 38, 49). However, intracellular ATP and arginine phosphate concentration gradients (indicative of diffusion limitation) were present in aerobic fibers at the high rates of ATP turnover characteristic of steady-state contraction (24).

To understand how diffusion influences cellular design, we have examined two metabolically distinct muscle fiber types (anaerobic light fibers and aerobic dark fibers) that undergo extreme hypertrophic growth in the blue crab Callinectes sapidus. Since the effects of diffusion should be more pronounced in fibers that undergo large changes in cellular dimensions, this model system enables us to reveal influences of diffusion likely present in many muscle fibers but not easily observed. The use of reaction-diffusion mathematical models and previously measured rates of ATP turnover allowed us to evaluate the functional role of developmental changes in cell structure in moderating the diffusion constraints imposed by hypertrophic fiber growth.

MATERIALS AND METHODS

Animals.

Juvenile blue crabs (C. sapidus, Rathbun) were collected by sweep netting in the Intracoastal Waterway behind Wrightsville Beach, NC; adult crabs were purchased from commercial fisherman. Animals were maintained in full-strength, filtered seawater (FSW; 35‰ salinity, 21°C) in aerated, recirculating aquariums and fed shrimp three times weekly. Carapace width and body mass were measured before use in all experiments. Only animals in the intermolt stage, as determined by the rigidity of the carapace, the presence of the membranous layer of the carapace, and the absence of a soft cuticle layer developing beneath the existing exoskeleton, were used (56). The protocols were reviewed and approved by the University of North Carolina Wilmington Institutional Animal Care and Use Committee (protocol no. 2006-021).

Exercise protocol.

Crabs were induced to undergo a burst swimming response, as described previously (6, 24, 30, 38). Briefly, crabs were held suspended in the air by a clamp in a manner that allowed free motion of the swimming legs, and small wire electrodes were placed in two small holes drilled into the mesobranchial region of the dorsal carapace. A physiological stimulator (Grass Instruments SD9, Astro Med, West Warwick, RI) was used to deliver a small-voltage pulse (80 Hz, 200-ms duration, 10 V/cm between electrodes) to the thoracic ring ganglia, which elicited a burst swimming response in the fifth pereiopods for several seconds following the stimulation. A single stimulation train was administered every 20–30 s until the animal was no longer capable of a burst response, which became evident when it responded by moving its legs at a notably slower rate.

Dissection.

Crabs were rapidly cut in half along the sagittal plane, and the dorsal carapace, heart, and reproductive and digestive organs were removed from each section. The gills and other supporting architecture were removed to expose the basal cavity, which houses the levator muscles of the fifth pereiopods (swimming legs).

Perfusion.

To illustrate hemolymph perfusion of the large dark and light fibers, five adult blue crabs injected with 125 μg of Alexa Fluor 594-labeled wheat germ agglutinin (WGA; Molecular Probes) in FSW were induced to undergo a burst exercise bout as described above and then rested in FSW for 10 min. They were subsequently injected with 50 μl of a suspension of 0.2-μm-diameter carboxylated fluorescent FluoSpheres (Molecular Probes) in 200 μl of FSW and exercised again. After 10 min of rest in FSW, the animals were killed, and individual basal levator swimming muscle fibers were mechanically isolated and removed. Anaerobic (light) fibers, which are used for burst swimming, and aerobic (dark) fibers, which are used to power sustained swimming, were examined (69). All image stacks and three-dimensional reconstructions of the fibers were generated using an Olympus FluoView 1000 laser scanning confocal microscope.

WGA is a lectin that binds to sialic acid and N-acetylglucosaminyl residues found on the basement membrane of the fiber sarcolemma and the blood vessel endothelium (73). Fluorescent microspheres, which behave as a solution at the relatively small size of 0.2 μm, completely fill vessel spaces and lodge within the smallest microvasculature, where they will remain throughout histological sectioning (66). The cardiovascular system of C. sapidus differs from that of vertebrate systems in that it is loosely defined as “partially closed,” rather than completely open (45). It has a system of arteries that branch into arterioles and, ultimately, form capillary-like structures. However, only a few of these small vessels form complete capillary beds; most have blind endings through which hemolymph empties into sinuses that bathe organs. When injected into the circulatory system of a blue crab, WGA percolates through the muscle tissue, labeling the sarcolemma of individual fibers (or subdivisions), thereby revealing regions that are in contact with hemolymph, while the microbeads remain within the smallest perfused spaces.

Histology.

To describe the ontogenetic changes in mitochondrial and nuclear distribution in light and dark fibers, fixed muscle fiber cross sections from juvenile and adult animals were labeled with the red-fluorescent mitochondrial probe MitoTracker Deep-Red 633 (Molecular Probes) and the blue-fluorescent nuclear probe 4′,6-diamidino-2-phenylindole (DAPI, Molecular Probes). Adult (n = 5) and juvenile (n = 5) animals were injected with ∼0.1 mg of Alexa Fluor 488 WGA to delineate fiber boundaries. Animals were exercised, allowed to rest for 10 min in FSW, and killed. Dark and light levator muscles were removed, fixed for 4–8 h in 4% paraformaldehyde in FSW, rinsed overnight in 25% sucrose, and then flash frozen in liquid nitrogen. Frozen sections were cut at 20 μm with a Leica Cryocut 1800. Sections were incubated for 10 min in 20 nM MitoTracker Deep-Red 633, rinsed in PBS, incubated for 30 min in 300 nM DAPI, and rinsed again for 3 min in PBS. Imaging and three-dimensional reconstruction were performed with an Olympus FluoView 1000 confocal microscope.

Fluorescence recovery after photobleaching.

Fluorescence recovery after photobleaching (FRAP) experiments were used to measure intracellular diffusion for the purposes of characterizing cytoplasmic connectedness within the fibers. Isolated light and dark fiber bundles from adult animals (n = 4) were arranged lengthwise across a rectangular petroleum jelly (Vaseline) well formed on a slide. Fibers were maintained at resting length and anchored beyond the edges of the well. Fibers in the well were incubated for 1 h with 100 μM calcein-AM (Molecular Probes) in FSW. Calcein, a membrane-permeable probe, is colorless and nonfluorescent until inside a cell, where endogenous esterases hydrolyze the calcein, rendering it fluorescent and negatively charged (thus, membrane impermeable). The petroleum jelly well was covered with a coverslip, with care taken to avoid flattening the fibers. FRAP measurements were then immediately performed with an Olympus FluoView 1000 confocal microscope.

Before each FRAP experiment, three-dimensional reconstructions were collected to ensure adequate dye distribution and homogeneity throughout the fiber. On the basis of these images, a uniformly fluorescent optical slice of muscle, ≥30 μm from the fiber surface, was chosen for each experiment. Diffusion coefficients were measured in the longitudinal (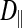) and radial (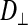) directions from each light and dark fiber examined (n = 4 per fiber type). The slide was rotated 90° between a longitudinal and a radial measurement to ensure that the time required to bleach the fiber was the same in both directions. The 488-nm laser was used at 1% intensity to obtain pre- and postbleach images of a 206 × 176 pixel (501 × 427 μm) region of the fiber. Five prebleach images, which provided average baseline fluorescence intensity, and 120 postbleach images, which were sufficient to chart complete recovery of the bleach region, were collected at 1.2-s intervals at a resolution of 10 μs/pixel. The laser was used at 100% intensity to bleach a 150 × 5 pixel (360 × 12 μm) rectangular region of interest (ROI). The bleached ROI was substantially longer than it was wide to ensure that recovery was only due to the diffusion of calcein in the direction of interest (i.e., longitudinally or radially). The bleached ROI was scanned 10 times at 200 μs/pixel to ensure proper bleaching (25–50% of prebleach intensity), and images were collected at 1.2-s intervals.

Postbleach fluorescence images were aligned, and Olympus FluoView version 1.6a software was used to extract a one-dimensional fluorescence intensity profile for a 1-pixel-wide line perpendicular to the bleached ROI, the ends of which reached sufficiently far outside the ROI as to incorporate a nonbleached intensity baseline. Analysis of these line series data describing the change in the bleaching profile over time was based on the approach described by Mullineaux et al. (48), in which the one-dimensional diffusion equation is

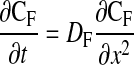(1)

where C_F is the fluorophore concentration, t is time, x is distance, and D_F is the diffusion coefficient of the fluorophore. Postbleach intensity values for all points along the line were subtracted from their corresponding average prebleach intensity values, yielding a one-dimensional bleaching profile to which a Gaussian curve was fit (with the assumption that the bleach profile was normal and the width of the bleach was very narrow compared with the length of the fiber). JMP version 4.0.4 (SAS institute, Cary, NC) was used to perform an iterative curve-fitting procedure in which the fluorescence intensity was estimated as a function of the linear position across the ROI, with the standard deviation and mean as floating variables. The fitted Gaussian curve was used to determine bleach depth (C) and the laser beam half-width (R_o) at an intensity of 1/e². To calculate diffusion coefficients, (C₀/C_t)² was plotted against time (t), where C₀ is the bleach depth at time 0 (immediately after bleach) and C_t is the bleach depth at time t. This yields a linear plot with a slope equal to 8D_F/R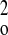(48).

Immunohistochemistry.

To describe the pattern of innervation in the dark and light fibers, immunohistochemistry was performed using an antibody to synapsin, a presynaptic vesicle-associated phosphoprotein, using methods modified from Buchner et al. (11).

The levator swimming muscle group was removed from four adults, fixed for 4–8 h in 4% paraformaldehyde in FSW, rinsed overnight in 25% sucrose, and then flash frozen in liquid nitrogen. Frozen 12- to 15-μm-thick sections were air-dried for 15 min and then incubated at room temperature for 2 h in blocking solution (2% goat serum, 1% BSA, 0.1% Triton X-100, 0.05% Tween 20, and 0.05% sodium azide in PBS). They were then incubated overnight at 4°C in the primary antibody to synapsin (mouse monoclonal anti-Drosophila SYNORF1) at a dilution of 1:5 (7.4 μg/ml) in PBS containing 1% BSA and 0.05% sodium azide. After three rinses in PBS containing 0.1% Triton X-100, sections were incubated for 1 h at 37°C in the secondary antibody (Alexa Fluor 488-labeled goat anti-mouse, Molecular Probes) at a concentration of 10 μg/ml in PBS containing 0.05% sodium azide and then washed three times in PBS. For controls, primary antibody, secondary antibody, or both were replaced with PBS. An Olympus FV1000 confocal microscope with the appropriate lasers and filters for the particular fluorochromes was used to collect all image stacks and three-dimensional reconstructions.

Transmission electron microscopy.

Mitochondrial fractional volume was calculated from electron micrographs of adult (n = 3) and juvenile (n = 3) light fibers collected using standard transmission electron microscopy techniques. Isolated light fiber bundles were placed at resting length in a primary fixative consisting of 1% glutaraldehyde and 4% paraformaldehyde in 0.063 M Sörenson's phosphate buffer (pH 7.38) (18, 53). The osmolarity of the fixative and all corresponding buffer rinses was adjusted by the addition of 10% sucrose and a trace amount of CaCl₂ to prevent changes in cell volume. Tissues were held in primary fixative for ≥24 h at room temperature and then rinsed for 15 min in Sörenson's phosphate buffer. This process was followed by a secondary fixation in 1% osmium tetraoxide in Sörenson's phosphate buffer for 2–3 h. Samples were then dehydrated with an ascending series (50%, 70%, 95%, 100%, 100%) of acetone and embedded in Spurr's epoxy resin (Electron Microscopy Sciences) (67). Samples were sectioned at 90 nm with a diamond knife on a Reichert Ultracut E and collected using a systematic random-sampling method (27) to ensure complete representation of the mitochondria throughout the muscle. Sections were stained with 2% uranyl acetate in 50% ethyl alcohol and Reynolds' lead citrate (55) and then examined with a Philips CM-12 transmission electron microscope operated at 80 kV. One section per grid was randomly chosen from each of five grids per animal, and one micrograph was taken from each of these sections. Negatives were digitized using a Microtek Scanmaker 4 negative scanner and processed with Adobe Photoshop version 7.0.

A stereological point-counting method was applied to the micrographs to determine the fractional volume of subsarcolemmal (SS) and intermyofibrillar (IM) mitochondria (27, 49). A point grid was superimposed on each image, and all points touching extracellular space were subtracted from the total number of points per micrograph. Points that landed on mitochondria were recorded as SS if the mitochondrion or mitochondrial cluster was between the sarcolemmal membrane and the myofibrils or as IM if the mitochondrion was located among the myofibrils, regardless of its proximity to the sarcolemmal membrane. The total number of SS and IM mitochondria was respectively divided by the total number of points that fell within intracellular space to determine SS fractional volume (SSFV) and IM fractional volume (IMFV).

Calculation of myonuclear domain, nuclei per millimeter, and nuclear number volume.

Single optical slices of DAPI-labeled 20-μm cross sections of light fibers from three adult and five juvenile WGA-injected animals (see above) were collected using the confocal microscope, and nuclei were counted and scored as SS or IM as described above for mitochondria. Intracellular SS nuclei were difficult to distinguish from nuclei in the extracellular space and in adjoining fibers, but differential interference contrast images and nuclear shape helped us determine whether peripherally located nuclei were truly intracellular. Fiber margins were traced using Adobe Photoshop, and resultant polygons were analyzed with Image Pro Plus version 6.1 to calculate fiber cross-sectional area (CSA), circumference, and mean diameter, as well as nuclear CSA and diameter (from fiber cross sections) and nuclear lengths (from longitudinal sections). The number of nuclei per millimeter of fiber (X) was calculated as described by Schmalbruch and Hellhammer (61), using the equation

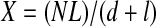(2)

where N is the number of myonuclei in a fiber cross section, L is the desired length of segment (i.e., 1 mm), d is the thickness of the section, and l is the mean length of a muscle nucleus. L was set at 1,000 μm, d was the optical thickness of each image (0.9–8.5 μm), and l was 13.0 and 16.8 μm for juveniles and adults, respectively. From this X value, we calculated the myonuclear domain [i.e., the volume of cytoplasm per myonucleus (Y)] using the equation from Rosser et al. (58)

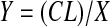(3)

where C is the cross-sectional area of the muscle fiber, L is the length of the fiber segment, and X is the number of myonuclei per millimeter of fiber determined from Eq. 2. To estimate number volume (number of nuclei per volume of fiber), we calculated the inverse of the myonuclear domain (Y) for SS and IM nuclei, respectively. Nuclear and mitochondrial stereological data were analyzed using Student's t-tests.

Reaction-diffusion mathematical model.

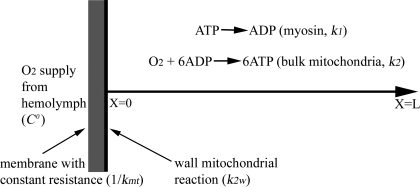
Reaction-diffusion models were developed to evaluate the influence of developmental changes in muscle structure on muscle metabolic function. The mathematical model used to evaluate aerobic metabolism was developed from the model described by Jimenez et al. (29) and extended for the system shown in Fig. 1, where O₂ is supplied at a fixed concentration (C⁰) and diffuses through a membrane with a fixed resistance (1/k_mt, where k_mt is the mass transfer coefficient for transport of O₂ from the hemolymph through the cell membrane), and it includes mitochondrial reactions at the fiber boundary as well as throughout the fiber. O₂ is consumed by a pseudohomogeneous second-order reaction at the mitochondria with 6 mol of ADP forming 6 mol of ATP for every 1 mol of O₂ by the overall reaction

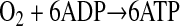(4)

Consideration of two populations of mitochondria allows us to examine the influence of mitochondrial distribution. One population (IM) is assumed to be uniformly distributed throughout the region from x = 0 to x = L, and the rate constant for this reaction reflects an averaged value accounting for the density of the mitochondria. The second population of mitochondria (SS) is clustered at the boundary of the cell at x = 0, and the rate constant for this reaction accounts for the density and activity of the mitochondria at this boundary. The ATP formed by the mitochondria is consumed by a cellular ATPase by a first-order reaction

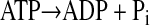(5)

The ATPase is also assumed to be uniformly distributed through the domain from x = 0 to x = L. The one-dimensional molar species balances for ADP, ATP, and O₂ valid in the region from x = 0 (boundary of the cell with hemolymph in the extracellular space) to x = L (center of the cell) are given by

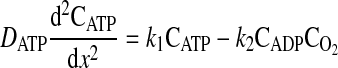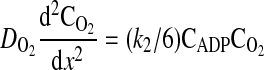(6)

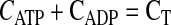where D is the diffusion coefficient, C is the concentration, C_T is the total concentration of ATP and ADP, k₁ is the rate constant governing the ATPase reaction, and k₂ is the rate constant for ATP production at the mitochondria. The boundary conditions for these equations are

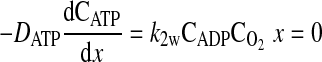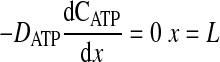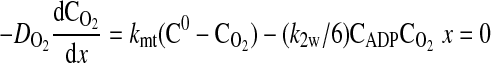(7)

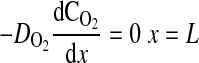where k_2w is the rate constant for ATP production at the fiber boundary and k_mt is the mass transfer coefficient for transport of O₂ from the hemolymph through the cell membrane. The first boundary condition reflects the fact that ATP is formed by the mitochondria at the boundary, and the second reflects symmetry about the center of the cell. The third boundary condition describes transport of O₂ across the cell membrane by diffusion with a linear driving force, where C⁰ is the concentration of O₂ in the hemolymph, and the consumption of O₂ to form ATP by the mitochondria clustered at the boundary. This boundary condition can be derived for the case of interfacial reaction and transport. The last boundary condition indicates that the O₂ distribution is symmetrical with respect to the center of the cell. The above-described system of equations is solved using MATLAB version 7.5.0.342 (Mathworks, Lowell, MA) to determine the spatially dependent concentrations and the flux at the boundary (x = 0), as well as the average concentrations of O₂ and ATP defined by

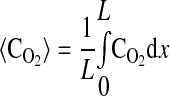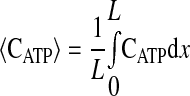(8)

Fig. 1.

Schematic of the reaction-diffusion mathematical model showing a one-dimensional spatial domain, where the position in the cell (x) ranges from x = 0 (sarcolemma) to x = L (fiber center), where L is segment length. O₂ is supplied at a fixed concentration (7.85 μM) and transported through a membrane (gray area) with a fixed resistance (1/k_mt, where k_mt is the mass transfer coefficient of O₂ transport from the hemolymph through the cell membrane). O₂ supplies a bulk population of mitochondria uniformly distributed throughout the region from x = 0 to x = L and a boundary population of mitochondria clustered at the fiber's edge (x = 0). The ATPase reaction (e.g., myosin) is distributed uniformly through the spatial domain from x = 0 to x = L. C⁰, O₂ concentration; k₁ and k₂, rate constants; k_2w, rate constant for ATP production at the fiber boundary.

The effectiveness factors (η) are determined following the methods discussed by Locke and Kinsey (41). Defined as the ratio of the rate of the reaction in the presence of diffusion to the rate of the reaction in the absence of diffusion, η can range from 1 (no limitation of reaction flux by diffusion) to 0 (complete limitation of reaction flux by diffusion). In the absence of diffusion limitations, Eqs. 6 and 7 can be shown to give

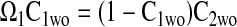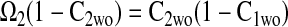(9)

where

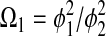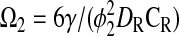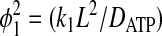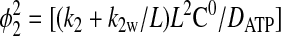(10)

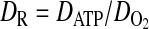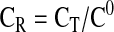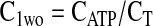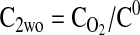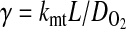Equation 9 leads to a quadratic equation, which can be easily solved for the nondimensional ATP and O₂ concentrations in the absence of diffusion limitations, C_1wo and C_2wo, respectively. All roots of the quadratic are real; however, only one root is within the physical domain of the problem. The reaction rates in the cases without and with diffusion limitations, respectively, are determined from

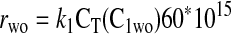(11)

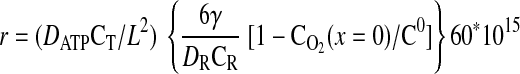(12)

where the units of k₁ are in s⁻¹, the units for C_T are in mmol/μm³, and the rate is in mM/min. In all calculations described in this report, the following parameters are fixed: D_ATP = 70 μm²/s, D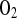= 1,160 μm²/s, C_T = 10⁻¹⁴ mmol/μm³, k_mt = 1,100 μm/s, and C⁰ = 7.85 μM.

The ratio of Eq. 12 to Eq. 11 was used to determine η for mitochondrial function. The concentration in Eq. 12 is determined by the numerical solution of Eqs. 6 and boundary conditions (Eq. 7) in MATLAB. The first set of calculations was determined using Eq. 9 to find the concentrations in the absence of diffusion limitations for various values of k₁, k₂, and k_2w. The resulting rates were determined by Eq. 11. Similar analysis was conducted in the case with diffusion limitations, whereby the numerical solution of Eq. 6 was used with Eq. 12. Since it was found that a range of combinations of k₁ and k₂ can give the same reaction rate, another set of calculations for the cases in the presence of diffusion was performed to determine the value of k₂ for various fixed values of k₁ that would match the experimentally determined reaction rate. In this set of computations, k₁ was set at fixed values from the smallest value that would satisfy the rate, and a root-finding method was used to determine the value of k₂ that would give the desired experimental rate. This procedure led to the maximal possible η that could be attained for any combination of rate and diffusion distance. The average concentrations of O₂ and ATP were determined in each of these cases (with fixed rate) using Eq. 8. Since a range of k₁ and k₂ can satisfy the rate, it is important to note that the average ATP and O₂ concentrations change; i.e., the average ATP concentration drops with increasing k₁.

To characterize the influence of diffusion on nuclear distribution, we evaluated an existing derivation of η with spherical geometry (Eqs. 12–32 in Ref. 19) for a range of diffusion coefficients and reaction rates. Here, we assumed a boundary source of nuclear products (e.g., RNA and proteins) and a uniform rate constant defining “consumption” across the myonuclear domain, which varied in distance from 14.5 μm (observed radius of the myonuclear domain) to 300 μm (radius if there were only SS nuclei in a large light fiber).

RESULTS AND DISCUSSION

Basal locomotor muscle.

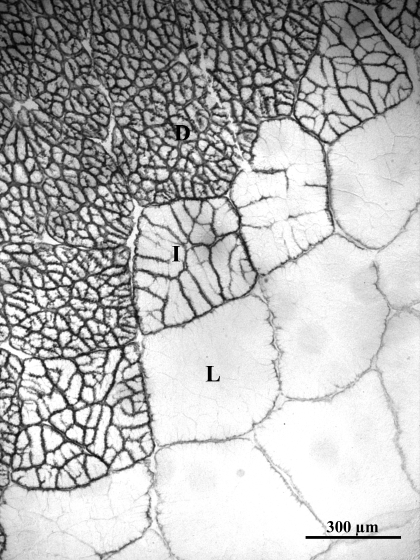
The blue crab has a number of anatomic modifications that give it an exceptional capacity for burst and steady-state swimming (65). Principal among these are the flattened, oar-like fifth pereiopods and the massive, basal locomotor musculature that powers the rotary motion of these appendages. Crustacean muscle fibers, similar to vertebrate muscle fibers, are distinctive in that they are multinucleated, postmitotic, and syncytial. During postmetamorphic development, fiber diameters in these muscles grow hypertrophically, increasing from <80 μm in juveniles to >600 μm in adults (6). The basal muscles are composed of three distinct fiber types: light fibers, which power anaerobic burst swimming; dark fibers, which power aerobically fueled endurance swimming; and a small number of intermediate fibers (69) (Fig. 2). The light fibers have very low mitochondrial densities, leading to a slow, aerobic recovery following anaerobic, burst contraction (6, 38). In contrast, the dark fibers have a network of mitochondria-rich subdivisions (69) that promote high rates of aerobic metabolism during sustained swimming. The subdivisions increase in number but maintain a constant, relatively small size (∼35 μm) during fiber growth (30).

Fig. 2.

Levator swimming muscle from Callinectes sapidus (adult) stained for endogenous peroxidase activity with a Vectastain Elite ABC kit (PBS buffer; catalog no. PK-6100, Vector Laboratories). Muscle consists of anaerobic light fibers (L) and highly subdivided aerobic dark fibers (D). A small fraction of moderately subdivided intermediate fibers (I) create a transition zone between dark and light fibers.

Anaerobic light fibers.

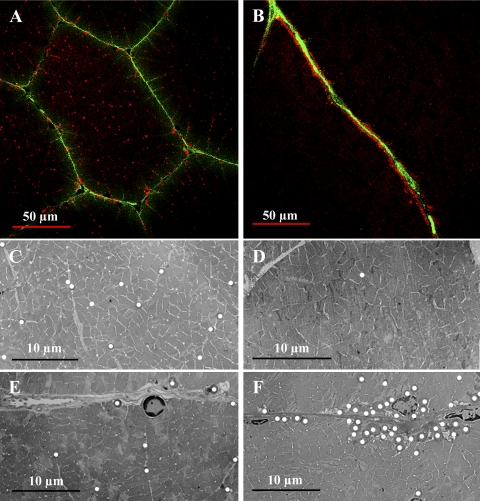
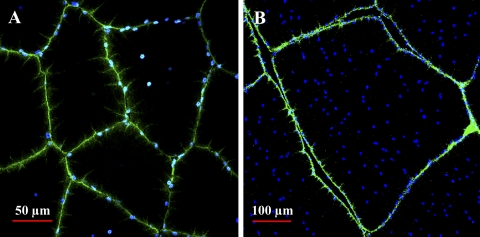
Mitochondrial and nuclear distribution in the anaerobic light fibers changes dramatically during growth. In small fibers from juveniles, mitochondria are uniformly distributed throughout the IM (Fig. 3, A and C) and SS (Fig. 3, A and E) regions of the cell, but in the large fibers from adults, mitochondria are found clustered almost exclusively at the sarcolemma (Fig. 3, B, D, and F). This pattern change was first noted qualitatively in blue crab muscle by Boyle et al. (6) and, more recently, was found in fish white muscle fibers that attain large sizes (49). Nuclei, on the other hand, show the opposite pattern during fiber growth. In the smallest juvenile fibers, nuclei were located exclusively in the SS region of the cell (Fig. 4A); as fiber size increased, however, nuclei were located in abundance in the SS region, as well as in the IM region (Fig. 4B). The nuclear distribution in the large fibers from adults is in striking contrast to the pattern in vertebrate skeletal muscle, where nuclei are typically found exclusively at the sarcolemma (9), although a response similar to hypertrophic growth has been observed in fish white muscle (S. T. Kinsey, unpublished observations).

Fig. 3.

Mitochondrial distribution in juvenile (A, C, and E) and adult (B, D, and F) anaerobic light fibers. A and B: cross sections of fixed light fibers from wheat germ agglutinin (WGA)-injected juveniles (A) and adults (B) labeled with the red-fluorescent probe MitoTracker Deep-Red 633, specific for mitochondria. Green-fluorescent WGA labeling indicates perfusion, which in the light fibers concurrently delineates fiber boundaries. C–F: transmission electron micrographs depicting mitochondrial distribution in subsarcolemmal (SS; E and F) and intermyofibrillar (IM; C and D) regions of juvenile (C and E) and adult (D and F) anaerobic light fibers. Mitochondria are marked with white circles. In small fibers of the juvenile, IM and SS mitochondria are distributed homogeneously; in large fibers of the adult, there is a high density of SS mitochondria, and IM mitochondria are sparse.

Fig. 4.

Nuclear distribution in juvenile (A) and adult (B) anaerobic light fibers. Cross sections of fixed light fibers from WGA-injected animals, which were treated with 4′,6-diamidino-2-phenylindole, a blue-fluorescent probe for nuclei. Green-fluorescent WGA staining identifies fiber sarcolemma. In the small fibers of the juvenile, nuclei are found almost exclusively at the fiber edge; in the large fibers of the adult, there is a high density of SS and IM nuclei.

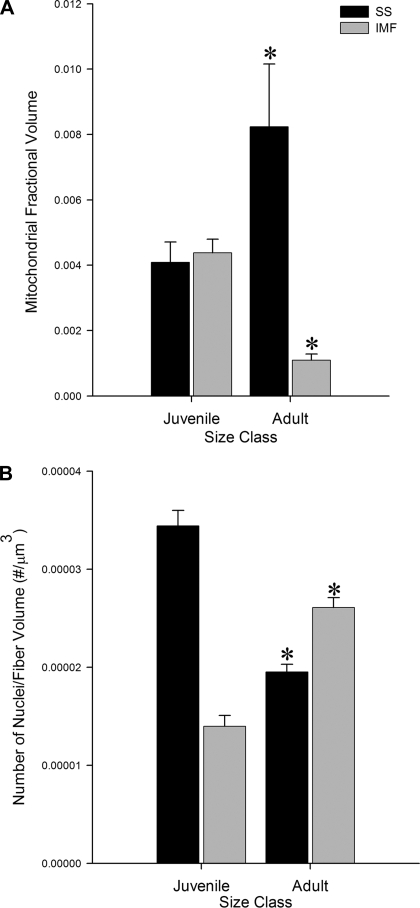
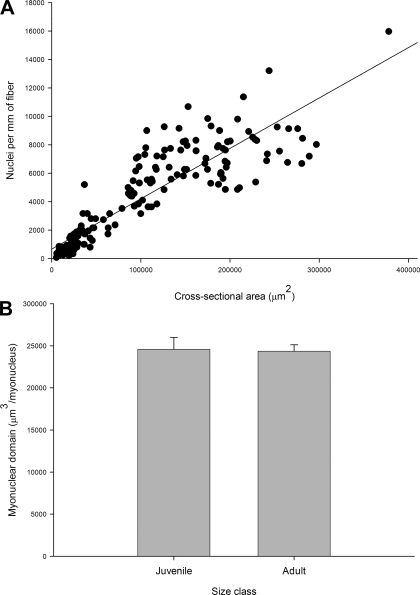
Stereological analyses revealed that the mitochondrial SSFV increased significantly, while the IMFV decreased significantly, during fiber growth (Fig. 5A). In contrast, nuclear SS number volume decreased significantly, while IM number volume increased significantly, during fiber growth (Fig. 5B). Neither the total (IM + SS) mitochondrial fractional volume nor the total nuclear number volume was significantly different between the juveniles and the adults. The unchanging total mitochondrial fractional volume is consistent with the minimal negative allometry of aerobic capacity with body mass in the blue crab light fibers (6). The constancy of total nuclear number volume reflects a direct relationship between the number of nuclei per millimeter of fiber and fiber CSA (Fig. 6A) and a myonuclear domain [the volume of cytoplasm in a cell that is serviced by a single nucleus (13)] that is not significantly different between juvenile and adult fibers (24,583.23 ± 1,412 and 24,356 ± 768 μm³, respectively; Fig. 6B). Although the nuclear distribution was quite different from that in vertebrate skeletal muscle, the myonuclear domain in muscle from blue crab was comparable to that of chicken (58), rat (3), and human (50) muscle. It is possible that our estimates of myonuclear domain are slightly in error because of the difficulty of classifying nuclei adjacent to the sarcolemma as truly intracellular or as extracellular satellite cell nuclei (23). However, this potential source of error does not alter our general findings, and misidentified nuclei likely comprise a small percentage of the total number of SS and IM nuclei (61).

Fig. 5.

Changes in mitochondrial and nuclear distribution during growth in light fibers. A: SS fractional volume (SSFV) and IM fractional volume (IMFV) of mitochondria in adult and juvenile light fibers. SSFV increases significantly (P < 0.05) and IMFV decreases significantly across size classes (P < 0.0001). B: SS number volume (SSNV) and IM number volume (IMFV) of nuclei in adult and juvenile light fibers. SSNV decreases significantly (P < 0.0001) and IMFV increases significantly across size classes (P < 0.0001). Values are means ± SE. *Significantly different across size class.

Fig. 6.

A: correlation between nuclear number per millimeter and fiber cross-sectional area. Nuclear number per millimeter increases significantly with fiber cross-sectional area (y = 669.79 + 0.035x, r² = 0.80, P < 0.0001), resulting in conservation of myonuclear domain during fiber growth (B). Values are means ± SE.

We suggest that mitochondria and nuclei undergo opposite patterns of redistribution during fiber growth as a result of contrasting diffusion constraints. Mitochondria require adequate diffusive flux of both O₂ to mitochondria and small metabolites between mitochondria and cytosolic ATPases. Thus the shift in mitochondria toward an SS distribution during fiber growth reflects the need to minimize diffusion distances for O₂ at the expense of larger diffusion distances for small metabolites. Nuclear function, on the other hand, is not directly dependent on O₂ supply but, rather, relies on the diffusion of slowly moving macromolecules between the nucleus and the cytosol that it serves. The increase in IM nuclei during fiber growth likely indicates a strategy to minimize transport distances for RNA and proteins in large-diameter fibers, although this constitutes a striking departure from the usual skeletal muscle paradigm of an exclusively SS nuclear distribution (9).

Reaction-diffusion models allow us to assess the influence of organelle distribution on cellular function. By varying the percentage of ATP production by the SS and IM mitochondrial populations, we were able to evaluate the effect of changing distribution on ATP turnover rates. Using previously measured maximal rates of aerobic metabolism in the light fibers (38), we found that the small, light fibers [with diffusive length scale (L) = 40 μm] had a high η when we assumed that 48% of the ATP production was via SS mitochondria (observed case) and when we assumed that all ATP production was via the IM mitochondria (no SS mitochondria; Table 1). Thus there was no effect of changing mitochondrial distribution from the near-uniform distribution that we observed to a truly uniform, hypothetical distribution over the short diffusion distances that characterize small light fibers. In contrast, the large light fibers (L = 300 μm) had a high η (little diffusion limitation) when 88% of ATP production was supplied by the SS mitochondria (observed case), whereas a greatly reduced η and a threefold lower rate of ATP turnover were observed when we assumed a uniform distribution with only IM mitochondria (Table 1). Therefore, in the large fibers that have longer maximal intracellular diffusion distances, clustering mitochondria at the sarcolemma permits a much higher rate of ATP turnover than does a uniform mitochondrial distribution. To our knowledge, this is the first demonstration that rates of aerobic flux can be enhanced simply by changing the position, but not the number, of mitochondria to offset diffusion limitation. However, it is also clear that there are limits on the extent to which the ontogenetic shift in distribution is effective, indicated by the reduced (but still high) η at the previously measured rates of ATP turnover. That is, the combination of fiber size, mitochondrial distribution, and blood Po₂ in adult animals appears to allow a maximal ATP turnover rate in the large light fibers that is very close to the observed rate.

Table 1.

Influence of mitochondrial distribution and subdivision of dark fibers on η, average nondimensional O₂ and ATP concentrations, k₁, and k₂ for small and large fibers

Length, μm	SS fraction, %	k1, s−1	k2, mM−1 ·s−1	Avg Nondimensional O2 Concn	Avg Nondimensional ATP Concn	η	ATP Turnover Rate, mM/min
Light fiber
40	48	0.0009	0.86	0.94	0.86	0.99	0.47
40	0	0.0009	0.86	0.90	0.86	0.99	0.46
300	88	0.005	0.186	0.55	0.16	0.77	0.47
300	0	0.005	0.186	0.20	0.05	0.26	0.16
Dark fiber
17.5	75	0.005	1.10	0.96	0.61	0.99	1.84
17.5	0	0.005	1.10	0.92	0.59	0.98	1.80
300	75	0.012	14.9	0.065	0.25	0.32	1.84
300	0	0.012	14.9	0.027	0.13	0.17	0.98

SS, subsarcolemma; k₁, ATPase rate constant; k₂, oxidative phosphorylation rate constant. Data are based on experimentally determined diffusion path lengths and phosphagen recovery rates (6, 24, 30, 38). Output was obtained at the lowest values of k₁ that would satisfy the observed rate, which maximized η. ATP turnover rate is fixed in the observed case (SS mitochondrial fraction =48, 88, or 75%), and k₁ and k₂ values from these observed cases are used in the hypothetical cases with only intermyofibrillar mitochondria (SS mitochondrial fraction = 0).

The redistribution of mitochondria observed in the light fibers leads to decreased diffusion path lengths for O₂, but at the expense of increasing intracellular diffusion distances for small metabolites, such as ATP and ADP. Although O₂ is a relatively small, rapidly diffusing molecule, it is found in low concentrations in the hemolymph around the basal muscle because of the low blood Po₂ characteristic of blue crabs (20, 43). Also, blue crabs lack myoglobin, which would increase the solubility of O₂ in the sarcoplasm and enhance diffusive flux to the mitochondria (51). Relocation of mitochondria to the fiber periphery, therefore, appears to avoid problems that may be associated with emerging O₂ gradients across the cell (42, 68) and leads to enhanced aerobic ATP flux (Table 1). This is consistent with our previous finding that postcontractile phosphagen recovery is not substantially limited by metabolite diffusion in the anaerobic light fibers (38). The effect of mitochondrial distribution is dependent on metabolic rate and diffusion distance, and it seems likely that the processes that govern the relative density of SS and IM mitochondria in blue crab muscles are also found in organisms that do not necessarily have large fibers (33, 42, 49, 68).

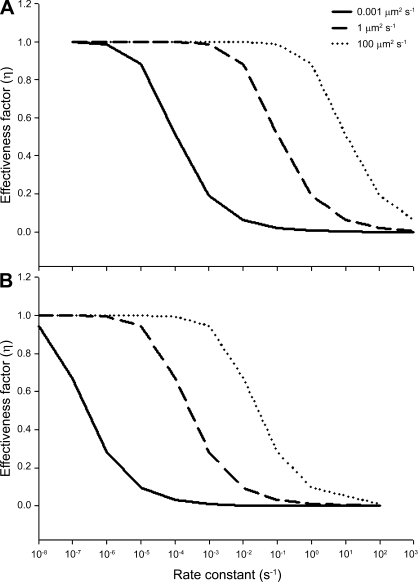
Nuclei (and their associated synthetic apparatus) are involved in the simultaneous transcription, translation, and diffusive flux of a variety of molecules ranging in size from small metabolites to larger macromolecules and, potentially, membrane-bound vesicles. To determine whether the distribution of nuclei in the anaerobic fibers was influenced by diffusion limitations, we modeled a simpler, existing derivation of η (19) at varying reaction rates for molecules with a range of diffusion coefficients (indicating a range of sizes). Figure 7 demonstrates that, at any specific η, changing the nuclear distribution during fiber growth, and thereby reducing diffusion distances, enhances the permissible rate constant for a given nuclear process by three orders of magnitude. This relationship holds for processes that entail diffusion coefficients characteristic of small molecules, macromolecules, or membrane vesicles. Although the high density of IM nuclei in large light fibers has not, to our knowledge, been seen in other organisms, it should be noted that extensive hypertrophy can lead to the occurrence of IM nuclei in vertebrate muscle as well (31, 58). Thus, diffusion constraints may govern the spacing of SS nuclei (9, 10) and the emergence and spacing of IM nuclei once fibers reach a threshold size.

Fig. 7.

Effect of changes in nuclear distribution on the rate constant for nuclear processes. A diffusion distance of 14.5 μm (observed radius of myonuclear domain; A) is compared with a distance of 300 μm (hypothetical case with only SS nuclei in an adult fiber; B). If the population of IM nuclei did not increase during light fiber hypertrophic growth there would be a three-order-of-magnitude-smaller rate constant that could be attained at any given effectiveness factor (η), for any diffusion coefficient.

Myonuclear domain size is thought to remain constant during the life of a muscle fiber (2, 3, 7, 8, 12, 17, 21), as nuclear number changes in response to hypertrophy (9, 28, 31, 44, 57, 59, 62) and/or atrophy (1, 25, 50, 70). Although comparable data for crustaceans are not available, Skinner (64) showed a ∼50% increase in DNA content per gram of protein during extreme atrophy coordinated with ecdysis. Atrophy of certain muscles is required before a molt cycle in crustaceans, so that larger muscles (e.g., those of the chelae) can be pulled through very small openings in the rigid exoskeleton. The observed change in DNA content per gram of protein would lead to a substantial, although temporary, increase in myonuclear domain. Over long periods of atrophy or hypertrophic growth, however, myonuclear domain conservation can be achieved with more than one arrangement of nuclei. By increasing nuclear density only at the fiber periphery during growth, as is typical in vertebrate systems, myonuclear domain can be conserved without a change in nuclear distribution. However, in cells that become as large as the anaerobic light fibers, implementation of this strategy may inhibit gene expression and/or protein synthesis by drastically increasing diffusion distances. By increasing the number of IM nuclei (vs. SS nuclei) with growth, as we observed in the blue crab light fibers, short diffusion distances can be conserved within each nuclear domain. We propose that it is not the myonuclear domain per se but, rather, a small maximal diffusion distance within that domain that is being conserved with growth. We found that the mean distance between any two myonuclei is 29.0 ± 0.5 and 28.6 ± 0.4 μm in juvenile and adult light fibers, respectively, which is consistent with nuclear spacing in mouse skeletal muscle with an exclusively SS distribution (9). Furthermore, Bruusgaard et al. (9, 10) used novel myonuclear labeling techniques and mathematical analyses to convincingly demonstrate that SS nuclei are not positioned randomly within a mouse muscle fiber but, rather, approximate an evenly spaced distribution, presumably to minimize transport distances.

Aerobic dark fibers.

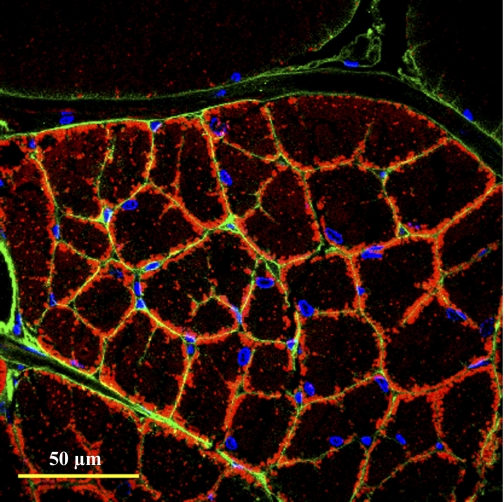
The capacity for aerobic swimming in the blue crab presumably entailed the evolution of the highly subdivided dark fibers from giant light fiber precursors, which had diffusion distances that were too great to support the high O₂ and metabolite diffusive flux needed for sustained swimming behavior (24, 30). Figure 8 is a micrograph of a dark fiber that is representative of juveniles and adults. Here, the WGA probe for sarcolemmal glycoproteins revealed intrafiber perfusion around each subdivision. This finding was further supported in muscle fibers from animals injected with WGA and fluorescent microspheres, where it is clear that hemolymph circulates between fiber subdivisions in the dark fibers but does not penetrate the adjacent light fibers (Fig. 9). Nuclei are located exclusively at the periphery of each subdivision, whereas mitochondria are primarily, but not exclusively, located at the subdivision periphery (Fig. 8). The pattern of organelle distribution within a dark fiber subdivision is reminiscent of mammalian skeletal muscle fibers (9, 33), which share similar dimensions and, therefore, similar diffusion constraints. In contrast to the light fibers, however, the dark fibers do not show dramatic changes in organelle distribution during growth. This is consistent with the observation that as these fibers grow hypertrophically, new subdivisions form and the effective diffusion distances do not change (30).

Fig. 8.

Aerobic dark fiber organelle distribution and perfusion. Transverse section of fibers from WGA-injected animals [to indicate perfusion pathways (green)] labeled for nuclei (blue) with 4′,6-diamidino-2-phenylindole and labeled for mitochondria (red) with MitoTracker Deep-Red 633. Nuclei are found exclusively at the subdivision edges and mitochondria at the edge and core of each subdivision. Intrafiber perfusion is indicated by complete WGA staining around each individual subdivision. Pattern is the same in small and large fibers.

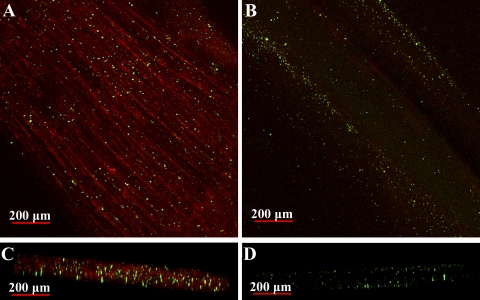
Fig. 9.

Pattern of hemolymph perfusion of dark (A and C) and light (B and D) levator fibers. Live animals were injected with a red-fluorescent Alexa 594-conjugated WGA and 0.2-μm yellow-green fluorescent microspheres. WGA binds to sarcolemmal (and vessel endothelial) glycoproteins, whereas microspheres become lodged in the smallest microvasculature of the muscle. A and B: 3-dimensional reconstructions (stacks) of whole fiber bundles. C and D: digitally reconstructed images of A and B, respectively, viewed in cross section. Fibers appear slightly flattened because of pressure from the coverslip. Intense WGA staining and substantial accumulation of microspheres inside the dark fibers indicate a high degree of intrafiber perfusion. Light fibers, however, exhibit very faint WGA staining and a lower abundance of microspheres (B and D), both of which occur primarily at the fiber edge. Beads that appear to be lodged inside the light fibers are likely located within fiber clefts.

We evaluated the interaction of metabolic organization and metabolic fluxes, as described above, in a subdivided and a hypothetical, nonsubdivided aerobic fiber. We incorporated rates of aerobic metabolism experimentally determined for the dark fibers (24). A high η was found for a single fiber subdivision (L = 17.5) in which 75% of the ATP production occurred via SS mitochondria (observed case) (30), as well as when only uniformly distributed, IM mitochondria were present (Table 1). Therefore, at these short diffusion distances, the experimental reaction rate can be attained with either mitochondrial distribution. However, the influence of mitochondrial distribution on η becomes sizable when ATP turnover increases to rates characteristic of other aerobic muscles. Our measurements of aerobic metabolism were based on postcontractile phosphagen resynthesis rates that likely underestimate maximal metabolic rate in the dark fibers for reasons described elsewhere (24). However, even at these relatively low rates of ATP turnover, the influence of subdividing the fiber is readily apparent. If subdivisions were not continuously formed during growth, which would result in a diffusion distance of ∼300 μm, aerobic fibers would yield η of only 0.32 when the SS mitochondrial population was 75%. Thus, in the absence of subdivisions, dark fibers cannot sustain even this modest rate of ATP turnover. As in the light fibers, η and ATP turnover rate decreased even further (0.17 and 0.98 mM/min, respectively) when there was no SS mitochondrial population (Table 1). Similarly, the distribution of nuclei throughout the fiber (at the periphery of each subdivision) again reduces diffusion distances and enhances nuclear reaction fluxes. The effective diffusion distance between nuclei in the dark subdivided fibers (17.5 μm) is similar to that for IM nuclei in the light fibers discussed above (14.5 μm). Therefore, we can again examine Fig. 7 to demonstrate that nuclear reaction rate constants for the observed short diffusion distances in the dark fibers are much higher than those in the hypothetical, unsubdivided case with only SS nuclei.

The subdivided structure of dark muscle raises the following question: What constitutes a fiber? A fiber is typically considered to share a common cytoplasm. Using the FRAP method, we therefore compared intracellular diffusion coefficients (of the small dye molecule calcein) between the dark, subdivided fibers and the light, nonsubdivided fibers as a probe for cytoplasmic connectedness between subdivisions. Intracellular diffusion coefficients for calcein could be calculated for movement in the longitudinal direction (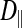; parallel to the fiber or subdivision) and the radial direction (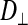; perpendicular to the fiber or subdivision). By comparing 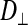between the two fiber types, we intended to determine whether intracellular diffusion in the dark fibers was, to any extent, impeded by the subdivision walls or whether the membrane permitted completely free cytoplasmic exchange.

In the light fibers, 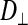was significantly lower than 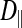(0.33 ± 0.06 × 10⁻⁶ vs. 1.31 ± 0.16 × 10⁻⁶ cm²/s, P < 0.0001), indicating an orientation dependence of diffusion in these fibers, and 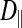was lower in the dark fibers (0.89 ± 0.093 × 10⁻⁶ cm²/s) than in the light fibers. These results are consistent with previous measurements of metabolite diffusion using pulsed-field gradient NMR in crustacean and fish muscle, which showed that subcellular barriers inhibit mobility more substantially in the radial than in the axial direction (34–37). Although this anisotropy has been demonstrated by pulsed-field gradient-NMR methods, to our knowledge, this is the first time this phenomenon has been observed using FRAP experiments. The measurement of 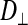, however, yielded an unexpected result. The long, thin rectangular bleached region was invariably encapsulated within a single dark fiber subdivision, and the subdivisions appeared to be completely isolated from one another (Fig. 10A). This pattern contrasts with that in the light fibers, which show a much faster recovery of fluorescence in the bleached region, indicative of rapid, unconstrained diffusion (Fig. 10B). Thus, diffusion of the fluorescent probe within the small volume of a dark fiber subdivision led to rapid equilibration, such that the entire subdivision became bleached. Furthermore, there was no detectable movement of unbleached fluorophore due to radial diffusion from adjacent subdivisions. It therefore appears that the membranes separating individual subdivisions do not allow free cytoplasmic exchange.

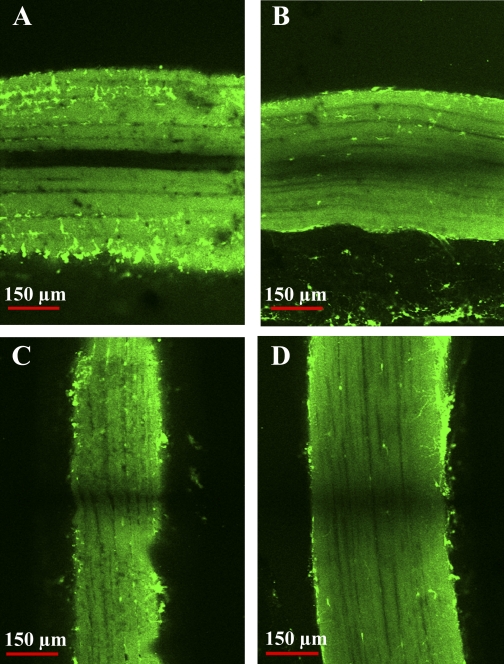
Fig. 10.

Immediate postbleach images of dark (A and C) and light (B and D) fibers during fluorescence recovery after photobleaching (FRAP). Fibers were incubated in the membrane permeable-dye calcein, which fluoresces green when hydrolyzed by intracellular esterases, and then subjected to a series of high-intensity bleach treatments. A and B: dark and light fiber postbleach images, respectively, from a FRAP experiment measuring radial diffusion coefficients. In dark fibers, calcein fluorophore (green) is thoroughly bleached within a single subdivision, and there is no radial diffusion into this bleached region, indicating cytoplasmic isolation. Light fibers exhibit some postbleach recovery via radial diffusion, indicative of cytoplasmic continuity throughout the fiber. C and D: images from measurements of axial diffusion coefficients. Pattern of recovery in the bleached region is similar between the dark (C) and light (D) fibers, indicating unhindered cytoplasmic exchange along the longitudinal axis in both fiber types. Subsequent images (not shown) demonstrate complete recovery of fluorescence in the bleached region.

These findings suggest that each subdivision functions as an independent metabolic unit, complete with mitochondria, nuclei, and thorough perfusion. From this perspective, the subdivisions would appear to constitute a fiber. However, fibers have metabolic and contractile functions. What then is the contractile functional unit: the subdivision or the fiber? There are ∼70 subdivisions per large dark fiber in an adult animal, and if the subdivisions are the contractile unit, we would expect a much greater neuromuscular synapse density in the dark fibers than the light fibers (an ∼70-fold increase if the innervation per fiber is constant). However, no such difference was observed (Fig. 11). Synapses were located in comparable densities at the sarcolemmal surface and within clefts that penetrate the interior of the light and dark fibers. Crustacean muscle is often multiterminally innervated (for review see Refs. 4 and 5), and motor axons travel deep into the sarcolemmal clefts to terminate in more central positions within the fiber (63). In addition, crustacean muscle fibers, in contrast to mammalian muscle fibers, often exhibit electrical continuity (52, 54) and can propagate membrane potentials via cytoplasmic connections between adjacent fibers (46). For this reason, it is difficult to use electrophysiological techniques to determine whether subdivisions are able to contract independently, but it is also more likely that all the subdivisions within a fiber contract in unison, making the whole fiber the contractile functional unit.

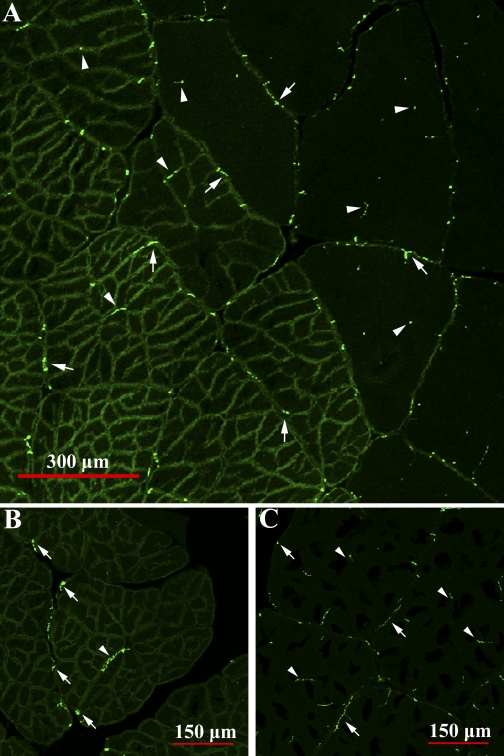
Fig. 11.

Muscle cross sections labeled with anti-SYNORF1, an antibody to the presynaptic vesicle-associated phosphoprotein synapsin, that reveal innervation patterns in light and dark levator fibers. For emphasis, labeling is shown in the transition zone of light and dark fibers (A) and in light (B) and dark (C) fibers independently. Inherent autofluorescent properties of the sarcolemma make the fiber boundaries visible. In both fiber types, synapses were visualized at the fiber sarcolemma (arrows) and inside the fiber core (within sarcolemmal clefts) and between subdivisions (arrowheads). Synapse density is not higher in dark fibers (left in A) than in light fibers (right in A), which would be expected if subdivisions were independent contractile units.

The above-described evidence suggests that aerobic dark fibers evolved from the anaerobic light fiber precursors by effective separation of the metabolic functional unit (fiber subdivision) from the contractile functional unit (whole fiber). The subdivisions therefore circumvent diffusion constraints associated with aerobic metabolic processes and can be considered a distinct metabolic unit. Contraction, on the other hand, which is not constrained by diffusive processes, is presumably carried out by the fiber as a whole as a result of electrical continuity between subdivisions.

Perspectives and Significance

The light and dark fibers of C. sapidus swimming muscles grow hypertrophically and reach dimensions in adult animals that are atypical of most cells. The two fiber types have evolved in fundamentally different ways to compensate for the changing role of diffusion during fiber growth. It is not known whether the ontogenetic changes in fiber design are controlled by diffusive processes per se or whether they represent part of a fixed developmental program. Nevertheless, it seems clear that the changes in fiber structure during development are a response to diffusion constraints, and they ameliorate many of the consequences of hypertrophic growth. Although the use of an extreme model system has revealed diffusion control of cell design that would be difficult to observe in traditional models, it is likely that the rules we describe here apply broadly. In fact, the present study appears to explain patterns that have long been observed in mammalian muscle fibers. Areas for future study would be a test of the generality of the observed patterns across many species and cell types, as well as characterization of the molecular basis of diffusion-driven muscle organization.

GRANTS

The anti-SYNORF1 antibody developed by E. Buchner was obtained from the Developmental Studies Hybridoma Bank developed under the auspices of the National Institute of Child Health and Human Development and maintained by the Department of Biological Sciences at the University of Iowa (Iowa City, IA). This research was supported by National Science Foundation Grants IOS-0316909 (to S. T. Kinsey), IOS-0719123 (S. T. Kinsey and R. M. Dillaman), and IOS-0315883 and IOS-0718499 (to B. R. Locke), National Institute of Arthritis and Musculoskeletal and Skin Diseases Grant R15-AR-052708 (to S. T. Kinsey), and a Sigma Xi Grant-in-Aid of Research (to K. M. Hardy).