Dehydration and the Dynamic Dimensional Changes within Dentin and Enamel

Abstract

Objectives

The objectives of this study were to quantify the dimensional changes in dentin and enamel during dehydration, and to determine if there are differences between the responses of these tissues from young and old patients.

Methods

Microscopic Digital Image Correlation (DIC) was used to evaluate deformation of dentin and enamel as a function of water loss resulting from free convection in air. Dimensional changes within both tissues were quantified for two patient age groups (i.e. young 18≤age≤30 and old 50≤age) and in two orthogonal directions (i.e. parallel and perpendicular to the prevailing structural feature (dentin tubules or enamel prisms)). The deformation histories were used to estimate effective dehydration coefficients that can be used in quantifying the strains induced by dehydration.

Results

Both dentin and enamel underwent contraction with water loss, regardless of the patient age. There was no significant difference between responses of the two age groups or the two orthogonal directions. Over one hour of free convection, the average water loss in dentin was 6% and resulted in approximately 0.5 % shrinkage. In the same time period the average water loss in the enamel was approximately 1% and resulted in 0.03% shrinkage. The estimated effective dehydration coefficients were -810 µm/m/(% weight loss) and -50 µm/m/(% weight loss) for dentin and enamel, respectively.

Significance

The degree of deformation shrinkage resulting from dehydration is over a factor of magnitude larger in dentin than enamel.

Introduction

There are many instances in which routine clinical practices can cause changes in the hydration of tooth tissues. For example, procedures commonly used for evaluating pulpal sensitivity using forced air, and in preparing surfaces for bonding, can cause dehydration. The water loss imposed by these procedures can result in shrinkage of dentin and enamel which, if restrained, can cause the development of undesired and potentially deleterious stresses. Consequently, dehydration and the resulting deformation within tooth tissues is a relevant clinical issue.

Previous studies have examined dimensional changes in dentin caused by complete dehydration. Van der Graaf and Ten Bosch [1] compared freeze-drying and drying of dentin in nitrogen at 60 and 100 °C. The treatments resulted in a reduction in weight by 9.0% to 10.5% and shrinkage of 1.7-2.0% and 1.4-1.7%, respectively, in the plane perpendicular and parallel to the tubules. In a study of demineralized coronal dentin by Carvalho et al., [2], dehydration was achieved in acetone, followed by further drying in hexamethyldisilazane, Peldri II, or using critical-point drying techniques. All three drying procedures caused dimensional changes with volumetric shrinkage between 15-20%, substantially higher than that of fully mineralized tissue. That indicates that the degree of shrinkage is a function of the tissue's microstructure. Of relevance here, there are structural changes that arise in dentin with the aging process. Specifically, after the third decade of life the lumens become progressively filled with mineral apatites in the formation of sclerotic dentin [3]. The process results in an overall increase in mineral content with age [4, 5], which may influence the nature of water loss during dehydration, as well as the rate and degree of shrinkage. No reported study has explored the potential for differences in dimensional changes in hard tissues of the tooth as a function of age.

Deformation within tooth tissues that results from free convection and temporary periods of water loss has been studied. In one innovative study, atomic force microscopy was adopted to examine the dimensional changes and deformation within dentin occurring during air-drying [6]. Though the dynamic strain response could not be documented due to limitations of the measurement resolution, the authors noted that the shrinkage strains within fully mineralized dentin were less than 0.5% over 24 hours. Moiré interferometry has also been used to evaluate dimensional changes in dentin in which the specimens were dehydrated over a period of hours and then rehydrated [7]. In specimens undergoing unconstrained shrinkage the strain gradients across the dentin-enamel junction were very high, and believed to result from differences between the water content of dentin and enamel and the corresponding differences in water loss. More recently, Kishen and Rafique [8] studied the dimensional changes in dentin undergoing free convection using moiré interferometry. While the major portion of water loss occurred within 2 hours, the strain history could not be quantified due to insufficient measurement resolution. These experiments demonstrated that the loss of free water occurs rapidly and that a highly precise measurement technique is required to quantify the consequent deformation history.

Despite the clinical relevance, no study has successfully documented the dynamic aspects of dimensional changes that occur in dentin or enamel during the early stage of dehydration. Therefore, in the present study dimensional changes resulting from dehydration of these two tissues were quantified using a microscopic optical technique. The purpose of this study was to quantify the dimensional changes in dentin and enamel during dehydration, and to compare the responses of these tissues from young and old patients.

Materials and Methods

Human premolars and molars were obtained from participating dental clinics in Shanghai, PRC according to approved protocols issued by the Institutional Review Board of Shanghai University and the University of Maryland Baltimore County. The teeth were placed in Hank's balanced salt solution (HBSS) immediately after extraction, and the patient's age and gender were recorded. A total of 10 teeth obtained from patients ranging in age from 22 to 63 years were divided into young (18≤age≤30: N=5) and old (50≤age: N=5) groups (Table 1). The terms used to describe the two ages were chosen mostly for convenience. “Old” dentin and enamel simply describes tissue that was obtained from a group of more mature patients with average age exceeding twice that of the younger group. The teeth were sectioned bucco-lingually using a slow speed diamond saw under continuous water-based coolant; two sections were made to obtain slices from the central region of the teeth with a thickness of approximately 2 mm (Fig. 1(a)). One of the sectioned surfaces was lightly abraded with #120 mesh silicon dioxide sandpaper. Additional sections were introduced to obtain specimens (beams) of either enamel or dentin with cross-section of 4 mm² (Fig. 1(a)). The specimens were maintained in HBSS at 21°C and tested within 3 weeks of tooth extraction.

Table 1.

Details of the dehydration models describing shrinkage in dentin and enamel. The entries for dentin and enamel highlighted in grey represent the effective dehydration coefficients assuming a linear model. The units for coefficients A₀ and B are m/m/(% water loss) and for coefficients A₁ are m/m/(% water loss)².

Group	Age (years)	Dentin						Enamel
		A0 (1) ×10ˆ-3	A1 (1) ×10ˆ-5	A0 (2) ×10ˆ-3	A1 (2) ×10ˆ-5	B (1) ×10ˆ-3	B (2) ×10ˆ-3	B (1) ×10ˆ-5	B (2) ×10ˆ-5
Young
Y1	22	-0.15	-3.82	-0.20	-2.91	-0.44	-0.43	-1.15	-4.13
Y2	24	0.09	-22.60	-0.01	-18.20	-1.10	-0.96	-2.90	-3.93
Y3	25	-0.14	-6.30	-0.09	-6.61	-0.42	-0.68	-7.27	-10.30
Y4	25	-1.80	9.02	-2.78	18.90	-0.86	-0.79	-17.50	-26.70
Y5	28	-0.74	3.79	-0.78	5.56	-0.62	-0.60	-6.82	-15.50
Avg.	25 (2)					-0.7 (0.3)	-0.7 (0.2)	-6.0 (6.3)	-10.5 (9.5)
Old
O1	50	-1.11	9.65	-1.09	8.9	-0.43	-0.46	-9.14	-10.40
O2	56	-1.79	4.03	-2.08	12.1	-1.59	-1.48	-23.80	-8.04
O3	59	-3.87	48.4	-4.49	75.2	-1.42	-1.45	-6.83	-8.70
O4	63	-1.79	17.9	-1.5	12.6	-0.81	-0.81	-15.00	-3.77
O5	63	-0.75	4.77	-0.99	6.04	-0.35	-0.49	-2.14	-12.60
Avg.	58 (5)					-0.9 (0.6)	-0.9 (0.5)	-11.4 (8.3)	-8.7 (3.3)

Figure 1.

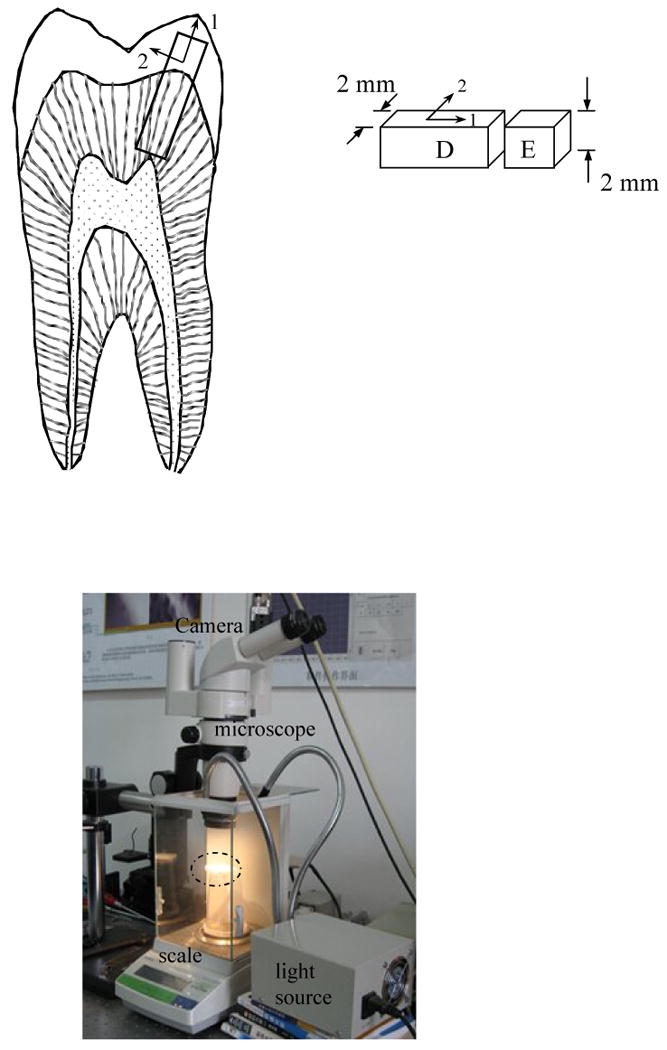
Details of the experimental approach

a) details of the specimen configuration. Note that the “1” and “2” directions correspond to the axes parallel and perpendicular, respectively, to the prevailing constituent.

b) the measurement system including optics (CCD camera, light source and microscope) and precision scale. The position of the specimen is located within the dashed enclosure.

Dimensional changes of the specimens resulting from dehydration were quantified using microscopic Digital Image Correlation (DIC). Due to its simplicity and versatility, DIC is becoming a method of choice in the evaluation of deformation within both soft [e.g. 9] and hard [e.g. 10] tissues. The optical arrangement consisted of a stereomicroscope (Nikon, Model SMZ 1000), a CCD camera (JAI Pulnix, Model TM-1400-CL) with resolution of 1392 × 1040 pixels and a personal computer with standard frame grabber. Details of the system and its operation are described elsewhere [11]. This optical unit was coupled with a precision digital scale (Mettler Toledo, Model AB 104-N) with a 100 g full-scale range and resolution and 0.1 mg, which enabled an estimate of the instantaneous moisture loss. The combination enabled simultaneous measurements of the displacement field and specimen weight via digital output to computer. The major components of the measurement system and their arrangement are shown in Figure 1(b). To perform experiments the sectioned specimens were removed from the HBSS, the surface of interest was coated liberally with blue indelible ink, blotted dry to remove excess surface moisture (and ink), and then placed atop the digital scale. The ink increased the natural contrast and decreased the translucency of the tissues to enable clear digital images to be acquired. The ink was water-based and only a very diffuse coating resided on the surface, thereby minimizing the opportunity for any influence to the moisture loss or shrinkage. At the beginning of the experiments a digital image of the specimen's surface was obtained and the weight recorded to document the “initial” or reference state. Thereafter, digital images of the specimens were acquired every 30 seconds and recorded along with the instantaneous weight for a period of up to 60 minutes at 25 ± 1°C, 45% relative humidity. The images were obtained using a magnification of 250×, resulting in a field of view of less than 0.75×1=0.75 mm².

In examination of the dentin and enamel specimens the first digital images obtained for each tissue served as the “undeformed image” (reference state), and all additional images obtained during dehydration are considered the “deformed” images. The displacement field within the field of view was determined from a correlation of the grayscale distribution of the deformed and reference images. Measurements of the in-plane displacements were obtained in two orthogonal directions, which by default were parallel and perpendicular to the dentin tubules or the enamel prisms. According to the field of view, the minimum displacement resolution without sub-pixel correlation was approximately 1 µm. The displacement distributions parallel and perpendicular to the structural feature of interest were fit with polynomial functions and the first derivatives of these functions with respect to physical distance were used in quantifying the strain distributions.

The strain fields in the dentin and enamel were used to determine functional dehydration coefficients describing the strain in terms of the amount of water loss. Similar to the techniques for quantifying thermal expansion/contraction, the strains were modeled according to

$${\epsilon }_i={\kappa }_i•\Delta H$$ (1)

where ε_i is the strain parallel (1-direction) or perpendicular (2-direction) to the feature of interest (Fig. 1(a)), ΔH is the fractional water loss in weight percent (100%·(initial weight – final weight)/initial weight), and κ_i is the dehydration coefficient where the subscript denotes the direction (parallel or perpendicular to the prevailing microstructure). For each tissue the dehydration coefficients in the two orthogonal directions were estimated from the respective average strain distribution in that direction according to

$${\kappa }_i={\left[A_o+A_1•\left(\Delta H\right)\right]}_i$$ (2)

where A_o and A₁ are curve fitting coefficients used in modeling the average strain as a function of the water loss. Note that Eqn. 2 accounts for nonlinear deformation that may arise with dehydration. A simpler linear approach was also used considering K_i as a constant (i.e. K_i =B_i) and not a function of the degree of moisture loss. Statistical differences in the components of shrinkage with respect to the two orthogonal directions and with respect to age were calculated using an ANOVA with Tukey's Honestly Significant Difference (HSD) test; significant differences were defined by p≤0.05.

Results

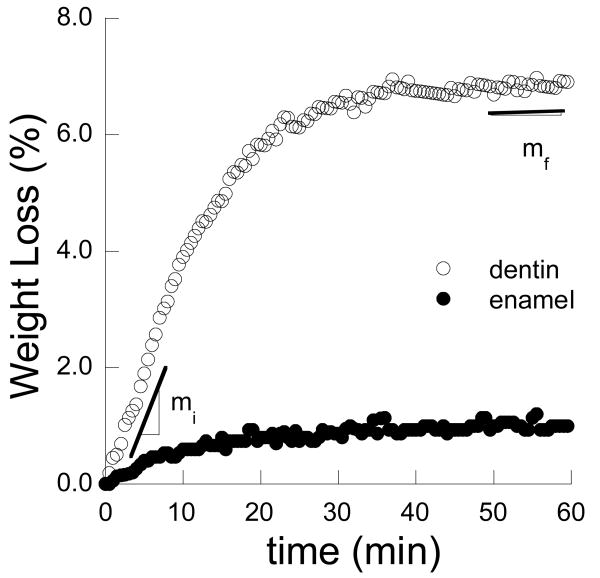
Dehydration of the dentin and enamel was quantified in terms of the percent weight loss and recorded as a function of time. Representative responses for the two tissues are shown in Figure 2. As expected, the rate of water loss was a maximum at the beginning of free convection (denoted by slope m_i) and decreased to a minimum (m_f) near the end of the one hour period. For dentin, the average initial and final rate of loss was 0.31±0.10 %/min and 0.04±0.02 %/min, respectively. The maximum and minimum rates of water loss in enamel were 0.07±0.03 %/min and 0.006±0.002 %/min, respectively. The rate of water loss in enamel was significantly smaller (p<0.0001) than in dentin.

Figure 2.

Dehydration history for a young dentin (22 year old) and enamel (25 year old) sample. Note the rate of moisture loss is denoted near the initiation (m_i) and completion (m_f) of the free convection cycle for dentin.

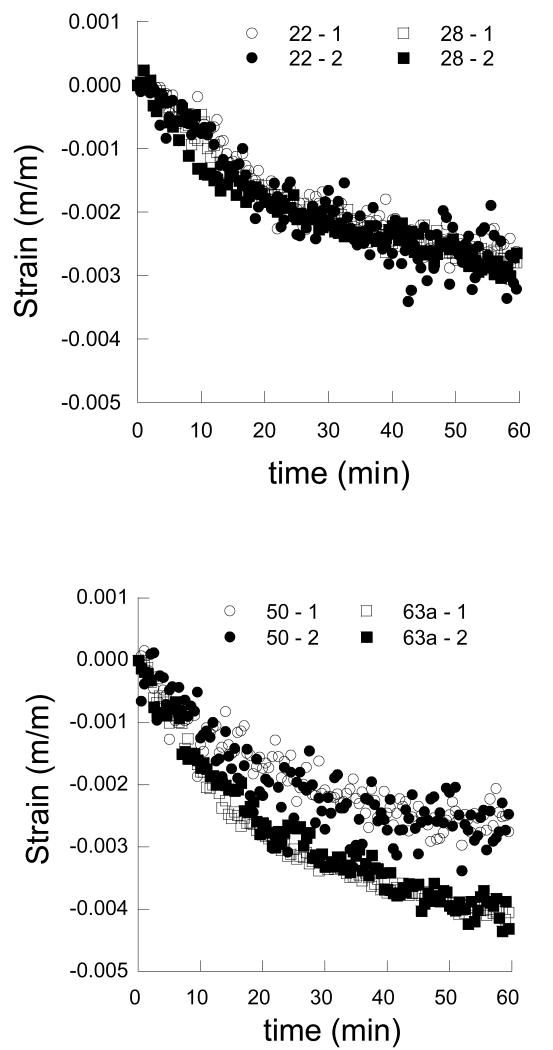
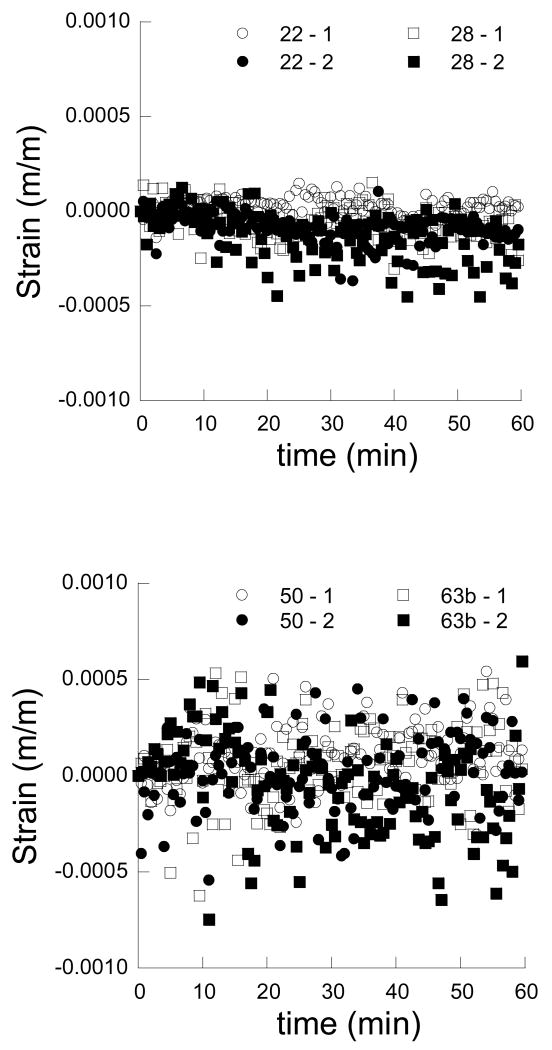
As a result of dehydration, the dentin and enamel samples underwent shrinkage in the two orthogonal directions, regardless of age. Representative strain responses for young and old dentin are shown as a function of time in Figures 3(a) and 3(b), respectively. Similarly, average strain distributions within young and old enamel are shown in Figures 4(a) and 4(b), respectively. Note that the strains within enamel are lower than those within the dentin and the disparity in shrinkage between the two tissues increases with time. In general, the strains resulting from dehydration of the dentin are a factor of magnitude higher than those in the enamel. Also evident in results of the enamel, the degree of variation in the strains (Fig. 4(b)) is greater than the average strain. The variation arises from three factors, namely: 1) the translucent nature of the tissue, 2) the corresponding difficulty in correlating images of the deformed enamel (during shrinkage) with the reference image at the start of free convection, and 3) the low magnitude of displacement in enamel relative to that caused by ambient vibration. As such, the measured responses for the enamel are less reliable than those obtained for dentin. Nevertheless, for both tissues the responses parallel and perpendicular to the prevailing microstructure in the “1” and “2” directions are equivalent (e.g. Fig. 3 and Fig. 4), thereby distinguishing that the responses are isotropic, regardless of age.

Figure 3.

The strain history in dentin as a function of time and moisture loss. Note that the “1” and “2” directions are parallel and perpendicular to the nominal dentin tubule direction, respectively.

a) strain history for young dentin including samples from a 22 year old and 28 year old individual

b) strain history for old dentin including samples from a 50 year old and 63 year old individual

Figure 4.

The strain history in enamel as a function of time and moisture loss. Note that the “1” and “2” directions are parallel and perpendicular to the nominal enamel prism axes, respectively.

a) strain history for young enamel including samples from a 22 year old and 28 year old individual

b) strain history for old enamel including samples from a 50 year old and 63 year old individual

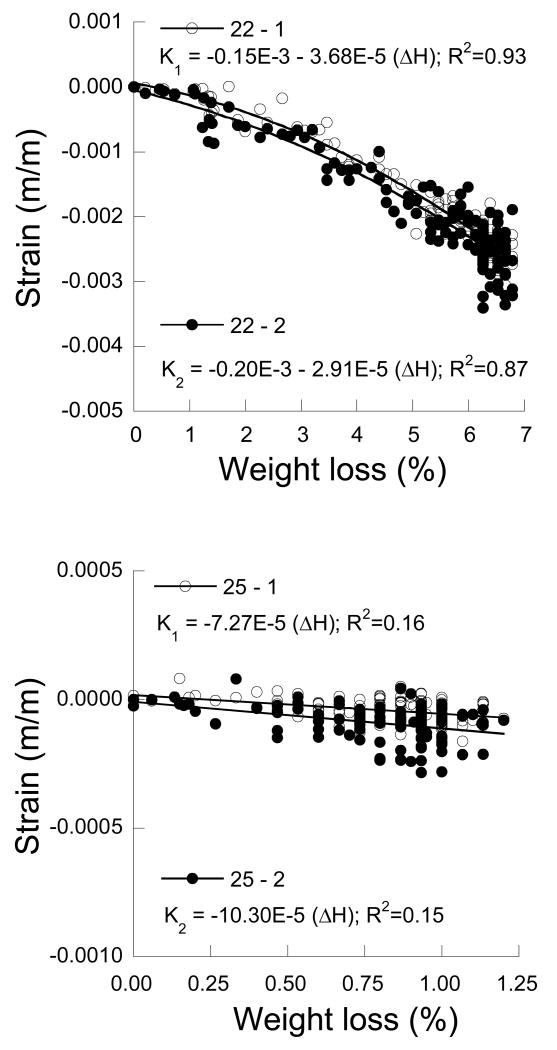
The strain history for the two tissues was also quantified in terms of the water loss by weight percent (ΔH). The strain distributions described in terms of ΔH for selected dentin and enamel samples are presented in Figures 5(a) and 5(b), respectively. There is a distinct nonlinearity evident in the strain distribution for dentin and an increase in the degree of deformation with increasing water loss. The strain distributions were used to estimate the dehydration coefficients (A_i) according to Eqn. 2 in the parallel and perpendicular directions. The coefficients obtained for the responses of each tooth accounting for nonlinear behavior are listed in Table 1. A statistical comparison of the coefficients was not conducted due to differences in the nonlinear behavior of the samples. A linear response was also assumed in modeling the deformation behavior where the dehydration coefficient is simply a constant. Using this approach, the estimated dehydration coefficients for dentin range from approximately -350 µm/m/(% water loss) to almost -1600 µm/m/(% water loss). Results for both measurement directions are listed in Table 1. Details of the statistical analysis are listed in Table 2. Note that the shrinkage behavior in the two directions was very consistent and there was no significant difference (p>0.05) in the dehydration contraction coefficients between the two measurement directions or the two age groups.

Figure 5.

The average strain history for a selected dentin and enamel samples in terms of the water loss.

a) dentin (22 year old)

b) enamel (25 year old)

Table 2.

Statistical comparisons of the linear dehydration coefficients. The units for the coefficients m/m/(% water loss). Quantities for dentin are ×10ˆ-3 and quantities for enamel are ×10ˆ-5, consistent with the presentation in Table 1.

Comparison by Orientation
	Age	1 direction	2 direction	Anova F	p value*
Dentin	Young	-0.7(0.3)	-0.7(0.2)	0.0006	0.98, NS
	Old	-0.9(0.6)	-0.9(0.5)	0.0028	0.96, NS
Enamel	Young	-6.0(6.3)	-10.5(9.5)	0.66	0.44, NS
	Old	-11.4(8.3)	-8.7(3.3)	0.45	0.52, NS
Comparison by Age
	Orientation	Young	Old	Anova F	p value*
Dentin	1 direction	-0.7(0.3)	-0.9(0.6)	0.44	0.67, NS
	2 direction	-0.7(0.2)	-0.9(0.5)	0.34	1.04, NS
Enamel	1 direction	-6.0(6.3)	-11.4(8.3)	0.82	0.39, NS
	2 direction	-10.5(9.5)	-8.7(8.3)	0.34	0.58, NS
Comparison of Pooled Data
		All Young	All Old	Anova F	p value*
Dentin		-0.69(0.23)	-0.93(0.50)	1.85	0.19, NS
Enamel		-9.25(8.09)	-10.04(6.13)	0.06	0.81, NS
		All Dentin	All Enamel	Anova F	p value
		-0.81(0.40)	-0.05(0.10)	61.27	0.0001**

^*NS = Non-significant

^**Significant

Due to the variation in strain within enamel evident in Figure 4 and Figure 5(b), only the linear model was used in characterizing shrinkage. Estimates of the dehydration coefficients for the two measurement directions for enamel are listed in Table 1. There was marked variation in the shrinkage coefficients for each of the measurement directions as evident from the standard deviations. Like dentin, there was also no significant (p>0.05) influence of measurement direction or age in the enamel responses as detailed in Table 2. Combining results from all ten samples and for the two different measurement directions, the average dehydration coefficients for the dentin and enamel were found to be −810±400 µm/m/(% weight loss) and −50±100 µm/m/(% weight loss), respectively. The difference between these two coefficients was significant (p<0.0001).

Discussion

Result of this investigation showed that microscopic DIC served as an effective technique for measuring the transient dimensional changes in dentin and enamel with loss of moisture despite the complexities posed by the small strains and moist surfaces. To the authors' knowledge the results for both the dentin and enamel presented here represent the first biaxial measurement of the dynamic shrinkage in these tissues during the onset of dehydration. Admittedly, there are rather large variations in the average strain obtained from dehydration of the samples in each age group, especially those for the enamel where the coefficient of variation (ratio of std. dev. to the average) is approximately 0.7. Nevertheless, the experimental approach did provide measures for comparison and new understanding that were previously unavailable. The recorded shrinkage for dentin after one hour of free convection (maximum shrinkage strain ≤ 1%) is approximately half of that reported earlier for complete dehydration [1]. Indeed, the weight loss in the dentin over the period of evaluation did not exceed 8%, which indicates that the dehydration process was incomplete. Nevertheless, the documented strain history for dentin (e.g. Fig. 3) illustrates that the rate of shrinkage undergoes a reduction with time. As dehydration is comprised of the loss of both free and bound water, the responses must primarily represent the dimensional changes associated with the loss of free water. Most certainly, the initial weight loss (e.g. Fig. 2) indicates loss of free water near the surface. In turn, the decrease in rate of shrinkage is attributed to the reduction in rate of evaporation as evident for both tissues in Figure 2. Water located farther from the surface must diffuse through a partially dried “cortex” that may become slightly rehydrated during the process, creating different kinetics.

According to the structural anisotropy exhibited by both dentin and enamel, one might expect that the dimensional changes in these tissues with water loss would be unique in the two orthogonal directions. Owing to the larger organic content of the dentin and the essentially transverse orientation of the collagen fibrils to the tubules [12], the largest strains were expected to develop transverse to the tubules. That was the nature of response documented in [6] after 24 hours of dehydration in air. Larger strains were noted perpendicular to the tubules in some of the dentin samples examined. But a comparison of results from all samples for the strains parallel and perpendicular to the tubules in dentin and prisms in enamel (Table 1) showed that there was no significant difference between results in the two directions (i.e. the shrinkage in both tissues is isotropic). The degree of variation in strain for the two measurement directions was similar. These results contradict those of Kinney et al., [6], which can be attributed to the shorter period of evaluation examined here and the difference in the nature of water loss that may have occurred. Overall, the comparison of responses suggests that loss of free water in dentin results in isotropic deformation whereas the loss of bound water and complete dehydration induces anisotropic deformation and more extensive shrinkage perpendicular to the tubules. That comment is speculative and requires further validation.

Considering that the distortion in dentin is associated with an increase in the interpeptide hydrogen bonding of collagen in the absence of water [13, 14], changes to the microstructure of dentin would be expected to be important to the shrinkage. A rise in the mineral content of the tissue may decrease the degree of free or bound water when fully hydrated and lower the extent of interfibril bonding upon dehydration. In turn, that would be expected to promote a reduction in shrinkage with water loss. Of relevance here, there is a rise in the overall mineral content of dentin with aging [4,5], which is at least partly due to the increase mineral filling the lumens. Also, earlier studies have shown that the degree of shrinkage in dentin increases with loss of mineral [2] suggesting that the rise in mineral with aging could promote a lower degree of shrinkage. But a comparison of the responses obtained for the two age groups showed that there was no significant difference in rate of water loss or in the dimensional changes with water loss. It should be noted that the maximum age of the old group was only 63 years and that none of the teeth were fully sclerotic. While there will be an increase in mineralization and filling of the tubules with increase in average age of the old group [15], these microstructural changes are not expected to cause substantial variation in the nature of shrinkage with dehydration. But again, the dimensional changes examined in this study were limited primarily to the loss of free water; they do not reveal if the shrinkage resulting from complete dehydration are different between the two age groups.

It is unlikely that free convection in any restorative procedure would extend over a period of one hour. But previous studies on dehydration have shown that air blasts can cause a 15 to 30 fold increase in the rate of water loss over that caused by free convection [16]. In fact, evaporation rates occurring under sustained air blasts can give rise to disruption of the odontoblasts and disruption of pulpal blood flow. Also, removal of the smear layer can double the rate of evaporative water loss [17], causing even further increase. That would suggest that the degree of water loss observed during the experiments (over one hour) could occur in less than one minute under high pressure air. As such, the magnitude of strains documented in this investigation is not completely unrelated to that of the strains that may develop in vivo.

The overall average shrinkage occurring in the dentin and enamel samples after completion of the one hour period of convection are approximately 5000 µm/m (0.5%) and 300 µm/m (0.03%), respectively. These values may have more physical meaning if they are considered in terms of stress. If an axial strain of that magnitude in dentin were restrained by a comparatively rigid body (e.g. a metal or ceramic), the corresponding normal stress (assuming tri-axial deformation and an elastic modulus of 20 GPa [18]) would exceed 100 MPa. As the tensile strength of dentin is 77 MPa parallel to the tubules and 112 MPa perpendicular to tubules (19), the stress might cause dentin to undergo microcracking. Similarly, assuming an elastic modulus for enamel of 80 GPa [20] the normal stress would exceed 25 MPa. This value is near the tensile strength of enamel when tested parallel to the prisms, and exceeds the 11 MPa tensile strength of enamel perpendicular to the direction of enamel prisms [21]. A tensile normal stress would develop during dehydration (resulting from exposure to air blasts or polar solvent (e.g. alcohol)). Assuming the dimensional changes are fully reversible, a compressive normal stress of equivalent magnitude would develop upon rehydration. Perhaps the most relevant mode of stress arising with changes in moisture content is shear at a bonded interface; the shear stress develops regardless of dehydration or rehydration. Assuming that the bonded medium exhibits an elastic modulus much smaller than dentin (e.g. a resin adhesive with modulus of 4 GPa for simplicity), the shear stress that develops in the resin due to contraction of dentin would approach 8 MPa. Though not large enough to cause shear failure, that value of shear stress can promote viscoelastic deformation in the resin or hybrid layer and contribute to the evolution of defects residing near the interface. There is further concern when considering the potential superposition of strains resulting from heat of a curing light or polymerization exotherms. Upon the dissipation of thermal energy there would be a contraction of the resin composite, while rehydration of the dentin and enamel would induce expansion of the two tissues. The synergism between these two components of deformation could exacerbate the integrity of the adhesive bond. Based on this rather rudimentary analysis, the importance of distortion resulting from hydration changes at the bonded interface should not be ignored.

The estimated dehydration coefficients obtained for dentin (B = -810 µm/m/(% water loss)) and enamel (B = -50 µm/m/(% water loss)) support estimates of the shrinkage strain over a fairly large range in dehydration. The coefficients are valid up to the degree of dehydration documented (i.e. 6% in dentin and 1% in enamel), but may not be reliable for conditions that cause more extensive water loss. Dimensional changes with rehydration were not quantified in the present study due to expected difficulties associated with movement of the specimen and consequent decorrelation of the digital images. Yet, studies examining the influence of dehydration on the mechanical behavior of dentin have shown that the changes resulting from loss of water are reversible, meaning that the mechanical behavior returned to the original state after rehydration [14,22]. That suggests that the dehydration coefficients can serve as first order estimates of the degree of expansion upon rehydration. But caution is warranted since the aforementioned studies were limited to a single dehydration/rehydration cycle, and arose after exposure to polar solvents, not free convection in air. Of equal importance, previous studies have identified that dehydration occurring in the presence of water-free polar solvents promotes an increase in the stiffness [23-25] and strength [26] of dentin that is attributed to the increase in interpeptide hydrogen bonding. The property changes are accompanied by shrinkage of the collagen matrix, which has been unrestricted in these previous measures of mechanical behavior. Stresses would develop if the shrinkage is restrained due to the change in boundary conditions resulting from bonding. Under cyclic loading this quasi-static stress attributed to dehydration would superpose with those applied externally and change the cyclic stress ratio. That could be detrimental as conditions that increase the stress ratio cause a significant decrease in the fatigue strength [27] and resistance to both the initiation and growth of fatigue cracks [28].

Although results of this investigation provide new understanding of the dynamic nature of dimensional changes in dentin and enamel with dehydration, there are a few limitations that should be discussed. Firstly, the deformation measurements for both dentin and enamel represent a surface response while the weight measurements used in calculating water loss represent a bulk response. Since the water loss at the surface is greater than within the interior the dehydration coefficients (Table 1) are liberal estimates of the strain with degree of water loss. There is a strain gradient from the center of the specimen to the interior that results from the variation in hydration. The surface strains are balanced on all four sides of the sample, which minimizes the development of out-of-plane distortion via bending. Thinner samples could be used to reduce hydration and strain gradients, but would be more likely to result in out-of-plane sample distortion (via bending or twisting) due to the reduction in moment of inertia of the sample. This 3-dimensional aspect of deformation would be more likely to inhibit the applicability of DIC or any other optical technique being considered for evaluation. Furthermore, the measurements performed on the dentin samples were taken with no regard to distance from the dentin enamel junction (DEJ). The dentin depth could be an important factor in the responses due to the decrease in the diameter and number of the lumens from the pulp to the DEJ, as well as a corresponding decrease in the ratio of peritubular to intertubular dentin. The decrease in intertubular dentin with depth results in a larger mineral/collagen ratio and that should result in lower shrinkage towards the pulp, provided that the increase in mineral/collagen ratio is high enough. Conversely, the large increase in tubule density in deep dentin increases the free water content to near 20% [29] and could cause an increase in shrinkage with distance from the DEJ. Further work is required to address this issue completely. Also, it was assumed that the orientation of the orthogonal axes defined by the microstructure is consistent with that established by the coordinates of the digital image, and that the orientation of the microstructure remains constant through the specimen. However, there is some potential variability (+/- 10°) that could contribute to the experimental noise in responses and the statistical nature of comparison in the two orthogonal directions. Lastly, the tissues examined in this study were obtained from caries-free third molars. Both the dentin and enamel were considered to be “fully mineralized”, but no measure of the actual mineral to collagen ratios were obtained. There is a rather large potential for the tissue adjacent to a newly placed restoration to be caries-affected and, therefore, to have lower mineral to collagen ratio than that measured here. Due to the higher levels of shrinkage reported in demineralized tissue [2], the partial loss of mineral should result in larger strains with dehydration, and potentially anisotropic behavior as well. These issues have clinical relevance and remain to be addressed in future studies.

Conclusions

The transient dimensional changes in dentin and enamel that result from dehydration were examined using microscopic Digital Image Correlation (DIC). Based on results of the investigation and a comparison of responses from young (18≤age≤30) and old (50≤age) tissue the following conclusions were drawn:

1. The average initial rate of loss in dentin was 0.31±0.10 %/min. At the end of one hour of free convection in air the rate of loss was 0.04±0.02 %/min. In enamel the rate of water loss was considerably smaller, with maximum and minimum rate of water loss of 0.07±0.03 %/min and 0.006±0.002 %/min, respectively.

2. Dehydration caused shrinkage of the dentin and enamel samples. The shrinkage strains in both tissues were isotropic and there was no significant difference in the dimensional changes between tissues from the young and old patients.

3. The average shrinkage strain in dentin reached 0.5% over one hour of dehydration and an average of 6% water loss by weight. Assuming a linear response, the effective dehydration coefficient for dentin was estimated to be κ_i = -0.81± (0.40) • 10^-3 [m/m/(% weight loss)].

4. The average shrinkage strain in the enamel reached 0.03% over one hour of dehydration and 1% water loss by weight. The effective coefficient of dehydration contraction for enamel was estimated to be κ_i= - 0.05(±0.10) • 10^-3 [m/m/(% weight loss)].