On Foundations of Discrete Element Analysis of Contact in Diarthrodial Joints

Abstract

Information about the stress distribution on contact surfaces of adjacent bones is indispensable for analysis of arthritis, bone fracture and remodeling. Numerical solution of the contact problem based on the classical approaches of solid mechanics is sophisticated and time-consuming. However, the solution can be essentially simplified on the following physical grounds. The bone contact surfaces are covered with a layer of articular cartilage, which is a soft tissue as compared to the hard bone. The latter allows ignoring the bone compliance in analysis of the contact problem, i.e. rigid bones are considered to interact through a compliant cartilage. Moreover, cartilage shear stresses and strains can be ignored because of the negligible friction between contacting cartilage layers. Thus, the cartilage can be approximated by a set of unilateral compressive springs normal to the bone surface. The forces in the springs can be computed from the equilibrium equations iteratively accounting for the changing contact area. This is the essence of the discrete element analysis (DEA). Despite the success in applications of DEA to various bone contact problems, its classical formulation required experimental validation because the springs approximating the cartilage were assumed linear while the real articular cartilage exhibited non-linear mechanical response in reported tests. Recent experimental results of Ateshian and his co-workers allow for revisiting the classical DEA formulation and establishing the limits of its applicability. In the present work, it is shown that the linear spring model is remarkably valid within a wide range of large deformations of the cartilage. It is also shown how to extend the classical DEA to the case of strong non-linearity if necessary.

1 Introduction

Cartilage is not an easy material to model its physical behavior under load. It is soft, multiphase, anisotropic, and inhomogeneous and its mechanical response to applied loads is essentially time-dependant (Huang et al, 2005). Nonetheless, attempts to describe mechanical behavior of the cartilage in a diarthrodial joint may not be hopeless and they are necessary for understanding the distribution of contact pressure. The latter is important for revealing the mechanisms of osteoarthritis, bone fracture and remodeling.

Mow et al (1980) treated cartilage as a biphasic material in their seminal work where a continuum mixture theory was used for mathematical modeling. Alternatively, a poroelasticity theory (Cowin, 1999; Coussy, 2004) can be used to describe articular cartilage. Both approaches are technically sophisticated and numerically complex. Analytical and semi-analytical solutions of the bone contact problems including cartilage (Ateshian et al, 1994; Ateshian and Wang, 1995; Donzelli et al, 1999) are restricted to simple geometries and linear materials what makes the problems tractable, while numerical solutions for more realistic contact surfaces that use commercial software (Wu et al, 1998; Han et al, 2005) are expensive and time-consuming.

Development of a reasonably simple numerical framework for modeling cartilage on the realistic contact surfaces should rely upon physically motivated simplifications of the mathematical model. The cartilage deforms in three stages: first – the early stage of instantaneous deformation, when the cartilage fluid bears most contact pressure; second – the transient stage, when the fluid starts moving; third – the steady stage, when mainly the solid phase of the cartilage supports the applied load. According to Mow et al (1980), the fluid flows out of the compressed region in about 5 seconds after loading, while Ateshian et al (1994), Ateshian, and Wang (1995) conclude that the fluid phase of cartilage plays a major role in providing load support during first 100−200 seconds after contact loading. Such diversity in the prediction of the fluid outflow is affected by the specific conditions of experiments and restrictive assumptions of analysis. What stage of the cartilage deformation, instantaneous, transient, or steady, dominates a load-bearing activity? This question has no simple answer.

Consider, for example, a hip joint under conditions of standing up, normal walking, and running. At the time of standing up an instantaneous pressure is applied at the top of the femoral head, which is supported by the cartilage fluid. If the standing position is not changing during few seconds then the fluid flows out of the compressed region and the steady state occurs. When a walking starts, an additional instantaneous load is applied to the hip joint producing extra instantaneous response of the remaining fluid, which starts flowing out of the compressed region. Since the period of the gait-cycle is shorter than the time of fluid transition then the steady response of the cartilage is achieved after a number of cycles when an additional amount of the cartilage fluid leaves the contact region of the femoral head with the acetabulum. When a running starts, additional inertia forces are applied to the hip joint producing further instantaneous response of the remaining fluid, which flows out of the compressed region and so on. Summarizing this example qualitatively it is possible to state that instantaneous and fluid-supported deformation of the cartilage occurs when the loading is changing while a steady and solid-supported deformation occurs when the loading is also steady – constant or cyclic. The time proportion of these two types of deformation depends on the character of the functional activity. Those, who are exposed to a monotonic and steady physical activity, seem to be more susceptible to the direct loading of the cartilage solid phase.

Since the transient stage gives intermediate contact pressure, it can be omitted from the analysis and only the initial, instantaneous, and the final, steady, stages are to be analyzed providing the bounds for contact pressure. It is important that while the instantaneous response, which is dominated by the elasticity of the fluid phase, can be considered linear, the steady response, which is dominated by the elasticity of the solid phase, should allow for finite elastic strains of the cartilage. The latter is the focus of the present work. Based on experimental results of Ateshian and his co-workers a ‘non-linear spring’ model of the articular cartilage is developed. It is found that the linearization of the nonlinear model is applicable to a surprisingly wide range of the engineering strain varying from zero to 25−30%. Normally, these strains cover the physiological range of the cartilage deformation. Nonetheless, we show how to modify the classical DEA to account for strains larger than 30%.

2 Discrete Element Analysis

2.1 Non-linear spring model

Ateshian et al (1997) and Huang et al (2005) performed experimental and theoretical analyses of the one-dimensional confined compression of articular cartilage. They found that the axial stress-stretch law for non-linear behavior of the specimen could be approximated as follows

$$\sigma =\frac{H_{A0}({\lambda }^2-1)}{2{\lambda }^{2\beta +1}}\text{exp}\left\{\beta ({\lambda }^2-1)\right\},$$ (1)

where σ is the axial Cauchy stress in the solid phase; λ is the axial stretch (other principal stretches equal unity); H_A0 and β are material parameters. These material parameters can be roughly estimated for the human and bovine articular cartilage: 0.3 ≤ H_AO ≤ 0.6; 0.05 ≤ β ≤ 0.6. Based on the analysis of Ateshian et al (1994), we assume that stretches are essentially uniform with depth of the cartilage layer. This allows introducing a non-linear spring with a uniform deformation along its length. Let the average spring stress be designated σ and the relative elongation of the spring is ε = Δh/h where h and h + Δh is the cartilage thickness before and after deformation accordingly. Then λ = ε + 1 and Eq. (1) takes the form

$$\sigma \left(\epsilon \right)=\frac{H_{A0}({(1+\epsilon )}^2-1)}{2{(1+\epsilon )}^{2\beta +1}}\text{exp}\left\{\beta ({(1+\epsilon )}^2-1)\right\}.$$ (2)

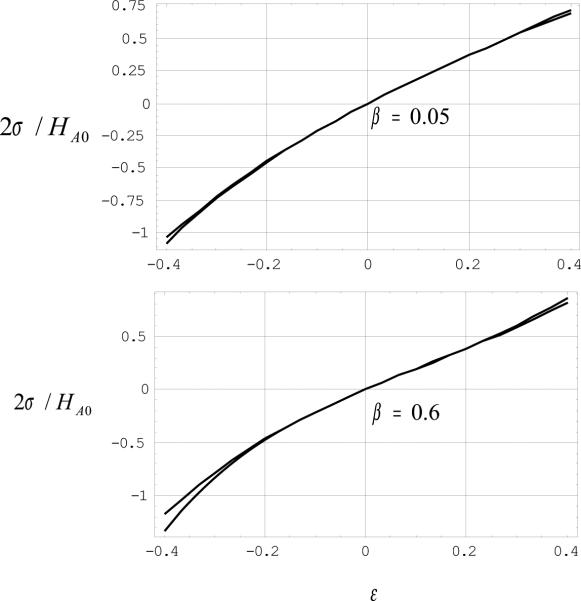
The graph of this formula is presented in Fig. 1 for the material parameters taking the limit values of the range 0.05 ≤ β ≤ 0.6. The positive values of the relative elongation (engineering strain) and the corresponding stresses are irrelevant, of course, because the springs are unilateral and they do not resist tension. However, the tension of the springs should be taken into account to provide robustness of the computational algorithm described below. The negative values of strains and the corresponding compressive stress are of interest. It is remarkable that the stress-strain curve is almost linear up to 30% strain while a slight deviation from the linearity emerges in the strain range of 30−40%, i.e. at the limits of the physiologically reasonable values of engineering strain. This observation gives an experimental validation for the classical discrete element analysis based on the linear spring approximation when engineering strains do not exceed 30%. If, however, the strains are about 30% or more the classical discrete element analysis should be modified as follows.

Figure 1.

Normalized stress versus engineering strain for articular cartilage: graphs of formulae (2) and (3) for the limit values of parameter β.

Remark 1. We use the experiment with the confined compression for calibration of the spring model. The confined compression means that the cross-section of the specimen does not change during its mechanical response and the stretches of the specimen are unit in the cross-sectional plane. This condition seems to ideally fit the spring model, which does not undergo cross-sectional changes during the deformation. The unconfined compression experiments would be difficult to interpret in the terms of the spring model because, in this case, there should be an interaction between the adjacent springs.

2.2 Numerical implementation

The original form of the non-linear spring definition presented by Eq. (2) is not attractive for computations. It can be expressed in a more attractive form by using power series about ε = 0:

$$\sigma \left(\epsilon \right)=\frac{H_{A0}}{2}(2\epsilon -{\epsilon }^2+(1+4\beta ){\epsilon }^3+O\left({\epsilon }^4\right)).$$ (3)

Equations (2) and (3) almost coincide with each other on the segment −0.4 ≤ ε ≤ 0.4 as can be easily observed in Fig.1 for the limit values of β. Of course, it is much simpler to manipulate Eq. (3) than Eq. (2) in all analytical transformations. Particularly, the density of the strain energy of the springs can be readily written down

$$w\left(\epsilon \right)=\int \sigma \left(\epsilon \right)d\epsilon ={\alpha }_1\frac{{\epsilon }^2}{2}+{\alpha }_2\frac{{\epsilon }^3}{3}+{\alpha }_3\frac{{\epsilon }^4}{4},$$ (4)

$$\{\begin{array}{cc}{\alpha }_1=H_{A0}\hfill & \hfill \\ {\alpha }_2=-H_{A0}∕2\hfill & ,\hfill \\ {\alpha }_3=H_{A0}(1+4\beta )∕2\hfill & \hfill \end{array}\phantom{\}}$$ (5)

where w(0) = 0 was assumed. There is no contact when the spring is in tension. This means that deformations with ε > 0 should be excluded from the considerations. The latter can be done by excluding the springs in tension from the contact zone. Changing the contact area iteratively it is possible to find the equilibrium state where all springs are compressed. It is important to emphasize, however, that the use of all formulae in the extended range of deformations (ε > 0) makes the intermediate computations robust.

Consider two rigid bodies 1 and 2, which are connected along the contacting surfaces by a layer of normal springs mimicking cartilage (Kawai, 1977; Genda et al, 2001). The total energy of the system can be written in the following form

$$\begin{array}{cc}\hfill & \Phi \left(\mathbf{u}\right)=\sum _{i=1}^N{S}_i{h}_i({\alpha }_1{\epsilon }_i^2∕2+{\alpha }_2{\epsilon }_i^3∕3+{\alpha }_3{\epsilon }_i^4∕4)\hfill \\ \hfill & -{\mathbf{u}}^T\mathbf{r},\hfill \end{array}$$ (6)

where the sum is over N surface elements with area S_i each; ε_i = Δh_i/h_i is a relative elongation of the normal spring associated with the ith element; Δh_i is the ith spring elongation and h_i is the ith element thickness – spring initial length; α₁, α₂, α₃ are material parameters defined in Eq. (5); u is a generalized vector of displacements and rotations of the considered rigid bodies, which takes the following form in the Cartesian coordinate system (x, y, z)

$${\mathbf{u}}^T=\{u_1,v_1,w_1,{\theta }_1,{\varphi }_1,{\chi }_1,u_2,v_2,w_2,{\theta }_2,{\varphi }_2,{\chi }_2\},$$ (7)

and r is a vector of the corresponding forces and moments, which may include the inertia forces as well,

$$\begin{array}{cc}\hfill & {\mathbf{r}}^T=\{F_{x1},F_{y1},F_{z1},M_{x1},M_{y1},M_{z1},F_{x2},F_{y2},F_{z2},\phantom{\}}\hfill \\ \hfill & \phantom{\{}{M}_{x2},M_{y2},M_{z2}\}.\hfill \end{array}$$ (8)

The relative displacement δ_i of the ith contact point (x_i, y_i, z_i) on the boundary surface of bodies 1 and 2 can be expressed as a linear function of the small relative displacements of the bodies

$${\delta }_i={\mathbf{B}}_i\mathbf{u},$$ (9)

where

$${\mathbf{B}}_i=[-IM1IM2]$$ (10)

where

$$\begin{array}{cc}\hfill M1& =\left[\begin{array}{ccc}\hfill 0\hfill & \hfill -(z_i-z_1)\hfill & \hfill (y_i-y_1)\hfill \\ \hfill (z_i-z_1)\hfill & \hfill 0\hfill & \hfill -(x_i-x_1)\hfill \\ \hfill -(y_i-y_1)\hfill & \hfill (x_i-x_1)\hfill & \hfill 0\hfill \end{array}\right]\hfill \\ \hfill M2& =\left[\begin{array}{ccc}\hfill 0\hfill & \hfill (z_i-z_2)\hfill & \hfill -(y_i-y_2)\hfill \\ \hfill -(z_i-z_2)\hfill & \hfill 0\hfill & \hfill (x_i-x_2)\hfill \\ \hfill (y_i-y_2)\hfill & \hfill -(x_i-x_2)\hfill & \hfill 0\hfill \end{array}\right]\hfill \end{array}$$

and I is the identity matrix.

Here (x₁, y₁, z₁) and (x₂, y₂, z₂) are the coordinates of the centroids of body 1 and 2 accordingly. It should not be missed that small displacements of the rigid bodies-bones (as compared to their size) can produce large elongations of springs-cartilage (as compared to their size).

Using Eq. (9) it is possible to find the relative spring elongations included in Eq. (6) as follows

$${\epsilon }_i=h_i^{-1}{\mathbf{n}}_i^T{\delta }_i=h_i^{-1}{\mathbf{n}}_i^T{\mathbf{B}}_i\mathbf{u},$$ (11)

where n_i is a unit normal at the ith point.

Substituting Eq. (11) in Eq. (6) and differentiating with respect to u it is possible to get the equilibrium equation

$$\begin{array}{cc}\hfill \mathbf{g}\left(\mathbf{u}\right)& ={\left(\frac{\partial \Phi }{\partial \mathbf{u}}\right)}^T\hfill \\ \hfill & =\sum _{i=1}^N{h}_i{S}_i({\alpha }_1{\epsilon }_i+{\alpha }_2{\epsilon }_i^2+{\alpha }_3{\epsilon }_i^3){\left(\frac{\partial {\epsilon }_i}{\partial \mathbf{u}}\right)}^T-\mathbf{r}\hfill \\ \hfill & =0,\hfill \end{array}$$ (12)

$$\frac{\partial {\epsilon }_i}{\partial \mathbf{u}}=\frac{1}{h_i}\frac{\partial }{\partial \mathbf{u}}{\mathbf{n}}_i^T{\mathbf{B}}_i\mathbf{u}=h_i^{-1}{\mathbf{n}}_i^T{\mathbf{B}}_i.$$ (13)

Substituting from Eqs. (11) and (13) in Eq. (12) it is possible to obtain a nonlinear system of discrete equations with respect to displacements u. The Newton-Raphson method can be used to solve this system. In order to do that we need to compute the tangent stiffness matrix

$$\mathbf{K}\left(\mathbf{u}\right)=\frac{\partial \mathbf{g}\left(\mathbf{u}\right)}{\partial \mathbf{u}}=\frac{\partial }{\partial \mathbf{u}}{\left(\frac{\partial \Phi \left(\mathbf{u}\right)}{\partial \mathbf{u}}\right)}^T.$$ (14)

It is possible to get the closed form expression for the tangent stiffness matrix. Indeed, considering Eq. (12) we have

$$\begin{array}{cc}\hfill \mathbf{K}\left(\mathbf{u}\right)& =\frac{\partial \mathbf{g}\left(\mathbf{u}\right)}{\partial \mathbf{u}}=\frac{\partial }{\partial \mathbf{u}}{\left(\frac{\partial \Phi \left(\mathbf{u}\right)}{\partial \mathbf{u}}\right)}^T\hfill \\ \hfill & =\sum _{i=1}^N\frac{S_i}{h_i}({\alpha }_1+2{\alpha }_2{\epsilon }_i+3{\alpha }_3{\epsilon }_i^2){\left({\mathbf{n}}_i^T{\mathbf{B}}_i\right)}^T\left({\mathbf{n}}_i^T{\mathbf{B}}_i\right).\hfill \end{array}$$ (15)

It is useful to rewrite this matrix in a more compact form

$$\mathbf{K}\left(\mathbf{u}\right)=\sum _{i=1}^N{c}_i\left(\mathbf{u}\right){\mathbf{D}}_i,$$ (16)

where

$$c_i\left(\mathbf{u}\right)=\frac{S_i}{h_i}({\alpha }_1+2{\alpha }_2{\epsilon }_i+3{\alpha }_3{\epsilon }_i^2).$$ (17)

$$\mathbf{D}={\left({\mathbf{n}}_i^T{\mathbf{B}}_i\right)}^T\left({\mathbf{n}}_i^T{\mathbf{B}}_i\right).$$ (18)

The Newton-Raphson method for solution of Eq. (12) takes the following form

$$\{\begin{array}{cc}\mathbf{K}\left({\mathbf{u}}^{\left(n\right)}\right){\Delta }^{\left(n\right)}=-\mathbf{g}\left({\mathbf{u}}^{\left(n\right)}\right)\hfill & \hfill \\ {\mathbf{u}}^{(n+1)}={\mathbf{u}}^{\left(n\right)}+{\Delta }^{\left(n\right)}\hfill & \hfill \\ n=0,1,\dots ,{\mathbf{u}}^{\left(0\right)}=0\hfill & \hfill \end{array}\phantom{\}}$$ (19)

The process can be terminated, for example, when

$$\frac{\mid \mid {\mathbf{u}}^{(n+1)}-{\mathbf{u}}^{\left(n\right)}\mid \mid }{\mid \mid {\mathbf{u}}^{(n+1)}\mid \mid }<\text{TOLERANCE}={10}^{-6},$$ (20)

where the norm is defined for any vector a as $\Vert \mathbf{a}\Vert =\sqrt{{\mathbf{a}}^T\mathbf{a}}$.

Remark 2. Strictly speaking there is a slight deviation of the third-order polynomial (3) from the original curve (2) in the limit case of parameter β = 0.6 in Fig.1. This deviation can be taken into account by using higher-order polynomials in the series expansion in (3). For the sake of simplicity we do not consider the higher-order polynomials though technically it can be readily done.

3 Discussion

Based on the experimental results of Ateshian and his coworkers we developed a nonlinear spring model for discrete element analysis of contact in diarthrodial joints. We showed, on the grounds of the nonlinear model, that the linear spring approximation is reasonable and, consequently, preferable for cartilage strains not exceeding 30% while larger strains require consideration of the physical nonlinearity of the cartilage. The validation of the classical DEA based on the linear spring approximation is probably the main result of the present work. Besides, we described a possible modification of the classical DEA that allow for taking this nonlinearity into account.

Evidently, the spring model presents a simplification of the real mechanical behavior of cartilage. This simplification does not allow for consideration of the interaction of fluid and solid phases within the cartilage. Neither the spring model allows accounting for the electro-chemo-mechanical coupling which takes place during deformation. In other words, the spring model is too crude to give insights into physical processes triggering the gross mechanical response of the cartilage. The drawbacks of the spring model should be stated and realized. It is crucial, at the same time, not to miss that the spring model is a very important computational tool concerning practical clinical applications. For example, contrary to more physically based approaches to modeling cartilage, the spring model allowed us to tackle the problem of the prediction of the collapse of the femoral head in developing osteonecrosis (Volokh et al, 2006). The collapse prediction required a preliminary massive analysis of the contact pressure distribution in the hip joint during activities of daily living (Yoshida et al, 2006). No other modeling approach, to the best of our knowledge, has been applied to a realistic contact problem to resolve issues occurring in orthopedic practice. It is our viewpoint that various approaches to modeling cartilage can be interpreted as the optical devices of different resolutions and there is no need to use a microscope where the naked eye is helpful.

Finally, we should mention that the discrete element method (springs) has been demonstrated to be accurate and efficient in the Hertzian contact problem as compared to the finite element method based on the classical elasticity formulation: Shih et al (1993); Stone et al (1996a); Stone et al (1996b). Even in non-cemented prosthetic implant and bone interface stress analysis, the discrete element method could readily provide qualitative information without the use of finite elements (Ide et al, 1989). A method similar to DEA was developed for modeling the knee contact by Blankevoort et al (1991).