Contrast Thresholds in Additive Luminance Noise: Effect of Noise Temporal Characteristics

Abstract

This study investigated how the temporal properties of additive luminance noise influence threshold contrast and affect estimates of equivalent noise and sampling efficiency. Threshold contrast was obtained from four visually normal observers for a 2-cycle-per-degree Gabor patch across a range of target durations in the absence and presence of additive luminance noise that was either static or dynamic. In addition, the temporal relationship between target and noise was either synchronous (simultaneous presentation of both) or asynchronous (noise duration longer than target duration). For both synchronous and asynchronous presentation modes, the extent of temporal integration differed for targets presented in dynamic vs. static noise. Furthermore, for a fixed-duration target, increasing the degree of temporal asynchrony between target and noise monotonically increased threshold contrast in dynamic noise, but had a non-monotonic effect on threshold contrast in static noise. For both dynamic and static noise, estimates of equivalent noise and sampling efficiency were dependent on the degree of temporal asynchrony between target and noise, presumably due to temporal integration of the noise. The observed differences between the effects of dynamic and static noise are consistent with a previous proposal that target detection in the presence of these two noise types tends to be governed by sustained-like and transient-like visual mechanisms, respectively.

1. Introduction

Spatial contrast sensitivity is typically measured using targets that are presented against a uniform field. However, it has been observed that visual deficits in individuals with ocular disorders may become more apparent when contrast sensitivity is measured in the presence of additive luminance noise. For example, early-stage glaucoma patients can have marked deficits in contrast sensitivity in the presence of additive luminance noise, whereas contrast sensitivity may not be significantly different from normal when measured against a field of uniform luminance (Yates, Leys, Green, Huang, Charlton, Reed, Di & Odom, 1995).

Moreover, information about the source of visual deficits can be obtained by comparing contrast sensitivity for targets that are presented in a relatively high level of additive luminance noise to contrast sensitivity for the same targets presented in the absence of noise (Legge, Kersten & Burgess, 1987; Pelli and Farell, 1999). By such a comparison, it is possible to factor an observer’s performance into two independent underlying components: (1) equivalent noise (N_eq), which is an estimate of the noise within the visual pathway, and (2) sampling efficiency, which represents the observer’s ability to make use of stimulus information optimally. This approach has been applied to the evaluation of vision loss in amblyopia (Huang, Tao, Zhou & Lu, 2007; Kiorpes, Tang & Movshon, 1999; Levi & Klein, 2003; Nordmann, Freeman & Casanova, 1992; Pelli, Levi & Chung, 2004; Xu, Lu, Qiu & Zhou, 2006) and in normal aging (Bennett, Sekuler & Ozin, 1999; Betts, Sekuler & Bennett, 2007).

A fundamental issue in the use of additive luminance noise is the temporal nature of the noise. In previous studies, the noise has been either static (a single unchanging noise field that is uncorrelated in space but correlated in time) or dynamic (a continuously changing noise field that is uncorrelated in either space or time). Recently, it has been observed that static and dynamic noise can bias performance toward different visual subsystems (Manahilov, Calvert & Simpson, 2003). Specifically, temporal integration functions for a Gabor patch of intermediate spatial frequency were consistent with detection by a transient-like visual mechanism when threshold contrast was obtained in static noise, and with a sustained-like visual mechanism when threshold contrast was obtained in dynamic noise.

A further consideration in the use of additive luminance noise is the temporal relationship between the test target and noise. In previous studies, this relationship has typically been either synchronous (simultaneous onset and offset of both target and noise) or asynchronous (target presentation embedded within a noise exposure of longer duration). The degree of temporal asynchrony is likely to be a major determinant of the effect of noise on visual performance. For example, threshold contrast was nearly independent of target duration when letter and word targets were presented in static noise that was synchronous with target presentation (Pelli, Burns, Farell & Moore-Page, 2006). In comparison, Manahilov and colleagues (2003) reported that contrast thresholds for Gabor patches of varying duration showed temporal integration when presented in static noise that was asynchronous with the target.

Given the varied use of different noise paradigms in previous studies, the purpose of the present study was to provide a systematic comparison of the effects of four basic paradigms of additive luminance noise on threshold contrast. These paradigms were asynchronous dynamic, asynchronous static, synchronous dynamic, and synchronous static luminance noise. First, temporal integration functions were obtained for a spatially band-limited test target of intermediate spatial frequency using these four noise paradigms in order to determine whether the differences in temporal integration observed by Manahilov et al. (2003) for targets presented in asynchronous dynamic and static noise extend to the synchronous presentation mode. Second, the effect of the magnitude of the temporal asynchrony between the target and noise was evaluated for both static and dynamic noise. Finally, the implications of the results for calculations of N_eq and sampling efficiency were considered.

2. Methods

2.1. Observers

Four individuals with normal best-corrected visual acuity participated in the study. Subjects S₁ and S₂, males, ages 27 and 61 yr, respectively, are the two authors. S₃ and S₄, females, both age 27 years, are practiced psychophysical observers who were naïve to the intent of the research. S₁, S₃, and S₄ have normal color vision, and S₂ has mild deuteranomaly. All experiments were approved by an institutional review board at the University of Illinois at Chicago, and written consent was obtained from each subject before testing. All four subjects participated in Experiment 1, which measured temporal integration functions using the four noise paradigms. S₁ and S₂ also participated in Experiment 2, which examined the effect of the degree of temporal asynchrony between target and noise on threshold contrast.

2.2. Stimuli and Testing System

Stimuli were generated by a Macintosh G4 computer and were displayed on an NEC monitor (FE2111SB) with a screen resolution of 1280 × 1024 and a 100-Hz refresh rate, driven by an ATI (Radeon 9000 Pro) video card with 10-bit DAC resolution. The temporal characteristics of the display were confirmed using an oscilloscope and photocell, and the display luminance was measured with a photometer (Minolta LS 110). Luminance values used during testing were derived from a linearized look-up table. The monitor, which was the only source of illumination in the room, was viewed monocularly through a phoropter with the subject’s best refractive correction.

The test stimulus was a Gabor patch, consisting of a sinusoidal grating with a spatial frequency of 2 cycles per degree (cpd) multiplied by a circular Gaussian window that was truncated at 3 standard deviations so that the pattern subtended 1.7 deg. The Gabor patch was presented in sine phase and had a spatial frequency bandwidth of approximately one octave at half-height. The Gabor patch was presented either in the center of a uniform field with a luminance of 50 cd/m², or in the center of a noise field of the same mean luminance. The contrast C of the Gabor patches was defined as Weber contrast:

$$C=(L_P-L_M)/L_M,$$ (1)

where L_P was the peak luminance of the Gabor patch in cosine phase and L_M was its mean luminance. The duration of the test stimulus ranged from 20 to 280 ms in approximately 0.15 log unit steps.

The noise field, which covered an area that was approximately 1.5 times larger than the Gabor patch, consisted of independently generated square checks with luminances drawn randomly from a uniform distribution, with a fixed root-mean-square (rms) contrast of 0.179. Each noise check subtended 0.083 deg by 0.083 deg, which corresponds to 6 noise checks per cycle of the Gabor patch, a value consistent with that used by others (e.g., Pelli et al., 2004). The check duration was 0.01 s (1 video frame). Noise spectral density was computed as the product of the squared rms noise contrast, the width and height of the noise checks, and the check duration (Legge et al., 1987). For dynamic noise, this yielded a noise spectral density (N) of 2.22 × 10⁻⁶ deg² s. For static noise, N was 2.22 × 10⁻⁴ deg² (the check duration was omitted from the calculation as per convention [Legge et al., 1987]).

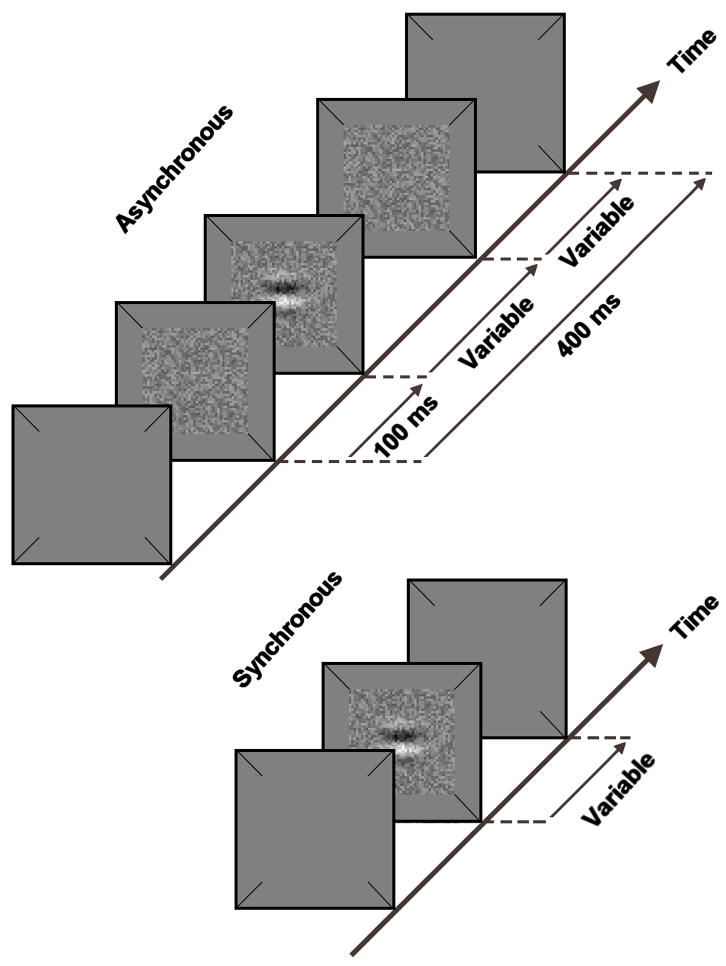
As illustrated in Fig. 1, the test stimulus and noise were presented either asynchronously (top) or synchronously (bottom). For the asynchronous paradigm of Experiment 1, the total noise duration was fixed at 400 ms, and the target onset was always delayed relative to the noise onset by 100 ms. For the synchronous paradigm, the target and noise were presented simultaneously. The noise field was changed every video frame for dynamic noise, whereas the noise field was constant throughout the presentation for static noise. This yielded four noise paradigms: 1) asynchronous dynamic, 2) asynchronous static, 3) synchronous dynamic, and 4) synchronous static. In Experiment 2, the target duration was fixed at either 20 or 280 ms, and the magnitude of the temporal asynchrony between target and noise was varied. In this case, the duration of the noise that preceded the onset of the test target was always equal to the noise duration following the target offset.

Figure 1.

Schematic illustration of the temporal sequences for the asynchronous (top) and synchronous (bottom) presentation modes of Experiment 1.

2.3. Procedure

A 30-s period of adaptation to a uniform field preceded each session, and a brief warning tone signaled the start of each stimulus presentation. The observer’s task was to judge the orientation of the Gabor patch, which was randomly either horizontal or vertical on each trial. No feedback was given. Threshold contrast was measured using the QUEST adaptive staircase procedure (Watson & Pelli, 1983), with 40 trials per condition and a targeted percent correct value of 82%. Pilot testing had determined that the staircases typically reached an asymptote within approximately 30 trials, but additional trials were added to ensure this was the case. Experiments were written in Matlab using the Psychophysics Toolbox extensions (Brainard, 1997).

In Experiment 1, one staircase estimate of threshold contrast was obtained from each observer at each of eight target durations for each of the four noise paradigms and also in the absence of noise. Noise paradigms were presented in a pseudo-random order, and the order of stimulus durations within a paradigm was randomized. In Experiment 2, three staircase estimates of threshold contrast were obtained for each of the two subjects as a function of the temporal asynchrony between target and noise for targets presented in both static and dynamic noise. In each session of Experiment 2, a single stimulus duration was presented, with the order of the durations chosen randomly across sessions. Within a session, the static and dynamic conditions were presented as separate blocks, with the order randomized, and the various temporal asynchronies were randomized within each block.

3. Results

3.1. Temporal integration functions

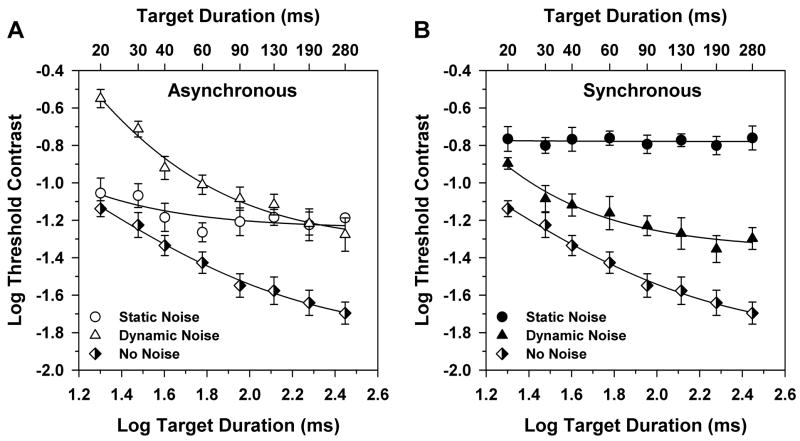
Fig. 2 plots mean log threshold contrast for the four observers as a function of log target duration in the absence of noise and in noise that was either asynchronous (Fig. 2A) or synchronous (Fig. 2B). The data for each condition were fit with the log form of the equation:

$$C_{\mathit{thr}}=C_{\mathit{min}}{(1+t_c/t)}^n,$$ (2)

where C_thr represents threshold contrast, t indicates target duration, C_min and t_c are parameters that control the vertical and horizontal position, respectively, of the function on a log-log plot, and n controls the slope of the initial time-dependent portion of the curve. This function is based on a model of spatiotemporal contrast integration described by Luntinen, Rovamo, and Näsänen (1995).

Figure 2.

Mean log threshold contrast as a function of log target duration for the four observers for the asynchronous (A) and synchronous (B) conditions, with targets presented either in static noise (unfilled and filled circles), dynamic noise (unfilled and filled triangles), or in the absence of noise (half-filled diamonds). Error bars indicate standard errors of the means (SEMs). Curves represent least-squares best fits of Eq. 2. Target durations in ms are indicated on the top x-axis.

The results shown in Fig. 2A agree well with those of Manahilov et al. (2003). In the absence of external noise (half-filled diamonds in each plot), the mean log threshold contrast decreased systematically with increasing target duration. In asynchronous dynamic noise (Fig. 2A, triangles), threshold contrast also decreased as the target duration increased, and thresholds for this condition were approximately 0.5 log unit higher than those for the noise-free condition, except at the two shortest target durations, where the threshold difference was slightly greater. However, in asynchronous static noise (Fig. 2A, circles), the log threshold contrast initially decreased slightly as the target duration was increased, but then became independent of the target duration for durations longer than approximately 40 ms. As a result, log threshold contrast in asynchronous static noise was similar to that of the noise-free condition at short target durations, but coincided with that for asynchronous dynamic noise at long target durations.

For synchronous dynamic noise (Fig. 2B, triangles), log threshold contrast decreased as the target duration increased, similar to the results for asynchronous dynamic noise shown in Fig. 2A. However, the overall effect of the noise was less for synchronous than for asynchronous dynamic noise. By comparison, log threshold contrast in synchronous static noise (Fig. 2B, circles) was independent of target duration over the entire range of durations. As a consequence, the threshold-elevating effect of the synchronous static noise was substantial at long target durations (approximately 0.9 log units above the noise-free condition). It is apparent from the results shown in Fig. 2 that static and dynamic noise can have quite different effects on temporal integration for both asynchronous and synchronous presentation modes, as Manahilov et al. (2003) observed previously using an asynchronous presentation mode.

3.2. Effect of temporal asynchrony

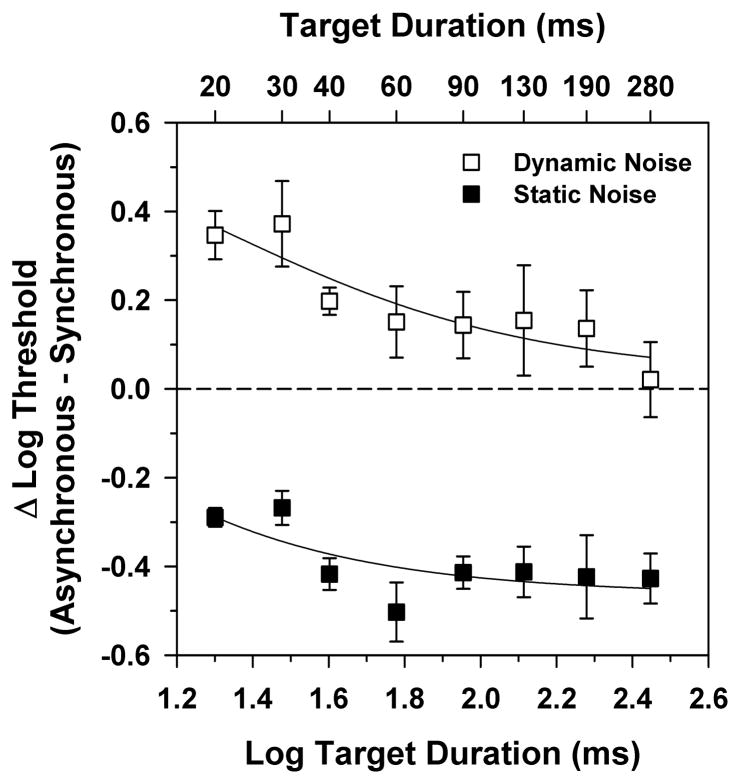
Further evidence for a fundamental difference between dynamic and static noise is presented in Fig. 3, which illustrates the effect of a temporal asynchrony between target and noise. In this figure, the threshold difference between the temporal integration functions obtained in asynchronous and synchronous noise (from Fig. 2) is plotted as a function of target duration for static (filled squares) and dynamic (unfilled squares) noise. The curves in Fig. 3 represent the difference between the respective fitted functions of Fig. 2. Differences greater than zero indicate that a temporal asynchrony between target and noise increased the threshold relative to the synchronous condition, whereas differences less than zero indicate that the temporal asynchrony produced a threshold decrease.

Figure 3.

Mean difference between the log threshold contrast values for the asynchronous and synchronous conditions of Fig. 2 as a function of log target duration for the four observers for either static noise (filled squares) or dynamic noise (unfilled squares). Error bars indicate ±1 SEM. Curves represent the differences between the corresponding fitted functions of Fig. 2. The horizontal dashed line indicates equality between the log threshold contrast values for the asynchronous and synchronous conditions. Target durations in ms are indicated on the top x-axis.

The difference functions for dynamic and static noise appear similar in overall shape. However, there is a fundamental distinction between the two. For targets presented in dynamic noise, the difference in log threshold between the asynchronous and synchronous conditions decreased as the target duration increased, whereas the difference increased slightly with increasing target duration for targets presented in static noise. The pattern of results for dynamic noise is to be expected, because the asynchronous and synchronous conditions became more similar as the target duration increased (given the fixed noise duration), so there should be less threshold difference between the two conditions at long target durations. However, the difference function for targets in static noise is paradoxical, in that, as the noise duration became more similar for the asynchronous and synchronous conditions, the threshold difference between the two conditions became larger.

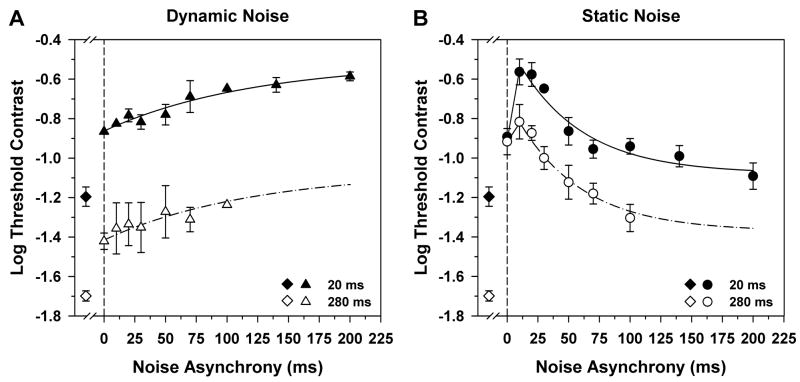
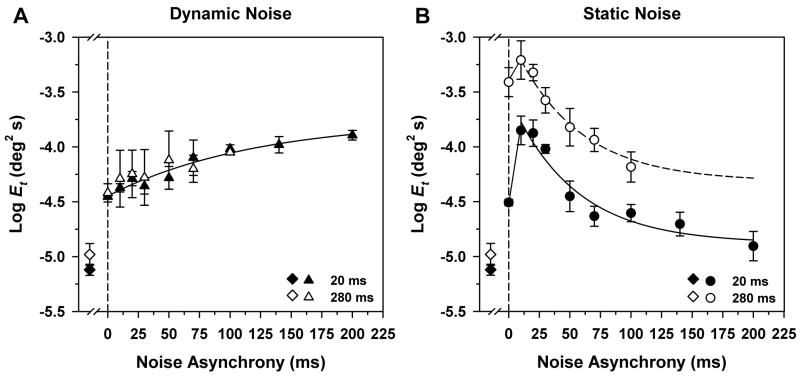
The results shown in Fig. 3 demonstrate that a temporal asynchrony had opposite effects on threshold contrast for targets presented in dynamic vs. static noise. However, it is not apparent from these data how threshold contrast varied as a function of the magnitude of the temporal asynchrony between target and noise. This relationship is illustrated in Fig. 4, which plots mean log threshold contrast for two observers as a function of the magnitude of the temporal asynchrony between the target and noise, for fixed target durations of 20 ms (filled symbols) and 280 ms (unfilled symbols). The abscissa in each plot in Fig. 4 indicates the duration of the noise that preceded the target, which in all cases was equal to the noise duration following the target. The vertical dashed line in each plot represents the synchronous condition. Data to the left of the dashed lines represent mean log threshold contrast in the absence of noise for the two target durations. There are fewer data points for the 280-ms test duration because the total presentation duration was arbitrarily limited to a value less than 500 ms in order to minimize the potential effect of eye movements.

Figure 4.

Mean log threshold contrast as a function of the magnitude of noise asynchrony for S₁ and S₂ for either dynamic (A) or static (B) noise, for target durations of either 20 ms (filled symbols) or 280 ms (unfilled symbols). Values on the x-axis indicate the duration of the noise preceding the target, which was always equal to the noise duration following the target. Vertical dashed lines indicate temporal synchrony between target and noise. Data points to the left of the vertical lines represent mean log threshold contrast in the absence of noise. Error bars indicate ±1 SEM. Solid curves represent least-squares best fits of exponential functions that were fit to the data for the 20-ms target as described in the text. Dot-dashed curves represent the same exponential functions displaced downward to minimize the least-squares errors from the data for the 280-ms target.

In dynamic noise (Fig. 4A), the log threshold contrast increased systematically for both target durations as the magnitude of the asynchrony increased. The solid curve in Fig. 4A represents an exponential function that was fit to the data for the 20-ms target duration. The dot-dashed curve represents the same exponential function shifted downward to minimize the mean squared error from the data for the 280-ms target. The magnitude of the vertical shift was 0.55 log unit, which represents partial temporal integration. The data sets for both target durations were well-fit by this exponential rise to saturation.

In static noise, by comparison (Fig. 4B), increasing the magnitude of the temporal asynchrony had a non-monotonic effect on the threshold contrast for both target durations. For the temporally synchronous condition (data points lying along the vertical dashed line), there was no appreciable difference between log threshold contrast values for the two target durations, which is consistent with the absence of temporal integration for the synchronous static condition (Fig. 2). When an asynchrony of 10 ms was introduced between target and noise, there was an increase in log threshold contrast that was greater for the 20-ms than for the 280-ms test target. This initial threshold increase was then followed by a systematic decrease in log threshold contrast with increasing asynchrony for both target durations.

The solid curve in Fig. 4B represents an exponential function that was fit to the data for the 20-ms target, which provides a satisfactory description of the data. The dot-dashed curve represents the same exponential function displaced downward to minimize the mean squared error from the data for the 280-ms target (shift of 0.29 log unit). Thus, the magnitude of temporal integration (i.e., vertical separation between the solid and dot-dashed curves) was considerably less for asynchronous static noise (Fig. 4B) than for asynchronous dynamic noise (Fig. 4A), in agreement with the results shown in Fig. 2.

The threshold contrast values of Figs. 4A and 4B were converted to threshold contrast energy (E_t), where contrast energy is defined as the integral over space and time of the squared signal function, given in units of deg² s (Legge et al., 1987). The results are plotted in Figs. 5A and 5B, which have the same conventions as Figs. 4A and 4B. In the absence of noise (leftmost data points in each plot), log E_t was nearly equivalent for the two target durations, indicating that stimulus contrast energy was the primary determinant of threshold. Similarly, in the presence of dynamic noise (Fig. 5A), threshold was also dependent on stimulus contrast energy at these two target durations. Increasing the magnitude of the temporal asynchrony between the target and dynamic noise systematically increased the value of E_t, and the extent of the increase was the same for both target durations. However, in the presence of static noise (Fig. 5B), stimulus contrast energy was not the determinant of threshold at the two target durations, given that the data sets for the two target durations were separated vertically. Furthermore, an increase in the magnitude of temporal asynchrony had a non-monotonic effect on E_t in the presence of static noise.

Figure 5.

Log threshold contrast and fitted functions of Fig. 4 replotted in terms of log threshold contrast energy (E_t). Other conventions are as in Fig. 4.

3.3. N_eq and sampling efficiency

The results shown in Fig. 5 have ramifications for estimates of N_eq and sampling efficiency. Pelli and Farell (1999) noted that N_eq and sampling efficiency can be derived by measuring threshold contrast energy in the absence of noise and in the presence of a high level of noise. Threshold contrast energy (E_t) is linearly related to the spectral density (N) of the additive luminance noise according to the relationship:

$$E_t=k(N+N_{eq}),$$ (3)

where k represents the slope of the function (e.g., Legge et al., 1987). If a line is fit to the two data points representing threshold contrast energy in the absence and presence of the noise, the negative of the x-intercept represents N_eq. Sampling efficiency (J) is reciprocally related to the slope of the fitted function according to the relationship:

$$J={({d^{\prime }}_c)}^2/k$$ (4)

where d′_c is the criterion level of detectability (Legge et al., 1987). In the present study, d′_c was 1.29 (Green and Swets, 1974).

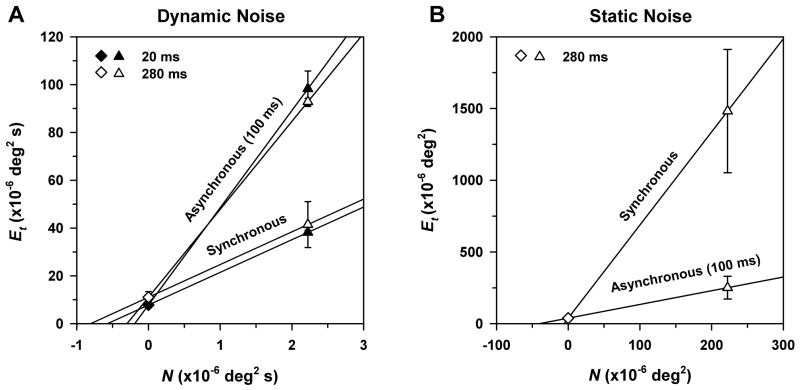
This analysis was applied to representative data from Fig. 5 in order to determine the relationship between temporal asynchrony, N_eq, and sampling efficiency. The results for dynamic noise are given in Fig. 6A. The filled and unfilled symbols in this plot represent threshold contrast energy vs. noise spectral density for target durations of 20 and 280 ms, respectively. Results are shown for the synchronous presentation mode and for an asynchronous condition in which the noise extended 100 ms before and after the test target. This was the largest magnitude of asynchrony for which data were available for both target durations. The functions for the synchronous dynamic condition were considerably shallower than for this particular asynchronous dynamic condition, and the lines intercepted the x-axis further from the origin. Thus, both N_eq and sampling efficiency were higher for synchronous than for asynchronous dynamic noise for both target durations.

Figure 6.

Mean threshold contrast energy (E_t) as a function of noise spectral density (N) for representative mean data from Fig. 5 for either dynamic (A) or static (B) noise, using target durations of both 20 and 280 ms (A) or only 280 ms (B), and for either the synchronous mode or an asynchronous mode in which the noise duration preceding and following the test target was 100 ms. Error bars indicate±1 SEM. Lines represent Eq. 3 and were used to derive the estimates of N_eq and sampling efficiency presented in Table 1.

Table 1 presents the values of N_eq and sampling efficiency for the 280-ms target presented in synchronous and asynchronous dynamic noise as derived from the mean data of Fig. 6A (results were similar for the 20-ms test target). Although these values of N_eq and sampling efficiency are for a particular temporal asynchrony between target and noise, it is apparent from the plots of Figs. 5A and 6A that all magnitudes of temporal asynchrony would yield lower values of N_eq and sampling efficiency than the synchronous condition, because the threshold signal energy increased systematically with increasing magnitude of asynchrony.

Table 1.

Values of N_eq and sampling efficiency derived from the mean data of Fig. 6 as described in the text.

Neq	Dynamic Noise	Static Noise
Synchronous	0.8 × 10−6 deg2 s	4.5 × 10−6 deg2
Asynchronous	0.3 × 10−6 deg2 s	29.1 × 10−6 deg2
Sampling Efficiency	Dynamic Noise	Static Noise
Synchronous	8.0%	12.1%
Asynchronous	2.8%	78.3%

For static noise, it is somewhat problematic to derive estimates of N_eq and sampling efficiency from the data of Fig. 5. One consideration is that, based on the different shapes of the temporal integration functions in static noise and in the noise-free condition (Fig. 2), it is likely that different visual mechanisms (i.e., transient-like and sustained-like mechanisms, respectively) mediated performance under these two conditions, as described by Manahilov et al. (2003). A second consideration is that the quantification of static noise typically does not incorporate noise duration (Legge et al., 1987), whereas the contrast energy of the brief targets does take target duration into account.

Nevertheless, for a target duration of 280 ms (the longest duration used here), the temporal integration functions in the absence of noise and in static synchronous and asynchronous noise have essentially reached an asymptote (Fig. 2), so that the threshold contrast energy for this long target duration may be considered to correspond to that of extended viewing, and can thus be specified in units of deg². On this basis, Fig. 6B plots target contrast energy vs. noise spectral density for the 280-ms test target for both synchronous static noise and for an asynchronous static noise condition in which there was 100 ms of noise preceding and following the target.

The function for synchronous static noise was considerably steeper than the function for this particular asynchronous condition, and the line intercepted the x-axis closer to the origin. Thus, both N_eq and sampling efficiency were lower for synchronous than for asynchronous static noise. This pattern of results is opposite that for dynamic noise (Fig. 6A), for which N_eq and sampling efficiency were highest for the synchronous condition. Table 1 gives the values of N_eq and sampling efficiency derived from the mean data of Fig. 6B for the 280-ms target presented in synchronous and asynchronous static noise. It is apparent from Table 1 that sampling efficiencies were higher for targets presented in static than in dynamic noise, regardless of the degree of temporal asynchrony. The units of N_eq are different for dynamic and static noise, however, so the values cannot be compared directly.

It would be of interest to extend this analysis to the data of Fig. 2 in order to derive N_eq and sampling efficiency as a function of target duration. However, several considerations suggest that this would be inappropriate. First, the data of Fig. 5A indicate that the magnitude of the temporal asynchrony between test target and dynamic noise should be held constant across test duration in order to derive N_eq and sampling efficiency properly. However, this was not the case for the data in Fig. 2, for which the noise duration was constant across varying target durations, resulting in a change in the magnitude of temporal asynchrony across conditions. Second, it is unlikely that the same visual mechanism mediated threshold contrast in static noise and in the noise-free condition, given the observed differences in the temporal integration functions for these conditions (Fig. 2). Third, the units of signal energy and noise spectral density were different for static noise. Consequently, the data of Fig. 2 were not analyzed using the approach of Pelli and Farell (1999).

4. Discussion

The aim of this study was to determine how the temporal characteristics of additive luminance noise influence threshold contrast and affect estimates of N_eq and sampling efficiency. The results demonstrate that dynamic and static noise can result in quite different temporal integration functions, whether the presentation mode is synchronous or asynchronous. Furthermore, introducing a temporal asynchrony between the target and noise has different effects on threshold contrast and threshold contrast energy depending on whether the noise is dynamic or static. These results have important implications for estimates of N_eq and sampling efficiency for targets presented in dynamic and static noise.

4.1. Temporal integration functions in dynamic and static noise

Our temporal integration data using an asynchronous mode of presentation (Fig. 2A) agree well with those of Manahilov et al. (2003). These investigators proposed that the relatively long time constant of temporal integration for targets of intermediate spatial frequency presented in asynchronous dynamic noise represents detection by a sustained-like (or parvocellular) visual mechanism. On the other hand, Manahilov et al. (2003) suggested that asynchronous static noise masks the sustained-like mechanism, so that detection under this condition would be mediated by the transient-like (or magnocellular) mechanism, which has a shorter time constant of integration.

The present results extend this difference between dynamic and static noise to temporal integration functions obtained with a synchronous mode of presentation (Fig. 2B). For threshold contrast obtained in synchronous dynamic noise, the time constant of temporal integration was relatively long, similar to that obtained in asynchronous dynamic noise (Fig. 2A). In comparison, threshold contrast was independent of target duration when measured in synchronous static noise. The flat threshold contrast function observed under this condition, which is consistent with previous reports (Rovamo, Kukkonen, Tiippana & Näsänen, 1993; Pelli et al., 2006), may result from a balance between temporal integration of the test target, which would be expected to decrease the threshold contrast, and temporal integration of the static noise, which would tend to increase the threshold contrast.

4.2. Magnitude of temporal asynchrony between target and noise

There were also fundamental differences between dynamic and static noise in terms of the effect of a temporal asynchrony between target and noise on threshold contrast. Relative to the synchronous condition, an asynchrony between the target and noise increased the threshold contrast in dynamic noise and decreased the threshold contrast in static noise (Fig. 3). The systematic increase in threshold contrast with increasing asynchrony of dynamic noise (Fig. 4A) indicates that there is temporal integration of dynamic noise when it extends beyond the target duration.

In comparison, an increasing temporal asynchrony had a non-monotonic effect on threshold contrast when targets were presented in static noise (Fig. 4B). The threshold elevation observed in static noise between the synchronous condition and a 10-ms asynchrony may be due to masking of the test target by the onset and offset of the nearly simultaneous noise field. The subsequent decrease in threshold contrast with increasing magnitude of asynchrony is paradoxical, given that there was a corresponding increase in the noise duration and thus a greater potential for temporal integration of the noise. It is possible that adaptation to the steady noise field during the longer noise presentations decreased the threshold contrast for the asynchronously presented test target.

There were also fundamental differences between dynamic and static noise when the effect of temporal asynchrony on threshold contrast energy was considered (Fig. 5). For targets presented in dynamic noise, the threshold was governed by stimulus contrast energy whether the presentation mode was synchronous or asynchronous (Fig. 5A). This was also the case for targets presented in the absence of noise. These results are consistent with energy models of threshold (reviewed by Mahahilov and Simpson, 1999). For static noise, however, thresholds were not dependent on stimulus contrast energy (Fig. 5B), at least at the two target durations used here.

4.3. Estimates of N_eq and sampling efficiency

The data of Fig. 6 and Table 1 indicate that estimates of both N_eq and sampling efficiency differed depending on whether the temporal relationship between target and noise was synchronous or asynchronous. Furthermore, the effect of a temporal asynchrony was quite different for dynamic and static noise. For targets presented in dynamic noise, an increase in the temporal asynchrony between target and noise resulted in a decrease in N_eq and sampling efficiency. For targets presented in static noise, however, there was an increase in N_eq and sampling efficiency with increasing temporal asynchrony. These findings provide further evidence that the noise integrates temporally when it extends beyond the target duration, and show that the effect of the temporal integration of the noise on threshold contrast differs depending on whether the noise is dynamic or static.

Our value of N_eq for a 280-ms target presented in asynchronous dynamic noise (0.3 × 10⁻⁶ deg² s) agrees well with the value of approximately 0.2 × 10⁻⁶ deg² s obtained by Legge et al. (1987) under their asynchronous dynamic noise condition. Legge et al. (1987) did not report N_eq for a test target presented in static synchronous noise in the absence of a luminance pedestal, but an extrapolation of their data suggests that our value of N_eq for a 280-ms target presented in synchronous static noise (4.5 × 10⁻⁶ deg²) is about an order of magnitude higher than theirs. Of note, in comparison to the present study, the noise characteristics and test targets were considerably different for the asynchronous dynamic and synchronous static conditions of Legge et al. (1987). These investigators did not measure thresholds in either synchronous dynamic or asynchronous static noise, so no comparison data are available for these conditions.

Our sampling efficiencies for targets presented in asynchronous dynamic noise (2.8%) and synchronous static noise (12.1%) are similar to those reported by Legge et al. (1987) for corresponding noise types (approximately 3% and 10%, respectively). The highest value of sampling efficiency in our study (78.3%) was obtained with asynchronous static noise. The high sampling efficiency that we observed under this condition is within the range reported by Burgess, Wagner, Jennings and Barlow (1981), who used static luminance noise. Overall, our data are consistent with the previous conclusion that sampling efficiencies are higher in static than in dynamic noise (Legge et al., 1987).

In summary, our results confirm and extend those of Manahilov et al. (2003) in demonstrating that dynamic and static noise can have quite different effects on threshold contrast as a function of target duration. The overall pattern of our results is consistent with their conclusion that, at an intermediate target spatial frequency, dynamic noise favors detection by a sustained-like mechanism, whereas static noise emphasizes detection by a transient-like mechanism. As a consequence, the same visual mechanism may not mediate performance in the presence and absence of noise, or across different target durations. This factor should be considered in interpreting values of N_eq and sampling efficiency derived from plots of threshold contrast energy in the presence and absence of additive luminance noise. Furthermore, for both dynamic and static noise, the potential for temporal integration of the noise as well as of the signal can affect estimates of N_eq and sampling efficiency and should be considered in their interpretation.