Abstract
In reverberant environments, acoustic reflections interfere with the direct sound arriving at a listener’s ears, distorting the spatial cues for sound localization. Yet, human listeners have little difficulty localizing sounds in most settings. Because reverberant energy builds up over time, the source location is represented relatively faithfully during the early portion of a sound, but this representation becomes increasingly degraded later in the stimulus. We show that the directional sensitivity of single neurons in the auditory midbrain of anesthetized cats follows a similar time course, although onset dominance in temporal response patterns results in more robust directional sensitivity than expected, suggesting a simple mechanism for improving directional sensitivity in reverberation. In parallel behavioral experiments, we demonstrate that human lateralization judgments are consistent with predictions from a population rate model decoding the observed midbrain responses, suggesting a subcortical origin for robust sound localization in reverberant environments.
INTRODUCTION
The ability to localize sound sources can be important for survival and facilitates the identification of target sounds in multi-source environments (Darwin, 2008; Kidd et al., 2005; Shinn-Cunningham, 2008). The auditory scenes that we perceive unfold in environments full of surfaces like walls, trees, and rocks (Huisman and Attenborough, 1991; Sakai et al., 1998). When an acoustic wave emanating from a sound source strikes a boundary surface, a fraction of the energy is reflected. The reflected waves themselves generate second order reflections, with the process repeating ad infinitum. The myriad of temporally overlapping reflections, perceived not as discrete echoes but as a single acoustic entity, is referred to as reverberation.
Reverberation poses a challenge to accurate sound localization. To estimate the location of a sound source with low frequency energy, such as speech, human listeners rely principally on tiny interaural time differences (ITDs) that result from the separation of the ears on the head (Macpherson and Middlebrooks, 2002; Wightman and Kistler, 1992). In a reverberant environment, reflected acoustic waves reach the listener from all directions, interfering with the direct sound. Under such conditions, the ear-input signals become decorrelated (Beranek, 2004) and the instantaneous ITD fluctuates (Shinn-Cunningham and Kawakyu, 2003). Because reverberant energy builds up over time, the directional information contained in the ear-input signals has a characteristic time course, in that ITD cues represent the true source location relatively faithfully during the early portion of a sound, but become increasingly degraded later in the stimulus.
In principle, listeners could accurately localize sounds in reverberation by basing their judgments on the directional information in the uncorrupted onset of the signals reaching the ears. Although human listeners can robustly localize sound sources in moderate reverberation (Hartmann, 1983; Rakerd and Hartmann, 2005), localization accuracy degrades in stronger reverberation (Giguere and Abel, 1993; Rakerd and Hartmann, 2005; Shinn-Cunningham et al., 2005b), suggesting that listeners are not immune to the ongoing, corrupted directional cues. To date, no one has studied the directional sensitivity of auditory neurons using stimuli with realistic reverberation. Thus, the degree to which auditory neurons maintain robust directional sensitivity in reverberation is unknown.
ITDs are initially coded in the auditory pathway as differences in relative spike timing between auditory nerve fibers on the left and right sides of the head. These timing differences are transformed to a rate code in the medial superior olive (MSO), where morphologically and physiologically specialized neurons (Grothe and Sanes, 1994; Scott et al., 2005; Smith, 1995; Svirskis et al., 2004) perform coincidence detection on convergent input from both sides of the head (Goldberg and Brown, 1969; Yin and Chan, 1990). Theoretically, the average firing rate of these coincidence detectors is equivalent to a cross-correlation of the input spike trains (Colburn, 1973).
The majority of neurophysiological studies of spatial processing have targeted the inferior colliculus (IC), the primary nucleus comprising the auditory midbrain (Aitkin et al., 1984; Delgutte et al., 1999; Joris, 2003; Kuwada et al., 1987; Kuwada and Yin, 1983; McAlpine et al., 2001; Rose et al., 1966; Stillman, 1971a; Yin et al., 1986). Multiple, parallel sound-processing pathways in the auditory brainstem converge in the IC (Adams, 1979; Oliver et al., 1995), making it a site of complex synaptic integration. Despite this complexity, the rate responses of low-frequency, ITD-sensitive IC neurons to broadband signals with a static interaural delay resemble the responses of ITD-sensitive neurons in the MSO (Yin et al., 1986) and are well-modeled as a cross-correlation of the acoustic ear-input signals, after accounting for cochlear frequency filtering (Hancock and Delgutte, 2004; Yin et al., 1987).
Here, we investigate the effects of reverberation on the directional sensitivity of low-frequency ITD-sensitive IC neurons. Consistent with the buildup of reverberation in the acoustic inputs, we show that directional sensitivity is better near the onset of a reverberant stimulus and degrades over time, although directional sensitivity is more robust than predictions from a traditional cross-correlation model of binaural processing that is insensitive to temporal dynamics in the reverberant sound stimuli. We further show that human lateralization judgments in reverberation are consistent with predictions from a population rate model for decoding the observed midbrain responses, suggesting that robust encoding of spatial cues in the auditory midbrain can account for human sound localization in reverberant environments.
RESULTS
Effects of reverberation on neural azimuth sensitivity
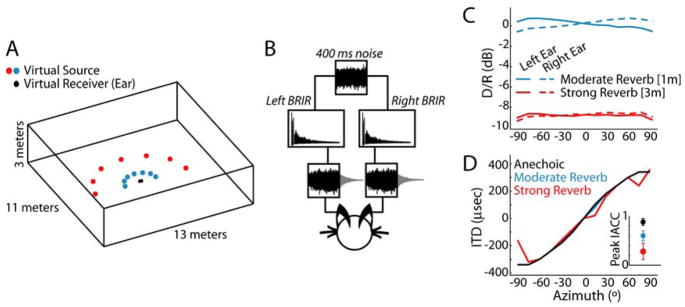
We used virtual auditory space simulation techniques (Fig. 1, Experimental Procedures) to study the directional response properties of 36 low-frequency, ITD-sensitive neurons in the IC of anesthetized cats. The virtual space stimuli simulated the acoustics of a medium-size room (e.g. a classroom), and were designed to contain only ITD cues, without any interaural level differences or spectral cues. Stimuli were synthesized for two distances between the sound source and the virtual ears (1m and 3m) in order to vary the amount of reverberation (“moderate” and “strong”). The ratio of direct to reverberant energy (D/R) decreased with increasing distance and was largely independent of azimuth for each distance simulated (Fig. 1C). Reverberation did not systematically alter the broadband ITD, estimated as the time delay yielding the maximum normalized interaural correlation coefficient (IACC) between the left and right ear-input signals (Fig. 1D). However, increasing reverberation did cause a systematic reduction in the peak IACC (Fig. 1D, inset), indicating increasing dissimilarity in the ear-input waveforms.
Figure 1. Properties of the virtual auditory space simulations.
A, Geometry of the virtual auditory environment. Reverberant binaural room impulse responses (BRIR) were simulated at two distances between source and receiver (1m and 3m). Anechoic (i.e., “no reverb”) BRIR were created by time-windowing the direct wavefront from the 1m reverberant BRIR.
B, To simulate a sound source at a given azimuth, a reproducible 400-ms broadband noise burst is convolved with the left and right BRIR and presented to the experimental subject over headphones.
C, Direct to reverberant energy ratio (D/R) vs. azimuth for reverberant BRIRs.
D, Broadband ITD vs. azimuth for each room condition, estimated as the time delay corresponding to the peak normalized interaural correlation coefficient (IACC). Inset, Peak IACC for each room condition. Error bars represent ±1 std across azimuths.
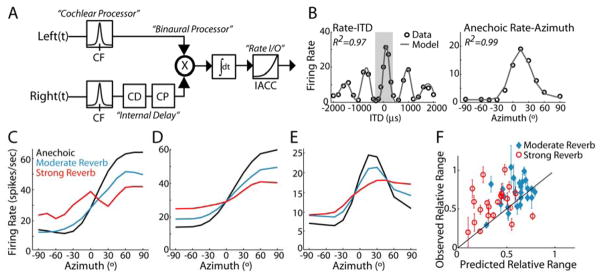
Figure 2A–C illustrates anechoic (i.e., “no reverb”) and reverberant rate-azimuth curves for three IC units. For anechoic stimuli (Fig. 2A–C, black curves), the shape of the rate-azimuth curve was determined by the unit’s sensitivity to ITD within the naturally occurring range (Supp. Fig. 1A–B), which corresponds to ± 360 μs for our virtual space simulations for cats. In many neurons, the discharge rate increased monotonically with azimuth (Fig. 2A–B), particularly in the sound field contralateral to the recording site, which corresponds to positive azimuths. Units with a non-monotonic dependence of firing rate on azimuth (Fig. 2C) generally peaked within the contralateral hemifield, consistent with the contralateral bias in the representation of ITD in the mammalian midbrain (Hancock and Delgutte, 2004; McAlpine et al., 2001; Yin et al., 1986).
Figure 2. Reverberation causes compression of neural rate-azimuth curves.
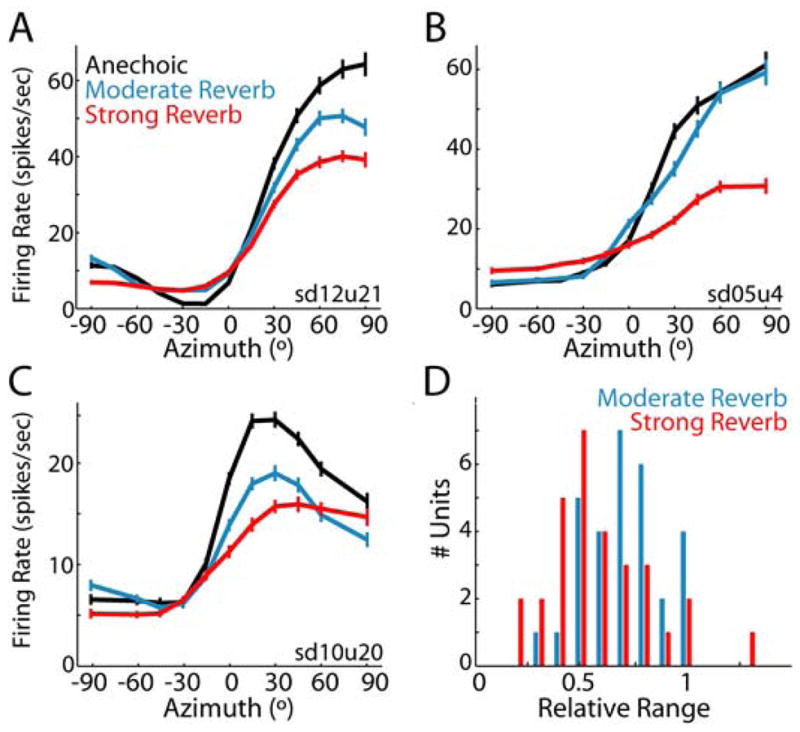
Anechoic and reverberant rate-azimuth curves (mean ± 1 standard error) for three IC neurons with CFs of A, 817 Hz, B, 569 Hz, C, 1196 Hz. D, Population histogram of relative range for each D/R (moderate reverb: n=30; strong reverb, n=30).
In reverberation, there was an overall tendency for the range of firing rates across azimuths to decrease with increasing reverberation, although the exact dependence varied across units. Typically, the effect of reverberation was graded (Fig. 2A, C); however, there were units for which moderate reverberation had essentially no effect on the rate response (Fig. 2B). Generally, the reduction in response range primarily resulted from a decrease in the peak firing rate; increases in minimum firing rates were less pronounced.
We quantified the overall compression of the rate-azimuth curves in reverberation using the relative range, which expresses the range of firing rates for a reverberant rate-azimuth curve as a fraction of the range of firing rates for that unit’s anechoic rate-azimuth curve. In reverberation, the relative range is generally less than 1 (Fig. 2D) and is significantly lower for the strong reverb than for the moderate reverb condition (paired t-test, p=0.001, n=24). An information theoretic measure of directional sensitivity, which is sensitive to the variability in spike counts as well as the mean firing rates, showed a similar dependence on reverberation strength (Supp. Fig. 2).
Reverberation could also alter the sharpness of azimuth tuning and – for units having a best ITD within the naturally occurring range – shift the best azimuth (Supp. Fig. 3). However, changes in these tuning parameters occurred in either direction and were not consistently observed in all units. The most consistent effect of reverberation across our neural population was the compression of the response range.
Directional sensitivity is better near stimulus onset in reverberation
Reverberant sounds have a characteristic temporal structure that is ignored when firing rates are averaged over the entire stimulus duration as in Figure 2. At the onset of a sound in a reverberant environment, the energy reaching a listener’s ears contains only the direct sound. Thus, the directional cues near the stimulus onset are similar for anechoic and reverberant virtual space stimuli (Fig. 3A–B). As reverberation build ups over time, reflections increasingly interfere with the direct sound energy at a listener’s ears and the directional cues for the reverberant stimuli become more corrupted. Accordingly, we expected neural directional sensitivity to be better during the early as opposed to the ongoing portion of a sound stimulus in reverberation. Figure 3C–D shows rate-azimuth curves for two IC neurons computed from the early (0–50 ms), ongoing (51–400 ms), and full (0–400 ms) neural response. The rate-azimuth curves have been normalized to the maximum rate within each time period to facilitate comparison. Consistent with the build-up of reverberation, the rate-azimuth curves computed from the early response are similar across room conditions (Fig. 3C–D, left), whereas substantial rate compression occurs for reverberant stimuli in the ongoing response (Fig. 3C–D, middle). This trend holds across our sample of low-frequency ITD-sensitive neurons (Fig. 3E). Directional sensitivity in both moderate and strong reverberation is significantly higher during the early as compared to the ongoing neural response epoch (paired t-test, moderate reverb: p=0.007, n=24; strong reverb: p<0.001, n=25).
Figure 3. Temporal dynamics of directional sensitivity in reverberation.
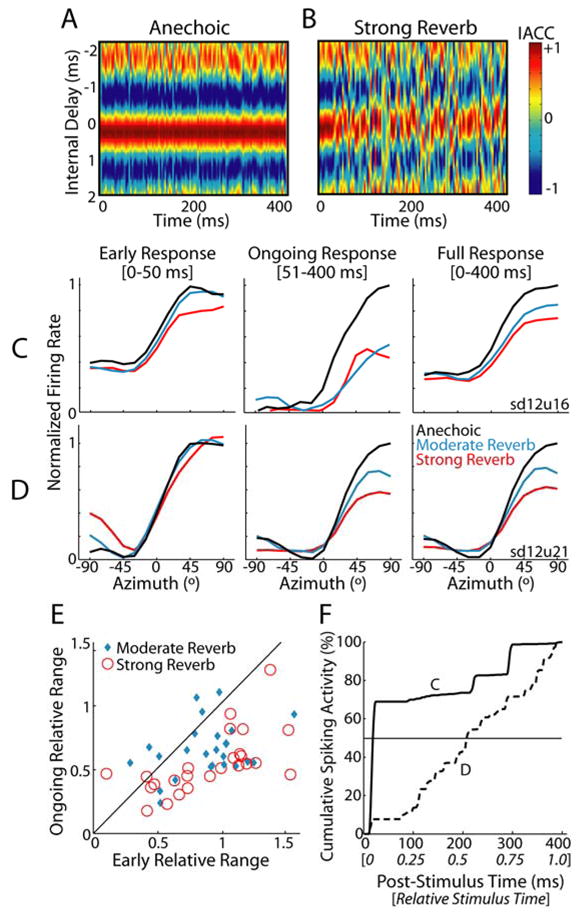
A, Short-term IACC across time for the 45° anechoic virtual space stimulus; hot colors indicate high correlation. Ear-input signals were simulated as in Fig. 1B and subsequently bandpass filtered (4th-order Gammatone filter centered at 1000 Hz) to simulate peripheral auditory processing. Short-term IACC was computed using a sliding 4-ms window.
B, Short-term IACC for the 45° strong reverb virtual space stimulus.
C,D Rate-azimuth curves for two IC neurons computed using the early (0–50 msec), ongoing (51–400 msec), and full (0–400 msec) neural responses. To facilitate comparison across time periods, firing rates have been normalized to the maximum anechoic firing rate, separately for each time period. Unit CFs are C, 747 Hz and D, 817 Hz.
E, Ongoing vs. early relative range for IC neuron population. Solid line indicates identity i.e., y=x.
F, Average cumulative peristimulus time histograms (cPSTHs) for the two neurons in panels C (solid line) and D (dashed line).
Previous studies of ITD-sensitivity in the mammalian IC have reported that neural onset responses show poorer ITD-tuning than ongoing neural responses (Geisler et al., 1969). Here, we have defined the ‘early’ response epoch as the first 50 ms of the neural response, which is substantially longer than what is generally considered the ‘onset’ response of a cell. Nonetheless, to prevent non-directional early responses from biasing our results, we removed units that showed no significant change in early discharge rate across azimuth (Kruskal-Wallis test, p>0.05); 6/36 units were removed from the statistical analysis and are not included in Figure 3E.
Role of temporal response dynamics
The relative contribution of the early and ongoing responses to the directional sensitivity measured over the entire stimulus duration (Fig. 3C–D, right) is determined by the distribution of spiking activity over the course of the stimulus. Many low-frequency ITD-sensitive IC neurons exhibit spike rate adaptation in response to a sustained acoustic stimulus, such that firing rates are higher during the earlier portion of the stimulus and decrease over time (Ingham and McAlpine, 2004; Nuding et al., 1999; Rees et al., 1997; Stillman, 1971b). Such “onset dominance” in neural processing reduces the contribution of less-reliable ongoing reverberant stimulus energy to temporally-integrated measures of directional sensitivity.
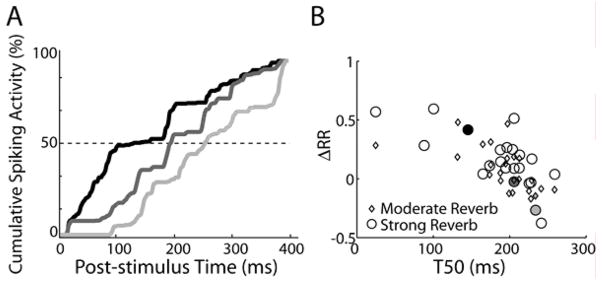
Figure 3F shows anechoic cumulative peristimulus time histograms (cPSTHs, see Experimental Procedures) for the same two units as in Fig. 3C–D. A unit with strong onset dominance (Fig. 3F solid line) has a cPSTH that rises rapidly shortly after stimulus onset. Accordingly, the full response for this unit is determined primarily by the early response (Fig. 3C). In contrast, a unit that fires in a sustained manner throughout the stimulus has a more linear cPSTH (Fig. 3F, dashed line); in this case, the full response exhibits a stronger resemblance to the ongoing neural response (Fig. 3D).
To quantify onset dominance in single units, we computed T50 -- the time post stimulus onset at which the cPSTH reaches 50% of its final value (Fig. 3F). A strongly onset-dominated unit has a small T50 (Fig. 3F, solid line) while a sustained unit has a T50 near the stimulus midpoint (Fig. 3F, dashed line). Across the neural population, the median T50 is significantly less than 0.5 (Wilcoxon signed-rank test, p<0.001, n=36), with the interquartile range spanning [0.31, 0.47]. This suggests that early directional responses typically contribute more to the overall directional sensitivity than the more-degraded ongoing directional responses.
If the response to a reverberant stimulus were governed primarily by neural response dynamics, we would expect onset-dominated units to show better directional sensitivity in reverberation than units with a sustained response. That is, we should observe a negative correlation between T50 and relative range. However, the correlation was not significant for either condition (moderate reverb: p=0.624; strong reverb: p=0.517), suggesting that other neural properties in addition to onset dominance influence directional sensitivity in reverberation.
Comparison to a Cross-Correlation Model
Previous investigations of low-frequency ITD-sensitive IC neurons have established that the rate response to interaurally-delayed broadband noise is well-described by a cross-correlation of the left and right ear-input signals, after accounting for peripheral frequency filtering and the nonlinear relationship between interaural correlation and firing rate (Hancock and Delgutte, 2004). Cross-correlation models essentially reduce all binaural processing (including interaural delays) to a change in the effective IACC computed over the entire duration of the stimulus. In general, firing rate changes monotonically with IACC in low-frequency IC neurons, although there is substantial variability in the degree of nonlinearity in the relationship (Albeck and Konishi, 1995; Coffey et al., 2006; Shackleton et al., 2005).
In a reverberant environment, reflections interfere with the direct sound wave, resulting in decorrelation of the ear-input signals [Fig. 1D, inset; see also (Hartmann et al., 2005; Shinn-Cunningham et al., 2005a)]. According to the cross-correlation model, this would qualitatively result in a compression of neural rate-azimuth curves, as observed in our neural data. We investigated whether a traditional cross-correlation model could quantitatively account for the degradation of directional sensitivity in reverberation.
We used a modified version of the Hancock and Delgutte (2004) cross-correlation model of ITD-sensitive IC neurons to generate predictions of reverberant rate-azimuth curves (see Experimental Procedures). The model is a cascade of linear peripheral frequency filtering and binaural cross-correlation followed by a nonlinear transformation of IACC to firing rate (Fig. 4A). The model parameters were fit for each individual unit using the rate-ITD and anechoic rate-azimuth data (Fig. 4B), and then fixed to predict responses to reverberant stimuli.
Figure 4. Average effective IACC poorly predicts directional sensitivity in reverberation.
A, Block diagram of the cross-correlation model, after Hancock and Delgutte (2004). Left and right ear-input signals are bandpass filtered to simulate cochlear processing. Right-ear signal is internally delayed through a combination of pure time delay (CD) and phase shift (CP), and the resulting IACC is converted to firing rate using a power-law nonlinearity.
B, Example model fits to the rate-ITD (left) and anechoic rate-azimuth (right) data for one IC unit (CF=1312 Hz). The shaded region in the left panel delineates the range of ITDs corresponding to ±90° in the right panel.
C–E, Model predictions of rate-azimuth curves for three IC neurons (same units as in Fig. 2A–C). For each neuron, model parameters were adjusted to minimize least-squared error between observed and predicted rate-ITD and anechoic rate-azimuth curves and subsequently fixed to generate predictions of reverberant rate-azimuth curves.
F, Observed vs. predicted relative range across the IC neuron population. Solid line indicates identity i.e., y=x. Error bars represent bootstrap estimates of ±1 std. of relative range for observed responses.
Figure 4C–E shows model predictions of reverberant rate-azimuth curves for the same three IC units as in Figure 2A–C. As expected, the model rate-azimuth curves are qualitatively similar to the measured reverberant rate-azimuth curves in that increasing reverberation causes more compression of the response. We quantified overall differences between observed and predicted directional sensitivity using the relative range (Fig. 4F). Across the population, the model predicts substantial variability in the relative range, which originates from variations in both frequency tuning and the nonlinear dependence of firing rate on IACC. Accurate model predictions for individual units would yield data points close to the identity line y=x in Figure 4F; however, there is a great deal of spread in the data with no significant correlation between observed and predicted relative range for either reverberation condition (moderate reverb: p=0.174, strong reverb: p=0.532). Moreover, a majority of the data points fall above the identity line, indicating that observed directional sensitivity is generally more robust (i.e., better) than model predictions. For both reverberation conditions, predicted directional sensitivity is significantly worse than observed directional sensitivity (one-tailed paired t-test, moderate reverb: p=0.02, n=24, strong reverb: p=0.005, n=24).
The cross-correlation model is not sensitive to the exact time course of short-term IACC; rather, its output depends only on the IACC averaged over the entire stimulus. In contrast, we have shown that onset dominance in neural responses emphasizes the earlier segments of the stimulus which, in reverberation, contain less-degraded directional information. Such neural processing would effectively attenuate the contribution of ongoing reverberant stimulus energy to the IACC measured at the output of the integrator in Figure 4A. Thus, we hypothesized that neural onset dominance could account for the inability of the model to predict directional sensitivity in reverberation.
To test the hypothesis, we examined the relationship between T50 and cross-correlation model error (defined as the difference between observed and predicted relative ranges, ΔRR). Positive values of ΔRR indicate robustness to reverberation (i.e., the cross-correlation model predicts more compression than was actually observed). Figure 5B shows a scatter plot of ΔRR versus T50; the filled symbols correspond to the cPSTHs plotted in Figure 5A. There is a significant negative correlation between the two metrics for both reverberation conditions (moderate reverb: r=−0.534, p=0.007; strong reverb: r=−0.612, p=0.003). Namely, units with smaller T50 (i.e., the most onset-dominated units) tend to be more robust to reverberation relative to model predictions than units with longer T50.
Figure 5. Onset dominance is related to robust directional sensitivity in reverberation.
A, cPSTHs for three IC neurons with CFs of 150 Hz (black), 741 Hz (dark gray), and 1551 Hz (light gray). T50 is defined as the time at which the cPSTH reaches 50% of its final value (intersection of cPSTH with dashed line).
B, Model prediction error (ΔRR) vs. T50 across the IC neuron population, where positive ΔRR indicate robustness to reverberation. The two metrics are inversely correlated (moderate reverb: p=0.007; strong reverb: p=0.003). Shaded symbols correspond to the units shown in A.
Despite the correlation, the substantial spread in the data suggests that onset-dominance cannot completely account for the inability of the cross-correlation model to predict directional sensitivity in reverberation. The cross-correlation model may be a poor predictor of directional sensitivity for stimuli with dynamic interaural time differences, in general (see Discussion). Nevertheless, these results suggest that onset dominance can improve directional sensitivity in reverberation.
Comparison to Human Psychophysics
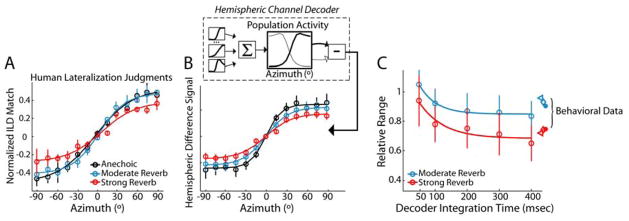
We measured human behavioral lateralization1 of virtual space stimuli nearly identical to those used in the neurophysiology experiments. Listeners adjusted the ILD of high-frequency narrowband noise until its perceived laterality subjectively matched that of each virtual space stimulus. Because the absolute range of pointer ILDs for azimuths spanning ±90° varied from subject to subject, we normalized the subjective lateral positions to their maximum for each subject. Figure 6A shows the normalized subjective lateral position as a function of stimulus azimuth. For all conditions, mean lateralization judgments vary nearly monotonically with virtual source azimuth. Listener judgments of source laterality are similar for the anechoic and moderate reverberation conditions. However, in strong reverberation, the range of lateralization judgments is noticeably compressed. This compression of perceived laterality resembles the reduction in relative range measured in single IC neurons.
Figure 6. Hemispheric decoding of IC neural responses accounts for lateralization behavior of human listeners.
A, Human lateralization judgments. Across-subject (n=3) mean (± 1 std) estimate of lateral position (i.e., normalized ILD-match) vs. stimulus azimuth.
B, Upper panel, Schematic of the population decoding model (see text for description). Lower panel, Hemispheric difference signal vs. azimuth. Error bars indicate bootstrap estimates of ±1 std.
C, Comparison of decoder and perceptual compression. Relative range of hemispheric difference signal (open circles) vs. the time interval over which firing rate is integrated in the hemispheric decoding model; solid lines indicate fits by decaying exponential. Error bars represent bootstrap estimates of ± 1 std. Relative range of human behavioral responses is plotted at the right edge of the panel (different symbols represent individual subjects).
In order to directly compare neural responses to the behavioral results, we implemented a hemispheric-difference decoding model (Hancock, 2007; McAlpine et al., 2001; van Bergeijk, 1962) using the empirically measured rate-azimuth curves from our neurophysiology experiments. The model (Fig. 6B, inset) estimates the lateral position of a sound source from the difference in the total activation between the two ICs. The choice of such a code [as opposed to a labeled line code, e.g. Jeffress (1948)] was motivated by the prevalence of monotonic rate-azimuth curves in our neural population, where a neuron’s best ITD lies outside of the naturally occurring range of ITDs (Supp. Fig. 1C, D).
The total population activity is computed for the ipsilateral IC by summing weighted rate-azimuth curves2 for all units in our sample of ITD-sensitive neurons. Assuming symmetry with respect to the sagittal plane in the neural activation patterns produced by sound sources located on opposite sides of the midline, the total population activity in the contralateral IC is derived by reflecting the ipsilateral population rate signal about the midline. The model output (hemispheric difference signal) is computed as the difference in population activity between the two ICs.
The main panel in Figure 6B shows the hemispheric difference signal for the anechoic and reverberant conditions. In all conditions, the hemispheric difference signal varies monotonically with stimulus azimuth. With increasing reverberation, the hemispheric difference signal becomes more compressed, as expected from the rate compression observed in individual units, and consistent with the main trend in the behavioral responses. However, for both anechoic and reverberant conditions, the hemispheric difference signal saturates more quickly for lateral source positions than the human laterality judgments (see Discussion).
We quantified compression of the hemispheric difference signal using the relative range. Figure 6C shows the relative range of the hemispheric difference signal (open circles) plotted as a function of the decoder integration time i.e., the time interval from stimulus onset over which we averaged the individual neuron’s firing rates to compute the hemispheric difference signal. The data are well fit by a single decaying exponential (solid curves). Because directional sensitivity is better during the earlier segment of a reverberant stimulus (Fig. 3E), the relative range is initially close to 1 and decreases over time, consistent with the buildup of reverberant energy in the stimulus.
The symbols at the right of Fig. 6C show the relative range of the lateralization estimates for individual human subjects. Both perceptual and decoder compressions show a similar dependence on reverberation strength. Quantitatively, the behavioral estimates show less compression than the hemispheric difference signal computed from the full neural response (0–400 ms), but more compression than that computed from only the early response (0–50 ms), suggesting that listener’s lateralization judgments are influenced by late-arriving stimulus energy. To the extent that listeners integrate information over early and ongoing response segments, onset dominance may reduce the effective contribution of the ongoing population response.
DISCUSSION
Our neurophysiological results show that the directional sensitivity of ITD-sensitive auditory midbrain neurons degrades over the duration of a reverberant stimulus, consistent with the buildup of reflected sound energy at a listener’s ears. We further find that onset dominance in temporal response patterns emphasizes the more reliable directional information in the early response, suggesting a role for this general feature of neural processing in improving directional sensitivity in reverberant environments. By comparing neural responses with human lateralization judgments, we find that the temporally integrated population rate response forms a possible neural substrate for robust sound localization in reverberation.
Dynamics of Directional Sensitivity in Reverberation
In a reverberant environment, reflections interfere with the direct sound arriving at a listener’s ears, causing the ear-input signals to become decorrelated. Thus, it is not surprising that we observed a more severe degradation in directional sensitivity with increasing reverberation for both single neurons in the auditory midbrain (Fig. 2D) and the cross correlation model (Fig. 4). However, the directional information in reverberation has a characteristic time course: it is relatively uncorrupted near the sound onset, before the arrival of reflections at a listener’s ears, and becomes more degraded as reverberation builds up over time (Fig. 3A–B). Our results show that neural directional sensitivity parallels this temporal pattern of cues in reverberation: Sensitivity is better during the early response than during the ongoing neural response (Fig. 3E).
The overall directional sensitivity computed from the average rate response will depend on the distribution of spiking activity over time. Since directional information is better near the stimulus onset, a beneficial processing strategy would be to give proportionally more weight to the response near the onset of a stimulus. This could be achieved by any mechanism that reduces responsiveness in the later portions of the stimulus. A majority of neurons in our population exhibited onset dominance in their temporal response patterns, where firing rates are initially high and decay over time. When directional sensitivity is computed by integrating spike activity over time, onset dominance is a basic mechanism for emphasizing the earliest activity periods, when directional information is most reliable.
The sound stimulus used in the present experiments was a sustained noise, hence had a single onset. Many natural sounds, including human speech and animal vocalizations are characterized by prominent amplitude modulations in the 3–7 Hz range (Houtgast and Steeneken, 1973; Singh and Theunissen, 2003), which functionally create multiple “onsets” over the duration of the stimulus. Indeed, the responses of IC neurons to sinusoidally amplitude modulated (SAM) sound stimuli typically show adaptation on every modulation cycle at low modulation frequencies (Krishna and Semple, 2000; Nelson and Carney, 2007; Rees and Moller, 1983). While onsets in natural sounds are thought to be crucial for speech reception in reverberant rooms (Longworth-Reed et al., 2009), they may also provide a listener with multiple “onset-dominated” epochs over which to integrate directional information and make localization judgments (so long as the reverberation time does not exceed the period of dominant amplitude modulations in the stimulus).
Physiologically, onset-dominance in the IC could be realized through any of several neural mechanisms, including synaptic depression (Wu et al., 2002), intrinsic dynamics of active membrane channels (Sivaramakrishnan and Oliver, 2001), delayed, long-lasting inhibition (Kuwada et al., 1989; McAlpine and Palmer, 2002; Nelson and Erulkar, 1963; Pecka et al., 2007; Tan and Borst, 2007) or adaptation already present in the inputs to the IC (Smith and Zwislocki, 1975). The present physiological data do not allow us to discriminate among these possible mechanisms.
Relationship between Onset Dominance and Echo Suppression
The ability of a listener to localize sounds accurately in reverberant environments is often attributed to the precedence effect, a phenomenon in which the perceived source location is dominated by the initial portion of a stimulus (Litovsky et al., 1999). Numerous studies have reported neurophysiological correlates of classic precedence phenomena in the IC (Fitzpatrick et al., 1999; Litovsky and Yin, 1998; Pecka et al., 2007; Spitzer et al., 2004; Tollin et al., 2004; Yin, 1994). The stimuli used in these studies consisted of a leading source (representing the direct sound) followed by a lagging source (representing a single acoustic reflection). Because most of these studies used very brief stimuli, the leading and lagging sounds did not overlap in time. Such conditions are an extreme oversimplification of realistic reverberation, in which thousands of reflections contribute to the energy at a listener’s ears over hundreds of milliseconds.
Typically, neurophysiological studies of the precedence effect report that responses to the lagging sound are suppressed over a range of delays between the leading and lagging sounds, consistent with the dominance of the leading sound in the perceived location. The present result suggest that onset dominance in neural responses helps provide a robust representation of the location of sound sources in reverberation when the neural response is averaged over much longer times than the separation between individual reflections. While there is a superficial similarity between onset dominance and echo suppression, the two sets of results are not comparable because we cannot isolate the response to individual reflections as done in studies of the precedence effect.
A possible dissociation between neural echo suppression and onset dominance is suggested by the effects of anesthesia. The time course of recovery from neural echo suppression is faster in unanesthetized compared to anesthetized animals (c.f. Tollin et al. 2004; Litovsky and Yin, 1998). In contrast, ongoing experiments in our laboratory suggest that the effects of reverberation on azimuth sensitivity are comparable in the IC of awake rabbit and anesthetized cat (Devore and Delgutte, 2008). Moreover, the dynamics of spike-rate adaptation, a possible mechanism underlying onset dominance appear not to be strongly affected by anesthesia in the IC (Ter-Mikaelian et al., 2007).
While robust encoding of ITD in reverberation and neural suppression of discrete echoes each embody the seminal notion of the “law of the first wavefront” (Wallach et al., 1949), they operate on different time scales. In fact, onset dominance and neural echo suppression may contribute independently to robust encoding of azimuth in reverberant environments. The neural mechanisms underlying echo suppression in transient stimuli undoubtedly affect the neural response in the early portion of reverberant stimuli. However, there is likely an additional process, operating over longer time scales, that integrates directional information over time, emphasizing the early, reliable spatial cues over ongoing cues that are more degraded by reverberation.
Other Factors Influencing Directional Sensitivity in Reverberation
Qualitatively, the effect of reverberation on neural responses is consistent with a cross-correlation model of binaural processing (Hancock and Delgutte, 2004; Yin et al., 1987), which predicts the average firing rate of IC neurons as a function of the effective IACC of the input signals (Fig. 3A). However, a quantitative comparison reveals that the predicted reduction in directional sensitivity is not correlated with the observed reduction, indicating that the model does a poor job at predicting directional sensitivity in reverberation. Moreover, the observed reduction in directional sensitivity was generally less than the predicted reduction (Fig. 4F), suggesting that additional mechanisms not included in the model provide neural robustness to reverberation. The difference between observed and predicted directional sensitivity was systematically related to onset dominance in neural temporal responses (Fig. 5B); however, the relation between onset dominance and model misprediction showed a lot of scatter, suggesting that additional factors beyond neural response dynamics play a role in the model’s shortcoming.
The cross-correlation model functionally reduces all processing of ear-input signals, including internal delay and reverberation, to changes in the effective interaural correlation. However, there is growing evidence that ITD-sensitive IC neurons receive convergent inputs from multiple brainstem coincidence detectors exhibiting different frequency and delay tuning (Fitzpatrick et al., 2000; McAlpine et al., 1998). Moreover, in addition to corrupting directional cues, reverberation also distorts the temporal envelopes of each ear-input signal. Temporal processing of stimulus envelope in the IC interacts with binaural processing in that manipulation of the stimulus envelope can cause changes in the firing rate of ITD-sensitive IC neurons even when IACC is unchanged (D’Angelo et al., 2003; Lane and Delgutte, 2005). Differences between model predictions and observed responses might be explained by differences between a single effective interaural correlation computation (as assumed in the model) and the actual computation performed by the IC cell on multiple inputs with different spectral, binaural, and temporal tuning characteristics.
Comparison to Psychophysics
The present results suggest that reverberation produces similar effects on the lateralization judgments of human listeners and on the directional sensitivity of IC neurons. A direct comparison of neural responses with human behavior requires explicit assumptions about how azimuth information is decoded from the rate responses of the neural population. Two basic classes of decoding models for sound lateralization have been analyzed: labeled-line models and hemispheric channel models. In labeled-line models (Fitzpatrick et al., 1997; Jeffress, 1948; Shackleton et al., 1992), the lateral position of a sound is determined by reading out the ITD corresponding to the centroid of activity in an array of neurons tuned to different ITDs. Such models require each tuned channel to transmit a label (i.e., the best ITD) to the decoder. In contrast, a hemispheric channel model determines the lateral position of a sound source by computing the difference of activity in two broadly tuned spatial channels, each representing subpopulations of neurons that preferentially respond to sound sources in one hemifield (Hancock, 2007; McAlpine et al., 2001; Stecker et al., 2005; van Bergeijk, 1962). Consistent with previous studies (Brand et al., 2002; Hancock and Delgutte, 2004; McAlpine et al., 2001), the majority of units in our population had monotonic rate-azimuth functions (Supp. Fig. 1C), with best delays outside the naturally-occurring range and almost exclusively in the contralateral hemifield (Supp. Fig. 1D), motivating our decision to implement a hemispheric channel decoder.
The model hemispheric difference signal was computed directly from the rate-azimuth curves measured in our sample of IC neurons. The range of the hemispheric difference signal decreased with increasing reverberation, mirroring the compression of human lateralization judgments (Fig. 6C). Ideally, human listeners would use only the information at the onset of the stimulus to make the lateralization judgment and would therefore be minimally affected by reverberation. The fact that lateralization judgments do show compression suggests that there may be an obligatory window of integration over which the lateral position is estimated. This possibility is intriguing, in that it suggests listeners may behave “suboptimally” given the available acoustic information. However, such behavior may be appropriate, considering that onset information can be unreliable due to masking by other sounds or internal noise. Thus, in everyday environments, optimal behavior may be to emphasize onsets, when detectable, but to also make use of ongoing information in case no onset information is available. Moreover, previous behavioral experiments have shown that human listeners are relatively insensitive to fast fluctuations in interaural correlation and appear to integrate binaural information over tens to hundreds of milliseconds when judging source direction (Grantham and Wightman, 1978). Psychophysical estimates of the length of the so-called “binaural temporal window” generally fall in the vicinity of 100 ms (Boehnke et al., 2002; Kollmeier and Gilkey, 1990). When we compared the human lateralization judgments to the hemispheric difference signal computed with different integration times (Fig. 6C), we found that decoder compression best matches perceptual compression for an integration window of 100–200 ms. To the extent that lateralization judgments result from the integration of population rate responses over time, onset dominance will emphasize the early stimulus segments during this integration, as was shown for individual units (Fig. 3C).
The azimuth dependence of the hemispheric difference signal was shallower at lateral azimuths than that of the human lateralization judgments (c.f. Fig. 6A–B). However, this result is very sensitive to model assumptions including the exact distribution of CFs and best ITDs, as well as the mapping between azimuth and ITD. Moreover, species differences may also play a role since we are comparing human psychophysical data with model predictions based on cat neural data.
Hemispheric channel models have been criticized due to the lack of anatomical and physiological evidence for this type of operation, with simpler, single hemisphere rate codes offered as an alternative (Joris and Yin, 2007). With the present data, we found that the inter-channel comparison was necessary to avoid non-monotonic responses at the most lateral source positions in the population rate response of each IC.
Theoretically, Jeffress-type models become more computationally powerful for animals with larger head sizes, including humans, while hemispheric decoding models work best for smaller animals such as cats (Harper and McAlpine, 2004). Because our neural data were not amenable to a straightforward implementation of a Jeffress-type decoding model for sound localization, we cannot say whether labeled-line models can explain lateralization performance in reverberation. However, our results show that hemispheric decoding models can indeed account for human lateralization in reverberant environments.
Conclusions
Our results show that reverberation degrades directional sensitivity both in single neurons and human listeners alike. Neural directional sensitivity is better during the earlier stimulus segments, when the signals at a listener’s ears are more reliable and less corrupted by reverberation. To the extent that listeners integrate directional information over time in estimating the position of a sound source, we have shown that onset dominance in neural responses enhances spatial cues that are most reliable, resulting in more robust estimates of source position. Overall, our findings suggest that robust encoding of directional information in the rate responses of subcortical auditory neurons is sufficient to account for the lateralization performance of human listeners.
EXPERIMENTAL PROCEDURES
Surgical Preparation
Healthy, adult cats were anesthetized with dial-in-urethane (75 mg/kg, i.p.) and prepared for acute single-unit recording from the auditory midbrain using surgical procedures described in Hancock and Delgutte (2004). All surgical and experimental procedures were approved by the Institute Animal Use and Care Committees at both the Massachusetts Eye and Ear Infirmary and the Massachusetts Institute of Technology.
Virtual Space Stimuli
Binaural room impulse responses (BRIRs) were simulated using the room-image method (Allen and Berkley, 1979; Shinn-Cunningham et al., 2001) for a pair of receivers separated by 12 cm slightly displaced from the center of a virtual room measuring 11×13×3 meters (Fig. 1A). The inter-receiver distance was chosen so that the range of ITDs in the direct sound spanned the range typically experienced by cats (±360 μs, Figure 1D). Because we did not include a model of the cat head in the simulations, the resulting BRIRs contained ITD but essentially no interaural level difference (ILD) cues. BRIRs were calculated for azimuths spanning the frontal hemifield (−90° to +90°) at distances of 1 and 3 m with respect to the midpoint of the receivers. Anechoic impulse responses were created by time-windowing the direct sound from the 1m reverberant BRIRs. Virtual auditory space stimuli were created by convolving the BRIRs with a 400-ms burst of exactly reproducible Gaussian broadband noise gated with 4-ms sin2 ramps (Fig. 1B).
Single Unit Recordings
Experimental procedures for recording activity from single units in the auditory midbrain were as described in Hancock and Delgutte (2004). When a single unit was isolated, we estimated its characteristic frequency (CF) using an automatic tracking procedure (Kiang and C. Moxon, 1974) and then determined the intensity threshold for diotic broadband noise. ITD-sensitivity for 200-ms broadband noise bursts (2/sec × 10 repeats) was characterized at ~15 dB above threshold. Typically, ITD was varied between ±2000μs in 200μs steps. Only ITD-sensitive units with low CFs (<2.5 kHz) were further studied with the virtual space stimuli, with responses for each of the three room conditions obtained in pseudorandom order (1/sec × 16 repeats at each azimuth).
Data Analysis
A rate-azimuth curve for each room condition was computed by averaging the number of spikes that occurred in a fixed temporal window, defined relative to stimulus onset, across all trials for each azimuth. Rate-azimuth curves were smoothed using a three point triangular smoothing filter having weights [1/6 2/3 1/6]. We computed average cumulative peristimulus time histograms (cPSTH) for each unit to obtain a metric of onset dominance in the response. Each 1 ms bin in the cPSTH represents the cumulative number of spikes up to the bin time in the anechoic PSTH. The cPSTH was computed over a 400 ms duration, with time zero corresponding to the first bin in the anechoic PSTH having an across-trial spike count distribution significantly different from that of spontaneous activity. Only azimuths that evoked mean firing rates ≥90% of the maximum rate across all azimuths were included in the average cPSTH in order to avoid including onset responses that often occur at unfavorable azimuths.
Single-Neuron Cross-Correlation Model
We used a cross-correlation model to predict reverberant rate-azimuth curves of IC units. For each unit, we fit the rate-ITD curve with a modified version of the Hancock and Delgutte (2004) cross-correlation model (Figure 4A). The original model used a parabolic function to transform IACC into firing rate. We modified this transformation to be a power function of the form:
where a, b, and p are free parameters (Coffey et al., 2006; Shackleton et al., 2005). This modification improved the model fits (as evaluated using R2).
To predict neural responses in reverberation, we first fit the six-parameter model to each unit’s rate-ITD curve using the lsqnonlin function in Matlab (The Mathworks, Natick, MA). We then refit the scaling parameters (a and b) to the anechoic rate-azimuth function (to compensate for differences in the duty cycle with which the measurements were made). Finally, we generated predictions of reverberant rate-azimuth curves by running the model with the appropriate virtual space stimuli as inputs. We only included units for which the goodness-of-fit (R2) for both rate-ITD and anechoic rate-azimuth data was at least 0.75 (8/36 units excluded).
Psychophysics
Four paid human subjects with normal hearing participated in the behavioral experiment. One of the four subjects failed the preliminary training procedure and was dismissed from the experiment. Experimental procedures were approved by the Boston University Charles River Campus Institutional Review Board.
Stimuli
BRIRs were created using the same methods and room characteristics as in the physiology experiments, except that the receivers were separated by 23 cm to achieve ITDs spanning the range typically encountered by a human (±690 μs). Virtual space stimuli were created by convolving the BRIRs with random 400-ms Gaussian lowpass noise bursts (4th order Butterworth filter with 2500-Hz cutoff) with 4-ms sin2 ramps.
Task
We used an acoustic pointing task to obtain a quantitative measure of stimulus laterality using the method of Best et al. (2007). Briefly, subjects adjusted the ILD of an acoustic pointer (200-Hz band noise centered at 3.0 kHz) until its perceived laterality matched that of a virtual space target. On each trial, the initial pointer ILD was randomly chosen from ±20 dB. The target and pointer were then played in alternation (500-ms interstimulus interval) until the subject indicated a match with a button press.
Data Analysis
We computed the mean ILD-match at each azimuth, for each condition, after rejecting outlying trials (defined as estimates more than ±3 standard deviations from the mean). We then fit sigmoid functions (using lsqnonlin in Matlab) to the individual subject responses and computed statistics using the fitted functions.
Acknowledgments
This work was supported by National Institutes of Health (NIH) Grants R01 DC002258 (BD), R01 DC05778-02 (BGSC), and core grant P30 DC005209 to Eaton Peabody Laboratory. S.D. was partially supported by NIH Grant T32 DC00038. We thank Connie Miller for surgical assistance and Lorraine Delhorne and Eric Larson for assistance with the behavioral experiments. Dr. Adrian K.C. Lee provided the ILD-pointer software and Dr. Jay Desloges provided the BRIR-simulation software. We additionally thank three anonymous reviewers who helped us to improve this manuscript.
Footnotes
Because they contain only a single binaural cue, the virtual space targets (and the ILD pointer) are generally perceived on an internal interaural axis and are not externalized outside the head. Hence, they are said to be lateralized instead of localized.
The weighting factors were used to adjust for slight differences between our empirical CF distribution and that found in a larger sample of low-frequency ITD-sensitive IC neurons (Hancock and Delgutte 2004). The weighting function was , where PHD (CF) is the lognormal distribution of CFs (with μ=6.5 and σ=0.31) fit to the Hancock and Delgutte (2004) data, and PPr es (CF) is the empirical CF distribution in our population. Our population contained proportionally fewer neurons around 500 Hz than the Hancock and Delgutte (2004) distribution.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Adams JC. Ascending projections to the inferior colliculus. J Comp Neurol. 1979;183:519–538. doi: 10.1002/cne.901830305. [DOI] [PubMed] [Google Scholar]
- Aitkin LM, Gates GR, Phillips SC. Responses of Neurons in the Inferior Colliculus to Variations in Sound-Source Azimuth. Journal of Neurophysiology. 1984;52:1–17. doi: 10.1152/jn.1984.52.1.1. [DOI] [PubMed] [Google Scholar]
- Albeck Y, Konishi M. Responses of neurons in the auditory pathway of the barn owl to partially correlated binaural signals. Journal of Neurophysiology. 1995;74:1689–1700. doi: 10.1152/jn.1995.74.4.1689. [DOI] [PubMed] [Google Scholar]
- Allen JB, Berkley DA. Image method for efficiently simulating small-room acoustics. J Acoust Soc Am. 1979;65:943–950. [Google Scholar]
- Beranek L. Concert Halls and Opera Houses. 2. New York: Springer-Verlag; 2004. [Google Scholar]
- Best V, Gallun FJ, Carlile S, Shinn-Cunningham BG. Binaural interference and auditory grouping. J Acoust Soc Am. 2007;121:1070–1076. doi: 10.1121/1.2407738. [DOI] [PubMed] [Google Scholar]
- Boehnke SE, Hall SE, Marquardt T. Detection of static and dynamic changes in interaural correlation. J Acoust Soc Am. 2002;112:1617–1626. doi: 10.1121/1.1504857. [DOI] [PubMed] [Google Scholar]
- Brand A, Behrand O, Marquardt T, McAlpine D, Grothe B. Precise inhibition is essential for microsecond interaural time difference coding. Nature. 2002;417:543–547. doi: 10.1038/417543a. [DOI] [PubMed] [Google Scholar]
- Coffey CS, Ebert J, Charles S, Marshall AF, Skaggs JD, Falk SE, Crocker WD, Pearson JM, Fitzpatrick DC. Detection of interaural correlation by neurons in the superior olivary complex, inferior colliculus and auditory cortex of the unanesthetized rabbit. Hearing Research. 2006;221:1–16. doi: 10.1016/j.heares.2006.06.005. [DOI] [PubMed] [Google Scholar]
- Colburn HS. Theory of binaural interaction based on auditory-nerve data. I. General strategy and preliminary results on interaural discrimination. J Acoust Soc Am. 1973;54:1458–1470. doi: 10.1121/1.1914445. [DOI] [PubMed] [Google Scholar]
- D’Angelo WR, Sterbing SJ, Ostapoff EM, Kuwada S. Effects of Amplitude Modulation on the Coding of Interaural Time Differences of Low-Frequency Sounds in the Inferior Colliculus. II. Neural Mechanisms. Journal of Neurophysiology. 2003;90:2827–2836. doi: 10.1152/jn.00269.2003. [DOI] [PubMed] [Google Scholar]
- Darwin CJ. Spatial hearing and perceiving sources. In: Yost WA, editor. Springer Handbook of Auditory Research: Auditory perception of sound sources. New York: Springer; 2008. [Google Scholar]
- Delgutte B, Joris PX, Litovsky RY, Yin TCT. Receptive Fields and Binaural Interactions for Virtual-Space Stimuli in the Cat Inferior Colliculus. J Neurophysiol. 1999;81:2833–2851. doi: 10.1152/jn.1999.81.6.2833. [DOI] [PubMed] [Google Scholar]
- Devore S, Delgutte B. Does spike rate adaptation mediate robust encoding of ITD in reverberation?. Paper presented at: Society for Neuroscience; Washington, DC. 2008. [Google Scholar]
- Fitzpatrick DC, Batra R, Stanford TR, Kuwada S. A neuronal population code for sound localization. Nature. 1997;388:871–874. doi: 10.1038/42246. [DOI] [PubMed] [Google Scholar]
- Fitzpatrick DC, Kuwada S, Batra R. Neural sensitivity to interaural time differences: beyond the Jeffress model. J Neurosci. 2000;20:1605–1615. doi: 10.1523/JNEUROSCI.20-04-01605.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fitzpatrick DC, Kuwada S, Kim DO, Parham K, Batra R. Responses of neurons to click-pairs as simulated echoes: Auditory nerve to auditory cortex. The Journal of the Acoustical Society of America. 1999;106:3460–3472. doi: 10.1121/1.428199. [DOI] [PubMed] [Google Scholar]
- Geisler CD, Rhode WS, Hazelton DW. Responses of inferior colliculus neurons in the cat to binaural acoustic stimuli having wide-band spectra. J Neurophysiol. 1969;32:960–974. doi: 10.1152/jn.1969.32.6.960. [DOI] [PubMed] [Google Scholar]
- Giguere C, Abel SM. Sound localization: effects of reverberation time, speaker array, stimulus frequency, and stimulus rise/decay. J Acoust Soc Am. 1993;94:769–776. doi: 10.1121/1.408206. [DOI] [PubMed] [Google Scholar]
- Goldberg JM, Brown PB. Response of binaural neurons of dog superior olivary complex to dichotic tonal stimuli: some physiological mechanisms of sound localization. J Neurophysiol. 1969;32:613–636. doi: 10.1152/jn.1969.32.4.613. [DOI] [PubMed] [Google Scholar]
- Grantham DW, Wightman FL. Detectability of varying interaural temporal differences. J Acoust Soc Am. 1978;63:511–523. doi: 10.1121/1.381751. [DOI] [PubMed] [Google Scholar]
- Grothe B, Sanes DH. Synaptic inhibition influences the temporal coding properties of medial superior olivary neurons: an in vitro study. J Neurosci. 1994;14:1701–1709. doi: 10.1523/JNEUROSCI.14-03-01701.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hancock KE. A physiologically-based population rate code for interaural time differences predicts bandwidth-dependent lateralization. In: Verhey J, editor. Hearing - from sensory processing to perception. Berlin: Springer Verlag; 2007. pp. 389–398. [Google Scholar]
- Hancock KE, Delgutte B. A Physiologically Based Model of Interaural Time Difference Discrimination. J Neurosci. 2004;24:7110–7117. doi: 10.1523/JNEUROSCI.0762-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harper NS, McAlpine D. Optimal neural population coding of an auditory spatial cue. Nature. 2004;430:682–686. doi: 10.1038/nature02768. [DOI] [PubMed] [Google Scholar]
- Hartmann WM. Localization of sound in rooms. Journal of the Acoustical Society of America. 1983;74:1380–1391. doi: 10.1121/1.390163. [DOI] [PubMed] [Google Scholar]
- Hartmann WM, Rakerd B, Koller A. Binaural Coherence in Rooms. Acta Acustica United With Acustica. 2005;91:451–462. [Google Scholar]
- Houtgast T, Steeneken HJM. The modulation transfer function in room acoustics as a predictor of speech intelligibility. Acustica. 1973;28:66–73. [Google Scholar]
- Huisman WHT, Attenborough K. Reverberation and attenuation in a pine forest. The Journal of the Acoustical Society of America. 1991;90:2664–2677. [Google Scholar]
- Ingham NJ, McAlpine D. Spike-Frequency Adaptation in the Inferior Colliculus. J Neurophysiol. 2004;91:632–645. doi: 10.1152/jn.00779.2003. [DOI] [PubMed] [Google Scholar]
- Jeffress LA. A place theory of sound localization. J Comp Physiol Psychol. 1948;41:35–39. doi: 10.1037/h0061495. [DOI] [PubMed] [Google Scholar]
- Joris P, Yin TC. A matter of time: internal delays in binaural processing. Trends Neurosci. 2007;30:70–78. doi: 10.1016/j.tins.2006.12.004. [DOI] [PubMed] [Google Scholar]
- Joris PX. Interaural time sensitivity dominated by cochlea-induced envelope patterns. J Neurosci. 2003;23:6345–6350. doi: 10.1523/JNEUROSCI.23-15-06345.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiang NYS, Moxon CE. Tails of tuning curves of auditory-nerve fibers. Journal of the Acoustical Society of America. 1974;55:620–630. doi: 10.1121/1.1914572. [DOI] [PubMed] [Google Scholar]
- Kidd G, Jr, Arbogast TL, Mason CR, Gallun FJ. The advantage of knowing where to listen. J Acoust Soc Am. 2005;118:3804–3815. doi: 10.1121/1.2109187. [DOI] [PubMed] [Google Scholar]
- Kollmeier B, Gilkey RH. Binaural forward and backward masking: evidence for sluggishness in binaural detection. J Acoust Soc Am. 1990;87:1709–1719. doi: 10.1121/1.399419. [DOI] [PubMed] [Google Scholar]
- Krishna BS, Semple MN. Auditory temporal processing: responses to sinusoidally amplitude-modulated tones in the inferior colliculus. J Neurophysiol. 2000;84:255–273. doi: 10.1152/jn.2000.84.1.255. [DOI] [PubMed] [Google Scholar]
- Kuwada S, Batra R, Stanford TR. Monaural and binaural response properties of neurons in the inferior colliculus of the rabbit: effects of sodium pentobarbital. J Neurophysiol. 1989;61:269–282. doi: 10.1152/jn.1989.61.2.269. [DOI] [PubMed] [Google Scholar]
- Kuwada S, Stanford TR, Batra R. Interaural phase sensitive units in the inferior colliculus of the unanesthetized rabbit. Effects of changing frequency. Journal of Neurophysiology. 1987;57:1338–1360. doi: 10.1152/jn.1987.57.5.1338. [DOI] [PubMed] [Google Scholar]
- Kuwada S, Yin TC. Binaural interaction in low-frequency neurons in inferior colliculus of the cat. I. Effects of long interaural delays, intensity, and repetition rate on interaural delay function. J Neurophysiol. 1983;50:981–999. doi: 10.1152/jn.1983.50.4.981. [DOI] [PubMed] [Google Scholar]
- Lane CC, Delgutte B. Neural correlates and mechanisms of spatial release from masking: single-unit and population responses in the inferior colliculus. J Neurophysiol. 2005:1180–1198. doi: 10.1152/jn.01112.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Litovsky RY, Colburn HS, Yost WA, Guzman SJ. The precedence effect. The Journal of the Acoustical Society of America. 1999;106:1633–1654. doi: 10.1121/1.427914. [DOI] [PubMed] [Google Scholar]
- Litovsky RY, Yin TCT. Physiological Studies of the Precedence Effect in the Inferior Colliculus of the Cat. I. Correlates of Psychophysics. J Neurophysiol. 1998;80:1285–1301. doi: 10.1152/jn.1998.80.3.1285. [DOI] [PubMed] [Google Scholar]
- Longworth-Reed L, Brandewie E, Zahorik P. Time-forward speech intelligibility in time-reversed rooms. J Acoust Soc Am. 2009;125:EL13–EL19. doi: 10.1121/1.3040024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macpherson EA, Middlebrooks JC. Listener weighting of cues for lateral angle: The duplex theory of sound localization revisited. J Acoust Soc Am. 2002;111:2219–2236. doi: 10.1121/1.1471898. [DOI] [PubMed] [Google Scholar]
- McAlpine D, Jiang D, Palmer AR. A neural code for low-frequency sound localization in mammals. Nature Neuroscience. 2001;4:396–401. doi: 10.1038/86049. [DOI] [PubMed] [Google Scholar]
- McAlpine D, Jiang D, Shackleton TM, Palmer AR. Convergent Input from Brainstem Coincidence Detectors onto Delay-Sensitive Neurons in the Inferior Colliculus. J Neurosci. 1998;18:6026–6039. doi: 10.1523/JNEUROSCI.18-15-06026.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McAlpine D, Palmer AR. Blocking GABAergic Inhibition Increases Sensitivity to Sound Motion Cues in the Inferior Colliculus. J Neurosci. 2002;22:1443–1453. doi: 10.1523/JNEUROSCI.22-04-01443.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson PC, Carney LH. Neural rate and timing cues for detection and discrimination of amplitude-modulated tones in the awake rabbit inferior colliculus. J Neurophysiol. 2007;97:522–539. doi: 10.1152/jn.00776.2006.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson PG, Erulkar SD. Synaptic Mechanisms of Excitation and Inhibition in the Central Auditory Pathway. J Neurophysiol. 1963;26:908–923. doi: 10.1152/jn.1963.26.6.908. [DOI] [PubMed] [Google Scholar]
- Nuding SC, Chen GD, Sinex DG. Monaural response properties of single neurons in the chinchilla inferior colliculus. Hear Res. 1999;131:89–106. doi: 10.1016/s0378-5955(99)00023-4. [DOI] [PubMed] [Google Scholar]
- Oliver DL, Beckius GE, Shneiderman A. Axonal projections from the lateral and medial superior olive to the inferior colliculus of the cat: a study using electron microscopic autoradiography. J Comp Neurol. 1995;360:17–32. doi: 10.1002/cne.903600103. [DOI] [PubMed] [Google Scholar]
- Pecka M, Zahn TP, Saunier-Rebori B, Siveke I, Felmy F, Wiegrebe L, Klug A, Pollak GD, Grothe B. Inhibiting the Inhibition: A Neuronal Network for Sound Localization in Reverberant Environments. J Neurosci. 2007;27:1782–1790. doi: 10.1523/JNEUROSCI.5335-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rakerd B, Hartmann WM. Localization of noise in a reverberant environment. In: Collet L, editor. Auditory signal processing: Physiology, Psychophysics, and models. Springer-Verlag; 2005. pp. 348–354. [Google Scholar]
- Rees A, Moller AR. Responses of neurons in the inferior colliculus of the rat to AM and FM tones. Hear Res. 1983;10:301–330. doi: 10.1016/0378-5955(83)90095-3. [DOI] [PubMed] [Google Scholar]
- Rees A, Sarbaz A, Malmierca MS, Le Beau FE. Regularity of firing of neurons in the inferior colliculus. J Neurophysiol. 1997;77:2945–2965. doi: 10.1152/jn.1997.77.6.2945. [DOI] [PubMed] [Google Scholar]
- Rose JE, Gross NB, Geisler CD, Hind JE. Some neural mechanisms in the inferior colliculus of the cat which may be relevant to localization of a sound source. J Neurophysiol. 1966;29:288–314. doi: 10.1152/jn.1966.29.2.288. [DOI] [PubMed] [Google Scholar]
- Sakai H, Sato S-i, Ando Y. Orthogonal acoustical factors of sound fields in a forest compared with those in a concert hall. J Acoust Soc Am. 1998;104:1491–1497. [Google Scholar]
- Scott LL, Mathews PJ, Golding NL. Posthearing Developmental Refinement of Temporal Processing in Principal Neurons of the Medial Superior Olive. J Neurosci. 2005;25:7887–7895. doi: 10.1523/JNEUROSCI.1016-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shackleton TM, Arnott RH, Palmer AR. Sensitivity to Interaural Correlation of Single Neurons in the Inferior Colliculusof Guinea Pigs. JARO - Journal of the Association for Research in Otolaryngology. 2005;6:244–259. doi: 10.1007/s10162-005-0005-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shackleton TM, Meddis R, Hewitt MJ. Across frequency integration in a model of lateralization. J Acoust Soc Am. 1992;91:2276–2279. [Google Scholar]
- Shinn-Cunningham BG. Object-based auditory and visual attention. Trends Cogn Sci. 2008;12:182–186. doi: 10.1016/j.tics.2008.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shinn-Cunningham BG, Desloge JG, Kopco N. Empirical and modeled acoustic transfer functions in a simple room: Effects of distance and direction. Paper presented at: 2001 IEEE Workshop on Applications of Signal Prcessing to Audio and Acoustics; New Pfaltz, New York. 2001. [Google Scholar]
- Shinn-Cunningham BG, Kawakyu K. Neural representation of source direction in reverberant space. Paper presented at: 2003 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics; New Pfaltz, NY. 2003. [Google Scholar]
- Shinn-Cunningham BG, Kopco N, Martin TJ. Localizing nearby sound sources in a classroom: Binaural room impulse responses. J Acoust Soc Am. 2005a;117:3100–3115. doi: 10.1121/1.1872572. [DOI] [PubMed] [Google Scholar]
- Shinn-Cunningham BG, Lin IF, Streeter T. Trading directional accuracy for realism. Paper presented at: Human-Computer Interaction International/1st International Conference on Virtual Reality.2005b. [Google Scholar]
- Singh NC, Theunissen FE. Modulation spectra of natural sounds and ethological theories of auditory processing. J Acoust Soc Am. 2003;114:3394–3411. doi: 10.1121/1.1624067. [DOI] [PubMed] [Google Scholar]
- Sivaramakrishnan S, Oliver DL. Distinct K currents result in physiologically distinct cell types in the inferior colliculus of the rat. J Neurosci. 2001;21:2861–2877. doi: 10.1523/JNEUROSCI.21-08-02861.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith PH. Structural and functional differences distinguish principal from nonprincipal cells in the guinea pig MSO slice. J Neurophysiol. 1995;73:1653–1667. doi: 10.1152/jn.1995.73.4.1653. [DOI] [PubMed] [Google Scholar]
- Smith RL, Zwislocki JJ. Short-term adaptation and incremental responses of single auditory-nerve fibers. Biol Cybernetics. 1975;17:169–182. doi: 10.1007/BF00364166. [DOI] [PubMed] [Google Scholar]
- Spitzer MW, Bala ADS, Takahashi TT. A Neuronal Correlate of the Precedence Effect Is Associated With Spatial Selectivity in the Barn Owl’s Auditory Midbrain. J Neurophysiol. 2004;92:2051–2070. doi: 10.1152/jn.01235.2003. [DOI] [PubMed] [Google Scholar]
- Stecker GC, Harrington IA, Middlebrooks JC. Location coding by opponent neural populations in the auditory cortex. PLoS Biol. 2005;3:e78. doi: 10.1371/journal.pbio.0030078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stillman RD. Characteristic delay neurons in the inferior colliculus of the kangaroo rat. Exp Neurol. 1971a;32:404–412. doi: 10.1016/0014-4886(71)90007-0. [DOI] [PubMed] [Google Scholar]
- Stillman RD. Pattern Responses of Low-Frequency Inferior Colliculus Neurons. Experimental Neurology. 1971b;33:432–440. doi: 10.1016/0014-4886(71)90034-3. [DOI] [PubMed] [Google Scholar]
- Svirskis G, Kotak V, Sanes DH, Rinzel J. Sodium along with low-threshold potassium currents enhance coincidence detection of subthreshold noisy signals in MSO neurons. J Neurophysiol. 2004;91:2465–2473. doi: 10.1152/jn.00717.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan ML, Borst JGG. Comparison of Responses of Neurons in the Mouse Inferior Colliculus to Current Injections, Tones of Different Durations, and Sinusoidal Amplitude-Modulated Tones 10.1152/jn.00174.2007. J Neurophysiol. 2007;98:454–466. doi: 10.1152/jn.00174.2007. [DOI] [PubMed] [Google Scholar]
- Ter-Mikaelian M, Sanes DH, Semple MN. Transformation of Temporal Properties between Auditory Midbrain and Cortex in the Awake Mongolian Gerbil. J Neurosci. 2007;27:6091–6102. doi: 10.1523/JNEUROSCI.4848-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tollin DJ, Populin LC, Yin TCT. Neural Correlates of the Precedence Effect in the Inferior Colliculus of Behaving Cats. J Neurophysiol. 2004;92:3286–3297. doi: 10.1152/jn.00606.2004. [DOI] [PubMed] [Google Scholar]
- van Bergeijk WA. Variation on a Theme of Bekesy: A Model of Binaural Interaction. The Journal of the Acoustical Society of America. 1962;34:1431–1437. [Google Scholar]
- Wallach H, Newman EB, Rosenzweig MR. The precedence effect in sound localization. J Am Psychol. 1949;57:315–336. [PubMed] [Google Scholar]
- Wightman FL, Kistler DJ. The dominant role of low-frequency interaural time differences in sound localization. The Journal of the Acoustical Society of America. 1992;91:1648–1661. doi: 10.1121/1.402445. [DOI] [PubMed] [Google Scholar]
- Wu SH, Ma CL, Sivaramakrishnan S, Oliver DL. Synaptic modification in neurons of the central nucleus of the inferior colliculus. Hear Res. 2002;168:43–54. doi: 10.1016/s0378-5955(02)00375-1. [DOI] [PubMed] [Google Scholar]
- Yin TC, Chan JC. Interaural time sensitivity in medial superior olive of cat. J Neurophysiol. 1990;64:465–488. doi: 10.1152/jn.1990.64.2.465. [DOI] [PubMed] [Google Scholar]
- Yin TC, Chan JC, Carney LH. Effects of interaural time delays of noise stimuli on low-frequency cells in the cat’s inferior colliculus. III. Evidence for cross-correlation. J Neurophysiol. 1987;58:562–583. doi: 10.1152/jn.1987.58.3.562. [DOI] [PubMed] [Google Scholar]
- Yin TC, Chan JC, Irvine DR. Effects of interaural time delays of noise stimuli on low-frequency cells in the cat’s inferior colliculus. I. Responses to wideband noise. J Neurophysiol. 1986;55:280–300. doi: 10.1152/jn.1986.55.2.280. [DOI] [PubMed] [Google Scholar]
- Yin TCT. Physiological correlates of the precedence effect and summing localization in the inferior colliculus of the cat. J Neurosci. 1994;14:5170–5186. doi: 10.1523/JNEUROSCI.14-09-05170.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]