Intermolecular electrostatic energies using density fitting

Abstract

A method is presented to calculate the electron-electron and nuclear-electron intermolecular Coulomb interaction energy between two molecules by separately fitting the unperturbed molecular electron density of each monomer. This method is based on the variational Coulomb fitting method which relies on the expansion of the ab initio molecular electron density in site-centered auxiliary basis sets. By expanding the electron density of each monomer in this way the integral expressions for the intermolecular electrostatic calculations are simplified, lowering the operation count as well as the memory usage. Furthermore, this method allows the calculation of intermolecular Coulomb interactions with any level of theory from which a one-electron density matrix can be obtained. Our implementation is initially tested by calculating molecular properties with the density fitting method using three different auxiliary basis sets and comparing them to results obtained from ab initio calculations. These properties include dipoles for a series of molecules, as well as the molecular electrostatic potential and electric field for water. Subsequently, the intermolecular electrostatic energy is tested by calculating ten stationary points on the water dimer potential-energy surface. Results are presented for electron densities obtained at four different levels of theory using two different basis sets, fitted with three auxiliary basis sets. Additionally, a one-dimensional electrostatic energy surface scan is performed for four different systems (H₂O dimer, Mg²⁺–H₂O, Cu⁺–H₂O, and n-methyl-formamide dimer). Our results show a very good agreement with ab initio calculations for all properties as well as interaction energies.

I. INTRODUCTION

The accurate evaluation of intermolecular interactions has been a field of intense study for some time. Several decomposition methods have been proposed in order to gain a deeper understanding of these interactions and their individual components.^1–12 The results obtained from these methods may be used for the development of empirical force fields for biomolecular simulations.^13,14 One of the most important contributions that is obtained from these decompositions is the electrostatic interaction, since it accounts for a large fraction of the interaction energy.¹⁴

In almost all decomposition methods the electronic electrostatic interaction is represented as a Coulomb interaction between two unperturbed monomer charge distributions, ρ^A and ρ^B,

$$E_{\text{Coul}}={\displaystyle \iint \frac{{\rho }^A(r_A){\rho }^B(r_B)}{\left|r_A-r_B\right|}d{r}_{A}d{r}_B.}$$ (1)

Historically, Eq. (1) has been approximated by using a multipole expansion, in which the Coulomb operator |r^A−r^B|⁻¹ is expanded in a Taylor series.¹⁵ The original molecular-centered expansion has been largely superseded by a distributed multipole expansion in terms of specific atomic or site contributions, due to its better convergence properties.^14,16,17 In order to employ this expression, the atomic or site-specific multipolar moments need to be determined by partitioning the wave function or the electronic density. A disadvantage of the multipolar expansion is that this approximation neglects the charge penetration effects which may be substantial at short range. This shortcoming may be overcome to an extent by using damping functions that correct the intermolecular interaction energy.^18,19

Equation (1) can also be solved without approximations with either numerical or analytical procedures. Gavezzotti has proposed a method that relies on the direct numerical integration over molecular electron density.²⁰ This method has been slightly modified by Ma and Politzer and employed for the calculation of electrostatic as well as induction intermolecular interaction energies.²¹ One disadvantage of these methods is that they require the generation of three-dimensional grids for the calculations which makes them computationally expensive and may result in numerical artifacts due to the finite nature of the grid. On the other hand, several methods that solve Eq. (1) analytically have also been proposed. These methods are used in the Morokuma-Kitaura decomposition,⁵ the constrained space-orbital variation (CSOV) method,⁶ and the symmetry-adapted perturbation theory (SAPT),⁸ among others.²² However, these methods are also computationally expensive since they involve the expansion of the density in terms of products of atomic orbitals leading to an order O(N⁴) operation.

As explained above, Eq. (1) may be approximated with a multipolar expansion that requires the partitioning of the wave function or the electronic density. The partitioning of electron density has been a field of intense research and a variety of methods have been proposed. Bader’s atoms in molecules (AIM) method divides the electron density into atomic basins which are defined as discrete regions in space that satisfy the boundary condition of zero flux.^23–25 The stockholder’s partitioning method proposed by Hirshfeld^26,27 divides the molecular electron density at each point into atomic contributions in proportion to their respective contributions to the promolecule density at that point. The atomic multipole moments may be determined for either of these decomposition methods by numerical integration.^28–30

Hansen and Coppens proposed a method for the partitioning of experimental electron density where the density in the crystal is modeled by a superposition of aspherical nucleus-centered pseudoatoms represented by Slater functions multiplied by spherical harmonics.³¹ In this method the electronic density is fitted by minimizing the self-overlap of the difference between the experimental and modeled densities. Atomic multipoles can be extracted from this fit. Similarly, the asymptotic density model (ADM) expands the electron density in atomic densities. This method employs Slater functions fitted using the molecular electrostatic potential from which cumulative atomic multipole moments are calculated.³²

Another method to partition the density is based on fitting the molecular electron density using site-centered auxiliary basis functions (generally centered on atoms).³³ In the early eighties, Hall and co-workers proposed using the density fitting (DF) method for the calculation of molecular properties.^34–37 They showed that by fitting the density in this way, molecular properties such as atomic moments may be calculated.

The DF procedure has been employed in many density-functional theory (DFT) programs for a very different purpose. This method has been shown to provide a way to avoid the costly calculation of four-center integrals.³⁸ Much research has been done in this area for the development of auxiliary basis sets for the fitting of the electron density, as well as of recursion algorithms to solve the required integrals.^39–42 Recently, this method has been extended to Hartree-Fock (HF) and post-HF methods to increase the computational speed.^43–47

In this contribution we present an implementation of the DF method for the determination of electron-electron and nuclear-electron intermolecular electrostatic interactions by separately fitting the unperturbed electron densities of the interacting monomers. The use of this method provides the advantage that the calculations are grid-free. Moreover, better accuracy may be obtained by increasing the size of the auxiliary basis set (ABS) used for the fit, or by including extra fitting sites such as bond midpoints. The use of the DF method results in a reduction in the order of the integral operation from O(N⁴) to O(N²). Furthermore, the DF method allows the calculation of intermolecular Coulomb interactions for electronic densities calculated from virtually any wave function for which a relaxed one-electron density matrix is available. Also, the accurate determination of Coulomb interactions requires the accurate determination of nuclear-electron interactions. We explore the accuracy of calculating the nuclear-electron interaction using the DF method, which to our knowledge has not been systematically investigated.

Initially, we test our implementation by calculating the molecular dipole moments for several molecules as well as the electrostatic potential and electric field for the water molecule with three different ABS. Subsequently, we present the results for the determination of the electrostatic interaction energy for ten water dimers^48,49 and compare these results with the exact values calculated with CSOV and SAPT.⁴⁹ Additionally, the penetration effects are tested by calculating one-dimensional electrostatic energy surface scans for four different systems.

II. METHODS

In this section we present the theory and computational details employed in the present study. In Sec. II A we provide a brief explanation of the density fitting method and its implementation. Subsequently, in Sec. II B we present the description of the intermolecular formalism based on the density fitting method. Finally, in Sec. II C we describe the particular details of the calculations.

A. Density fitting

As explained in Sec. I, the use of ABS for density fitting has been a field of intense study. This method relies on the use of auxiliary basis functions to expand the molecular electron density. Briefly, the electron density may be fitted by minimizing the Coulomb self-interaction energy of the error:^38–41

$$E_2=\frac{1}{2}{\displaystyle \iint \frac{[\rho (r_1)-\tilde{\rho }(r_1)][\rho (r_2)-\tilde{\rho }(r_2)]}{\left|r_1-r_2\right|}d{r}_{1}d{r}_2,}$$ (2)

where the approximate density ρ̃(r) is expanded in primitive Cartesian Gaussian functions

$$\tilde{\rho }(r)={\displaystyle \sum _k{x}_{k}k(r).}$$ (3)

Inserting Eq. (2) into Eq. (1) and using the linear combination of atomic orbitals (LCAO) expansion for the density, $\rho (r)={\displaystyle {\sum }_{\mu \nu }{P}_{\mu \nu }}{\varphi }_{\mu }(r){\varphi }_{\nu }^{*}(r)$ (Ref. ⁵⁰), we obtain

$$\begin{array}{cc}{E}_2=& \frac{1}{2}{\displaystyle \sum _{\mu ,\nu }{\displaystyle \sum _{\sigma ,\tau }{P}_{\mu \nu }{P}_{\sigma \tau }\langle \mu \nu \left|\right|\sigma \tau \rangle -{\displaystyle \sum _l{x}_l{\displaystyle \sum _{\mu ,\nu }{P}_{\mu \nu }\langle \mu \nu \left|\right|l\rangle }}}}\\ & +\frac{1}{2}{\displaystyle \sum _k{\displaystyle \sum _l{x}_k{x}_l\langle k\left|\right|l\rangle .}}\hfill \end{array}$$ (4)

By minimizing Eq. (4) with respect to the expansion coefficients x_l, a linear system of equations is obtained:

$$\frac{\partial E_2}{\partial x_l}=-{\displaystyle \sum _{\mu ,\nu }{P}_{\mu \nu }\langle \mu \nu \left|\right|l\rangle +{\displaystyle \sum _k{x}_k\langle k\left|\right|l\rangle ,}}$$ (5)

which may be used for the determination of the coefficients

$$\mathbf{X}={\mathbf{A}}^{-1}\mathbf{b},$$ (6)

where b_l=∑_μ,νP_μ,ν〈μ,ν||l〉 and A_kl=〈k||l.

These expressions have been implemented by the authors in a FORTRAN 90 code developed for the present study. All the required integrals are calculated using the McMurchie-Davidson recursions.⁵¹ Since A is symmetric and positive definite it may be diagonalized to obtain its inverse. In this case we employ a modification of the matrix inverse similar to a singular value decomposition (SVD) procedure⁵² by setting the inverse of the eigenvalue to zero if it is below a certain cutoff. If the cutoff for the eigenvalues is set too high, some details of the electron density may be lost. On the other hand, if the threshold is too low, numerical instabilities may become a problem.

As explained above, the auxiliary fitting functions are generally centered only on atoms for the fitting procedure. However, since we are interested in investigating the accuracy of this method, in the present implementation the ABS used for the fitting procedure may be centered on alternate sites (such as bond midpoints) in addition to the atomic sites.³⁶

B. Intermolecular interactions

In order to calculate the intermolecular Coulomb interaction between two molecules it is necessary to determine the nuclear-nuclear (N-N), nuclear-electron (N-e), and electron-electron (e-e) contributions to the Coulomb energy^53,54

$$E_{\text{Intermol}}=E_{N-N}+E_{N-e}+E_{e-e}.$$ (7)

By making use of the approximate molecular electron density [Eq. (3)] we can calculate the intermolecular Coulomb energy as

$$\begin{array}{cc}{E}_{\text{Intermol}}=& \frac{Z_A{Z}_B}{r_{AB}}+{\displaystyle \int \frac{Z_A{\tilde{\rho }}^B(r_B)}{r_{AB}}dr+{\displaystyle \int \frac{Z_B{\tilde{\rho }}^A(r_A)}{r_{AB}}dr}}\\ & +{\displaystyle \int \frac{{\tilde{\rho }}^A(r_A){\tilde{\rho }}^B(r_B)}{r_{AB}}dr,}\hfill \end{array}$$ (8)

where Z_A represents the nuclei on molecule A, ρ̃^A represents the approximate density of molecule A, Z_B represents the nuclei on molecule B, and ρ̃^B represents the approximate density of molecule B.

Thus, the total intermolecular Coulomb interaction E_Intermol can be calculated by separately fitting the unperturbed electron density of each monomer to obtain the approximate electron densities, ρ̃^A and ρ̃^B. Once the approximate densities for each monomer have been determined, all terms in Eq. (8) may be calculated. It is important to note that while the least-squares-fitting procedure guarantees good e-e intramolecular energies, it does not guarantee good N-e, or intermolecular e-e interaction energies a priori.

Also, note that because of the definition for the approximate density [Eq. (3)], the integrals for the N-e and e-e terms are only one- and two-center integrals, respectively. This results in a simplification of Eq. (1) since the four-center integrals required for the electronic Coulomb interaction are effectively reduced to two-center ones, which results in an order O(N²) operation.

C. Computational details

Relaxed one-electron molecular densities for the test cases were obtained from ab initio calculations performed with HONDO 95, CADPAC, and GAUSSIAN 98.^54–57 The electron densities for the molecular properties were determined at the B3LYP/6-31G* level of theory. For the determinations of the ten water dimers, the calculations were performed at four levels of theory: B3LYP, MP2, MP3, and BD,^58–61 with the 6-31G* and augmented correlation-consistent polarized valence triple zeta (aug-cc-pVTZ) basis sets. Finally, the one-dimensional (1D) surface scans were performed at the B3LYP/6-31G* level only. All molecular geometries for the dipole moment tests were optimized at the B3LYP/6-311G* level. The geometries for the ten water dimers were taken from van Duijneveldt-van de Rijdt et al.⁴⁹

The calculated density matrices were used as input for the program described in Sec. II A. In all cases the density fit was done with three different auxiliary basis sets (ABS). The first two correspond to DGAUSS’ A1 and P1 Coulomb fitting ABS.^62,63 The final ABS, denoted as g03, was obtained from the automatic fitting utility from GAUSSIAN 03.⁶⁴ The g03 ABS were obtained by using the 6-311G** basis sets for the corresponding atoms.⁶⁵ Due to the extensive size of this last ABS, the f function orbitals were deleted and only the s and spd functions were retained. In the case of the P1 set, the original basis sets contain only s and d basis functions; in this study the d functions were expanded to represent spd shells.^62,63 In all cases a cutoff of 10⁻⁸ was employed for the SVD part of the fitting procedure.

The calculated ab initio molecular properties were determined with GAUSSIAN 98.⁵⁷ In all cases the density matrices for the DF determination of the molecular properties were obtained from the same calculation as the ab initio molecular properties. For the CSOV electrostatic analysis,⁶ all calculations were performed with a modified version of the HONDO 95 package.^54,55 All density matrices used for the density fit in the intermolecular calculations involving DFT densities were obtained from the HONDO 95 CSOV calculations. For the post-HF density matrices, namely MP2, MP3, and BD, all density matrices were calculated with the CADPAC package.^56,60,61

III. RESULTS

In this section we present the results obtained with the DF method compared with ab initio calculations. In Sec. III A several molecular properties calculated with ab initio and DF methods using the three ABS are discussed. This provides a test of the implementation of the DF formalism as well as of the quality of the ABS. Subsequently, the results for the intermolecular electrostatic interactions are presented in Sec. III B. Initially, we present the analysis of the error for the e-e and N-e intermolecular energies with respect to cutoff to investigate the accuracy of the fitting method. This is followed by the results for the determination of the intermolecular Coulomb energy for ten water dimers as well as for the one-dimensional surface scans.

A. Molecular properties

As explained in Sec. II A, the ABS used for the fitting procedure may be placed on atomic as well as other sites. In order to determine if the use of extra fitting sites improves the accuracy of the DF calculations, two sets of molecular dipole calculations were performed. In the first, only atomcentered ABS were employed. For the second set, additional fitting functions were placed on the bond midpoints (MP) involving hydrogen and heavy atoms.

Table I shows the calculated dipoles from the ab initio method as well as the ones obtained with the DF procedure using all three auxiliary basis sets for several molecules. On average the error between the ab initio and DF dipoles is less than 0.1 D for most of the molecules tested. A systematic improvement for the dipole is observed going from A1 to P1 and finally to g03 which is the biggest ABS tested. The inclusion of MP also results in more accurate results compared with the original ab initio calculations (see Table I). Note that the worst case for the calculated dipoles is CH₃CH using the A1 ABS where the DF result is 0.275 D below the ab initio one; the inclusion of MP improves this result.

TABLE I.

Dipole moments for several molecules.

	ab initio	A1	P1	g03	A1a	P1a	g03a
LiH	5.547	5.666	5.706	5.654	5.540	5.639	5.647
HF	1.843	1.873	1.818	1.835	1.842	1.847	1.841
CO	0.033	0.016	0.005	0.041	0.035	0.048	0.038
NH3	1.845	1.884	1.967	1.902	1.907	1.900	1.895
H2O	2.096	2.087	2.157	2.097	2.109	2.101	2.095
CH3SH	1.738	1.463	1.710	1.749	1.575	1.729	1.744
formate	0.820	0.845	0.856	0.813	0.827	0.787	0.823

^aUsing midpoints with heavy-atom ABS on H-X bonds. All dipole moments in Debye.

The electric field for water at a series of points from the nuclei is presented in Table II. As expected, the results show a systematic improvement with ABS size. Based on our previous results for the dipole moments, MP were employed for the DF electric-field determinations.

TABLE II.

Calculated electric field for water molecule from ab initio and density fitting (in au). All calculations were done at the B3LYP/6-31G* level. All density fitting calculations were done with midpoints using O ABS.

	ab initio			A1			P1			g03
Ctr. Coord.	X	Y	Z	X	Y	Z	X	Y	Z	X	Y	Z
(.1,.0,.0)	191.615	0.000	0.000	191.810	0.000	0.00019	1.702	0.000	0.000	191.620	0.000	0.000
(.0,.1,.0)	−0.227	191.831	0.000	−0.312	191.960	0.000	−0.251	191.857	0.000	−0.225	191.836	0.000
(.0,.0,.1)	−0.231	0.000	192.317	−0.313	0.000	192.452	−0.255	0.000	192.340	−0.228	0.000	191.316
(.0,.0,.2)	−0.284	0.000	41.836	−0.279	0.000	41.788	−0.275	0.000	41.845	−0.280	0.000	41.833
(.0,.0,.5)	−0.142	0.000	3.979	−0.147	0.000	3.993	−0.139	0.000	3.974	−0.139	0.000	3.974
(.0,.0,.7)	−0.081	0.000	1.070	−0.086	0.000	1.067	−0.079	0.000	1.069	−0.080	0.000	1.069
(.0,.0,1.0)	−0.043	0.000	0.119	−0.043	0.000	0.121	−0.043	0.000	0.121	−0.042	0.000	0.121
(.0,.0,1.5)	−0.019	0.000	−0.035	−0.019	0.000	−0.033	−0.019	0.000	−0.033	−0.019	0.000	−0.034
(.0,.0,2.0)	−0.010	0.000	−0.021	−0.010	0.000	−0.021	−0.010	0.000	−0.020	−0.010	0.000	−0.021
(.0,.0,3.0)	−0.004	0.000	−0.005	−0.003	0.000	−0.005	−0.003	0.000	−0.005	−0.003	0.000	−0.005

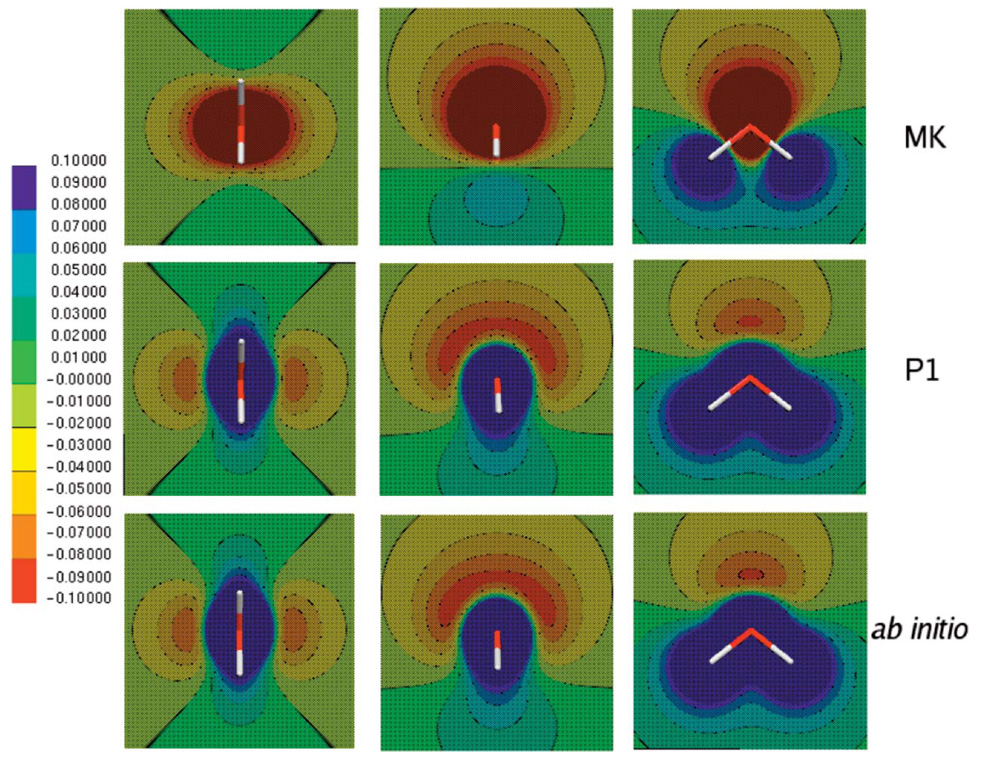
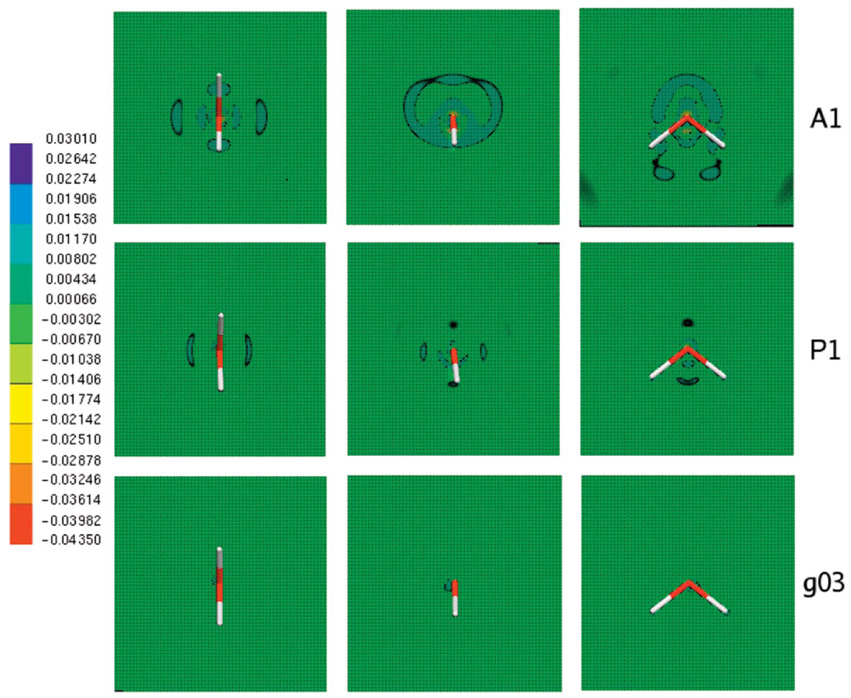
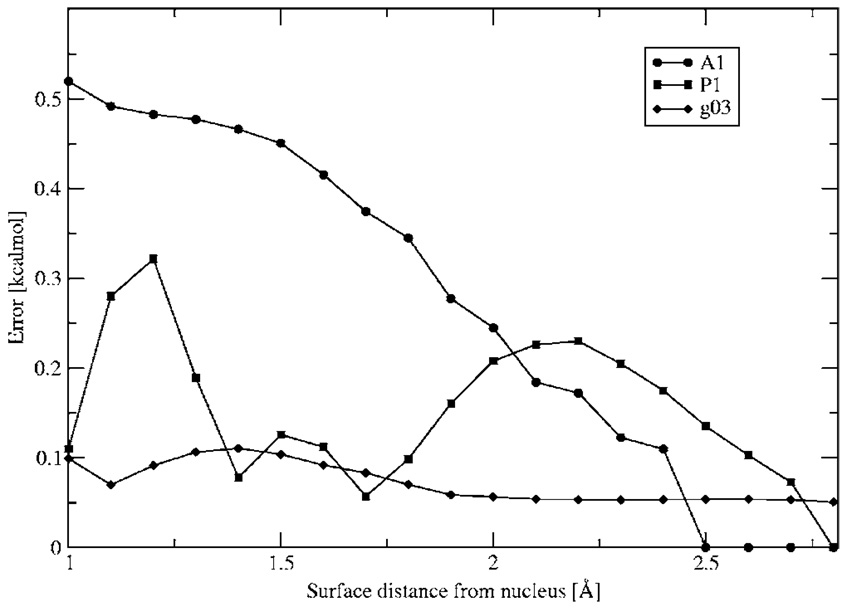
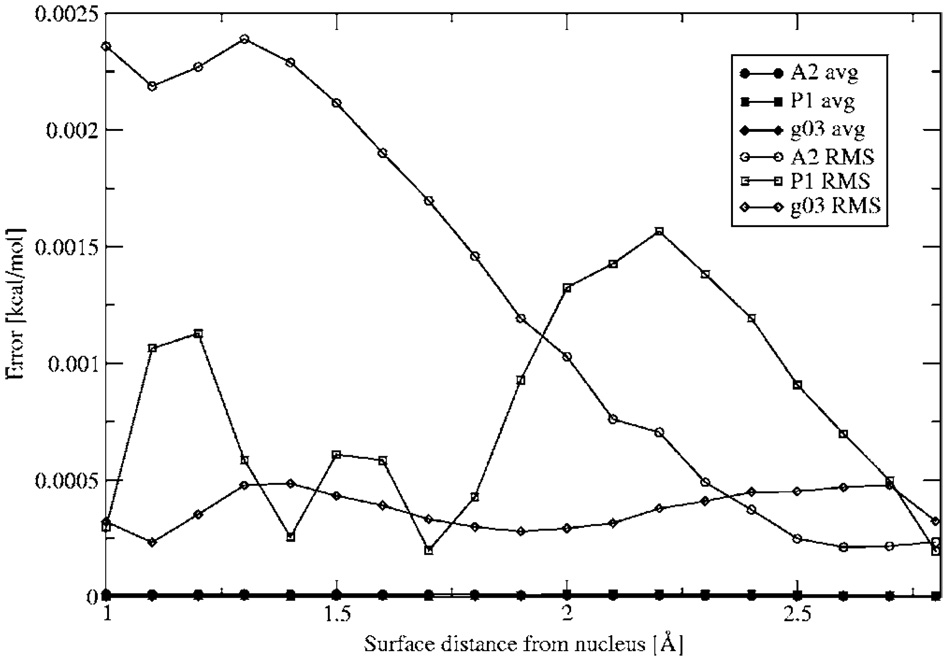
Figure 1 shows the electrostatic potential calculated from Merz-Kollman-fitted charges, DF method, and ab initio calculations for three different orientations along the molecular plane. In all cases the DF method provides a better description of the electrostatic potential even at close range. The electrostatic potential difference between the ab initio and DF calculations is shown in Fig. 2. It is interesting to note that, as expected, the results improve with ABS, with g03 giving the best results compared with the ab initio electrostatic potential. The maximum error for all ABS for the electrostatic potential calculation is around 0.5 kcal/mol with average and root-mean-square (rms) errors below 2.5 × 10⁻³, 1.5 × 10⁻³, and 5 × 10⁻⁴ for A1, P1, and g03, respectively (see Fig. 3 and Fig. 4).

FIG. 1.

(Color) Electrostatic potential maps for the water molecule calculated from Merz-Kollman-generated charges (MK), P1 fitted density, and ab initio calculation. All calculations and fittings were done at the B3LYP/6-31G* level with a fine grid (120 × 120 × 120 points). The density fitting results were obtained using midpoints with O ABS.

FIG. 2.

(Color) Water molecule electrostatic potential difference maps for density fitting with respect to ab initio. All calculations and fittings were done at the B3LYP/6-31G* level with a fine grid (120 × 120 × 120 points). All density fitting results were obtained using midpoints with O ABS.

FIG. 3.

Maximum absolute error in electrostatic potential between DF and ab initio calculations. All errors in kcal/mol.

FIG. 4.

Average and root-mean-square absolute error in electrostatic potential between DF and ab initio calculations. All errors in kcal/mol.

B. Intermolecular electrostatics

We now present the results for the intermolecular electrostatic interactions. First, we investigate the absolute error for the e-e and N-e intramolecular energies with respect to cutoff between DF and ab initio for the water molecule to determine the accuracy of the fitting procedure. Subsequently, the results for intermolecular calculations on ten water dimers^48,49 for DFT and post-HF calculations are presented. These ten dimers provide a rigorous test for any intermolecular electrostatic approach because only high-accuracy ab initio methods (such as SAPT⁸) are able to calculate the energies of these selected stationary points. Finally, the electrostatic energy surface scans for four molecular systems are discussed.

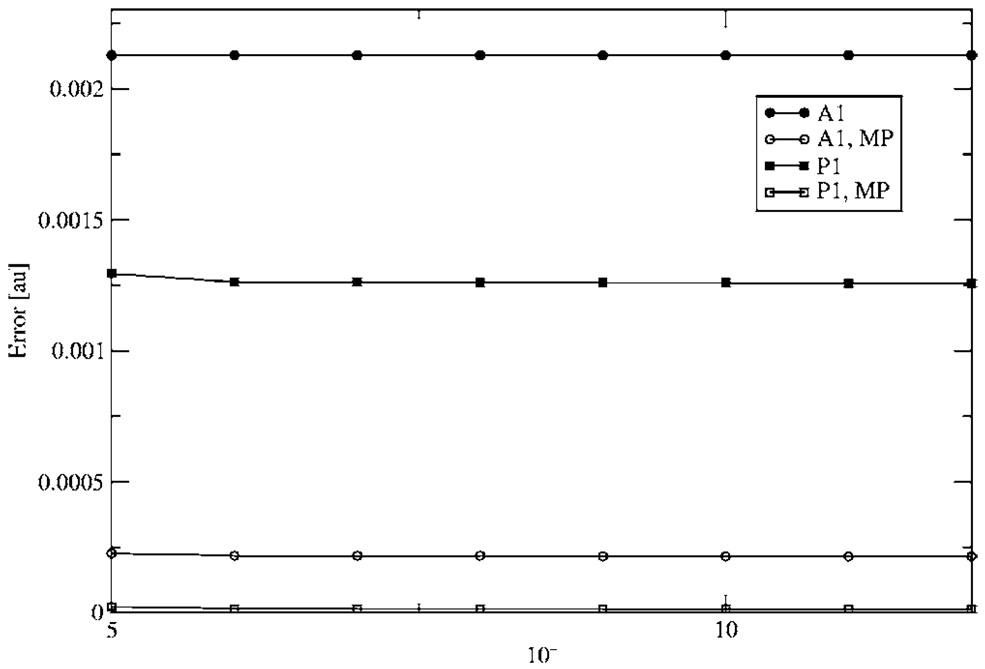
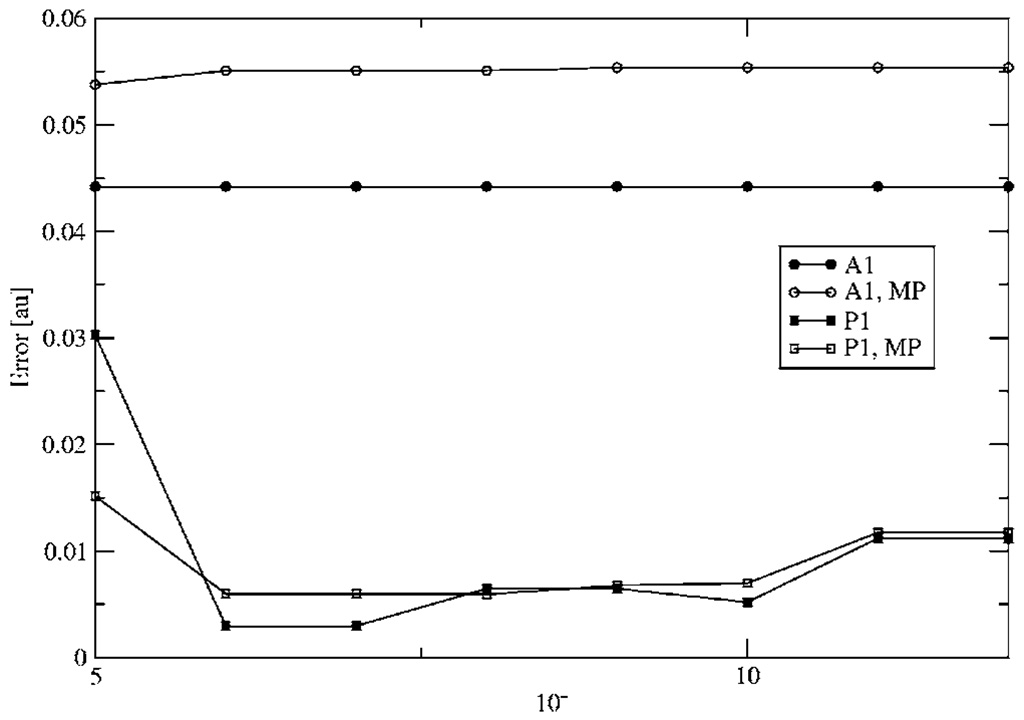
Figure 5 and Figure 6 show the calculated error in the e-e and N-e intramolecular energies, respectively for a single water molecule. As can be seen, the inclusion of MP dramatically reduces the error. In this case, the N-e intramolecular energy error is roughly twenty times as large as the e-e. This is due to the fact that the ABS tested are designed to reproduce the e-e Coulomb interaction. Therefore in the case of the N-e energy, the error may be due to a poor representation of the core density and its interaction with the nuclei. However, it is important to note that for intermolecular electrostatic calculations the distance for the N-e interactions are larger, which results in a decrease in the error.

FIG. 5.

Electron-electron intramolecular energy error with respect to eigen-value cutoff.

FIG. 6.

Nuclear-electron intramolecular energy error with respect to eigen-value cutoff.

The intermolecular Coulomb interaction energy for a series of ten water dimers has been calculated using the DF method. Based on the results for the molecular properties (see Sec. III A), we have decided to further investigate if the size of the ABS on the fitting sites improves the final results for these dimers. Four different sets of DF intermolecular determinations were performed for the water dimers. The first consists only of ABS centered on atoms with O ABS on the oxygen atom and H ABS on the hydrogen atom. In the second set the ABS on the H atoms are replaced by O ABS. The third and fourth sets include MP with H ABS and O ABS, respectively. In all cases all three ABS have been studied.

Table III and Table IV show the intermolecular Coulomb energies obtained from densities calculated at the B3LYP/augcc-p VTZ level (values in parentheses correspond to B3LYP/6-31G* calculations). Intermolecular Coulomb energy determinations using SAPT at the coupled-cluster theory with single and double excitations (CCSD) and MP3 levels,⁴⁹ CSOV at the B3LYP level, multipoles up to quad-rupole, and damping function corrected multipoles (EMTP*)¹⁹ are also presented for comparison.

TABLE III.

Intermolecular energies for water dimer (in kcal/mol) in several geometries as defined in van Duijneveldt-van de Rijdt et al. (Ref.⁴⁹). All results calculated with B3LYP/aug-cc-pVTZ (values in parentheses correspond to B3LYP/6-31G*). For the density fitting result the fitted densities were obtained from the exact DFT calculation (CSOV). MP=midpoints.

Level of theory	Water dimer geometry
	1	2	3	4	5
SAPT (CCSD)a	−8.023	−6.725	−6.494	−6.699	−5.688
SAPT (MP3)a	−8.081	−6.814	−6.601	−6.733	−5.776
CSOV (DFT)	−8.109(−8.224)	−6.854(−7.022)	−6.643(−6.908)	−6.727(−6.150)	−5.768(−5.507)
Multipoles, MP	−6.15	−5.08	−4.91	−4.86	−4.17
EMTP*, MPb	−8.03	−6.85	−6.67	−7.26	−6.67
A1	−7.361(−8.076)	−6.148(−6.758)	−5.961(−6.575)	−6.297(−6.506)	−5.552(−5.721)
A1, (O)c	−7.319(−7.067)	−6.206(−5.984)	−6.031(−5.879)	−6.343(−6.088)	−5.485(−5.466)
A1, MP (H)d	−8.259(−9.889)	−7.065(−8.447)	−6.895(−8.285)	−6.414(−6.159)	−5.656(−5.377)
A1, MP (O)e	−8.063(−7.817)	−6.871(−6.657)	−6.668(−6.568)	−6.031(−5.669)	−5.123(−5.034)
P1	−8.890(−8.415)	−7.477(−7.144)	−7.294(−7.059)	−6.774(−6.269)	−5.992(−5.759)
P1, (O)c	−8.216(−8.283)	−6.932(−7.090)	−6.710(−6.979)	−7.137(−6.437)	−6.082(−5.745)
P1, MP (H)d	−8.235(−8.243)	−6.914(−7.028)	−6.686(−6.910)	−6.488(−6.160)	−5.563(−5.524)
P1, MP (O)e	−8.149(−8.241)	−6.897(−7.059)	−6.689(−6.956)	−6.726(−6.242)	−5.642(−5.582)
g03	−8.112(−8.210)	−6.886(−7.009)	−6.696(−6.897)	−6.663(−6.259)	−5.900(−5.612)
g03, (O)c	−8.613(−8.339)	−7.405(−7.121)	−7.254(−7.011)	−6.463(−6.063)	−5.801(−5.455)
g03, MP (H)d	−8.117(−8.222)	−6.863(−7.041)	−6.663(−6.933)	−6.733(−6.187)	−5.803(−5.539)
g03, MP (O)e	−8.048(−8.231)	−6.838(−7.022)	−6.647(−6.909)	−6.566(−6.169)	−5.760(−5.514)

^aReference⁴⁹.

^bMultipole determination corrected by damping function (Ref.¹⁹).

^cReplacing Hydrogen ABS on H atoms by oxygen ABS.

^dUsing hydrogen ABS on midpoints.

^eUsing oxygen ABS on midpoints.

TABLE IV.

Intermolecular energies (continued) for water dimer (in kcal/mol) in several geometries as defined in van Duijneveldt-van de Rijdt et al. (Ref.⁴⁹). All results calculated with B3LYP/aug-cc-pVTZ (values in parentheses correspond to B3LYP/6-31G*). For the density fitting result the fitted densities were obtained from the exact DFT calculation (CSOV). MP=midpoints.

Level of theory	Water dimer geometry
	6	7	8	9	10
SAPT (CCSD)a	−5.327	−4.964	−1.546	−4.809	−2.696
SAPT (MP3)a	−5.442	−4.923	−1.513	−4.830	−2.762
CSOV (DFT)	−5.440(−5.355)	−4.865(−4.356)	−1.635(−1.338)	−4.953(−4.846)	−2.866(−3.157)
Multipoles, MP	−3.97	−3.47	−1.09	−3.42	−2.04
EMTP*, MPb	−6.53	−5.15	−1.47	−4.90	−2.88
A1	−5.312(−5.480)	−4.491(−4.738)	−1.113(−1.430)	−4.246(−4.813)	−2.420(−2.993)
A1, (O)c	−5.187(−5.288)	−4.053(−4.269)	−1.101(−1.355)	−4.315(−5.034)	−2.377(−3.165)
A1, MP (H)d	−5.402(−5.155)	−4.232(−4.121)	−1.112(−1.318)	−4.248(−4.999)	−2.383(−3.224)
A1, MP (O)e	−4.840(−4.878)	−3.979(−4.106)	−1.075(−1.307)	−4.200(−4.812)	−2.387(−3.085)
P1	−5.762(−5.693)	−4.653(−4.318)	−0.980(−1.050)	−4.544(−4.472)	−2.496(−2.902)
P1, (O)c	−5.634(−5.514)	−4.925(−4.240)	−1.555(−1.283)	−5.410(−5.165)	−2.940(−3.241)
P1, MP (H)d	−5.250(−5.380)	−5.262(−4.650)	−1.752(−1.324)	−5.000(−4.866)	−2.769(−3.123)
P1, MP (O)e	−5.271(−5.413)	−4.831(−4.244)	−1.571(−1.220)	−5.121(−5.065)	−2.932(−3.285)
g03	−5.691(−5.460)	−5.493(−4.415)	−1.684(−1.336)	−4.620(−4.818)	−2.732(−3.115)
g03, (O)c	−5.627(−5.320)	−4.159(−4.320)	−1.064(−1.326)	−4.222(−4.833)	−2.499(−3.167)
g03, MP (H)d	−5.492(−5.379)	−5.082(−4.410)	−1.636(−1.363)	−5.062(−4.838)	−2.945(−3.159)
g03, MP (O)e	−5.517(−5.358)	−5.368(−4.333)	−1.650(−1.360)	−4.714(−4.867)	−2.769(−3.170)

^aReference ⁴⁹.

^bMultipole determination corrected by damping function (Ref.¹⁹).

^cReplacing hydrogen ABS on H atoms by oxygen ABS.

^dUsing hydrogen ABS on midpoints.

^eUsing oxygen ABS on midpoints.

As expected, the g03 ABS shows the best agreement with respect to the CSOV results in all cases. Note that for all ten dimers, the use of MP with the heavy-atom ABS provides the best agreement with the CSOV calculations. The average error in kcal/mol for the best DF calculation (using MP with O ABS) is 0.470(0.298), 0.075(0.090), and 0.119(0.012) for the A1, P1, and g03 ABS, respectively. The worst error in kcal/mol among all ten dimers for these calculations are 0.886(0.532) for A1, 0.169(0.219) for P1, and 0.503(0.023) for g03 (see Table V). Note that the average error in electrostatic interaction energies determined by multipole expansion is 1.47 kcal/mol. This average error is reduced to around 0.3 kcal/mol when a damping function is employed;¹⁹ however, this function has been also fitted to compensate short-range exchange-repulsion energies (Piquemal et al. ⁵⁴).

TABLE V.

Absolute error in intermolecular Coulomb energy (in kcal/mol) for calculated water dimers using O ABS on midpoints calculated with B3LYP/aug-cc-pVTZ (values in parentheses correspond to B3LYP/6-31G*) (see Table III and Table IV). Errors are reported with respect to CSOV calculation.

Water dimer geometry	A1	P1	g03
1	0.046(0.407)	0.040(0.017)	0.061(0.007)
2	0.017(0.365)	0.043(0.037)	0.016(0.000)
3	0.025(0.340)	0.046(0.048)	0.004(0.001)
4	0.696(0.532)	0.001(0.092)	0.161(0.019)
5	0.645(0.473)	0.126(0.075)	0.008(0.007)
6	0.600(0.477)	0.169(0.058)	0.072(0.003)
7	0.886(0.250)	0.034(0.112)	0.503(0.023)
8	0.550(0.031)	0.054(0.118)	0.025(0.022)
9	0.753(0.034)	0.168(0.219)	0.239(0.021)
10	0.479(0.072)	0.066(0.128)	0.097(0.013)
Average	0.470(0.298)	0.075(0.090)	0.119(0.012)

Another advantage of the DF method is that the fit can be performed for electronic density obtained at any level of theory that produces a relaxed one-electron density matrix. Table VI shows the calculated intermolecular electrostatic results for densities obtained with three post-HF methods: MP2, MP3, and Brueckner doubles (BD) using the aug-cc-pVTZ basis set. In this case, all DF calculations were done with MP using O ABS. As before, the largest ABS provides the most accurate results with respect to the ab initio SAPT calculations. The average errors are around 0.5 for A1, 0.11 for P1, and 0.1 kcal/mol for g03 at all three levels of theory (see Table VII). It is important to point out that the average error for these calculations is above the one obtained with the DFT densities, especially with the 6-31G* basis set. The reason is that all the ABS employed in the present study are designed to work with double-zeta basis sets such as 6-31G*.

TABLE VI.

Intermolecular energies (in kcal/mol) for water dimer in several geometries as defined in van Duijneveldt-van de Dijdt et al. (Ref.⁴⁹) for post-HF calculated densities. All results calculated with aug-cc-pVTZ basis set (level of theory in square brackets). For the density fitting results the fitted densities were obtained from the exact calculation as noted on each row using midpoints with oxygen ABS.

Level of theory	Water dimer geometry
	1	2	3	4	5	6	7	8	9	10
SAPT (CCSD)a	−8.024	−6.726	−6.493	−6.699	−5.688	−5.327	−4.964	−1.546	−4.808	−2.696
SAPT (MP3)a	−8.081	−6.814	−6.601	−6.733	−5.776	−5.442	−4.923	−1.513	−4.830	−2.762
A1 [MP2]	−8.016	−6.778	−6.552	−6.075	−5.105	−4.792	−4.025	−1.082	−4.146	−2.296
P1 [MP2]	−8.133	−6.841	−6.620	−6.755	−5.637	−5.246	−4.814	−1.631	−5.018	−2.804
g03 [MP2]	−8.061	−6.813	−6.607	−6.608	−5.749	−5.477	−5.361	−1.606	−4.642	−2.654
A1 [MP3]	−7.841	−6.656	−6.452	−5.904	−4.995	−4.708	−3.919	−1.085	−4.112	−2.339
P1 [MP3]	−8.000	−6.782	−6.593	−6.586	−5.572	−5.228	−4.566	−1.422	−4.900	−2.803
g03 [MP3]	−7.956	−6.768	−6.590	−6.453	−5.694	−5.464	−5.075	−1.485	−4.563	−2.674
A1 [BD]	−7.842	−6.638	−6.424	−5.902	−4.967	−4.668	−3.919	−1.076	−4.087	−2.297
P1 [BD]	−7.987	−6.743	−6.540	−6.582	−5.525	−5.161	−4.621	−1.458	−4.899	−2.773
g03 [BD]	−7.933	−6.724	−6.534	−6.446	−5.643	−5.394	−5.141	−1.525	−4.551	−2.638

^aReference ⁴⁹.

TABLE VII.

Absolute error in intermolecular Coulomb energy (in kcal/mol) for the calculated water dimers with post-HF fitted densities (see Table VI). MP2 and MP3 errors are reported with respect to MP3 calculation from (Ref. ⁴⁹), and the BD errors are reported with respect to CCSD.

Water dimer geometry	MP2			MP3			BD
	A1	P1	g03	A1	P1	g03	A1	P1	g03
1	0.065	0.032	0.020	0.240	0.081	0.125	0.182	0.037	0.091
2	0.036	0.027	0.001	0.158	0.032	0.046	0.088	0.017	0.002
3	0.049	0.019	0.006	0.149	0.008	0.011	0.069	0.047	0.041
4	0.658	0.022	0.125	0.829	0.147	0.280	0.797	0.117	0.253
5	0.671	0.139	0.027	0.781	0.251	0.082	0.701	0.143	0.025
6	0.650	0.196	0.035	0.734	0.214	0.022	0.659	0.166	0.067
7	0.898	0.109	0.438	1.004	0.357	0.152	1.045	0.343	0.177
8	0.431	0.118	0.093	0.428	0.091	0.028	0.470	0.088	0.021
9	0.684	0.188	0.188	0.718	0.070	0.267	0.721	0.091	0.257
10	0.466	0.042	0.108	0.423	0.041	0.088	0.399	0.077	0.058
Average	0.461	0.089	0.104	0.546	0.129	0.110	0.513	0.113	0.099

Van Duijneveldt-van de Rijdt et al.⁴⁹ have suggested that since the value of k_BT at room temperature is around 0.6 kcal/mol, an average error of 0.24 kcal/mol should be a reasonable requirement for analytical model potentials. It is important to note that for our DF calculations, the average error obtained with the P1 and g03 basis sets are below the 0.24 kcal/mol threshold.

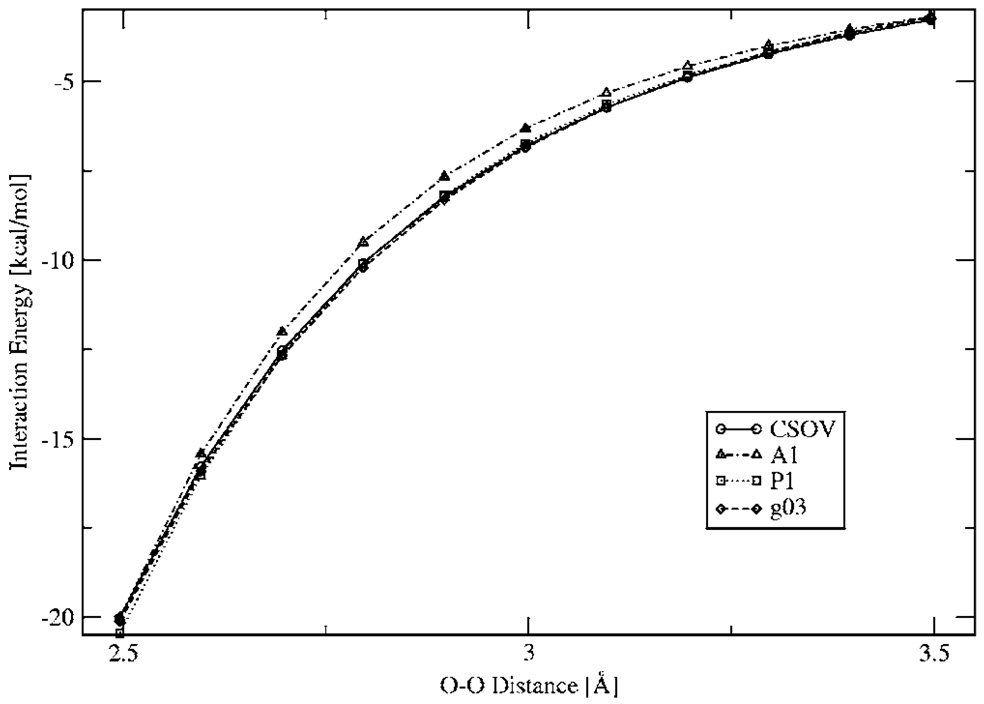
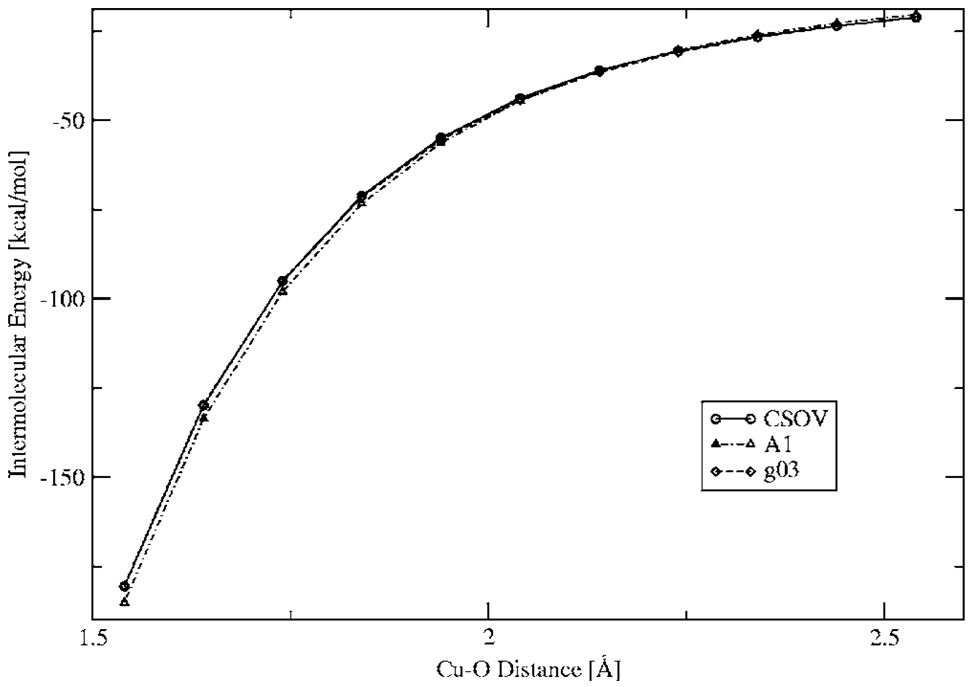
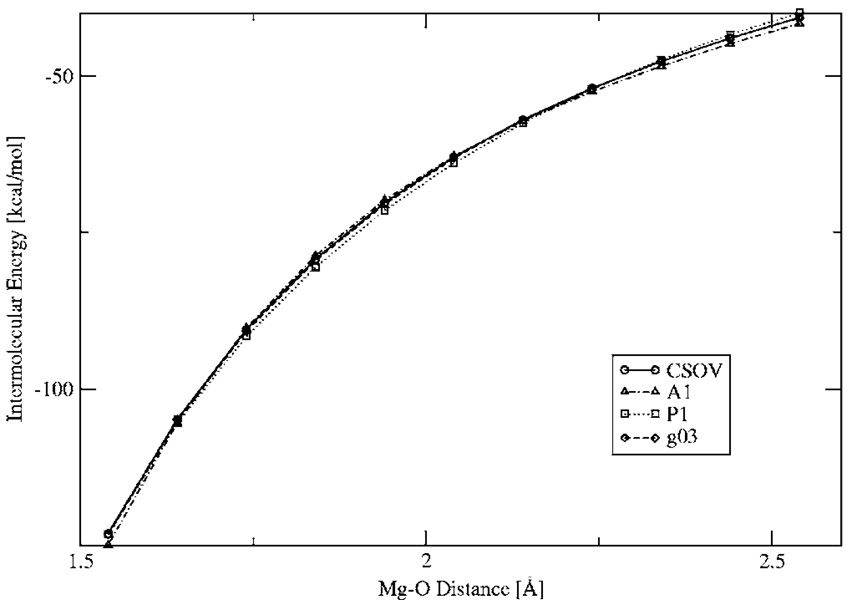
Finally, in order to test how the penetration effects affect the results for the DF intermolecular calculations, several electrostatic energy surface scans were performed. Figure 7–Figure 9 show the intermolecular electrostatic interaction for the structure 1 H₂O dimer, Mg²⁺–H₂O, and Cu⁺–H₂O, respectively, for a range of distances. As can be seen from these surfaces, the DF calculations for all three ABS show very good agreement with the ab initio results, including at short range. In the case of the Cu⁺–H₂O, only calculations with the A1 and g03 ABS are presented because there are no P1 ABS available for Cu.

FIG. 7.

Water dimer (structure 1) Coulomb interaction energies for a range of distances.

FIG. 9.

Cu⁺-water Coulomb interaction energies for a range of distances.

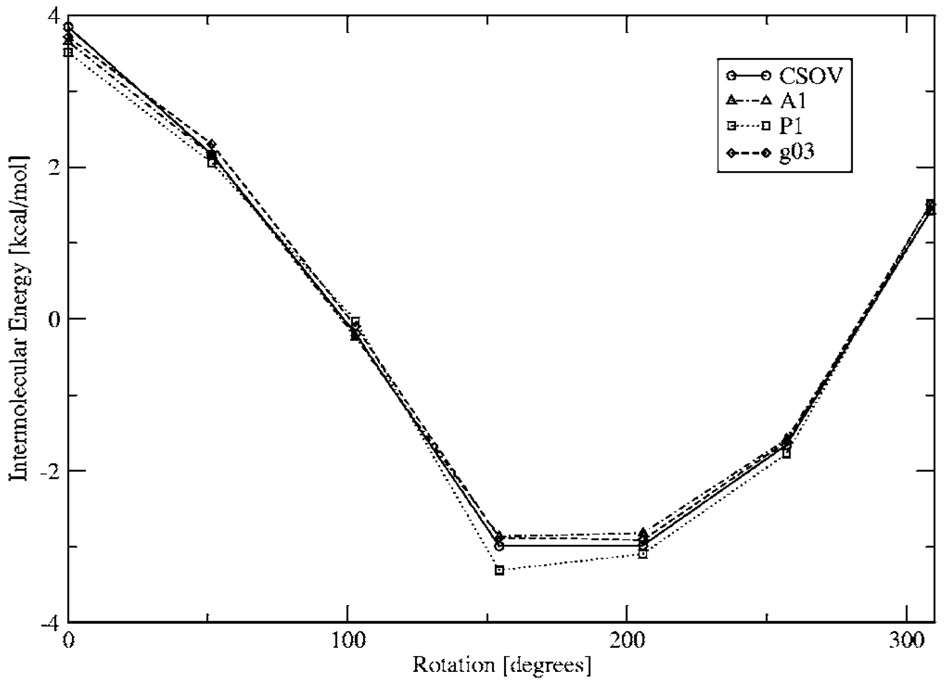
The DF intermolecular electrostatic interactions also show very good agreement with respect to rotation, as shown by the results obtained for the n-methyl-formamide dimer calculations (see Fig. 10). As can be seen, when one of the n-methyl-formamide molecules is rotated while keeping the other one fixed, the intermolecular electrostatic interaction goes from repulsive to attractive. In all cases all three ABS reproduce the ab initio trend. Note that in the case of P1, there is a slight deviation at the minimum.

FIG. 10.

N-methyl-formamide dimer Coulomb interaction energies rotating about one of the fragments.

It is expected that the present algorithm should be as fast (or faster) than SAPT or CSOV calculations. In all cases at least two matrix diagonalizations are needed, which for small molecules may be the limiting step in the procedure. As the system size increases, the calculation of the four-center two-electron Coulomb integrals will become the time-consuming step in the case of the SAPT and CSOV procedures. However, in the case of the DF method, due to the nature of the algorithm, these integrals are only two-center two-electron which are much faster to calculate. In addition, the memory usage for the DF method is expected to be reduced in comparison with SAPT or CSOV.

Moreover, note that the implementation of this algorithm should be straightforward on available quantum codes that provide density fitting capability. In this case the auxiliary coefficients would already be available from the self-consistent-field (SCF) cycle, and the only remaining step for the calculation of the intermolecular interaction would be the calculation of the terms in Eq. (8). Additionally, it has been shown that the density fitting method can be applied to relatively large systems.⁶⁶

IV. CONCLUSIONS

We have presented a method based on DF that provides an accurate and efficient way to calculate intermolecular electrostatic interaction energies. The use of the DF method for the fitting of the molecular density for each unperturbed monomer results in a simplified intermolecular Coulomb energy expression of the order O(N²). The calculated results show that the size of the auxiliary basis set employed in the fitting procedure is very important to obtain accurate results. The accuracy of the calculations is also improved by performing the fit on atomic and additional sites such as bond midpoints. This method provides a straightforward procedure for the determination of intermolecular electrostatic interactions from molecular densities calculated from any wave function where a one-electron density matrix is available. Furthermore, this method provides a new way to study ab initio electrostatic interaction energies in large systems and to estimate the transferability of electrostatic parameters in point charge or multipole-based force fields.

The DF method was tested by calculating the molecular dipoles for a series of molecules as well as the electric field and electrostatic potential for the water molecule. In all cases the largest ABS (g03) provided the best results compared with ab initio results. Intermolecular electrostatic interactions were calculated at four different levels of theory: B3LYP, MP2, MP3, and BD using two different basis sets (6-31G* and aug-cc-pVTZ) for ten water dimers. The fitting procedure for these ten dimers was performed with three different auxiliary basis sets. The average errors for the DFT results are 0.470(0.298), 0.075(0.090), and 0.119(0.012) for the A1, P1, and g03 ABS, respectively. In the case of the post-HF densities, the average errors are around 0.5 for A1, 0.11 for P1, and 0.1 kcal/mol for g03 at all three levels of theory. In the case of the best DF results, the calculated average errors are below the 0.24-kcal/mol threshold proposed by van Duijneveldt-van de Rijdt et al.⁴⁹ The penetration effect was tested by performing a potential-energy surface scan for four systems; in all cases the intermolecular energies calculated with DF reproduce the CSOV ones, including those at close range.

FIG. 8.

Mg²⁺-water Coulomb interaction energies for a range of distances.