FastTree: Computing Large Minimum Evolution Trees with Profiles instead of a Distance Matrix

Abstract

Gene families are growing rapidly, but standard methods for inferring phylogenies do not scale to alignments with over 10,000 sequences. We present FastTree, a method for constructing large phylogenies and for estimating their reliability. Instead of storing a distance matrix, FastTree stores sequence profiles of internal nodes in the tree. FastTree uses these profiles to implement Neighbor-Joining and uses heuristics to quickly identify candidate joins. FastTree then uses nearest neighbor interchanges to reduce the length of the tree. For an alignment with N sequences, L sites, and a different characters, a distance matrix requires O(N²) space and O(N²L) time, but FastTree requires just O(NLa + N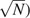) memory and O(N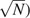log (N)La) time. To estimate the tree's reliability, FastTree uses local bootstrapping, which gives another 100-fold speedup over a distance matrix. For example, FastTree computed a tree and support values for 158,022 distinct 16S ribosomal RNAs in 17 h and 2.4 GB of memory. Just computing pairwise Jukes–Cantor distances and storing them, without inferring a tree or bootstrapping, would require 17 h and 50 GB of memory. In simulations, FastTree was slightly more accurate than Neighbor-Joining, BIONJ, or FastME; on genuine alignments, FastTree's topologies had higher likelihoods. FastTree is available at http://microbesonline.org/fasttree.

Introduction

Inferring phylogenies from biological sequences is the fundamental method in molecular evolution and has many applications in taxonomy and for predicting structure and biological function. In general, sequences are identified as homologous and aligned, and then a phylogeny is inferred. Large alignments can be constructed efficiently, in time linear in the number of sequences, by aligning the sequences to a profile instead of to each other, as with position-specific Blast or hmmalign (Schaffer et al. 2001; http://hmmer.janelia.org/).

Given an alignment, Neighbor-Joining and related minimum evolution methods are the fastest and most scalable approaches for inferring phylogenies (Saitou and Nei, 1987), (Studier and Keppler, 1988), (Desper and Gascuel, 2002). All these methods rely on a distance matrix that stores an estimate of the evolutionary distance between each pair of sequences. Computing an entry in the distance matrix requires comparing the characters at each position in the alignment and hence requires O(L) time, where L is the number of positions. Thus, the distance matrix takes O(N²L) time to compute, where N is the number of sequences, and O(N²) space to store.

Given a distance matrix, Neighbor-Joining performs a greedy search for a tree of minimal length, according to a local estimate of the length of each branch (Gascuel and Steel 2006). More specifically, Neighbor-Joining begins with the tree as a star topology, and it iteratively refines the tree by joining the best pair of nodes together, until the tree is fully resolved. Each step considers O(N²) possible joins, so the standard Neighbor-Joining algorithm requires O(N³) time to infer a tree from a distance matrix. This can be reduced to O(N²) or O(N²logN) time, either by using heuristics to consider fewer joins (Elias and Lagergren 2005, Evans et al. 2006) or by using additional O(N²) memory (Simonsen et al. 2008, Zaslavsky and Tatusova 2008). FastME is another minimum evolution method that takes only O(N²) time (Desper and Gascuel 2002). With any of these optimized methods, the O(N²L) time to compute the distance matrix dominates the time.

As DNA sequencing accelerates, the memory and CPU requirements of the distance matrix approach are becoming prohibitive. For example, an alignment of full- length 16S ribosomal RNAs (rRNAs) contains over 160,000 distinct sequences (DeSantis et al. 2006; http://greengenes.lbl.gov). Similarly, the MicrobesOnline database, which provides phylogenies for all protein families from prokaryotic genomes, contains protein families with over 100,000 distinct sequences (Alm et al. 2005; http://www.microbesonline.org/). The distance matrix for families with 100,000–200,000 members requires 20–80 GB of memory to store (a 4-byte floating-point value for each of N(N −1)/2 pairs). Although computers with this much memory are available, the typical node in a compute cluster has an order of magnitude less memory. Furthermore, DNA sequencing technology is improving rapidly, and the distance matrix's size scales as the square of the family's size, so we expect these problems to become much more severe. Finally, most of the methods that construct a tree from a distance matrix in O(N²) time, such as FastME and the exact O(N²) implementations of Neighbor-Joining, require additional O(N²) memory.

Whatever the method used, inferred phylogenies often contain errors, and so it is important to estimate the reliability of the result (Nei et al. 1998). The standard method to estimate reliability is to use the bootstrap: to resample the columns of the alignment, to rerun the method 100–1,000 times, to compare the resulting trees to each other or to the tree inferred from the full alignment, and to count the number of times that each split occurs in the resulting trees (Felsenstein 1985). (A split is the two sets of leaves on either side of an internal edge.) Unfortunately, bootstrapping is a minimum of 100 times slower than the underlying phylogenetic inference, and comparing the trees to each other is also a nontrivial computation. In principle, the resampled trees could be compared with the original tree in O(N²) time and O(N) space by hashing the splits in the tree. However, the tree comparison tools that we are aware of require O(N³) time and O(N²) space.

Although building phylogenetic trees for large gene families is challenging, it is important to do so and not just to build trees for small sets of selected homologs. Analyzing all the sequences is important for taxonomy, for predicting gene function, for classifying environmental DNA sequences, and for identifying functional residues (Eisen 1998, Lichtarge et al. 2003, Engelhardt et al. 2005, von Mering et al. 2007). Furthermore, omitting sequences might change the biological interpretation of the result, especially in prokaryotes: because of horizontal gene transfer, it is difficult to know which homologs are relevant without building a tree. Finally, for Web sites that support interactive use of phylogenetic trees, it is desirable to compute trees for all the genes beforehand (Li et al. 2006; http://www.treefam.org/; http://www.microbesonline.org/).

Our Approach

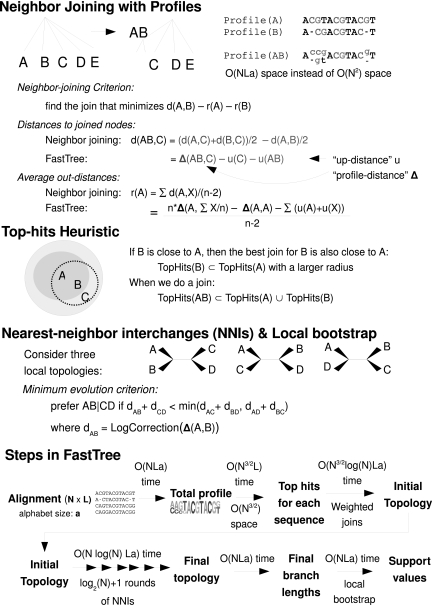
We present FastTree that uses four ideas to reduce the space and time complexity of inferring a phylogeny from an alignment (fig. 1). First, FastTree implements Neighbor-Joining by storing profiles for the internal nodes in the tree instead of storing a distance matrix. Each profile includes a frequency vector for each position, and the profile of an internal node is the weighted average of its children's profiles. For example, if we join two leaves i and j, and i has an A at a position and j has a G, then the profile of ij at that position will be 50% A and 50% G (and 0% for other characters). The intuition behind using profiles is that the average of the distances between the sequences in two subtrees A and B equals the distance between profile(A) and profile(B) because profile(A) is the average of the sequences in A. FastTree uses these profiles to compute the distances between internal nodes in the tree and also the total distance from a node to all other nodes, which is also required for Neighbor-Joining. The profiles require a total of O(NLa) space, where a is the size of the alphabet (20 for protein sequences and 4 for nucleotide sequences), instead of O(N²) space for the distance matrix. However, the time required for Neighbor-Joining with exhaustive search rises from O(N³) to O(N³La) because every distance has to be recomputed on demand in O(La) time.

Second, FastTree uses a combination of previously published heuristics (Elias and Lagergren 2005, Evans et al. 2006) and a new “top-hits” heuristic to reduce the number of joins considered. Whereas traditional Neighbor-Joining considers O(N³) possible joins and optimized variants have considered O(N²) possible joins (the size of the distance matrix), FastTree considers O(N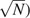logN) possible joins. Thus, in theory, FastTree takes O(N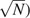log(N)La) time. In practice, FastTree is faster than computing the distance matrix. These heuristics require additional O(N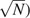) memory, raising the total storage requirement for FastTree to O(NLa +N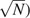), which is still much less than O(N²).

Third, FastTree refines the initial topology with nearest neighbor interchanges (NNIs). Given an unrooted tree ((A, B), (C, D)), where A, B, C, and D may be sub-trees rather than individual sequences, FastTree compares the profiles of A, B, C, and D and determines whether alternate topologies ((A, C), (B, D)) or ((A, D), (B, C)) would reduce the length of the tree. These NNIs are similar to those of FastME, although FastME uses a distance matrix (Desper and Gascuel 2002). FastTree's NNIs take O(N log(N)La) additional time and O(NLa) additional space. In practice, the NNIs take much less time than computing the initial topology, and they improve the quality of the tree.

Fourth, FastTree computes a local bootstrap value for each internal split ((A, B), (C, D)) by resampling the columns of the profiles and counting the fraction of resamples that support ((A, B), (C, D)) over the alternate topologies ((A, C), (B, D)) or ((A, D), (B, C)). The local bootstrap has been used for maximum likelihood trees (Kishino et al. 1990) but cannot be used with distance matrices. Computing the local bootstrap takes O(bNLa) time, where b is the number of bootstrap samples. Even with 1,000 resamples, this takes less than a minute for an alignment of over 8,000 protein sequences and 394 columns. Thus, local bootstrap gives FastTree an additional 100-fold speedup over distance matrix methods, in which the entire computation must be repeated for each sample. However, the local bootstrap should be interpreted more conservatively than the traditional bootstrap. Whereas traditional bootstrap estimates the probability that the split is correct (Efron et al. 1996), local bootstrap estimates the probability that the split is correct if we assume that A, B, C, and D are subtrees of the true tree.

Below, we describe FastTree in more detail. Then, we show that in realistic simulations, FastTree is slightly more accurate than other minimum evolution methods such as Neighbor-Joining, BIONJ, or FastME. On genuine alignments, FastTree topologies tend to have higher likelihoods than topologies from other minimum evolution methods, which also suggests that FastTree gives higher quality results. For both simulated and genuine alignments, FastTree's heuristics do not lead to any measurable reduction in quality. For large families, FastTree requires less CPU time and far less memory than computing and storing a distance matrix. Finally, we show that the local bootstrap is a good indicator of whether each split in the inferred topology is correct, and it is orders of magnitude faster than the traditional bootstrap. We believe that FastTree is the first practical method for computing accurate phylogenies, including support values, for alignments with tens or hundreds of thousands of sequences.

Materials and Methods

FastTree

A rough outline of FastTree is shown at the bottom of figure 1. Before we explain how FastTree implements Neighbor-Joining, we explain how it computes distances between sequences and how it computes distances between profiles. We then explain how it computes distances between internal nodes and how it calculates the Neighbor-Joining criterion, which is used to select the best join. We also describe the heuristics that it uses to reduce the number of joins that it considers. Finally, we explain the steps after Neighbor-Joining: NNIs, the local bootstrap, and estimating the branch lengths for the final topology. For formulas, derivations, and technical details, see supplementary note 1 (Supplementary Material online).

FIG. 1.—

Overview of FastTree.

Distances between Sequences

FastTree uses both corrected and uncorrected distances. FastTree corrects the distances for multiple substitutions during NNIs, computing final branch lengths, and local bootstrap, but not during Neighbor-Joining. For nucleotide sequences, FastTree's uncorrected distance d_u is the fraction of positions that differ, and the corrected distance is the Jukes–Cantor distance 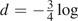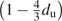. For protein sequences, FastTree estimates distances by using the BLOSUM45 amino acid similarity matrix (Henikoff S and Henikoff JG 1992) and a log correction inspired by that of scoredist (Sonnhammer and Hollich 2005). We scaled the BLOSUM45 similarity matrix into a dissimilarity matrix such that the average dissimilarity between each amino acid and a random amino acid is 1 if we use the nonuniform amino acid frequencies of biological sequences. The uncorrected distance d_u between two sequences is the average dissimilarity among nongap positions, and the corrected distance is d = −1.3 × log(1 − d_u). The intuitive justification is that the term within the logarithm ranges from 1 for identical sequences to an expected value of 0 for unrelated sequences, as with Jukes–Cantor distances for nucleotide sequences. For both nucleotide and protein sequences, FastTree truncates the corrected distances to a maximum of 3.0 substitutions per site, and for sequences that do not overlap because of gaps, FastTree uses this maximum distance.

Distances between Profiles

FastTree uses profiles to estimate the average distance between the children of two nodes. The profile distance at each position is the average dissimilarity of the characters. The uncorrected distance between two profiles is then the average of these position-wise distances, weighted by the product of the proportion of nongaps in each of the two profiles. FastTree computes the distance between two profiles in O(La) time by using the eigendecomposition of the dissimilarity matrix.

The profile distance is identical to the average distance if the distances are not corrected for multiple substitutions and if the sequences do not contain gaps. For example, if we join two sequences A and B together, then the profile distance

Of course, we do wish to correct for multiple substitutions, and in practice, large alignments always contain gaps. In these cases, the profile-based average becomes an approximation of the average distances used in traditional minimum evolution methods.

First, consider the issue of correcting distances for multiple substitutions with a formula of the form d ∝ −log(1− d_u). The average corrected distance between A and BC is (d(A,B) + d(A,C))/2 or the average of two logarithms. However, FastTree cannot compute this average of logarithms from the profiles. Instead, FastTree uses the logarithm of averages. This is a close approximation if the distances are short or if the distances are similar. If the distances are large, then distances between profiles may be more accurate than averages of distances (Müller et al. 2004).

Second, consider what happens if the sequences contain gaps. FastTree records the fraction of gaps at each profile position, and when computing distances, FastTree weights positions by their proportion of nongaps. Traditional Neighbor-Joining implicitly weights the ungapped columns more highly. For example, consider an alignment with A = C-, B = GG, and C = CC: Δ(AB,C) = 2/3, but (d_u(A,B) + d_u(A, C))/2 = 1/2. Both approaches treat gaps as missing data, and it is not obvious which is preferable.

Distances between Internal Nodes

Neighbor-Joining operates on distances between internal nodes rather than on average distances between the members of subtrees. For example, after joining nodes A and B, Neighbor-Joining sets

FastTree instead sets the profile of AB to 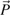(AB) =(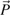(A) + 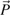(B))/2 and computes the distance between nodes with

where Δ(i,j) is the profile distance and u(i) is the “up-distance,” or the average distance of the node from its children. u(i) = 0 for leaves, and for balanced joins, u(ij) = Δ(i,j)/2. This profile-based computation gives the exact same value of d_u(i,j) as Neighbor-Joining after any number of joins, as long as distances are not corrected for multiple substitutions and the sequences contain no gaps.

FastTree actually uses weighted joins, as in BIONJ (Gascuel 1997), rather than the balanced joins. In BIONJ, the weight of each join depends on the variance of the distance between two joined nodes, which can also be computed from the profiles. Also, with weighted joins, the formula for the up-distances becomes more complicated.

Calculating the Neighbor-Joining Criterion

Given the distances between nodes, Neighbor-Joining selects the join that minimizes the criterion d_u(i,j) −r(i) −r(j), where i, j, and k are indices of active nodes that have not yet been joined, d_u(i,j) is the distance between nodes i and j, n is the number of active nodes, and

r(i) can be thought of as the average “out-distance” of i to other active nodes (although the denominator is n−2, not n − 1). Traditional Neighbor-Joining computes all N out-distances before doing any joins, which takes O(N₂) time, and updates each out-distance after each join, which also takes O(N²) time overall. To avoid this work, FastTree computes each out-distance as needed in O(La) time by using a “total profile” T which is the average of all active nodes’ profiles, as implied by

(Δ(i,i) is the average distance between children of i, including self-comparisons.) If there are gaps, then this is an approximation. FastTree computes the total profile at the beginning of Neighbor-Joining in O(NLa) time, updates it incrementally in O(La) time, and recomputes it every 200 joins to avoid round-off error.

Notice that FastTree does not log correct the distances during Neighbor-Joining. We considered doing so, but it reduced FastTree's accuracy. Perhaps the profile-based out-distances become inaccurate: the out-distance is an average of both far and small values, and so the log correction of the average distance is a poor estimate of the average of the log-corrected distances.

Selecting the Best Join

FastTree uses heuristics to reduce the number of joins considered at each step to less than O(n). We first explain the “top-hits” heuristic. For each node, FastTree records a top-hits list: the nodes that are the closest m neighbors of that node, according to the Neighbor-Joining criterion. By default, m =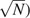. Before doing any joins, FastTree estimates these lists for all N sequences by assuming that if A and B have similar sequences, then the top-hits lists of A and B will largely overlap. More precisely, FastTree computes the 2m top hits of A, where the factor of two is a safety factor. Then, for each node B within the top m hits of A that does not already have a top-hits list, FastTree estimates the top hits of B by comparing B to the top 2m hits of A. In theory, this takes a total of O(N²L/m + NmL) = O(N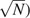L) time to compute and O(Nm) = O(N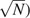) space to store.

FastTree restricts the top-hits heuristic to ensure that a sequence's top hits are only inferred from the top hits of a “close enough” neighbor. Because of these restrictions, it is not clear how many sequences will have O(m) close neighbors and it is not clear if the initial computation of top-hits lists will truly take O(N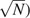L) time. However, for large alignments, it takes less time than computing the distance matrix, so in practice it takes less than O(N²L) time.

FastTree maintains these top-hits lists during Neighbor-Joining. First, after a join, FastTree computes the top-hits list for the new node in O(mLa) time by comparing the node to all entries in the top-hits lists of its children. Second, after a join, some of the other nodes’ top hits may point to an inactive (joined) node. When FastTree encounters these entries, it replaces them with the active ancestor. Finally, as the algorithm progresses, the top-hits lists will gradually become shorter as joined nodes become absent from lists. Thus, FastTree periodically “refreshes” the top-hits list by comparing the new node to all other nodes and also by comparing each of the new node's top hits to each other. Each refresh takes O(nLa + m²La) time and ensures that the top-hits lists of O(m) other nodes are of full length and up-to-date, so FastTree performs O(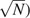) refreshes, and they take a total of O(N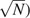La) time.

Besides storing the list of top hits for each node, FastTree also remembers the best-known join for each node, as in FastNJ (Elias and Lagergren 2005). FastTree updates the best-known join whenever it considers a join that involves that node. For example, while computing the top hits of A, it may discover that A,B is a better join than B,best(B).

Based on the best joins and the top-hits lists, FastTree can quickly select a join. First, FastTree finds the best m joins among the best-known joins of the n active nodes, without recomputing the Neighbor-Joining criterion to reflect the current out-distances. In principle, this can be implemented in O(mlog N) time per join by using a priority queue. (FastTree simply sorts the entries, which adds O(Nlog N) time per join or O(N² log N) time overall.) For those m candidates, FastTree recomputes the Neighbor-Joining criterion, which takes O(mLa) time, and selects the best. Furthermore, FastTree does a local hill-climbing search to find a better join, as in relaxed Neighbor-Joining (Evans et al. 2006): given a join AB, it considers all joins AC or BD, where C is in top-hits(A) or D is in top-hits(B). This can be beneficial because the out-distances change after every join, so the best join for a node can change as well. In theory, this takes O(logn) iterations (Evans et al. 2006), O(mlog(n)La) time per join, or O(N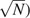log(N)La) time overall. Thus, it takes FastTree a total of O(N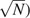log(N)La) time to maintain the top-hits lists and to select all the joins.

Nearest Neighbor Interchanges

After FastTree constructs an initial tree with Neighbor-Joining, it uses NNIs to improve the tree topology. During each round, FastTree tests and possibly rearranges each split in the tree, and it recomputes the profile of each internal node. The profiles can change even if the topology does not change because FastTree recomputes the weighting of the joins.

By default, FastTree does log₂(N) + 1 rounds of NNIs. We chose a fixed number of rounds, instead of iterating until no more NNIs occur, to ensure fast completion. We chose roughly log₂(N) rounds so that, on a balanced topology, a misplaced node could migrate all the way across the tree.

The minimum evolution criterion prefers ((A, B), (C, D)) over alternate topologies ((A, C), (B, D)) or ((A, D), (B, C)) if d(A,B) + d(C,D) < d(A,C) + d(B,D) and d(A,B) + d(C,D) < d(A,D) + d(B,C). Here, FastTree uses log-corrected profile distances, rather than distances between nodes. The profile distances do not account for the distances within the nodes, but this does not affect the minimum evolution criterion as it increases all distances d(A, ·) by the same amount.

For larger topologies, FastTree must compute profiles for additional subtrees before doing this computation. For example, consider the topology ((A, (B, C)), D, E). After Neighbor-Joining, FastTree has profiles for the internal nodes BC and ABC as well as for the leaves, but to test the split BC versus ADE requires the profile for DE. FastTree computes the profile for DE by doing a weighted join of D and E, using the weighting of BIONJ for a 4-leaf tree (Gascuel 1997). FastTree stores these additional profiles along the path to the root and reuses them when possible. (FastTree computes an unrooted tree but stores it as a rooted tree.) To ensure that a round of NNIs takes O(NLa) time and at most O(NLa) additional space, FastTree visits nodes in postorder (it visits children before their parents).

Local Bootstrap

To estimate the support for each split, FastTree resamples the alignment's columns with Knuth's 2002 random number generator (http://www-cs-faculty.stanford.edu/knuth/programs/rng.c). FastTree counts the fraction of resamples that support a split over the two potential NNIs around that node, much as it does while using NNIs to improve the topology. If a resample's minimum evolution criterion gives a tie, then that resample is counted as not supporting the split.

Branch Lengths

Once the topology is complete, FastTree computes branch lengths, with

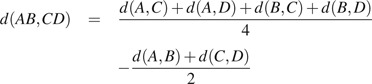for internal branches and

for the branch leading to leaf A, where d are log-corrected profile distances.

Unique Sequences

Large alignments often contain many sequences that are exactly identical to each other (Howe et al. 2002). Before inferring a tree, FastTree uses hashing to quickly identify redundant sequences. It constructs a tree for the unique subset of sequences and then creates multifurcating nodes, without support values, as parents of the redundant sequences.

Testing FastTree

Sources of Alignments

We obtained sequences of members of Clusters of Orthologous Groups (COG) gene families (Tatusov et al. 2001) and members of Pfam PF00005 (Finn et al. 2006) from the fall 2007 release of the MicrobesOnline database (http://www.microbesonline.org/). We aligned the sequences to the family's profile, using reverse position-specific Blast for the COG alignment (Schaffer et al. 2001) and hmmalign for the PF00005 alignment (http://hmmer.janelia.org/). As the profiles only include positions that are present in many members of the family, these alignments do not contain all positions from the original sequences. The 16S rRNA alignment is from greengenes and is trimmed with the greengenes mask (DeSantis et al. 2006; http://greengenes.lbl.gov).

To simulate alignments with realistic phylogenies and realistic gaps, we used the COG alignments. In each simulation, we selected the desired number of sequences from a COG alignment, we removed positions that were over 25% gaps, we estimated a topology and branch lengths with PhyML (Guindon and Gascuel 2003), we estimated evolutionary rates across sites with PHYLIP's proml (http://evolution.genetics.washington.edu/phylip.htm), we simulated sequences with Rose (Stoye et al. 1998), and we reintroduced the gaps from the original alignment. For simulations of 5,000 sequences, we used FastTree instead of PhyML and we assigned evolutionary rates at random. For N = 10, we simulated 3,100 alignments (10 independent runs per family); for N = 50, we simulated 3,099 alignments; for N = 250, we simulated 308 alignments; for N = 1,250, we simulated only 92 alignments because some PhyML jobs did not complete, and for N = 5,000, we simulated 7 alignments, as only seven families contained enough nonredundant sequences. See supplementary note 2 (Supplementary Material online) for technical details.

CPU Timings

All programs used a single thread of execution. We used a computer with two dual-core 2.6-GHz AMD Opteron processors and 32 GB of RAM. However, for the two long-running maximum likelihood jobs in table 6, we used a computer with a 2.4-GHz Intel Q6600 quad-core processor and 8 GB of RAM. The two machines have similar performance (about 20% different for FastTree).

Table 6.

CPU Time and Memory Usage for Computing Distances, Trees, and Support Values

Program	Support	COG2814		PF00005		16S rRNA
		h	GB	h	GB	h	GB
FastTree 1.0	None	0.06	0.16	0.52	0.3	16.3	2.4
FastTree 1.0	Local 1,000	0.08	0.16	0.56	0.3	17.3	2.4
Log-corrected distancesa		0.05	0.13	0.71	2.8	33.1	49.9
Maximum likelihood distancesb		138	0.72	≈ 3, 000	—	≈ 5, 000	—
Clearcut 1.0.8c	None	0.06	0.22	1.44	5.2	≈ 28.6	≈ 52
RapidNJ 1.0.0c	None	0.05	2.2	≈ 0.9	≈ 55	≈ 22.1	≈ 549
FastME 1.1c	None	0.51	4.2	≈ 12.5	≈ 105	≈ 138	≈ 1, 000
QuickTree 1.1c	None	0.24	0.16	22.7	2.9	≈ 1, 500	≈ 47
QuickTree 1.1d	Boot 100	63.5	0.71	≈ 104	≈ 15.5	≈ 105	≈ 254
BIONJc	None	32.9	0.44	≈ 820	≈ 10.9	≈ 105	≈ 110
PhyML 3e	Approximate	> 1,000	9.5	—	—	—	—
	likelihood ratio test
RAxML VI 1.0f	None	> 1,000	0.70	—	—	—	—
Consenseg	Boot 100	1.09	0.36	118	9.4	≈ 3, 700	≈ 94

NOTE.—aLRT, approximate likelihood ratio test.

^aThe time to compute the distances between all N² pairs of sequences in the alignment, as implemented by the authors, and the space required to store the N(N – 1)/2 distinct entries of the distance matrix. For nucleotide sequences, these are the same as Jukes–Cantor distances.

^bFor protein sequences, we used PHYLIP's protdist and default options (JTT model, no variation of rates across sites). For nucleotide sequences, we used PHYLIP's dnadist with the F84 model and gamma-distributed rates.

^cThese timings include half of the time to compute N² log-corrected distances because the method requires a distance matrix but each pair of sequences only needs to be considered once.

^dUsing QuickTree's built-in implementation of %different distances and of global bootstrap.

^eFor best performance, we used no variation of rates across sites.

^fFor best performance, we used no variation of rates across sites and the fast hill-climbing option (-f d.). For an initial topology, we used the BIONJ tree.

^gThis does not include the time to compute the resampled trees.

To estimate performance on large alignments, we extrapolated from the largest feasible alignment for that method and its theoretical complexity. Inferring a tree from a distance matrix requires O(N²) space and either O(N²) time (FastME and RapidNJ; Simonsen et al. 2008), O(N²logN) time (Clearcut), or O(N³) time (QuickTree and BIONJ). Computing bootstrap values from resampled trees with PHYLIP's consense or with QuickTree's built-in bootstrap requires O(N²) space and O(N³) time. For QuickTree, which identifies and removes duplicate sequences, we used the number of unique sequences rather than the total number.

Results

Topological Accuracy in Simulations

We tested FastTree and other methods for inferring phylogenies on simulated protein alignments with realistic topologies, realistic gaps, varying evolutionary rates across sites, and between 10 and 5,000 sequences. The simulated alignments ranged from 64 to 1,009 positions (median 304), with 9% gaps, and on average, pairs of sequences within these alignments were 33% identical. For each alignment and for each method, we counted the proportion of splits that were correctly inferred.

As shown in table 1, FastTree was significantly more accurate than other minimum evolution methods but was 1–2% less accurate than PhyML, a maximum likelihood method (Guindon and Gascuel 2003). We will show that FastTree scales to far larger alignments than current maximum likelihood methods can handle. Furthermore, most of the splits that disagree between minimum evolution and maximum likelihood trees are poorly supported (Nei et al. 1998). This is true in our simulations as well, even for the splits that PhyML inferred correctly but FastTree missed (data not shown). Thus, the practical effect of these differences may be much less than 1–2%.

Table 1.

Topological Accuracy of Tree-Building Methods on Simulated Protein Alignments with Gaps

	Topological Accuracy
Method	Distances	n = 10	n = 50	n = 250	n = 1,250	n = 5,000
PhyML	JTT	0.744a	0.771a	0.817a	0.801a	—
FastTree	Log-corrected	0.724b	0.763b	0.797b	0.778b	0.763b
FastME	Log-corrected	0.716c	0.754c	0.796b	0.777b	0.753c
BIONJ	Log-corrected	0.725b	0.754c	0.766c	0.730c	0.723c
BIONJ	JTT	0.701c	0.758c	0.777c	0.737c	0.731c
BIONJ	JTT + Γ	0.567c	0.625c	0.737c	0.697c	—
QuickTree	Log-corrected	0.716c	0.746c	0.760c	0.726c	0.716c
QuickTree	%Different	0.673c	0.678c	0.699c	0.672c	0.655c
Clearcut	Log-corrected	0.682c	0.733c	0.755c	0.723c	0.715c

^aSignificantly more accurate than FastTree (P < 0.01, paired t-test)

^bNot significantly different from FastTree (P > 0.01, paired t-test)

^cSignificantly less accurate than FastTree (P < 0.01, paired t-test)

After FastTree, the next best method was FastME, which like FastTree uses NNIs according to the minimum evolution criterion (Desper and Gascuel 2002). Depending on the number of sequences, FastTree was slightly but significantly more accurate than FastME, or the two methods were tied. FastTree was up to 4% more accurate than BIONJ, a weighted variant of Neighbor-Joining (Gascuel 1997), when run with FastTree's log-corrected distances. BIONJ with log-corrected distances was about as accurate as BIONJ with maximum likelihood distances from PHYLIP's protdist, so FastTree's distance measure is adequate. Maximum likelihood distances that were estimated using a model with gamma-distributed rates gave poor results. FastTree was 1–5% more accurate than QuickTree, an implementation of traditional Neighbor-Joining (Howe et al. 2002), and 4–6% more accurate than Clearcut, an implementation of relaxed Neighbor-Joining (Evans et al. 2006). Clearcut is more scalable than the other distance matrix methods but not as scalable as FastTree (see below).

We obtained similar results with a standard set of simulations of ungapped nucleotide alignments (Desper and Gascuel 2002) or with ungapped protein simulations (supplementary tables 1 and 2; Supplementary Material online). Furthermore, FastTree was more accurate than BIONJ regardless of how strongly the tree deviated from the molecular clock or how divergent the sequences were (Supplementary fig. 1; Supplementary Material online).

These simulations also confirm that topologies can be inferred even when there are many more sequences than sites (Bininda-Emonds et al. 2001). The alignments with 5,000 sequences contained just 197–384 sites, yet FastTree identified 76.3% of the splits correctly.

Effectiveness of FastTree's Approximations and Heuristics

The simulations also let us test the internals of FastTree. First, FastTree's Neighbor-Joining phase should give roughly the same results as BIONJ with uncorrected distances. In practice, the two methods had very similar accuracies, as did FastTree's Neighbor-Joining with exhaustive search (table 2). Thus, FastTree's accuracy was not affected by its approximations to handle gaps or by its heuristics to reduce the number of joins considered. Heuristic search was also over 100 times faster: for an alignment of 1,250 proteins with 338 positions, the Neighbor-Joining phase of FastTree took 1,551 s with exhaustive search but only 8 s with heuristic search.

Table 2.

The Topological Accuracy of Variants of FastTree on Simulated Protein Alignments with Gaps

	Topological Accuracy
Method	N = 250	N = 1, 250	N = 5, 000
FastTree, default settings	0.797	0.778	0.763
FastTree + extra NNI (20 rounds)	0.797	0.778	0.763
FastTree's Neighbor-Joining (no NNI)	0.734	0.702	0.698
FastTree, exhaustive search, no NNI	0.733	0.701	—
BIONJ, uncorrected distances	0.731	0.699	0.694
BIONJ, log-corrected distances	0.766	0.730	0.723

Second, using uncorrected distances only reduced the accuracy of BIONJ by around 3% (table 2). This is consistent with a previous simulation study of realistic topologies and protein alignments (Hollich et al. 2005). Because using uncorrected distances leads to relatively few errors, FastTree can correct these errors by doing a few rounds of NNIs. Adding more rounds of NNIs did not increase accuracy (table 2).

Quality of Trees for Genuine Alignments

To test the quality of FastTree's results on genuine protein families, we inferred topologies for alignments of 500 randomly selected sequences from large COGs. These alignments ranged from 65 to 1,009 positions, and within each alignment, the average pair of sequences was 27% identical. To quantify the quality of each topology, we used PhyML to optimize the branch lengths and compute the log likelihood. We ran PhyML with the Jones, Taylor, and Thorton (JTT) model of amino acid substitution and four categories of gamma-distributed rates.

In table 3, we report the average difference in log likelihood between that method's trees and FastTree's trees. The methods are sorted by the average difference. All the distance matrix methods gave significantly worse average likelihoods than FastTree (paired t-test, all P < 1⁰ −20). Furthermore, as in the simulations, FastTree's approximations and heuristics did not reduce the quality of the trees (supplementary table 3; Supplementary Material online). Overall, we found that for these genuine alignments, FastTree's topologies were of high quality.

Table 3.

The Relative Log Likelihoods of Topologies Inferred for 310 Genuine Protein Alignments of 500 Sequences Each

Method	Distances/model	Average log likelihood	Lower likelihood than FastTree(%)
PhyML/FastTreea	JTT + Γ4b	440.7	0
FastTree	Log-corrected	0.0	—
FastME	Log-corrected	– 165.2	86
BIONJ	JTT	– 404.3	95
BIONJ	Log-corrected	– 426.1	> 99
QuickTree	Log-corrected	– 495.3	> 99
Clearcut	Log-corrected	– 532.2	99
QuickTree	%Different	– 667.0	100
BIONJ	JTT + Γ	– 1,576.1	99

^aPhyML 3 with FastTree as the starting tree.

^bΓ₄ means four categories of sites with gamma-distributed rates.

We also tested the quality of FastTree trees for sets of 500 nonredundant sequences from a large 16S rRNA alignment (DeSantis et al. 2006; http://greengenes.lbl.gov). To quantify the quality of each topology, we used PhyML with the Hasegawa–Kishino–Yano 85 model, which accounts for the higher rate of transitions over transversions, and four categories of gamma-distributed rates. FastTree found topologies with higher likelihoods than most of the distance matrix methods (table 4). FastME did outperform FastTree slightly if given maximum likelihood distances that account for the higher rate of transitions than transversions. Distinguishing transitions from transversions might further improve FastTree's topologies.

Table 4.

The Relative Log Likelihoods of Topologies Inferred for 100 Genuine 16S rRNA Alignments of 500 Sequences Each

Method	Distances/model	Average log likelihood	Lower likelihood than FastTree(%)
PhyML	HKY85 + Γ4	510.4	0
PhyML	HKY85	358.4	5
FastME	F84 + Γ	59.9	34
FastTree	Jukes–Cantor	0.0	—
FastME	Kimura	– 7.4	53
FastME	Jukes–Cantor	– 71.7	70
BIONJ	F84 + Γ	– 749.1	100
BIONJ	Kimura	– 781.0	100
BIONJ	Jukes–Cantor	– 843.9	100
QuickTree	F84 + Γ	– 878.8	100
Clearcut	F84 + Γ	– 905.1	100
QuickTree	Jukes–Cantor	– 941.1	100
Clearcut	Jukes–Cantor	– 982.3	100

NOTE.—HKY, Hasegawa–Kishino–Yano.

CPU Time and Memory Required to Infer Trees

We tested FastTree and other methods on a protein alignment from the COG database (COG2814), a domain alignment from PFam (PF00005), and a trimmed alignment of full-length 16S rRNAs (Tatusov et al. 2001; Finn et al. 2006; http://greengenes.lbl.gov). These alignments contain roughly 8,000–150,000 distinct sequences (table 5). Running the distance matrix methods on the larger alignments was not feasible, so we extrapolated from smaller alignments (see Materials and Methods). The actual or estimated CPU time and memory usage are shown in table 6.

Table 5.

Genuine Alignments for Performance Testing

Alignment	COG2814	PF00005	16S rRNA
Type	Protein	Protein	Nucleotide
#Sequences	10,610	52,927	167,547
#Distinct	8,362	39,092	158,022
#Columns	394	214	1,287
%Gaps	10.8	15.2	4.3

The maximum likelihood methods we tested, PhyML 3 (Guindon and Gascuel 2003) and RAxML VI (Stamatakis 2006), did not complete in 50 days on the smallest of these problems, which took FastTree about 3 min. (Despite the high usage of virtual memory by PhyML, both PhyML and RAxML ran at over 99% CPU utilization.) Even for COG alignments of just 1,250 proteins, PhyML 3 typically took over a week. Thus, current maximum likelihood methods do not scale.

Most of the methods require a distance matrix as input, so in practice, the running time is the time to compute a distance matrix plus the time to infer a tree. As shown in table 6, FastTree is over 1,000 times faster than computing maximum likelihood protein distances. For the 16S rRNA alignment, FastTree is as fast as computing Jukes–Cantor distances and over 100 times faster than computing maximum likelihood distances with gamma-distributed rates.

For the 16S alignment, the only method other than FastTree that seems practical is Clearcut: all the other methods would require over 1,000 h or over 500 GB of memory. Clearcut itself is very fast—we estimate that it might take only 12 h to infer a tree from the 16S distance matrix. However, Clearcut requires a distance matrix, and FastTree is faster than Clearcut once the cost of computing the distance matrix is included. Clearcut would also require over 50 GB of memory—20 times as much as FastTree—which makes it impractical for us to run. Furthermore, Clearcut seems to be less accurate than FastTree (tables 1, 3, and 4).

Effectiveness and Speed of the Local Bootstrap

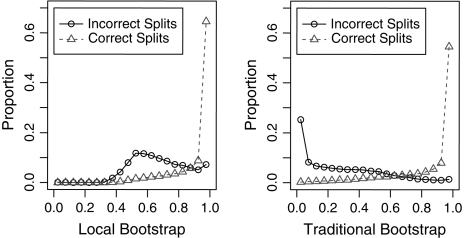
To test whether FastTree's local bootstrap can identify which splits are reliable, we used the protein simulations with 250 sequences. We also computed the traditional bootstrap: we used PHYLIP's seqboot to generate resampled alignments, we ran FastTree on each resample, and we counted how often each split in the original tree was present in the resampled trees. For both methods, we used 1,000 resamples. As shown in figure 2, both methods were effective in identifying correct splits. If we define “strongly supported” as a local bootstrap of ≥95%, then 65% of the correct splits were strongly supported. Conversely, 97% of the strongly supported splits were correct.

FIG. 2.—

Distribution of support values for simulated alignments of 250 protein sequences with gaps. We compare the distribution of FastTree's local bootstrap and the traditional (global) bootstrap for correctly and incorrectly inferred splits. The right-most bin contains the strongly supported splits (0.95–1.0)

To quantify how effective the measures were in distinguishing correct splits, we used the area under the receiver operating characteristic curve (AOC; DeLong and Clarke-Pearson 1998). The AOC is the probability that a true split will have a higher support value than an incorrect split, so a perfect predictor has AOC = 1 and a random predictor has AOC = 1/2. The traditional bootstrap had an AOC of 0.933 versus 0.875 for the local bootstrap. Overall, the local bootstrap is not quite as sensitive as the traditional bootstrap, but it is a strong indicator of which splits are correct.

The local bootstrap was far faster than the traditional bootstrap and required far less memory. The traditional bootstrap takes 100 times longer than tree inference plus the time to compare the trees to each other. For the 16S rRNA alignment, performing the tree comparisons with PHYLIP's consense would take months and would require over 90 GB of memory (table 6). In contrast, FastTree computed the local bootstrap in an hour and 2.4 GB.

Discussion

Large Alignments

We have relied on profile-based multiple sequence alignment as the most practical method for large families. However, profile-based alignment is believed to be less accurate than progressive alignment. Thus, whenever possible, biological inferences from these large trees should be confirmed with smaller, higher quality alignments. This also allows the use of slower but more accurate tree-building methods and tests. For example, MicrobesOnline.org includes interactive tools for browsing large trees, for selecting relevant sequences, and for building progressive alignments and maximum likelihood trees with those sequences.

Scaling to a Million Sequences

FastTree computes trees for the largest existing alignments, with on the order of 100,000 sequences, in under a day. However, given the rapid rate of DNA sequencing, we expect that alignments with 1,000,000 sequences will soon exist. For such large alignments, the major memory requirement will be the top-hits lists, which take O(N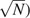) space. For 1 million sequences, this will be about 20 GB. In contrast, the distance matrix for a million sequences would take 2 TB of memory. FastTree's running time should scale by between O(NlogN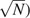) and O(N²), so inferring a tree for a million rRNA sequences should take 2–4 weeks. Tuning the top-hits heuristic might reduce this time.

Conclusions

FastTree makes it practical to infer accurate phylogenies, including support values, for families with tens or hundreds of thousands of sequences. These phylogenies should be useful for reconstructing the tree of life and for predicting functions for the millions of uncharacterized proteins that are being identified by large-scale DNA sequencing. FastTree executables and source code are available at http://www.microbesonline.org/fasttree; FastTree trees for every prokaryotic gene family are available in the MicrobesOnline tree-browser (http://www.microbesonline.org/); and a FastTree tree for all sequenced full-length 16S rRNAs is available from the FastTree Web site and will be included in the next release of greengenes (http://greengenes.lbl.gov).

Supplementary Material

Supplementary notes 1 and 2, Tables 1–3 and figure 1 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).