Modeling Confidence and Response Time in Recognition Memory

Abstract

A new model for confidence judgments in recognition memory is presented. In the model, the match between a single test item and memory produces a distribution of evidence, with better matches corresponding to distributions with higher means. On this match dimension, confidence criteria are placed, and the areas between the criteria under the distribution are used as drift rates to drive racing Ornstein-Uhlenbeck diffusion processes. The model is fit to confidence judgments and quantile response times from two recognition memory experiments that manipulated word frequency and speed versus accuracy emphasis. The model and data show that the standard signal detection interpretation of z-transformed receiver operating characteristic (z-ROC) functions is wrong. The model also explains sequential effects in which the slope of the z-ROC function changes by about 10% as a function of the prior response in the test list.

Over the last 15 years, receiver operating characteristic (ROC) functions, as defined by signal detection theory (SDT; Green & Swets, 1966), have often been used to interpret recognition memory data. ROC analyses have been used extensively to test memory models, to guide the development of memory models, and to argue for and against single versus dual process retrieval models.

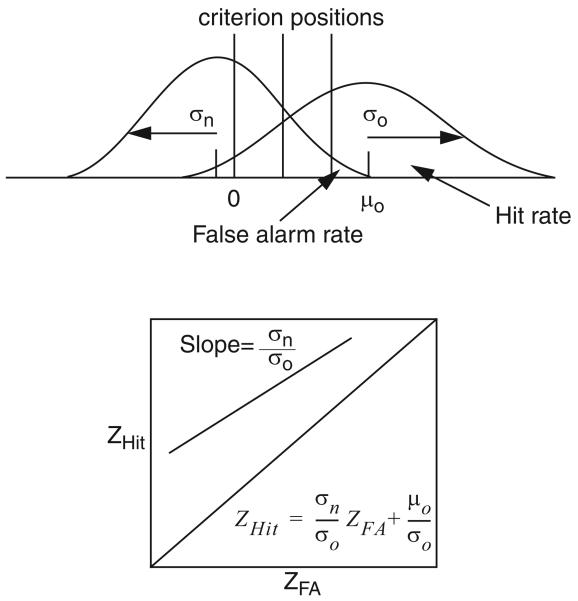
In a recognition memory experiment, a list of words is studied and the study list is followed by a list of test words. In a standard two-choice experiment, subjects are asked to decide whether or not the test words appeared in the study list. To model this judgment with SDT, a single criterion value is placed on a dimension that represents the degree to which a test item matches information in memory. If the match value is above the criterion, an “old” response is produced; and, if it is below, a “new” response is produced. Changes in the placement of the decision criterion are used to model the effects of bias toward one or the other of the two choices. In Figure 1, there are two normal distributions, one for old items and one for new items, with unequal standard deviations. The figure shows three possible confidence criteria. For each one, the hit rate is the proportion of “old” responses to studied stimuli and the false-alarm rate is the proportion of “old” responses to new stimuli. If the criterion is moved from the right to the left, from the rightmost criterion in Figure 1 to the middle or leftmost criterion, both the hit and false-alarm rates increase. ROC functions are obtained by plotting hit rates against false-alarm rates for each criterion. If the proportions of hits and false alarms are transformed to z-scores, then a plot of Z_Hit versus Z_FA produces a straight line with the slope equal to the ratio of the standard deviations: σ_N/σ_O, as illustrated in the bottom panel of Figure 1.

Figure 1.

An illustration of the standard signal detection model with one normal distribution for old stimuli and another for new stimuli, the z-ROC plotted from the two distributions, and the equation relating the z-transformed hit and false-alarm rates. μ_o is the mean of the distribution for old words and σ_o and σ_n are the standard deviations for the distributions of old and new words respectively. Z_Hit = z-score of the hit rate; Z_FA = z-score of the false-alarm rate.

In a confidence judgment procedure, subjects are asked to rate their confidence that a test item is old or new. The same match dimension is assumed as for the two-choice task, but instead of one criterion, there are several. The position of the match value relative to these confidence criteria determines the confidence response. For a confidence judgment task with four confidence categories, the three criteria might be placed as in Figure 1 to partition the match dimension into four response regions. To form a z-transformed receiver operating characteristic (z-ROC) function, hit and false-alarm rates are computed first for the rightmost, highest confidence old category, then for the two rightmost categories (adding the number of responses in the two categories), then for the three rightmost, and so on. Just as for the two-choice task, if the distributions are normal, the z-ROC function is linear with a slope that equals the ratio of standard deviations, as in the bottom panel of Figure 1.

In most of the recent applications of ROC functions in memory research, the probabilities of hits and false alarms have been the only dependent variable used to test models. Another major dependent variable, response time (RT), has not been considered. The few attempts to model both RTs and probabilities have either not been fit explicitly to data or they have not been widely applied. Most importantly, they have not provided any direct linkage between RTs, SDT, and ROC data.

As will be discussed in detail below, once the proportions of responses in each confidence category are modeled jointly with the RTs for each category, theoretical conclusions that consider only the proportions of responses become invalid. Crucially, the model we propose allows different sources of noise to be independently estimated. All sources of noise are not combined into a single value, as with SDT. When the multiple sources of noise are identified, they can be separated away from the information that is of theoretical interest—the information from memory that guides old–new and confidence judgment responses.

In this article, we present a model (the RTCON model) for confidence judgments in recognition memory that is designed to simultaneously explain ROC functions and RT distributions for each of the confidence categories in an experiment. In the model, when a test word is presented, it is matched against information in memory. The degree to which a test item matches is not a single value. Instead it is represented by a normal distribution. Confidence criteria divide the distribution into regions, one for each confidence category. The area under the normal distribution for each confidence category determines the rate at which evidence is accumulated. For each category, there is a criterial amount of evidence such that when the criterion is met, a response is made. The accumulator that first reaches its criterion amount of evidence determines which confidence judgment is made.

In the sections below, we first review previous attempts to model confidence judgments and RTs and then turn to a review of SDT approaches to memory.

RT and Confidence

In early efforts to combine confidence judgments and RTs for two-choice tasks, Volkmann (1934) and Reed (1951) suggested that a confidence judgment is a function of RT. Audley (1960) explicitly proposed that confidence judgments are determined by random walk processes. The more steps toward a response criterion, the slower the RT. (Note that the number of steps in a discrete model is the analog of time in a continuous model.) The problem with using number of steps in a random walk model is that the model predicts that the RT distributions for the different confidence categories will be nonoverlapping. This is because the amount of evidence for a decision is the same for all responses at a boundary (e.g., Edwards, 1965; Laming, 1968; Pleskac & Busemeyer, 2007). For example, high-confidence responses will be fast and low-confidence responses will be slow, and a fast response cannot be a low-confidence response (although the distributions might overlap slightly as a result of variability in encoding or response output processes). The RT distributions from our experiments, described below, and other experiments (e.g., unpublished RT results from Ratcliff, McKoon, & Tindall, 1994, Experiments 3 and 4) almost completely overlap and so this type of model is ruled out (see the more complete discussion in Vickers, 1979). Two other random walk models (Audley & Pike, 1965; Laming, 1968, p. 86) have also been proposed for tasks that involve more than two choices, but neither has been fully developed or applied to experimental data.

Another class of models, balance-of-evidence models (Vickers, 1979), has been applied to experiments in which, for each test item, subjects first make an old/new judgment and then a confidence judgment. Evidence is accumulated in two counters (cf., LaBerge, 1962) and which counter first reaches its criterial amount of evidence determines the old/new response. The confidence judgment is then determined by the difference in accumulated evidence between the two counters, in other words, the balance of evidence. To calculate the difference in evidence, the system must have access to the amounts of evidence in each of the counters (Vickers, 1979; Vickers & Lee, 1998, 2000). There has been relatively little evaluation of this model using RT and confidence judgment data.

Pleskac and Busemeyer (2007) recently extended the diffusion model to accommodate confidence ratings. As with the balance-of-evidence models, this model is tailored to a paradigm in which confidence judgments follow an initial two-alternative decision. The initial two-alternative decision is modeled with a standard diffusion process. After the process reaches a boundary for the initial yes–no decision, there is an additional period of evidence accumulation, and confidence ratings are based on the position of the process at the end of this period. The model makes predictions about RTs for the two-choice task but makes no predictions about RT for the confidence judgments. The confidence RT will always be a constant. Pleskac and Busemeyer speculate that their model could be extended to a paradigm in which subjects make a single selection from a confidence scale if one assumes that subjects make an implicit two-alternative decision and then select a confidence level. However, these suggestions have not been translated into an explicit model.

For memory research, the focus of this article, Van Zandt and colleagues (2000; Merkle & Van Zandt, 2006; Van Zandt & Maldonado-Molina, 2004) have proposed a balance-of-evidence Poisson counter model as the basis for confidence judgments and RTs. In this model, unit counts arrive in two accumulators at exponentially distributed times. The accumulator that reaches criterion first determines the old/new decision, and then the difference in evidence between the terminated winning accumulator and the nonterminated losing accumulator is used to make the confidence judgment.

Both the Vickers (1970) accumulator model and the Poisson counter models were evaluated for two-choice tasks by Ratcliff and Smith (2004), who found that neither model satisfactorily accounted for the distributions of correct and error RTs or accuracy values. Also, the Poisson counter confidence model appears to be unable to account for the shapes of the RT distributions for the confidence categories (Van Zandt, 2000, Figure 11). In particular, the predicted confidence distributions appear to be much less skewed than the empirical data.

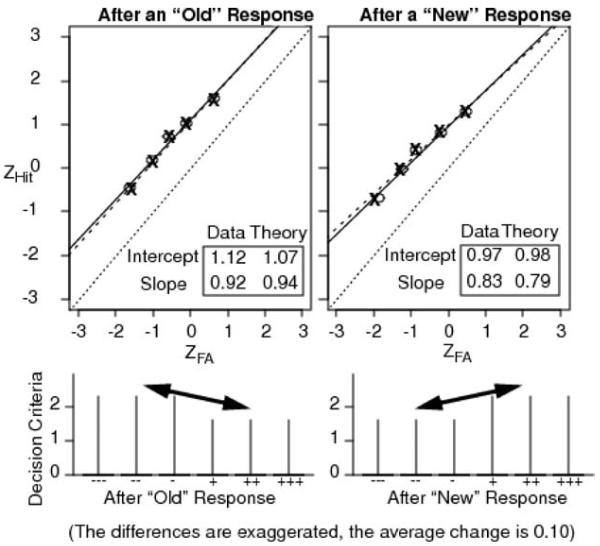
Figure 11.

In the top panel, two z-ROC functions for responses preceded by an “old” response or a “new” response. The bottom panels show how the model accounts for this. For the confidence categories, “−−−” is high-confidence new, “+++” is high-confidence old, and the other symbols represent lower confidence responses. Z_Hit = hit rate z-score; Z_FA = false-alarm rate z-score.

In a different kind of model, Juslin and Olsson (1997) attempted to explain RTs, accuracy, and confidence judgments with assumptions similar in spirit to the runs model (Audley, 1960). Evidence was sampled at equally spaced time steps and a response was made when the amount of evidence in a window of the last k samples was greater than one criterion or lower than another criterion. Confidence judgments were then determined by the variability in the samples represented by the proportion of evidence samples greater than zero versus the proportion less than zero. This model was critiqued by Vickers and Pietsch (2001), who showed that the relationship between accuracy and RT as a function of speed–accuracy instructions was not correctly predicted nor was the relationship between RT and confidence judgments.

The balance-of-evidence models are primarily designed to explain confidence judgments that are made after old/new decisions. They would need to be modified to explain performance when subjects make only a confidence judgment decision, not an old/new decision followed by a confidence judgment decision.

Even when confidence judgments are made after old/new decisions, these models have a serious problem: The confidence judgment is a second decision, after the old/new decision, and it could be based on a separate process that does not use the information accumulated to make the yes/no decision. The confidence judgment might be completely independent of the first decision, or it might be partially dependent on it (e.g., Baranski & Petrusic, 1998). In the majority of experiments in memory research, subjects make only a confidence judgment, not a yes/no response. Our model was developed to explain performance with this procedure.

Signal Detection Theory and Recognition Memory

There has been a long history of applying SDT to recognition memory, starting with Egan (1958). Egan found linear z-ROC functions with slopes of about 0.7, consistent with normal distributions of match for old and new items with unequal standard deviations (see also Wickelgren & Norman, 1966). Although Egan used normal distributions, Banks (1970) and Lockhart and Murdock (1970) showed that linear z-ROC functions are consistent with other kinds of distributions, for example, exponential distributions. With exponential distributions, the slope would not be the ratio of standard deviations, as it is if the distributions are normal.

In the experimental literature, linear z-ROCs (or functions in-distinguishable from linear) are a typical finding. However, there have been some cases in which the z-ROC functions have been systematically nonlinear, and these have inspired theoretical development (Arndt & Reder, 2002; DeCarlo, 2002; Malmberg & Xu, 2006; Ratcliff et al., 1994; Rotello, Macmillan, & Van Tassel, 2000; Yonelinas, Dobbins, & Szymanski, 1996). Several theories have focused on accommodating U-shaped z-ROC functions, sometimes seen in recognition memory experiments and commonly seen in associative recognition and source memory experiments (Glanzer, Hilford, & Kim, 2004; Hilford, Glanzer, Kim, & DeCarlo, 2002; Kelley & Wixted, 2001; Qin, Raye, Johnson, & Mitchell, 2001; Slotnick & Dodson, 2005; Slotnick, Klein, Dodson, & Shimamura, 2000; Wixted, 2007; Yonelinas, 1997, 1999).

U-shaped functions violate SDT's assumption of normal distributions. Theorists have responded by elaborating SDT. One such elaboration is the dual process model (Yonelinas, 1994), which attempts to explain recognition memory performance in terms of a standard signal detection process plus a “recollection” process. For the SDT process, the distributions of match values for old and new items are normally distributed with equal variance. For the recollection process, a threshold retrieval process recovers qualitative details from the learning event. In this model, subjects respond based on recollection on some proportion of trials and degree of match on the other trials. The joint influence of recollection and degree of match leads to a U-shaped z-ROC function, and empirical nonlinear functions are taken as evidence for the dual-process approach. Alternatively, DeCarlo (2002, 2003) showed that U-shaped functions can be produced if the distributions of match values are probability mixtures of two different distributions, for example, distributions from items that were attended during study versus items that were not attended at study (see Kelley & Wixted, 2001, for a similar approach).

In both DeCarlo's (2002, 2003) and Yonelinas's (1994) proposals, the nonlinearity of z-ROC functions has been used to draw conclusions about the nature of memory evidence. In Yonelinas's model, evidence comes from two qualitatively different processes; and, in DeCarlo's model, it comes from a mixture of qualitatively similar processes. As we will demonstrate, our model can produce nonlinear z-ROC functions without assuming two qualitatively different processes or mixtures of processes. It follows, then, that z-ROC shapes cannot be used to directly infer the nature of evidence from memory.

There have also been attempts to directly link SDT to RT in the recognition memory literature. The hypothesis was that the nearer the quality of evidence from a stimulus to the criterion, the longer the RT (e.g., Murdock, 1985; Norman & Wickelgren, 1969). However, this approach fails to capture the shapes of RT distributions, and it fails to account for the relative speeds of correct and error responses (see Ratcliff, 1978; Ratcliff, Van Zandt, & McKoon, 1999).

The Two-Choice Diffusion Model and Signal Detection Theory

Ratcliff's two-choice diffusion model has been successful in explaining accuracy values and RT distributions for correct and error responses in a wide variety of tasks (Ratcliff, 1978, 1988, 2006; Ratcliff & McKoon, 2008; Ratcliff & Rouder, 1998; Ratcliff et al., 1999). In the model, evidence toward the decision criteria, one criterion for one of the possible responses and the other criterion for the other possible response, is accumulated over time. The accumulation process is noisy, with noise normally distributed. The rate at which evidence is accumulated, the drift rate, is determined by the quality of the information from the stimulus. For example, in a perception experiment, the drift rate is determined by the quality of perceptual information. In a recognition memory experiment, the drift rate is determined by the match between a stimulus and memory. The quality of the information from stimuli of the same type (e.g., the high-frequency words in a recognition memory experiment) varies across trials (with a normal distribution). In other words, drift rate varies across trials. A criterion, the drift-rate criterion, is set such that if the quality of the stimulus information is above the criterion, evidence accumulates toward one of the decision criteria; and, if it is below, evidence accumulates toward the other decision criterion. The drift rate criterion is exactly analogous to the criterion in SDT (Ratcliff, 1978, 1985; Ratcliff et al., 1999).

For two-choice decisions, the diffusion model's interpretation of ROC functions is quite different from the SDT interpretation despite their similarities— both using normal distributions of stimulus information. The diffusion model has two types of adjustable criteria: the two-response decision criteria and the drift-rate criterion. Manipulating either or both of these can produce ROC functions. Hit and false-alarm proportions can be altered by moving the starting point of the evidence accumulation process from nearer one of the decision criteria to nearer the other decision criterion. This is optimal for random walk and diffusion models for a single condition in the sense that it produces the highest overall accuracy in the minimum average decision time (e.g., Laming, 1968). However, hit and false-alarm proportions can also be altered by moving the drift rate criterion from nearer the mean evidence for new items to nearer the mean evidence for old items. This is exactly the same as changing the criterion in SDT. The two possibilities are identifiably different because moving the starting point shifts the leading edge of the RT distribution more, whereas moving the drift criterion shifts the leading edge less (Ratcliff, 1978, 1985; Ratcliff et al., 1999; for a detailed review, see Ratcliff & McKoon, 2008). These differences between SDT and the diffusion model are key. For the diffusion model, ROC functions can be produced by changing the starting point between the decision criteria, changing the drift criterion, or both.

A second difference between the SDT and diffusion model interpretations of ROC functions is that in SDT there is only one source of noise, noise in the distributions of stimulus quality. In the diffusion model, there are three sources that affect accuracy: the noise across trials in the quality of evidence from a stimulus (the noise in drift rates across trials), the noise in the accumulation of evidence process, and the noise in the criteria (or equivalently, in the starting point). The three sources of noise are identifiable. In SDT, these sources of noise cannot be separated; and so ROC functions cannot be uniquely attributed to noise in stimulus quality (see McNicol, 1972).

More specifically, in the diffusion model, the effects of noise in the distributions of stimulus quality can be attenuated by noise in the decision criteria (or starting point), noise in the accumulation-of-evidence process, or both. For example, suppose that the slope of the z-ROC function was 0.8. In standard SDT, this would mean that the ratio of the standard deviations of the match distributions for new versus old test items would be 0.8. But if there were also within-trial noise in the diffusion process and between-trial noise in the decision criteria, then these sources of variability would add to the noise in the stimulus information. The diffusion process noise and criterion noise affect all item types, which makes the variability for old and new items more similar when all noise sources are conflated (as they are in SDT). The true ratio of the standard deviations in just the stimulus information would then have to be smaller than 0.8.

Modeling Confidence Judgments

A bias that has guided our model development is that each response category requires a separate response (separate key press); and so each must correspond to a separate unit that accumulates evidence to a decision criterion. Thus, we assume that each confidence category has a different diffusion process accumulating evidence to a different decision criterion. This means that each diffusion process has a different drift rate and we need to have some way of relating match values from memory to drift rate in a way that is more constrained than simply assuming six different drift rates for each stimulus type in an experiment. We chose to constrain the models using an SDT representation in which the output from a match of a test item with memory is a normal distribution (not a single value). On this match dimension, confidence criteria are placed, and the areas under the normal distribution between criteria represent accumulation rates in diffusion processes.

Our proposal is that there is no access to position of the process in any accumulator prior to the process terminating (e.g., Ratcliff, 2006). This is in contrast to the proposals discussed above that assume that confidence is computed from the difference in evidence between a terminated process and the competing process that did not terminate (Van Zandt, 2000; Vickers, 1979) or that confidence is based on the position of a binary process some time after a yes/no decision has been made (Pleskac & Busemeyer, 2007).

In simple decision making-tasks, it is well accepted that there are multiple sources of noise in processing, as there are in the diffusion model discussed above. First, there is perceptual or memory noise so that the encoding of the stimulus or the match between a test item in memory is not the same on every trial of the same type. Second, there is noise added by the decision process. Third, there is criterion noise such that the decision criteria do not have the same values on each trial. A major advantage of sequential sampling models is that these sources of noise are identifiable. As just mentioned, this contrasts with SDT in which these sources of noise are not identifiable.

The fact that there are multiple sources of noise in the model has important consequences both for z-ROC functions and for the two-choice diffusion model. Because the multiple sources of variability in our model are identifiable, the slope of the z-ROC is a function not only of variability in memory strength across trials but also of decision variability, criterion variability, and even decision criterion settings.

A Description of the RTCON Model

In a confidence judgment experiment, each confidence category requires a different response (a different key press). In the RTCON model, evidence from a stimulus is accumulated to decision criteria, with different criteria for each category. Unlike the balance-of-evidence models discussed above, there is no access to information as it accumulates (e.g., Ratcliff, 2006). Our model is a natural extension of two earlier approaches: racing diffusion processes (Ratcliff et al., 2007; Smith, 2000; Usher & McClelland, 2001) and distributed representations of information in memory (Ratcliff, 1981). The model has some global similarity to the model for RT in absolute identification by Brown, Marley, Donkin, and Heathcote (2008), which uses a different representation of information but has racing accumulators, though they are deterministic rather than stochastic, as in the model here. Note that in the cases in which models with two racing diffusion processes and the standard diffusion model have been fit to two-choice data, the two tend to mimic each other with the standard diffusion model fitting numerically a little better (Ratcliff, 2006; Ratcliff & Smith, 2004; Ratcliff, Thapar, Smith, & McKoon, 2005).

Output From the Match Process

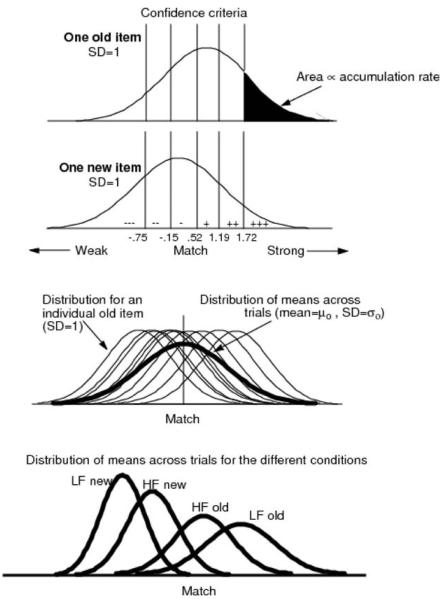
The output of the process that matches a test item against memory is not a single discrete value. Instead, it is a distribution over the match dimension (cf. Ratcliff, 1981, for similar assumptions about the distribution of letter representations over ordinal position in the perceptual matching task). The assumption that each individual item produces a distribution of match is the key to how the model works. The top panel of Figure 2 illustrates the distribution for one old test item and the second panel illustrates the distribution for one new test item. For all test items, these distributions are normal with SD = 1.0. The lines on the two panels are the confidence criteria for six confidence categories, to be discussed below.

Figure 2.

The top two panels show distributions of match for a single old test item and a single new test item, respectively. The vertical lines are possible positions for decision categories, with the same confidence criteria for each. The third panel shows the distributions for tests of single items (thin lines) and the distribution of their means across trials (bold line). The bottom panel shows the distributions of means for the four categories of test items in Experiment 1. For the confidence categories, “−−−” is high-confidence new, “+++” is high-confidence old, and the other symbols represent lower confidence responses. HF indicates words with high probability of occurrence in English, and LF indicates low-frequency words.

We assume that for the same item type, from trial to trial, it is impossible to produce identical distributions over match values. This was an early assumption by Ratcliff (1978) and subsequently proved necessary for diffusion models to correctly account for the relative speed of correct and error responses (Ratcliff, 1981; Ratcliff et al., 1999). For items in the same condition (e.g., high-frequency words), the positions (means) of their normal distributions vary across trials, as shown in the third panel of Figure 2. The fine lines are the distributions for individual test items, each with the same standard deviation, and the bold line is the distribution of their means across trials. For our first experiment, the distributions of the means for the four conditions in the experiment are shown in the bottom panel of the figure. The variability in the means of the distributions from trial to trial is similar to the variability that is assumed in SDT. But, as we show later, the ratios of the standard deviations in the RTCON model are not the same as the SDT ratios provided by the slopes of the z-ROC functions. Further discussion of the differences in the means and standard deviations of these distributions will be presented below.

The Decision Process

The confidence criteria divide the match dimension into regions, one for each confidence category. The size of a region, that is, the area under the curve for the region, provides the drift rate for the diffusion decision process for that confidence category. The confidence criteria for six categories are illustrated in the top two panels of Figure 2. In the top panel, the black region is the area under the curve and drift rate for highest confidence old test items.

Figure 3 shows how the distribution of match for a single test item is mapped to the decision process. The top panel illustrates that the decision criteria for the different confidence categories can be different from each other. The confidence criteria divide the match dimension into regions. For example, the black area in the middle panel determines drift rate for the highest confidence “old” response, the area immediately to its left determines drift rate for the medium confidence “old” response, and the next area to the left determines drift rate for the lowest confidence “old” response. The top panel shows the six accumulators and the amount of evidence in each at some point in time before any of them have reached criterion. The far right area in the top panel is relatively large, so its drift rate is relatively large, so the amount of evidence that has been accumulated in the highest confidence “old” category is relatively large. The area in the category to the immediate left is smaller, so the drift rate is smaller, so the amount of evidence in the medium confidence old category is smaller. However, we stress that because the accumulation process is noisy, the accumulator with the most evidence at this time point will not necessarily be the one that wins.

Figure 3.

The top panel shows accumulators for six confidence categories with the amount of evidence accumulated in each at some point in time. The decision criteria for each accumulator are also shown. The equation shows the change in evidence as a function of time, where v is the drift rate, k is the decay rate, x(t) is the position of the accumulator at time t, dt is the size of the time steps, and σ is the within-trial noise. The middle panel shows how six match values map into the amounts of evidence, that is, how they map into drift rates for the diffusion decision process. The black area determines the drift rate for the highest confidence old category. The bottom panel shows how narrow versus wide separations of confidence criteria (the black areas on the left and right distributions) can lead to large versus small drift rates. For the confidence categories, “−−−” is high-confidence new, “+++” is high-confidence old, and the other symbols represent lower confidence responses.

Unlike SDT, the values of the confidence criteria are not uniquely identifiable from the proportions of responses in the confidence categories because the decision criteria can trade off against the confidence criteria. For example, the proportion of responses in one of the confidence categories can be decreased either by moving the confidence criteria closer together or by increasing the decision criterion for that category. In the RTCON model, the constraints provided by RT largely eliminate tradeoffs between the decision and confidence criteria as we show using Monte Carlo simulations later.

Decision Process Dynamics

Each accumulator implements an Ornstein-Uhlenbeck (OU) diffusion process with normally distributed noise in the accumulation process. The OU process adds a decay factor to the standard diffusion process. As a function of the amount of evidence in an accumulator, a term, kx, is subtracted from the drift rate. k is the decay constant (in units of 1/ms) and it is multiplied by the current amount of evidence, x. In modeling RT distributions with racing diffusion processes, if decay is set to zero (i.e., a Wiener diffusion process), the tails of the distribution are not skewed out enough. This contrasts with the diffusion process with one accumulation process in which estimates of the OU decay parameter are zero (Ratcliff & Smith, 2004).

The equation for the change in evidence, dx(t), for a small time step, dt, is

$$\mathit{dx}\left(t\right)=a(v-\mathit{kx}\left(t\right))\mathit{dt}+\sigma \surd \left(\mathit{dt}\right)$$ (1)

where v is the drift rate (in units of 1/ms) derived from the area between confidence criteria (where drift rates sum to 1), k is the decay rate (in units of 1/ms), a is the scaling parameter, σ²dt is the coefficient of the diffusion process, representing within trial noise (σ² in units of 1/ms), and x is the current position in the process, that is, the current amount of evidence in the accumulator (Brown, Ratcliff, & Smith, 2006). The parameters (except for drift rate) are the same for all the accumulators. In implementing the model, we replaced the continuous equation in Equation 1 with one that uses small discrete steps to approximate the continuous model as is shown in Figure 3. In this form, dx(t) is replaced by Δx(t) and dt is replaced by Δt, where these latter terms refer to small discrete steps. Evidence in this model is not allowed to fall below zero; if it were to fall below zero at a particular iteration of the model, it is reset to zero.

Justification for Using a Distribution of Match Values for a Test Item Instead of a Single Value

For each confidence category, we use the area under the distribution of match to drive drift rate, not the height of the distribution or position on the match dimension. This means that if there is a large area between two of the confidence criteria, there is a lot of evidence for that confidence judgment. In contrast, if the height of the function (i.e., one component of a likelihood computation) or position was used, there would be no way of making one confidence response highly probable, the next not probable and the next one highly probable. This is illustrated in the left bottom panel of Figure 3; the black area represents a judgment that is unlikely, but the two to either side of it are more likely because their areas are larger. If height were used, the middle category would have the highest probability, the judgment corresponding to the black area a lower probability, and the area to the left of the black area a still lower probability. However, subjects vary in how they distribute responses across confidence categories. For a given category, some subjects might make very few responses, whereas others might make many. In the bottom panel of Figure 3, the heights of the black areas in the two figures are much the same, but the proportion of responses in them is different. Similarly, if the position on the match dimension were used (e.g., strength), the match values for the two cases in the bottom panel of Figure 3 would produce much the same values of match. Our model captures the differences in response proportions by using area under the curve between confidence criteria.

Drift rates strongly depend on memory strength in the RTCON model. As individual item memory distributions shift to the right (i.e., as strength increases), high drift rates shift from the low end of the response scale (on the “sure new” side) to the high end of the response scale (on the “sure old” side). For an item with very high strength, much of the distribution will fall above the highest confidence criterion, leading to a very high drift rate for the highest confidence old response.

It is a little unusual to assume that the area under the distribution leads to drift rates (but see Gomez, Ratcliff, & Perea, 2008; Ratcliff, 1981). An area should not be construed as representing the probability that an item has that drift rate because all items have to be assigned drift rates. We see no compelling reason that a traditional quantity, such as some value of strength, can be the only possible quantity that can drive a decision process. To understand how area could drive the decision process, suppose that a comparison for a single item involves multiple samples from the distribution of evidence. When a random sample from the distribution falls between the confidence criteria corresponding to an accumulator, then a small fixed increment is added to that accumulator. Then, an accumulator that corresponds to a large area would receive a larger number of increments and, hence, a higher drift rate than an accumulator that corresponds to a small area. It is possible to speculate how this might be accomplished neurophysiologically: If each accumulator (i.e., finger in this case) is fed by a spatially represented motor area, then differences in the number of neurons contributing to each accumulator might correspond to the area under the curve between the confidence criteria (with more neurons corresponding to a larger area). Of course, these are metaphors, and more would be needed to integrate the model with neural models or even neurophysiology (e.g., Ratcliff et al., 2007).

Predictions From the RTCON Model

Generating predictions from the model requires simulations because there are no exact solutions for RTs or confidence judgments. For the predictions presented here, we used 20,000 simulations for each condition in an experiment (e.g., high/low-frequency words, old/new test item).

Recognition memory confidence judgment experiments often produce data for which z-ROC functions are linear with slopes less than 1. Our model must be capable of producing this pattern of results at the same time that it fits the RT distributions for each of the confidence categories. The model must also be capable of producing nonlinear z-ROC functions because individual subjects can produce nonlinearity consistently across the conditions of an experiment (Malmberg & Xu, 2006; Ratcliff et al., 1994). As pointed out above, in the traditional SDT analysis, if a z-ROC slope is different from 1, then the match distributions must have different standard deviations for old versus new test items. Our model does not have this requirement.

The reason the RTCON model does not have the requirement is that z-ROC slopes different from 1 can be produced by differences in the decision criteria for the confidence categories. These differences can produce slopes different from 1 even when the standard deviations in the match distributions are the same for old and new test items. If the decision criteria increase from the high-confidence new category to the high-confidence old category and the standard deviation in match across trials is the same for old and new items, then the z-ROC slope will be less than 1. Differences in decision criteria can be separated from differences in the standard deviations of the old and new items' distributions because these two possibilities have distinctly different signatures in the location and spread of RT distributions. If one of the decision criteria increases and all the others remain the same, the RT distribution shifts and spreads towards longer RTs and fewer responses occur in the corresponding confidence category. If the standard deviation of a match distribution increases, then the proportions of responses in the middle confidence categories tend to decrease and the proportions in the extreme categories tend to increase with only small changes in the RT distributions.

Figure 4 shows predicted z-ROC functions, values of the decision criteria, and across-trial distributions of match values. Panels A, B, and C show the behavior of the model when the old and new item distributions have equal standard deviations. In Panel A, the decision criteria are all equal to each other. In Panel B, the decision criteria increase from the “sure new” category on the left to the “sure old” category on the right, and the slope of the z-ROC function is less than 1, 0.84. Panel C shows the additional effect of increasing the mean of the old item distribution, an even larger decrease in the slope, to 0.59 (e.g., Heathcote, 2003; Hirshman & Hostetter, 2000). Slopes greater than 1 can be obtained in the same way if the decision criteria decrease from “sure new” to “sure old.” The important point of this demonstration is that, for the B and C panels, the standard deviations of the old and new distributions are equal to each other but the slopes of the z-ROC functions are less than 1. This means that, in the framework of the RTCON model, the standard SDT interpretations of z-ROC slopes are wrong. They do not necessarily represent the ratio of the standard deviations of the distributions of match across trials for new and old test items.

Figure 4.

This figure illustrates how decision criteria and the old and new item distributions of evidence interact in the model to produce predictions. The bold lines and the bold text represent the changes in the values or predictions from the values in Panel A. In Panel A, the standard deviations in the across-trial memory distributions (i.e., the distributions of the means of the single-item evidence distributions) are equal and so are the decision criteria. The z-ROC function is linear with slope = 1. In Panels B and C the decision criteria are not equal. This produces a decrease in the slope of the z-ROC function. Panel D shows the effect of increasing the standard deviation in match across trials for old items, which produces a decrease in z-ROC slope. Note that the slope is not the ratio of the across trial distribution standard deviations. Panels E and F show how nonlinear z-ROC functions can be produced by altering decision criteria settings. For the confidence categories, “−−−” is high-confidence new, “+++” is high-confidence old, and the other symbols represent lower confidence responses. μ_o and μ_n are the means of the old and new across-item memory evidence distributions; σ_o and σ_n are their standard deviations. Z_Hit = z-score of the hit rate; Z_FA = z-score of the false alarm rate.

Panel D shows what happens when the distributions of match across trials for old and new test items have unequal standard deviations. If the old item distribution has the larger standard deviation and the decision criteria have the same values across the confidence categories, then the slope of the z-ROC function is less than 1, but again it is not the ratio of the standard deviations. The slope is attenuated, closer to 1 than the ratio of the standard deviations. This occurs because the other sources of variability in the model combine with variability from the distributions of match (as in standard SDT with criterion variability, McNicol, 1972, pp. 199-204). The ratio of new and old item distribution standard deviations will rarely match the slope of the z-ROC. If the values of the two old- and new-item standard deviations increase, the z-ROC slope will approach the ratio. But these are not free to vary; they are estimated in fits to the data.

Panels E and F show ways in which the model can produce nonlinear z-ROC functions. An inverted-U-shaped function is produced when the values of the confidence criteria are larger for the middle than the end categories, and a U shape is produced when the middle criteria have lower values than the end criteria. Nonlinear functions are often obtained, especially for the data from individual subjects. For example, in the studies by Ratcliff et al. (1994), some subjects showed U-shaped z-ROC functions, and others showed inverted-U-shaped functions, and these shapes were consistent across the conditions of the experiment.

It is important to remember that the RTCON model makes strong predictions about the RT distributions for each confidence category, although the predictions are not discussed here because their relationship to z-ROC functions is not simple and easy to understand. However, it must be stressed that the RT distributions severely constrain the model. The model must accurately predict both the proportions of responses in each confidence category and the RTs in each category: The predictions for ROC functions can be obtained only when all aspects of the data are fit simultaneously.

The simulations presented in Figure 4 demonstrate that the RTCON model is able to produce a wide range of z-ROC shapes, including linear, U-shaped, and inverted-U-shaped functions. This flexibility is a virtue given that all of these functional forms have been observed, but critics may conclude that the model is overly flexible and can fit any arbitrary z-ROC pattern. Critically, this conclusion ignores the additional constraints placed on the model by RT data. We performed a simulation to demonstrate the impact of RT data on the model's flexibility in accommodating z-ROC form. We generated data from parameters that produce a roughly linear z-ROC. We then hand adjusted the proportions to create an inverted-U shape in the z-ROC, but we left the RT quantiles unaltered. We fit the model to this adjusted dataset either fitting only the response proportions or fitting both response proportions and RT quantiles. When the model was fit to response proportions only, the predicted proportions matched the curved z-ROC function. Of course, we would never want the model to be fit to such a limited dataset, but this shows that the model is capable of producing the nonlinear z-ROC function. When the model was fit jointly to response proportions and RT quantiles, the predicted z-ROC function was more linear than the target data—predictions in the middle of the function missed low, whereas predictions at the end of the function missed high. Fitting reaction time quantiles that were appropriate for a linear z-ROC constrained the model so that it could not dramatically depart from linearity and so could not fit the contrived z-ROC curvature.

Fitting the Model to Data

In Experiment 1, presented below, there are four conditions (high-and low-frequency, old and new test words) and because RT quantiles are fit, there are 140 degrees of freedom in the data. In the model for these conditions, there are 24 parameters free to vary.

From Equation 1, there are three parameters that describe the change in amount of evidence as a function of time in the accumulation process that are common to all accumulators: the scaling parameter (a) accumulation rate, the standard deviation of the diffusion decision process as evidence is accumulated over time (the square root of the diffusion coefficient; σ), and decay (k). The scaling parameter was fixed at .1 in the first experiment. There are five confidence criteria (placed on the match dimension to give six confidence categories) and six decision criteria (one for each category). T_er is the duration of all the nondecision components of processing combined (e.g., encoding the test word, memory access, response output). The nondecision component and the decision criteria vary across trials (just as in the two-choice model, Ratcliff, 1978; 1981; Ratcliff & McKoon, 2008; Ratcliff et al., 1999). The nondecision component varies uniformly with range s_t (see Ratcliff, Gomez, & McKoon, 2004; Ratcliff & Tuerlinckx, 2002 for justification) and the decision criteria vary uniformly with the same range for each of them (s_z).

In our experiment with the four conditions (high- and low-frequency, old and new test words), the differences among them are determined by the mean values of match for the four conditions, with the mean of the high-frequency new items set to zero. The match values are normally distributed across trials with standard deviations, σ_ho, σ_hn, σ_lo, and σ_ln, where the subscripts h, l, o, and n refer to high frequency, low frequency, old, and new, respectively.

We used a straightforward method for fitting the model to data. First, we chose some set of parameter values (that produced predictions somewhere near the data) and generated predictions for the proportion of responses in each confidence category and their RTs. Then the parameters were adjusted until the predictions matched the data as closely as possible, using the robust simplex function minimization method (Nelder & Meade, 1965).

For simulation of the process given by Equation 1, we used the simple Euler's method with 10-ms steps (cf. Brown et al., 2006; Usher & McClelland, 2001). Response proportions and .1, .3, .5, .7, and .9 RT quantiles were generated for each confidence category for each condition of the experiment using 20,000 iterations of the decision process for each condition. The results were checked with 1-ms steps to make sure there were no serious deviations as step size was reduced so as to more accurately approximate the continuous diffusion process. All differences between parameter values for the two sets of fits for the different step sizes were less than 10%.

For each evaluation of the model, a chi-square statistic is computed over each bin between the quantiles and outside the extreme quantiles for the six confidence categories (see Ratcliff & Tuerlinckx, 2002). Specifically, .1 probability mass lies outside each of the .1 and .9 quantile RTs, and .2 probability mass lies between the .1, .3, .5, .7, .9 quantile RTs, and this leads to six bins per confidence category. The chi-square statistic uses the number of observations in these six bins as the observed values. For the expected values, the quantile RTs from the data and the RT distributions from the model are used to find the proportion of responses predicted from the model between these quantile RTs. Then these are multiplied by the total number of observations to give the expected proportions. The standard chi-square value is computed from (O-E)²/E, where O denotes the observed frequency and E denotes the expected frequency. There are six bins per confidence category, with six confidence categories, which gives 36 degrees of freedom, but the 36 numbers have to add to 1, which reduces degrees of freedom to 35. With four types of items (as in Experiment 1), this gives a total number of degrees of freedom of 140.

In other work (e.g., Ratcliff & Smith, 2004), we have found that the Wilks likelihood ratio chi-square statistic, G², produces almost identical fits to those using the chi-square statistic. These two statistics are asymptotically equivalent, i.e., they approach each other as the number of observations becomes large (see Jeffreys, 1961). A third statistic, the Bayesian Information Criterion (BIC; Schwarz, 1978), can be derived from the G-square statistic. The BIC takes into account the number of parameters in a model (see Ratcliff & Smith, 2004, for application of BIC to evaluation of sequential sampling models). The best fit of a single model to a single data set according to the G-square statistic is also the best fit according to the BIC. Until competitive model testing is needed, these methods are essentially equivalent for our purposes.

For a set of starting values for the parameters and a range in each of the starting values, the simplex routine computes a set of N + 1 values of chi-square where N is the number of parameters. A set of ranges in the parameter values is also provided to the routine, in our case, 20% of each parameter value. N of the chi-squares use the starting parameter values, but with one parameter value perturbed away by the range provided to the routine. The remaining chi-square has all the parameters perturbed. The simplex routine then determines which chi-square is the largest and adjusts the parameter values to make it smaller. The largest of the N + 1 values is again determined from the new parameter values, and parameter values are again adjusted. This process continues until some tolerance level in the change in the parameter values and a tolerance level in the change in chi-square is reached (the parameter values change by less than .001% percent and chi-square less than 0.1, say), or the maximum number of iterations is reached. In our fitting programs, we let the process reach a minimum and then restart it, in our case, seven times, with the parameter values for the new run being the parameter values for the old run with a new 20% range on the values.

The process is not guaranteed to reach a global minimum, i.e., the best fit. In fact, we often have to rerun the program changing the starting values because the program gets stuck in a flat part of the parameter space (i.e., the value of chi-square does not change much if the parameter values are perturbed). However, the main point is that the quality of the fit shows how well the model can do. It might be able to do better, but it can do at least as well as presented below. The predictions of the model are then generated from a separate version of the fitting program. If the fits are adequate, then we have demonstrated the adequacy of the model.

From our experience with the model, it is unlikely that a completely different set of parameter values will produce a better fit. The issue is: if a different set of values produces a better fit, the parameter values might produce a different interpretation of, for example, the relationship between the across trial variability in the familiarity distributions and z-ROC functions. However, we have each written a separate fitting program and tried a wide range of parameter values to see if better fits could be obtained. We believe we are pretty near the optimum values.

Experiment 1

Experiment 1 was designed to provide enough data to allow the model to be evaluated. To this end, subjects were tested on between 8 and 10 sessions. Experiment 1 used a standard recognition memory paradigm with confidence judgments as responses. Subjects studied lists of pairs of words, each list followed by a recognition test of single words. Pairs were used on the study lists to encourage subjects to encode the words as strongly as possible. Study and test words were displayed on a PC monitor. The study and test words were either high in Kucera-Francis frequency or low. In each study list, half the words were high frequency and half low, and in each test list, there were equal numbers of old and new, high- and low-frequency words. For every test item, subjects were asked to make a confidence judgment on a 6-point scale, from sure new to sure old.

Method

Subjects

Ten undergraduate students from Ohio State University participated and earned $10 for each completed session. Two subjects completed 10 sessions, one completed 9 sessions, six completed 8 sessions, and one completed 7 sessions. The first session for each subject was considered practice and not included in the analyses.

Materials

The stimuli were drawn from a pool of 814 high-frequency words and 859 low-frequency words. High-frequency words ranged from 78 to 10,595 occurrences per million (M = 323.25; Kucera & Francis, 1967). Low-frequency words ranged from 4 to 6 occurrences per million (M = 4.41). Each study list was constructed by randomly selecting (without replacement) 16 high-frequency words and 16 low-frequency words from the pools. The words were randomly paired to create 16 pairs such that the two words of a pair were both either high frequency or low frequency. Each pair was presented twice in the study list, with at least one other pair intervening. Four pairs (two high and two low frequency) served as buffer items for the study list, presented in the first two and the last two positions of the list. The remaining 12 pairs (6 high and 6 low frequency) were randomly assigned to the middle study list positions. Test lists consisted of the 24 nonbuffer words from the study list (12 high and 12 low) along with 12 high-frequency and 12 low-frequency new words. Test words appeared on the screen one at a time in random order.

Procedure

Each experimental session lasted approximately 45 minutes and consisted of a response-key practice block followed by 10 study/test blocks. Subjects responded using the Z, X, C, comma, period, and slash keys on the PC keyboard, which were marked with stickers labeled “−−−”, “−−”, “−”, “+”, “++”, and “+++”, respectively. Subjects placed the ring, middle, and index fingers of their left hand on the “−−−”, “−−”, and “−” keys and the index, middle, and ring fingers of their right hand on the “+”, “++”, and “+++” keys. Subjects were instructed to use this mapping of fingers to response keys throughout the entire experiment.

For each item in the response-key practice, a response key label (e.g., “+++”) appeared on the computer screen and subjects were required to press the indicated key as quickly as possible. A message reading “TOO SLOW” appeared on the screen following any response with a latency longer than 800 ms. The response practice block contained 20 repetitions of each of the six response key labels for a total of 120 trials. The labels appeared in a random order with the constraint that the same label could not be repeated on successive trials. RT quantiles for the practice/calibration blocks of trials did not show significant differences across the different keys.

After the response-key practice, subjects completed the study/test recognition memory blocks. Subjects initiated the beginning of each study list by pressing the spacebar. Each word pair was displayed for 1,800 ms followed by 50 ms of blank screen. A message prompting subjects to press the space bar to begin the test list appeared immediately after the final study-list pair. Each test word remained on the screen until a response was made. Subjects were instructed to hit one of the “−” keys to indicate that the test word was not on the study list and one of the “+” keys to indicate that it was. They were also told to use the keys to report their degree of confidence that their response was correct, with more +'s or −'s reflecting a higher level of confidence. Subjects were encouraged to respond both quickly and accurately. They were told to use the confidence ratings in any way they pleased to best reflect their confidence in each decision. They were not told that they had to use all of the response keys. They received accuracy feedback such that the word “ERROR” appeared on the screen for 1 s following an incorrect response. An incorrect response was defined as a −, −−, or −−− response to an old item or a +, ++, or +++ response to a new item.

Results

There are five main results, discussed in detail below: First, the model fits the proportions of responses in each confidence category and their RT quantiles well. Second, because the model fits response proportions, it also fits z-ROC functions. Third, the model fit the data well for subjects that showed linear as well as inverted-U-shaped z-ROC functions. Fourth, the model accommodated the data when the slopes of the z-ROC functions were quite different from the ratios of the standard deviations in the distributions of match values. Fifth, the model accommodated sequential effects; the slope of the z-ROC function was different for responses following an “old” response than a “new” response.

Quantile RTs and response proportions

Figure 5 shows the quantile RTs for the six confidence categories. The “sure new” category is labeled 1 and the “sure old” category is labeled 6. Five quantiles are shown, the RTs for the .1, .3, .5, .7, and .9 quantiles. For all the confidence categories, the differences between the .7 and .9 quantiles are somewhat larger than the differences between the .1 and .3 quantiles, reflecting the right skew that is commonly obtained in RT experiments. There are only small differences in the quantiles across the confidence categories, although the higher quantiles do show somewhat larger differences than the lower quantiles. The reason that the RT distributions are relatively similar in location and spread is likely due to the amount of practice we gave the subjects.

Figure 5.

Response time (RT) quantiles plotted against six confidence categories. The x-axis shows confidence: 1 is high-confidence new and 6 is high-confidence old.

Figure 6 shows the fits of the model to the data. The black dots are RT quantiles (same as in Figure 5) and the Xs are the model's fits for them. Each of the six columns of quantiles is the data for one of the six confidence categories, from “sure new” (−−−) to “sure old” (+++). The x-axis shows the proportions of responses in each of the confidence categories. The tick marks on the x-axis (the small scales around each response proportion) are the ranges from x − .125 to x + .125 (illustrated in the box at the bottom of the figure). The ellipses represent how much variability there is in each quantile for each confidence category, in other words, the variability that would be observed if the experiment were repeated with different subjects. The variability estimates were calculated with a bootstrap computation. Five hundred sets of data were generated from data randomly chosen (with replacement) from the 10 real subjects' data (RTs and proportions of responses for each confidence category). From these data, the standard errors in the RT quantiles and response proportions were calculated. They are displayed in Figure 6, with 2-SE ellipses around each data point. In each case, the predictions made by the model from its best-fitting parameter values fall within the 2-SE ellipses.

Figure 6.

Response time (RT) quantiles for experimental data (black dots) and predictions of the model from fits to the data (Xs) are plotted against the proportions of responses in each confidence category. The tick marks on the x-axis represent a common range of proportion from the data value minus 0.125 to the data value plus 0.125, as illustrated in the box at the bottom of the figure. The ellipses represent 2-SE confidence regions around the data points derived from the bootstrap method described in the text. For the confidence categories, “−−−” is high-confidence new, “+++” is high-confidence old, and the other symbols represent lower confidence responses.

We examined whether we needed variability in decision criteria from trial to trial (decision criteria were assumed to be uniformly distributed with range s_z), variability in confidence criteria, or both. We refit the model with no variability in decision criteria and variability in confidence criteria (uniformly distributed, but not allowing any criterion to cross a neighbor) and found roughly equivalent fits. Allowing both to vary provided about the same goodness of fit as for variability only in decision criteria. For this reason we decided to only allow decision criteria to vary from trial to trial. But this does not mean that confidence criteria do not vary from trial to trial, rather the goodness of fit for this experiment is not improved by allowing them to vary. Future experiments may require such variability.

Parameter values

The model was fit to the data for individual subjects and to the data averaged over subjects. The best-fitting parameter values for the group data were similar to the averages of the parameter values for the individual subjects (Tables 1 and 2). The standard deviations in the parameter values that are shown in the tables are the standard deviations across individual subjects. In only one case is there a difference between the two sets of parameter values that is larger than one standard deviation. Thus, at least for this experiment, fitting group data gives about the same values as fitting individual subject data.

Table 1.

Parameter Values for Experiment 1

Statistic	Ter	st	σ	Decay k	Scale a	LF New μln	LF New σln	HF New μhn	HF New σhn	HF Old μho	HF Old σho	LF Old μlo	LF Old σlo
Fit to mean data	543	248	0.186	0.29	0.1	−0.47	0.44	0.00	0.62	1.08	0.95	1.70	1.13
Means over subjects	536	262	0.177	0.32	0.1	−0.44	0.48	0.00	0.63	1.05	0.96	1.64	1.07
SD over subjects	66	96	0.019	0.04	0.0	0.15	0.10	0.00	0.13	0.29	0.10	0.30	0.19
Monte Carlo means	541	249	0.178	0.29	0.1	−0.48	0.44	0.00	0.64	1.05	0.99	1.65	1.16
Monte Carlo SDs	2	6	0.002	0.00	0.0	0.02	0.01	0.00	0.03	0.05	0.05	0.06	0.06

Note. T_er is the mean duration of nondecision processes; s_t is the range of variation in the nondecision response time component; σ is the standard deviation in evidence accumulation; k is the decay coefficient; a is the scaling factor applied to the drift rates; LF denotes low frequency words; HF denotes high frequency words; μ and σ give the mean and standard deviation of the across-trial match distributions for each item type.

Table 2.

Confidence and Decision Criteria and Decision Criterion Range for Experiments 1 and 2

		Confidence criteria					Decision criteria						Decision criterion range
Experiment and group	Statistic	c1	c2	c3	c4	c5	d1	d2	d3	d4	d5	d6
Experiment 1	Fit to mean data	−1.01	−0.19	0.44	1.41	2.30	2.44	2.32	2.35	2.77	2.25	2.34	1.13
	Means over subjects	−1.04	−0.17	0.44	1.32	2.28	2.28	2.20	2.25	2.57	2.16	2.21	1.04
	SD over subjects	0.10	0.03	0.05	0.25	0.15	0.17	0.12	0.39	0.13	0.15	0.28	0.23
Monte Carlo recovery simulations	Monte Carlo means	−1.00	−0.19	0.44	1.39	2.31	2.41	2.25	2.29	2.67	2.20	2.27	1.16
	Monte Carlo SDs	0.02	0.01	0.01	0.02	0.03	0.03	0.02	0.03	0.03	0.03	0.04	0.03
Experiment 2, speed	Fit to mean data	−1.12	−0.16	0.66	1.54	2.70	2.86	1.95	2.24	2.66	2.01	2.65	0.11
Experiment 2, accuracy	Fit to mean data	−1.12	−0.16	0.66	1.54	2.70	4.32	3.31	3.59	4.14	3.74	3.88	0.11

Note. In Experiment 2, the values of all confidence criteria (c₁–c₅) and the decision criterion range were constrained to be the same in the speed and accuracy conditions. c₁–c₅ are the confidence criteria used to derive drift rates from match distributions; d₁–d₆ are the decision criteria that terminate the accumulation race.

z-ROC functions

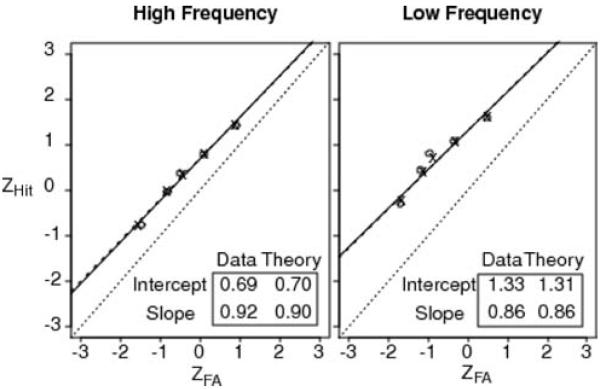
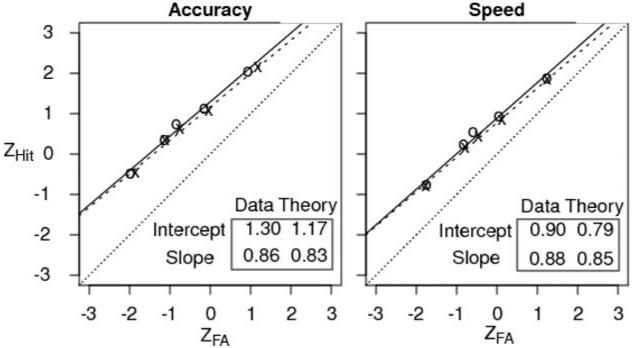
Figure 7 shows the z-ROC functions for the group data (the circles in the figure) and the values predicted by the model (the Xs in the figure). The middle diagonal line is a reference line with slope 1. The ROC function from the data and the function predicted from the model are the lines to the upper left of the reference line. The model's predictions are so close to the data that the two functions almost completely overlap for both slope and intercept. The predicted and observed functions are slightly nonlinear with inverted ⋃ shapes. The slopes are less than 1, slightly lower for low-frequency words (0.86) than high-frequency words (0.92). A paired-samples t test showed that the frequency effect on slope was significant, t(9) = 3.93, p < .01.

Figure 7.

z-ROC functions for the data from Experiment 1 (the data in Figure 6). The circles are the data and the Xs are the model predictions. The diagonal dotted line is a reference with slope 1 and intercept 0. There are two straight line fits to the data and the predictions from the model (solid and dashed lines, respectively), but these coincide so they largely overlap. Z_Hit = hit rate z-score; Z_FA = false-alarm rate z-score.

It is important to stress that the model's predictions for the z-ROC functions are completely constrained by the proportions of responses in each confidence category and the quantile RTs. This means that the parameters of the model cannot be adjusted to produce better fits to the z-ROC functions without affecting the fits for all of the data, the response quantiles and proportions for each confidence category and each experimental condition. The z-ROC functions can be calculated only after the model generates its best fitting values for the response proportions and quantile RTs.

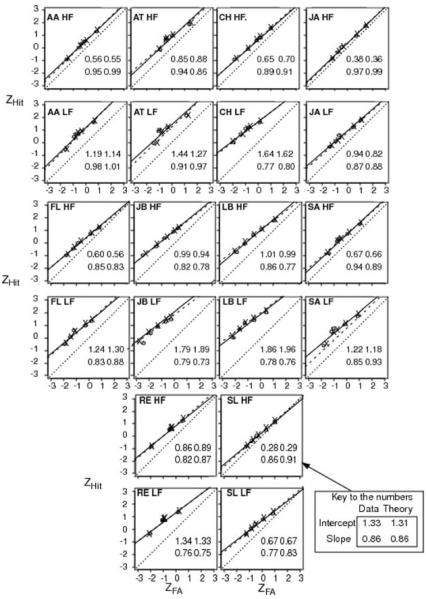
Figure 8 shows the observed and predicted z-ROC functions for high- and low-frequency words for each of the subjects individually. The slopes vary from 0.76 to 0.98 across subjects and frequency conditions. The z-ROC functions are inverted ⋃ shapes for some of the subjects (e.g., AT, LB, and SA). In general, the observed and predicted slopes and intercepts are close to each other.

Figure 8.

z-ROC functions as in Figure 7 plotted for all the individual subject data and model predictions. The first two initials identify the participant. HF = high-frequency words; LF = low-frequency words; Z_Hit = hit rate z-score; Z_FA = false-alarm rate z-score.

As discussed in the introduction, the slope of a z-ROC function has previously been taken as a direct measure of the ratio of the standard deviations in match values for old and new test items. For our experiment, this was not the case. The ratio of the standard deviations in match across trials that was estimated from the model's best-fitting parameter values (for the group data) was 0.39 for low-frequency words and 0.65 for high-frequency words. In the individual subject fits, the standard deviation ratios for high- and low-frequency words were significantly different, t(9) = 4.66, p < .01. The ratios from the RTCON model are quite different from the standard deviations that would be calculated directly from the data's z-ROC functions, 0.86 and 0.92, respectively. So, as discussed earlier, when RTs are taken into account and when there are multiple sources of noise in processing, then the SDT mapping between distributions of match values and z-ROC slopes is not valid.

Individual differences

In other research in which RT distributions have been examined for confidence judgments or, more generally, tasks that provide one of several possible responses (e.g., absolute identification, Brown et al., 2008), different patterns of RT data are sometimes obtained. Murdock (1974) and Murdock and Dufty (1972) presented results that showed that mean RT increased by 500 ms going from high-confidence to low-confidence responses (see also Norman & Wickelgren, 1969; Ratcliff & Murdock, 1976). One possible explanation of these results is that subjects make a judgment about high confidence and then move to lower confidence decisions (e.g., the conveyor belt model makes this assumption explicitly; Murdock, 1974, p. 271; Murdock & Anderson, 1975).

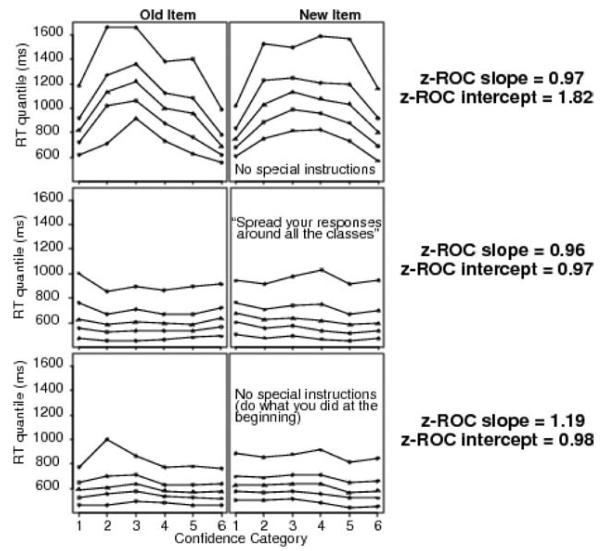
In piloting the experiments reported here, we ran a few subjects in this experiment first with a set of sessions with instructions to use categories as they wished, then sessions in which they were told to spread their responses across categories, and finally revert to how they performed the task originally. The results for one subject are shown in Figure 9. Initially, there was a huge bow in all RTs, then with the “spread responses across categories” instruction, the bow disappeared, and finally the subject was unable/unwilling to perform as he did in the first set of sessions. One other subject out of 5 showed the same kind of bow in the initial set of sessions, the other 3 showed data very much like those in Figure 5.

Figure 9.

Quantile probability functions for one subject showing the effects of different instructions as described in the text. RT = response time.

These results show that, for an individual, performance may be under strategic control and that subjects may evaluate some of the response categories first and then evaluate some of the others a little later. But it is clear that performance can be under strategic control and that individual differences can be large. Note that the RTCON model cannot accommodate the large bow in the leading edge of the distribution coupled with a bow in the other quantiles that is not too much larger than the leading edge bow. When the model produces a bow in the leading edge, it produces a much larger bow in the higher quantiles, unlike the data for the subject in the top panel of Figure 9.

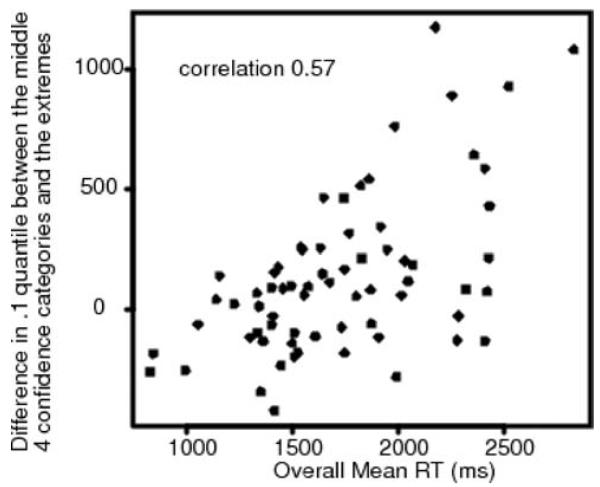
To investigate the bowing effect in a little more detail, we examined the difference in the .1 quantile RTs in the middle four confidence categories and the extreme two confidence categories in the data from Experiments 1 and 2 of Glanzer, Kim, and Hilford (1999). These correspond to the two extreme categories and the middle four categories in the top panel of Figure 9. Figure 10 shows the difference in the .1 quantile RTs averaged over all conditions in the experiment plotted against mean RT for all the subjects in the two experiments. The plot shows that a number of subjects (maybe half) show little bow in the leading edge, but there are some subjects who show a large bow. But the size of the bow is a function of mean RT. This means that the bow is more pronounced when mean RT is larger, which is consistent with our contention that the bow might be the result of strategic effects or sequential evaluation (first, decide whether the stimulus belongs in a high-confidence category, then, if not, decide about lower confidence categories). The Glanzer et al. experiments used one session of data with unpracticed subjects. Figure 10 shows that without practice, mean RTs (for all except 2 or 3 individual subjects) are much larger than those in Experiment 1 (which has means around 700 ms). In fact, about 14 subjects in Glanzer et al.'s experiments have means three times those in Experiment 1. It is hard to believe that there is only a single decision process running when the mean RT is over 2 s and the .9 quantile RT is well over 3 s.

Figure 10.

A plot of the difference in the .1 quantile response times (RTs) for the two extreme (high-confidence) confidence categories and the middle four categories (lower confidence) against overall mean RT for 68 subjects from Glanzer et al. (1999) Experiments 1 and 2. A difference above zero on the y-axis means that the RTs for the middle categories are larger than for the two extreme categories.

In an additional analysis, we present the accuracy of responses in the six confidence categories (see Table 3). This shows that accuracy increases as confidence increases, as is found in other studies (e.g., Mickes, Wixted, & Wais, 2007).

Table 3.

Response Accuracy as a Function of Confidence Category

Experiment and condition	Confidence category
	−−−	−−	−	+	++	+++
Experiment 1	.79	.73	.67	.64	.73	.84
Experiment 2: Accuracy	.90	.78	.73	.63	.74	.93
Experiment 2: Speed	.79	.72	.69	.60	.68	.84

“−−−”is high confidence new and “+++” is high confidence old and the other symbols represent lower confidence responses.

Sequential effects

An important prediction from standard SDT is that the ROC slope should not change as a function of the prior response. This prediction comes from the assumption that the slope of the z-ROC function measures the ratio of standard deviations for noise and signal distributions (in the memory application here, new and old item match distributions) and the standard deviations should not change as a function of prior response. Even if the signal and noise distributions were not normal, there should be no change in the slope as a function of the prior response. However, the z-ROC slopes from the experiment reported here did change as a function of the prior response. Figure 11 shows the functions (averaged over high and low word frequency) for responses following an “old” response and following a “new” response.¹ The slopes differ by 0.09. This is a large difference: Differences between slopes of 0.8 and 1.0 have fueled a great deal of theoretical work in evaluating global memory models. In standard SDT, the interpretation of the 0.09 difference would have to be that the standard deviations of the old and/or new distributions change a great deal depending on the prior response.

In contrast, the RTCON model accommodates the sequential effects observed in the experiment while fitting response proportions (and hence ROC functions) and RT quantiles. The data used for fitting are averaged response proportions and RT quantiles over word frequency and subjects. For the best fits to the data, all parameters other than the decision criteria were fixed and the fits showed the decision criteria changed by about 5% between an “old” previous response and a “new” previous response. The change in the criteria for prior “old” minus prior “new” were, in order from “sure new” to “sure old,” 0.116, 0.004, 0.108, −0.110, −0.072, and −0.198. The “new” decision criteria were higher when the previous response was “old,” and the “old” decision criteria were higher when the previous response was “new,” as illustrated in the bottom panel of Figure 11 (note that the sizes of the differences in decision criteria displayed in Figure 11 are exaggerated). Analyses of sequential effects in the two-choice diffusion model are similar and the effects are explained by changes in criteria (Ratcliff, 1985; Ratcliff et al., 1999).

A sequential effect on the slopes of z-ROC functions is not unique to our experiment. Table 4 shows the same analysis carried out on six different published experiments, some that used high-versus low-frequency words and some that manipulated encoding strength (study time or number of repetitions). For each experiment, changes in slope as a function of prior response were computed for each condition and averaged. The slopes and intercepts in Table 4 result from 40 different conditions in the experiments, with no cases in which the slope after an “old” response was less than the slope after a “new” response. In each experiment, the slope of the z-ROC function differed as a function of the prior response by about 0.1.

Table 4.

Slope of the z-ROC Function as a Function of Prior Response

Experiment	Slope after an “old” response	Slope after a “new” response
Ratcliff, McKoon & Tindall (1994), Experiments 3, 4, & 5.	0.83	0.71
Glanzer et al. (1999), Experiment 1 & 2	0.88	0.79
Ratcliff, Sheu, & Gronlund (1992), Experiment 1	0.88	0.81
Experiment 1 above	0.92	0.83

Sequential effects on z-ROC slopes parallel the findings of studies that have explicitly manipulated response bias in a confidence judgment procedure. Van Zandt (2000) varied the proportion of test items for which the correct response was “old” versus “new” and the relative rewards associated with “old” and “new” responses. After an old/new response, a confidence judgment was produced. The z-ROC slopes were larger in conditions that biased positive responding (high proportion of old test words or a large reward for old responses) than conditions that biased negative responding (low proportion of old test words or a large reward for new responses). Similar effects have been observed in perceptual signal detection tasks (Balakrishnan, 1998; Mueller & Weidemann, 2007). The sequential effects we obtained in our experiment are consistent with the biases just described; subjects are biased to use the same response as the previous trial. This yields higher slopes after yes responses and lower slopes after no responses. As outlined above, the RTCON model explains this slope effect in terms of the values of the decision criteria. Variation in decision criteria also provides a qualitative explanation for Van Zandt's (2000) data.

The fact that, within an experiment, the z-ROC slope can change considerably for each condition of an experiment as a function of the prior response poses serious problems for any effort to use z-ROC slopes to interpret memory processes. It is difficult to imagine how changes in slope come about in SDT in which slope is interpreted as a direct measure of the relative standard deviations of the noise and signal distributions. For our model, it is natural for decision criteria to vary as a function of prior response; and, in our experiment, such variation was enough to explain differences in slope. We do not propose a model for the behavior of decision criteria; that is something that has not been done successfully for models of two-choice decisions (see discussion in Ratcliff & McKoon, 2008). However, these results show what kinds of behavior of parameter values such a model should aim to explain (e.g., Triesman & Williams, 1984).

Fits to individual subject data

Turning to the fits of the model to the data from individual subjects, the mean chi-square value was 443 with a SD of 104. The mean, 443, is 2.6 times the critical value (168.6). This indicates a mismatch between theory and data. The size of the mismatch is about what has been obtained in other experiments with diffusion models. For the two-choice decision model, Ratcliff, Thapar, Gomez, and McKoon (2004) examined how large misses between model and data had to be in order to produce increases in chi-square values as large as 2 to 3 times the critical value. They did this because the chi-square goodness of fit values were typically 2–3 times the critical value. They found that a miss as large as .1 in the proportion of responses between quantiles would be large enough to produce an addition to the chi-square as large as the critical value. Specifically, for the observed data, for the .3, .5, and .7 quantiles, there is .2 probability mass between them. If, for one of the conditions, the predicted proportions between these quantiles changed from .2 and .2 to .1 and .3, the addition to chi-square was as large as the critical value. This suggests that relatively small systematic deviations in the quantile RTs are enough to produce the observed inflated chi-square values.

We performed an analysis similar to that of Ratcliff et al. (2004) using the data from the experiment reported here. We generated a simulated data set using the average parameter values across subjects and a sample size corresponding to eight sessions of data. The chi-square of a fit to these data with the true parameter values was 155. We then perturbed each quantile reaction time by 10 ms. We randomly selected whether each quantile was increased or decreased with equal probability. This slight perturbation of the quantile data increased the chi-square to 410. This demonstration shows that minor sources of variation outside of those incorporated into the model can lead to large increases in chi-square. Thus, the fairly high chi-squared values from individual subject fits do not undermine the quality of the fits and should not be considered evidence against the model. In contrast, modest alterations to the response proportions had only minor effects on the chi-square values.

In summary, although the chi-square values are significant, the goodness of fit values are adequate in the context of other sequential sampling models for RT and accuracy.

Correlations among parameter values

If there were large correlations among the best-fitting parameter values, then our interpretations of the differences in parameter values that we found would be suspect. For example, we might offer an interpretation of the difference between two parameters when, in fact, the difference was caused by other, correlated, parameters.

To check this, we examined covariances among parameter values using Monte Carlo simulations. The same method used to generate predicted data for model fits was used here to generate data from simulated subjects. The number of simulations per condition was not 20,000, as in fitting the model to data, but, instead, the average numbers of observations for each subject in the experiment: 900 observations for each of the four conditions defined by high- and low-frequency words and old and new test words. Data for 50 simulated subjects were generated using the parameter values for the best fits to the group data (see Tables 1 and 2). We fit the model to each simulated data set to obtain the best-fitting parameter values for each set and then calculated the correlations among the values.

Results showed no strong tradeoffs in parameter values. The largest correlations (.49, .53, .59) were correlations between the standard deviation of the noise in the accumulation of evidence process (i.e., in the diffusion coefficient) and three of the confidence criteria (the correlations for the other three confidence criteria were smaller). There were a few correlations between decision criteria and confidence criteria that reached around .4, but they were not consistently high across all the decision and confidence criteria.

The lack of systematic tradeoffs indicates that the model's parameters are reasonably identifiable. Although this investigation is by no means exhaustive, it does indicate that, for the parameter values we obtained, the model does not suffer from large tradeoffs among parameters.

Goodness of fit and parameter recovery

We used the 50 sets of parameter values recovered from the Monte Carlo study just described to assess how well the model recovers true parameter values, that is, the values used to generate the simulated data. The starting values used in the fitting program were between 10 and 30% different from the values used to generate the data. The means and standard deviations across the 50 simulations are shown in Tables 1 and 2. There were no significant differences between the parameters used to generate the data and those recovered. The chi-square statistic for the data from this experiment has 140 degrees of freedom, as described earlier. For the chi-square statistic, the mean value for 140 degrees of freedom is 139.3 with an upper .95 confidence limit (the critical value .05) of 168.6 and a lower confidence limit of 113.7.

The mean chi-square value for the fits to the 50 sets of Monte Carlo data was 120.5 with a SD of 21.1. There were 6 out of 50 values that had chi-square values that were significant and there were 18 out of 50 values of chi-square that were below the lower .05 chi-square limit (only 8 of those were below the .01 level). This indicates to a small degree that the model can accommodate noise in the data (i.e., accommodate differences in the data that come from variability). But in general, even though the model is quite complicated, with 24 free parameters for this data set, parameter recovery is surprisingly good.

Experiment 2

In Experiment 1, the RTs are much shorter than those usually reported for confidence judgments in recognition memory experiments. We attribute the speed of responses in Experiment 1 to training on the response keys and an emphasis on both speed and accuracy. It is possible that the bowed pattern of RT results (e.g., Figure 9, top panel) is more typical of regular processing and that we have simply eliminated RT differences by emphasizing speed. Experiment 2 is designed to address this issue by manipulating speed–accuracy instructions in an experiment similar to Experiment 1; in fact, Experiment 2 follows Experiment 1 in most details apart from instructions. We might expect that only decision criteria change in moving from speed to accuracy instructions.

Method

Subjects

Four Ohio State University undergraduate students participated. Subjects earned $10 for each session. Subjects completed between 8 and 11 sessions, and the first session for each subject was ecluded from all analyses.

Materials and procedure

This experiment used the same materials as in Experiment 1, and the procedures matched Experiment 1 except for the manipulation of a speed versus accuracy emphasis. Instruction conditions were randomly assigned to blocks under the constraint that five test blocks were completed with a speed emphasis and five were completed with an accuracy emphasis in each session. The initial instructions informed subjects that their responding should always be relatively fast and accurate but that on some blocks they would be asked to sacrifice accuracy to improve speed and on other blocks they would be asked to sacrifice speed to improve accuracy. Throughout the experiment, the test signal indicated whether speed or accuracy should be emphasized on the upcoming test. On speed blocks, subjects saw a “TOO SLOW” message each time they took more than 900 ms to respond. No feedback regarding the accuracy of their responses was provided. On accuracy blocks, subjects saw an “ERROR” message for each incorrect response. No feedback regarding response speed was provided.

Results and Discussion

Two subjects had low frequencies of responses (e.g., less than 5) in high-confidence categories, so we aggregated over high- and low-frequency words. Even so, there were still some response categories with few observations. To remedy this problem, we pooled adjacent responses to estimate RT quantiles for any response category with below 15 responses for a subject. For example, if a subject had only 10 “−−−” responses for old items, the quantile for this response would be computed by pooling the 10 reaction times with the reaction times for a “−−” response to old items. Similarly, when a subject made fewer than 15 “+ + +” responses, quantiles were based on the pooled RTs from “+ +” and “+ + +” responses. Pooling was required for 4 of 36 sets of quantiles for one subject and 5 of the 36 for another subject. No quantiles had to be pooled for the other two subjects. The model was fit to four types of items: old and new items in both the speed and accuracy conditions. Just as in the first experiment, having four item types results in 144 total response frequencies and 140 degrees of freedom in the data. Table 3 presents accuracy as a function of confidence and shows the same pattern as in Experiment 1, namely that accuracy increases as confidence increases.

We can compare the changes in the RT data between this experiment and two-choice experiments in the literature. In Experiment 2, going from speed to accuracy instructions, averaging over all conditions (six confidence categories for both old and new items), the .1 quantile RT changed from 515 ms to 623 ms (a 108 ms difference), the median RT changed from 609 ms to 762 ms (a 153-ms difference), and the mean RT changed from 622 ms to 773 ms (a 151-ms difference). For the two-choice recognition memory task for young subjects in Ratcliff, Thapar, and McKoon (2004), subjects studied high- and low-frequency words either once or three times (Experiments 1 and 2 here had two presentations of each word). Averaged over all conditions and subjects, the difference in the .1 quantile RT was 76 ms (569 ms versus 635 ms), the difference in the median RT was 90 ms (650 ms versus 740 ms), and the difference in mean RT was 113 ms (670 ms vs. 783 ms). Ratcliff and Smith (2004) presented fits of a dual diffusion model to a speed–accuracy manipulation in a lexical decision task (Wagenmakers, Ratcliff, Gomez, & McKoon, 2008). In this experiment, averaged over all conditions and subjects, the difference in the .1 quantile RT was 102 ms (409 ms versus 511 ms), the difference in the median RT was 151 ms (506 ms versus 657 ms), and the difference in mean RT was 193 ms (528 ms vs. 771 ms). These results show that the changes in the RT distributions in our six-choice task and these two two-choice tasks show about the same pattern.

The lexical decision experiment in Ratcliff and Smith (2004) was fit by one model with racing diffusion processes with only the decision criteria changing. In the application of our confidence judgment model, as in the Ratcliff and Smith application with the two-choice model, all parameters defining characteristics of the accumulation process were held constant across speed and accuracy instructions. The only parameters allowed to change between the two conditions were the values of the decision criteria.

Figure 12 shows the observed and predicted z-ROCs. The empirical functions show that the speed/accuracy manipulation changed the z-ROC intercept by about 30% (the intercept can be compared with d′ from two-choice SDT because, if the signal and noise distributions have the same variance, the intercept is d′). This is not too different from the result from Ratcliff and Smith's (2004) lexical decision experiment in which overall d′ values for speed versus accuracy instructions were 3.09 versus 2.06, averaging over all conditions. But this was larger than the difference in Ratcliff et al.'s, 2004, recognition memory experiment which had d′ for accuracy versus speed conditions of 1.97 and 1.71 averaging over all conditions. This indicates better memory performance when test instructions emphasized accuracy. Slopes were about the same in the two instruction conditions and the predicted points show a good fit to accuracy overall. For both conditions, the intercepts of the functions for the model predictions showed the appropriate effect of instruction condition, but the fitted values underestimated the intercept by a little over 10%. Theoretical slopes were close to empirical slopes.

Figure 12.

Experimental and predicted z-ROC functions for speed and accuracy conditions for the data from Experiment 2. Z_Hit = hit rate z-score; Z_FA = false-alarm rate z-score.

Figure 13 shows the probability-quantile plots. The empirical RT quantiles (dots) show a similar pattern to the first experiment. RTs are relatively stable across confidence categories, with only a small increase (if any) from the high-confidence to low-confidence responses. Furthermore, this pattern characterized both the speed and accuracy conditions, suggesting that the pattern is not created simply because subjects overemphasize the quickness of their decisions. As discussed above, RTs were substantially shorter with speed instructions than with accuracy instructions, including a large shift in the .1 quantile RT. The Xs in Figure 13 show the model predictions. In general, the model provided a good fit to the empirical proportions and response quantiles with perhaps the only exception a slight overestimation of the .9 quantile RT with accuracy instructions. Parameter values are reported in Tables 2 and 5. Overall, parameter values are similar to those generated for fits to the data from Experiment 1. In all, there were 26 free parameters to fit the 144 response frequencies.

Figure 13.

Response time (RT) quantiles for experimental data (black dots) and fits of the model to the data (Xs) are plotted against the proportions of responses in each confidence category. The tick marks on the x-axis represent a common range of proportion from the data value minus 0.1 to the data value plus 0.1, as illustrated in the box at the bottom of the figure. For the confidence categories, “−−−” is high-confidence new, “+++” is high-confidence old, and the other symbols represent lower confidence responses.

Table 5.

Parameter Values for Experiment 2

Ter	st	σ	Decay k	Scale a	New μn	New σn	Old μo	Old σo
569	252	0.194	0.17	0.061	0.0	0.84	2.11	1.12

Note. T_er is the mean duration of nondecision processes; s_t is the range of variation in the nondecision response time component; σ is the standard deviation in evidence accumulation; k is the decay coefficient; a is the scaling factor applied to the drift rates; μ following “new” or “old” is the mean of the across-trial match distribution for new items and old items, respectively; σ following “new” or “old” is the standard deviation of the across-trial match distribution for new items and old items, respectively.

The relative standard deviations of the new-item and old item memory evidence distributions tell a similar story to those in the first experiment. Old-item evidence was always more variable than new item evidence, and the ratio was 0.75. This contrasts with the slope of the z-ROC function, which averaged 0.87 and, as in Experiment 1, the standard deviation ratio was substantially lower than the z-ROC slopes. Once again, z-ROC slope makes old- and new-item evidence variability appear more similar than the results of the RT model. This is the expected result, because the z-ROC analysis combines multiple sources of variation that the RT model estimates separately.

General Discussion

The RTCON model proposed in this article is intended to explain recognition memory performance when subjects are asked to make confidence judgments. The model successfully combines the two parts of the data, the proportions of judgments in each confidence category and their RTs. The model coherently integrates a diffusion decision process with a unidimensional measure of the degree of match between a test item and memory. There are three features of the model that are responsible for its success. First, each of the confidence categories accumulates evidence in its own accumulator. Second, evidence is accumulated as an OU diffusion process with a modest amount of decay. Third, the output of the process that matches a test item against memory produces a distribution of memory evidence. Confidence criteria divide the distribution into areas, one for each confidence category (Figure 2). The area between the confidence criteria determines the drift rate for the accumulator corresponding to the confidence category and the drift rate determines RTs. In this way, RTs are constrained by the same confidence criteria that determine confidence judgments.

We used simulations of the RTCON model to demonstrate that common z-ROC interpretations based on accuracy-only models are invalid. Specifically, traditional SDT holds that the slope of the z-ROC function equals the ratio of the standard deviations in memory evidence for new and old items. In RTCON, this relationship breaks down because z-ROC slope is affected by a number of factors other than characteristics of the memory evidence distributions, including nonmnemonic sources of variability and changes in decision criteria. Accuracy-based theories also draw simple links between z-ROC shape and memory processes; for example, nonlinear z-ROCs mark the presence of processes such as signal mixing (DeCarlo, 2002) or recollection (Yonelinas, 1994). In RTCON, a variety of z-ROC shapes can be produced based on changes in the decision criteria (see Figure 4) without any changes in the underlying memory evidence. In experimental data, the slope of the z-ROC is usually less than 1. In the fits to data we have performed so far, this, to a large degree, is the result of a wider distribution of match values for old items relative to new items. But, we reiterate, the ratio of the standard deviations in the match distributions is not the same as the slope of the z-ROC function.

Although we used the RTCON model to reveal problems with accuracy-only models, the resulting conclusions are in no way dependent on the details of RTCON. Consider the primary reasons why standard interpretations do not apply to the RTCON model: The RTCON model implements several sources of variability other than variability in memory processes, and the model produces responses based on accumulated evidence using decision criteria. Decades of development in RT models suggests that any successful model will have these properties (Ratcliff & Smith, 2004). Thus, standard z-ROC interpretations will change for any model that is capable of predicting RT data.

Of course, the RTCON model not only reveals problems with accuracy-only models, it also represents a first step in the development of models that can accommodate RTs for confidence judgments. We evaluated the model's ability to fit recognition confidence datasets with manipulations of word frequency (Experiment 1) and speed–accuracy emphasis (Experiment 2). In both cases, the model fit the data well. For all the conditions in Experiment 1, the predicted RT quantiles and response proportions are within 2 standard errors of the data (the ellipses shown in Figure 6). The model also accommodated the effect of word frequency on the z-ROC slope, i.e., lower slopes for low-frequency words (see Figure 7). The model accounts for the data from individual subjects as well as the data averaged across subjects. In Experiment 2, the model reproduced the effects of speed–accuracy emphasis on both z-ROC intercepts and full RT distributions by changing only the position of the decision criteria. Taken together, these results are promising and suggest that memory researchers can begin to capitalize on the powerful constraints introduced by RT data in model development.

It is important to understand that, although the model has a relatively large number of parameters, the parameters are interrelated throughout the structure of the model. This means that if the predictions miss one data point, the miss cannot be remedied by adjusting one parameter to bring the misprediction into line. A change in one parameter alters predictions across some or all of the conditions in an experiment.

The model is also identifiable for the parameter values from fits to our data. There are no strong correlations across parameter values for the parameter ranges from fits to the data from our experiments. This means that the model does not allow effects that should be explained by changes in one parameter to be accommodated by changes in a different parameter. Furthermore, we showed that the model was unable to jointly fit RT distributions and response proportions when the proportions were artificially adjusted to form a nonlinear z-ROC function.

In the RTCON model, drift rates are determined both by the quality of memory evidence and the position of the confidence criteria. Holding the confidence criteria constant, drift rates for “higher” confidence responses tend to dominate when memory evidence is high because, if the memory evidence distribution is shifted far to the right, most of its mass will lie in the region associated with a high-confidence response, leading to a high drift rate. With a constant memory strength, drift rates will also change with changes in the position of the confidence criteria. As Figure 3 demonstrates, drift rates are higher when the decision region associated with a response is wider. Widening a decision region has a large effect on the probability of using the response and a small effect on the RTs. For example, in one simulation using parameter values similar to those in Experiment 1, we increased the width of the region for a “+ +” category by .5, which led to a .21 increase in the probability of the response (.15 to .36), but with only about a 10 ms decrease in mean RT. In a second simulation, we took the same parameter values and increased the mean of the old item distribution so that the proportion of high-confidence “old” responses increased from .14 to .56. Mean RT for the high-confidence responses decreased from 665 ms to 632 ms. The relatively small effects on RT occur because the processes are racing. Accumulators with lower drift rates only win the race when they terminate unusually quickly as a result of noise in the diffusion process. Even when an accumulator has a low drift rate, higher drift rates for competing accumulators keep all responses relatively fast because the high drift ones will usually win. As a result, moving from a high to a low drift rate on one accumulator can substantially decrease response proportions without leading to a large decrease in RT. Another consequence of this competition mechanism is that responses for all response categories are faster when one accumulator gets a high drift rate than when drift rates are evenly distributed across accumulators.

Drift rates will also be affected by the number of response categories. For example, with a four-level response scale there would be only four response regions and each would cover a larger area than the six response regions shown in Figure 3. Simulations suggest that the effect of number of response regions on RT is subtle, i.e., only about a 20 to 30 ms decrease in mean RT going from a six-category to a four-category scale. However, it is also possible that other parameters might change in going from six to four response categories.

It may seem unusual that confidence criteria affect drift rates, but this property is shared by the two-choice diffusion model and has contributed to this model's success in fitting data from a wide range of two-choice decision tasks. Specifically, the diffusion model includes a drift criterion that defines the zero point in drift— evidence values above the criterion have positive drift rates and evidence values below the criterion have negative drift rates, with the magnitude given by the distance from the criterion (Ratcliff, 1985; Ratcliff & McKoon, 2008).

Model Mimicking and Constraints

We have assumed that decision criteria have variability across trials but confidence criteria are fixed. However, we have also found that if variability is put in the confidence criteria (with the restriction that the criteria cannot cross) and removed from the decision criteria, all the fits are about as good. Therefore, variability in either class of criteria mimic each other and cannot be uniquely identified. However, we do not see this as a problem unless some theoretical issue depends on identifying the source of variability.

We have performed a modest number of investigations into what aspects of the functional form of distributions in the RTCON model are critical for its behavior and what aspects can be changed without affecting the qualitative behavior of the model. First, we changed the distributions across trials of nondecision time and decision boundaries from uniform distributions to truncated normal distributions (with range truncated at plus and minus 2.5 SDs in the full normal distribution). The standard deviations matched those of the uniform distributions. Another assumption that might be critical is the assumption of normal distributions in the distributions of match across trials. Instead, we assumed back-to-back exponential distributions (a double exponential distribution). Again, the standard deviation matched the standard deviation in the normal distributions of match in the original model fits to data. Simulated data were generated and the original model fit to the simulated data. The largest deviation between predictions from the original model fit to the simulated data and the simulated data was about 2% in response proportion and about 27 ms in RT. Across all response proportions, the mean deviation was less than 1% and across all RT quantiles, the mean miss was 6 ms. This shows that the functional form of the distributions of nondecision time, mean match values across trials, and decision boundaries is not critical, at least for parameters around the values for fits to our data.

Predictions for z-ROC Slopes

Our claim is that recognition memory performance can only be understood with a model that simultaneously accounts for confidence judgments and RTs. A critical implication of this is that the standard SDT interpretation of confidence data is not valid. The slopes of z-ROC functions cannot be used as indices of match values or as measures of the relative standard deviations of old and new item distributions. Once there is a decision mechanism that takes into account RTs, then the interpretation of z-ROC functions changes. Noise in the process that accumulates evidence and noise in the decision criteria combine with noise in match values to make the slope of the z-ROC function from the model predictions closer to 1 than the ratio of the standard deviations for new and old test items. Because the model identifies the different sources of noise, it solves the problem of criterion variability that is inherent in SDT (see McNicol, 1972, p. 199; Norman & Wickelgren, 1969).

Many researchers have used z-ROC slopes to test global memory matching models, a popular class of memory models (for a review, see Clark & Gronlund, 1996). Many of these models predict a larger standard deviation in match values for old than new test items (Ratcliff, Sheu, & Gronlund, 1992). They also predict that the difference in the standard deviation values should increase as memory for old test items becomes stronger (e.g., items are repeated or studied for more time). If the z-ROC slope were truly the ratio of new to old item standard deviations, this prediction could be tested by evaluating whether the z-ROC slope decreases as old items are strengthened. Some previous research has found that the slope does change in this way (Glanzer & Adams, 1990; Glanzer et al., 1999; Ratcliff et al., 1994; Yonelinas, 1997). Other research has found equivocal results, either slopes decreasing with increased strength of old items or no effect at all on slopes (Glanzer et al., 1999, Experiments 1, 2, and 4; Heathcote, 2003; Hirshman & Hostetter, 2000; Ratcliff et al., 1994, 1992; Stretch & Wixted, 1998). The equivocal results for manipulations of study time and item repetition have been cited as strong evidence against the global matching models (Ratcliff et al., 1994, 1992). However, according to the model we propose in this article, the equivocal findings are not as diagnostic as previously believed. The problem, as we have pointed out, is that there is no way with SDT to separate out the various sources of variability. The sources are combined, and so the slope of a z-ROC does not measure the relative standard deviations of old and new item distributions.

For our experiments, the z-ROC slopes decreased from 0.92 for high-frequency test items to 0.86 for low-frequency test items and average 0.87 for the speed and accuracy conditions in Experiment 2. This difference does not reflect the differences in the standard deviations of the old and new test item distributions: The ratio of the across trial standard deviations in the match distributions are 0.66 and 0.30 for high- and low-frequency test items and 0.75 for the speed and accuracy conditions in Experiment 2 in the model (Tables 1 and 5).

Relationship Between Decision Criteria and Confidence Criteria

As discussed above, in contrast to traditional SDT, the RTCON model involves two distinct types of criteria. The confidence criteria determine how memory evidence is translated into accumulation rates and the decision criteria determine the amount of evidence the accumulators must achieve for a response to be produced. These correspond to the drift criterion and decision criteria in the two-choice diffusion model (Ratcliff, 1985; Ratcliff et al., 1999). In principle, either or both types of criteria could be influenced by manipulations of response bias, such as the proportion of old versus new items on a test and the relative payoffs and penalties associated with “old” versus “new” responses. Although there is no a priori reason for predicting which type of criteria should change to accommodate a bias manipulation, the two types are separately identifiable in fits to data. For example, changing the decision criteria more dramatically impacts the RT quantiles than changing the confidence criteria. Specifically, RT distributions are fast and compact when decision criteria are low versus slow and skewed when decision criteria are high. Moreover, changes in the different types of criteria have distinct influences on the ROC data. Changes in bias can be achieved in two ways: Confidence criteria can be set at low (liberal) or high (conservative) values. Alternatively, decision criteria can be relatively low on the “old” side of the scale and relatively high on the “new” side of the scale for liberal responding, and vice versa for conservative responding. With the confidence criteria strategy, z-ROC slope increases as responding moves from liberal to conservative. With the decision criteria strategy, z-ROC slope decreases as responding moves from liberal to conservative. Thus, each type of parameter has a unique signature in the resulting predictions, and researchers can determine which type of criteria is influenced by a bias manipulation through fits to empirical data.

Large Numbers of Confidence Categories

Mickes et al., (2007) had subjects rate the strength of test items in a standard recognition memory task on a 20-point scale (Experiment 1) or a 100-point scale (Experiment 2). They directly calculated the standard deviation of ratings given to old items versus new items and found that the ratios closely matched estimates of the standard deviation ratio based on z-ROC slope. The results seem to provide independent validation of the z-ROC estimates, which contradicts our claim that z-ROC slopes are much closer to 1 than actual ratios of standard deviations in memory evidence.

To apply the RTCON model to the Mickes et al. (2007) data from Experiment 2, the model would need 100 racing accumulators for the 100 confidence categories. However, this assumes that the number of internal confidence categories used by subjects matches the number of categories in the response scale. Research in absolute identification suggests that subjects are able to competently use a maximum of seven or eight response categories. We find it unlikely that subjects in Mickes et al. truly discriminated between ratings of, for example, 75 and 77. Indeed, some of the subjects reported compressing the scale explicitly by, for example, only using ratings that were multiples of 5. There is little evidence in the Mickes et al. results that establishes that subjects were using all of the confidence ratings.

To see if subjects could have been using many fewer response categories, we simulated the 100 category data using a standard signal detection process with nine criteria. The nine criteria were used to produce 10 equally spaced response categories and these categories were distributed across the 100-point scale randomly from trial to trial. Following Mickes et al., the ratings were collapsed into 6 categories and the z-ROC slope closely matched the ratio of standard deviations of the old and new item rating distributions. Thus, the Mickes et al. results can be obtained from a model that uses a fraction of the number of experimental response categories, and this suggests that the RTCON model does not need to use tens or hundreds of accumulators in tasks that require that many categories. These results also indicate that increasing the number of categories to 20 or 100 does not produce a direct measure of the standard deviations of memory evidence distributions. Regardless of the number of ratings, responses are the output of a decision process that is subject to both decision noise and criterial noise.

Noise in the SDT Decision Criterion

Mueller and Weidemann (2008) recently developed a model that adds noise in the decision criteria to the basic SDT model (e.g., McNicol, 1972). This model can accommodate results that are problematic for basic SDT, such as the changes in ROC shape (or, equivalently, z-ROC slope) that come about from manipulations of bias (Balakrishnan, 1998; Van Zandt, 2000). Their model is similar to ours in spirit in that changes in z-ROC slope can be produced by changes in decision parameters. Both approaches highlight the importance of modeling sources of variation. We go beyond Mueller and Weidemann's approach by including variability in the accumulation of evidence process and variability in decision criteria. Our results indicate that the additional model constraints imposed by RT data allow identification of the separate sources of variability.

Dual Process Models

There are several implications of the success of the RTCON model for the dual process/single process debate in recognition memory. It is clear that subjects can use a recall (or recollection) process to retrieve contextual information if asked to do so and that this information can be used in a recognition decision (Heathcote, Raymond, & Dunn, 2006; Rotello et al., 2000). However, the recall process can be significantly slower than an assessment of match between a test item and memory (Gronlund & Ratcliff, 1989; McElree, Dolan, & Jacoby, 1999). Furthermore, there is no guarantee that it will be used in standard recognition memory tasks. For example, in a study by Gronlund and Ratcliff, information about how words were paired together at study, information that is likely to be retrieved by a recall mechanism, was not available until later in processing than match information. Also, it played a large role only in decisions in which the discrimination task required it. Specifically, it was used in associative recognition, where the task was to decide if two words had been paired at study. But it was not used when the task was simply to decide whether both words had been studied (in same or different pairs).

Our model is highly consistent with the view that recall (or recollection) is not routinely used in item recognition; there is only a single match process. Our model is also consistent with the view that there are two processes in item recognition, a recall process and a match process, both continuous, both available at the same point in the time course of processing, and both contributing to match distributions (e.g., Squire, Wixted, & Clark, 2007). However, the RTCON model offers something that dual process models like this do not: an explanation of processing. Dual process models have attempted to demonstrate that there are two qualitatively different processes and they have used these to explain considerable amounts of empirical and neurophysiological data. But the models go no further in understanding the two components themselves. There is no model of familiarity and no model of recollection. The need to understand processing seems to be finessed by the two process dichotomy.

Conclusion

In the wider context of sequential sampling models, the RTCON model jointly explains RTs and confidence judgments just as other sequential sampling models have jointly explained RTs and accuracy. Analyses that are based on only one of the dependent variables are almost certainly wrong in the architectures of cognitive processes that they postulate. We see this model as being the first in this class that handles these dependent variables, and we hope this sets a standard for other models to surpass. In this article, we have demonstrated how applications of SDT to recognition memory—applications that depend only on confidence judgments and not RTs—are misleading. Skeptics of sequential sampling models for two-choice tasks have pointed to the fact that the models have not explained confidence judgments, an additional dependent variable to accuracy and RT. Here we have addressed this criticism.