A Feedback Model Explains the Differential Scaling of Human Postural Responses to Perturbation Acceleration and Velocity

Abstract

Although the neural basis of balance control remains unknown, recent studies suggest that a feedback law on center-of-mass (CoM) kinematics determines the temporal patterning of muscle activity during human postural responses. We hypothesized that the same feedback law would also explain variations in muscle activity to support-surface translation as perturbation characteristics vary. Subject CoM motion was experimentally modulated using 34 different anterior–posterior support-surface translations of varying peak acceleration and velocity but the same total displacement. Electromyographic (EMG) recordings from several muscles of the lower limbs and trunk were compared to predicted EMG patterns from an inverted pendulum model under delayed feedback control. In both recorded and predicted EMG patterns, the initial burst of muscle activity scaled linearly with peak acceleration, whereas the tonic “plateau” region scaled with peak velocity. The relatively invariant duration of the initial burst was modeled by incorporating a transient, time-limited encoding of CoM acceleration inspired by muscle spindle primary afferent dynamic responses. The entire time course of recorded and predicted muscle activity compared favorably across all conditions, suggesting that the initial burst of muscle activity is not generated by feedforward neural mechanisms. Perturbation conditions were presented randomly and subjects maintained relatively constant feedback gains across all conditions. In contrast, an optimal feedback solution based on a trade-off between CoM stabilization and energy expenditure predicted that feedback gains should change with perturbation characteristics. These results suggest that an invariant feedback law was used to generate the entire time course of muscle activity across a variety of postural disturbances.

INTRODUCTION

The neural mechanisms responsible for the formation and modification of muscle activity for standing balance control are not well understood. Previous studies have described how muscle activity changes in response to variations in support-surface perturbations using descriptive measures, such as mean electromyographic (EMG) activity during fixed time periods or EMG onset and offset latencies (Brown et al. 2001; Diener et al. 1988; Maki and Ostrovski 1993; Szturm and Fallang 1998). Joint torques have also been demonstrated to change under varying biomechanical conditions (Bothner and Jensen 2001). However, it has been difficult to interpret the observed changes in muscle activity with respect to either the underlying neural mechanisms or the functional biomechanical outputs because the relationship between sensory inflow due to a postural perturbation and the resulting muscle activity is not known. Although joint torque trajectories can be predicted using biomechanical models (Alexandrov et al. 2001; Kuo 1995; Park et al. 2004; Peterka 2000; van der Kooij et al. 1999), muscle activity cannot be directly inferred from joint torques (Gottlieb et al. 1995).

A simple neuromechanical model describing the sensorimotor transformation between postural perturbation characteristics and muscle activity can describe the entire time course of muscle activity in normal and sensory-loss cats (Lockhart and Ting 2007), as well as in healthy human adults (Welch and Ting 2008) during postural responses to support-surface perturbations. The model represents an explicit formulation of the hypothesis that temporal patterns of muscle activity are formed by overlapping contributions of center-of-mass (CoM) acceleration, velocity, and position trajectories; each kinematic signal is weighted by feedback gain magnitudes that are specific to each subject and muscle. Because of the different temporal dynamics across kinematic signals, the feedback model predicts that the contributions of CoM acceleration, velocity, and displacement feedback will have distinct temporal signatures and always affect different portions of evoked muscle activity. By appropriately choosing three feedback gains on CoM acceleration, velocity, and displacement, as well as a common time delay, we previously reproduced several temporal patterns of muscle activation that varied across muscles and subjects (Lockhart and Ting 2007; Welch and Ting 2008). The model was also used to predict temporal patterns of muscle activation using an optimal trade-off between CoM stabilization and energy efficiency. Although the optimal patterns were similar to those found in trained cats (Lockhart and Ting 2007), naïve human subjects used temporal patterns of muscle activity that deviated from the optimal pattern but could nonetheless result from the same feedback structure (Welch and Ting 2008).

The predictions arising from this feedback hypothesis may be consistent with prior studies investigating perturbation-dependent changes in muscle activity, when considered in light of potential experimental limitations in altering perturbation acceleration and velocity independently. Previous studies remain somewhat inconclusive about the effects of perturbation acceleration on postural response activity, perhaps because acceleration levels were either not directly measured (and may therefore be inaccurately reported) or did not vary independently of perturbation velocity. For example, the initial EMG burst amplitude has been shown to scale with perturbation velocity, whereas the plateau region varies with perturbation displacement (Diener et al. 1988); however, acceleration was not directly measured or varied. Our feedback model suggests that although there may be a contribution of perturbation velocity in the initial burst, the earliest muscle activity is primarily due to perturbation acceleration (Lockhart and Ting 2007; Welch and Ting 2008). Because the initial acceleration of a perturbation is difficult to manipulate independently of perturbation velocity using traditional motion-control algorithms (see methods), prior studies may not have sufficiently isolated the effects of perturbation acceleration and velocity on postural responses. However, consistent with the predicted effects of perturbation acceleration, EMG amplitudes and joint torques have been shown to depend on the “smoothness” of the initial perturbation trajectory (Brown et al. 2001; Siegmund et al. 2002; Szturm and Fallang 1998) and the deceleration impulse at the end of the perturbation (Bothner and Jensen 2001), affecting the timing of the termination of the postural response (Carpenter et al. 2005; McIlroy and Maki 1994).

In the current study, we developed a series of perturbations to test whether perturbation velocity and acceleration have different and independent effects on temporal patterns of muscle activity during postural responses to discrete perturbations, as predicted by our model (Lockhart and Ting 2007; Welch and Ting 2008). To compare our results with previous studies, we first used traditional EMG measures to assess how muscle activity scales with perturbation characteristics during specific time periods of the postural response across conditions. We then performed the same analyses on simulated EMG signals to test whether these results were consistent with the hypothesis that subjects use the same set of feedback gains across all perturbation conditions. Next, we investigated whether the entire time course of muscle activity across conditions could be reproduced by the feedback model. We demonstrate that the initial burst of muscle activity is well reproduced by feedback on CoM acceleration for perturbations with short-duration acceleration impulses, but is not well reproduced when perturbation accelerations are extended in time. We hypothesized that this discrepancy could result from the transient encoding of acceleration by muscle spindles and improved model fits to data by truncating acceleration feedback after a fixed duration. Using this improved model, we finally demonstrate that subjects used constant feedback gains across conditions, rather than modifying them according to an optimal trade-off between CoM stabilization and energy expenditure.

METHODS

Seven healthy subjects (five male, two female), ages 19.4 ± 1.4 yr (mean ± SD), were recruited from the Georgia Institute of Technology student population to participate in an experimental protocol that was approved by both the Georgia Institute of Technology and Emory University Institutional Review Boards. All subjects signed an informed consent form before participating. Subjects stood with weight evenly distributed on two force plates (AMTI, Watertown, MA) installed on a movable platform that could translate in the horizontal plane. Subjects focused vision to a scenic view 4.6 m away and were instructed to cross their arms at chest level and react naturally to the support-surface perturbations.

Experimental protocol

To test the effects of varying CoM acceleration and velocity on muscle activity evoked during postural responses, we presented subjects with a set of ramp-and-hold perturbations that translated the support surface in the anterior–posterior direction. Perturbations were applied using a custom-designed perturbation platform (Factory Automation Systems, Atlanta, GA) driven by servo motors and controlled by industrial motion controllers. These perturbations varied the relationship between peak acceleration and velocity by either maintaining constant peak velocity while varying peak acceleration or maintaining constant peak acceleration while varying peak velocity. However, using traditional motion-control algorithms that minimize the error between the desired and actual trajectories of the device, we found that changing the acceleration characteristics of the ramp-and-hold trajectory produced the predicted changes in peak acceleration, but also caused correlated changes in peak velocity, as well as overshoot in the displacement trajectory (Fig. 1A). We thus developed two sets of perturbations where platform velocity and acceleration were varied independently while maintaining a 12-cm total excursion (Fig. 1, B and C). Perturbation characteristics spanned a range of velocities (5-cm/s steps between 25 and 40 cm/s) and accelerations (0.1-g steps between 0.1 and 0.6 g) that were varied independently in both forward and backward directions for a total of 34 perturbation types. Due to controller limitations, certain velocity–acceleration combinations were excluded from the experimental design (see Fig. 4 for included experimental conditions).

FIG. 1.

Example of variations in perturbation characteristics. A: using a standard controller, unforeseen covariation of peak perturbation velocity and acceleration, as well as positional overshoot, occurs. Our custom platform and controller allowed the independent variation of peak perturbation velocity and acceleration. B: in constant peak acceleration perturbations, the initial acceleration profile and the peak acceleration magnitude was the same across all perturbations. Peak velocity was varied by extending the duration of the acceleration pulse. C: in constant peak velocity perturbations, peak acceleration was varied to maintain the same acceleration impulse across perturbations, causing each perturbation to reach the same peak velocity at different rates. Total platform displacement was constant in all perturbations and exhibited no positional overshoot. For each column, line styles indicate representative perturbations with different platform motion characteristics.

FIG. 4.

Joint motion varies with perturbation characteristics. Intersubject mean peak angular deflections of the ankle (A), knee (K), and hip (H) joints, measured in degrees, are illustrated for each experimental condition in the backward direction. Error bars indicate 1SD of the mean.

After a set of 20 acclimatization trials at an intermediate perturbation level (35 cm/s at 0.4 g) in both directions, five replicates of each perturbation condition were administered in random order, for a total of 170 perturbations per subject. Intertrial time varied randomly between 5 and 15 s. A minimum of 5 min seated rest was enforced between each set of 60 perturbations to reduce muscle fatigue. Only those trials in which subjects were able to maintain balance without stepping were included in further analyses; conditions requiring a stepping response were replicated at random until five nonstepping trials were achieved or until the total number of experimental perturbations exceeded 210 trials. Results from one experimental condition (25 cm/s at 0.3 g) have been previously published (Welch and Ting 2008).

Data collection

Platform acceleration and position, surface EMGs, and ground reaction forces were collected at 1,080 Hz, synchronized with body segment kinematics collected at 120 Hz (Fig. 2). Platform acceleration was measured using a three-dimensional accelerometer directly mounted onto the platform (Analog Devices, Norwood, MA). Platform signals were low-pass filtered at 30 Hz (third-order zero-lag Butterworth filter). Platform velocity was then calculated by the numerical differentiation of filtered platform position measured using a linear variable differential transformer (MTS Systems, Cary, NC). Surface EMG (Konigsberg Instruments, Pasadena, CA) was collected from 15 muscles in the legs and trunk on the right side of the body unless otherwise indicated: TA, tibialis anterior (bilateral); MG, medial gastrocnemius (bilateral); SOL, soleus; VLAT, vastus lateralis; RFEM, rectus femoris; SEMB, semimembranosus; SEMT, semitendinosus; BFLH, long head of biceps femoris; BFSH, short head of biceps femoris; ES, erector spinae (bilateral); RA, rectus abdominis (bilateral). Silver/silver chloride disc electrodes were placed at a 2-cm interelectrode distance according to standard EMG electrode placement guidelines (Basmajian and Blumenstein 1980). EMG signals collected bilaterally are reported using the suffixes “-R” and “-L” to indicate right and left legs, respectively. Raw EMG signals were high-pass filtered at 35 Hz (third-order zero-lag Butterworth filter), demeaned, half-wave rectified, and low-pass filtered at 40 Hz (first-order zero-lag Butterworth filter). Body segment kinematics were derived from a custom 25-marker set that included head–arms–trunk (HAT), thigh, shank, and foot segments (Vicon, Centennial, CO). Ankle, knee, and hip joint angular kinematics were calculated as the intersegment angles in the sagittal plane. CoM displacement was calculated from kinematic data as a weighted sum of segmental masses (Winter 2005). This displacement waveform was low-pass filtered at 50 Hz (third-order zero-lag Butterworth filter) and numerically differentiated to derive the CoM velocity trajectory. Ground reaction forces were low-pass filtered at 100 Hz (third-order zero-lag Butterworth filter). CoM acceleration was then calculated as the difference between ground reaction force divided by subject mass and platform acceleration.

FIG. 2.

Representative postural response to a forward support-surface translation. Muscles were activated in a coordinated fashion to produce forces to counteract the perturbation (left), returning the posture to an upright position, usually within 1 s of the perturbation onset (right). The shaded areas on electromyographic (EMG) traces represent the initial burst (IB) and plateau region (PR) periods of muscle activity.

Data analysis

SCALING OF MUSCLE ACTIVITY TO PERTURBATION CHARACTERISTICS.

Changes in muscle activity due to the manipulation of perturbation characteristics were determined by examining mean muscle activity during specific time periods as reported in several previous studies (Diener et al. 1988; Henry et al. 1998; Maki and Ostrovski 1993). Because the characteristic temporal features of the EMG response vary between conditions, recorded EMGs following postural perturbations were examined during two consecutive 150-ms time periods following the onset of activity in each muscle, corresponding to the initial burst (IB) and plateau region (PR) of muscle activity (Fig. 2). To increase the temporal resolution of the analysis, each time period was then further subdivided to create a total of four 75-ms periods following muscle onset (APR1–APR4), where IB is a combination of APR1 and APR2 and PR is a combination of APR3 and APR4. Muscle onset time was determined as the time point at which muscle activity exceeded the mean activation level during the quiet background period plus 2SDs of the mean and was verified manually. For each subject, mean EMG levels during each time period were calculated for each muscle and normalized to the maximum EMG observed in that muscle over all conditions. To examine the scaling of muscle responses with perturbation characteristics, we performed a three-way ANOVA (velocity × acceleration × subject) on the mean EMG data during each period. For those muscles significantly affected by perturbation characteristics, we computed the slopes of the scaling relationships by performing linear regression analysis of mean EMG to peak perturbation acceleration and velocity. ANOVA results were evaluated at a significance level of α = 0.05, adjusted with a Bonferroni correction for multiple comparisons (α = 0.0125; n = 4). All averaged data are presented as means ± SD.

FEEDBACK PREDICTIONS AND RECONSTRUCTIONS OF MUSCLE ACTIVITY.

We predicted the entire time course of muscle activity using four different formulations of the hypothesis that CoM kinematic signals are linearly combined in a feedback manner to generate muscle activity. For all of the formulations, the horizontal displacement (p), velocity (v), and acceleration (a) of the CoM were subject to a common time delay (λ) to simulate neural transmission and processing time. Simulated muscle activity (EMG_p) was then formed by the linear combination of each delayed CoM signal weighted by a feedback gain (k_a, k_v, k_p)

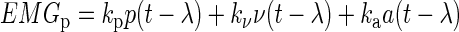(1)

The simulated muscle activity was half-wave rectified to produce a nonnegative EMG prediction, and converted to a muscle torque using a first-order muscle model, which counteracted the disturbance torque (Lockhart and Ting 2007; Welch and Ting 2008). All analyses were conducted over a 1.1-s time interval, beginning 100 ms before platform motion. In all simulations, feedback parameters were restricted such that 0 < k_i < 100 and 60 < λ < 250. Parameters for all of the formulations are listed and briefly described in Table 1.

TABLE 1.

Feedback model parameters for each model formulation

Symbol	Description	Value
A. System Identification Pendulum Model
μm	Weight for maximum deviation between simulated and measured EMG signals at any time point	1,000 N·m/s
μs	Weight for error between simulated and measured EMG signals over time	10 N·m/s
wp	Weight for final pendulum position	0 N
wv	Weight for final pendulum velocity	0.08 N·s
wa	Weight for final pendulum acceleration	0.02 N·s2
B. Jigsaw Models
μm	Weight for maximum deviation between simulated and measured EMG signals at any time point	10 N·m/s
μs	Weight for error between simulated and measured EMG signals over time	1 N·m/s
C. Optimal Feedback Model
ρ	Weight for level of EMG activation over time	20 N·m/s
qp	Weight for deviations of pendulum position over time	0.05 N/s
qv	Weight for deviations of pendulum velocity over time	50 N
qa	Weight for deviations of pendulum acceleration over time	1 N·s
ωp	Weight for final pendulum position	0 N
ωv	Weight for final pendulum velocity	0.08 N·s
ωa	Weight for final pendulum acceleration	0.02 N·s2

W = [w_p w_v w_a], Q = diag [q_p q_v q_a], and Ω = [ω_p ω_v ω_a]. The final simulation time (t_end) was 1.1 s for all models. Listed parameters are described in detail in Welch and Ting (2008).

FEEDBACK MODEL RECONSTRUCTION OF MUSCLE ACTIVITY.

Similar to our prior studies (Lockhart and Ting 2007; Welch and Ting 2008), we first used a computational model of balance control that simulated the body motion using a lumped mass on a single-link inverted pendulum scaled to each subject's mass and CoM height (Fig. 3A). We used this neuromechanical model to identify a feedback delay (λ) and three feedback gains (k_i) to best reproduce the entire time course of recorded muscle activity for each muscle in each experimental condition. An optimization was performed to minimize the difference between the recorded and simulated muscle activity, while ensuring the stability of the inverted pendulum

(2)

The first term penalized the error between the simulated and recorded EMG signal over time as represented by the vector e_m with weight μ_s. The second term penalized the maximum deviation between the simulated and measured EMG signals at any single point in time with weight μ_m. The final term penalized nonzero final states of the inverted pendulum x = [p v a]^T with weight W, promoting a final pendulum configuration resembling quiet upright stance.

FIG. 3.

Feedback models for postural control. A: the standing human was modeled as an inverted pendulum on a cart that was perturbed using recorded perturbation acceleration trajectories. Horizontal pendulum acceleration, velocity, and displacement trajectories were subject to a common time delay and scaled by the corresponding feedback gain. The resulting delayed and weighted kinematic signals were summed and rectified to predict temporal patterns of muscle activity. A first-order muscle model was used to generate the resulting muscle torque to counteract the perturbation. The time constant of the muscle model was defined as τ = 40 ms and the muscle model gain was A = 4mh kg·m⁻²·s⁻¹, where m is the mass (in kg) of the subject and h is the height of the subject's center of mass (CoM, in m). B: in the model-free jigsaw analysis, recorded CoM kinematic signals were used to directly reconstruct EMG patterns. Predicted muscle activity was generated as a linear combination of the recorded kinematic signals (CoM acceleration, velocity, and displacement) at a common time delay.

SCALING OF PREDICTED MUSCLE ACTIVITY WITH PERTURBATION CHARACTERISTICS.

Using subject-specific feedback gains and delay, we also used this model to make predictions of muscle activity, assuming that the feedback gains were fixed across conditions. For each subject, the feedback gains and delay for an intermediate perturbation condition (35 cm/s at 0.4 g) were used to generate predicted muscle activation patterns for all experimental conditions. The localized changes in the temporal patterns of muscle activity predicted by the constant-gain feedback model were then compared with those recorded experimentally. The goodness of fit between recorded EMG and constant-gain EMG predictions was evaluated for each muscle to determine whether a feedback law with constant gains was sufficient to account for the observed variations in muscle activity with perturbation characteristics.

MODEL-FREE RECONSTRUCTION OF MUSCLE ACTIVITY.

Because of the possibility that the inverted pendulum model simulations may not adequately reproduce the actual CoM kinematics, we also used a model-free “jigsaw” method of reconstructing muscle activity directly from experimentally measured CoM kinematics in each condition (Fig. 3B). This approach was not subject to the strict biomechanical constraints imposed on the CoM kinematics by the inverted-pendulum model, but rather shifted and scaled recorded CoM acceleration, velocity, and displacement signals to match recorded EMG patterns. For each muscle and perturbation condition, a feedback delay (λ) and three feedback gains (k_i) that best reproduced the entire time course of recorded muscle activity were found by minimizing the difference between the jigsaw reconstruction and the recorded EMG pattern

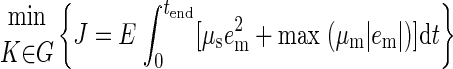(3)

This cost function is identical to Eq. 2, but excludes the final term required to achieve an upright pendulum configuration at the end of simulation.

TRANSIENT ACCELERATION ENCODING.

An additional variant of the model-free method was created to account for mismatches between reconstructed and recorded muscle activity in low-velocity/acceleration conditions. We hypothesized that muscle spindles transiently encode acceleration when a muscle is stretched starting from rest, with the encoding ending abruptly as force and strain accumulate within the fiber. Although the mechanisms for such a “stiction” response are not known, it could be caused by the rapid detachment of cross-bridges (Getz et al. 1998; Henatsch 1971). Our “jigsaw with stiction” method was used to investigate the possible role of transient acceleration encoding due to spindle stiction on the postural response. We empirically modeled the muscle spindle stiction response by allowing acceleration encoding for a 75-ms time period after the onset of platform acceleration. Specifically, acceleration feedback was eliminated between 175 and 300 ms following platform motion onset. This permitted a 100-ms neural processing delay before muscle onset and 75 ms of acceleration encoding before the elimination of acceleration feedback. Feedback gains and delay were then chosen as with the “jigsaw” method, using a cost function that minimized the difference between the reconstructed and recorded EMG patterns (Eq. 3).

Similarly, we simulated transient acceleration encoding in the feedback model by limiting the duration of the acceleration feedback to the first 75 ms following the onset of EMG activity. We then recomputed the predicted EMG time courses and scaling relationships derived from constant-gain simulations.

OPTIMAL FEEDBACK MODEL.

Finally, we used the feedback model with stiction to predict muscle activation patterns for each perturbation condition based on an optimal trade-off between CoM stabilization and neural effort. For each condition, the feedback delay (λ) was set to 100 ms and three feedback gains (k_i) were chosen to minimize total muscle activation and the kinematic deviation of the pendulum from the initial upright configuration, without regard to experimentally recorded data (Lockhart and Ting 2007; Welch and Ting 2008).

COMPARISON OF FEEDBACK GAINS ACROSS MODELS.

To determine whether humans respond optimally to support-surface translations, we compared the variations in each subject's feedback parameters across conditions to those predicted by the optimal control model. Each model resulted in a unique set of three feedback gains and one time delay for each subject, condition, and muscle. For each model and subject, we assessed the goodness of fit between predicted and recorded EMG signals using both the coefficient of determination (r²) and the uncentered coefficient of determination (variability accounted for [VAF]). Next, we performed three-way ANOVA (velocity × acceleration × subject) on each feedback parameter, at a significance level of α = 0.05, to determine whether these feedback parameters remained constant or changed with perturbation velocity and acceleration. We finally performed regression analysis of the mean feedback parameters across subjects with respect to peak velocity and acceleration to reveal any significant scaling relationships.

RESULTS

Summary

In response to a variety of support-surface perturbations of equal displacement, the initial EMG burst in multiple muscles scaled linearly with peak perturbation acceleration, while the later plateau region of EMG scaled linearly with peak perturbation velocity. Similar scaling trends were found in simulated EMG signals based on a simple CoM feedback model. The temporal pattern of EMG signals was similar to recorded EMG signals during anterior-posterior support-surface translations over a wide range of perturbation magnitudes that evoke a range of kinematic strategies (e.g., ankle, mixed, and hip strategies) for balance recovery. However, the initial burst of activity in recorded EMG signals had a relatively fixed duration that only followed CoM acceleration for a limited period of time. We corrected for this discrepancy by incorporating a time-limited feedback reponse to CoM acceleration in the model, inspired by muscle spindle afferent dynamics. With this correction, a relatively invariant set of model feedback gains was sufficient to characterize the changes in the temporal patterns of muscle activity recorded across all experimental conditions.

Scaling of muscle activity to perturbation characteristics

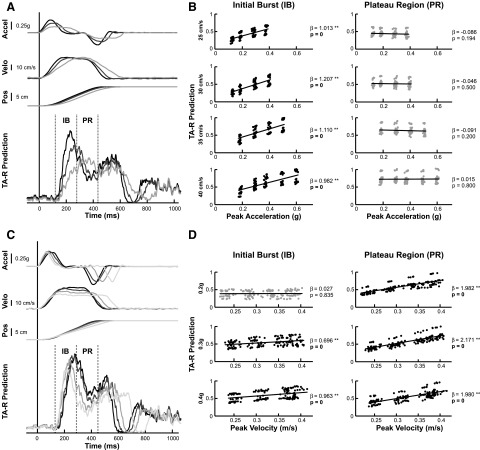
In response to support-surface translations in the sagittal plane, subjects activated muscles throughout the lower limbs and trunk to counteract perturbation-induced postural sway. Subjects exhibited postural sway in the opposite direction of platform motion, characterized by coordinated joint motions about the ankle, knee, and hip that varied across perturbation conditions (Fig. 4), spanning the continuum from “ankle” to “hip” strategies (Runge et al. 1999). The continuum of joint motions across conditions was characterized predominantly by changes in maximum hip deflection (P < 0.02), with ankle and knee deflection remaining constant across conditions (P > 0.24). Subjects typically returned to an upright configuration within 1 s. Here, we will primarily discuss EMG analysis results for the right ankle dorsiflexor tibialis anterior (TA-R) during forward perturbations and for the right ankle plantar flexor medial gastrocnemius (MG-R) during backward perturbations; these muscles serve as major agonists and their results are representative of the findings across all muscles. In response to forward perturbations, the postural response in TA-R was characterized by an initial burst of EMG, after a latency of 119 ± 22 ms, followed by a sustained plateau region of tonic activity (Fig. 5). Similarly, in response to backward perturbations, MG-R exhibited an initial burst at a latency of 136 ± 49 ms, followed by a plateau region. In all muscles, muscle onset latencies were significantly affected by platform acceleration (P < 0.006; except bilateral ES), but not by platform velocity (except bilateral TA: P < 0.003; SEMB: P = 0.008). The magnitude and shape of the EMG patterns varied considerably between conditions (Fig. 5, A and C).

FIG. 5.

Scaling of muscle activity with perturbation characteristics. A: example variations of right-leg tibialis anterior (TA-R) EMG to perturbations of varying peak acceleration (Accel, 0.2–0.5 g), with constant peak velocity (Velo, 35 cm/s) and total displacement (Pos, 12 cm). Vertical lines indicate the time window evaluated for the IB and PR time bins of muscle activity. B: the linear regression of mean TA-R EMG across all subjects during the IB and PR time bins to peak platform acceleration. Each data point represents the mean EMG level for one successful trial of one subject. Results from the linear regression analysis are indicated by slope (β) and P values. Significant slopes: *P < 0.01 and **P < 10⁻⁵, with data points in black and P values in bold font. Conditions with insignificant regression slopes are indicated by gray data points. C: example variations of TA-R EMG to perturbations of constant peak acceleration (0.4 g), varying peak velocity (25–40 cm/s), and constant total displacement (12 cm). D: the linear regression of mean TA-R EMG across all subjects during the IB and PR time bins to peak platform velocity.

The effects of perturbation acceleration and velocity on EMG activity were temporally separated within the time course of the postural response, as exemplified by TA-R EMG (Fig. 5). In perturbations of varying peak acceleration with constant peak velocity, IB activity increased with perturbation acceleration (Fig. 5A, example of TA-R response at 30 cm/s). This was true for multiple velocity levels (Fig. 5B) and for all 15 muscles recorded in both forward and backward perturbations (Table 2). Across subjects, the mean slope of IB activity with respect to peak acceleration was 0.56 ± 0.16 g⁻¹ for TA-R and 0.41 ± 0.27 g⁻¹ for MG-R. In contrast, PR muscle activity did not vary with peak acceleration at low velocities in TA-R, but some scaling was found at higher velocities (Fig. 5B). This scaling appears to be due to the variation of muscle activity in early, rather than the late, PR time period (Fig. 5A). Scaling of PR activity with peak acceleration was found in only 4 of 15 muscles for forward perturbations and in 12 muscles for backward perturbations (Table 2).

TABLE 2.

ANOVA P values for EMG response to peak acceleration and peak velocity

Muscle	Forward Perturbations				Backward Perturbations
	Initial Burst		Plateau Region		Initial Burst		Plateau Region
	Peak Accel	Peak Velo	Peak Accel	Peak Velo	Peak Accel	Peak Velo	Peak Accel	Peak Velo
TA-L	<10−16	0.009	0.089	<10−16	<10−15	0.54	<10−6	<10−8
MG-L	<10−3	0.76	0.42	<10−3	<10−4	0.016	<10−4	<10−12
TA-R	<10−15	0.03	0.26	<10−16	<10−8	0.39	0.002	<10−9
MG-R	<10−5	0.09	0.001	<10−9	<10−6	0.77	<10−4	<10−9
SOL	<10−5	<10−5	0.11	0.005	<10−8	0.002	0.002	<10−16
VLAT	<10−6	0.64	0.009	<10−9	<10−4	0.092	<10−4	<10−8
RFEM	<10−16	0.40	0.010	0.002	<10−6	0.001	0.001	<10−8
SEMB	<10−15	<10−3	0.092	<10−10	<10−15	0.039	<10−10	<10−16
SEMT	<10−14	0.001	0.040	<10−9	<10−16	0.22	<10−6	<10−16
BFLH	<10−10	0.004	0.26	<10−10	<10−6	0.54	0.031	0.0031
BFSH	<10−10	0.018	0.41	<10−9	<10−15	0.18	0.017	<10−3
ES-L	<10−7	0.006	0.23	0.20	0.0022	0.10	<10−4	<10−16
ES-R	<10−6	0.007	0.058	0.004	<10−4	0.89	<10−3	<10−10
RA-L	<10−6	0.42	0.005	<10−8	<10−7	0.10	0.13	<10−5
RA-R	<10−3	0.47	0.71	<10−5	<10−6	0.35	0.008	0.002

P values indicated in bold are significant at P < 0.0125 for n = 4 comparisons. For all muscles during all periods, the subject factor was significant (P < 10⁻⁵) and the interactions between velocity and acceleration were not significant (P > 0.045).

For perturbations of constant peak acceleration and varying peak velocity, IB activity was constant, while PR activity increased with perturbation velocity (Fig. 5C, example of TA-R response at 0.4 g) at all acceleration levels (Fig. 5D). Significant scaling of IB activity with peak velocity was found in only 7 muscles for forward perturbations and in 2 muscles for backward perturbations (Table 2). Significant scaling of PR activity with peak velocity was found in 14 of 15 muscles for forward perturbations and in all muscles for backward perturbations (Table 2). In contrast to the scaling of PR activity with peak acceleration described earlier, the scaling of PR activity with peak velocity appears to be due to variations in muscle activity during the later portion of the PR time period (compare Fig. 5, A and C). Across subjects, the slope of PR muscle activity with respect to peak velocity was 2.25 ± 0.72 s/m for TA-R and 1.35 ± 0.80 s/m for MG-R.

Inspection of the EMG signals suggests that the effects of peak acceleration are limited to early PR and the effects of velocity to late PR. Accordingly, a higher-resolution analysis demonstrated that EMG activity evolved from scaling with acceleration in the early periods to scaling with velocity in the later periods (Table 3). The slope of the TA-R response with respect to peak perturbation acceleration was highest in APR1 and decreased in APR2 across all velocity levels. In APR3 and APR4, the scaling with peak acceleration was not significant, except for APR4 at the highest velocity level (Table 3). In contrast, the slope of the TA-R response with respect to peak perturbation velocity was not significant in APR1, significant for two velocity levels in APR2, and increased significantly across all velocity levels between APR3 and APR4 (Table 3). Although the effects of acceleration and velocity may be temporally segregated at the earliest and latest time periods investigated, their influences can overlap at intermediate time points. The changes in slope with respect to acceleration and velocity are thus consistent with the predictions of a feedback model where the activity is formed by the different time courses, rather than simply the peak magnitudes, of CoM acceleration and velocity (van der Kooij and de Vlugt 2007).

TABLE 3.

Postural response scaling in TA-R evolves temporally from acceleration to velocity scaling

Level	Postural Response Period
	APR1	APR2	APR3	APR4
Velocity	Acceleration scaling slope, g−1
25 cm/s	0.74*	0.67*	0.31	0.07
30 cm/s	0.85*	0.61*	0.04	−0.08
35 cm/s	0.45*	0.31†	0.26	0.28
40 cm/s	0.39*	0.30*	0.13	0.41*
Acceleration	Velocity scaling slope, s/m
0.2 g	0.07	0.40	1.37*	2.21*
0.3 g	−0.07	0.75†	1.84*	2.39*
0.4 g	−0.24	0.81†	1.39*	2.31*

Significant regression slopes are in bold, with the significance levels denoted

^*(P < 10⁻⁵) and

^†(P < 0.05).

Scaling of predicted muscle activity to perturbation characteristics

To determine whether a feedback law with constant feedback gains could reproduce the observed variations in muscle activity across conditions, we used subject-specific feedback gains from a perturbation of intermediate magnitude (Table 4) to predict the muscle activity in all perturbation conditions. The variations in the predicted EMG signals were qualitatively similar to those recorded from experimental subjects—the earlier regions of muscle activity, including the initial burst, varied in response to changes in perturbation acceleration (Fig. 6A), whereas the later regions of muscle activity varied in response to changes in peak velocity (Fig. 6C).

TABLE 4.

Subject-specific parameters and gains from model predictions of TA-R activity for forward perturbation (35 cm/s at 0.4 g)

Subject	Mass m, kg	CoM Height h, m	Feedback Gains
			kp, cm−1	kv, s/cm	ka, s2/m	λ, ms
A	73	1.04	3.8	1.40	0.15	79
B	58	1.06	6.5	0.56	0.11	60
C	76	1.15	2.3	1.60	0.13	98
D	70	1.08	5.4	0.78	0.09	105
E	65	1.05	12.8	0.70	0.17	82
F	73	1.17	7.5	0.67	0.12	77
G	81	1.23	6.9	0.93	0.13	116

FIG. 6.

Scaling of muscle activity predicted by a constant feedback gain pendulum model. A: example variations of simulated TA-R EMG to perturbations of varying peak acceleration (Accel, 0.2–0.4 g), with constant peak velocity (Velo, 35 cm/s) and total displacement (Pos, 12 cm). B: the linear regression of mean simulated TA-R EMG across all subjects during the IB and PR time bins to peak platform acceleration. Significant slopes: *P < 0.01 and **P < 10⁻⁵. Conditions with insignificant regression slopes are indicated by gray data points. C: example variations of simulated TA-R EMG to perturbations of constant peak acceleration (0.4 g), varying peak velocity (25–40 cm/s), and constant total displacement (12 cm). D: the linear regression of mean simulated TA-R EMG across all subjects during the IB and PR time bins to peak platform velocity.

The differential scaling of IB and PR activity with peak perturbation acceleration and velocity was predicted by model simulations using constant feedback gains. At all velocity levels, model-predicted IB activity varied linearly with peak perturbation acceleration, whereas activity during PR showed no significant scaling with peak perturbation acceleration (Fig. 6B). The slopes of model-predicted IB muscle activity to peak acceleration were generally larger than those in experimental subjects and were similar across all velocity levels, in contrast to experimental data where the slope of IB activity to peak acceleration decreased at higher velocities (Fig. 5B). The model did not predict the occasional scaling of PR activity with peak acceleration that was observed experimentally in some muscles (compare Fig. 5B to Fig. 6B). At constant acceleration levels, the model predicted scaling of the IB activity with peak perturbation velocity at higher accelerations and demonstrated strong scaling of PR muscle activity with peak perturbation velocity (Fig. 6D). The slopes of the scaling relationship between PR activity and velocity were similar to those found for experimental data (Fig. 5D).

Reconstruction of muscle activity using the feedback model

To determine the source of the discrepancies between the scaling of model-derived predictions and measured muscle activity in IB and PR, we investigated the goodness of fit between the model-derived temporal patterns of muscle activity and those recorded experimentally. Although the model adequately reproduced the recorded EMG signals for the intermediate perturbation from which the feedback gains were determined (35 cm/s at 0.4 g), model predictions deviated from the measured EMG signals when feedback gains were held constant across all perturbation levels. In particular, the initial burst of activity was similar for higher peak acceleration levels in experimental subjects compared with the model predictions (cf. black and dark gray traces in Figs. 5A and 6A). However, the duration of the platform acceleration impulse is extended at low acceleration levels; similarly, model predictions for these conditions exhibit a slow rise in EMG, with the initial activity extending for a long duration, well into the PR time period (Fig. 6A). Experimental data did not reflect this widening of the initial burst, but rather exhibited initial activity that was much shorter in duration than predicted by the model at low peak acceleration levels (cf. gray and light gray traces in Figs. 5A and 6A). Accordingly, the temporal EMG patterns predicted by the constant-gain model matched recorded EMG signals best at higher accelerations and did not produce good matches at low accelerations levels (Fig. 7). Across conditions, constant-gain EMG predictions resembled bilateral TA EMG reasonably well in all subjects (VAF = 0.75 ± 0.10), whereas the predictions of triceps surae and proximal leg and trunk muscles resulted in less successful matches to experimental data (triceps surae: VAF = 0.67 ± 0.11; proximal: VAF = 0.58 ± 0.17) and produced simulation results with as low as 27 and 6% VAF, respectively.

FIG. 7.

Comparison of the time course of recorded EMGs to those predicted by a constant-gain pendulum model. The same feedback gains chosen to match subject responses at an intermediate perturbation level (35 cm/s at 0.4 g) were used to predict temporal patterns of muscle activity across all perturbation conditions. The time course of the predicted (solid black) muscle activation pattern is compared with the recorded EMG patterns (gray, mean ± SD) for low- (left column) and high-velocity/acceleration conditions (right column). Three representative comparisons are shown to illustrate the range of observed results among subjects and muscles: TA-R (right-leg tibialis anterior), SEMT (right-leg semitendinosus), and RA-R (right rectus abdominis). Goodness-of-fit is indicated by the coefficient of determination (r²) and uncentered coefficient of determination (variability accounted for [VAF]).

When feedback parameters were allowed to vary with experimental condition, we observed improvements in the fit between model predictions and experimental data (Fig. 8A). The resulting simulated muscle activity accounted for >61% of the variability in ankle muscle activity (SOL and bilateral TA and MG) across all subjects and conditions (VAF = 0.86 ± 0.05). Activity in proximal leg and trunk muscles was generally well reconstructed (VAF = 0.82 ± 0.11), although activity in some conditions was poorly reconstructed (all VAF >27%) due to the overprediction of muscle activity, especially during the plateau region of the response. Because the low level of activity in these muscles was insufficient to maintain the pendulum in the upright configuration and each muscle was analyzed individually, the optimization procedure increased muscle activity to satisfy this stringent biomechanical constraint (e.g., SEMT, SEMB, RA, and ES).

FIG. 8.

Comparison of the time course of recorded EMGs to those predicted by system identification using the pendulum model. For each perturbation condition, feedback gains were chosen to match the EMG response in each muscle and each subject. A: the time course of the model-derived (solid black) muscle activation pattern is compared with the recorded EMG patterns (gray, mean ± SD) for low- (left column) and high-velocity/acceleration conditions (right column). Three representative comparisons are shown to illustrate the range of observed results among subjects and muscles: TA-R (right-leg tibialis anterior), VLAT (right-leg vastus lateralis), and RA-R (right rectus abdominis). Goodness of fit is indicated by the coefficient of determination (r²) and uncentered coefficient of determination (VAF). B: the acceleration of the inverted pendulum model corresponding to simulated muscle activity (black) is compared with recorded CoM motion (gray) for the low- (left column) and high-velocity/acceleration conditions (right column).

In general, model predictions were best matched to experimental data in conditions with accelerations >0.2 g. In these conditions, pendulum kinematics were well matched to recorded CoM kinematics (kinematic VAF >66%; kinematic VAF = 0.87 ± 0.08), despite the fact that kinematic matching was not specified in the cost function. Still, the reconstruction of muscle activity from those conditions with accelerations ≤0.2 g resulted in good matches to recorded EMG; however, the kinematics of the pendulum often differed substantially from the recorded CoM kinematics (kinematic VAF >38%; kinematic VAF = 0.68 ± 0.15). For low peak accelerations, experimentally recorded COM acceleration trajectories mimicked the wide duration impulse of the platform acceleration waveform (Fig. 8B). Because the initial burst of experimental EMG was always of short duration, the model was thus unable to match both CoM acceleration and EMG signals in the same condition at low peak accelerations. Instead, model-derived EMG patterns matched the short initial burst of the EMG signals by deviating pendulum motion substantially from the actual CoM acceleration in the same condition (Fig. 8B).

Model-free reconstruction of muscle activity

To remove the influences of mismatched CoM acceleration predictions from the model-based reconstruction of EMG, we directly scaled and summed recorded CoM kinematic signals to best reproduce the measured EMG signals using the jigsaw model. Like the simulated EMG signals derived from the pendulum model, jigsaw EMG signals consisted of an initial burst of activity followed by a plateau region, with a time course similar to that of recorded EMG data (Fig. 9). The jigsaw EMG reconstructions reproduced recorded EMG with >55% VAF in all muscles and subjects for all conditions (VAF = 0.90 ± 0.06). However, in perturbations with peak acceleration ≤0.2 g, jigsaw EMGs also resulted in wide, low-magnitude initial burst regions compared with recorded EMG signals. This discrepancy between the jigsaw EMG signals and the recorded data was more pronounced in subjects and muscles where EMG signals had well-defined initial burst regions (e.g., all muscles for Subjects A and G; ankle muscles for all subjects). Although the VAF across all conditions was not improved when these perturbation conditions were removed from the analysis (VAF = 0.90 ± 0.05), the minimum VAF across conditions increased from 55 to 66%.

FIG. 9.

Comparison of the time course of recorded EMGs to those predicted by a model-free analysis. In the “jigsaw model,” recorded CoM kinematic signals are used to directly reproduce recorded EMG signals using 3 gains and a delay. The time course of the jigsaw-derived (solid black) muscle activation pattern is compared with the recorded EMG patterns (gray, mean ± SD) for low-(left column) and high-velocity/acceleration conditions (right column). Three representative comparisons are shown to illustrate the range of observed results among subjects and muscles: TA-R (right-leg tibialis anterior), SEMT (right-leg semitendinosus), and RA-R (right rectus abdominis). Goodness of fit is indicated by the coefficient of determination (r²) and uncentered coefficient of determination (VAF).

Transient acceleration encoding

The addition of transient acceleration encoding significantly improved the match between model-derived and recorded EMG patterns for all muscles (Fig. 10), but did not qualitatively alter the predictions regarding the scaling of muscle activity with perturbation acceleration and velocity. With stiction, the goodness of fit between jigsaw and recorded EMG improved in conditions with accelerations ≤0.2 g (P < 10⁻¹⁶), as well as in those with accelerations >0.2 g (P < 10⁻²⁹). The observed improvements to model reconstructions were most pronounced in subjects and muscles with strong, well-defined initial burst regions, resulting in well-matched model reconstructions.

FIG. 10.

Comparison of the time course of recorded EMGs to those predicted by a model-free analysis with a transient acceleration contribution. In the “jigsaw model with stiction,” the recorded CoM acceleration signal is truncated to limit its contribution to 75 ms. The time course of the model-derived (solid black) muscle activation pattern is compared with the recorded EMG patterns (gray, mean ± SD) for 4 velocity/acceleration combinations. Antagonistic pairs on each body segment are shown to illustrate the range of observed results among subjects and muscles: TA-R (right-leg tibialis anterior), MG-R (right-leg medial gastrocnemius), VLAT (right-leg vastus lateralis), SEMT (right-leg semitendinosus), RA-R (right rectus abdominis), and ES-R (right erector spinae). Goodness of fit is indicated by the coefficient of determination (r²) and uncentered coefficient of determination (VAF).

When transient acceleration encoding was added to the constant-gain inverted-pendulum model, the scaling of IB muscle activity with peak perturbation acceleration and the scaling of PR activity with peak velocity was similar to that observed in experimental subjects. Also, the slope of initial burst scaling remained larger in the constant-gain model compared with experimental data (data not shown). As before, PR activity was predicted to scale with peak acceleration, although this was not observed experimentally.

Optimal feedback predictions compared with feedback gain variations across conditions

To achieve an optimal trade-off between postural stability and energetic efficiency, the optimal model predicts the changing of feedback gains with both peak perturbation acceleration and velocity (P < 10⁻¹⁶ for all gains) (Fig. 11). In contrast, the jigsaw model with stiction demonstrates the relative invariance of the feedback gains necessary to reconstruct recorded temporal patterns of muscle activity across conditions (P > 0.10 for k_v and k_p). Although we observed small variations in acceleration gain with peak perturbation acceleration (Fig. 11A) and variations in all feedback gains with peak perturbation velocity (Fig. 11B; P < 10⁻³ for all gains), these trends were inversely related to those predicted by the optimal feedback model.

FIG. 11.

Comparison of feedback gains that characterize recorded EMG signals to an optimal solution. A: the linear regression of optimal and jigsaw CoM acceleration, velocity, and position feedback gains (k_a, k_v, k_p) to peak perturbation acceleration is illustrated at each velocity level (0.25–0.4 m/s). Data points indicate the intersubject mean of the feedback gain for each condition. B: the linear regression of optimal and jigsaw feedback gains to peak perturbation velocity is illustrated at each acceleration level (0.2–0.4 g).

DISCUSSION

Across postural strategies that incorporate different joint motions, we reproduced the entire time course of muscle activity using constant, delayed feedback gains on CoM acceleration, velocity, and displacement in a simple inverted-pendulum model. This suggests that different temporal muscle activation patterns across individuals, muscles, and perturbation conditions have a common underlying neural mechanism of low dimension. The feedback model explains the differential scaling of muscle activity during various time periods of postural responses to perturbation acceleration and velocity. These scaling relationships may have been previously masked or misinterpreted as a result of limitations in the control of perturbation devices, which we circumvented through careful manipulations of perturbation characteristics. As in prior studies, we show that the initial burst of muscle activity during postural responses is relatively invariant compared with later time periods in the postural response. However, we hypothesize that the limited duration of the initial burst reflects the dynamics of afferents that transiently encode acceleration information, rather than a feedforward motor pattern.

Feedback control of muscle activity for posture

Although feedback models of posture predicting joint torques have been implemented previously, only through the direct examination of muscle activity were we able to reveal potential neural mechanisms for postural control because many different temporal patterns of muscle activity can produce similar kinematic trajectories and joint torques (Gottlieb et al. 1995). Without the use of acceleration feedback in our model, realistic muscle activity patterns do not emerge in simulations of either human (Welch and Ting 2008) or cat responses (Lockhart and Ting 2007). However, as in animals with large-fiber sensory neuropathy, muscle activation patterns lack an acceleration feedback component yet produce similar patterns of CoM kinematics (Lockhart and Ting 2007). The destabilizing effects of neural processing and transmission delays may be mitigated by the phase-leading acceleration feedback to muscle activity, allowing prior postural feedback models to transform joint angle changes instantaneously into joint torques.

Together with studies investigating the sensory integration mechanisms in balance control, our results support the hypothesis that the CNS uses a multisensory estimate of task-level variables, such as CoM motion, to produce and modulate muscle activity during postural control. Here, we used a single-link pendulum model of postural control to investigate, in principle, whether muscle activity could be characterized by a feedback mechanism; future studies will be necessary to validate the generality of the model to different postural perturbation paradigms and strategies. Although cats use quadrupedal stance, they may be adequately modeled as an inverted pendulum during support-surface translations because the mass of the trunk is large and all four legs primarily change in orientation but not length (Macpherson et al. 1989; Scrivens et al. 2008). However, in humans, the body can literally act as a single-link pendulum during ankle-strategy responses (Peterka 2000), but undergoes multijoint motions for mixed- and hip-strategy responses to larger perturbations. The fact that our single degree-of-freedom model can still predict individual muscle responses when the individual joint motions do not mirror those of the CoM supports the idea that, rather than being activated by feedback circuits local to a particular joint, muscles across the body are modulated using an estimate of CoM motion in a feedback manner. Similarly, it has been shown that the hand trajectory is well controlled in reaching tasks (Adamovich et al. 2001; Tseng et al. 2002) and global variables such as hand direction, velocity, and endpoint force are encoded in the primate motor cortex (Georgopoulos et al. 1986, 1992; Scott and Kalaska 1997). Even at the level of the spinal cord, global variables such as leg length, orientation, velocity, and endpoint force are computed from the ensemble of sensory receptor information (Bosco and Poppele 1997, 2001; Bosco et al. 1996; Lemay and Grill 2004; Poppele et al. 2002).

As the critical task-level biomechanical variable defining the motion of the body, the direction of CoM motion has been shown to reliably predict the directional tuning of muscles across postural perturbation conditions where any single sensory signal would fail to predict the appropriate muscle response. These studies demonstrate that not only local proprioceptive signals but also vestibular and visual information are insufficient to robustly predict the ensuing muscle activity for the full suite of postural responses. Rotations (pitch and roll) versus translations (horizontal plane) of the support surface that elicit similar patterns of muscle activation induce opposite changes in joint angles, but similar changes in CoM displacement in both humans and cats (Carpenter et al. 1999; Diener et al. 1983; Gollhofer et al. 1989; Nardone et al. 1990; Nashner 1977; Ting and Macpherson 2004). Similarly, spatial patterns of muscle activation in the legs, trunk, and neck during automatic postural responses cannot be attributed to any single somatosensory or vestibular signal, but require multisensory integration, whether subjects are standing (Carpenter et al. 1999; Inglis and Macpherson 1995; Keshner et al. 1988; Ting and Macpherson 2004) or seated (Forssberg and Hirschfeld 1994; Keshner 2003).

Here, we extend these results to demonstrate that the formation of the time course of muscle activity across multiple joints may also be derived from a global (rather than local) multisensory estimate of postural destabilization, as encapsulated by CoM kinematics (Ting 2007). The initial direction of changes in joint kinematics on perturbation was not conserved within each condition—even within the same subject—consistent with previous studies demonstrating that CoM kinematics are more tightly regulated in postural control than are individual joint angles (Allum and Carpenter 2005; Brown et al. 2001; Gollhofer et al. 1989; Krishnamoorthy et al. 2003; Szturm and Fallang 1998). Especially in slower perturbations, the measurable changes in joint velocity and acceleration occurred too late to be useful in the formation of muscle activity through delayed-feedback processes. Further, joint kinematic changes did not scale linearly with platform motion characteristics as did muscle activity, suggesting that local joint changes may be inappropriate for the feedback control of balance. Thus despite the obvious limitation of our current analysis, which allowed only a single muscle to be investigated at a time, it is unlikely that a multiple-link pendulum model could reproduce the muscle activity based on a set of constant local feedback gains.

The fact that muscles across the body appear to be modulated by a common set of variables related to CoM kinematics is consistent with a low-dimensional, hierarchal feedback control law (Todorov 2004), where task-level variables modulate the activity of muscle synergies (Ting 2007; Ting and McKay 2007). Such a neural architecture has been shown to emerge from the principles of optimal feedback control (Chhabra and Jacobs 2006; Todorov and Jordan 2002). Muscle synergies that coactivate multiple muscles across the body in fixed proportions have been identified in postural responses to perturbations in cats and humans and their activity is modulated by both the direction of the postural disturbance and the postural strategy (Ting and Macpherson 2005; Torres-Oviedo and Ting 2007; Torres-Oviedo et al. 2006). Muscle synergies can activate anatomical agonists and antagonists in varying proportions, possibly explaining the scaling of “antagonist” muscles with perturbation characteristics observed in the current study. Further, because individual muscles may be simultaneously activated by multiple muscle synergies, different feedback gains can occur across anatomical agonists, as we observed here. Indeed, muscle synergy activity (M-modes) has been correlated to anterior–posterior CoM motion during anticipatory postural adjustments (Krishnamoorthy et al. 2003). Clearly, more complex, multisegmental models will be necessary to more fully understand the multimuscle coordination and biomechanics required for different kinematic balance strategies (Alexandrov et al. 2001; Horak and Nashner 1986; Runge et al. 1999). Further, the generality of such task-level postural control needs to be tested in other types of perturbation that alter CoM kinematics through mechanisms different from the moving floor paradigm studied here.

Scaling of muscle activity to perturbation characteristics

Regardless of whether local or global variables are used in postural control, the ability of our model to reproduce the temporal patterns of muscle activity for postural responses to support-surface perturbations provides a useful framework for understanding variations in muscle activity across perturbation conditions. Our experimental methods and data may also serve to better clarify the scaling relationships of the initial burst reported previously by Diener and colleagues (1988). Consistent with their findings, simulated muscle activation patterns exhibited velocity dependence during the late portions of the initial burst of muscle activity, as well as throughout the plateau region, with the effects of displacement predominant only in the late plateau region. The scaling of muscle activity during the initial burst with peak perturbation acceleration, versus velocity as reported by Diener, may be explained not only by differences in the control of the experimental apparatus, but also by the interactions and temporal overlap between acceleration and velocity feedback contributions.

Covariation of perturbation acceleration and velocity is typical of many perturbation paradigms in prior studies (Maki and Ostrovski 1993; Szturm and Fallang 1998), possibly resulting from the use of controllers in which only the displacement trajectory is specified (Brown et al. 2001). Positional overshoot and an underdamped “ringing” in the acceleration are also common (Fig. 1A). Additionally, initial platform acceleration can be relatively invariant on a hydraulically actuated platform, even when the reference trajectory is smoothed, possibly due to the minimum aperture opening on the servo valve (Ting and Macpherson, unpublished results). On such devices, the initial perturbation acceleration can be altered only by shortening the initial acceleration burst (Lockhart and Ting 2007). Thus it is important that perturbation acceleration be directly measured, rather than inferred from either the desired or recorded displacement trajectory.

Our analysis also reveals that the acceleration and velocity feedback gains that reproduce the observed variations in muscle activity are relatively invariant across perturbation conditions, although interactions can arise in a standard statistical analysis from the overlapping contributions of acceleration and velocity feedback in each time period. We demonstrated that when peak velocity is held constant, the initial burst scales with the peak perturbation acceleration. However, the scaling relationship with perturbation acceleration changes slope with different peak velocity levels, demonstrating an interaction effect. As in Diener et al. (1988), we find velocity scaling to be present in the initial burst only if data are pooled across all conditions; if segregated by acceleration level, when the peak acceleration is increased, the muscle activation increases to a larger but constant level with respect to velocity (Fig. 5D). A similar acceleration scaling result can be observed in the plateau region if data are pooled together, but not when separated by velocity level.

Transient acceleration encoding

Although our findings suggest that acceleration information is used in postural control, it is not known how acceleration is encoded within the nervous system. The initial burst of muscle activity remains present following vestibular loss (Inglis and Macpherson 1995; Runge et al. 1998). In contrast, sensory loss in the group I range eliminates the initial burst of the postural response, which can be explained by the absence of acceleration feedback within the framework of our model (Lockhart and Ting 2007), implicating Golgi tendon organs, cutaneous receptors, and muscle spindles. Although Golgi tendon organs respond to muscle contractile force, it is not clear that they produce a transient response to stretch when situated physiologically (Jami 1992). Rapidly adapting cutaneous receptors have an acceleration-like dynamic response to pressure or stretch of the skin (Johansson et al. 1992) and modulate motor response to slipping and during finger–object interactions (Johansson and Westling 1987; Macefield et al. 1996). Further, plantar mechanoreceptors in the foot may transmit shear force information that is proportional to horizontal accelerations when stimulated by the onset of platform motion (Maki and Ostrovski 1993; Morasso et al. 1999).

Muscle spindle primary afferents also exhibit a burst in firing frequency at the onset of muscle stretch that has been shown to scale with stretch acceleration (Schafer 1967) and may represent the local acceleration of the part of the muscle in which the spindle is embedded (Schafer and Kijewski 1974). This acceleration response may result from stiction within the intrafusal fiber when it is stretched from an isometric state (Jansen and Matthews 1962; Lennerstrand and Thoden 1968) and disappears when the muscle is first shortened and then stretched (Gregory et al. 1987; Haftel et al. 2004; Houk et al. 1992; Huyghues-Despointes et al. 2003). The end of this acceleration response could result from the breaking of actin–myosin complexes as force within the fiber increases (Henatsch 1971) or the detaching of cross-bridges in a prepower stroke phase at a critical strain level (Getz et al. 1998).

The duration of the initial burst in spindle firing frequency also varies with respect to the acceleration and velocity characteristics of the stretch. In fast stretches (∼12% resting length/s), the initial burst consists of a few spikes, lasting only tens of milliseconds (Haftel et al. 2004). However, in slow stretches (∼0.2% resting length/s), the initial burst can be much broader, lasting up to 500 ms (Cordo et al. 2002). Using published human muscle morphometric data for TA (Maganaris et al. 1999), we estimate that the TA stretches in the present study to be about 1–2% resting length/s. During these long initial bursts, the firing frequency decays in a quasi-exponential shape (Cordo et al. 2002), similar to the force transients in muscle fibers when stretched (Getz et al. 1998). The initial burst may thus transiently encode acceleration; the initial burst of muscle activity reliably followed CoM acceleration trajectory when the acceleration burst was shortened (Lockhart and Ting 2007), but not when it is lengthened in the present study. Although our simple truncation of acceleration encoding to 75 ms improved model fits to experimental data, more information about the mechanisms that determine the duration and shape of the initial burst of muscle primary afferents may further improve the agreement between our simulation results and experimental data.

Invariant versus optimal feedback gains for postural control

Our results demonstrate that humans use a set of invariant feedback gains in response to a wide range of postural perturbations, even when different kinematic strategies are used. Here, we found that, regardless of how similar the nominal response of our subjects was to the optimum (Welch and Ting 2008), they did not alter their feedback gains according to an optimal feedback solution when perturbations were presented randomly. We hypothesize that the different joint motions emerged from musculoskeletal dynamics due to the linear scaling of muscle activity in response to perturbation characteristics imposed by the constant feedback gains. This is consistent with the idea that the ankle and hip strategies represent the extremes of a continuous spectrum of postural responses (Alexandrov et al. 2001; Creath et al. 2005; Horak and Nashner 1986; Runge et al. 1999). Although small variations in the feedback gains were found across different velocities, these variations were inversely related to those predicted by the optimal solution specific for each perturbation condition. It is possible that these small variations represent some biases in the perturbations themselves, in the sensory receptor mechanisms, or in the data analysis algorithms. We hypothesize that the feedback gains would change if perturbations were presented predictably, rather than randomly, consistent with the previously observed habituation to postural perturbations, whereby the same perturbation may evoke different response magnitudes and response strategies (Chong et al. 1999; Hansen et al. 1988; Horak et al. 1989; Timmann and Horak 1997). If so, the feedback gains identified here may reflect the “central set” of a subject, which determines the amplitude of postural responses to perturbation (Horak 1996; Keshner et al. 1987).

GRANTS

This research was supported by National Institutes of Health Grants HD-046922-01S1 and NS-053822.